Introduction

Background

With the trend of world energy "coal falling and gas rising," natural gas with the characteristics of environmental friendliness has been paid more and more attention. At present, China's natural gas production is dominated by conventional natural gas, but there are abundant reserves of unconventional natural gas such as shale gas and coalbed methane, which will be the substitutes of conventional natural gas in future. The technically recoverable resources of shale gas in China are about 36 × 1012, accounting for 15% of the total global shale gas resources and 1.6 times that of conventional natural gas. The development prospect of shale gas is very broad. Shale gas with the characteristics of low porosity and low permeability is an unconventional natural gas that mainly exists in dark shale or high-carbon shale in an adsorbed or free state (Wei et al. 2021). Although deep shale gas resources in China are widely distributed, the area geological background and conditions of shale gas enrichment and distribution are relatively complex. In recent years, with the rapid development of horizontal drilling and hydraulic fracturing technology, the development potential of shale gas has been greatly improved, and it has gradually become one of the most promising energy sources (Gao and You 2015b).

In fact, an important problem faced by shale gas production is that the well pressure and production are high in the early stage of production, but the well pressure and production decrease rapidly with the increase in production time. In order to effectively cope with the rapid decline of production during shale gas production, shale gas fields are usually developed on a rolling basis, and new wells are merged year by year, but the incorporation of new wells can easily cause pressure fluctuations in the gathering and transportation system and even lead to "backoff" (Drouven and Grossmann 2017). In the process of shale well development, with the continuous reduction in formation pressure, when the well pressure is lower than the gas transmission pressure, theoretically the well will not be able to produce and will be abandoned. Therefore, the production cycle of the well can be prolonged by means of timely reduction in the wellhead pressure. Pressurized mining technology is a common way to reduce wellhead pressure. In this paper, an optimization model is developed to solve the problem of how to pressurize a shale gas field.

Related work

The success of the "shale gas revolution" in North America has profoundly changed the supply pattern of the global energy market (Liu and Li 2018). The development of shale gas is therefore increasingly valued, and many scholars have conducted researches on different problems arising from the development of shale gas.

The gas storage methods of shale gas reservoirs are mainly free gas and adsorbed gas. Free gas mainly determines the initial gas production period of the well, and adsorbed gas mainly dictates the stable production period of the well. Therefore, by increasing the production capacity through large-scale hydraulic fracturing, the stable production period of shale gas can be longer and the development value can be better Loucks et al. (2009). Drouven and Grossmann (2017) proposed a mixed-integer linear, two-stage stochastic programming model for optimal design of shale well development and refracturing. Cafaro et al. (2016) established a continuous-time nonlinear programming model based on a predictive function and a discrete-time, multi-period MILP to solve the refracturing planning problem. Cafaro et al. (2018) proposed a continuous-time optimization model different from Cafaro et al. (2016) for multiple refracturing over the life of shale wells.

Hydraulic fracturing is a crucial step in shale gas production. In this process, a large amount of water is required to configure fracturing fluid, and the related water management issues have been attracted much attention. Gregory et al. (2011) explored the water management challenges of hydraulic fracturing to produce shale gas, including water use, management, and disposal. Yang et al. (2014) developed a two-stage mixed integer linear programming model (MILP) for solving water management problems in shale gas fields. Gao and You (2015a) discussed the optimal design and operation of water pipe networks for shale gas production. Carrero-Parreño et al. (2018) raised a new water management optimization model. The model explicitly takes into account the effect of high concentrations of total dissolved solids and their temporal variation in the body of impaired water. Cafaro and Grossmann (2021) combined multi-well development planning with the design of water distribution networks to maximize the reuse of damaged water from fracturing wells.

As the development of shale gas is becoming increasingly common, issues such as shale gas development planning, design and supply chain have also been paid more attention. Cafaro and Grossmann (2014) first promoted a mixed integer nonlinear programming model (MINLP) for long-term planning of the shale gas supply chain. Subsequently, Drouven and Grossmann (2016) extended on this basis, and proposed a new superstructure to solve the problem of shale gas development. The model takes into account the discrete dimensions of pipeline diameters and compressors, expanding the scope of shale gas development problems. Guerra et al. (2016) established mathematical formulas and measures for a comprehensive optimization framework for shale gas resource assessment, while integrating the design and planning of shale gas supply chain and water management. With the increasing prominence of environmental problems, the consideration of environmental impact factors has been added to the relevant research. Ren et al. (2019) used a dual-objective programming model to optimize freshwater use and flowback water control, considering uncertainties at each stage to achieve the best trade-off between economic and environmental goals. Colin-Robledo et al. (2019) proposed a mathematical programming formula for an integrated shale gas natural gas supply chain that maximizes profits while addressing the minimization of overall environmental impact. Caballero et al. (2020) employed an integrated water management model that discusses key trade-offs between best practices from an economic and environmental perspective. The above studies provide many reference solutions for shale gas development and supply chain design, but there are few studies on pressurization of shale gas gathering and transportation systems.

Scholars have also carried out a lot of research on the optimization design of oil and gas gathering and transportation pipeline networks, mainly focusing on the optimization of pipeline network topology parameters, and the optimization of pressure pressurization at a given pressure pressurization position. Zhou et al. (2014a, b) studied the optimization of the coalbed methane gathering and transportation system by adopting the staged optimization method based on its technological characteristics and the status quo of mining and production. The topology of oil & gas gathering and transportation pipeline network is usually complex, and a reasonable optimization of the layout can effectively reduce the total investment of oil and gas fields. Wei et al. (2016) established a mathematical model for the optimal design of the gathering and transportation pipeline network considering factors such as the topology layout and pipe diameter of the pipeline network. Compared with the manual design scheme, the optimized scheme can save 13.9% of the investment cost. Liu et al. (2016) applied a hierarchical optimization strategy to optimize a multilevel star-tree style oil and gas gathering and transportation network. Zhang et al. (2017) built a generic MILP considering terrain and obstacle conditions. The optimal topology, the location of the central processing facility, the diameter and the path of each pipeline are obtained by solving the model. Zhou et al. (2020) proposed a MINLP model with the minimum total cost as the objective function to optimize the star-access-ring pipeline network. Hong et al. (2019) established an integrated MILP for gathering and transportation pipelines in response to the neglect of hydraulic characteristics in previous studies. Hong et al. (2020) developed a MILP model for optimizing multi-period onshore gas field gathering and transportation network systems to figure out the location of central processing facility, pipeline installation and topology, wellsite-CPF connection mode, flowrate of each pipeline, and working pressure of each node at each time period. Montagna et al. (2021) constructed a MINLP model for unconventional oil & gas gathering and transportation network design, and proposed a bilayer decomposition-based solution algorithm to solve the model.

In the production process of oil and gas fields, the total operating cost of the gathering and transportation system largely depends on the operating cost of the compressors in the pipeline network. Zhou et al. (2014a, b) proposed a superstructure-based mixed integer programming method to optimize the design of the pipeline network with the goal of minimizing the total cost of the compressor project. Liu et al. (2014) considered compressor’s outlet pressure and quantity as decision variables to minimize the energy consumption of the pipeline network, and used dynamic programming to solve the optimization model. Drouven and Grossmann (2017) developed a MINLP to determine the optimal timing of wells in shale gas gathering and transportation systems and the compressor power required to transport the produced shale gas to long-distance pipelines. Wang (2019) successfully completed the frequency conversion test of the power frequency high-speed reciprocating compressor through risk identification, test plan formulation and control parameter determination for the reciprocating compressor in the coalbed methane gathering and transportation system. Liu et al. (2020) modeled a dynamic network using rigorous thermodynamic equations to determine the optimal dynamic operation of the pipeline to minimize compression costs. Zagorowska et al. (2020) proposed an optimization model for compressor parallel operation mode. However, there are few studies on the pressurization scheme of the shale gas gathering and transportation system, and the pressurization is a process that every shale gas field has to go through. In general, although predecessors have carried out certain research on the optimization of gathering and transportation systems, the previous methods cannot be directly introduced into the problem of combined pressurization optimization of shale gas gathering and transportation systems.

Contributions

  1. (1)

    A MINLP model is established to solve the combined pressurization optimization problem of shale gas gathering and transportation systems.

  2. (2)

    Considering the mutual comparison of different combined supercharging methods, the advantages of combined supercharging are described.

  3. (3)

    An actual case is introduced to verify the validity of the model, which has certain guiding significance for the selection of supercharging scheme in actual production.

Paper organization

This article is elaborated according to the following structure. Section 2 describes the mathematical problem; Sect. 3 clarifies the model assumptions and introduces the mathematical model; Sect. 4 introduces the solution algorithm to solve the problem; Sect. 5 gives an example and proves the validity of the model; The final section draws conclusions.

Problem description

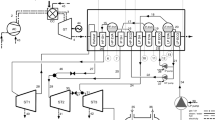
In view of the different placement of compressors, shale gas pressurization methods can be divided into distributed pressurization and centralized pressurization. Distributed compressor station (CS) is to set the CS at the well site or platform, and send low-pressure shale gas into the gas production pipeline; centralized CS is to set the compressor station at the multi-well gas gathering station or the gas gathering station. The shale gas is collected at the multi-well gas gathering station or the gas gathering terminal and then sent to the gas gathering pipeline. Distributed pressurization can be further divided into well pressurization and platform pressurization. Centralized pressurization can be divided into area pressurization, gas gathering station pressurization, dehydration station centralized pressurization and first station centralized pressurization. Among them, the three pressurization methods (gas gathering station pressurization, dehydration station centralized pressurization and first station centralized pressurization) are the same without considering the high and low pressure distribution. All of the upstream low-pressure shale gas flows to the gas gathering station, the dehydration station or the first station for centralized pressurization. The above three pressurization methods can be collectively referred to as station pressurization. The way of pressurization at area points is called area pressurization, that is, centralized pressurization can be simplified into area pressurization and station pressurization. As shown in Fig. 1, the pressurization modes of the shale gas gathering and transportation system are divided into four types.

  1. (1)

    Well pressurization: install pressurization equipment (generally mainly referred to as compressors) at a single shale gas well or wells that are put into production at the same time to pressurize the low-pressure shale gas in the shale gas block.

  2. (2)

    Platform pressurization: install pressurization equipment at the shale gas platform to pressurize medium or low-pressure gas.

  3. (3)

    Area pressurization: install pressurization equipment at the shale gas area point to pressurize the low-pressure area of the shale gas field.

  4. (4)

    Station pressurization: install pressurization equipment at the shale gas station to pressurize low-pressure shale gas.

Fig. 1
figure 1

Description of combined pressurization optimization of shale gas gathering and transportation system

Full size image

In order to better express the four pressurization modes, the nodes of the pipe network were classified and defined. The set of wells is W, the set of platforms is G, the set of area points is N, the set of stations is S, the four types of locations are collectively referred to as node I, and the set is \(I = W \cup G \cup N \cup S\). Candidate pressurization locations are grouped into well \(w \in W\), platform \(g \in G\), area point \(n \in N\), station \(s \in S\), and node \(i \in I\). The set of all pipe sections is \(A = \left\{ {(i,\,j)|i \in I,\,j \in I} \right\}\), and the pipe section (i, j) represents the pipe section between node i and node j. Similarly, define the set of similar pipe sections: the set of well-to-platform pipe sections is \({\text{WGA}} = \left\{ {(w,\,g)|w \in W,\,g \in G} \right\}\), the set of platform-to-node pipe sections is \({\text{GIA}} = \left\{ {(g,\,i)|g \in G,\,i \in I} \right\}\), the set of node-to-area point pipe sections is \({\text{INA}} = \left\{ {(i,\,n)|i \in I,\,n \in N} \right\}\), and the set of node-to-area pipe sections is \({\text{ISA}} = \left\{ {(i,\,s)|i \in I,\,s \in S} \right\}\). The compressor units type set is \(Y = \left\{ {y|y \in Y} \right\}\). The shale gas gathering and transportation pipeline network is a whole. The low-pressure gas source and the high-pressure gas source share a set of gathering and transportation pipeline network, regardless of the high and low pressure distribution.

Mathematical model

Objective function

The total compressor unit cost is defined as the compressor unit purchase cost and operating cost, as shown in Eq. (1).

$$\min \, F = F_{{{\text{cc}}}} + F_{{{\text{oc}}}}$$
(1)

where, \(F\) is the total cost of compressor units, 104 Yuan; \(F_{{{\text{cc}}}}\) is the compressor unit purchase cost, 104 Yuan; \(F_{{{\text{oc}}}}\) is the compressor unit operation cost, 104 Yuan.

Purchase cost

Compressor unit purchase cost is the cost of purchasing different types of compressor units, as shown in Eq. (2).

$$F_{{{\text{cc}}}} = \sum\limits_{y \in Y} {\sum\limits_{i \in I} {b_{{i,{\kern 1pt} y}} z_{i,\,y} \alpha_{i,\,y} } }$$
(2)

where, \(b_{i,\,y}\) is the active if type y compressor is installed at node i; \(z_{i,\,y}\) is the compressor number of type y installed at node i; \(\alpha_{i,\,y}\) is the price of type y compressor installed at node i, 104 Yuan/set.

Operating cost

Compressor unit operating cost is the cost of energy consumption during compressor operation, as shown in Eq. (3).

$$F_{{{\text{oc}}}} = \sum\limits_{i \in I} {N_{i} r_{i} }$$
(3)

where, \(N_{i}\) is the operating power of compressor at node i, kW; \(r_{i}\) is the operating price of compressor at node i, 104 Yuan/kW.

Constraints

Pipe pressure and flowrate constraints

  1. (1)

    Pressure drop constraints of shale gas pipelines

The pressure drop constraints for shale gas pipelines are expressed in Eq. (4).

$$Q_{i,\,j} = 5033.11\,d_{i,\,j}^{8/3} \left[ {\frac{{(p_{i|(i,\,j)} )^{2} - (p_{j|(i,\,j)} )^{2} }}{{Z_{i,\,j} \Delta_{i,\,j} T_{i,\,j} L_{i,\,j} }}} \right]^{0.5} \quad \forall (i,j) \in A,\,i \ne j$$
(4)

where, \(Q_{i,\,j}\) is the volume flow rate of the pipe section (i, j), m3/d; \(d_{i,\,j}\) is the inner diameter of the pipe section (i, j), cm; \(p_{i|(i,\,j)}\) is the starting pressure of the pipe section (i, j), MPa; \(p_{j|(i,\,j)}\) is the end pressure of the pipe section (i, j), MPa; \(Z\) is the gas compression factor in the average pressure and average temperature of the pipe section; \(\Delta\) is the relative density of shale gas; \(T_{i,\,j}\) is the average thermodynamic temperature of shale gas in the pipe section (i, j), K; \(L_{i,\,j}\) is the pipe length of the pipe section (i, j), km.

  1. (2)

    Maximum pressure constraints

Due to friction loss, the pressure at the starting point of the pipe section is the largest, and only the starting pressure of the pipe section (i, j) needs to be pressure limited, as expressed in Eq. (5).

$$p_{i|(i,\,j)} \le p_{\max } \quad \forall (i,\,j) \in A,\,i \ne j$$
(5)

where, \(p_{\max }\) is the maximum pressure that the pipe section (i, j) can withstand, MPa.

  1. (3)

    Minimum pressure constraints

To ensure the normal flow of shale gas, a minimum pressure constraint needs to be added, as shown in Eq. (6).

$$p_{j|(i,\,j)} \ge p_{\min } \quad \forall (i,\,j) \in A,\,i \ne j$$
(6)

where, \(p_{\min }\) is the minimum end pressure of the pipe section (i, j), MPa.

  1. (4)

    Pipe section constraints

Pipe section flow can be represented by other node flows. The pipe section flow constraint is to link the flow at node i (or node j) with the flow at pipe section (i, j), as shown in Eq. (7).

$$q_{i|(i,\,j)} = Q_{i,\,j} = q_{j|(i,\,j)} \quad \forall (i,\,j) \in A,\,i \ne j$$
(7)

where, \(q_{i|(i,\,j)}\) is the volume flow rate of the node i of the pipe section (i, j), m3/d; \(q_{j|(i,\,j)}\) is the volume flow rate of the node j of the pipe section (i, j), m3/d.

Compressor constraints

  1. (1)

    Compressor suction pressure

The suction pressure of the compressor at node i is equal to the pressure at node i, as shown in Eq. (8).

$$p_{i} = p_{i}^{{{\text{in}}}} \quad \forall i \in I$$
(8)

where, \(p_{i}\) is the pressure at node i, MPa. \(p_{i}^{{{\text{in}}}}\) is the suction pressure of the compressor at node i, MPa.

  1. (2)

    Compressor discharge pressure

The discharge pressure of the compressor at node i is equal to the starting pressure of the downstream pipe section, as shown in Eq. (9).

$$p_{i}^{{{\text{out}}}} = p_{i\,|\,(i,\,j)} \quad \forall i \in I,\,\forall (i,\,j) \in A,\,i \ne j$$
(9)

where, \(p_{i}^{{{\text{out}}}}\) is the discharge pressure of the compressor at node i, MPa.

  1. (3)

    Compression ratio

The compression ratio is the ratio of the compressor discharge pressure to the suction pressure, as shown in Eq. (10).

$$\varepsilon_{i} = \frac{{p_{i}^{{{\text{out}}}} }}{{p_{i}^{{{\text{in}}}} }}\quad \forall i \in I$$
(10)

where, \(\varepsilon_{i}\) is the compression ratio of the compressor at node i.

  1. (4)

    Compressor power

The compressor power is expressed in Eq. (11). If the compression ratio is greater than 1, the node i needs to install a compressor for pressurization. The compressor installation decision variable \(b_{i}^{y} = 1\), and \(N_{i}\) is assigned a positive value. If the pressure ratio is less than or equal to 1, the compressor decision variable \(b_{i}^{y} = 0\), and the compressor unit stops running. The gas will not go through the compressor, but go directly to the downstream pipe section from the adjacent pipeline through the separator, \(N_{i} = 0\).

$$N_{i} = 16.745\,p_{i}^{{{\text{in}}}} q_{i} \frac{k}{k - 1}(\varepsilon_{i}^{{\frac{k - 1}{k}}} - 1)\frac{{Z_{i}^{{{\text{in}}}} + Z_{i}^{{{\text{out}}}} }}{{2Z_{i}^{{{\text{in}}}} }}\frac{1}{\eta }\quad \forall i \in I$$
(11)

where, \(q_{i}\) is the volume flow rate at node i, m3/min; \(k\) is the gas specific heat ratio; \(Z_{i}^{{{\text{in}}}}\) is the gas compression factor under the suction condition of the compressor at node i; \(Z_{i}^{{{\text{out}}}}\) is the gas compression factor under the discharge condition of the compressor at node i; \(\eta\) is the compressor efficiency.

  1. (5)

    Constraints on the number of compressors

The number of compressors is restricted as shown in Eq. (12).

$$z_{i,\,y} = \frac{{N_{i} }}{{N_{{\text{y}}} }}\quad \forall i \in I,\,\forall y \in Y$$
(12)

where, \(N_{{\text{y}}}\) is the maximum operating power, kW/set.

Throttling constraints at wells and platforms

  1. (1)

    Throttling ratio at wells

The well throttling ratio is used to judge whether throttling is required at well w, as represented in Eq. (13). If the throttling ratio is less than 1, the wellhead needs throttling, and the compressor decision variable \(b_{{{\text{w,}}\,{\text{y}}}} = 1\) at well w; if the throttling ratio is equal to 1, the wellhead does not need throttling, and the compressor decision variable \(b_{{{\text{w,}}\,{\text{y}}}} = 0\) at well w.

$$\delta_{{\text{w}}} = \frac{{p_{{{\text{w}}|({\text{w}},\,{\text{g}})}} }}{{p_{{\text{w}}} }}\quad \forall w \in W,\,\forall (w,\,g) \in {\text{WGA}}$$
(13)

where, \(\delta_{{\text{w}}}\) is the throttle ratio at well w; \(p_{{\text{w}}}\) is the pressure at well w, MPa; \(p_{{{\text{w|(w,}}\,{\text{g}})}}\) is the starting pressure of the pipe section (w, g), MPa.

  1. (2)

    Throttling ratio at platforms

The platform throttling ratio is used to judge whether throttling is required at platform g, as shown in Eq. (14). If the throttling ratio is less than 1, all wells in the platform need to be throttled, and the compressor decision variable \(b_{{{\text{g,}}\,{\text{y}}}} = 1\) at the platform g; Otherwise, if the throttling ratio is equal to 1, the wellhead does not need throttling, and the compressor decision variable \(b_{{{\text{g,}}\,{\text{y}}}} = 0\) = 0 at the platform g.

$$\delta_{{\text{g}}} = \frac{{p_{{{\text{g|(g,}}\,{\text{j)}}}} }}{{p_{{\text{g}}} }}\quad \forall g \in G,\,\forall (g,\,j) \in {\text{GIA}}$$
(14)

where, \(\delta_{{\text{g}}}\) is the throttle ratio at platform g; \(p_{{\text{g}}}\) is the pressure at platform g, MPa; \(p_{{{\text{g}}|({\text{g,}}\,{\text{j}})}}\) is the starting pressure of the pipe section (g, j), MPa.

Pressure balance constraints

  1. (1)

    Pressure balance constraints at platforms

If the platform is pressurized, all wells in the platform need to be pressurized together, which requires the pressure of all wells in the platform to be unified. At this time, the suction pressure of the compressor at platform g is equal to the minimum pressure of all wells in the platform, as shown in Eq. (15).

$$p_{{\tau (g)^{ + } }}^{\min } = p_{{\text{g}}} \quad \forall g \in G$$
(15)

where, \(\tau (g)^{ + }\) is the collection of wells belonging to platform g; \(p_{{\tau (g)^{ + } }}^{\min }\) is the minimum pressure of all wells belonging to the platform, MPa.

  1. (2)

    Pressure balance constraints at area points within a shale gas block

The pressure at the area point n is equal to the end pressure of the pipe section (i, n), as shown in Eq. (16).

$$p_{{{\text{n|(i,}}\,{\text{n)}}}} = p_{{\text{n}}} \quad \forall n \in N,\forall (i,n) \in {\text{INA}}$$
(16)

where, \(p_{{{\text{n|(i,}}\,{\text{n)}}}}\) is the end pressure of the pipe section (i, n), MPa; \(p_{{\text{n}}}\) is the pressure at area point n, MPa.

  1. (3)

    Pressure balance constraints at stations

The pressure at station s is equal to the end pressure of the pipe section (i, s), as shown in Eq. (17).

$$p_{{{\text{s|(i,}}\,{\text{s)}}}} = p_{{\text{s}}} \quad \forall s \in S,\,\forall (i,\,s) \in {\text{ISA}}$$
(17)

where, \(p_{{{\text{s|(i,}}\,{\text{s)}}}}\) is the starting pressure of the pipe section (i, s), MPa; \(p_{{\text{s}}}\) is the pressure at station s, MPa.

Uniqueness constraints for pressurization at the well or pressurization at the platform

In the actual pressurization scheme, if pressurization at the platform is adopted, the wells in the platform will no longer be pressurized at a single well. Similarly, if a single well or wells that are put into production at the same time is pressurized, the platform where they are located will no longer be pressurized at the platform, and the constraints are shown in Eq. (18).

$$a_{{{\text{i,}}\,{\text{j}}}} b_{{{\text{w,}}\,{\text{y}}}} b_{{{\text{g,}}\,{\text{y}}}} = 0\quad \forall w \in W,\,\forall g \in G,\,\forall y \in Y,\,\forall (i,\,j) \in A$$
(18)

where, \(a_{{{\text{i,}}\,{\text{j}}}}\) is the elements in the connection relationship matrix of the pipe section (i, j).

Flow constraints at wellheads

The throughput rate at well w is equal to the initial well flow rate, as shown in Eq. (19).

$$q_{{\text{w}}}^{0} = q_{{\text{w}}} = q_{{{\text{w|(w,}}\,{\text{g)}}}} \quad \forall w \in W,\,\forall (w,\,g) \in {\text{WGA}}$$
(19)

where, \(q_{{\text{w}}}^{0}\) is the initial volume flow rate of at well w, m3/d.

Solution approach

The combined pressurization optimization model of shale gas gathering and transportation system not only includes Boolean variables for judging whether a node is installed with compressors, but also nonlinear pressure drop constraints, as well as other continuous and discrete variables. Therefore, the problem generated by the model is a MINLP problem, and the software that can solve such problems at present include GAMS, AMPL, NEOS and AIMMS. Among them, GAMS is an optimization modeling software based on interactive database theory and mathematical programming, which consists of a language compiler and an integrated efficient solver for formulating, solving and analyzing optimization problems (Amosa et al. 2021). It has been successfully applied in many fields, such as power system and power equipment (Orejuela Luna and Espinosa Gualotuña 2018; Montoya et al. 2018; Zaro and Alqam 2019), cost of hybrid energy storage system (Das and Kumar 2017), pump-valve optimization of complex large-scale water distribution system (Skworcow et al. 2014), multi-objective exhaust pipe of thermoacoustic engine (Tartibu et al. 2015), optimization of wastewater treatment network (Galan and Grossmann 1998) and optimization of shale gas gathering and transportation pipeline network (Drouven and Grossmann 2017). GAMS is flexible and versatile; it can easily and safely change the details in the model, allowing the description of the model to be independent of the algorithm used to solve the problem. It is specially designed for optimization problems such as linear, nonlinear and mixed integer. It is more obvious in large and complex problems. Therefore, this paper adopts GAMS to model and solve the model.

Case study

Known parameters

In this paper, an actual shale gas field is selected as a case study to verify the model proposed. The gathering and transportation pipeline network in this shale gas field block consists of 8 platforms, 1 station and 8 pipeline sections, as shown in Fig. 2. The pipeline network in the block has a branch-like structure, and there are both wells put into production earlier and wells put into production later, for example, there are 6 wells on H3 platform, 3 wells are put into production first (H3-a), and the other 3 wells are put into production later (H3-b).

  • (1) Pipe parameters

Fig. 2
figure 2

Pipeline network structure

Full size image

Pipe parameters are represented in Table 1.

  • (2) Historical production data of wells and pressure of gas-gathering stations

Table 1 Pipe parameters
Full size table

The production data of a single shale gas well are shown in Fig. 3. The initial pressure of the well is 25.31 MPa. After 1 year of gas production, the pressure drops to about 5.08 MPa, and after 954 days, the pressure drops to 1 MPa and does not change. The production data of a single shale gas well are shown in Fig. 3. The initial pressure of the well was 25.31 MPa. After 1 year of gas production, the pressure dropped to about 5.08 MPa. After 954 days, the pressure dropped to 1 MPa and did not change. The initial flow rate of the well is 10 × 104 m3/d. During the drainage production period (0 to 310 days in this block), the flow rate was maintained at 10 × 104 m3/d; after 310 days, the flow rate decreased rapidly, and gradually stabilized at 2000 days. The output pressure of the station is 5.68 MPa.

  • (3) Number of wells, production parameters and time to come into operation

Fig. 3
figure 3

Shale gas well production data

Full size image

The actual production situation of a 300 days period of the shale gas block was selected for research, and four periods (Period) of T1, T2, T3 and T4 were divided according to the degree of pressure attenuation. The number of wells and production parameters in the platform at each time period are shown in Table 2.

Table 2 Number of wells and production parameters
Full size table

  • (4) Component of shale gas

The composition of shale gas is shown in Table 3.

Table 3 Shale gas composition
Full size table

  • (5) Power and prices of compressors

The purchase prices of different types of compressors are listed in Table 4. The price of electricity required for the operation of the compressor unit is 0.67 Yuan/(kW·h).

Table 4 Compressor price
Full size table

Analysis of results at different times

Due to the pressure decay characteristics of shale gas, the pressure requirements of shale gas blocks in different periods will also be quite different. According to the actual production situation of shale gas, a reasonable selection of the pressurization scheme can effectively save operating costs. As shown in Table 5, platform pressurization, area pressurization and station pressurization are selected and combined to form four different combination forms. Well pressurization is not considered here, because well pressurization can be equivalent to platform pressurization in some special cases, which will be discussed in the next section.

Table 5 Combination forms of pressurization
Full size table

Optimization results

The solution results obtained by each combination at different times, the solution time, and the number of constraints, variables and nonzero elements in the iterative process are shown in Table 6.

Table 6 Solution results obtained by each combination at different times
Full size table

Solution result analysis

The solutions of each combination at different times are shown in Fig. 4. Different colored circles in the grid indicate whether there is a solution. The numbers in each circle represent the number of locations that need to be pressurized at that time and combination. It can be seen that with the increase in the production time of shale gas blocks, the number of pressurized positions obtained by each combination method shows an upward trend, and there are also obvious differences between different combination methods. Form 1, Form 2 and Form 3 cannot meet the pressurization requirements at every moment, while Form 4 can solve the corresponding combined pressurization scheme at each moment. Form 1, Form 2 and Form 3 are composed of two different pressurization methods, and Form 4 is composed of three pressurization methods. Therefore, the combination of more pressurization methods can better cope with the impact of changing pressurization demands in shale gas blocks.

Fig. 4
figure 4

Solution results of each combination form at different periods

Full size image

Analysis of pressurization type

The combined pressurization scheme obtained by each combination form at different times is shown in Fig. 5. It can be seen from the figure that shale gas blocks have different demands on the pressurized position at different times. For example, during T1, the entire shale gas block only needs to pressurize the platform or station to meet the pressure demand. In the T2 period, not only area points need to be pressurized, but also stations need to be pressurized. Therefore, Form 1 and Form 2, which do not contain both area point and station pressurization methods, cannot meet the pressure requirements of shale gas blocks.

Fig. 5
figure 5

Pressurization types of each combination at different periods

Full size image

Similarly, the platform needs to be pressurized during the T3 period, while Form 3 does not include platform pressurization, which cannot meet the pressure requirements of shale gas blocks. During the T4 period, the platform and area points need to be pressurized at the same time, while Form 2 and Form 3 do not include the pressurization method of platforms and area points at the same time. Therefore, none of them can meet the pressure demand of shale gas blocks.

It should be noted that, among all the combinations in each time period, there are eight cases where the pressurization position is a platform, six cases where the pressurization position is a station, and only four cases when the pressurization position is a reginal point. Therefore, from the perspective of pressurization position, including platform pressurization and station pressurization, it can better cope with changes in pressurization demand for shale gas blocks.

Comparative analysis of different combinations

In the analysis of the previous section, it is suggested that there are few positions that need to be pressurized in the early stage, and various combinations can meet the pressurization requirements. However, with the increase in production time, more and more places need to be pressurized, and only the combination of more pressurization methods can meet the pressurization requirements. Therefore, in this section, according to the production situation in the T4 period, the well pressurization is added for research. It is worth noting that well pressurization and platform pressurization belong to the same position, that is, well pressurization is to pressurize some wells in the platform, and platform pressurization is to pressurize all wells in the platform. For comparative analysis, three different combinations of well pressurization, platform pressurization, area pressurization and station pressurization are formed, as shown in Table 7. Form 4 is the same as Form 4 in Table 5, and the other two well- pressurized ones are named Form 5 and Form 6 in turn.

Table 7 Combination forms of pressurization
Full size table

Iterative analysis of the solution process

Since all combined pressurization methods use the same mathematical model, we take Form 4 as an example to analyze the entire solution process. There are a total of 276 constraints (189 equality constraints, 87 inequality constraints), 237 variable numbers and 681 nonzero numbers in the model. The MINLP problem generated by the optimization model is solved by calling the solver DICOPT in GAMS. During the solution process, the computer divides the MINLP problem into two sub-problems, nonlinear programming (NLP) and mixed integer programming (MIP). The NLP sub-problem is solved by CONOPT, and the MIP sub-problem is solved by CPLEX. Every time the iterative solution of NLP and MIP is completed, it is a main iteration. At the beginning of the first main iteration, the first (relaxed) NLP is set up for iterative solution, then the first MIP is set up for iterative solution, and finally the solution result is obtained and the first main iteration process is ended. Then the subsequent main iterations are performed in sequence. Such main iterations are performed 20 times in total, and the NLP searches for a feasible solution at the 14th main iteration. Finally, at the 20th main iteration, the search is stopped due to the main iteration limit, the solution is completed normally, and an optimal integer solution is found. The main iteration process is shown in Fig. 6.

Fig. 6
figure 6

Iterative process

Full size image

Comparison of pressurization positions

The distribution of compressors under the three combinations is shown in Fig. 7.

  1. (1)

    For Form 4, compressors are arranged at 6 platforms, 2 area points and 1 station, respectively, which require a large number of compressors, and the pressurization positions are scattered, almost all over the entire shale gas block.

  2. (2)

    For Form 5, the compressors are arranged at 6 wells, 1 area point and 1 station, respectively, the number of compressors required is less than that of the first type, and the locations requiring pressurization are more concentrated.

  3. (3)

    For Form 6, the compressors are arranged at 3 platforms, 2 wells, 1 area point and 1 station, respectively, the number of compressors required is minimal, and the locations requiring pressurization are relatively concentrated.

Fig. 7
figure 7

Distribution of compressor units under different combinations

Full size image

It reveals that Form 6 is significantly better than Form 4 and Form 5, reflecting the advantages of the combined pressurization method considering both well pressurization and platform pressurization in the pressurization of shale gas gathering and transportation systems. More centralized pressurization locations and fewer compressors save manpower and material resources in managing and maintaining the entire pressurization system.

Operating power comparison

The operating power and operating cost of each pressurization position under different combinations are shown in Fig. 8. The total operating power of the compressors of Form 4, Form 5 and Form 6 is 2961.893, 2940.093 and 2945.613 kW, respectively, and the compressor operating power at the station is higher than that at other locations. This is because the compressor at the station needs to pressurize the shale gas in the entire block, and the amount of shale gas that needs to be processed is much larger than other pressurization locations. The number of pressurization positions is 9, 8 and 7, respectively. Form 4 has the largest number of pressurization positions and the total operating power of the compressor, while Form 6 has the least number of pressurization positions, and the total operating power of the compressor is also moderate.

Fig. 8
figure 8

Operating power and operating cost of each pressurization position under different combinations

Full size image

Since only 3 platforms contain wells that are put into production at different times, and each platform is put into production in two batches, although the comparison is not very obvious, the advantages of Form 6 can also be seen. If there are more platforms containing wells with different periods of production, and the well periods of production are more spread out, the advantage of the Form 5 is diminished, and it requires more compressors to meet the gas delivery requirements. Compared with the Form 5, the Form 4 has less compressors, but because more shale gas needs to be pressurized, the compressor operation cost is higher, and it is not the most economical solution. Form 6 combines the advantages of Form 4 and Form 5 with fewer pressurization positions required and a moderate total compressor operating cost.

Comparison of compressor configurations

The compressor configuration for each pressurization position is shown in Table 8. The compressor configuration is closely related to the pressure difference between the inlet and outlet of the compressor and the processing capacity. For example, platform H4 in Form 4 is smaller than the compressor inlet and outlet pressure difference and processing capacity of the station, so the compressor power configured at platform H4 is also smaller. Although the pressure difference between the inlet and outlet of the compressor in Well H5-b in Form 5 is larger than that of the station, its processing capacity is much smaller than that of the station, so the compressor power configured at the station is higher. The processing capacity of the platform H5 compressor in Form 6 is smaller than that of the well H4-a, but its inlet and outlet pressure difference is much larger than that of the well H4-a, which leads to a higher power compressor installed at the platform H5.

Table 8 Compressor configuration and unit cost
Full size table

The compressor configuration at each boost position affects the unit cost. The higher the power and the number of compressors, the higher the cost. The running costs of the Form 4, Form 5 and Form 6 are 142.56 × 104 Yuan, 141.84 × 104 Yuan and 142.56 × 104 Yuan, respectively. Although the number of compressors and compressor power under the three combinations are different, their operating costs are all maintained at about 142 × 104 Yuan, which makes the total cost of the compressor directly affected by its purchase cost. Form 5 has the highest purchase cost of the compressor at 777 × 104 Yuan. Although the Form 5 requires fewer compressors than the Form 4, the Form 5 requires more high-power compressors, making the Form 5 more expensive to purchase. Form 6 has the lowest purchase cost of compressors at 727 × 104 Yuan, due to the fact that it requires the least number of compressor sets (only 7 compressors). There is no doubt that Form 5 has the highest total compressor cost of 918.84 × 104 Yuan, and Form 6 has the lowest total compressor cost of 869.56 × 104 Yuan. Therefore, the optimization results fully show that the combined pressurization method considering both well pressurization and platform pressurization is superior to the other two combined methods.

Conclusions

In this paper, a variety of pressurization methods are considered, and the total cost of compressor units is used as the objective function to establish a combined pressurization optimization mathematical model of the shale gas gathering and transportation system, then the optimization model is verified and analyzed for the shale gas block. The main conclusions are as follows:

  1. (1)

    A mixed-integer nonlinear optimization model of combined pressurization for shale gas gathering and transportation system is proposed. The model considers various pressurization methods, optimizes the appropriate pressurization mode for the system, and more importantly, can effectively guides the selection of the actual pressurization scheme.

  2. (2)

    Based on the actual production conditions of a shale gas block, Form 4 is significantly better than Form 1, Form 2 and Form 3 in the face of the impact of shale gas pressure attenuation, and includes a combination of platform pressurization and station pressurization, which can better meet the pressurization needs of different periods.

  3. (3)

    When well pressurization and platform pressurization are considered at the same time, more concentrated pressurization positions and fewer compressors are obtained by optimization, which reflects the advantages of the combined pressurization method in the pressurization of shale gas gathering and transportation systems. This model is not only applicable to the shale gas block studied in this paper, but also applicable to the combined pressurization optimization problem of gathering and transportation systems in other blocks.

  4. (4)

    Although compared with previous work, our model has achieved great progress and can be used as an effective tool for determining shale gas boosting scenarios. However, it can be further improved. In future work, the production decline curve can be introduced into the model according to the development characteristics of the gas reservoir, so as to obtain a more realistic booster scheme.