Introduction

Knowing the reservoir parameters, such as its permeability, provides an adequate reservoir management. Well testing is a conventional way to estimate those parameters. During this procedure, fluid is extracted from the reservoir and pressure data is measured. In such a process, the wellbore is open, fluid is produced and, thus, pressure decreases (Bela et al. 2021).

There are different models of oil reservoirs to consider during a production test. In this work, a multilayered radially composite reservoir was considered, i.e., there are different regions of permeability in each layer. In addition, there is formation crossflow, which is the main contribution of such. Formation crossflow, which is different than crossflow in the wellbore, is defined in this work as the semipermeable-wall system described by Gao and Deans (1983). A nonzero vertical permeability between every two adjacent layers is considered.

There are a few works considering a stratified composite reservoir, i.e., without formation crossflow but including different regions of permeability (Bixel et al. 1963; Closmann and Ratliff 1967; Bittencourt Neto et al. 2020; Shi et al. 2020b) and also there are some works that account for formation crossflow (Ehlig-Economides and Joseph 1987; Bourdet et al. 1985; Prijambodo et al. 1985; Gao and Deans 1983; Shi et al. 2020a).

However, the currently available solutions for well testing regarding multiple regions and transient time for multilayered reservoir with formation crossflow are limited to a model with only two distinct regions of permeability and for a naturally fractured reservoir (Shi et al. 2020a). In addition, such work considers only regions of equal radii.

Thus, the novelty of the present work is combining a composite reservoir system with multiple distinct permeability regions and formation crossflow for a multilayered reservoir under single-phase flow. Moreover, the multiple regions of distinct permeability considered in each layer can have different radii, which is also an important contribution of this research.

One of the main and primary researches on single-phase flow was the one proposed by Lefkovits et al. (1961). In this work, an analytical model was proposed, where the properties, such as thickness, permeability, and porosity could be different in each layer. Formation damage was also considered. However, only wellbore crossflow was considered, which is when there is communication between two layers strictly through the well. Such reservoirs are denoted as commingled systems.

Different from the commingled system, the model for multilayered systems involving interlayer formation crossflow is the one considered in this present research. For such a model, the interflow at the interface between all layers should be considered in the formulation.

The formulation regarding the interflow between layers for the present research was derived from Ehlig-Economides and Joseph (1987). In this paper, an analytical model was developed considering a reservoir with an arbitrary number of communicating layers under single-phase flow, i.e., formation crossflow along with all layers. Properties could also be different from layer to layer, however, there were no different regions within each layer. In this work Ehlig-Economides and Joseph (1987), both formation damage and wellbore storage were considered. Furthermore, an approximate solution was derived for both short and long times. This work was developed in the Laplace field and used numerical inversion of Laplace transforms, more specifically, the Stehfest Algorithm (Stehfest 1970) in order to find a pressure response in the real field. The first work to use the Stehfest Algorithm, was the one proposed by Tariq et al. (1978).

The analytical model developed by Ehlig-Economides and Joseph (1987) was strongly based on the one proposed by Gao and Deans (1983), and the results for both are similar. Both works showed that after a period of time, the reservoir with formation crossflow could be described as an equivalent single layer system. In the present research, the same could be observed.

The study presented by Prijambodo et al. (1985), also included formation crossflow and it considered a two-layer cylindrical reservoir. In addition, this work presented an analysis for producer wells and considered damaged regions for its results. It showed that the flowing pressure response at the well at early times can be divided into three flow periods; The first one shows that the reservoir behaves as if there was no crossflow. The second one, a transitional period, shows that the pressure response depends on the contrast between horizontal permeabilities and on the degree of communication between layers. During the third period, the reservoir behaves like a single-layer system, like the results presented in Ehlig-Economides and Joseph (1987) and Gao and Deans (1983).

Another work regarding formation crossflow is presented by Lu et al. (2019). The authors proposed a model based on Green functions for crossflow reservoirs. However, unlike the present work, the latter considered the reservoir to be homogeneous, that is, without the different regions of permeability, moreover, the model contemplates only reservoirs with two layers, while the present model allows an arbitrary number of layers.

Finally, the work proposed by Bourdet et al. (1985) also included formation crossflow. It was entirely done in the real field and proposed an analytical model for a two-layer reservoir. It also considers wellbore storage and skin effects. In addition, it includes a dual-porosity and permeability model description.

A radially composite reservoir is considered in the present work, i.e., the presence of different regions of permeability within each layer. There are a few studies on radially composite media. The first was proposed by Bixel et al. (1963). They considered a 2D infinite two-zone reservoir to solve the pressure diffusion equation. The work proposed by Closmann and Ratliff (1967) also considered a composite radial single-layered reservoir model. Likewise, the work proposed by (Bittencourt Neto et al. 2020) considered a composite radial reservoir, however, a two-layered model was considered. For this paper (Bittencourt Neto et al. 2020), like in the present work, the formulation was developed in the Laplace domain.

Similar to the analytical model developed by Bittencourt Neto et al. (2020), the work proposed by Shi et al. (2020b) also considered two distinct regions, and the model was developed in the Laplace field. In this paper, a field application is discussed in detail and the results show that the pressure derivative type curve during the new flow regimes stage can identify the vertical combined boundary effect, which is characterized by a dual-layered reservoir with different boundary types. All these works (Shi et al. 2020b; Bittencourt Neto et al. 2020; Closmann and Ratliff 1967; Bixel et al. 1963 did not consider formation crossflow.

A more recent work in naturally fractured reservoirs developed an analytical model considering formation crossflow in a multilayered reservoir with two distinct regions of permeability (Shi et al. 2020a). In a naturally fractured reservoir the flow takes place in two stages: from the rock matrix to the fractures and then from the fractures to the well. The region near the wellbore has different properties due to acid stimulation, which allows the existence of two distinct regions of permeability in each layer (Shi et al. 2020a).

In addition to developing a model to combine a composite multilayered reservoir and formation crossflow like was done before Shi et al. (2020a) for 2 regions, the present model is innovative as it considers multiple regions within each layer that can have different radii. Finally, the proposed model can be used to calculate the equivalent permeability of the reservoir, and this model was validated by comparison with a commercial flow simulator.

The next section of this paper, "Model description" Section, describes the model’s hypothesis. "Mathematical formulation" Section presents the mathematical analysis of the problem. "Model validation" section is reserved for the model validation, and finally, "Equivalent permeability" section presents the summary and conclusions.

Model description

Consider an infinite, laterally isotropic, multilayered, radially composed reservoir. In each one of its n layers denoted by j, there are \(m_j\) distinct regions of permeability denoted by i, and each permeability value will be denoted by \(k_{ji}\). There may be formation crossflow in between all layers’ adjacencies. All the formulation was done in consistent units.

In the model, each layer has a single phase flow of a fluid with viscosity (\(\mu\)) that is constant, and also constant and small total compressibility (\(c_{t}\)) in all layers. In addition, the porosity (\(\phi _{j}\)) may have a different value in each layer, as well as the thickness (\(h_{j}\)). Constant flow rate at the well is considered. Formation damage and wellbore storage will be disregarded. Consider \(\varDelta p_{ji}=p_{i}-p_{ji}\), the flow in each region i of each layer \(j=1,2,\ldots ,n\) is governed by the following diffusion equation (Bourdet et al. 1985; Ehlig-Economides and Joseph 1987):

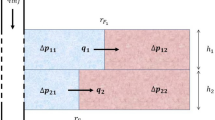
$$\begin{aligned} (kh)_{ji} \nabla ^2 \varDelta p_{ji} =\, &(\phi h)_{j} c_t \mu \frac{\partial \varDelta p_{ji}}{\partial t} + (\varDelta p_{ji} - \varDelta p_{(j-1)i})X_{j-1}^{i} \nonumber \\&- (\varDelta p_{(j+1)i}-\varDelta p_{ji})X_{j}^{i} \end{aligned}$$
(1)

In order to define the coefficient of semipermeability \(X_ {j}^{i}\), first consider that the radii of the regions of permeability are all equal for each layer j. Figure 1 illustrates that problem for a 2 layers and 2 regions case. Notice that the radii \(r_{12} \text { and } r_{22}\) are considered to be infinite:

Fig. 1
figure 1

Two layered model with regions of equal radii

Full size image

Then, each coefficient of semipermeability \(X_ {j}^{i}\) is defined as Ehlig-Economides and Joseph (1987):

$$\begin{aligned} X_{j}^{i} = \frac{2}{2[(\varDelta h_j)/k_v{_{j}^{i}}]+\chi _{j}^{i}+\chi _{j+1}^{i}} \end{aligned}$$
(2)

For \(j=1,\ldots ,n\) and \(i=1,\ldots ,m_j\). In this case, \(m_j=m_{j+1}\) for all \(j=1,\ldots ,n-1\).

\(\varDelta h_j\) and \(k_v{_{j}^{i}}\) are the thickness and the permeability of the shale between layers j and \(j+1\), \(\chi _{j}^{i} = \frac{h_j}{k_{z_j}^i}\), where \(k_{z_j}^i\) is the vertical permeability of layer j in region i. Notice that the thickness of the shale ( \(\varDelta h_j\)) can be zero and the coefficient of semipermeability will not be necessarily zero in this case.

Also notice that \(X_ {n}^{i}=0\) and if there is no crossflow between layers j and \(j+1\), then \(X_ {j}^{i}=0\).

Fig. 2
figure 2

Two layered model with regions of different radii

Full size image

Now, if the radii of adjacent regions in layers j and \(j+1\) are different, there will be coefficients of semipermeability that relate to different regions. Figure 2 illustrates that problem for a case considering two layers and two regions. The radii \(r_{12} \text { and } r_{22}\) are considered to be infinite.

Notice that, in Fig. 1 the semipermeability coefficient \(X_ {1}^{2}\) relates region 2 from layer 1 and region 2 from layer 2. Then, in that case, \(X_ {1}^{2}\) is given by:

$$\begin{aligned} X_{1}^{2} = \frac{2}{2[\varDelta h_1/k_{v_1}^{2}]+\chi _{2}^{2}+\chi _{1}^{2}} \end{aligned}$$
(3)

where \(\chi _{2}^{2} = \frac{h_2}{k_{z_2}^2}\) and \(\chi _{1}^{2} = \frac{h_1}{k_{z_1}^2}\).

However, in the example illustrated in Fig. 2, \(X_ {1}^{2}\) relates different regions of permeability. In this case, \(X_ {1}^{2}\) relates region 2 in layer 1 and region 1 in layer 2. Then, \(X_ {1}^{2}\) is given by:

$$\begin{aligned} X_{1}^{2} = \frac{2}{2[\varDelta h_1/k_{v_1}^{2}]+\chi _{2}^{1}+\chi _{1}^{2}} \end{aligned}$$
(4)

where \(\chi _{2}^{1} = \frac{h_2}{k_{z_2}^1}\) and \(\chi _{1}^{2} = \frac{h_1}{k_{z_1}^2}\).

Then, \(X_ {j}^{i}\) can be defined generally (for equal and different radii cases) as:

$$\begin{aligned} X_{j}^{i} = \frac{2}{2[(\varDelta h_j)/k_v{_{j}^{i}}]+\chi _{j}^{i_j}+\chi _{j+1}^{i_{j+1}}} \end{aligned}$$
(5)

where regions \(i_j\) and \(i_{j+1}\) can represent equivalent or different regions for layers j and \(j+1\).

The example described in Fig. 2, considers three coefficients of permeability. Then, each interface can be extended to the other layer and the problem can be treated as one with three distinct regions in each layer, where the radii of the three regions are the same in both layers.

Consider now, \(m_j\) to be the number of regions in layer j. From the examples discussed above, it is possible to see that even if the numbers of the regions are the same for two connected layers, i.e., \(m_j\) = \(m_{j+1}\), the radius of each one of these \(m_j\) regions can still be different.

Let \(r(j,1)\text {, }r(j,2)\text {, }r(j,3), \ldots , r(j,m_j)\) be the radii of the regions in layer j and for layer \(j+1\), \(r(j+1,1)\text {, }r(j+1,2)\text {, }r(j+1,3), \ldots , r(j+1,m_{j+1})\).

Let s be the number of incidents where \(r(j,l)=r(j+1,k)\), then, it is possible to show that the number of \(X_{j}^{i}\) semipermeability coefficients in the adjacency between layers j and \(j+1\) is \(m_j+m_{j+1}-1-s\).

For example, in Fig. 3, the first two layers represented have, respectively, three and four regions. Also, r(1, 2) and r(2, 3) are the only values that coincide (\(r(1,2)=r(2,3)\)). That is, \(m_1=3\), \(m_2=4\) and \(s=1\). Hence, there are \(3+4-1-1 = 5\) crossflow coefficients within these layers.

Fig. 3
figure 3

Reservoir with n connected layers and many regions of permeability

Full size image

After having each semipermeability coefficient well defined, consider the following equation:

$$\begin{aligned} \alpha = \Big ( \sum \limits _{j=1}^{n}(m_{j}-1)\Big )-s \end{aligned}$$
(6)

Then, extending each interface to all reservoir’s layers and creating artificial regions, illustrated in Fig. 4, this problem can be reduced to one where \(\alpha\) is the number of regions with equal radii.

Fig. 4
figure 4

\(\alpha\) extensions of the regions in each layer

Full size image

It is important to define well each semipermeability coefficient \(X_{j}^{i}\) for the \(\alpha\) regions, i.e., observing correctly the permeability regions it is relating.

After all layers have been divided into \(\alpha\) regions, there might be regions with the same \(X_{j}^{i}\) coefficients. For example, it is possible to see that in Fig. 4\(X_{1}^{1}=X_{1}^{2}\), because both of the coefficients relate region 1 in layer 1 with region 1 in layer 2.

Notice that there are \(m_j+m_{j+1}-1-s\) different values of \(X_{j}^{i}\) and \(\alpha -(m_j+m_{j+1}-1-s)\) repeated values for each adjacency.

Mathematical formulation

Considering the previous hypotheses and denoting \(m =\alpha\) (number of regions), the model description is given by the diffusion equation (1) and its suitable boundary conditions:

  • The Initial Condition (I.C.) which occurs at time \(t=0\) and reflects that the reservoir is in equilibrium, that is, the pressure is the same in all layers (apart from the hydrostatic effect).

  • The Internal Boundary Condition (I.B.C), which is related to well-flowing conditions during the test.

  • The External Boundary Condition (E.B.C), which refers to the flow behavior at the extreme limit of the reservoir and in this work, an infinite-like reservoir is considered.

Then, the following equation model the problem for all layers \(j=2,\ldots ,n-1\) and regions \(i=1,\ldots ,(m-1)\):

PDE:

$$\begin{aligned} (kh)_{ji} \nabla ^2 \varDelta p_{ji} =\,&(\phi h)_{ji} c_t \mu \frac{\partial \varDelta p_{ji}}{\partial t} \nonumber \\&+ (\varDelta p_{ji} - \varDelta p_{(j-1)i})X_{j-1}^{i} - (\varDelta p_{(j+1)i}-\varDelta p_{ji})X_{j}^{i} \end{aligned}$$
(7)

Consider \(\kappa _{ji}=k_{ji} h_j\) and \(\omega _{j}=\phi _j h_j\). When \(j=1\), the PDE is:

$$\begin{aligned} \kappa _{1i} \nabla ^2 \varDelta p_{1i} = \omega _{1} c_t \mu \frac{\partial \varDelta p_{1i}}{\partial t} - ( \varDelta p_{2i}- \varDelta p_{1i})X_{1}^{i} \end{aligned}$$
(8)

And for \(j= n\), the PDE is:

$$\begin{aligned} \kappa _{ni} \nabla ^2 \varDelta p_{ni} = \omega _{j} c_t \mu \frac{\partial \varDelta p_{ni}}{\partial t} + ( \varDelta p_{ni} - \varDelta p_{(n-1)i})X_{n-1}^{i} \end{aligned}$$
(9)

For all layers \(j=1,\ldots ,n\) and all regions \(i=1,\ldots ,(m-1)\) there is the initial condition:

$$\begin{aligned}&IC: \varDelta p_{ji}(r,0) = 0 \end{aligned}$$
(10)

For all layers \(j=1,\ldots ,n\) and region \(i=1\) the inner boundary condition Lefkovits et al. (1961):

$$\begin{aligned}&IBC: q_{ji} = \frac{2 \pi (kh)_{ji} r }{\mu } \Big ( \frac{\partial \varDelta p_{ji}}{\partial r} \Big ) \bigg |_{r = r_{w}} \end{aligned}$$
(11)

And for all layers \(j=1,\ldots ,n\) and region \(i=m\) the external boundary condition:

$$\begin{aligned}&EBC: \lim _{r \rightarrow \infty } \varDelta p_{ji}(r,t) = 0 \end{aligned}$$
(12)

Consider \(j=1,\ldots ,n\) and \(i=2,\ldots ,m\). There are coupling conditions relating the regions \(i-1\) and i in each layer j, which must be defined in order to properly solve the problem. To guarantee that the pressure and flow rate profiles are continuous, the coupling conditions between the regions (CCR) are defined by imposing that the pressure and the flow rate must be equal at the interface between them Nie et al. (2011):

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\varDelta p_{j(i-1)}(r = r_{j(i-1)},t) = \varDelta p_{ji}(r = r_{j(i-1)},t)\\ &{}q_{j(i-1)}=q_{ji} \end{array}\right. } \end{aligned}$$
(13)

Using Darcy’s law it is possible to rewrite the flow rate relation of the CCR so that :

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\varDelta p_{j(i-1)}(r = r_{j(i-1)},t) = \varDelta p_{ji}(r = r_{j(i-1)},t)\\ &{}\Big ( r\frac{\partial \varDelta p_{j(i-1)}}{\partial r} \Big ) |_{r=r_{j(i-1)}} = \frac{(kh)_{ji}}{(kh)_{j(i-1)}}\Big ( r\frac{\partial \varDelta p_{ji}}{\partial r} \Big ) |_{r=r_{j(i-1)}} \end{array}\right. } \end{aligned}$$
(14)

where \(j = 1, \ldots , n\) and \(i = 1, \ldots , m\).

The coupling condition between layers (CCL) is obtained considering that the pressure drop is equal in the layers along the well (except for the hydrostatic effect) and that the flow rate at the well is given by the sum of the flows of each layer, that is Bittencourt Neto et al. (2020):

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\varDelta p_{(j-1)1} (r = r_{w},t) = \varDelta p_{j1}(r = r_{w},t)\\ &{}q = q_{11} + q_{21} + \ldots + q_{n1} \end{array}\right. } \end{aligned}$$
(15)

Once again, using the Darcy’s law, the flow rate CCL equation can be rewritten as:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\varDelta p_{(j-1)1} (r = r_{w},t) = \varDelta p_{j1}(r = r_{w},t)\\ &{}\frac{q\mu }{2\pi r_{w}} = \sum \limits _{j=1}^{n} {\kappa _{ji}\frac{\partial \varDelta p_{ji}}{\partial r} \big |_{r = r_{w}}} \end{array}\right. } \end{aligned}$$
(16)

To find the pressure solution, the Laplace transform will be applied to equations (7) through (16) and the solution will be first calculated in such space. Then, the Stehfest Algorithm (Stehfest 1970) is used to find the solution in the real field.

Consider \(\kappa _{ji} = k_{ji}h_{j}\) and \(\omega _{j} = \phi _{j}h_{j}\) to facilitate the analysis, \(\varDelta {\overline{p}}\) to be the Laplace transform of the pressure variation and u to be the Laplace’s variable. Now, for layers \(j=1,\ldots ,n\) and regions \(i=2,\ldots ,m-1\) the following equation is given in the Laplace field:

ODE:

$$\begin{aligned} \kappa _{ji} \nabla ^2 \varDelta {\overline{p}}_{ji} =\,&\omega _{j} c_t u \mu \varDelta {\overline{p}}_{ji} \nonumber \\&+ ( \varDelta {\overline{p}}_{ji} - \varDelta {\overline{p}}_{(j-1)i})X_{j-1}^{i} - ( \varDelta {\overline{p}}_{(j+1)i}- \varDelta {\overline{p}}_{ji})X_{j}^{i} \end{aligned}$$
(17)

For layers \(j=1,\ldots ,n\) and region \(i=1\):

$$\begin{aligned}&IBC: {\overline{q}}_{ji} = \frac{2 \pi \kappa _{ji} r u }{\mu } \Big ( \frac{\partial \varDelta {\overline{p}}_{ji}}{\partial r} \Big ) \bigg |_{r = r_{w}} \end{aligned}$$
(18)

For layers \(j=1,\ldots ,n\) and region \(i=m\):

$$\begin{aligned}&EBC: \lim _{r \rightarrow \infty } \varDelta {\overline{p}}_{ji}(r,t) = 0 \end{aligned}$$
(19)

The coupling conditions between regions in the Laplace field are given below (Bittencourt Neto et al. 2020; Nie et al. 2011):

$$\begin{aligned} CCR:{\left\{ \begin{array}{ll} &{}\varDelta {\overline{p}}_{j(i-1)}(r = r_{j(i-1)},t) = \varDelta {\overline{p}}_{ji}(r = r_{j(i-1)},t)\\ &{}\Big ( r\frac{\partial \varDelta {\overline{p}}_{j(i-1)}}{\partial r} \Big ) |_{r=r_{j(i-1)}} = \frac{\kappa _{ji}}{\kappa _{j(i-1)}}\Big ( r\frac{\partial \varDelta {\overline{p}}_{ji}}{\partial r} \Big ) |_{r=r_{j(i-1)}} \end{array}\right. } \end{aligned}$$
(20)

For \(j = 1, \ldots , n\) and \(i = 2, \ldots , m\).

The coupling conditions between layers in the Laplace field are given below Bittencourt Neto et al. (2020):

$$\begin{aligned} CCL:{\left\{ \begin{array}{ll} &{}\varDelta {\overline{p}}_{(j-1)1} (r = r_{w},t) = \varDelta {\overline{p}}_{j1}(r = r_{w},t)\\ &{}\frac{{\overline{q}}\mu }{2 \pi u \sum \limits _{j=1}^{n}{\kappa _{j1}}} = \sum \limits _{j=1}^{n} {\Big (r\frac{\partial \varDelta {\overline{p}}_{j1}}{\partial r} \Big ) \big |_{r = r_{w}}} \end{array}\right. } \end{aligned}$$
(21)

For \(j=2,\ldots ,n\).

The pressure general solution in the Laplace field is well known in terms of modified Bessel functions. They are given below for region i in layer j Ehlig-Economides and Joseph (1987):

$$\begin{aligned} \varDelta {\overline{p}}_{ji} = A_{j}^{i}K_0(\sigma _{ji}r) + B_{j}^{i}I_0(\sigma _{ji}r) \end{aligned}$$
(22)

Applying the EBC in the equation above, for \(i=m\):

$$\begin{aligned} \lim _{r \rightarrow \infty }\Big [ A_{j}^{i}K_0(\sigma _{ji} r) + B_{j}^{i}I_0(\sigma _{ji} r) \Big ] = 0 \implies B_{j}^{i}=0 \end{aligned}$$
(23)

Hence, the following equations for the general pressure solution are given:

For regions \(i=1,\ldots ,m-1\):

$$\begin{aligned} \varDelta {\overline{p}}_{ji} = A_{j}^{i}K_0(\sigma _{ji}r) + B_{j}^{i}I_0(\sigma _{ji}r) \end{aligned}$$
(24)

For region \(i=m\):

$$\begin{aligned} \varDelta {\overline{p}}_{ji} = A_{j}^{i}K_0(\sigma _{ji}r) \end{aligned}$$
(25)

Using the solutions above, it can be seen that \(\nabla ^2\varDelta {\overline{p}}_{ji} = \sigma ^2_{ji}\varDelta {\overline{p}}_{ji}\). Hence, replacing this equivalence in the ODE (17) Ehlig-Economides and Joseph (1987):

$$\begin{aligned}&\kappa _{ji} \sigma ^2_{ji}\varDelta {\overline{p}}_{ji} - \omega _{ji} c_t \mu u\varDelta {\overline{p}}_{ji}+(\varDelta {\overline{p}}_{ji} - \varDelta {\overline{p}}_{(j-1)i})X_{j-1}^{i} \nonumber \\&\qquad - (\varDelta {\overline{p}}_{(j+1)i}-\varDelta {\overline{p}}_{ji})X_{j}^{i} = 0 \end{aligned}$$
(26)

And rearranging the equation above for each region i:

$$\begin{aligned}&(\kappa _{ji} \sigma ^2_{ji} - \omega _{ji} c_t \mu u -X_{j-1}^{i} - X_{j}^{i})\varDelta {\overline{p}}_{ji}\nonumber \\&\qquad +X_{j-1}^{i} \varDelta {\overline{p}}_{(j-1)i} - X_{j}^{i}\varDelta {\overline{p}}_{(j+1)i} = 0 \end{aligned}$$
(27)

This is a homogeneous linear system for each region i where the nontrivial solution is wanted, that is, \(\varDelta {\overline{p}}_{ji}\ne 0\). That is true only if each matrix below is singular, and that implies that its determinant must vanish:

$$\begin{aligned} a^{i}_{jk}= {\left\{ \begin{array}{ll} X_{j-1}^{i}, &{} \text {for } k=j-1; \,j>1,\\ \kappa _j \sigma ^2 - \omega _{ji} c_t \mu u - X_{j-1}^{i} - X_{j}^{i}, &{} \text {for } k = j,\\ X_{j}^{i}, &{} \text {for } k=j+1;\, j<n,\\ 0, &{} \text {for } k \ne j-1,\,j, \text {or } j+1. \end{array}\right. } \text { For } i=1,\ldots ,m. \end{aligned}$$
(28)

To find the values of \(\sigma _{ji}\) by vanishing the determinant of each matrix above is equivalent to finding the eigenvalues \(\kappa _{ji} \sigma ^2\) of each matrix below:

$$\begin{aligned} b^{i}_{jk}= {\left\{ \begin{array}{ll} -X_{j-1}^{i}, &{} \text {for } k=j-1;\, j>1,\\ \omega _{ji} c_t \mu u + X_{j-1}^{i} + X_{j}^{i}, &{} \text {for } k = j,\\ -X_{j}^{i}, &{} \text {for } k=j+1;\, j<n,\\ 0, &{} \text {for } k \ne j-1,\,j, \text {or } j+1. \end{array}\right. } \text { For } i=1,\ldots ,m. \end{aligned}$$
(29)

This equivalence is true because:

$$\begin{aligned} a^{i}_{jk} = b^{i}_{jk}-eig(b^{i}_{jk})I \end{aligned}$$
(30)

where I is the identity matrix, and, consequently:

$$\begin{aligned} det(a^{i}_{jk})=0 \implies det(b^{i}_{jk}-eig(b^{i}_{jk})I)=0 \end{aligned}$$
(31)

Then, finding \(\sigma _{ji}\) is equivalent to extracting the square root of the eigenvalue of \(b^{i}_{jk}\) then, dividing it by \(\kappa _{ji}\):

$$\begin{aligned} \sigma _{ji}=\sqrt{\frac{ eig(b^{i}_{jk})}{\kappa _{ji}}} \end{aligned}$$
(32)

Now, with the values of \(\sigma _{ji}\) calculated, the pressure coefficients can be determined. It can be seen in equations (24) and (25), that there are \((2m-1)n\) coefficients. The relations provided by the coupling conditions between layers and regions are, precisely, that many.

The first n relations are provided by using the pressure solutions for region 1 (24) in the CCL pressure and flow rate equations:

Pressure CCL:

$$\begin{aligned}&A_{j-1}^{1}K_0(\sigma _{(j-1)1} r_{w}) + B_{j-1}^{1}I_0(\sigma _{(j-1)1} r_{w}) \nonumber \\&\quad = A_{j}^{1}K_0(\sigma _{j1} r_{w}) + B_{j}^{1}I_0(\sigma _{j1} r_{w}) \end{aligned}$$
(33)

For \(j=2,...,n\).

Flow rate CCL:

$$\begin{aligned} \frac{q\mu }{2\pi u r_{w}} =&\sigma _{11}\kappa _{11}(-A_{1}^{1}K_0(\sigma _{11} r_{w}) + B_{1}^{1}I_0(\sigma _{11} r_{w}))\nonumber \\&+\ldots +\sigma _{n1}\kappa _{n1}(-A_{n}^{1}K_0(\sigma _{n1} r_{w}) + B_{n}^{1}I_0(\sigma _{n1} r_{w})) \end{aligned}$$
(34)

The other \((2m-1)n-n\) equations left are provided by using pressure solutions (24) and (25) in the CCR pressure and flow rate equations:

Pressure CCR:

$$\begin{aligned}&A_{j}^{i-1}K_0(\sigma _{j(i-1)} r_{j(i-1)}) + B_{j}^{i-1}I_0(\sigma _{j(i-1)} r_{j(i-1)}) \nonumber \\&\quad = A_{j}^{i}K_0(\sigma _{ji}r_{j(i-1)}) + B_{j}^{i}I_0(\sigma _{ji} r_{j(i-1)}) \end{aligned}$$
(35)

For \(i = 2,\ldots ,m-1\).

$$\begin{aligned}&A_{j}^{i-1}K_0(\sigma _{j(i-1)} r_{j(i-1)}) + B_{j}^{i-1}I_0(\sigma _{j(i-1)} r_{j(i-1)}) \nonumber \\&\quad = A_{j}^{i}K_0(\sigma _{ji} r_{j(i-1)}) \end{aligned}$$
(36)

For \(i = m\).

Flow rate CCR:

$$\begin{aligned}&A_{j}^{i-1}K_1(\sigma _{j(i-1)} r_{j(i-1)}) - B_{j}^{i-1}I_1(\sigma _{j(i-1)} r_{j(i-1)}) \nonumber \\&\quad = \frac{\kappa _{ji}\sigma _{ji}}{\kappa _{j(i-1)}\sigma _{j(i-1)}}\Big (A_{j}^{i}K_1(\sigma _{ji} r_{j(i-1)}) - B_{j}^{i}I_1(\sigma _{ji} r_{j(i-1)})\Big ) \end{aligned}$$
(37)

For \(i = 2,\ldots ,m-1\).

$$\begin{aligned}&A_{j}^{i-1}K_1(\sigma _{j(i-1)} r_{j(i-1)}) - B_{j}^{i-1}I_1(\sigma _{j(i-1)} r_{j(i-1)}) \nonumber \\&\quad = \frac{\kappa _{ji}\sigma _{ji}}{\kappa _{j(i-1)}\sigma _{j(i-1)}}\Big (A_{j}^{i}K_1(\sigma _{ji} r_{j(i-1)})\Big ) \end{aligned}$$
(38)

For \(i = m\).

Using the relations above, a linear system can be set up in order to calculate the pressure coefficients:

$$\begin{aligned} \begin{bmatrix} A_{1}^{1} \\ B_{1}^{1} \\ A_{1}^{2} \\ B_{1}^{2} \\ \vdots \\ A_{1}^{m_1} \\ A_{2}^{1} \\ B_{2}^{1} \\ A_{2}^{2} \\ B_{2}^{2} \\ \vdots \\ A_{2}^{m_2} \\ \vdots \\ A_{n}^{1} \\ B_{n}^{1} \\ A_{n}^{2} \\ B_{n}^{2} \\ \vdots \\ A_{n}^{m_n} \\ \end{bmatrix} = M^{-1} \begin{bmatrix} q \mu /(2\pi r_{w}u) \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ \vdots \\ 0 \\ 0\\ 0 \\ 0\\ \vdots \\ 0\\ \end{bmatrix} \end{aligned}$$

where the matrix M above is defined by the \((2m-1)n\) equations (35) to (38). Finally, it is possible to find a solution in the Laplace field for the pressure variation at the wellbore:

$$\begin{aligned} \varDelta {\overline{p}}_{wf} = A_{1}^{1}K_0(\sigma _{11}r_{w}) + B_{1}^{1}I_0(\sigma _{11}r_{w}) \end{aligned}$$
(39)

The Stehfest Algorithm (Stehfest 1970) is used to invert this solution into the real field.

Model validation

The results for the wellbore pressure profile for the proposed analytical model are presented in this section. The accuracy of the proposed solution was testified by comparing it with the commercial finite difference-based flow simulator IMEX (CMG 2010).

As an input for the numerical simulation, a radial grid was considered. The grid is more refined in the region closest to the wellbore, which is the region most affected by its presence. The oil model used in the simulator was blackoil. For all cases, formation crossflow is considered between the adjacent layers.

The following parameters were considered:

  • 4 days (96 hours) injection period.

  • Flow rate at the wellbore was defined as \(500\text { m}^3\text {/day}\).

  • Initial pressure was defined as \(300\text { kgf/cm}^2\).

  • The wellbore radius was considered to be \(r_{w} = 0.108\text { m}\) in all cases.

  • The vertical permeability was considered to be equal to the horizontal permeability for all cases.

  • Porosity was defined as \(\phi =0.2\) for all cases

  • The thickness of the shale between the layers (\(\varDelta h\)) is considered to be zero in all cases for both the analytical and the numerical models.

The other parameters can be found in Table 1 for all cases considered:

Table 1 Analyzed Cases
Full size table

In the graphs of all cases, there are the pressure changes and its derivative curves for the analytical and numerical solution. The pressure derivatives are calculated with respect to the logarithm of time. It is important to analyze the behavior of the pressure derivative as well, in order to properly interpret the results of the test.

Consider the curve composed of blue circles to be the analytical solution for pressure variation and the curve composed of red circles to be the analytical solution for pressure derivative. For the numerical solutions, the yellow stars curve represents the pressure variations and the purple stars the derivative curve.

First, consider case A with two layers and two regions, and the radii of the regions are equal. Pressure and pressure derivative curves for the analytical model solution and numerical solution are presented in Fig. 5:

Fig. 5
figure 5

Analytical and numerical pressure variation and derivative solutions for case A

Full size image

It is possible to see a close agreement between the analytical and numerical simulated curves.

Also, this graph represents clearly the two distinct flow regimes. One for early times and the second one for later times. They reflect the distinct regions of permeability impacting the pressure and derivative curves.

Region 1 has a permeability value of 1000 mD and the second region has a permeability value of half of that, 500 mD. This directly affects the pressure change and its derivative curves. Indeed, for the initial times, the pressure curve only notices the presence of the first region of permeability. After that, it reflects the second region, doubling the value of the derivative curve.

Ccase B considers two layers and two regions like in the previous case; however, for this case the radii of the regions are distinct. This problem can be treated as a three regions of equal radii case.

Case B graphs are given in Fig. 6:

Fig. 6
figure 6

Analytical and numerical pressure variation and derivative solutions for case B

Full size image

The region of permeability 500 mD for layer 1 has 10m, and in layer 2, it has 228m and the region of permeability 550 mD for layer 1 has 228m, and in layer 2, it has 10m. Hence, the created artificial region 2 has a permeability value of 550 mD for layer 1 and 500 mD for layer 2 and for that region the presence of formation crossflow will have a greater impact than in the other regions which have the same values of permeability for both layers.

Notice that the numerically simulated curves reflect a greater presence of the formation crossflow, since its curves are slightly below than in the analytical model’s. However, the behaviors of the curves are still very similar.

Finally, case C is considered, three layers and three regions with distinct radii are considered. Since the radii for all regions are different, the number of different semipermeability coefficients is five for this example.

Case C graphs are given in Fig. 7:

Fig. 7
figure 7

Analytical and numerical pressure variation and derivative solutions for case C

Full size image

The numerical and analytical curves are relatively close. The fact that the value of permeability at the final regions for all layers is lower than the value at the initial regions causes the derivative curves to increase with time.

In all three cases, it is possible to observe the proximity between the analytical solution and the numerical data, hence, the presented analytical model is able to describe the pressure behavior in multilayered radial composite reservoirs during the production periods.

Equivalent permeability

The pressure measured at the well is directly linked to the equivalent permeability (\(k_{\text {eq}}\)). In that sense, another way to evaluate the efficiency of the model presented in this work is by estimating the equivalent permeability.

For a multilayered reservoir, like presented in Cobb et al. (1972), it is given by:

$$\begin{aligned} k_{\text {eq}} = \frac{\sum \limits _{j=1}^{n}k_jh_j}{\sum \limits _{j=1}^{n}h_j} \end{aligned}$$
(40)

Since the model presented here reduces the cases of different regions radii into one with regions of equal radii, then the derivative profile enables the computation of equivalent permeabilities that combine the respective regions of the layers. That is, to obtain the first equivalent permeability, region 1 of layer 1 is combined with region 1 of layer 2 and so on.

Using the source line logarithmic approximation, the following equation is used to estimate the equivalent permeability (Cobb et al. 1972):

$$\begin{aligned} {\overline{k}}_{\text {eq}} = \frac{q \mu _o}{2h_Tm} \end{aligned}$$
(41)

where m is the constant derivative level and \(h_T\) is the total thickness.

In Table 2, the estimated and real equivalent permeabilities are presented for the cases considered in the previous section along with the percentage errors:

Table 2 Real and estimated equivalent permeability values and percentage error for cases A to C
Full size table

Most cases presented errors less than 1\(\%\). This indicates that the proposed formulation may be useful in obtaining reservoir parameters.

Impact of formation crossflow

In order to observe the impact of formation crossflow in the pressure response, a case considering formation crossflow will be compared to one with the same reservoir properties, however, without formation crossflow. For these cases, the vertical and horizontal permeabilities will be considered to be different. The values of the parameters can be found in Table 3:

Table 3 Impact of Crossflow: Analyzed Cases
Full size table

To better perceive the impact of formation crossflow, very distinct values of permeabilities from one layer to another are considered. Figure 8 shows the graph results for the pressure change and pressure derivative for cases \(D_1\) and \(D_2\).

Fig. 8
figure 8

Pressure variation and derivative solutions for cases \(D_1\) and \(D_2\)

Full size image

It is possible to see that after some time the curves become more apart from each other, that behavior is possibly explained by the impact of the formation crossflow. Notice that in the case of considering formation crossflow, it is not possible to identify the radial flow regime. In Fig. 9, the pressure derivative curves can be observed closer:

Fig. 9
figure 9

Pressure derivative solutions for cases \(D_1\) and \(D_2\)

Full size image

The difference between the curves for cases \(D_1\) and \(D_2\) are more noticeable in Fig. 9.

Finally, Table 4 presents the estimated and real equivalent permeabilities considering the first region of permeability, for cases \(D_1\) and \(D_2\), along with the percentage errors:

Table 4 Real and estimated equivalent permeability values and percentage error for cases \(D_1\) and \(D_2\)
Full size table

Case \(D_1\), which considers the presence of formation crossflow, has an estimated \(k_{eq}\) value closer to the real \(k_{eq}\) value.

Summary and conclusions

Based on the analytical solution proposed by Ehlig-Economides and Joseph (1987), this work proposed a formulation that combined the presence of formation crossflow with having different coupling regions of permeability along with each layer for multilayered reservoirs under single-phase flow.

The model here suggested can be applied to a variety of cases. Cases with equal and different radii of regions of permeability, cases including skin factor and wellbore storage and it even can be extended to model cases including multilayered reservoir systems under two-phase fluid flow. The model can include skin factor and wellbore storage straightforwardly because the solution is provided in Laplace space, and the model can be extended to a two-phase model by considering different properties concerning the fluids for each region. In addition, properties such as thickness and porosity can be considered as variables in the model and be different for each region. Furthermore, a model considering a continuous pressure to obtain the flow rate at the wellbore can be derived from the model here presented. In that sense, this work is quite robust and dynamic.

For a set of cases, a comparison was made between the analytical solution and numerical simulation, and it was possible to see the agreement between them. The pressure response, along with other features, such as equivalent permeability, show a good agreement in the comparison for all cases.