Introduction

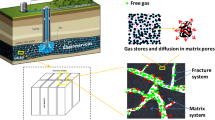
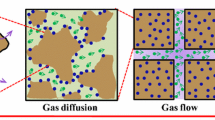
Coalbed methane, as a high-quality new energy, has the characteristics of high calorific value, no pollution, and good safety (Xue 2015). It has developed rapidly in China in the past ten years. Unlike the conventional natural gas reservoirs, coal seams are both source rock and reservoir rock which exhibits a conspicuous dual-porosity property (Li et al. 2020), especially for medium–high-rank coals. Methane is mainly stored on the surface of micropores (matrix system) in an adsorption state under initial reservoir conditions and desorbs and subsequently transfers through macropores (cleat system) once reservoir pressure drops below a certain level (desorption pressure) (Fan et al. 2018). Practically, the permeability of matrix system is negligible while the cleat system is the primary migration channel of coalbed methane (Dong et al. 2019). Stress-induced permeability changes in conventional rocks have been in-depth investigated previously (Wang et al. 2010, 2012). However, permeability dynamics exhibit unique different characteristics in coals due to gas adsorption/desorption phenomenon. In the process of coalbed methane exploitation, the permeability is mainly affected by effective stress and matrix shrinkage. Many studies and production experiences show that permeability is the key to coalbed methane production (Durucan et al. 1986; Tao et al. 2014). Permeability is sensitive to effective stress and matrix shrinkage during CBM exploitation. With the decrease of reservoir pressure, the importance of these two effects on the permeability of coal reservoir changes dynamically (Zhao et al. 2020). During the depletion of CBM reservoir, a reduction in permeability will occur due to the increasing effective stress imposed to the coal seam (Lin et al. 2020). However, this reduction will be opposed or even offset by the permeability enhancement resulting from the matrix shrinkage associated with methane desorption (Yan et al. 2020).

For in-situ CBM reservoir, it is generally considered to be in uniaxial strain state, and the lateral boundary in this state is fixed (zero lateral strain) (Chen et al. 2015; Liu et al. 2014). Because the overburden is constant when CBM is exhausted, the vertical stress remains constant. Uniaxial strain condition was first proposed by Geertsma in 1966 to describe the deformation of reservoir during depletion (Geertsma 1966). In his work, it was assumed that with continuous production, the reservoir deformation was mainly in the vertical direction because its lateral size was larger than the vertical one (Mitra et al. 2012; Liu et al. 2020). In 1998, Palmer and Mansoori extended this boundary to coalbed methane reservoirs to simulate the permeability changes during depletion (Palmer et al. 1998). A theoretical permeability change prediction model (P&M model) is proposed from the rock mechanics point of view, which considers both effective stress change and matrix shrinkage effect. Since then, based on the assumption of uniaxial strain, a series of permeability dynamics models have been proposed (Table 1). Among which Shi-Durucan (S&D) model and Cui-Bustin (C&B) model gained much attention and popularity (Feng et al. 2016; Shi et al. 2004; Cui et al. 2005). The common characteristics among P&M, S&D, and C&B models lie in that all are developed for uniaxial strain conditions. Liu et al. presented a model that explicitly considers fracture-matrix interaction during coal deformation processes based on a newly proposed internal swelling stress concept (Liu et al. 2010). In this concept, the effect on permeability of partial separation of matrix blocks by fractures that do not completely cut through the whole matrix is first examined. Liu’s model is also developed for uniaxial conditions.

Table 1 Classic coal permeability models
Full size table

Apart from the hypothesis of uniaxial stress condition, the assumption of constant volume of underground formation was also used for developing analytical permeability model. Massarotto et al. suggested that coalbed methane reservoirs are actually under a constant volume condition and stated that an essentially constant volume of the coal reservoir was maintained by the methan and tensile strength of the overburden across the reservoir and over time. A simplified model based on this philosophy was lately proposed that is complex in equation form but calls for less parameters (Manssarotto et al. 2009). However, the application of constant volume theory in permeability prediction till now is far behind of that of uniaxial strain conditions.

In general, the permeability evolution models can be classified into two categories: porosity-based and stress–strain-based permeability models (Ma et al. 2011). For the porosity-based models, the permeability was correlated with porosity through cubic laws (Palmer and Mansoori 1998; Palmer 2009; Wei et al. 2015), For the stress–strain-based model, the permeability evolution was related to the effective stress variation through the exponential function (Shi and Durucan 2004, 2005), On this basis, a dynamic model of permeability evolution in CBM well development is established considering the effective stress effect and matrix shrinkage effect (Cui and Bustin 2005; Zhang and Tong 2008; Zhang and Wang 2008; Zhou et al. 2009; Liu and Rutqvist 2010).

However, most of the rock mechanics parameters used in the existing models are measured from the core in the laboratory, which ignores the scale effect of the change of mechanical parameters from the core scale to the reservoir scale, which is easy to cause large errors. In this paper, a new method is introduced based on the surface physicochemical principle (linking the reduced strain of gas adsorption with the change of coal solid surface energy). This method does not need to take the reduced strain of adsorption as the necessary input, thus eliminating the associated laborious and expensive laboratory measurements. Proposed a new theoretical dynamic model for coal permeability during CBM production based on the assumptions of matchstick geometry of the coal and uniaxial strain condition (Meng et al. 2018). A mathematical model of strain permeability under the coupling action of effective stress and matrix shrinkage is established. The gas-sorption-induced strain is treated as directly analogous to the change of surface energy of coal solids. Model validation was conducted by fitting the public data, followed by sensitivity analysis. The model was then incorporated into a CBM reservoir simulator and succeeded in history matching gas and water rate for a CBM well in Ordos basin.

Mathematical Model

Permeability model

As in Fig. 1, the coal seams are assumed to be ideal bundled-matchstick geometry (Shi et al. 2004).

Fig.1
figure 1

A matchstick geometry for coal seams

Full size image

The matrix shrinkage associated with methane desorption in coal seams can be treated as directly analogous to the volumetric thermal contraction of thermoelastic porous medium (Palmer et al. 1998). According to the derivation of the stress–strain relationship for a homogenous, isotropic thermoelastic porous medium, the stress–strain relationship for isothermal coal seams can be written as

$$\begin{gathered} \varepsilon_{ij} = \frac{1}{2G}\left[ {\sigma_{ij} - \frac{\upsilon }{1 + \upsilon }\sigma_{c} \delta_{ij} } \right] - \frac{\alpha }{3K}p\delta_{ij} - \frac{1}{3}\varepsilon_{V} \delta_{ij} \hfill \\ \hfill \\ \end{gathered}$$
(1)

where

$$\alpha = 1 - \frac{K}{{K_{s} }}$$
(2)
$$\sigma_{c} = \sigma_{xx} + \sigma_{yy} + \sigma_{zz}$$
(3)
$$\varepsilon_{b} = \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz}$$
(4)

α is the Boit coefficient; σc is the confining pressure, MPa; εb is the bulk volumetric strain, MPa; G is the shear modulus, MPa; ν is the drained Poisson’s ratio, K is the macroscopic bulk modulus, MPa; Ks is the solid grain bulk modulus, MPa; p is the pore pressure, MP; εV is the macroscopic volumetric matrix shrinkage strain induced by coalbed methane desorption; δij is the Kronecker delta, is zero when i ≠ j and one when i = j; subscript i, j = x、y、z.

Note that the shear modulus G and the bulk modulus K are related to Young’s modulus E and Poisson’s ratio ν, respectively, through isotropic elasticity theory (Palmer et al. 1998).

$$G = \frac{E}{2(1 + \upsilon )}$$
(5)
$$K = \frac{E}{3(1 - 2\upsilon )}$$
(6)

Solving σc in Eq. (1)

$$\varepsilon_{xx} { = }\frac{1}{2G}\left[ {\sigma_{xx} - \frac{\upsilon }{1 + \upsilon }\sigma_{c} } \right] - \frac{\alpha }{3K}p - \frac{1}{3}\varepsilon_{V}$$
(7-1)
$$\varepsilon_{yy} { = }\frac{1}{2G}\left[ {\sigma_{yy} - \frac{\upsilon }{1 + \upsilon }\sigma_{c} } \right] - \frac{\alpha }{3K}p - \frac{1}{3}\varepsilon_{V}$$
(7-2)
$$\varepsilon_{zz} { = }\frac{1}{2G}\left[ {\sigma_{zz} - \frac{\upsilon }{1 + \upsilon }\sigma_{c} } \right] - \frac{\alpha }{3K}p - \frac{1}{3}\varepsilon_{V}$$
(7-3)

Adding both sides of Eqs. (7-1), (7-2), and (7-3), one obtains

$$\varepsilon_{xx} { + }\varepsilon_{yy} { + }\varepsilon_{zz} { = }\frac{1}{2G}\left[ {\sigma_{xx} + \sigma_{yy} + \sigma_{zz} - \frac{3\upsilon }{{1 + \upsilon }}\sigma_{c} } \right] - \frac{\alpha }{K}p - \varepsilon_{V}$$
(8)

Substituting Eqs. (3) and (4) into Eq. (8), one obtains

$$\varepsilon_{{\text{b}}} { = }\frac{1}{2G}\left[ {\sigma_{{\text{c}}} - \frac{3\upsilon }{{1 + \upsilon }}\sigma_{c} } \right] - \frac{\alpha }{K}p - \varepsilon_{V}$$
(9)

Substituting Eqs. (5) and (6) into Eq. (9), and σc is gotten as follows

$$\sigma_{{\text{c}}} = \left[ {\varepsilon_{{\text{b}}} + \frac{\alpha }{K}p + \varepsilon_{V} } \right]\left[ {\frac{{{1 + }\upsilon }}{1 - 2\upsilon }} \right]2G = \left[ {\varepsilon_{{\text{b}}} + \frac{\alpha }{K}p + \varepsilon_{V} } \right]\left[ {\frac{E}{1 - 2\upsilon }} \right]$$
$$\sigma_{c} = \frac{E}{1 - 2\upsilon }\left( {\varepsilon_{b} + \varepsilon_{V} } \right) + 3\alpha p$$
(10)

Substituting Eqs. (5), (6), and (10) into Eq. (1), one obtains

$$\begin{gathered} \varepsilon_{ij} = \frac{1}{2G}\sigma_{ij} - \frac{1}{2G}\frac{\upsilon }{1 + \upsilon }\left[ {\frac{E}{1 - 2\upsilon }\left( {\varepsilon_{b} + \varepsilon_{V} } \right) + 3\alpha p} \right]\delta_{ij} - \frac{\alpha }{3K}p\delta_{ij} - \frac{1}{3}\varepsilon_{V} \delta_{ij} \\ = \frac{1}{2G}\sigma_{ij} - \frac{1}{2G}\frac{\upsilon }{1 + \upsilon }\frac{E}{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} - \left( {\frac{1}{2G}\frac{3\upsilon }{{1 + \upsilon }} + \frac{1}{3K}} \right)\alpha p\delta_{ij} - \left( {\frac{1}{2G}\frac{\upsilon }{1 + \upsilon }\frac{E}{1 - 2\upsilon } + \frac{1}{3}} \right)\varepsilon_{V} \delta_{ij} \\ = \frac{1}{2G}\sigma_{ij} - \frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} - \left( {\frac{1 + \upsilon }{E}} \right)\alpha p\delta_{ij} - \frac{1 + \upsilon }{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \delta_{ij} \\ = \frac{1}{2G}\sigma_{ij} - \frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} - \frac{1}{2G}\alpha p\delta_{ij} - \frac{1 + \upsilon }{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \delta_{ij} \\ \end{gathered}$$

Then, one obtains

$$\begin{gathered} \sigma_{ij} = 2G\varepsilon_{ij} + 2G\frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} + \alpha p\delta_{ij} + \frac{{2G\left( {1 + \upsilon } \right)}}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \delta_{ij} \\ =2G\varepsilon_{ij} + 2G\frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} + \alpha p\delta_{ij} + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \delta_{ij} \\ { = }2G\varepsilon_{ij} + 2G\frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} \delta_{ij} + \alpha p\delta_{ij} + K\varepsilon_{V} \delta_{ij} \\ \end{gathered}$$
(11)

where the terms on the left-hand sides of Eq. (11) are known as the effective stresses.

Substituting Eqs. (5) and (6) into Eq. (9), and solving for εb yields

$$\varepsilon_{b} = \frac{1}{2G}\sigma_{c} \left[ {\frac{{{1 - 2}\upsilon }}{1 + \upsilon }} \right] - \frac{\alpha }{K}p - \varepsilon_{V} = \frac{1}{3K}\sigma_{c} - \frac{\alpha }{K}p - \varepsilon_{V}$$
$$\varepsilon_{b} = \frac{1}{K}\left( {\frac{1}{3}\sigma_{c} - \alpha p} \right) - \varepsilon_{V}$$
(12)

Considering the coal sample as a porous medium containing solid volume Vs and pore volume Vp, the bulk volume can be defined as Vb = Vp + Vs and the porosity is given byφ = Vp/Vb. According to Eq. (12), the volumetric evolution of coal-bearing porous medium can be described in terms of the bulk volume strain and the pore volume strain, respectively. The bulk volume strain increment and the pore volume strain increment can be expressed as (Zimmerman et al. 2000)

$$d\varepsilon_{b} = - \frac{{dV_{b} }}{{V_{b} }} = \frac{1}{K}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) - d\varepsilon_{V} = \frac{1}{K}\left( {\frac{1}{3}d\sigma_{c} - dp} \right) + \frac{1}{{K_{s} }}dp - d\varepsilon_{V}$$
(13)
$$d\varepsilon_{p} = - \frac{{dV_{p} }}{{V_{p} }} = \frac{1}{{K_{p} }}\left( {\frac{1}{3}d\sigma_{c} - \beta dp} \right) - d\varepsilon_{V} = \frac{1}{{K_{p} }}\left( {\frac{1}{3}d\sigma_{c} - dp} \right) + \frac{1}{{K_{\phi } }}dp - d\varepsilon_{V}$$
(14)

where

$$b = 1 - K_{p} /K_{\varphi }$$
(15)

β is a dimensionless effective stress coefficient. According to the bulk modulus characteristic of the porous frame defined by Brown and Korringa, the pore compressibility can be expressed as (Zimmerman et al. 2000; Berryman 1992)

$$c_{\phi } = \frac{1}{{K_{\phi } }} = - \frac{1}{{V_{p} }}\left( {\frac{{\partial V_{p} }}{\partial p}} \right)_{{\sigma_{c} }}$$
(16)

The pore bulk modulus Kp can be shown to be dependent of K, Ks, and the porosityφ for linear poroelasticity (Berryman 1992; Zimmerman et al. 1986). The relation is known in general that

$$\frac{\phi }{{K_{p} }} = \frac{1}{K} - \frac{1}{{K_{s} }}$$
(17)

According to Eq. (2), we can write Eq. (17) as

$$\frac{1}{{K_{p} }} = \frac{\alpha }{\phi K}$$
(18)

Using the definition of porosity, the porosity change of deforming coal seams can be described in terms of the bulk volume strain and the pore volume strain

$${\text{d}}\phi = {\text{d}}\left( {\frac{{V_{p} }}{{V_{b} }}} \right) = \phi \left( {\frac{{{\text{d}}V_{p} }}{{V_{p} }} - \frac{{{\text{d}}V_{b} }}{{V_{b} }}} \right)$$
(19)

Substituting Eqs. (2), (13), (14), and (18) into Eq. (19) yields

$$\frac{{{\text{d}}\phi }}{\phi } = \frac{{{\text{d}}V_{p} }}{{V_{p} }} - \frac{{{\text{d}}V_{b} }}{{V_{b} }} = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - dp} \right) + \left( {\frac{1}{{K_{s} }} - \frac{1}{{K_{\phi } }}} \right)dp$$
$$\begin{gathered} = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp + \alpha dp - dp} \right) + \frac{1}{{K_{s} }}dp - \frac{1}{{K_{\phi } }}dp \\ = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \frac{\phi - \alpha }{{\phi K}}\left( {\alpha - 1} \right)dp + \frac{1}{{K_{s} }}dp - \frac{1}{{K_{\phi } }}dp \\ = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp - \frac{K}{{K_{s} }}dp} \right) + \frac{1}{{K_{s} }}dp - \frac{1}{{K_{\phi } }}dp \\ = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \left( {1 - \frac{\phi - \alpha }{\phi }} \right)\frac{1}{{K_{s} }}dp - \frac{1}{{K_{\phi } }}dp \\ = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \frac{\alpha }{{\phi K_{s} }}dp - \frac{1}{{K_{\phi } }}dp \\ = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \left( {\frac{\alpha }{{\phi K_{s} }} - \frac{1}{{K_{\phi } }}} \right)dp \\ \end{gathered}$$
$$\frac{{{\text{d}}\phi }}{\phi } = \frac{\phi - \alpha }{{\phi K}}\left( {\frac{1}{3}{\text{d}}\sigma_{c} - \alpha dp} \right) + \left( {\frac{\alpha }{{\phi K_{s} }} - \frac{1}{{K_{\phi } }}} \right){\text{d}}p$$
(20)

Generalized Terzaghi’s effective stress law as follow (Nur and Byerlee 1971)

$$\frac{{\sigma_{xx}^{e} + \sigma_{yy}^{e} + \sigma_{zz}^{e} }}{3} = \frac{{\sigma_{xx} + \sigma_{yy} + \sigma_{zz} }}{3} - \alpha p$$
(21)
$$\sigma^{e} = \sigma_{xx}^{e} + \sigma_{yy}^{e} + \sigma_{zz}^{e}$$
(22)

where σe is the volumetric effective stress and σije is the effective stress tensor.

Using this definition, Eq. (20) can be written as

$$d\phi = \frac{\phi - \alpha }{K}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \left( {\frac{\alpha }{{K_{s} }} - \frac{\phi }{{K_{\phi } }}} \right)dp = \frac{\phi - \alpha }{K}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) + \frac{\alpha - \phi }{{K_{\phi } }}dp$$
$$\frac{d\phi }{{\phi - \alpha }} = \frac{1}{K}\left( {\frac{1}{3}d\sigma_{c} - \alpha dp} \right) - \frac{1}{{K_{\phi } }}dp = \frac{1}{3K}d\sigma^{e} - \frac{1}{{K_{\phi } }}dp$$
(23)

Assuming constant K and Kφ, integrating Eq. (23) yields

$$\phi = \alpha + \left( {\phi_{0} - \alpha } \right)\exp \left[ {\frac{1}{3K}\left( {\sigma^{e} - \sigma_{0}^{e} } \right) - \frac{1}{{K_{\phi } }}\left( {p - p_{0} } \right)} \right]$$
(24)

where \(\phi_{0}\) is the initial fracture porosity, \(\sigma_{0}^{e}\) is the initial effective stress, and p0 is the initial reservoir pressure.

Furthermore, Eq. (24) can be approximated using Taylor's expansion as:

$$\phi { = }\phi_{0} + \left( {\phi_{0} - \alpha } \right)\left[ {\frac{1}{3K}\left( {\sigma^{e} - \sigma_{0}^{e} } \right) - \frac{1}{{K_{\phi } }}\left( {p - p_{0} } \right)} \right]$$
(25)

On the assumption that reservoirs are under uniaxial strain conditions, that is, εxx = εyy = 0, the effective horizontal stress σxxe or σyye is gotten as follows:

According to Eqs. (3), (21), and (22) we can write Eq. (26) as

$$\frac{{\sigma_{xx}^{e} + \sigma_{yy}^{e} + \sigma_{zz}^{e} }}{3} = \frac{{\sigma_{xx} + \sigma_{yy} + \sigma_{zz} }}{3} - \alpha p$$
$$\begin{gathered} \sigma_{xx}^{e} = \sigma_{xx} - \alpha p \hfill \\ \sigma_{yy}^{e} = \sigma_{yy} - \alpha p \hfill \\ \sigma_{zz}^{e} = \sigma_{zz} - \alpha p \hfill \\ \end{gathered}$$
(26)

According to Eq. (5), Eq. (6), and Eq. (11) we can write Eq. (27) as

$$\sigma_{xx} - \alpha p{ = }2G\varepsilon_{xx} + \frac{E}{1 + \upsilon }\frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} { = }\frac{E}{1 + \upsilon }\frac{\upsilon }{1 - 2\upsilon }\varepsilon_{b} + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V}$$
(27)

Taking the difference between Eq. (7-3) and Eq. (7-1), one obtains

$$\varepsilon_{zz} - \varepsilon_{xx} { = }\varepsilon_{b} { = }\frac{1}{2G}\left[ {\sigma_{zz} - \sigma_{xx} } \right]$$
(28)

Substituting Eq. (26) and Eq. (28) into Eq. (27), and solving for \(\sigma_{xx}^{e}\) yields

$$\begin{gathered} \sigma_{xx} - \alpha p{ = }\sigma_{xx}^{e} = \frac{E}{1 + \upsilon }\frac{\upsilon }{1 - 2\upsilon }\left[ {\frac{1}{2G}\left( {\sigma_{zz} - \sigma_{xx} } \right)} \right] + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \\ = \frac{E}{1 + \upsilon }\frac{\upsilon }{1 - 2\upsilon }\left[ {\frac{1}{2G}\left( {\sigma_{zz}^{e} - \sigma_{xx}^{e} } \right)} \right] + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \\ = \frac{\upsilon }{1 - 2\upsilon }\left( {\sigma_{zz}^{e} - \sigma_{xx}^{e} } \right) + \frac{E}{{3\left( {1 - 2\upsilon } \right)}}\varepsilon_{V} \\ \end{gathered}$$

Transposing and reducing, one obtains

$$\sigma_{xx}^{e} { = }\sigma_{yy}^{e} { = }\frac{\upsilon }{1 - \upsilon }\sigma_{zz}^{e} + \frac{E}{{3\left( {1 - \upsilon } \right)}}\varepsilon_{V}$$
(29)

and the effective stress increment becomes

$$\begin{gathered} \sigma^{e} = \sigma_{xx}^{e} { + }\sigma_{yy}^{e} + \sigma_{zz}^{e} \hfill \\ = \frac{1 + \upsilon }{{1 - \upsilon }}\sigma_{zz}^{e} + \frac{2E}{{3\left( {1 - \upsilon } \right)}}\varepsilon_{V} \hfill \\ = \frac{1 + \upsilon }{{1 - \upsilon }}\left( {\sigma_{zz}^{{}} - \alpha p} \right) + \frac{2E}{{3\left( {1 - \upsilon } \right)}}\varepsilon_{V} \hfill \\ = \frac{1 + \upsilon }{{1 - \upsilon }}\sigma_{zz}^{{}} - \frac{1 + \upsilon }{{1 - \upsilon }}\alpha p + \frac{2E}{{3\left( {1 - \upsilon } \right)}}\varepsilon_{V} \hfill \\ \end{gathered}$$
$$\sigma^{e} - \sigma_{0}^{e} = - \frac{1 + \upsilon }{{1 - \upsilon }}\alpha \left( {p - p_{0} } \right) + \frac{2E}{{3\left( {1 - \upsilon } \right)}}\left( {\varepsilon_{V} - \varepsilon_{V0} } \right)$$
(30)

The substitution of Eq. (30) into Eq. (25) leads to

$$\phi { = }\phi_{0} + \left( {\alpha - \phi_{0} } \right)\left[ {\frac{1}{{K_{\phi } }}\left( {p - p_{0} } \right) + \alpha \frac{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{{E\left( {1 - \upsilon } \right)}}\left( {p - p_{0} } \right) - \frac{2}{3}\frac{1 - 2\upsilon }{{1 - \upsilon }}\left( {\varepsilon_{V} - \varepsilon_{V0} } \right)} \right]$$
(31)

In the limit of incompressible grains, that is,\(\alpha \to 1\), thus, a model similar to the P&M model is yielded:

$$\phi = \phi_{0} + \left( {1 - \phi_{0} } \right)\left[ {\frac{1}{{K_{\phi } }}\left( {p - p_{0} } \right) + \frac{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{{E\left( {1 - \upsilon } \right)}}\left( {p - p_{0} } \right) - \frac{2}{3}\frac{1 - 2\upsilon }{{1 - \upsilon }}\left( {\varepsilon_{V} - \varepsilon_{V0} } \right)} \right]$$
(32)

To derive the coal matrix shrinkage strain, we use the Bangham equation, which relates the change of strain of a porous body with a change of surface energy. This thought of equivalence was first mentioned and verified by Bangham and his associates (Bangham 1952). Their experimental results showed that upon the reduction of the free surface energy by the adsorption of gases and vapors, as calculated from the Gibbs adsorption isotherm, the solid increases in size by amounts of the order of 0.5% in one dimension. It has been shown in the case of charcoal and coal that, within the limits of accuracy of the experiments, the percentage linear expansion of the solid is directly proportional to a change in the free surface energy per unit area. The form of the equation is:

$$\varepsilon { = }\rho_{c} S\Delta \gamma /E$$
(33)

where ε is the strain change of coal solid; ρc is the density of coal, t/m3; S is specific surface area, m2/t; △γ is the change of surface energy of coal solid, J/m2, which is caused by the adsorption/desorption of gas to/from the surface of coal solid. According to Gibbs equation, △γ can be written as:

$$\Delta \gamma { = }\gamma_{0} - \gamma = \int_{0}^{p} {\Gamma RT{\text{d}}\ln p}$$
(34)

where γ0 and γ is the surface energy of coal solid under vacuum condition and after adsorbing gases, respectively, \(\Gamma = V/V0S\), the difference between surface concentration and bulk phase concentration; combining Eq. (33) with Eq. (34) results in:

$$\varepsilon_{V} = \frac{{\rho_{c} RT}}{{V_{0} E}}\int_{0}^{p} \frac{V}{p} {\text{d}}p$$
(35)

V in Eq. (35) can be gained from equation of Langmuir isotherm adsorption:

$$V = \frac{{bpV_{L} }}{bp + 1}$$
(36)
$$\varepsilon_{V} = \frac{{\rho_{c} RT}}{{V_{0} E}}\int_{0}^{p} {\frac{1}{p}\frac{{bpV_{L} }}{bp + 1}{\text{d}}p} = \frac{{\rho_{c} V_{L} RT}}{{V_{0} E}}\int_{0}^{p} {\frac{1}{bp + 1}{\text{d}}\left( {bp} \right)} = \frac{{\rho_{c} V_{L} RT}}{{V_{0} E}}\ln \left( {bp + 1} \right)$$
(37)

For the case of CBM production, during the process of depressurization when pressure falls from critical desorption pressure pr to p, the change of strain is obtained from Eq. (37):

$$\Delta \varepsilon = \varepsilon_{V} - \varepsilon_{V0} = \frac{{V_{L} \rho_{c} RT}}{{V_{0} E}}\left[ {\ln \left( {bp + 1} \right) - \ln \left( {bp_{r} + 1} \right)} \right] = \frac{{V_{L} \rho_{c} RT}}{{V_{0} E}}\ln \left( {\frac{bp + 1}{{bp_{r} + 1}}} \right)$$
(38)

where VL is Langmuir volume constant, m3/t; b is Langmuir pressure constant, MPa−1; T is absolute temperature, K; R is universal gas constant, 8.3143 J/(mol⋅K); V0 is gas molar volume under standard condition, 22.4L/mol; pr is critical desorption pressure, MPa.

The following relationship for the effective stress change is obtained:

$$\phi = \phi_{0} + \left( {1 - \phi_{0} } \right)\left[ {c_{\phi } \left( {p - p_{0} } \right) + \frac{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{{E\left( {1 - \upsilon } \right)}}\left( {p - p_{0} } \right) - \frac{2}{3}\frac{1 - 2\upsilon }{{1 - \upsilon }}\frac{{V_{L} \rho_{c} RT}}{{V_{0} E}}\ln \left( {\frac{bp + 1}{{bp_{r} + 1}}} \right)} \right]$$
(39)

Assume that the fracture permeability varies as the porosity as follows (Pan et al. 2012)

$$\frac{k}{{k_{0} }} = \left( {\frac{\phi }{{\phi_{0} }}} \right)^{3} = \left\{ {1 + \frac{{1 - \phi_{0} }}{{\phi_{0} }}\left[ {c_{\phi } \left( {p - p_{0} } \right) + \frac{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{{E\left( {1 - \upsilon } \right)}}\left( {p - p_{0} } \right) - \frac{2}{3}\frac{1 - 2\upsilon }{{1 - \upsilon }}\frac{{V_{L} \rho_{c} RT}}{{V_{0} E}}\ln \left( {\frac{bp + 1}{{bp_{r} + 1}}} \right)} \right]} \right\}^{3}$$
(40)

Our model bears a similarity with P&M (Eq.41) and S&D model (Eq.42) in the composition of equation, i.e., all models include two parts controlling permeability dynamics, the stress effect sector, and matrix shrinkage sector. However, the theoretical basis of our model is reliable, the form is simple and the parameters involved in the model are easy to obtain, and hence, eliminates the elaborate as well as expensive work of determination of lithologic parameters including constrained modulus M bulk modulus K and isotherm parameter sorption-induced strain εl (εg in S&D model); On the other hand, the commonly used prediction models such as P&M model is established based on the assumption that porosity is much less than 1, for coal reservoirs of the high porosity, the calculation of the model will appear bigger error, while our model to make up for the defects, also can be applied to coal reservoir of the high porosity, which has a much wider application scope.

P&M model:

$$\frac{k}{{k_{0} }} = \left[ {1 + \frac{{c_{m} }}{{\phi_{0} }}\left( {p - p_{0} } \right) + \frac{{\varepsilon_{L} }}{{\phi_{0} }}\left( {\frac{K}{M} - 1} \right)\left( {\frac{bp}{{1 + bp}} - \frac{{bp_{0} }}{{1 + bp_{0} }}} \right)} \right]^{3}$$
(41)

S&D model:

$$\left\{ {\begin{array}{*{20}c} {\sigma - \sigma_{0} = - \frac{\upsilon }{1 - \upsilon }\left( {p - p_{0} } \right) + \frac{{E\varepsilon_{g} }}{{3\left( {1 - \upsilon } \right)}}\left( {\frac{bp}{{1 + bp}} - \frac{{bp_{0} }}{{1 + bp_{0} }}} \right)} \\ {k = k_{0} e^{{ - 3c_{\phi } \left( {\sigma - \sigma_{0} } \right)}} \;\;\;\;\;\;\;\quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ \end{array} } \right.$$
(42)

CBM reservoir model

The following set of partial differential equations are given to formulate the water and gas flows (Zhang et al. 2009):

$$\nabla \cdot \left[ {\lambda \frac{{k_{rg} k_{f} }}{{\mu_{g} B_{g} }}\nabla \left( {p_{g} - \rho_{g} gH} \right)} \right] + q_{vmf} - q_{vg} = \frac{\partial }{\partial t}\left( {\frac{{\phi_{f} S_{g} }}{{B_{g} }}} \right)$$
(43)
$$\nabla \cdot \left[ {\lambda \frac{{k_{rw} k_{f} }}{{\mu_{w} B_{w} }}\nabla \left( {p_{w} - \rho_{w} gH} \right)} \right] - q_{vw} = \frac{\partial }{\partial t}\left( {\frac{{\phi_{f} S_{w} }}{{B_{w} }}} \right)$$
(44)
$$\frac{{\partial V_{m} }}{\partial t}{ = } - \frac{{1}}{\tau }\left[ {V_{m} - V_{E} \left( {p_{g} } \right)} \right]$$
(45)
$$q_{{vm{\text{f}}}} = - \rho_{c} \frac{{\partial V_{m} }}{\partial t}$$
(46)

where λ is the unit conversion factor; pl is the fracture pressure for the l-phase; kf is the fracture permeability; krl is the l-phase relative permeability; μl is the l-phase viscosity; Bl is the l-phase formation volume factor; ρl is the l-phase density; Sl is the l-phase saturation for the fracture system; t is time, ϕf is the fracture porosity; qvl is the l-phase volumetric flow rate per unit volume reservoir; l = g, w; H is the elevation; Vm is the average gas concentration; τ is adsorption time; qvmf is the desorbed gas flow rate through the coal matrix per unit volume reservoir; ρc is the coal density; and VE is the equilibrium methane concentration, which can be described by Langmuir isotherm as follows:\(V_{E}\)

$$V_{E} {(}p_{g} {) = }\frac{{V_{L} p_{g} }}{{p_{L} + p_{g} }}$$
(47)

VL, pL are the Langmuir volume and pressure constants, respectively.

In this paper, we use the closed outer boundary and constant pressure inter boundary conditions. The auxiliary equations are given as:

$$p_{c} = p_{g} - p_{w}$$
(48)
$$S_{w} + S_{g} = 1$$
(49)

where pc is the capillary pressure between gas and water phases.

In time, we use a fully implicit formulation solved at every time step with an Orthomin method preconditioned with incomplete LU decomposition (Zhang et al. 2009), in which pressure and saturation are both solved implicitly. At each iteration step, the porosity and permeability (along three dimensions of x, y, z) is updated with Eqs. (39) and (40), respectively.

Model validation

Validation with field data

MCGovern once presented a general pressure-dependent permeability multiplier curve for the San Juan basin coalbeds (Fig. 2), which turns out to be cut out for model validation in this paper. Figure 1 demonstrates a permeability ratio k/k0 up to a factor of 7 as reservoir pressure drops from 5.516 to 0.069 MPa after the reservoir is largely dewatered (MCGovern 2005). It’s noted that the data by McGovern was once used by Shi and Durucan for verifying their model and the value of reservoir parameters used in this study are primarily determined based on Shi’s work (Table 2).

Fig. 2
figure 2

Model validation with field data

Full size image
Table 2 Reservoir parameters used for model validation
Full size table

Though coal seams are practically under-saturated at initial conditions (the volume of adsorbed methane is less than that corresponding to initial pressure p0 on Langmuir curve), in this study, we found that an assumption of the critical pressure pr to be 8.0 MPa yields a good agreement with the field data. This assumption is to, some extent feasible due to large degree of depressurization. As a matter of fact, validation of Shi’s model was achieved by varying initial reservoir pressure from 8.27 to 11.38 MPa.

To derive the Langmuir volume, we directly borrowed the αs(CH4) = 0.00038 that was used for history matching the flue-gas- injection micropilot in Shi. This leads to a VL of 34 m3/t. It is worth pointing out that laboratory researches on coal sorption properties have demonstrated a phenomenon referred to as adsorption/desorption hysteresis, i.e., (Bush et al. 2003), the desorption curve does not follow exactly the adsorption curve under decreasing and increasing pressure, respectively. This hysteresis results in a decrease in Langmuir pressure in depressurization process compared with that in pressurization process. Since the primary recovery of CBM from underground reservoir is a depressurization process, it is recommended that desorption curve be applied when simulating permeability performance during primary recovery. Therefore, the value of PL used by Shi (4.31 MPa) was induced to 3 MPa to better simulate the permeability performance (Shi et al. 2004).

Comparison with previous models

Palmer and Mansoori reported a good history matching of the bottom-hole pressure and gas production rate for a CBM well in San Juan basin with a permeability curve with strong rebound at lower pressure drawdown, which conforms to curve 3 in Fig. 3. Later, Shi and Durucan gave the permeability responses with S&D and P&M models based on the history matched data. In their research, the initial porosity and pressure were set to 0.00085 and 10.4 MPa, respectively, and the simulation results are plotted in Fig. 3. We can see that the S&D model generates a much stronger rebound at lower drawdown pressure than the P&M model, but both failed to yield a good match.

Fig. 3
figure 3

Comparison with P&M model and S&D model

Full size image

Mavor and Vaughn reported in-situ permeability changes from drill-stem and shut-in tests in three wells in San Juan Fruitland formation coal seams (Mavor et al. 1998). As is noted previously, isotherm parameters exhibit some kind of difference due to adsorption/desorption hysteresis, and hence, we modified Mavor’s VL to 31m3/t and PL to 2.8 MPa. Assume a normal pressure and temperature gradient, an in-situ pressure of 10.4 MPa corresponds to a temperature of about 330 K. The simulation result was demonstrated in Fig. 3. It is indicated that the newly developed model yields a much better match compared with the above two models.

Sensitivity analysis and discusses

The influence of different factors on the permeability ratio k/k0 was evaluated by the gray relation theory (Liu et al. 2004), and the closeness of correlation between different sequences is determined by the level of similarity of their corresponding geometric configurations. In this research, the sequence of influence factor i (i = 1, 2,…, 9) and that of k1/k0 (k1 corresponds to a reservoir pressure of p1 = 0.5 MPa) are set as the behavior sequence Xi and the feature sequence X0, respectively. The integrated incidence degree is adopted as a quantitative index to represent the closeness of each behavior and feature sequence. The influence factor with a greater integrated incidence degree exerts a more profound effect on permeability when reservoir pressure drops from p0 to p1. The base value and range of each factor are listed in Table 3.

Table 3 Integrated incidence degree between k1/k0 and influence factors
Full size table

Figure 4 shows the value variation of integrated incidence degree between k1/k0 and influence factors. We can see that the initial porosity, coal density, and temperature have relatively high integrated incidence degrees (0.638 at the lowest), which indicates that these three parameters exhibit a dominant influence on the permeability model.

Fig. 4
figure 4

Integrated incidence degree of each influence factor

Full size image

To examine the performance of permeability dynamics, we tried different combinations of parameters and found four sets (Table 4) are quite typical in generating four distinctive dynamic curves (Fig. 5). Coal seams were assumed to be saturated by pure methane, and hence, desorption pressure was equal to initial reservoir pressure of 6.1 MPa. Both adsorption and desorption processes are simulated. In the region p < 6.1 MPa, curve 1 displays a proximately exponential increase with decreasing pressure, and results in an increase of more than fourfold, while curve 2 displays a progressive decline. In case 3, permeability exhibits descending trend at initial pressure drawdown period and then rebounds strongly at lower pressure drawdown (about 1 MPa) and up to a factor of 2.16 at 0.15 MPa, more than doubling the initial permeability. Curve 4 shows a relatively “flat” trend in both adsorption and desorption processes, indicating little variation of permeability.

Table 4 Combination of parameters in illustrating permeability dynamics
Full size table
Fig. 5
figure 5

Permeability dynamics versus pore pressure

Full size image

The occurrence of varied shapes of dynamic curves is probably attributed to the mutual interference of stress effect and matrix shrinkage. In the primary recovery of CBM reservoir, pore pressures decline gradually, resulting in an increase in effective stress and methane desorption. The former effect tends to shrink the pore volume while the latter can enhance that. If those two effects are evenly matched, permeability will exhibit negligible changes (Curve 4). Once the stress effect is much stronger than matrix shrinkage, permeability will decline without rebound. By contrast, permeability will increase enormously without decline stage if matrix shrinkage exerts a predominant control.

Field application

Hancheng area in the southeast margin of Ordos basin is one of regions possessing coalbed methane exploration and development potential. The 3# coal seam in the Permian Shanxi Formation and the 5#, 11# coal seams in the Carboniferous Taiyuan Formation are the main target formations for coalbed methane recovery.

History matching of gas and water production rate for a CBM well WL1 in Hancheng area was conducted by a coalbed methane simulator incorporated with the proposed permeability model. The 3#, 5# coal seams are penetrated and drained by well WL1. Reservoir parameters are listed in Table 5.

Table 5 Parameters used in the simulation
Full size table

The simulated gas and water production curves, as shown in Fig. 6, are consistent with the field observations, indicating a fairly fine performance of the proposed model.

Fig. 6
figure 6

History matching results for CBM well WL1 in Ordos basin

Full size image

The dynamic change curves of coal permeability were illustrated in Fig. 7 during the coalbed methane development, which demonstrates an overall higher permeability in the near-wellbore region than in the far-field region. At the early stage of dewatering, permeability experiences a 10% decrease in near-wellbore region, which affects the drainage of water adversely. After about 150 days of drainage, permeability in this region begins to rebound. It is also the case with far-wellbore region except for the beginning time and amplitude of the rebound.

Fig. 7
figure 7

Permeability dynamics in near-wellbore and far-field regions

Full size image

It is also interesting to point out that fluctuation of gas production rate has a close relation to near-wellbore permeability dynamic changes. Comparing Fig. 6(b) with Fig. 7, a fairly fine correspondence between those two curves can be found, i.e., the ascension/decline sections on gas rate curve have a corresponding congruent trend on permeability curve in near-wellbore region. After a drainage period of 150 days, permeability in near-wellbore region begins to rebound. We can also see that after about 5.5 years of drainage, permeability rebounds and then exceeds initial value (k/k0 > 1) and average gas production rate climbs from less than 2000m3/d to 2300m3/d.

Conclusion

A new dynamic model of coal permeability was developed by the physical chemistry theory that relates desorption to changes of surface energy and the equivalence assumption between sorption-induced and surface-induced strains. The advantages of the new model over the previous include demand for less input parameter and allowing for application under variable temperatures. Model validation with published data indicates a fine performance of the new model. Following incorporating the model to a CBM numerical simulator, we succeeded in history match gas and water production rate for a CBM well in Ordos basin. Simulation results showed a close relation between the gas production rate changes and permeability dynamics.