Introduction

About 60% of the world’s oil reserves are located in fractured carbonate reservoirs (Akbar et al. 2000). One of the major topographical features of the carbonate reservoirs is karsts which are characterized by the presence of vugs, factures and caves formed by the mechanical and chemical erosion of the rock surface by the surface water (Jackson 1997). These highly permeable free-flow karst features provide great economic benefits to oil operators as they not only provide storage volume for the hydrocarbons but also allow for their free movement. They also directly affect the efficiency of the EOR processes as these karst conduits influence the movement of the injected fluid inside the reservoir (Trice 2005). Many paleokarstic oil and gas reservoirs and water aquifers can be found around the world. Some of the major examples are Hainaut carbonate and sulphate karstic aquifer (Licour 2014), Raspo Mare reservoir (Bellentani et al. 2016; Gauchet and Corre 1996), gas reservoirs of Sinian (Zou 2013), Yarqon-Taninim aquifer (Dafny et al. 2010), Buda thermal karst system (Albert et al. 2015), a giant Middle Eastern oil field located offshore in the Arabian Gulf (Dabbouk et al. 2002), Tahe oil reservoir in Tarim Basin in China (Li et al. 2016; Peng et al. 2009), Kharyaga field in Russia (Khvatova et al. 2012), and a karstic reservoir in the Brazilian pre-salt field (Correia et al. 2019).

Numerical modelling of flow in karst reservoirs is challenging due to the presence of non-Darcian free-flow elements such as vugs, fractures and caves which makes the Darcy model inapplicable. The complexities in modelling flow in karsts are exacerbated by the fact that the location of the interfaces between the porous medium and the free-flow medium is not known. The simplest approach developed to model the coupled flow in porous and free-flow media is the Multiple Interacting Continua (MINC) approach introduced in 1985 (Pruess and Narasimhan 1985). It is based on the dual porosity method (Odeh 1964; Warren and Root 1962). In this method, the fractures and the matrix blocks are grouped into two separate but interacting continua. This method has been widely used (Bai et al. 1993; Kossack and Gurpinar 2001; Wu and Pruess 1988; Wu et al. 2006), to model flow through fractured and vuggy aquifers and reservoirs. Effective Continuum Model (ECM) (Wu 1999; Wu and Finsterle 1996) is a modification to MINC and does not require detailed fracture and matrix geometric properties and their spatial distribution. The MINC method, although computationally more effective, may not be accurate as it simplifies the flow patterns in fractured rocks. The discontinuum model or the Darcy-Stokes model attempts to model flow in karst reservoirs by employing the Navier–Stokes equation in the free-flow region and the Darcy equation in the porous region. The BJS boundary condition is then used to model the interface between the porous region and the free flowing region (Beavers et al. 1970; Beavers and Joseph 1967). Several research papers have used the Darcy-Stokes model to simulate flow in karst reservoirs (Arbogast and Brunson 2007; Arbogast and Gomez 2009; Arbogast and Lehr 2006). Peng et al. (2009) developed a streamline numerical model for Darcy-Stokes to model two-phase flow in Tahe fractured reservoir. They however pointed out that they found it very difficult to obtain convergence when solving the same problem using a finite difference scheme rather than streamline simulation. An embedded discrete karst model (EDKM) was developed to model flow in carbonate reservoir with megakarstic structure. The EDKM models uses a single porosity model with two grid domains representing the karst and matrix properties. Special connections are then applied to represent transmissibility between the matrix and the karst medium (Correia et al. 2020). The EDKM model is an extension of the EDFM model (Moinfar et al. 2014).

A single continuum approach using the Brinkman equation (Brinkman 1949) is used to model the effect of flow in free-flow regions and in the porous regions. It is a hybrid formulation which can mimic the effect of the Stokes’ equation in the caves and the Darcy equation in the porous media. The Brinkman model has been widely used to model single-phase flow in fractured reservoirs and aquifers (Bi et al. 2009; He et al. 2015; Jamal et al. 2019; Krotkiewski et al. 2011; Ligaarden et al. 2010; Mohamed et al. 2015; Popov et al. 2009, 2007). Brinkman model is however computationally very expensive as it simultaneously solves three transport equations and one mass conservation equation to model flow in the reservoir. One approach to minimize the simulation time is to use the Darcy model which incorporates the transport equation inside the mass conservation equation and therefore requires the solution of only one parabolic partial differential equation to model flow in the aquifer. The value of the permeability for the free-flow region is obtained by the equation \(k = \frac{{r^{2} }}{12}\), where r is the size of the cave opening. This however does not provide reliable estimates of velocity in the caves (Field 1997). The actual velocity profile in free flowing regions as modelled by the Stokes equation should have a parabolic shape; however, the Darcy model generates a flat piston-like profile, which is not accurate. Consequently, some approaches were developed to provide fairly accurate solutions while taking advantages of the computational inexpensiveness of the Darcy model. These include the sector modelling approach (Jamal and Awotunde 2018), the Darcy model with estimated permeability (DMEPD) approach (Youssef and Awotunde 2019), and the Darcy model with optimized permeability distribution (DMOPD) approach (Jamal and Awotunde 2020). The DMOPD approach works on the principle that the Darcy model can be made to mimic the velocity profile obtained using the Brinkman model by dividing the free-flow region into zones and then assigning different values of permeability to each zone. The distribution is such that the central zone has the maximum value of permeability and this gradually decreases as one moves towards the walls of the caves. The DMOPD model initially solves the Brinkman model on the whole reservoir for the first timestep, and this is followed by estimating the permeability distribution in the cave which gives the best match of the velocity profile obtained using the Darcy model to the one obtained using the Brinkman model. Any global optimization algorithm can be used for estimating the permeability distribution. Finally, the Darcy model is solved for the remaining timesteps using the values of permeability obtained after estimation.

Modelling single-phase flow using the Brinkman model or the Darcy-Stokes method is computationally very expensive. This expense further increases while attempting to model two-phase flow as the number of unknowns increases. An another challenge that arises when modelling two-phase flows through open channels using the Stokes/Brinkman equation is to manage the interface between two phases as there is a sharp change between the density and viscosity of fluid on either side of the interface. Two main methods that are used to model the moving interface are the volume of fluid (VOF) method and the level-set method (Bilger et al. 2017; Dai et al. 2017; Olsson and Kreiss 2005). An additional auxiliary equation is required to track the interface. This further increases the complexity of the problem.

In this paper, we introduce the TP-DMOPD model (Two-Phase Darcy’s Model with Optimized Permeability Distribution), in an attempt to simply the simulation of two-phase flows in karst reservoirs consisting of megakarstic features such as caves. Under this method, the permeability in the caves is estimated while assuming that a single-phase fluid is flowing in the reservoir. Once the permeability distribution is obtained, a two-phase Darcy model is solved to obtain the pressure and saturation distributions in the reservoir. Two examples have been presented to show the application of the TP-DMOPD model. The accuracy of the results is then compared with Darcy model. Results indicated that the Darcy model predicted a later breakthrough of water at the producers when compared to the TP-DMOPD model.

Mathematical models for fluid flow in the reservoir

Single-phase Brinkman model

Single-phase flow in karst reservoirs is solved by the combination of a mass conservation equation and the Brinkman equation. The mass conservation equation is given by

$$\frac{\partial (\phi \rho )}{{\partial t}} + \nabla \cdot (\rho \vec{u}) = \frac{\rho q}{{V_{b} }}$$
(1)

where \(\rho\) is the density of the fluid \(\left( {ML^{ - 3} } \right)\), \(\phi\) is the porosity (fraction), \(\vec{u}\) is the velocity vector \(\left( {LT^{ - 1} } \right)\),\(q\) is the volumetric flow rate \(\left( {L^{3} T^{ - 1} } \right)\), \(V_{b}\) is the volume of each grid \(\left( {L^{3} } \right)\), and \(t\) is the time.

The Brinkman equation (Brinkman 1949) is given as

$$\nabla p + \mu \overline{\overline{K}}^{ - 1} \vec{u} - \mu_{{{\text{eff}}}} \nabla^{2} \vec{u} = 0$$
(2)

where \(p\) is the pressure \(\left( {ML^{ - 1} T^{ - 2} } \right)\), \(\mu\) is the fluid viscosity \(\left( {ML^{ - 1} T^{ - 1} } \right)\), \(\overline{\overline{K}}\) is the permeability tensor \(\left( {L^{2} } \right)\), \(\vec{u}\) is the velocity vector \(\left( {LT^{ - 1} } \right)\), and \(\mu_{{{\text{eff}}}}\) is the effective fluid viscosity. The values of \(\overline{\overline{K}}\) and \(\mu_{{{\text{eff}}}}\) are assigned depending on whether the location being modelled is in the cave or inside the porous media. When \(\mu_{{{\text{eff}}}} = \mu\) and \(\overline{\overline{K}} \to \infty\), the second term in Eq. 2 drops out and it takes the form of the Stokes equation which can be used to model flow in caves. Similarly, when \(\mu_{{{\text{eff}}}} = 0\) and \(\overline{\overline{K}} = \overline{\overline{K}}\) (\(\ne \infty\)), the third term (viscous shear) drops out and Eq. 2 then takes the form of Darcy equation. This can then be used to model flow in the porous medium. Equations 1 and 2 yield a system of four equations that when solved together yields the values of pressure, and the three component velocities (\(u_{x}\), \(u_{y}\) and \(u_{z}\)) in the reservoir.

Single-phase Darcy model

Henri Darcy developed an equation (Darcy 1856) that together with mass conservation equation (Eq. 1) can be used to solve flow in reservoirs. The Darcy equation is given as

$$\nabla p + \mu \overline{\overline{K}}^{ - 1} \vec{u} = 0$$
(3)

In Eq. 3, the value of permeability in the caves is obtained from the equation

$$k = \frac{{r^{2} }}{12}$$
(4)

where r is the size of the cave opening. Equation 4 is obtained when the equation for flow between two parallel plates (Poiseuille’s equation) is compared to the single-phase Darcy equation. Equations 1 and 3 together yields four separate equations which when solved can simulate flow in reservoirs. However, the advantage of using the Darcy model is that the method of solution can be simplified by substituting the Darcy equation (Eq. 3) into the mass conservation equation (Eq. 1). This yields a single parabolic equation given by (Chen 2007; Ertekin et al. 2001)

$$\frac{\partial (\phi \rho )}{{\partial t}} - \nabla \cdot \left( {\frac{{\rho \overline{\overline{K}} }}{\mu }\nabla p} \right) = \frac{\rho q}{{V_{b} }}$$
(5)

Equation 5 can be used to obtain the pressures at every location in the reservoir. Once the pressure values are calculated, Eq. 3 can be solved explicitly to obtain the velocities.

Two-phase Darcy model

The Darcy model can simulate two-phase flow in a reservoir. Equation 5 is modified for each phase and can be written as

$$\frac{{\partial (\phi \rho_{o} S_{o} )}}{\partial t} - \nabla \cdot \left( {\frac{{\rho_{o} k_{ro} \overline{\overline{K}} }}{{\mu_{o} }}\nabla p_{o} } \right) = \frac{{\rho_{o} q_{o} }}{{V_{b} }}$$
(6)
$$\frac{{\partial (\phi \rho_{w} S_{w} )}}{\partial t} - \nabla \cdot \left( {\frac{{\rho_{w} k_{rw} \overline{\overline{K}} }}{{\mu_{w} }}\nabla p_{w} } \right) = \frac{{\rho_{w} q_{w} }}{{V_{b} }}$$
(7)

where the subscripts o and w refer to oil and water phase, respectively, \(k_{ro}\) and \(k_{rw}\) are the relative permeabilities of oil and water, respectively. The two-phase equations (Eqs. 6 and 7) can also be represented in terms of formation volume factors as follows (Ertekin et al. 2001):

$$\frac{{\partial (\phi b_{o} S_{o} )}}{\partial t} - \nabla \cdot \left( {\frac{{b_{o} k_{ro} \overline{\overline{K}} }}{{\mu_{o} }}\nabla p_{o} } \right) = \frac{{b_{o} q_{o} }}{{V_{b} }}$$
(8)
$$\frac{{\partial (\phi b_{w} S_{w} )}}{\partial t} - \nabla \cdot \left( {\frac{{b_{w} k_{rw} \overline{\overline{K}} }}{{\mu_{w} }}\nabla p_{w} } \right) = \frac{{b_{w} q_{w} }}{{V_{b} }}$$
(9)

where \(b_{0} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {B_{o} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${B_{o} }$}}\) and \(b_{w} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {B_{w} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${B_{w} }$}}\), \(B_{o}\) is the formation volume factor of oil and \(B_{w}\) is the formation volume factor for water. Two auxiliary equations are required to further close the equation. They are

$$S_{o} + S_{w} = 1$$
(10)
$$p_{c} = p_{o} - p_{w}$$
(11)

where \(p_{c}\) is the capillary pressure and is given as the difference between the pressures of the non-wetting phase and the wetting phase. Once the pressure and saturation in the reservoir are determined, the velocities of the oil and water phases can be calculated explicitly by using the following equations

$$\nabla p_{o} + \mu_{o} k_{ro}^{ - 1} \overline{\overline{K}}^{ - 1} \vec{u}_{o} = 0$$
(12)
$$\nabla p_{w} + \mu_{w} k_{rw}^{ - 1} \overline{\overline{K}}^{ - 1} \vec{u}_{w} = 0$$
(13)

Well modelling

In Eqs. 6–9, \(q_{o}\) and \(q_{w}\) are the oil and water rates at reservoir conditions. The oil and the water rates can be calculated from bottom hole pressure using the following relations (Chen 2007)

$$q_{o} = WI\lambda_{o} \left( {p_{o} - p_{BHP} } \right)$$
(14)
$$q_{w} = WI\lambda_{w} \left( {p_{w} - p_{BHP} } \right)$$
(15)

where

$$WI = \frac{2\pi kh}{{\ln \left( {\frac{{r_{eq} }}{{r_{W} }}} \right)}}$$
(16)

and the mobility terms \(\lambda_{o}\) and \(\lambda_{o}\) are given as,

$$\lambda_{o} = \frac{{k_{ro} }}{{\mu_{o} }}$$
(17)
$$\lambda_{w} = \frac{{k_{rw} }}{{\mu_{w} }}$$
(18)

In Eq. 16, \(r_{w}\) is the wellbore radius and \(r_{{{\text{eq}}}}\) is the equivalent radius and can be calculated from the Peaceman’s formula as

$$r_{eq} = 0.14\sqrt {\Delta x^{2} + \Delta y^{2} }$$
(19)

where \(\Delta x\) and \(\Delta y\) are the grid block length and width, respectively.

The total fluid rate \(\left( {q_{L} } \right)\) being produced by any producer is given as

$$q_{L} = q_{o} + q_{w}$$
(20)

The two-phase Darcy model with optimized permeability distribution (TP-DMOPD) approach

The TP-DMOPD approach is developed to model two-phase flow in karst reservoirs consisting of megakarstic features such as caves. Under this approach, the caves are partitioned into an odd number of regions or zones \(\left( {n_{c} } \right)\). This ensures that there is \(\frac{{n_{c} - 1}}{2}\) zones around the central zone. The total number of zones depends on the maximum number of grids present along the width of the cave. The central zone is assigned a maximum value of permeability, as this is indicative of the peak of a parabolic velocity profile. The permeability ratios in each zones are then obtained by using an optimization algorithm to obtain a match between the velocity in the caves obtained for a single-phase flow using Brinkman model and the velocity computed by the Darcy model. The permeability in each zone when divided by the maximum permeability calculated from Eq. 4 (permeability of the central zone) yields the permeability ratio. The objective function to be minimized is given by,

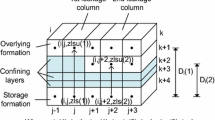
$$\Psi \left( {\vec{\alpha }} \right) = \frac{1}{\kappa }\left\| {\vec{u}_{BE} - \vec{u}_{D} } \right\|_{2}$$
(21)

where \(\vec{u}_{BE}\) is the vector of velocities for all the grids inside the caves generated by solving the single-phase Brinkman model, \(\vec{u}_{D}\) is the vector of velocities for all the grids inside the caves generated by solving the single-phase Darcy model, \(\kappa\) is the length of the velocity vectors, and \(\vec{\alpha }\) consists of permeability ratios that need to be estimated by the optimization algorithm. The minimum and maximum values of the search space for the permeability ratios are kept between 0.01 and 1. The minimum value assures that the permeability values do not become zero and the maximum value assures that the permeability of surrounding zones does not become greater than the permeability of the central zone. Figure 1 displays an example of partitioning of caves in a reservoir. The caves have been divided into 9 zones. A central zone along with four zones on either side of it.

Fig. 1
figure 1

Zonation of the caves in the TP-DMOPD approach: a full reservoir model, b the caves have been portioned into 5 zones, c a zoomed in section of cave in b focusing on the cave partitions

Full size image

The steps required to model two-phase flow in karsts using the TP-DMOPD model are listed as follows:

  1. 1.

    Initially, the single-phase Brinkman model (Eqs. 1 and 2) is solved for the whole reservoir for a single timestep to obtain the pressure and velocity distribution in the reservoir.

  2. 2.

    The caves are then partitioned into an odd number of zones and the central zone is assigned a maximum permeability value obtained from Eq. 4.

  3. 3.

    The permeability ratios are then computed using an optimization algorithm such that the velocity obtained inside the caves by solving the single-phase Darcy model (Eq. 5) gives a very good match to the velocities obtained from step 1.

  4. 4.

    The permeabilities of each zone are then computed by multiplying the permeability ratio obtained with the permeability of the central zone.

  5. 5.

    The two-phase Darcy model (Eqs. 8–11) is then used to solve the pressure distribution in the reservoir.

  6. 6.

    The velocities for both the phases can then be obtained by solving Eqs. 12 and 13

Example applications

Example 1

The first example used to show the effectiveness of the TP-DMOPD model consists of a 2D reservoir consisting of a single cave (shown in red) surrounded by porous media (shown in blue) (Fig. 2). All the boundaries of the reservoir are considered as no-flux boundaries. This means that no fluid can enter or leave the reservoir system at any time. The reservoir dimensions are \(1220\,{\text{m}} \times 41\,{\text{m}} \times 1.5\,{\text{m}}\left( { \approx 4003\,{\text{ft}} \times 134.5\,{\text{ft}} \times 5\,{\text{ft}}} \right)\) and it has been discretized into \({40} \times 41 \times 1\) grids. The reservoir is initially at a pressure of 4000 psi. The initial water saturation is 35%. The porous media is assumed to be homogenous having a permeability of 40 md and a porosity of 25%. Water is injected into the reservoir by a single injection well located in grid block (1, 10). The injection well is operated at a BHP of 5000 psi. The reservoir fluid is produced by a production well operating at a BHP of 2000 psi. The producer is located in grid block (20, 32).

Fig. 2
figure 2

Reservoir used for Example 1

Full size image

Zonation of the cave and estimation of permeability ratios (Example 1)

The cave demarcated by the red region (Fig. 2) is split into 21 separate zones (Fig. 3). One central zone with a maximum permeability value obtained using Eq. 4, and 10 zones located on either side of the central zone. To estimate the permeability ratios in the reservoir, the fluid is assumed to be in a single-phase (water only). The viscosity of water is assumed to be 1cp and the density is assumed to be 62.4 lb/ft3. The permeability ratios were estimated by the differential evolution algorithm. The termination criteria for the optimization run were defined as 1500 function evaluations. Figure 4 shows that the objective function was sufficiently minimized, which indicates that the velocities obtained using the Brinkman model match those obtained using the Darcy model (Fig. 4). Figure 5 displays the estimated permeability ratios along with the permeability values obtained for each zone. Figure 6 compares the velocity profiles inside the cave for a single-phase fluid obtained using the three modelling techniques. It can be observed that the TP-DMOPD model gives an excellent match to the Brinkman model indicating that the optimization strategy was able to provide good estimates for the permeability ratios. The Darcy model however produces a more flattened shape compared to the Brinkman model and the DMOPD model. For a single-phase flow, the time taken to run the Brinkman’s model for each timestep is 0.895 s whereas the time taken to run the Darcy model and the DMOPD model after the history matching process is about 0.092 s per timestep. This means that the DMOPD model is about 9.7 times faster than the Brinkman’s model for this particular example. The time taken to run the Darcy model and the DMOPD model is similar because DMOPD is essentially running the Darcy model but with improved permeability distribution.

Fig. 3
figure 3

Zonation of the cave

Full size image
Fig. 4
figure 4

Values obtained when minimizing the objective function for example 1

Full size image
Fig. 5
figure 5

Figure displaying the estimated permeability ratios for each zone along with the permeability values obtained for Example 1

Full size image
Fig. 6
figure 6

Single-phase fluid velocities within the cave obtained using the three different techniques

Full size image

Modelling of two-phase flow (example 1)

The permeability values obtained from the estimation stage of the TP-DMOPD model are then used to model two-phase flow in the karst reservoir (Eqs. 8–11). The correlations that have been used to calculate the fluid properties are listed in Eqs. 22–28

$$b_{o} = e^{{5 \times 10^{ - 6} \left( {p_{o} - 14.7} \right)}}$$
(22)
$$b_{w} = e^{{5 \times 10^{ - 7} \left( {p_{w} - 14.7} \right)}}$$
(23)
$$\mu_{o} = 5e^{{2 \times 10^{ - 6} \left( {p_{o} - 14.7} \right)}}$$
(24)
$$\mu_{w} = e^{{6 \times 10^{ - 8} \left( {p_{w} - 14.7} \right)}}$$
(25)
$$k_{ro} = 0.93\left( {1 - S_{n} } \right)^{2.5}$$
(26)
$$k_{rw} = 0.5S_{n}^{3.5}$$
(27)

where

$$S_{n} = \frac{{S_{w} - S_{wc} }}{{1 - S_{wc} - S_{or} }}$$
(28)

where \(S_{wc}\) is the connate water saturation and it is assumed to be 20%, \(S_{{{\text{or}}}}\) is the residual oil saturation and is assumed to be equal to 10%. The Capillary pressure is assumed to be zero. The numerical solution was run for 1500 days using a timestep size of 1 day. A fully implicit finite difference method is employed and the Newton–Raphson method is used to solve the set of nonlinear simultaneous equations generated from Eqs. 8–11.

Figure 7 shows the plot of water saturation obtained after 300 days of running the simulation. It can be observed from the figure that the TP-DMOPD model generates a sharp parabolic profile of the water saturation inside the cave whereas the Darcy model leads to a more flattened, piston-like flow profile. The parabolic profile generated using the TP-DMOPD model allows for a quicker breakthrough of water at the production well. We can observe that the injected water has reached the production well when using the TP-DMOPD model, this is however not the case when using the Darcy model (Fig. 7). Figure 8 compares the water cuts obtained at the producer using the two modelling techniques. It can be observed from Fig. 8 that breakthrough of the injected water at the producer occurs after 300 days when flow in the reservoir is modelled using the TP-DMOPD model whereas when the flow is modelled using the Darcy model the breakthrough is delayed by 90 days and occurs 390 days after the start of the simulation. Figure 9 compares the production rate of oil and water at the producer. It is observed for both the cases that after breakthrough the oil production starts to decrease and the water production starts to increase.

Fig. 7
figure 7

Water saturation map after 300 days obtained using a TP-DMOPD model, b Darcy model

Full size image
Fig. 8
figure 8

Comparison of water cut obtained from the two modelling techniques

Full size image
Fig. 9
figure 9

Comparison of oil and water rates obtained from a TP-DMOPD model, b Darcy model

Full size image

Figure 10 displays the oil and water velocities after 100 days from the start of the simulation obtained using both the modelling techniques. The velocities are measured at a location which is 1000ft inside of the left boundary of the reservoir. It is observed that the TP-DMOPD model generates a velocity profile which is more parabolic in shape whereas the Darcy model generates a more flat shape. For both the cases, the oil velocity is higher than the water velocity because the average water saturation after 100 days at the location where the velocities are measured is 35% which is same as the initial saturation which means that the water front has not yet reached the location. After 1500 days (Fig. 11), the average water saturation at the same location obtained from both the techniques is greater than 50% and therefore more preference is now given to flow of water and the water velocity becomes greater than the oil velocity.

Fig. 10
figure 10

Comparison of oil and water velocities obtained after 100 days using a TP-DMOPD model, b Darcy model

Full size image
Fig. 11
figure 11

Comparison of oil and water velocities obtained after 1500 days using a TP-DMOPD model, b Darcy model

Full size image

All the three models generate a system of linear equations which is solved using the LU factorization method. The computational performance of the TP-DMOPD model can be compared to the Brinkman model by calculating the computational complexity of solving this set of linear equations. The computational complexity of LU can be given by

$${\text{Cost}} \approx \frac{2}{3}n^{3}$$
(29)

where \(n\) is the total number of unknowns in the system. For this particular example, the cost for solving the Brinkman’s model was calculated to be equal to \(6.043 \times 10^{11}\) whereas the cost for solving the DMOPD or the Darcy Model is equal to \(2.352 \times 10^{10}\), which is about 25 times less when compared to the Brinkman model. The cost of solving for the DMOPD and Darcy model is less than the Brinkman model because Brinkman has separate equations for pressure, saturation, and velocities for oil and water in each primary axes in the linear system whereas the DMOPD only solves for the pressures and saturations in the linear system and the velocities are obtained explicitly using Eqs. 12 and 13.

Example 2

This example consists of a meandering cave embedded in a heterogeneous reservoir (Fig. 12). The white portion in the figure represents the caves. The width of the cave is about 35 ft \(\left( { \approx 11\,{\text{m}}} \right)\). All the boundaries of the reservoir are considered as no-flux boundaries. The reservoir dimensions are \(2000\,{\text{ft}} \times 2000\,{\text{ft}} \times 25\,{\text{ft}}\) and it has been discretized into \(400 \times 400 \times 1\) grids. The reservoir is initially at a pressure of 4000 psi. The initial water saturation is 35%. Water is injected into the reservoir through four injectors at a rate of 400 bbls/day. The reservoir fluid is produced through 5 producers (4 producers are located in the caves and 1 producer is located in the porous media) at a rate of 200 bbls/day. The locations of the wells are displayed in Fig. 12.

Fig. 12
figure 12

Reservoir used for Example 2

Full size image

Zonation of the cave and estimation of permeability ratios (Example 2)

The cave demarcated by the white region (Fig. 12) is split into 7 separate zones (Fig. 13). One central zone with a maximum permeability value obtained using Eq. 4, and 3 zones located on either side of the central zone. The permeability ratios are estimated by assuming single-phase (water) flow in the reservoir. The viscosity of water is assumed to be 1cp and the density is assumed to be 62.4 lb/ft3. The permeability ratios were estimated by employing the differential evolution (DE) algorithm. The termination criteria for the optimization were defined as 400 function evaluations. Figure 14 (minimization of the objective function) indicates that there is a satisfactory match between the velocities obtained using the Brinkman model to those obtained using the Darcy model. Figure 15 displays the estimated permeability ratios and the permeability values for each zone. For a single-phase flow, the time taken to run the Brinkman’s model for each timestep is 2232.7 s whereas the time taken to run the Darcy model and the DMOPD model after the history matching process is about 58.85 s per timestep. This means that the DMOPD model is about 37.9 times faster than the Brinkman’s model for this particular example.

Fig. 13
figure 13

Figure showing the zonation of the caves: a full model, b zoomed in section of the cave

Full size image
Fig. 14
figure 14

Values obtained when minimizing the objective function for example 2

Full size image
Fig. 15
figure 15

Figure displaying the estimated permeability ratios for each zone along with the permeability values obtained for Example 2

Full size image

Modelling of two-phase flow (example 2)

The permeability values obtained from the estimation stage of the TP-DMOPD model are then used to model two-phase flow in the karst reservoir (Eqs. 8–11). The correlations used to calculate the fluid properties are listed in Eqs. 22–28. The simulation was run for 200 days using a timestep size of 10 days. Figure 16 displays the saturation plot obtained at the end of 200 days. Figure 17 compares the water cut values obtained when using the TP-DMOPD model to the values obtained when using the Darcy model for all the 5 producers. The x-axis (time) for all the plots in Fig. 17 has been zoomed in to show the region of interest. For the producers located in the caves (P2–P5), we observe a faster breakthrough of the injected water when the reservoir is modelled using the TP-DMOPD model. The producer P1 is located in the porous region and it is far away from all the injectors and therefore has not produced any water for the duration considered. For this particular example, the cost for solving the Brinkman’s model was calculated to be almost equal to \(5.869 \times 10^{17}\) whereas the cost for solving the TP-DMOPD or the Darcy Model is equal to \(2.184 \times 10^{16}\), which is about 27 times less when compared to the Brinkman model.

Fig. 16
figure 16

Water saturation map after 200 days of production

Full size image
Fig. 17
figure 17

Comparison of water cut obtained from the two modelling techniques for: a producer 1, b producer 2, c producer 3, d producer 4 and e producer 5

Full size image

Conclusion

The existing models to simulate two-phase flow in karst reservoirs are computationally very expensive and difficult to model. In view of this, a two-phase Darcy model with optimized permeability distribution (TP-DMOPD) approach was proposed to model flow in karst reservoirs. The TP-DMOPD model is a modification to the already existing DMOPD model, which was developed to model single-phase flow in karst aquifers consisting of megakarstic features such as caves. In the TP-DMOPD method, initially, the caves are divided into different zones and the permeability ratio of each zone is estimated by matching velocity of fluid obtained inside the caves using the Brinkman model to that obtained using the Darcy model. A global optimization algorithm is used to perform the estimation. In this paper, we have used the differential evolution (DE) algorithm as the optimizer. During the estimation process, the fluid inside the reservoir is assumed to be single-phase (water). Once the permeability ratios are estimated and the permeability values are calculated, the two-phase Darcy model is used to solve the pressure and saturation distribution inside the reservoir.

Two reservoir models were used to compare the solutions obtained from the Darcy model to the results obtained from the TP-DMOPD model. For both the examples, the injected water travelled faster in the caves when the TP-DMOPD model was employed. The Darcy model consistently predicted a later breakthrough of the injected water at the producers when compared to the TP-DMOPD model.