Introductions

Natural gas exploration and development contributes to the progress of industrial productivity (Resnikoff 2011; Wang et al. 2021). In natural gas exploration and development, its production prediction and risk quantification are important topics, which is of great significance for the development of the energy exploitation plan and adjustment of the development strategy Research is currently being conducted extensively around the world regarding the prediction of long-term oil and natural gas production and risk quantification. Attention is given to the research of oil and gas resource growth prediction and risk quantification (Farzaneh-Gord et al. 2021).

In the Sichuan Basin, the Sinian gas reservoir is the most abundant area of conventional natural gas resources. The natural gas resources in the area reach \(2.62 \times 10^{12} {\text{m}}^{3}\) and the proven rate is 28.5%. Furthermore, the proven recovery degree of reserves is only 1.4%, belonging to the early and middle stages of resource exploration (Shi et al. 2020; Li et al. 2015). The Sinian gas reservoirs have a strong resource base and potential for exploration and development, which can promote increased natural gas production and associated benefits in the Sichuan Basin. In addition, the Sinian gas reservoir in the Sichuan Basin is expected to become the largest integrated carbonate gas field in China.

However, the geological characteristics of the reservoir, such as the strong heterogeneity of the reservoir and the complex pressure system, do not contribute to determining the future scale of the gas reservoir production. Meanwhile, the key to efficient gas reservoir development is to determine the production scale by reasonable research methods (Zhang et al. 2021a; Zeng et al. 2021). Therefore, strengthening research to predict the growth of natural gas production and risk quantification in the Sinian gas reservoir in the Sichuan Basin further clarifies the research and resource development potential in this area. Moreover, it has a positive impact on natural gas production planning.

Many studies are currently available on the prediction model of natural gas reserves and production, such as the peak prediction method, the production composition method, and the reservoir numerical simulation method (Li et al. 2021; Qiao et al. 2021). Among them, the peak prediction method is the most commonly used method for predicting medium- and long-term natural gas production (Zheng et al. 2020; Bataee et al. 2014). The prediction results of natural gas reserves and production obtained by the peak prediction method are more in line with the macro-trend of production growth (Zhang et al. 2021b; Wang et al. 2020a). Khanmohammadi and Saadat-Targhi 2019 proposed a method for modifying the model index given the disadvantage that the traditional Weibull production prediction model is greatly affected by the E index. The results show that the peak production of natural gas will occur around 2050, and the peak natural gas production will be \(\left( {1453 - 1750} \right) \times 10^{8} {\text{m}}^{3}\). (Zeng et al. 2020) used the GM(1,3) gray model to predict the multi-cycle parameters of the natural gas reserve curve and replaced the parameters in the multi-cycle Hubbert equation to predict the growth trend of natural gas reserves. The results show that the improved GM(1,3) gray model can improve the prediction accuracy of natural gas reserves. Sun et al. 2021 established a multi-cycle HCZ prediction model and described the model solving steps and evaluation method for the prediction results. The results show that the peak of world gas production will be reached around 2031, with a peak production of about \(4.04 \times 10^{12} {\text{m}}^{3}\) and the ultimate recoverable reserves about \(359.21 \times 10^{12} {\text{m}}^{3}\). Wang et al. 2018 introduced the ultimate recoverable reserves (URR) into the multi-cycle Gauss model as a boundary condition for predicting the growth trend of natural gas production. The results show that URR is the main control factor for determining the future production trend. The peak production is \(\left( {710 - 760} \right) \times 10^{8} {\text{m}}^{3}\).

There are many research methods for risk quantification of gas reserves and production, including the probability method, the neural network method, the fuzzy clustering method, etc. (Bulut and Zcan 2021; Wen et al. 2019). Among them, the probability method is widely used in the quantitative analysis of the risks of natural gas production. For areas with a low degree of natural gas exploration and development, the probability method can be used to predict, based on the existing data, the realization probability of different natural gas reserves and production targets in the future. Wang et al. 2020b determined the reserves of individual wells in narrow reservoirs of ultra-low permeability based on the probability method. The reserve of a block or reservoir is characterized by the probability distribution of the reserves of one well. Mahdizadeh and Goharshadi 2013 established a mathematical model for evaluating production by considering the action mechanism of different risk factors on planning objectives. The Monte Carlo simulation method was introduced to realize the production probability simulation. The risk-level evaluation matrix is established using two indices of the production target realization probability and the discrete degree. Ding 2018 used the probability method to analyze the influence of different distribution functions of each parameter on the results of the calculation of geological reserves. The results show that there are few samples of the oil-bearing area and the effective oil layer thickness, and it is convenient to calculate the distribution probability using the triangular distribution function.

It is obvious that gas production predictions and production risk quantification are independent research topics. Therefore, in the manuscript, these two topics are first combined. That is, a quantitative analysis of production risk based on the production prediction results is performed. It can provide a quantitative basis for guiding natural gas research and development.

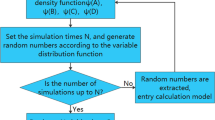
The working steps are as follows (Fig. 1). Firstly, the Hubbert and Gauss models are used to calculate the rules for the growth of natural gas production under different URR scenarios. Then, based on the Monte Carlo simulation method, the probability distribution of production in each year is calculated. Finally, the production risk evaluation matrix is established according to the probability of realization P and the dispersion degree C. The production risk of natural gas is systematically quantified, which gives a reliable basis for planning the realization of production targets.

Fig. 1
figure 1

Research flowchart of natural gas production prediction and risk quantification

Full size image

Theory of natural gas production prediction and risk quantification

Theory of natural gas production prediction

Hubbert prediction model

The Hubbert model is a common life cycle model for predicting the peak of natural gas production. The model has the following features (Tilton 2018).

After the oil and gas fields are put into operation, production starts from 0, grows with time, and reaches the peak value. Production then declines with the extension of development time until resources are depleted. As the development time approaches infinity, the area of the production time curve is equal to the final recoverable field reserves.

The formula of Hubbert model is as follows:

$$ P = \frac{{{\text{URR}}}}{{1 + e^{{ - b\left( {t - t_{m} } \right)}} }} $$
(1)

where \(P\) is cumulative production (\(10^{8} {\text{m}}^{3} /{\text{a}}\)); URR is the ultimate recoverable reserves (\(10^{8} {\text{m}}^{3}\)); \(t\) is production time; \(t_{m}\) is the peak production time; and \(b\) is the peak slope.

By taking the derivative of Formula (1) with respect to t, a formula for calculating the annual production can be obtained as follows:

$$ Q = \frac{dP}{{dt}} = \frac{{b \times URR \times e^{{ - b\left( {t - t_{m} } \right)}} }}{{\left[ {1 + e^{{ - b\left( {t - t_{m} } \right)}} } \right]^{2} }} $$
(2)

where \(Q\) is annual production (\(10^{8} {\text{m}}^{3} /{\text{a}}\)).

When \(t = t_{m}\), the production growth reaches the peak. Meanwhile, the cumulative production \(P\) has the greatest change rate, i.e., \(dP/dt\) is the maximum. Then

$$ Q_{m} = b \times {\text{URR}}/4 $$
(3)

where \(Q_{m}\) is the peak annual production (\(10^{8} {\text{m}}^{3} /a\)).

Formula (3) is converted to \({\text{URR}} = 4Q_{m} /b\) and substituted in formula (2). The formula for calculating the annual production of the Hubbert model can be obtained (Wang et al. 2016).

$$ Q = \frac{{2Q_{m} }}{{1 + \cos \,h\left[ {b\left( {t - t_{m} } \right)} \right]}} $$
(4)

The variation of the Hubbert model curve starts from a slight increase, then maintains stabilization close to the peak time, and finally falls rapidly to the depletion of resources.

Gauss prediction model

Similar to the Hubbert model, the Gauss model is symmetrical and belongs to the life cycle growth curve (Cao et al. 2021). The Gauss model formula is as follows:

$$ f\left( t \right) = \frac{1}{{s\sqrt {2\pi } }}e^{{ - \left( {t - \mu } \right)^{2} /2s^{2} }} $$
(5)

where \(\mu\) is the mean value, and \(s\) is the standard deviation.

In the process of natural gas exploitation, the cumulative production in the interval \(\left( {0 - \infty } \right)\) during the exploitation time t is considered as URR. By multiplying the distribution density function \(f\left( t \right)\) and the \({\text{URR}}\), the formula for calculating annual production \(Q\) can be obtained (Zhang and Zhao 2021).

$$ Q = \frac{{{\text{URR}}}}{{s\sqrt {2\pi } }}e^{{ - \left( {t - \mu } \right)^{2} /2s^{2} }} $$
(6)

Take the derivative of formula (6) with respect to \(t\).

$$ \frac{dQ}{{dt}} = \frac{{{\text{URR}}}}{{s\sqrt {2\pi } }}e^{{ - \left( {t - \mu } \right)^{2} /2s^{2} }} \left( { - \frac{t - \mu }{{s^{2} }}} \right) $$
(7)

When production peaks, the rate of change in annual production \(dQ/dt = 0\).

$$ t_{m} = \mu $$
(8)

By substituting Formula (8) into Formula (6), the peak annual production \(Q_{m}\) can be obtained.

$$ Q_{m} = \frac{{{\text{URR}}}}{{s\sqrt {2\pi } }} $$
(9)

By substituting Formulas (8) and (9) into Formula (6), a formula for the annual production of the Gauss model can be obtained.

$$ Q = Q_{m} e^{{ - \left( {t - t_{m} } \right)^{2} /2s^{2} }} $$
(10)

where \(s\) can represent the peak fluctuation degree to some extent.

Theory of production risk quantification

Monte Carlo probability method

The Monte Carlo method of probability is based on probability theory and the theory of mathematical statistics. The basic idea of this method is to establish a model for calculating the probability. Then, the statistical characteristics of the probability are obtained by a sampling test. An approximate result of the probability of realization was obtained.

When the Monte Carlo method is used for probability calculation, the problem to be solved must first be transformed into the expected value of a certain probability model. Then, the model is randomly sampled, enough random numbers are chosen and the problem to be solved is statistically analyzed (Ed et al. 2020).

Suppose that the random variable \(f\left( x \right)\) follows the distribution density function \(\psi \left( x \right)\), the mathematical expectation of \(f\left( x \right)\) is as follows:

$$ E = \int\limits_{{x_{0} }}^{{x_{1} }} {f\left( x \right)\psi \left( x \right)dx} $$
(11)

The N sample points \(x_{i}\) are stochastically chosen in terms of the distribution density function \(\psi \left( x \right)\); the arithmetic mean value of the function \(f\left( {x_{i} } \right)\) homologous to the sample points is taken as the value of the integral estimate.

$$ \overline{{E_{N} }} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} f\left( {x_{i} } \right) $$
(12)

The values of the variables are chosen stochastically in terms of the probability distribution density function. Through the amounts of repeated simulations of independent variables, a probability density distribution can be obtained and process of calculating the random sampling of variables can be realized.

The assumption of the application of the Monte Carlo simulation is the determination of the mathematical model of the objective function and the probability distribution of the variables in the model. Each parameter generates the amounts of random sample points in terms of a given probability distribution. The sample points are substituted into the model. Then, the probability density distribution of the objective function can be obtained. The specific steps are as follows:

Step 1 Establishment of the mathematical formula of the simulated target.

Step 2 Determination of the main independent model variables.

Step 3 Determination of the probability distribution function of the variables, including normal distribution, exponential distribution, triangular distribution, uniform distribution, and other functions).

Step 4 Determination of the simulation times, random sampling according to the variable distribution function and input into the analysis model.

Step 5 Final determination of the probability distribution and statistical characteristics of the target variables through sufficient simulation time.

Risk-level evaluation matrix

Two indicators are needed to evaluate the risk level of production, namely realization probability \(P\) and production dispersion degree \(C\). The production dispersion degree \(C\) represents the degree of difference between this production value and another, i.e., degree of change in production caused by change in production risk factors [30]. Thus, the lower the \(C\) value is, the less the risk factors affect production. The greater the stability of production, the lower the production risk level.

The formula of production dispersion degree \(C\) can be expressed as:

$$ C = 1 - \mu /s $$
(13)

where \(\mu\) represents the mean value, and \(s\) represents the standard deviation.

The risk assessment matrix is established by a comprehensive consideration of the two evaluation indices P and C. Production risks are divided into four levels (Fig. 2). According to the prediction results of natural gas production, production risk can be comprehensively quantified.

Fig. 2
figure 2

Production risk rating evaluation matrix

Full size image

The corresponding relationship between the regions of the production risk matrix and the judgment criteria for assessing the level of risk is as follows:

Risk level I (dark green area in Fig. 1): The production target is very achievable. Judgment criteria: production realization probability P > 80%, and dispersion degree C ≤ 5%.

Risk level II (light green area in Fig. 1): The production target is easy to achieve. Judgment criteria: 50% ≤ P ≤ 80%, and C ≤ 10%; or P > 80%, and 5% < C ≤ 10%.

Risk level III (yellow area in Fig. 1): The production target is relatively easy to achieve. Judgment criteria: 20% ≤ P < 50%, and C ≤ 10%; or P > 50%, and 10% < C ≤ 25%.

Risk level IV (red area in Fig. 1): The production target is not easy to achieve. Judgment criteria: P < 20%; 20% ≤ P < 50%, and C > 10%; or C > 25%.

Prediction of natural gas production in Sinian gas reservoirs

Estimate of URR

The Sinian gas exploration and development period are relatively short, with a production curve starting in 2012 (Fig. 3). The natural gas production curve currently maintains rapid growth, which is in line with the trend of the Hubbert and Gauss prediction models (Formulas (4) and (10)) in the early stage of the curve growth. Therefore, these two prediction models can be used to predict gas production in the Sinian gas reservoirs.

Fig. 3
figure 3

Production growth trend of Sinian gas reservoir over the years

Full size image

The URR range for ultimate recoverable reserves must be estimated prior to the prediction of natural gas production. The rapid growth of natural gas production indicates that resource exploitation is still at an early stage of exploration and development (Fig. 3). Due to the short time of research and development of the Sinian gas reservoir, knowledge of the gas reservoir is not enough. Therefore, URR is simply estimated by a numerical calculation method.

Geological research has determined that the natural gas resource of the Sinian gas reservoir is \(2.62 \times 10^{12} {\text{m}}^{3}\). By analyzing the gas reservoirs in the Sichuan Basin, the above range of the natural gas discovery rate and recovery factor are chosen. According to the current technical conditions of natural gas exploration and production in the Sichuan Basin, the proven rate of natural gas reservoir is in the range of 40–60%, i.e., the cumulative proven reserves at the end of the life cycle are \(\left( {1.048 - 1.572} \right) \times 10^{12} {\text{m}}^{3}\). The recovery of natural gas is about 60% in the Sichuan Basin, which corresponds to recoverable reserves in the range \(\left( {6288 - 9432} \right) \times 10^{8} {\text{m}}^{3}\). In addition, due to the limitations of the technical conditions, the conversion rate of URR from recoverable reserves to the ultimate recoverable reserves is about 60%, so that the estimated URR range is \(\left( {3770 - 5660} \right) \times 10^{8} {\text{m}}^{3}\). In particular, as the understanding of the Sinian gas reservoirs in the Sichuan Basin deepens, the URR calculation URR needs to be improved.

Prediction of natural gas production growth trend

The Hubbert and Gauss models are used to predict the peak production in the Sinian gas reservoirs at a proven rate of 40–60%. Discovery rates of 40%, 45%, 50%, 55%, and 60% were selected to calculate URR values corresponding to each discovery rate (Table 1). The growth trend of natural gas production in the Sinian gas reservoirs is then studied according to the five discovery rate scenarios.

Table 1 Correlation analysis of production prediction results
Full size table

The different URR values are substituted in Formulas (4) and (10) to obtain the natural gas production growth formula (Formulas (14) and (15)) and natural gas production prediction results (Figs. 3a and 4a) based on the Hubbert and Gauss models. Formulas (14) and (15) are production growth formulas for the Hubbert and Gauss models, respectively. These two formulas include the model parameters (peak annual production \(Q_{m}\), peak production time \(t_{m}\), peak slope \(b\), and standard deviation \(s\)) under different URR conditions. The above-mentioned formulas correspond to Figs. 3a and 4a, respectively.

$$ Q = \left\{ {\begin{array}{*{20}c} {\frac{2 \times 109}{{1 + \cos \,h\left[ {0.116\left( {t - 2036} \right)} \right]}},{\text{URR}} = 3770 \times 10^{8} {\text{m}}^{3} } \\ {\frac{2 \times 164}{{1 + \cosh \left[ {0.154\left( {t - 2036} \right)} \right]}},{\text{URR}} = 4240 \times 10^{8} {\text{m}}^{3} } \\ {\frac{2 \times 206}{{1 + \cos \,h\left[ {0.175\left( {t - 2036} \right)} \right]}},{\text{URR}} = 4716 \times 10^{8} {\text{m}}^{3} } \\ {\frac{2 \times 243}{{1 + \cos \,h\left[ {0.187\left( {t - 2036} \right)} \right]}},{\text{URR}} = 5188 \times 10^{8} {\text{m}}^{3} } \\ {\frac{2 \times 284}{{1 + \cosh \left[ {0.201\left( {t - 2036} \right)} \right]}},{\text{URR}} = 5660 \times 10^{8} {\text{m}}^{3} } \\ \end{array} } \right. $$
(14)
$$ Q = \left\{ {\begin{array}{*{20}c} {140 \times e^{{ - \left( {t - 2036} \right)^{2} /\left( {2 \times 10.77^{2} } \right)}} ,{\text{URR}} = 3770 \times 10^{8} {\text{m}}^{3} } \\ {178 \times e^{{ - \left( {t - 2036} \right)^{2} /\left( {2 \times 9.489^{2} } \right)}} ,{\text{URR}} = 4240 \times 10^{8} {\text{m}}^{3} } \\ {215 \times e^{{ - \left( {t - 2036} \right)^{2} /\left( {2 \times 8.766} \right)}} ,{\text{URR}} = 4716 \times 10^{8} {\text{m}}^{3} } \\ {250 \times e^{{ - \left( {t - 2036} \right)^{2} /\left( {2 \times 8.290^{2} } \right)}} ,{\text{URR}} = 5188 \times 10^{8} {\text{m}}^{3} } \\ {285 \times e^{{ - \left( {t - 2036} \right)^{2} /\left( {2 \times 7.933^{2} } \right)}} ,{\text{URR}} = 5660 \times 10^{8} {\text{m}}^{3} } \\ \end{array} } \right. $$
(15)
Fig. 4
figure 4

Prediction results of natural gas production based on Hubbert model

Full size image

To deeply analyze the law of growth of natural gas production with URR, the law between the model parameters and URR should be studied. Therefore, 100 different URR values are evenly extracted within the estimated range of \({\text{URR}} = \left( {3770 - 5660} \right) \times 10^{8} {\text{m}}^{3}\) (“Estimate of URR” section). These URR values are replaced in Formulas (4) and (10) to obtain the different results of production prediction (Figs. 4a and 5a), and the corresponding values of the model parameters (Figs. 4b and 5b) are extracted. Due to the large number of production prediction results, only the results of five URRs are presented in this paper. It contains the upper and lower boundary values of the URR range for predicting the boundary of future production.

Fig. 5
figure 5

Prediction results of natural gas production based on Gauss model

Full size image

The production prediction results in Figs. 4a and 5a are very similar. Therefore, both results can be analyzed simultaneously. When the URR increases, the peak production value increases together with it, and the time of peak production is always in 2036, namely \(t_{m} \equiv 2036equiv 2036\). In 2021–2051 period, the production growth curve is axisymmetric with respect to \(t = 2036\).

As shown in Fig. 4b, with the growth of URR, the peak production \(Q_{m}\) and parameter \(b\) of the Hubbert model show a stepwise growth trend. As the URR rises to a certain value, the parameter increases rapidly and then slightly. In Fig. 5b, with increasing URR, the production peak \(Q_{m}\) of the Gauss model increases linearly. The numerical curve of the parameter \(s\) maintains a relatively smooth downward trend, and the decline rate gradually decreases. Variations in model parameters can reflect the production variation. Therefore, when the URR growth rate is the same, the production prediction results of the Gauss model have a smoother production growth trend than the Hubbert model.

According to the growth rate of production, the process of future production growth can be divided into four stages. That is, the stage of production increase (2021–2031), the stage of production stabilization (2032–2040), the stage of rapid decline in production (2041–2050), and the stage of slow decline in production (2051–2070). In 2023–2031, production increased rapidly with passing years. In 2032–2036, production rises steadily and reaches peak production in 2036. In 2036–2040, production declines steadily. In 2041–2050, production declines rapidly. After 2050, the production curve begins to slowly decline and gradually approaches zero. In particular, the production curves converge at the point in 2050 where the annual production is \(Q = 60 \times 10^{8} {\text{m}}^{3}\). Therefore, 2050 is considered the dividing line between the stage of rapid decline and slow decline in production.

To compare the accuracy of the results of production prediction, a correlation analysis should be introduced. An analysis of the correlation between the Hubbert model and historical data was performed, and the same is true for the Gauss model. As can be seen from Table 1, the correlation coefficient of the two models is close to 1, and the corresponding production prediction results are very accurate. However, the correlation coefficient of the Gauss model prediction results is higher than that of the Hubbert model under each URR. A higher correlation coefficient means better prediction. Therefore, the prediction data of the Gauss model were selected as the production prediction results of the Sinian gas reservoir. The production prediction results under different URR conditions are presented in Table 2.

Table 2 Production prediction results of Sinian gas reservoirs under different URRs
Full size table

Comprehensive evaluation

The low level of research and development degree of the Sinian gas reservoir leads to many unknown factors. Therefore, the URR of ultimate recoverable reserves is considered to be the dominant factor influencing the trend of production variation. The estimated URR range is brought into Hubbert and Gauss models for production prediction. The results of the correlation analysis proved the accuracy of the prediction. A model for predicting the production growth trend of the Sinian gas reservoir at different proven rates has been established, which can provide a theoretical basis for planning gas exploration. Preliminary results show that the Sinian gas reservoir will continue to grow rapidly over the next 10 years and will reach peak production in 2036.

Quantification of gas production risk in Sinian gas reservoirs

Calculation of production realization probability based on Monte Carlo method

As described in “Prediction of natural gas production growth trend” section, the future production growth process can be divided into four stages. That is, the stage of increased production (2021–2031), the stage of stabilized production (2032–2040), the stage of rapid decline in production (2041–2050) and the stage of slow decline in production (2051–2070). Therefore, it is necessary to calculate the probability of production realization for different stages.

To clearly illustrate the impact of URR on production prediction results, the four-stage prediction results in Fig. 5a are locally amplified. The results of URR production prediction for different years in different stages can be obtained (Fig. 6).

Fig. 6
figure 6

URR- production prediction results

Full size image

The production increase stage in Fig. 6a is taken as an example to briefly describe the meaning of the URR-production prediction results. Figure 6a contains a bar and dot chart. Among them, bar charts with different colors represent the production of different years. The midpoint at the top of a bar chart constitutes a point plot. Details of the bar chart are as follows.

The colors of the columns and their corresponding lines represent different years. The abscissa of the column is the URR corresponding to the production. The length of different colored columns represents the difference between the production and the adjacent years. The ordinate at the top of the column represents the annual production. For example, the light blue bar chart corresponds to 2030. Among them, the URR coordinate of the blue column in the upper right direction is 5660. The ordinate at the top is 213.90. The bottom ordinate is 192.88. The length of the blue column can be calculated as 21.02. And adjacent to the 2029 corresponding color column. That is, when \({\text{URR}} = 5660 \times 10^{8} {\text{m}}^{3}\), the annual production of 2030 \(Q = 213.90 \times 10^{8} {\text{m}}^{3}\), and the difference between it and 2029 \(Q = 192.88 \times 10^{8} {\text{m}}^{3}\) is \(\Delta Q = 21.02 \times 10^{8} {\text{m}}^{3}\).

The Monte Carlo method described in “Monte Carlo probability method” section is used to calculate the different probabilities of production realization for each year in the four stages. The process of calculating the probability is introduced by taking the production calculation process in 2030 as an example. The Gauss equation of production calculation in Formula (10) is used as a mathematical model of probability simulation, and URR is the main independent variable that affects production. The URR value was obtained from uniform extraction (“Prediction of natural gas production growth trend” section). Therefore, uniformly distributed URR values are randomly selected many times. The URR extraction number is set as 100,000. For each extracted URR value, the corresponding \(Q_{m}\) and \(t_{m}\) are obtained from Fig. 4b, respectively. Then, \(Q_{m}\), \(t_{m}\), and \(t = 2030\) are substituted in Formula (10) to obtain the production Q in 2030.

After a sufficient time of production calculation, the distribution probability \(Q\) is calculated. The corresponding cumulative probability is obtained by accumulation, i.e., the production realization probability. Since the URR is evenly distributed, the accuracy of production probability statistics can be guaranteed. Figure 7 shows the results of production realization probability for representative years in the four stages.

Fig. 7
figure 7

Calculation of the production realization probability in different years

Full size image

Table 3 shows the results of production realization probability at different stages of the year. Cumulative probability represents the probability that the production will reach the corresponding scale, so the cumulative probability is also the realization probability. In 2030, “\({\text{P}}80 = 89.34 \times 10^{8} {\text{m}}^{3} /{\text{a}}\)” represents an 80% probability that \(89.32 \times 10^{8} {\text{m}}^{3} /{\text{a}}\) will be reached. Gas production is calculated in the 0–100% probability range. The risk of production in different probability intervals is quantified. Production corresponding to P80 is guaranteed production, P50 is average production, and P20 is ideal production. The production simulation can provide the realization probability of different gas development goals, which has an important reference and guidance for the formulation of the research and development plans and feasibility analysis of the Sinian gas reservoir.

Table 3 Production realization probability calculation results of different stage years
Full size table

Evaluation of production risk level based on matrix analysis

To quantify the risk of natural gas production in the Sinian gas reservoirs, the risk matrix (“Risk level evaluation matrix” section, Fig. 1) should be introduced to evaluate the level of production risk. According to the probability calculation method in “Evaluation of production risk level based on matrix analysis” section, the production distribution probability and the realization probability curve are obtained for four stages in each year. The mean value \(\mu\) and the standard deviation \(s\) of the annual production are calculated according to the distribution probability curve. Furthermore, the dispersion degree \(C\) of the annual production is calculated according to Formula (13).

In the stage of production increase and production rapid decline, \(5\% < C \le 10\%\). For that period, the corresponding annual production of \(P > 80\%\) is in the risk level II; \(20\% \le P < 50\%\) is in the risk level III; and \(P < 20\%\) is in the risk level IV.

In the stage of production stabilization and production slow decline, \(10\% < C \le 25\%\). For that period, the corresponding annual production of \(P > 50\%\) is in the risk level III, while \(P \le 50\%\) is in the risk level IV.

According to the range of \(C\) values in different stages, the production realization probability curve for each year in four stages is superimposed with different regions of the risk matrix. The risk levels of the production target for different stages and years are obtained (Fig. 8).

Fig. 8
figure 8

Production risk rating evaluation

Full size image

As can be seen from Fig. 8, with increasing production value, the corresponding realization probability decreases, and the production realization probability curve gradually approaches the area of higher risk. According to the quantitative results of production risk in different stages, the realization probability and the risk level of different production in each year can be obtained directly. The level of production risk represents the difficulty of achieving the production target. Therefore, a quantitative study of production risk based on probability calculation and matrix analysis can provide a theoretical basis for analyzing the feasibility of natural gas production targets at different time nodes.

Comprehensive evaluation

Quantitative study of natural gas production risk is based on the results of production prediction. On the premise of URR uniform distribution, the distribution of production probabilities in each year is analyzed. The productivity of natural gas at different time points is studied. The production realization probability \(P\) and dispersion degree \(C\) are introduced into the evaluation matrix as evaluation indices. Risk grade evaluation of annual production in different stages of production growth is conducted. The risk of the natural gas production target has been comprehensively analyzed.

At present, the knowledge about the Sinian gas reservoir in the Sichuan Basin is relatively shallow. In this paper, production prediction takes URR as the only influencing factor. The criteria for establishing a risk grade evaluation matrix are not fully combined with the research and development of gas reservoirs. Therefore, with the research and development of the Sinian in the future, the methods of production prediction and risk matrix should be updated to contribute to the continuous development of natural gas production.

Summary and conclusions

  • (1) URR was introduced into the Hubbert and Gauss models to predict the gas production growth in the Sinian gas reservoirs. Correlation analysis is used to confirm that the prediction results of the Gauss model are more accurate. According to the production growth rate, the production growth process can be divided into four stages. The consequences of production prediction reveal that gas production in the Sinian gas reservoirs will reach a peak range of \(\left( {140 - 285} \right) \times 10^{8} {\text{m}}^{3} /{\text{a}}\) in 2036. Production will be stable from 2032 to 3040, and the URR exploitation degree is about 60% at the end of the production stabilization stage.

  • (2) A quantitative study of production risk based on the production prediction consequences can offer a more quantitative basis for gas exploration. Through the Monte Carlo simulation, the probability of production realization \(P\) in each year was obtained with URR as the influencing factor. By combining \(P\) with the dispersion degree \(C\), a risk level evaluation matrix is established, which promotes the establishment of a target risk quantization system of gas production in the Sinian gas reservoirs.