Introduction

The quantification of natural gas exploration risks is an essential task in gas field exploration and development. It is vital for guiding gas field exploration, formulating development schemes, and determining the scale of investment. However, studies to quantify the risk of natural gas production are still in the initial phase. Therefore, further optimization is needed to introduce mathematical methods to quantify the risks of natural gas production.

Natural gas is an important energy source and strategic material, and its exploration and development are widely being performed. Attia M M (Tarom et al. 2017; Herndon 2016) et al. predicted that the natural gas production in the Barnett block in the USA would reach 200 × 108 m3 in 2030 and that the annual natural gas production will exceed the annual crude oil production in the peak period. By 2035, gas production will reach 250 × 108 m3; annual gas production will remain at 280 × 108 m3 until 2050. Abudeif A M (Attia et al. 2015; Abudeif et al. 2016) et al. analyzed the petrophysical properties and hydrocarbon potential of conventional gas peaks in the Bari field to predict their full life cycle. The results show that the peak time of the predicted production would be in 2055 with a peak production of 485.49 × 108 m3 and a relatively stable production period of 17 years. Radwan A E (Radwan et al. 2020, 2021) et al. analyzed the formation structure and oil and gas potential in the Suez Basin and then analyzed the growth trend of natural gas reserves in this area. The forecast results show that the proved reserves will peak in 2047, reaching 368.49 × 108 m3 with a proved rate of 36.4%. Therefore, the quantification of the natural gas production risk is beneficial to the progress of natural gas exploration and development.

Risk assessment of production targets of gas reservoirs offers an important means of improving gas field management levels, detecting existing exploration and development problems, and achieving efficient and rational development of gas reservoirs. The Carboniferous gas reservoir in eastern Sichuan, China, has a cumulative natural gas production of 135.06 × 108 m3, a recovery percent above 50%, and a reserves-to-production ratio of 24:1 (Resnikoff 2011; Alipour et al. 2019). It has made a huge contribution to building a 30 × 108 m3 natural gas mining area and natural gas industry in southwest China in the past seven decades. In this context, strengthening the risk assessment of the production targets of the Carboniferous gas reservoir in eastern Sichuan will promote natural gas exploration and the development of oil and gas fields in southwest China (Long et al. 2020).

However, the geological characteristics of the Carboniferous gas reservoirs, such as complex structures, low porosity, low permeability fissures, and high heterogeneity, make it difficult to accurately estimate the gas reservoir production scale and hinder the risk assessment of the gas reservoir’s production. Therefore, a detailed risk evaluation of the production targets of the Carboniferous gas reservoir in eastern Sichuan should be performed to obtain the theoretical basis for natural gas exploration and the development of gas reservoirs with complex geological conditions.

Risk factors affecting natural gas production include objective risk factors (e.g., geological conditions and the size of reserves) and risk factors in decision-making (e.g., technical level and planning and implementation) (Hu et al. 2015). Objective risk factors can be identified but cannot be artificially changed, while risk factors in decision-making can be adjusted by modifying the natural gas exploration scheme. The risk factors for natural gas production are diverse, which makes quantifying the risk of natural gas production targets challenging. For this reason, when selecting the optimal mathematical method for quantifying the risk of natural gas production, attention must be paid to the merits and demerits of each mathematical model and the specificity of each risk factor (Yadua et al. 2020).

Many methods are currently available to study the risk factors for natural gas production, including the Monte Carlo probability method, the neural network method, the analytical hierarchy process (AHP), and the fuzzy clustering method (Zheng and Liu 2019). Syed Z (Syed and Lawryshyn 2020) performed a risk assessment of natural gas production using the Monte Carlo probability method. Through random simulation of the probability distribution functions of different risk factor variables, they qualitatively evaluated the uncertainty of the gas reservoir parameters and the production scales corresponding to different risks. It was found that the results of the probability distribution of production, calculated by the probability method, facilitated decision-making on investment in natural gas reservoirs and the formulation of development schemes. Farzaneh-Gord M (Farzaneh-Gord et al. 2021) introduced the artificial neural network method with a highly linear predictive capability and an error back-propagation (BP) algorithm, which was applied to simulate the mapping relationship between the production risk factors and natural gas well production. They also built a mathematical computational model for natural gas well production based on the BP neural network model. According to the prediction results, the average relative error between the results calculated by this method and the values measured by the physical flow meter on site was 3.33%. In addition, the relative errors of more than 80% of the data points fell within ± 5%, and therefore, the prediction accuracy was high. Xp A (Xp et al. 2021) comprehensively examined several parameters based on the characteristics of tight sand reservoirs and eventually selected porosity, permeability, zone of flowage index, and shale content as characteristic reservoir parameters. Based on this, they classified reservoirs into five types using the fuzzy K-means clustering method. They compared the discriminant analysis method and the decision tree method in terms of their discrimination accuracy and chose the decision tree method to build a quantitative method for reservoir classification assessment. The results show that the quantitative evaluation model built according to the decision tree method is suitable for the research and development of natural gas. Liu S (Liu et al. 2019) comprehensively investigated five critical evaluation parameters affecting natural gas production from shale gas reservoirs. By analyzing the shale gas data of the Barnett block, the weight coefficients of these parameters were obtained and a suitable risk evaluation system of natural gas production targets for this block was built.

The diversity of risk factors results in high complexity of risk quantification. For this reason, the merits and demerits of each mathematical model and the specificity of risk quantification must be considered when selecting the optimal mathematical method for quantifying the risk of natural gas production (Wu et al. 2020). Monte Carlo simulation is a method used for statistical analysis of natural gas production risks under different risk factor combinations. In this paper, four risk factors are selected by the analytic hierarchy process (AHP) as the decision-making risk factors to analyze the average annual production in the stable production stage of the Carboniferous gas system in eastern Sichuan. The Monte Carlo production simulation is carried out with a self-established annual production calculation formula in the stable production stage to determine the production scale with different risk factors. The sensitivity of risk factors with different cumulative probability intervals is analyzed by using the fuzzy comprehensive evaluation method. According to the results of the risk sensitivity analysis, the influence of the change of the risk factor curve on the natural gas production curve is estimated.

Theories on risk quantification of natural gas production

When quantifying the risk of natural gas production based on the probability method, it is necessary to identify the probability distribution of production risk factors according to their values. The variation of their values can be used to generate many values of risk factors with the same probability of distribution using a random number generator. Based on the probability distribution of all risk factors, the probability distribution of natural gas production can be predicted. Furthermore, the probability distribution function of production can be used to calibrate the risk of the event occurrence. This method of calculating probability statistics is referred to as the Monte Carlo simulation.

Quantifying natural gas production risk requires an objective and accurate evaluation of various risk factors, which involves the generation, calculation, and processing of numerous data points on risk factors. Thus, the Monte Carlo simulation is applied to quantify natural gas production risks.

Principle of Monte Carlo simulation

Monte Carlo simulation, also called random sampling, is often used to solve the probability or expectation of a target problem (Gonzaga et al. 2019). The basic idea is to introduce independent parameters of a variable with a certain probability distribution into an existing or self-built mathematical model for the target variable, which gives the function of the probability distribution of the target variable and clarifies the effects of multiple parameters on the target variable.

When the distribution density function of a random variable \(f\left( x \right)\) is \(\psi \left( x \right)\), the mathematical expectation of the variable can be expressed as follows:

$$E = \mathop \smallint \limits_{{x_{0} }}^{{x_{1} }} f\left( x \right)\psi \left( x \right)dx$$
(1)

\(N\) sampling points \(x_{i}\) are randomly extracted according to the distribution density function \(\psi \left( x \right)\), and the arithmetic average of the function values \(f\left( {x_{i} } \right)\) corresponding to these sampling points is adopted as the estimated integral value.

$$\overline{{E_{N} }} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} f\left( {x_{i} } \right)$$
(2)

Similarly, for a target function with multiple variables, the values of the variables are randomly extracted sequentially according to the probability distribution density function of each variable. The probability density distribution of the target function is obtained by an extensive, repeated, and independent simulation of variable values. The Monte Carlo simulation can be used to calculate the random sampling of multiple variables (Mehana et al. 2020).

The Monte Carlo simulation is superior to conventional numerical integration in terms of the sampling calculation process of multiple variables (dimensions). In the single integration scenario, the computational efficiency of the Monte Carlo simulation is slightly lower than that of conventional numerical integration. However, with the increase in the number of integration variables (dimensions), the computational efficiency of conventional numerical integration shows an exponential decline, while that of Monte Carlo simulation basically remains constant. The Monte Carlo simulation is far superior to conventional numerical integration when the number of integration variables (dimensions) reaches four (Sheng et al. 2021). The risk quantification system for natural gas production is huge and requires a comprehensive evaluation of multiple risk factors. This is because the risk quantification system can be assessed objectively, accurately, and comprehensively only when a numerical analysis is performed for each risk factor to identify their mathematical laws. Therefore, the Monte Carlo simulation is more applicable to quantify natural gas production risks.

The main steps of the Monte Carlo simulation are as follows:

Step 1: Build a mathematical model for problem-solving;

Step 2: Define the probability distribution density function of each variable in the model;

Step 3: Perform a random sampling of model variables according to the probability distribution density function; and.

Step 4: Replace the extracted random variables in the model to solve the problem.

The mathematical model for the Monte Carlo simulation can be an existing mathematical formula or a mathematical formula derived in accordance with the characteristics of the problem to be solved. The key to Monte Carlo simulation is to determine the probability distribution density function of the variable, which requires improving the existing probability distribution density function according to the variation of the value of the variable. Then, the distribution function of each variable can be obtained more accurately.

The probability distribution density functions commonly used in Monte Carlo simulation include Gaussian distribution, triangular distribution, Poisson's distribution, and binomial distribution functions, among which the Gaussian distribution function is more frequently used.

The Gaussian model is a lifecycle-based growth curve often used in oil and gas field research. The Gaussian function is symmetric in shape, and its curve tends to be gentle (Yu et al. 2011).

More precisely, the Gaussian curve first increases slightly, then rises sharply, followed by a slow increase. After reaching its peak, the curve begins to decline in a symmetric pattern. The Gaussian model is often used to study the probability distribution of oil and gas production and other parameters in oil and gas fields. It is classified into single-cycle and multi-cycle Gaussian models, which depend on the number of peaks (Hubbert 1949). The relationship between probability distribution and parameters in the Gaussian single-cycle model is expressed as follows:

$$N = N_{m} \cdot e^{{ - \left( {t - t_{m} } \right)^{2} /2s^{2} }}$$
(3)

where \(N\) is the probability distribution; \(N_{m}\) is the peak probability distribution;\(t\) is the value of the parameter corresponding to the probability distribution; \(t_{m}\) is the value of the parameter corresponding to the peak probability distribution; and \(s\) is the model parameter, which can represent the range of peak fluctuations to some extent, but is not the same as the standard deviation.

The traditional multi-cycle Gaussian model can be expressed as follows:

$$N = \mathop \sum \limits_{i = 1}^{k} N_{mi} \cdot e^{{ - \left( {t - t_{mi} } \right)^{2} /2s_{i}^{2} }}$$
(4)

where k is the overall cycle index; and i is the number of cycles, i.e., the parameter subscript of a cycle index. For instance, when i = 3, \(N_{mi}\) denotes the annual newly increased proved reserves peak of the third cycle.

Multi-cycle scenarios often appear in studies on the probability distribution of oil and gas fields. Consequently, the multi-cycle Gaussian model is often used to investigate the probability distribution of various parameters.

Fuzzy comprehensive evaluation (FCE)

When quantifying the risk of natural gas production targets, a sensitivity analysis needs to be performed to investigate the effects of different risk factors on production targets. As the laws governing the relationship between risk factors and production are still unclear, FCE should be introduced to measure the weights of different production risk factors. FCE is a comprehensive evaluation method based on fuzzy mathematics. It converts a qualitative evaluation into a quantitative one according to the membership theory of fuzzy mathematics, in order to perform a comprehensive evaluation of things or objects restrained by multiple factors. Since it can comprehensively analyze multiple risk factors, it is applicable for the synthetic analysis of the sensitivity and other fuzzy information of risk factors (Zhang and Feng 2018; Guan et al. 2019). The principle of FCE is described as follows:

$$\left\{ {\begin{array}{*{20}c} {B = W \times R} \\ {R = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {r_{11} } \\ {r_{21} } \\ \end{array} } & {\begin{array}{*{20}c} {r_{12} } \\ {r_{22} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & {r_{1j} } \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {r_{2j} } \\ \end{array} } \\ \end{array} } \\ \vdots & \vdots & {\begin{array}{*{20}c} \ddots & \vdots \\ \end{array} } \\ {r_{i1} } & {r_{i2} } & {\begin{array}{*{20}c} \ldots & {r_{ij} } \\ \end{array} } \\ \end{array} } \right]} \\ \end{array} } \right.$$
(5)

where \(B\) is the evaluation result, i.e., membership of the evaluation object to the evaluation grade; \(W\) is the weight of an evaluation index, i.e., the weighted fuzzy matrix of the index; \(R\) is the membership of an evaluation index, i.e., the fuzzy relation matrix; \(r_{ij}\) is the value in the ith row and jth column of the fuzzy relation matrix \(R\), i.e., the preference membership of the ith factor to the jth evaluation object.

To solve the weights of different indices for assessing the evaluation result, the first step is to obtain the fuzzy relation matrix R. Regarding the parameters of the evaluation index, data of different dimensions cannot be directly used. Therefore, the next step is to unify the data dimensions by standardizing the index data collected according to the principles of preference. Specifically, the principles of preference include the principles “the greater, the better,” “the smaller, the better,” and “the closer to a constant, the better” (Liu et al. 2020).

The standardized model based on the principle “the greater, the better” is expressed by Formula (6).

$$r_{ij} = \frac{{X_{ij} - X_{{i,{\text{min}}}} }}{{X_{{i,{\text{max}}}} - X_{{i,{\text{min}}}} }}$$
(6)

The standardized model based on the principle of “the smaller, the better” is expressed by Formula (7).

$$r_{ij} = \frac{{X_{{i,{\text{max}}}} - X_{ij} }}{{X_{{i,{\text{max}}}} - X_{{i,{\text{min}}}} }}$$
(7)

The standardized model based on the principle “the closer to a constant, the better” is expressed by Formula (8).

$$r_{ij} = \frac{{{\text{min}}\left( {X_{ij} ,X} \right)}}{{{\text{max}}\left( {X_{ij} ,X} \right)}}$$
(8)

In Formulas (6–8), \(X_{{{\text{min}}}}\) is the minimum among all \(X_{ij}\) s of each index; \(X_{{{\text{max}}}}\) is the maximum among all \(X_{ij}\) s of each index; and \(X\) is a constant. The fuzzy relation matrix R can be obtained after standardization. The evaluation result B is given and substituted into Formula (5) for calculating the weight (W) of each evaluation index.

Then, by standardizing the fuzzy weight matrix \(W\), the sensitivity of different risk factors \(\alpha_{i}\) can be obtained. The standardized formula is as follows:

$$\alpha_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{i} }}$$
(9)

where \(\alpha_{i}\) is the sensitivity of the ith risk factor; \(w_{i}\) is the ith value of the fuzzy weight matrix \(W\); and \(n\) is the number of values of \(W\).

Monte Carlo simulation of risks of natural gas production

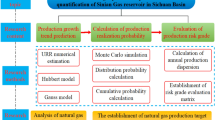
Before performing the Monte Carlo simulation of natural gas production, a mathematical computing model should be built for the target function (natural gas production) to determine the probability distribution of the model variables. After that, many random samples can be generated according to the probability distribution of different parameters. Finally, they are substituted in the model to obtain the probability density distribution curve of the target function. The specific steps are described below and illustrated in Fig. 1:

Fig. 1
figure 1

Monte Carlo simulation process for quantifying the risk of natural gas production

Full size image

Step 1: Build a mathematical computing model for natural gas production (“Evaluation of natural gas production uncertainty based on the probability method Section”);

Step 2: Determine and select the main model variables;

Step 3: Define the probability distribution functions of variables according to their laws of variation; and.

Step 4: Determine the number of simulations N, perform random sampling according to the probability distribution functions of the variables, substitute the random samples in the model, and identify the probability distribution and statistical characteristics of the target variable based on a sufficient number of simulations.

Risk quantification of natural gas production in the Carboniferous gas reservoir of eastern Sichuan

In this study, a Carboniferous gas reservoir in the eastern Sichuan Basin was chosen as the research area. The target area covers 25 exploration and development blocks. Natural gas production and production parameters in these 25 blocks are adopted as original training samples to perform the Monte Carlo simulation, thus obtaining the probability distribution of the production and the production risk factors.

Different blocks of natural gas have different sizes of reserves and require different times of exploration and development, which makes their direct analysis impossible. The stage of exploration and development of natural gas, depending on the growth rate of production, can be further divided into three stages, namely the rising stage, the stable stage, and the declining stage. Among them, the rising stage is a stage with a low degree of resource exploration. The developers’ understanding of resource allocation during this stage is insufficient to fully prioritize the greatest potential of the area being explored. The stable stage is characterized by stable exploration and development of resources. The developers’ understanding of resource allocation during this stage becomes mature, and they can properly leverage the area's full potential. The declining stage is a stage with a declining rate of resource utilization, which can be mainly attributed to the gradual depletion of reserves in the area.

It is clear that the status of gas production in the stable stage can best reflect its resource potential, which is not affected by exploration and development time. Thus, the average annual production in the stable stage is adopted as a criterion for quantifying the risk of natural gas production.

Evaluation of natural gas production uncertainty based on the probability method

Risk quantification factors should be rationally selected to investigate the effects of risk factors on the annual average production Q during the stable stage and to quantify the natural gas production risks using multi-parameter analysis. AHP can be used to select risk factors for the natural Carboniferous gas production target. Figure 2 shows an AHP chart of risk factors consisting of three layers:

Fig. 2
figure 2

AHP—Selection of risk factors for natural gas production

Full size image

Layer 1: Target layer. The overall target of “risk quantification of the natural gas production planning target” is determined;

Layer 2: Criterion layer. The risks of natural gas production are classified into four major types, i.e., resource scale risk (ZY), geological development risk (KF), planning and deployment risk (GH), and technical level risk (JS). Among them, ZY and KF are objective risk factors that can be identified but cannot be changed artificially. GH and JS are decision-making risk factors that can be identified and artificially changed. Risk factors in decision-making are usually chosen to quantify risks when formulating natural gas planning schemes. Natural gas development and utilization rates can be improved by adjusting risk factors in decision-making according to quantification results;

Layer 3: Risk index layer. The major types of risk factors in the criterion layer can be classified into many minor types of risk factors according to the principle of natural gas exploration and development. For illustration, only 14 risk factors are listed in Fig. 2.

Planning and implementation are significantly influenced by JS in the exploration and development process. The two risks are highly correlated and have low independence. Therefore, only the production risk factor under JS is selected to construct the mathematical model. The following formula for the average annual production in the stable stage is taken as the target function for the Monte Carlo simulation of natural gas production:

$$Q = \frac{ABDJL}{C} \times 100\%$$
(10)

where \(Q\) is the annual production in the stable stage, in \(10^{8} {\text{m}}^{3} /{\text{year}}\); \(A\) is the production rate in the stable production stage, in %; \(B\) is the number of gas production years during the stable production stage, in years; \(C\) is the recovery degree during the stable production stage, in %; \(D\) is the average production of a kilometer-deep well, in \(10^{4} {\text{m}}^{3} /\left( {{\text{km}} \times {\text{well number}}} \right)\); \(J\) is the number of productive wells in the stable stage, dimensionless; and \(L\) is the average productive well burial depth, in \({\text{km}}\).

Among the above production parameters, the number of productive wells \(J\) and the average productive well burial depth \(L\) are objective risk factors that can be identified during research and development but cannot be changed artificially. The other four factors, the production rate \(A\), the number of gas production years \(B\), the recovery degree \(C\), and the average production of a kilometer-deep well \(D\), are decision-making risk factors that can be adjusted based on human decisions through modification of the exploration and development scheme of natural gas. For this reason, the four decision-making risk factors A, B, C and D are adopted in this study to investigate the production risks through the Monte Carlo simulation.

The key to accurate calculation of production by the Monte Carlo probability method is to accurately select the statistical model of parameters and determine the probability distribution curve of each parameter. According to the statistical law of actual natural gas exploitation data and previous experience, the multi-cycle Gaussian model of formula (4) is used to conduct characteristic analysis and probability distribution fitting for the sample points of Carboniferous natural gas production risk factors. The distribution probability density functions of the four production risk factors are calculated. The data of the natural gas production risk factors were obtained from the natural gas exploration and development data of Carboniferous gas reservoirs. The data in each natural gas region of the carboniferous gas reservoir were obtained from the Exploration and Development Research Institute of the PetroChina Southwest Oil and Gas Field Company, which collected and sorted the data. Formulae (11–14) are the probability density functions of the distribution of the four production risk factors, A, B, C, and D, respectively.

$$Q = 4.01e^{{ - \frac{{\left( {A - 4.214} \right)^{2} }}{{2 \times 7.410^{2} }}}} + 1.31e^{{ - \frac{{\left( {A - 2.488} \right)^{2} }}{{2 \times 9.737^{2} }}}} + 0.71e^{{ - \frac{{\left( {A - 6.566} \right)^{2} }}{{2 \times 7.039^{2} }}}} + 0.38e^{{ - \frac{{\left( {A - 8.424} \right)^{2} }}{{2 \times 6.147^{2} }}}} + 0.38e^{{ - \frac{{\left( {A - 10.654} \right)^{2} }}{{2 \times 5.401^{2} }}}}$$
(11)
$$Q = 2.485e^{{ - \frac{{\left( {B - 13.91} \right)^{2} }}{{2 \times 6.676^{2} }}}}$$
(12)
$$Q = 2.45e^{{ - \frac{{\left( {C - 43.94} \right)^{2} }}{{2 \times 8.514^{2} }}}} + 1.41e^{{ - \frac{{\left( {C - 26.97} \right)^{2} }}{{2 \times 11.09^{2} }}}} + 0.555e^{{ - \frac{{\left( {C - 51.75} \right)^{2} }}{{2 \times 10.23^{2} }}}}$$
(13)
$$Q = 2.14e^{{ - \frac{{\left( {D - 2.381} \right)^{2} }}{{2 \times 9.045^{2} }}}} + 2.14e^{{ - \frac{{\left( {D - 3.904} \right)^{2} }}{{2 \times 18.19^{2} }}}} + 0.425e^{{ - \frac{{\left( {D - 8.703} \right)^{2} }}{{2 \times 1.56^{2} }}}}$$
(14)

The four subgraphs in Fig. 3 represent the distribution probability and cumulative probability density functions of the four production risk factors, respectively. The red histogram is the distribution probability density function, which corresponds to the multi-cycle Gaussian equation of risk factors in Formulae (11–14). The black curve is the cumulative probability density function, which is obtained by the one-time accumulation of the distribution density function. The probability densities of the four risk factors are all consistent with the multi-cycle Gaussian model. It can be seen that the distribution probability density equation of different production risk factors has different multiple cycles.

Fig. 3
figure 3

Probability distribution of four production risk factors

Full size image

The number of simulations is set at 10,000. According to the probability density function of the distribution of production risk factors, random numbers are cyclically extracted and replaced in the target production function expressed by Formula (10). The average annual production of the Carboniferous gas reservoir in the stable stage is calculated, and the probability distribution curve of the average annual production in the stable stage is obtained by simulation. As shown in Fig. 4, the probability distribution of the annual production in the stable stage is similar to those of the four risk factors, including the distribution probability shown by continuous histograms and the cumulative probability shown by smooth curves. Specifically, the red zone indicates the maximum probability interval that corresponds to the annual production in the stable stage. The interval has an annual production range of \(\left( {43.43 - 126.35} \right) \times 10^{8} {\text{m}}^{3} /{\text{year}}\), a minimum distribution probability of 3.65%, a maximum distribution probability of 4.56%, an average distribution probability of 3.65%, and a cumulative probability range of 14.59–92.88%.

Fig. 4
figure 4

Monte Carlo simulation results of average annual natural gas production in stable stage

Full size image

In the probability curve of the average annual production in the stable stage, the cumulative probability indicates the possibility of a production that exceeds a certain scale. For instance, “\({\text{P}}90 = 48.06 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” means that the production predicted by the model has a 90% probability of exceeding \(48.06 \times 10^{8} {\text{m}}^{3} /{\text{year}}\), as shown in Table 1. In this study, natural gas productions of different cumulative probability intervals (0–100%) are calculated, and the risk quantification of the average annual productions is performed with respect to different probability intervals. The production corresponding to the cumulative probability P90 is the verified production. The production corresponding to the cumulative probability P50 is the benchmark production. The production corresponding to the cumulative probability P10 is the peak production. The results of the production simulation can be used to obtain the probability of achieving different targets of natural gas development and production, thus providing guidelines for formulating and optimizing gas field research and development schemes.

Table 1 Average annual natural gas production under different cumulative probabilities
Full size table

Sensitivity analysis of production risk factors

To analyze the impact of risk factors on production, it is necessary to conduct a sensitivity analysis of production risk factors. The first step is to obtain the risk factors of the annual production growth curve during the stable production stage, i.e., the production curve with the same probability as the risk factor. Growth curve analysis should adopt the same principle of probability analysis. That is, when analyzing the risk factor, each time the value of the risk factor of a certain probability is substituted, it is also necessary to substitute the other three risk factor values of the same probability. For instance, if the cumulative probability corresponding to the substituted stable-stage production rate is 90%, the cumulative probabilities corresponding to the other risk factor values should also be 90%. By substituting the values of the risk factors with different cumulative probabilities into the target function of the production expressed by Formula (10), growth curves of different production risk factors vs. the average annual production in the stable stage can be obtained.

As shown in Fig. 5, the light red histograms are distribution probabilities corresponding to different values of risk factors. Red curves are production risk factor–production growth curves. Green curves are production risk factor–cumulative probability curves. With the increase in the risk factor values, the growth curves of various production risk factors vs. average annual production in the stable stage increase continuously and show constant changes in the slope. That is, the effects of the four risk factors in decision making on the production constantly change. The cumulative probability curves also decrease with the increase in value of risk factors. The height of the distribution probability histogram can reflect the extent of change in the slope of the corresponding cumulative probability curve. Different values of risk factors correspond to different cumulative probability intervals and distribution probabilities.

Fig. 5
figure 5

Production risk factors—average annual production growth curve in stable stage

Full size image

Notably, different risk factor values correspond to different cumulative probability intervals and distribution probabilities. Thus, the sensitivity analysis of single-risk factors requires the selection of factors and production from different cumulative probability intervals for risk research.

To perform a sensitivity analysis of production risk factors, it is necessary to rank the correlation coefficients between production risk factors and production. A high correlation coefficient between the risk factor and production means that the risk factor is sensitive to production. Production simulation results based on the Monte Carlo probability method are mainly influenced by the production rate in the stable production stage \(\left( A \right)\), the number of gas production years during the stable production stage \(\left( B \right)\), the recovery degree during the stable production stage \(\left( C \right)\), and the average production of a kilometer-deep well \(\left( D \right)\). As can be seen from the model formula, relationships between different production risk factors and the average annual production in the stable stage are multiply–divide relationships. Thus, different variables have the same sensitivity in relation to the model, and the sensitivity of different factors to the production results is mainly based on the uncertainty of the variables themselves.

Sensitivity analysis reveals the sensitivity of different risk factors to production. The value (positive or negative) of the sensitivity of risk factors characterizes the direction of influence of the risk factor on production. That is, the higher the absolute positive (negative) value of the risk factor, the higher the sensitivity of the risk factor to the production, and vice versa.

As shown in Fig. 5, with the change in value of risk factors, the slope of the risk factor–production growth curve keeps changing, that is, the influence degree of the four decision-making risk factors on the production also keeps changing. The different values of risk factors correspond to different cumulative probability intervals. Therefore, to perform sensitivity analysis on the average annual production target in the stable production stage, five production risk factors–production growth curves with different cumulative probability intervals are selected for risk analysis. The fuzzy comprehensive evaluation method of formula (5) is used to obtain the sensitivity coefficient \(w_{i}\) of different risk factors to determine the influence degree of risk factors in different cumulative probability intervals on production.

The production probability interval has a great influence on the sensitivity analysis of risk factors. So divide the whole probability interval 5 equally. Five cumulative probability intervals are 80–100%, 60–80%, 40–60%, 20–40%, and 0–20%. Then, sensitivity analysis is performed for the five probability intervals. The selection of this probability interval is artificial. In the actual exploration and development work, suitable probability interval can be selected according to the scale of natural gas production.

To perform the sensitivity analysis of risk factors according to the principle of single-factor analysis, the cumulative probability interval is first selected, and then, one risk factor is selected each time. The other production risk factors are kept constant at the central probability values of the cumulative probability interval. P90 means that the cumulative probability interval is 80–100% and that the central probability is 90%, and so on for the other probability intervals. Single-risk factors with different probabilities are consecutively substituted in formula (10) at different cumulative probability intervals to analyze the sensitivity of each risk factor to the production. Finally, the sensitivity analysis charts of all cumulative probability intervals are obtained.

Figure 6 shows the results of the sensitivity analysis of different cumulative probability intervals. The broken line graphs are risk factor–production sensitivity curves that show the effect of risk factor variation on production variation. Histograms characterize the sensitivity of risk factors to production. The slope of the broken line graph illustrates the variation of the annual production in the stable stage relative to the cumulative probability of the risk factor. This variation is codetermined by the sensitivity coefficient \(\alpha_{i}\) and the risk factor variation \(\Delta x_{i}\) of the risk factor. The height of the histogram characterizes the magnitude of the sensitivity coefficient \(w_{i}\) of the corresponding risk factor.

Fig. 6
figure 6figure 6

Sensitivity analysis of production risk factors with different cumulative probability intervals

Full size image

As seen from Fig. 6, the sensitivity of the risk factors varies significantly in different probability intervals. However, the production is significantly affected by the production risk factors \(A\) (production rate in the stable production stage) and \(D\)(average production of a kilometer-deep well), that is, these two factors have the highest sensitivity. The sensitivity of production risk factor \(D\) is higher than that of \(A\). The production risk factor \(C\) (recovery degree during the stable production stage) has the least sensitivity in all probability intervals. Within the range of 0–20% probability, the sensitivity of production risk factor \(B\)(number of gas production years during the stable production stage) is the highest. The risk factor sensitivity ranking of the entire probability interval is as follows: average production of a kilometer-deep well \(\left( D \right)\) > production rate in the stable production stage \(\left( A \right)\) > number of gas production years during the stable production stage \(\left( B \right)\) > recovery degree during the stable production stage \(\left( C \right)\). Different intervals of cumulative probability correspond to the annual productions in the stable stage, which are limited by the four decision-making risk factors to varying degrees.

Two parameters, the sensitivity coefficient \(w_{i}\) and the risk factor variation \(\Delta x_{i}\), are selected to comprehensively compare the risk factors in terms of sensitivity. The sensitivity coefficient \(w_{i}\) characterizes the effect of risk factors on production. The risk factor variation \(\Delta x_{i}\) represents the variation of risk factors in a certain probability interval. As shown in Table 2, the product of the sensitivity coefficient \(w_{i}\) and the risk factor variation \(\Delta x_{i}\) characterizes the variation of the average annual production in the stable stage in the current probability interval under the effect of a risk factor.

Table 2 Sensitivity analysis parameters of different cumulative probability intervals
Full size table

For instance, in the probability interval of 80–100%, the stable-stage production rate has a sensitivity coefficient \(w_{i} = 2.7655\) and a risk factor variation \(\Delta x_{i} = 1.4154\), indicating that the variation of the stable-stage production rate in this probability interval is \(1.4155\% .\) The product of \(w_{i}\) and \(\Delta x_{i}\) characterizes the slope size of the risk factor–production sensitivity curve corresponding to the stable-stage production rate. The production variation \(\Delta Q = 3.9144 \times 10^{8} {\text{m}}^{3}\) implies that the variation of the stable-stage production rate in this probability interval leads to a production variation of \(3.9144 \times 10^{8} {\text{m}}^{3}\). It is important to note that different production risk factors have significantly different values. For example, in the entire probability interval of 0–100%, the maximum value of the stable-stage production rate is 12.00%, while that of the stable-stage production life is 27.50 years (Fig. 3). Therefore, different risk factor–production sensitivity curves have different slopes. For this reason, the sensitivity coefficient \(w_{i}\) is chosen to characterize the sensitivity of different risk factors to the production. The histogram of sensitivity degree \(\alpha_{i}\), which represents the proportion of sensitivity coefficient \(w_{i}\) of different risk factors, is used to intuitively describe the risk factors.

Production improvement planning based on risk factors’ sensitivity analysis

To better understand the effect of sensitivity analysis on natural gas production planning, production improvement planning is investigated Figure 7. shows the different production plans based on risk factor sensitivity analysis results. That is, a high production realization target is set under the current productivity level, and risk factors in decision-making are adjusted according to the results of the sensitivity analysis. The purpose is to investigate the adjustment measures of the development planning scheme necessary to realize the production targets and to further analyze the feasibility of achieving the production targets.

Since the sensitivity of risk factors varies greatly in different probability intervals, five cumulative probability intervals are selected to analyze the production improvement planning based on the sensitivity analysis of risk factors, which are 80–100%, 60–80%, 40–60%, 20–40%, and 0–20%. To more clearly characterize the parallel displacement of the risk factor curves in the figure, the original probability intervals are expanded by 10% from the upper or lower limit, i.e., 70–100%, 50–80%, 30–60%, 10–40%, and 0–30%. In general, the results of the sensitivity analysis are limited by the probability intervals and constitute the basis of production improvement planning. Therefore, production planning in a new probability interval should follow the laws of sensitivity analysis.

The cumulative probability interval of 70–100% can be taken as an example to illustrate the decision-making steps for production improvement planning.

  1. (1)

    Setting the production realization target in the cumulative probability interval of 70–100%. As shown in Table 1, the central probability production “\({\text{P}}90 = 48.06 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” in the cumulative probability interval of 70–100% is selected as the realized production scale, and “\({\text{P}}80 = 59.92 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” is adopted as the production realization target. The production realization target and the current level of productivity should be within the probability interval of 80–100%;

  2. (2)

    Evaluation of production improvement requirements. Improving the production from the realized production scale “\({\text{P}}90 = 48.06 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” to the production realization target “\({\text{P}}80 = 59.92 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” requires an increment of “\(11.86 \times 10^{8} {\text{m}}^{3} /{\text{year}}\);”

  3. (3)

    Selection of risk factors in production decision-making. As shown in Fig. 6a, the production risk factors \(\left( {\text{A}} \right)\) and \(\left( D \right)\) are the two most sensitive risk factors within the probability range of 80–100%, so they are selected to formulate the production improvement planning. Within the probability range of 0–30%, the two risk factors with high sensitivity, \(\left( B \right)\) and \(\left( D \right)\), are selected for production improvement planning (Fig. 7).

  4. (4)

    Parallel displacement of the decision-making risk factor probability curves. The first step is to determine how much the two decision-making risk factors need to be improved based on the sensitivity coefficient \(w_{i}\) of each risk factor in the probability interval of 80–100% (Table 2), i.e., whether the risk factor \(A\)(the production rate in the stable production stage) needs to be improved by 4.29%, or whether the risk factor \(D\)(the average production of a kilometer-deep well) needs to be improved by \(2.18 \times 10^{4} {\text{m}}^{3} /\left( {{\text{km}} \times {\text{well number}}} \right)\). Next, two new decision-making risk factor probability curves are produced through corresponding parallel displacement.

  5. (5)

    Realization of the production target. Two new Monte Carlo simulations are performed. The probability curve of one risk factor in decision-making is substituted in Formula (10) after parallel displacement, while the other risk factors in decision-making remain constant. The probability curves also show a productivity increment of “\(11.86 \times 10^{8} {\text{m}}^{3} /{\text{year}}\).” This demonstrates that the realized production scale “\({\text{P}}90 = 48.06 \times 10^{8} {\text{m}}^{3} /{\text{year}}\)” can be improved to the production target “\({\text{P}}80 = 59.92 \times 10^{8} {\text{m}}^{3} /{\text{year}}\).”

Fig. 7
figure 7figure 7

Production planning based on risk factor sensitivity analysis results

Full size image

Notably, \(A\), \(B\), \({\text{C}},\) and \(D\) are all risk factors in decision-making, and their values can be changed by adjusting the development planning scheme. Thus, the probability curves of the risk factors can be parallel displaced to change their probability distribution in order to analyze the effect of adjusting the production risk factors on production growth.

Table 3 shows the natural gas production improvement planning data for all cumulative probability intervals. The realization of the production target under the current productivity level is considered in the same probability interval, and the risk factor variation \(\Delta x_{i}\) is inversely proportional to the sensitivity coefficient \(w_{i}\). In the probability interval of 0–30%, extremely low probabilities of the production and the risk factors lead to small sensitivity coefficients, for which the risk factors must change drastically to achieve the production target. Therefore, it is difficult to achieve the planning target in this probability interval. In the practical formulation and adjustment of the planning scheme, the probability of realization can be determined according to the overall production scale of the exploration and development unit. Highly sensitive risk factors in decision-making can be selected and adjusted according to the production scale and the laws of realization, thus achieving the production target more easily.

Table 3 Summary of the production planning results
Full size table

Conclusions

In this paper, analytic hierarchy process (AHP) is employed to select four decision-making risk factors, i.e., production rate \(\left( A \right)\), gas production life \(\left( B \right)\), recovery degree \(\left( C \right)\), and average productivity of a kilometer-deep well \(\left( D \right)\) in the stable production stage to analyze the annual average production of a Carboniferous system in eastern Sichuan. The probability distribution functions of the four risk factors are calculated through the multi-cycle Gaussian model. The annual natural gas production with different probabilities is obtained by the Monte Carlo probability simulation method and the calculation formula of annual production in the stable production stage. The maximum probability range of the annual production is \(\left( {43.43 - 126.35} \right) \times 10^{8} {\text{m}}^{3} /{\text{year}}\), and the corresponding probability range is 14.59–92.88%.

Based on the probability distribution of natural gas production and risk factors, four kinds of risk factor–production growth curves are deduced. The sensitivity analysis of single risk factors with different probability intervals is performed using the fuzzy comprehensive evaluation method. In the entire probability interval, the more sensitive risk factors are the average production of a kilometer-deep well (D) and the production rate in the stable production stage (A). Through sensitivity analysis of these two risk factors, the risk factor adjustment measures needed to achieve the production target can be obtained. Furthermore, the results of this study can provide theoretical and data support for natural gas production planning.