Introduction

Concerns regarding anthropogenic CO2 emissions are strongly growing. Tackling the increasing atmospheric CO2 concentrations has become the top priority on political and environmental agendas worldwide. Carbon capture and storage has been identified as a major technology that aims at addressing the climate change dilemma (Metz et al. 2005). It signifies a midterm mitigation strategy for the next few decades, until new energy concepts are developed on a relevant scale, for example the solar conversion of CO2 into synthetic fuels (Kirsch et al. 2020). In carbon capture and storage, carbon dioxide is captured from a source of emission, purified, compressed, transported and injected into geological formations for storage (Surampalli et al. 2015). Potential geological formations for carbon storage include unminable coal seams (Ma et al. 2017), saline aquifers (Michael et al. 2009), depleted oil and gas reservoirs (Godec et al. 2011) and shales (Busch et al. 2008; Kang et al. 2011). On the other hand, the total primary energy supply has amounted to a total of approximately 14 × 106 kilo-tons of oil equivalent in 2017 (IEA, 2017), indicating an increasing demand on energy. Due to the declining production rates of conventional reservoirs, unconventional oil and gas resources are considered potential sources of future energy (Stark et al. 2007). Despite their abundance, unconventional reservoirs are characterized by low permeability and are therefore more challenging in terms of hydrocarbon recovery (Sheng 2020). Technological advances have indeed improved the profitability of tight reservoirs by increasing the connectivity between the rock matrix and wellbore through the so-called hydraulic fracturing and horizontal drilling (Tovar et al. 2014); however, large volumes of unrecovered hydrocarbons remain trapped within the formation. Therefore, the application of enhanced oil and enhanced gas recovery technologies is still required to further improve the displacement of remaining hydrocarbons (Sheng 2015). Carbon dioxide assisted recovery technologies such as supercritical extraction (Jin et al. 2017), CO2 injection either via huff and puff (Alfarge et al. 2018) or CO2 flooding (Wang et al. 2010) exploit the favorable physical and chemical properties of CO2 at reservoir conditions, where it commonly exists above its critical point (31.1 °C, 7.38 MPa). Supercritical CO2 (sc-CO2) is characterized by high diffusivity, low viscosity and higher miscibility in crude oils relative to other gases (Lan et al. 2019) and is consequently responsible for promoting oil phase swelling (Samara and Jaeger 2021), as well as the reduction in viscosity and interfacial tension (IFT) (Perera et al. 2016), which contribute to improved displacement of residual oil that would otherwise remain unrecovered. Additionally, in unconventional organic-rich formations such as coalbeds, application of enhanced gas recovery takes advantage of the preferential adsorption of CO2 on organic matter relative to CH4, which leads to the desorption of CH4 and consequently enhancing methane recovery (Prusty 2008). This mechanism has also proven effective in gas shale formations (Godec et al. 2014; Tao and Clarens 2013). As a result, coupling of carbon storage with enhanced oil and gas recovery could result in the double benefit of achieving higher hydrocarbon recovery factors and the reduction of greenhouse gases through storing CO2 geologically (Liu et al. 2019).

Specific challenges arise in the case of oil and gas recovery from shales due to their extremely narrow pores, where the pore size can be in the order of nanometers (Nojabaei et al. 2013). In small confined pores, the capillary pressure is significantly large (Teklu et al. 2014) and is responsible for the entrapment of hydrocarbons within the pore space. On the other hand, due to the strong interactions of CO2 with reservoir liquid and solid phases, the situation can be changed in favor of mobilizing the oil and gas trapped in these tight formations. Therefore, the fundamental parameters and prevailing mechanisms which govern fluid displacement and CO2 storage need to be quantified. Several studies have investigated wettability alteration in systems comprising CO2, brines and conventional rocks (Arif et al. 2019; Mutailipu et al. 2019; Yekeen et al. 2020). However, studies involving shales are still rare in the literature. The assessment of shale wettability is either achieved through imbibition tests (Lan et al. 2015, 2014; Yassin et al. 2017) or contact angle measurements. For instance, the impact of pressure and temperature on shale wettability was investigated by (Arif et al. 2016) using the sessile drop method. They reported an increasing contact angle with increasing CO2 pressure yet a reduced contact angle with increasing temperature. Shengli shale was investigated by (Pan et al. 2018). They examined the impact of pressure and salinity on the contact angle. They reported higher contact angles at higher pressures and in brines with higher salinity. In black shales (Yekeen et al. 2021) reported a decreasing contact angle at higher temperatures and an increasing contact angle in higher salinity brines and at higher pressures. Although (Shojai Kaveh et al. 2016) also reported an increasing contact angle with pressure, contrary to what had been reported earlier regarding salinity, they found lower contact angles with increasing salinities. The discrepancy in these findings may very well be attributed to the variability in minerology, organic matter and thermal maturity of the investigated shales which further hinders the advancement toward an undisputed understanding of shale wettability (Sharifigaliuk et al. 2021). As far as fluid–fluid interactions are concerned, several studies investigated IFT in binary systems comprising brine and CO2. The reported findings thereof are consistent and reveal a direct relation between IFT and salinity and an inverse relation between IFT and pressure. These studies are summarized in Table 1.

Table 1 Summary of previous studies on CO2-brine IFT
Full size table

In spite of the aforementioned studies, a systematic work that considers all the participating phases (hydrocarbons, aqueous and solid phases), as well as their interactions, that further enables the derivation of a complete and direct picture on the situation in tight reservoirs—especially oil shales—is still lacking in the literature. This knowledge gap is addressed by this work with a special focus on the utilization of CO2 in oil recovery from Jordanian shale formations and their potential use for CO2 storage. The first aim of the current study is to investigate fluid–fluid and rock–fluid interactions at pressures up to 40 MPa through the measurement of IFT in CO2-brine systems at conditions that have not been investigated so far, the measurement of IFT in a system comprising CO2 and oil extracted from Jordanian shale, quantifying wettability alteration of the relevant system, as well as the assessment of CO2 adsorption and gas diffusion. Up to the best of our knowledge, no experimental work that verifies the relation between CO2 adsorption and wettability alteration of shale surfaces can be found in the literature. This experimental verification signifies the second objective of the work at hand.

Materials

Fluid phases

For this study, model brines of different NaCl concentrations were prepared, representing the main ions present in formation brines. The solutions were prepared by adding NaCl to deionized water at concentrations of 3 wt% and 10 wt% and stirred for 15–30 min at 300 rpm to ensure homogeneity and their complete dissolution. The monovalent ion concentrations were chosen based on the fact that they fall in the range of those that are present in unconventional reservoirs and that are relevant to carbon storage (Pan et al. 2018; Saraji et al. 2014), with the aim of assessing the impact of ion concentration on the system under investigation.

The oil phase under investigation was obtained by supercritical CO2-extraction from rocks taken from Sultani reservoir. The extraction was carried out in a laboratory-scale unit (volume 4 L, Pmax 69 MPa, Tmax 150 °C Eurotechnica, Germany) described elsewhere (Samara et al. 2019). The extracted fluid was centrifuged for 10 min at 3000 rpm and room temperature using a centrifuge (Multifuge X1R, Thermo scientific- UK) to form two completely separate phases, one comprising the extracted formation oil and one comprising the extracted formation brine that was not further used in this study. Carbon dioxide was provided by Westfalen AG, Germany, at a purity of 99.99%.

Solids

Shale samples were obtained from the outcrop of Al-Sultani deposit located in the central region of the Hashemite Kingdom of Jordan. For the sorption tests, a sample was cut into a nearly spherical shape with a diameter of 8.3 mm. The spherical shape facilitates the application of a mathematical approach of transient mass transfer and enables the estimation of an overall diffusion coefficient. Wetting tests were performed on a natural untreated rock sample. For the X-ray diffraction (XRD) test, powdered samples were loaded into the diffractometer with Cu Kα radiation and a nickel filter (Empyrean—Malvern Panalytical, UK), in a 2θ range of ≈ 10°–90°. Figure 1 shows the XRD pattern.

Fig. 1
figure 1

Sultani shale mineralogical composition

Full size image

According to the XRD analysis, Sultani shale is majorly composed of calcite, followed by Quartz, Dolomite and Pyrite, which is in line with the earlier findings of (Li et al. 2019) whose tests were performed on samples taken from the same reservoir. The porosity of Sultani shale is reported by (Samara et al. 2019) to be around 20% with poor connectivity among the pores.

Methods

Sorption

Gas sorption on the rock surface was determined using a magnetic suspension balance (MSB) (TA instruments, Germany) in a compressed CO2 environment. The MSB is coupled to a high-pressure view cell by Eurotechnica GmbH (Pmax 45 MPa, Tmax 150 °C) that is used to observe the sample during the measurement, e.g., for any volume change taking place. The measurements are taken at 40 °C and 60 °C and a pressure range of 5 to 30 MPa. Temperature and pressure conditions are maintained constant throughout the entire sorption procedure. An electronically controlled magnetic coupling is used to transmit the weight of the sample inside the high-pressure test cell to a microbalance located outside and subject to atmospheric conditions. The sample weight is recorded as a function of time, pressure and temperature by a data acquisition software. More details on this method can be found in (Fujii et al. 2009). Upon pressurization, the sample will increase in weight over time due to gas adsorbing on the surface of the solid sample. Given the tightness of the rock, a homogeneous poreless but gas-permeable solid matter is assumed in order to enable the quantification of mass transfer by applying Fick’s law of diffusion. An analytical approach that describes nonstationary diffusion of a gas into a solid sphere is provided by (Crank 1975) as per Eq. 1:

$$\left( {\frac{{M_{t} }}{{M_{\infty } }}} \right) = 1 - \frac{6}{{n^{2} }}\mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{n^{2} }}{\text{exp}}\left( { - Dn^{2} \pi^{2} t/a^{2} } \right),$$
(1)

where Mt/M∞ is the mass of CO2 as a function of time t, n is the running index of the series, a is the radius of the sphere and D is the apparent diffusion coefficient. Under the assumption that the weight increase is merely the result of CO2 sorption into the sample, the theoretical course of CO2 mass uptake as described by Eq. 1 is adjusted by changing the apparent diffusion coefficient value until both the theoretical and experimental curves agree.

In order to remove any residual adsorbed gases and any moisture present in the solid rock, evacuation of the high-pressure autoclave containing the sample is performed prior to pressurization. Subsequently, the autoclave is pressurized up to the designated test conditions and gas sorption begins to take place. The test is carried out until a constant value of the weight is attained.

The errors associated with measurement of CO2 adsorption and diffusion coefficient are attributed to uncertainty in pressure and temperature readings, uncertainty of the starting weight signal, buoyancy effects, the extraction of soluble matter by sc-CO2 and humidity. The pressure is determined by calibrated pressure sensors at a precision of ± 0.2 bar. The temperature is determined by thermocouples at a precision of ± 0.1 °C. Directly after pressurizing the autoclave, the mass measurements are subject to an error which stems from the time needed for pressure and temperature equilibration. The error associated with this phenomenon is considered the most important, where a deviation of  5% is possible, i.e., the real adsorbed CO2 mass—in other words, the difference between the initial mass reading and final mass reading—could be up to 5% higher. The error resulting from buoyancy was not corrected, the reported results are those of the excess and not the absolute isotherms. Last but not least, as the sample is placed in an atmosphere of pressurized CO2, the extraction of fluids present in the sample pores by means of sc-CO2 may lead to a lower apparent adsorption. To eliminate the error associated with this process, the tests are conducted on samples that have already undergone extraction prior to sorption measurements. All together the uncertainty in the sorption and diffusivity data is in the range of  1 to + 6%.

Interfacial tension

To measure the IFT of the respective fluid mixtures the pendant drop method was employed. Measurements of IFT were performed using a high-pressure view cell (PDE 1700 MD-H by Eurotechnica GmbH, Germany, wetted material (Hastelloy), Pmax 69 MPa, Tmax 200 °C, internal volume of 25 ml) as described in (Jaeger et al. 2010). The pendant drop method depends on drop shape adjustment when the gravity and surface forces are in equilibrium at constant T and P conditions. A calibrated thermocouple is located 10 mm from the drop inside the view cell and measures the temperature to an accuracy of ± 0.1 °C. A pressure transducer with an accuracy of ± 0.1 bar is used to measure the pressure inside the view cell. A charge-coupled device (CCD) camera records the drop shape and a drop shape analysis program-ADVANCE (Krüss GmbH, Germany)-is used to evaluate the drop profile based on the axisymmetric drop shape analysis (ADSA) technique described elsewhere (Saad and Neumann 2016). The experimental drop profile is adapted to a theoretical profile via the Young–Laplace equation which describes the surface curvature of a liquid drop as explained in (Song and Springer 1996) by adjusting the IFT.

Determination of IFT by means of drop shape analysis requires knowledge of the densities of the participating fluid phases. The density of the oil was measured as a function of pressure and temperature using a high-pressure oscillating tube densitometer (DMA 4200 M, Anton Paar, Austria, Pmax = 50 MPa, accuracy: ± 0.2 kg/m3 and ± 0.05 °C). The density of CO2 as a pure fluid is determined as a function of pressure and temperature using the GERG2008 equation of state (Kunz and Wagner 2012). Brine densities were adapted from (Liu et al. 2017) who calculated the density under similar conditions based on the empirical model developed by (Duan and Sun 2003).

A mini-dosing device with a volume of 2.5 ml is charged with the drop liquid and is connected to the view cell by means of a thin capillary. The liquid is dispensed through the thin capillary which has a diameter that allows formation of drops of appropriate shape. As previously described in (Samara et al. 2019), the tip of this capillary is located inside the view cell at the center of the two opposite pressure-resistant glass windows. After heating the view cell to the designated temperature, temperature equilibration is ensured by waiting 30 min before introducing fresh CO2. The view cell is then pressurized until the targeted pressure is reached. The cell is left again for approximately 10 to 15 min until temperature and pressure equilibration is achieved before forming a drop at the tip of the capillary. The experimental uncertainty associated with the pendant drop method may result from different factors of influence that comprise the following: errors in pressure and temperature measurement, error due to density difference between the adjacent gas and liquid phases, the uncertainty associated with the numerical analysis of the drop shape, as well as the presence of contaminants in the measurement system.

The error in determining the density difference between adjacent fluid phases is associated with the uncertainty in determining the density of the gas saturated liquid, which amounts to ± 0.5% in the current work. This results in an IFT measurement uncertainty in the order of ± 1%. Regarding the error associated with the drop shape factor, according to (Song and Springer 1996), the highest accuracy of the method is obtained at a shape factor in the range of 0.5–0.7. When the drop is too spherical, a shape factor below 0.5 is obtained and the standard deviation increases considerably. Contaminations may influence the results and lead to erroneous IFT measurements, therefore prior to IFT tests, the system was confirmed to be contaminant free by the measurement and validation of tap water IFT at atmospheric conditions (~ 72 mN/m). All in all, the mean deviation resulting from all aforementioned sources of uncertainty amounts to a maximum of ± 2% in the IFT range of 10–25 mN/m. Below 10 mN/m this error may increase to a value of ± 5% due to larger uncertainties, especially those associated with a drop shape factor falling out of the desirable range mentioned earlier.

Wetting

The wetting behavior was evaluated with the same setup as used in the previous sub-section. The sessile drop method is applied to determine the contact angle (CA) between the prepared brines and the surface of the rock in a compressed CO2 atmosphere. As previously described in (Samara et al. 2019), these drops are recorded by a CCD camera and evaluated by the CA module of the drop shape analysis software ADVANCE (Krüss GmbH, Germany) in order to determine the three-phase CA. The error in CA measurement is mainly due to the use of a non-ideal surface as the tests were performed on natural, untreated rocks to preserve the native nature of the rocks. The images have been evaluated using different methods of drop profile approximation and CA mean values were calculated with uncertainties of ± 2°. Figure 2 shows a sessile drop of the 3 wt% NaCl brine on the Sultani rock samples.

Fig. 2
figure 2

Sessile drop of 3 wt% NaCl brine on Sultani shale at 26 MPa and 60 °C

Full size image

Results and discussion

Oil-CO2 interfacial tension

The driving force for any extraction process is the solubility of the targeted solute in the solvent. Increasing the pressure and temperature of CO2 as a solvent above the critical point causes a considerable increase in its density and consequently affects its solvating power. Increasing the density of CO2 translates to an increased interaction between the molecules of both the solvent and the solute, which ultimately leads to an increase in solubility (Ahmad et al. 2019). Aside from the favorable consequences of CO2 dissolution into the oil such as oil swelling and viscosity reduction (Li et al. 2013), its impact on interfacial tension (IFT) is relevant for mobilizing the oil and increasing its recovery. Interfacial tension is related to the capillarity pressure (Pc) within the pores via the Young–Laplace Eq. 2 (Arif et al. 2016):

(2)

where бlf is the IFT between the reservoir liquid and CO2, θ is the CA between the fluid interface and the rock at the three-phase contact point and r is the pore radius. Therefore, a reduction in the IFT results in reducing the capillary pressure and consequently an increase in oil recovery. The oil –CO2 IFT at 60 °C is shown in Fig. 3.

Fig. 3
figure 3

Interfacial tension between extracted oil and CO2 as a function of pressure at 60 °C

Full size image

At low to moderate pressures, the IFT course is dominated by the interaction of CO2 with the light compounds of the crude oil, this is indicated by a steep slope that is qualitatively similar to that observed for a gas condensate/CO2 system as reported in (Wang et al. 2019), where complete miscibility is reached at moderate pressures below 15 MPa. This can be attributed to the reduction in the intermolecular distance between CO2 and the oil as pressure increases, thereby increasing the intermolecular forces between them (Yang et al. 2015). Additionally, this signifies increased solubility of CO2 in the oil and consequently a reduced IFT (Hemmati-Sarapardeh et al. 2014; Rezk and Foroozesh 2019). On the other hand, the leveling off of the curve at high pressure (around 14 MPa) shows a typical IFT course that signifies the presence of heavier components. This is in line with the findings of (Yang and Gu 2005; Yang et al. 2015). The heavier fractions of oil exhibit less mutual solubility with CO2 (Marufuzzaman and Henni 2015) and therefore a considerable reduction in IFT can no longer be observed.

Brine-CO2 interfacial tension

In order to understand the phase behavior between injected CO2 and formation brine, the IFT of a binary system comprising CO2 and model brines has been investigated. Figure 4 shows the IFT between CO2 and two different brines (3 wt% and 10 wt% NaCl) at 60 °C.

Fig. 4
figure 4

CO2-NaCl brine interfacial tension as a function of pressure and salinity at 60 °C. For comparison, literature data are also plotted (Chalbaud et al. 2009), (Liu et al. 2017))

Full size image

It is observed that the IFT decreases as pressure increases for both NaCl concentrations. At pressures up to 20 MPa, the decrease in IFT is significant. This is attributed to the fact that as pressure increases, CO2 solubility in brine considerably increases at low to moderate pressures (Duan et al. 2006; Duan and Sun 2003). On the other hand, at elevated pressures the slope of IFT reduction decreases until a further drop in IFT is hardly observable. At higher pressures, CO2 becomes increasingly incompressible and the influence of pressure on CO2 density declines (Δρ/ΔP is reduced). This in turn influences the solubility of CO2 in the brine and explains why the IFT curves level off (Mosavat et al. 2014). It is worth mentioning that the pressure at which constant IFT values are observed is independent of the brine salinity, which is in line with the work of (Chalbaud et al. 2009). Their findings could also be confirmed in terms of the influence of the salinity: Fig. 4 shows that the isobaric IFT is also higher for the brine with the higher salinity. This is explained by the spatial distribution of monovalent ions (Na+) in the aqueous phase and its impact on the interfacial configuration of water molecules (Aggelopoulos et al. 2011). Cations have no affinity to the liquid–gas interface and are therefore repelled from the respective front, consequently accumulating in the aqueous solution. As a result, water molecules located at the interface migrate toward the aqueous bulk phase to solvate the cations in what is also known as ion hydration (Chalbaud et al. 2009; Levin and Flores-Mena 2001), and therefore the number of water molecules available to interact with the CO2 is reduced (Mirchi et al. 2014). This results in a reduction of mutual solubility and accordingly a higher CO2-brine IFT is observed for brines with higher salt concentration (Bachu and Bennion 2009).

The brine concentration in this study is almost similar to that investigated by (Chalbaud et al. 2009) (10.5 wt%), the reported values there show lower IFT at low pressures due to the higher temperature (71 °C). Conversely, as the pressure increases beyond 10 MPa, IFT undergoes an inversion and is higher at higher temperature, which is a known phenomenon (Chalbaud et al. 2009; Li et al. 2012a) and is also related to the density behavior of CO2. Brines with similar concentrations were investigated by (Liu et al. 2017) at 60 °C; however, only two IFT measurements are reported for each brine, which makes it difficult to evaluate and explain the existing discrepancy. On the other hand, IFT measurements reported in this work are consistent among each other. A more comprehensive comparison to previously published values is not possible because IFT measurements at high pressures are lacking in the literature for brines with similar salinity at 60 °C.

Sorption

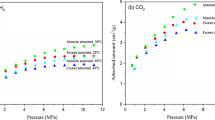
Sorption measurements have been successively conducted on the same sample described in the materials section. The sample had already undergone extraction in order to minimize any interference by fluids originally present in the rock such as oil or formation brine which occupy the pore space, consequently reducing the surface area available for the CO2 to adsorb (Rani et al. 2019). The sorption kinetics of CO2 on Sultani shale is exemplarily depicted in Fig. 5. Sorption kinetics are used to determine the adsorption capacity of the shale as per Eq. 1 in the methods section. After a strong initial increase, the adsorbed CO2 mass reaches equilibrium at around 200 min. Figure 6 shows the adsorption capacity of CO2 as wt% of the rock at two temperatures (40 °C and 60 °C) as a function of pressure as well as the bulk densities of CO2 as calculated by GERG2008 equation of state (Kunz and Wagner 2012).

Fig. 5
figure 5

CO2 adsorption kinetics on Sultani shale at 15 MPa and 40 °C

Full size image
Fig. 6
figure 6

Density of bulk phase CO2 and CO2 adsorption capacity of Sultani shale as a function of pressure at 40 °C and 60 °C

Full size image

At a constant temperature, the adsorption isotherms show a strong increase in adsorption capacity near the critical state of CO2. This increase is related to the sharp increase in CO2 density as it changes from the gaseous state to the supercritical state (Klewiah et al. 2020). However, this increase is only observed until a certain pressure is reached. For both investigated temperatures, the adsorption capacity peaks at 20 MPa with no significant difference over values measured at 15 MPa: In the gravimetric sorption measurement method, the net increase in mass uptake is a superposition of two forces; the adsorption of gas molecules on the adsorbent (positive), and the buoyancy force that acts against the latter (negative) (Gasparik et al. 2014). The buoyancy force is given in Eq. 3 (Abdul Kareem et al. 2018):

$$F_{B} = V_{s} \cdot \rho_{{{\text{bulk}}}} \cdot g,$$
(3)

where FB is the buoyant force, Vs is the sample volume, ρbulk is the density of bulk CO2 and g is the gravitational acceleration. At lower pressures, the density of the bulk phase (ρbulk) is low and therefore the buoyant force acting upward on the sample can be neglected. However, as the pressure increases, ρbulk increases, consequently increasing the buoyant force and the excess adsorption isotherm appears to be lower (Fujii et al. 2010), which occurs beyond 20 MPa.

On the other hand, at low pressure the adsorption capacities at 40 °C is higher than 60 °C. Conversely, as the pressure increases, the adsorption capacity at 60 °C appears to be higher. This can also be justified by the buoyancy effect as follows: At high pressure the occupancy of sorption sites by the adsorbed molecules is already high, and therefore it may be assumed that the density of the adsorbed phase does not increase much with pressure and the volume of adsorbed phase remains relatively constant. Consequently, the density of bulk CO2 determines the magnitude of change in buoyancy forces interfering with the adsorption capacity. From Fig. 6, it is observed that ρbulk at 40 °C is higher than that for 60 °C. This implies that the effect of buoyancy forces on the sample is higher at 40 °C than 60 °C and increases at higher pressure. As a result, the buoyancy-induced error on the 40 °C adsorption isotherm is larger compared to the 60 °C isotherm. Therefore, excess isotherm correction would yield higher absolute adsorption isotherms for 40 °C. This is in line with what was stated in ref (Fujii et al. 2010), who reported a higher buoyancy effect at 50 °C compared to 100 °C. However, the conversion of the excess isotherm to an absolute isotherm with buoyancy correction cannot be determined as neither the exact volume of adsorbed CO2 (Vads)—which increases the volume of the sample—nor the density of the adsorbed CO2 layer (ρads) can be measured.

Figure 7 depicts the apparent diffusion coefficients (D) as estimated using Eq. 1. The results show that as CO2 transitions from the gaseous state into the supercritical state, the diffusion coefficient is reduced. Additionally, it is also observed that the dominating diffusion mechanism is self-diffusion, since the experimental values qualitatively follow the first approximation of the rigid sphere model as described by Chapman and Cowling in (Jost 1952). This model estimates the coefficient of self-diffusion and is given in Eq. 4:

$$D_{11} = 1.2\frac{\mu }{\rho },$$
(4)

where µ and ρ are the gas dynamic viscosity and density, respectively, at given pressure and temperature conditions. This therefore implies that the diffusion—unlike surface diffusion and Knudsen diffusion—is independent of the pore diameter.

Fig. 7
figure 7

CO2 diffusion coefficient as a function of pressure at 40 °C and 60 °C

Full size image

It can also be observed that while at 5 MPa the coefficient is higher for the higher temperature; the opposite is observed at higher pressures. However, at both temperatures, the diffusion coefficient is observed to slightly increase with increasing pressure at supercritical conditions. Following Eq. 4 and in accordance with the experimental findings, the dynamic viscosity at lower temperature (40 °C) is the dominating effect at higher pressures for which it may be inferred that friction between molecules of the same type enhances diffusion whereas it is well known that in binary diffusion the opposite occurs.

Wettability analysis

Wettability of a fluid-rock system affects the distribution and flow of fluids within the reservoir. It signifies the preferential affinity of the rock toward one of the fluids present in the reservoir. Wetting is correlated with the capillary pressure (Pc) by means of the contact angle (CA), θ and the interfacial tension бlf in Eq. 2. Young’s equation correlates the CA to the IFT between the different phases comprising a reservoir system and is presented in Eq. 5 (Shojai Kaveh et al. 2016):

(5)

where бsf is the IFT between the solid and CO2, бsl is the IFT between the solid and liquid (brine), бlf is the IFT between reservoir liquid (brine) and CO2 and θ is the CA at the point of three-phase contact. In the literature, several classifications of wetting behavior exist in terms of CA values like those reported in (Fanchi 2018; Schön 2011). Those reported in (Schön 2011) are considered here, where rock surfaces are classified into water wet when 0° < θ < 70°, intermediate wet when 70° < θ < 110°, and oil wet when 110° < θ < 180°. In the context of this study, the wetting of the reservoir rock by model brines in the presence of CO2 is investigated as shown in Fig. 8.

Fig. 8
figure 8

Contact angle measurement of brines on Al-Sultani shale in a CO2 atmosphere at 60 °C

Full size image

For the 3 wt% NaCl brine, it is observed that the CA is an increasing function of pressure. This is, however, only valid for moderate pressures ranging between 10 and 20 MPa. At higher pressures, the CA decreases with increasing pressure. This can be attributed to the following: The CA is the result of the superposition of IFT between CO2, brine and rock as indicated by Eq. 5 (Espinoza and Santamarina 2010). By examining Fig. 6, it can be seen that the adsorption capacity of CO2 on the rock surface increases until a pressure of 20 MPa is reached, beyond which the adsorption capacity declines. The adsorption of CO2 molecules on the rock surface reduces the IFT between CO2 and the rock surface (бsf) and results in a higher CA according to Eq. 5. Figure 4 shows that the IFT between the CO2 and the brine (бlf) decreases until 20 MPa is reached. Referring back to Eq. 5, this would imply a reduction in the CA, however, that is not the case; therefore, it can be assumed that the effect of бsf is more pronounced than that of бlf in determining CA. Beyond 20 MPa, бsf decreases but бlf is relatively constant and therefore a reduction in CA is observed. All of this explains the transition of rock wettability from being intermediate wet at 10 MPa to being CO2 wet for the range of 16 to 26 MPa and the reversal of wettability again at 30 MPa (intermediate wet). This behavior is in line with the findings reported by (Arif et al. 2017; Shojai Kaveh et al. 2016) where it was observed that increasing the pressure makes the system more CO2 wet.

From a general point of view, brine salinity does not seem to impact the wettability as the rock is classified as intermediate wet at 10 MPa and CO2 wet at 20 MPa with both brines. However, the difference in CA measurements could be explained as follows: Examining Fig. 4 and Eq. 5 once again, it can be seen that a higher бlf increases the CA (бlf, 10 wt% > бlf, 3 wt%), which explains why the brine with the higher salinity exhibits higher CA at the respective pressures. This is also in line with the findings of (Arif et al. 2017) who measured CA and similarly showed an increasing CA for higher salinity brines on calcite, which is a major constituent of Al-Sultani shale as confirmed by the XRD results.

Conclusion

In the current study, the phase behavior and mutual interactions of binary and ternary fluid–solid systems have been investigated in view of their significance for oil extraction and CO2 storage. A series of tests have been conducted to assess the CO2 adsorption capacity of the rock, the CO2-oil and CO2-brine IFT along with the wettability of the rock surface at elevated pressures. In line with previous findings, the CO2-brine and CO2-oil IFT decrease as a function of pressure as mutual solubility is enhanced. The results also indicate that the CO2-oil IFT reaches a semi-plateau at 15 MPa beyond which no further reduction is observed. This implies that oil recovery will not be drastically enhanced when pressures higher than 15 MPa are applied. The CO2-brine IFT plateau also implies that the storage of CO2 at pressures higher than 20 MPa will not promote the dissolution of higher amounts of CO2 into the reservoir brine. Additionally, the IFT is observed to be an increasing function of salinity, which suggests that reservoirs with low salinity brines are more suitable for the application of carbon storage due to enhanced solubility trapping. This is also implied by the higher water wetting of low salinity brine, which promotes better capillary trapping of CO2 as a residual discontinuous phase below the brine.

Measurements of CA also reveal that water wetting decreases with increased pressure until an inversion occurs beyond 20 MPa, which is consistent with the adsorption tests that reveal a maximum adsorption capacity at 20 MPa, beyond which the excess adsorption isotherms drop, suggesting that this is the decisive property to explain the maximum in CA. Further, the diffusion coefficient is observed to qualitatively follow the rigid sphere model which estimates the coefficient of self-diffusion, implying that self-diffusion is the dominating mechanism in the process of mass transfer. As a general conclusion, it may be stated that increasing the pressure up to 20 MPa has mainly positive effects on oil mobility as well as CO2 storage capacity, which also takes its maximum value at the respective pressure where it may be inferred that the amount of stored CO2 via the so-called solubility and adsorption trapping mechanisms is maximized, indicating optimum process conditions of 20 MPa while the temperature interestingly exhibits only little influence.