Introduction

Impact of salinity on foamability and foam stability

The main technologies of enhanced oil recovery (EOR) in carbonate reservoirs are CO2, N2, and hydrocarbon gas injections (Memon et al. 2020). Gas fingering and early gas breakthrough can be prevented by injecting a foamy surfactant solution to reduce gas mobility and redirect gas flow (Spirov and Rudyk 2015).

The choice of surfactants for foam injection depends on their ability to withstand the harsh conditions of oil reservoirs such as high salinity, temperature, and pressure. The structure and stability of foams are determined by the ability of surfactant molecules to stabilize foam films, which depends on the type of surfactant and its concentration in the solution (Varade and Ghosh 2017). Foam stability decreases at higher temperature, but increases at higher salinity (Fuseni et al. 2018; Kahrobaei and Farajzadeh 2019).

An increase in salt concentration causes a decrease in the repulsion between the charged head groups of surfactant molecules. This leads to an increase in the adsorption and concentration of surfactant molecules at the interface and the binding of salt ions to the adsorbed surfactant ions. This results in subsequent compression of the electrostatic double layer (EDL) and a decrease in surface and interfacial tensions (Ruckenstein and Bhakta 1996). The surface tension gradient changes the tangential stress along the interface and reduces the rate of film thinning (Firouzi and Nguyen 2014). The foam lamellas become rigid and resistant to local deformation or rupture when thinning. Instead of collapse, a transition to a stable state occurs (Varade and Ghosh 2017).

Increase in foam stability due to a decrease in the foam collapse rate in saline surfactant solutions has been shown in experimental studies using bubble columns, but the bubbles size and initial foam volume decrease (Varade and Ghosh 2017; Behera et al. 2014; Nasr et al. 2020). For each type of surfactant solution, there is a limiting salinity, above which the lamellas rupture.

The results of experiments in bubble column cannot be directly transferred to a foam flow through the porous medium, which is determined by several global factors such as fluids velocity, pregenerated foam texture, gas fraction, length of core sample, geometry of porous channels, and permeability (Nguyen et al. 2000).

Foam formation is typically investigated in foam-flooding experiments (foam scans) through core samples at constant total flow rates and different gas fractions (fg).

The measured pressure gradient is converted into the apparent viscosity using Darcy’s equation:

$$ \mu_{{{\text{app}}}} = \frac{k}{{u_{t} }}\frac{{\left| {\Delta P} \right|}}{L} $$
(1)

where k (m2) is the core permeability, \(u_{t}\) (m3/s) is the total Darcy velocity, ∆P (Pa) is the pressure drop over the core, and L (m) is the core length.

Apparent viscosity increases with increasing dP and permeability and decreasing velocity for the specific core sample. dP and apparent viscosity are also dependent on foam viscosity, foamability, and foam stability. The presence of salt in the solution increases the viscosity of the flowing fluid but may inhibit foamability.

Data on salt tolerance obtained from foam core-flooding experiments are reported for several surfactants. The improved oil recovery has been reported in the presence of 22% of total dissolved solids for an ethoxylated amine surfactant (Elhag et al. 2018), Ethomeen C12 (Cui et al. 2016), and Duomeen TTM (Jian et al.2019). At 20% salinity, good foaming ability and foam stability have been observed for a system consisting of polyoxyethylene ether sulfonate and sulfobetaine (Sun et al. 2016) and for a system consisting of a hydrophone and alkoxy chain type (Puerto et al. 2012).

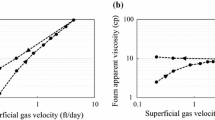
Most core-flooding experiments are conducted through sandstones with relatively high porosity and permeability. Higher apparent viscosity is achieved with higher permeability rock samples (Kahrobaei and Farajzadeh 2019). A point close to fg of 0.8 or 0.9, at which the rising curve falls sharply, indicates a transition foam quality, separating the low- and high-quality regimes. For example, an increase in apparent viscosity with increasing fg is observed in the Berea sandstone at 90 mD (Kapetas et al. 2016) and in the Fontainebleau sandstone at 55 mD (Gassara et al. 2017). However, permeability and pore geometry can have a significant impact on the shape of the apparent viscosity curve and transition foam quality. For the Fontainebleau sandstone with permeabilities of 121, 368, and 465 mD (Gassara et al. 2017) and for the Sister Berea sandstone at 160 mD (Kapetas et al. 2017), \(\mu_{{{\text{app}}}}\) is close to constant in low-quality regime. For the Bandera Gray sandstone at 6 mD, \(\mu_{{{\text{app}}}}\) decreases over most of fg range (Kapetas et al. 2017).

Carbonate rocks have relatively high porosity with lower permeability compared to sandstone rocks. The blocking capacity of foams increases with increasing permeability, which allows fractures or cavities to be plugged, solving the problem of channeling in heterogeneous formations. Foam can also be diverted from high-permeability zones to unswept zones in the upper part of reservoirs due to gravity override (Ma et al. 2013). The foam flow in a low-permeability medium is restricted by a narrow porous space. In our previous study, IOS foam formation was observed for 50 mD Indiana limestone with up to 8% NaCl and 0.6 gas fraction (Rudyk et al. 2019). No foam was formed at 9–11% NaCl.

To investigate whether foam can form at even lower permeabilities, the salinity effect on foam flow through tight Indiana limestone of 10 mD permeability is presented for internal olefin sulfonate (IOS) in the range of 1–12% NaCl (10–120 g/L NaCl) and compared to similar experiments with 50 mD Indiana limestone.

Materials and methods

Materials

The tests are carried out using Indiana Limestone of 10 mD of permeability purchased at Kochurek company. The diameter x length = 3.81 cm × 26 cm, porosity is 13.5%, and core pore volume (PV) is 40 cm3. Nitrogen (N2) gas and carbon dioxide (CO2) gas both with a purity of 99.98% are purchased from Oman Gas Company. The internal olefin sulfonate (IOS) Enordet 322 surfactant is provided by Shell Chemical. The surfactant concentration of 0.5% IOS is added in NaCl solution at the salinity of 1, 5, 8, 10, and 12% NaCl for the core-flooding experiments.

Experimental procedure

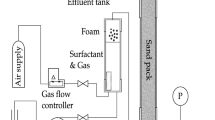
The core flood rig built for this study is shown schematically in Fig. 1. All the details of the operational procedure are given in (Rudyk et al. 2019). A limestone core sample in a coreholder is placed horizontally in an oven at 60 °C. An ICS hydraulic pressure pump is used to generate a confining pressure of 2000 psi. Nitrogen gas is injected at a total flow rate of 0.2 and 0.3 cm3/min to match the gas injection rate of the target oil field. For a specific total flow rate and gas fraction (gas fraction), the gas flow rates are calculated under normal conditions and then converted to 400 psi, as set by the Back-Pressure Regulator (BPR).

Fig. 1
figure 1

Layout of the experimental setup

Full size image

The surfactant solution and N2 gas are injected simultaneously at a constant total flow rate \(\left( {q_{t} } \right)\), liquid flow rate \(\left( {q_{l} } \right)\), and gas flow rate \(\left( {q_{g} } \right)\), corresponding to a specific gas fraction (fg). Gas and liquid flow rates for specific gas fractions are shown in Fig. 2. Injection continues until steady-state pressure is observed for the selected gas fraction (fg), which occupies at least 4 pore volumes of the injected fluid. The dP is measured, and apparent viscosity \((\mu_{{{\text{app}}}} )\) is calculated by Eq. 1.

Fig. 2
figure 2

Experimental gas flow rate (qg) and liquid flow rate (ql) of surfactant solution at the total flow rates of 0.2 cm3/min and 0.3 cm3/min and gas fractions (fg)

Full size image

The foam exiting the system is collected in a graduated cylinder at atmospheric pressure and laboratory temperature. The foam flow is recorded using a camera for the examination of foam texture. The length of the foam droplets (Ld) at the end of the pipe before falling is measured at each gas fraction (fg).

Results and discussion

dP and apparent viscosity at 1–12% NaCl

Experiments are performed using IOS surfactant solutions with 1, 5, 8, 10, and 12% NaCl to measure dP, calculate apparent viscosity, and observe the foam texture at the exit from the system. The permeability calculated prior to each foam scan is 10 mD for surfactant solutions at 1, 5, and 8% NaCl and 5 mD at 10% and 12% NaCl. The foam scans are performed using two total flow rates of 0.2 and 0.3 cm3/min.

An example of a foam scan is shown for 10% NaCl at 0.2 cm3/min in Fig. 3. Gas fractions are tested in a random order to reduce the effect of the previous state. Compared to the tests using 50 mD limestone described in (Rudyk et al. 2019, 2021), the curves are exceptionally smooth for all gas fractions. The fluctuations usually increase with increase in gas fraction as bursting gas bubbles affect the outlet pressure measurements. They are only noticeable at fg = 0.5, because in this test the surfactant solution in the supply container runs out. At the beginning of the next fg, dP remains at the same value as in the test at the previous fg for some time until all the previously formed foam has been displaced.

Fig. 3
figure 3

Foam scan at 10% NaCl and total flow rate of qt = 0.2 cm3/min, as example. Gas fractions (fg) are tested in random order

Full size image

dP and apparent viscosity (\(\mu_{app}\)) are plotted versus corresponding gas fraction in Fig. 4. Linear decreasing trends in the graphs of apparent viscosity allow comparison with the liquid flow rates (ql) shown in Fig. 2. The corresponding total flow rates are indicated by dashed lines across the apparent viscosity graphs in Fig. 4.

Fig. 4
figure 4

dP and apparent viscosity (μ app) at specific gas fraction (fg) obtained in foam scans at 1, 5, 8, 10 and 12% NaCl. Dashed lines in the plots of μ app vs. fg indicate the ql lines for qt = 0.2 and 0.3 cm3/min in Fig. 2. Breakdown points that can signify transition foam quality are shown as a circles with black borders. The arrows indicate the shift of breakdown points between two total flow rates

Full size image

At 1% NaCl, both dP graphs of 0.2 and 0.3 cm3/min decrease linearly starting at fg = 0.3 at about 400 psi (Fig. 4a). The slightly different slopes are caused by the difference in total flow rate. Both \(\mu_{{{\text{app}}}}\) graphs at 1% NaCl also closely follow the ql lines of the respective total flow rates, except for two points: fg = 0.2 at 0.3 cm3/min and fg = 0.3 at 0.2 cm3/min (Fig. 4b). The apparent viscosity does not exceed 0.04 Pa s and 0.02 Pa s at 0.3 cm3/min and 0.2 cm3/min, respectively. Both dP and \(\mu_{{{\text{app}}}}\) of 0.3 cm3/min are higher than of 0.2 cm3/min.

At 5% NaCl, the dP graph of 0.2 cm3/min decreases linearly within 0.2–0.6 fg interval but deviates from the general trend at 0.7 and 0.9 (Fig. 4c). The graph of 0.3 cm3/min is on average close to 440 psi in the 0.2–0.5 range but decreases at higher fg values. On each graph, two inflection points can be observed: 0.6 and 0.8 on the graph of 0.2 cm3/min and 0.5 and 0.7 on the graph of 0.3 cm3/min. This leads to the effect that the dP graphs of 0.2 cm3/min and 0.3 cm3/min have similar shape, but the graph of 0.3 cm3/min is visually shifted by 0.1 in the direction of decreasing fg. After conversion of dP to apparent viscosity, the graphs shift in such a way that the inflection points have similar values: on average 0.028 Pa s and 0.02 Pa s for the first and second inflection points, respectively (Fig. 4d). Only two points 0.6 and 0.9 deviate from the ql line at 0.2 cm3/min. The deviation from the ql line of 0.3 cm3/min is significant in the range of 0.4–0.7. The dP of 0.3 cm3/min is higher than of 0.2 cm3/min, but the opposite is true for apparent viscosity.

At 8% NaCl, the dP graph of 0.2 cm3/min decreases linearly in the range of 0.2–0.7, sharply decreasing at higher values (Fig. 4e). The dP graph of 0.3 cm3/min decreases almost to linear, starting from 0.4. Linear intervals on the \(\mu_{{{\text{app}}}}\) graphs have different slopes, which fully correspond to the slopes of the ql lines for the corresponding total flow rates (Fig. 4f). The dP of 0.3 cm3/min is higher than that of 0.2 cm3/min, but the apparent viscosity of 0.2 cm3/min is higher than that of 0.3 cm3/min.

The highest dP does not exceed 420 psi and 516 psi at 0.2 cm3/min and 0.3 cm3/min, respectively, and the apparent viscosity of 0.06 Pa s at both 5% and 8% NaCl.

At 10% NaCl, the dP graphs decrease over the entire range of gas fraction. An increase is observed at fg = 0.6 for 0.2 cm3/min and fg = 0.5 for 0.3 cm3/min (Fig. 4g). As with 5% NaCl, the graphs have similar shapes, but the graph of 0.3 cm3/min is shifted from 0.2 cm3/min by 0.1 in the direction of decreasing fg. This shift can also be observed in the graphs of apparent viscosity (Fig. 4h). Points 0.5 and 0.9 at 0.3 cm3/min and points 0.6 and 0.9 at 0.2 cm3/min deviate from the corresponding ql lines. dP does not exceed 200 psi and 300 psi for 0.2 cm3/min and 0.3 cm3/min, respectively, and an apparent viscosity of 0.01 Pa s. Both dP and apparent viscosity are higher for 0.3 cm3/min.

At 12% NaCl, dP is above 800 psi for 0.2 cm3/min and above 940 psi for 0.3 cm3/min, which is close to the 1000 psi limit pressure for this equipment. For both total flow rates, dP is close to constant in the 0.2–0.5 range, decreasing with high gas fraction. As with lower salinities, bends are observed at 680 psi on average at 0.6–0.7 for 0.2 cm3/min and 0.7–0.8 for 0.3 cm3/min. dP is higher for 0.3 cm3/min, while the apparent viscosity is higher for 0.2 cm3/min. The shape of the graphs for 12% NaCl differs from the graphs for lower salinities, showing a Newtonian plateau at low fg and a decrease at high fg values.

Taking into account the permeability of 10 mD, calculated before testing 1, 5, and 8% NaCl and 5 mD before testing 10% NaCl and 12% NaCl, the maximum apparent viscosity is 0.01 Pa s at 10% NaCl and 0.04 Pa s at 12% NaCl.

For all salinities, dP of 0.3 cm3/min is higher than of 0.2 cm3/min, as for ql and qg in Fig. 2. However, apparent viscosity of 0.3 cm3/min is higher than of 0.2 cm3/min for 1% and 10% NaCl due to low dP. In contrast, the apparent viscosity at 0.2 cm3/min is higher than at 0.3 cm3/min for 5, 8, and 12% NaCl due to high dP. This shows that the dP values affect the dependence of apparent viscosity on the total flow rate when converting dP to apparent viscosity. Thus, the dependence of the apparent viscosity on the total flow rate may not be as straightforward as for dP and may vary from case to case.

Dependence of dP and \(\mu_{{{\text{app}}}}\) on salinity

The dP and apparent viscosity are compared for the specific total flow rates in Fig. 5. For both total flow rates, the dP and \(\mu_{{{\text{app}}}}\) increase in the following order of salinity: 10%, 1%, 5% and 8%, and 12%. The graphs of 5% and 8% NaCl overlap closely at both total flow rates showing insensitivity to salinity. Compared to 5% and 8% NaCl, dP of 12% NaCl at both total flow rates is significantly higher, but the apparent viscosity does not show such a significant difference.

Fig. 5
figure 5

Salinity effect on the dP and apparent viscosity for Indiana limestone of 10 mD: a and b qt = 0.2 cm3/min; c and d qt = 0.3 cm3/min. The data of Indiana limestone of 50 mD are added for comparison (Rudyk et al. 2019). Dashed lines indicate \(f_{g}^{{{\text{tr}}}}\) at 5% and 10% NaCl

Full size image

The results of 0.3 cm3/min are compared with our previous results for 50 mD limestone at 1, 5, and 8% NaCl (Fig. 5c, d). For 50 mD, dP and \(\mu_{{{\text{app}}}}\) increase in the following order: 8, 1, 5% NaCl. Compared to 1% NaCl, dP and \(\mu_{{{\text{app}}}}\) were higher at 5% NaCl due to higher foam density and viscosity and lower at 8% NaCl due to reduced foamability (Rudyk et al. 2019).

For the same salinities of 1, 5, and 8% NaCl, dP in the experiment with 10 mD limestone is higher by about 100–400 psi than with 50 mD limestone dependent on fg, while the apparent viscosities of 1% and 5% NaCl are higher for 50 mD (Fig. 5c, d). The graphs for 8% NaCl are close and have similar shapes for both 10 mD and 50 mD (Fig. 5d). The slopes are sharper for \(\mu_{{{\text{app}}}}\) graphs of 50 mD limestone in higher gas fraction regime (dotted lines).

The limiting salinity for IOS foam formation through 50 mD Indiana limestone and 255 mD Berea sandstone was determined at 8% NaCl as fine foam was observed up to 0.7 (Rudyk et al. 2019, 2020). At the higher salinity of 9% and 10% NaCl, only slight pressure drops of less than 10 psi and single bubbles bigger 0.4 cm in diameter were observed. At the same 10% and 12% NaCl, dP and apparent foam viscosity through limestone of 10 mD limestone are much higher, compared to 50 mD limestone.

The experiments are not conducted above 12% NaCl due to lack of surfactant. Therefore, the highest salinity level at which the foam is formed for 10 mD limestone is taken as 12% NaCl. Thus, the lower permeable system of the limestone pore space significantly increases the salinity limit at which the foam can form.

Kukizaki and Baba 2008 found a linear correlation between foam bubble sizes and membrane pore diameters formed in different surfactant solutions. The pore walls support the existence of lamellas and smaller bubbles, which would otherwise transform into larger bubbles due to gas diffusion caused by the pressure drop across the bent lamellas (Nguyen et al. 2000). However, if the slip between the bubbles and the grain wall is significant, as for aqueous foams, the yield stress of the foam due to low permeability may be negligible and the foam flows freely. Therefore, the increased limiting salinity, which is 12% NaCl at 10 mD compared to 8% NaCl at 50 mD and 255 mD, can be explained by a narrower porous system acting as a membrane.

On the other side, the presence of salt in the surfactant solution reduces foamability, making the foam texture coarser as fg is increased, but the foam lamellas become denser, more viscous and stable up to the limiting salinity. For example, the \(\mu_{{{\text{app}}}}\) of foam in brine is 1.5–3 times higher than in deionized water, starting from fg = 0.5 (Cui et al. 2016). In addition, the deposition of salt and surfactant in a porous medium can reduce permeability leading to an increase in dP and apparent viscosity.

Thus, the very low dP and apparent viscosity at 10% NaCl can be explained by the reduced foamability, while the very high dP and apparent viscosity at 12% NaCl by the higher viscosity of the saline solution.

The difference between total flow rates can be expected to be eliminated by Darcy’s equation after dP is converted to apparent viscosity, resulting in overlapping of \(\mu_{{{\text{app}}}}\) graphs at different total flow rates. However, they do not overlap at any salinity in Figs. 4 and 5, even with such a small difference in total flow rates. Most of the literature data also indicate the flow rate dependence (Nguyen et al. 2000).

According to Fig. 4, dP of 0.3 cm3/min is higher than of 0.2 cm3/min for all salinities. At low dP, dividing by the total flow rate using Eq. 1 keeps the apparent viscosity graph of higher total flow rates above the lower ones like for 1 and 10%. At high dP, dividing by the total flow rate shifts the apparent viscosity graphs for lower flow rates above the higher total flow rates like for 5%, 8%, and 12% NaCl. We previously observed such a shift in experiments with 50 mD Indiana limestone (Rudyk et al. 2019). For example, the dP value measured at different pressures and the total flow rate at 5% NaCl were close. After conversion to apparent viscosity, the graphs of lower total flow rate shifted significantly higher the higher total flow rate.

Transition foam quality

Transition foam quality divides the foam scan into a low-quality regime (low gas fraction) and a high-quality regime (high gas fraction) using the criterion of maximum apparent viscosity. In most publications, the apparent viscosity increases with fg up to transition foam quality at fg = 0.9 (Farajzadeh et al. 2015). Some researchers did not find experimentally either the lower limit of the limiting capillary pressure regime, or the sharp boundary of the low-quality regime (Nguyen et al. 2000).

The criterion of breakdown point at maximum apparent viscosity can be applied to both graphs of 12% NaCl which are constant up to 0.5 for 0.2 cm3/min and 0.6 for 0.3 cm3/min and decrease at higher fg (Fig. 5a, c). The graphs of 5% and 8% NaCl at 0.3 cm3/min do not vary significantly at lower fg (Fig. 5c). Breakdown points of 0.4 can be selected as transition foam quality (\(f_{g}^{{{\text{tr}}}}\)) for 8% NaCl and 0.5 for 5% NaCl.

However, the graphs of 5% and 8% at 0.2 cm3/min linearly decrease up to 0.6 and 0.7, respectively, before breaking down (Fig. 5a). In addition, the graphs have more linear shape at 0.2 cm3/min, than at 0.3 cm3/min. This indicates that the foam creates a higher resistance to flow through the porous channels at 0.3 cm3/min, while the foam arranges quickly enough to more freely pass through the porous medium at 0.2 cm3/min. Likewise, both graphs at 10% NaCl decrease linearly over the entire fg range. Humps can be observed at the same fg as at 5% NaCl for both total flow rates.

Similar to 1% NaCl, a linear decrease over almost the entire fg range was previously observed for 50 mD limestone at 8% NaCl (Rudyk et al. 2019) and for the low foaming Soloterra 963 surfactant (Rudyk et al. 2021). Thus, the transition foam quality is 0.4 for 0.2 cm3/min and 0.3 for 0.3 cm3/min at 1% NaCl, which implies that almost all graphs are in high-quality regime.

Transition foam quality shifts along fg axis depending on the permeability or the total flow rate. An increase in \(f_{g}^{{{\text{tr}}}}\) with increasing total flow rate has been reported in (Alvarez et al. 2001). For Indiana limestone of 50 mD, we also observed a shift in \(f_{g}^{{{\text{tr}}}}\) to higher values with increasing total flow rate (Rudyk et al. 2019).

With increase in total flow rate, we observed a shift in \(f_{g}^{{{\text{tr}}}}\) to higher values for IOS surfactant, but to lower values for Soloterra 963 when injecting through 50 mD limestone (Rudyk et al. 2019, 2021).

However, all graphs of 0.3 cm3/min are shifted toward decreasing fg by 0.1 compared to 0.2 cm3/min, with the exception of 12% NaCl. This may be due to the higher foam viscosity at a lower total flow rate.

Shifts of \(f_{g}^{{{\text{tr}}}}\) toward higher fg with increasing permeability are noted in (Farajzadeh et al. 2015). Indeed, \(f_{g}^{{{\text{tr}}}}\) of 0.5 for 10 mD limestone is lower than 0.6 for 50 mD limestone or 0.7 for 255 mD Berea sandstone, all at 5% NaCl and 0.3 cm3/min (Rudyk et al. 2019, 2020).

Dependence dP and \(\mu_{{{\text{app}}}}\) on ql and qt

Liquid or gas flow rates can affect foam flow in different ways, even if they are fractions of the total flow rate. The gas flow rate is reported to mainly regulate the foam flow but it depends on the regime (Behera et al. 2014; Alvarez et al. 2001). Most of the authors agreed that gas velocity is the governing factor in low-quality regime and liquid velocity in high-quality regime. According to Osterloh and Jante (1992), dP was linearly proportional to gas velocity in low-quality regime and dependent on liquid velocity in high foam quality regime. According to Ettinger and Radke (1992), dP was linearly proportional to liquid velocity in high-quality regime.

The linearity of the graphs of dP or \(\mu_{{{\text{app}}}}\) over a significant range of gas fraction allows determining that they follow the lines of liquid flow rate of the corresponding total flow rates.

The dP and \(\mu_{{{\text{app}}}}\) are plotted depending on the corresponding ql in Fig. 6. Four dP graphs of 5% and 8% NaCl at both total flow rates are superimposed, showing a low sensitivity of dP to differences in salinity and total flow rate. The dP graphs of 1% and 10% NaCl do not overlap while they are close for 12% NaCl (Fig. 6a).

Fig. 6
figure 6

Salinity effect on the dP and apparent viscosity for Indiana limestone of 10 mD: a dashed line is a mean function for dP of four curves (5% and 8% NaCl of qt = 0.2 and 0.3 cm3/min); b dashed lines are mean functions for specific salinity and two total flow rates (0.2 and 0.3 cm3/min)

Full size image

The opposite picture can be observed for apparent viscosity plots (Fig. 6b). The overlapping of apparent viscosity graphs of 0.2 and 0.3 cm3/min at 1% and 10% NaCl (low dP) shows that the influence of the total flow rate has been eliminated, resulting in the overlapping of apparent viscosity graphs (Fig. 6b). Mean function for 0.2 cm3/min and 0.3 cm3/min begins at (0;0) like at 1% NaCl for 50 mD limestone, while the mean functions of higher salinities have higher y-intersections.

In contrast, the \(\mu_{{{\text{app}}}}\) graphs for 5% and 8% NaCl are not grouped by equal salinity. They are grouped according to equal total flow rates, which can be explained by the insensitivity of the foam to the difference in salinity in this range. The line of mean function for 0.2 cm3/min is higher than for 0.3 cm3/min for 5, 8, and 12% NaCl. The lines of the mean functions of 1% NaCl and the two total flow rates for 5 and 8% NaCl are almost parallel.

It can be concluded that ql is the factor that controls foam flow for 10 mD limestone in high-quality regime because it starts at \(f_{g}^{{{\text{tr}}}}\) less than 0.5 for most of graphs. However, the line of mean function of 0.2 cm3/min for 5 and 8% NaCl crosses the low-quality regime and not the high-quality regime if \(f_{g}^{{{\text{tr}}}}\) is determined at breakdown points of 0.7 for 8% NaCl and 0.6 for 5% NaCl. Then, for these cases, the opposite conclusion can be made that ql is the governing factor in the low-quality regime and, probably, the gas flow rate in the high-quality regime. On the other hand, breakdown points could be mistaken for \(f_{g}^{{{\text{tr}}}}\) because they do not meet the criterion for maximum apparent viscosity. The sharp decrease at higher fg can be caused by changes in foam texture in the intermediate state between the fine and coarse foam. Gauglitz et al. (2002) explained such fluctuations as a third, unstable steady state, in which the state of the foam spontaneously changes due to perturbation of the pressure gradient. Similar deviations were also observed for the surfactant Soloterra 963 in a similar experiment using 50 mD limestone (Rudyk et al 2021).

In the described experiment, the decreasing functions of the dP and \(\mu_{{{\text{app}}}}\) demonstrate that the foam flow is highly dependent on the liquid flow rate, which can be used to simulate the foam flow. The linear correlations between apparent viscosity and ql allow prediction of \(\mu_{{{\text{app}}}}\) at most fg values. Deviations, however, are expected at the highest and lowest ql and corresponding fg.

Length of foam droplets

A high dP can be produced with a flow of very coarse foam due to the high viscosity of the saline solution and the low rock permeability. A high dP alone and the resulting high apparent viscosity do not necessarily signify the generation of a strong foam.

However, the fine foam is more effective in gas trapping and blocking. Since the foam cannot be seen inside the coreholder, attempts have been made to find a relationship between bubble size at the exit and mobility reduction (Nguyen et al. 2000). A correlation between the bubble size of the foam exiting the core and the dP is reported in (Tang and Kovscek 2006).

Instead of bubble size, we measured the length of the foam droplets before they fall to indicate the viscosity of the flowing foam at the outlet because the bubble size often exceeds 0.5 cm. (Rudyk et al. 2020). It has been found that the length of the foam droplet is inversely proportional to the apparent viscosity, that is, higher apparent viscosity is accompanied by shorter foam droplets. The length of foam droplets (Ld) is plotted vs. fg in Fig. 4 for the specific salinity. As the foam droplet length increases, the foam texture changes from very fine to coarse in the fg range from 0.2 to 0.9.

Almost linearly, \(\mu_{{{\text{app}}}}\) decreases and Ld increases in the range of 0.4–0.9 for 0.2 cm3/min and in the range of 0.3–0.8 for 0.3 cm3/min at 1% NaCl (Fig. 4b, k). A similar picture is observed for 8% NaCl at 0.2 cm3/min, for which the Ld and apparent viscosity change in opposite directions (Fig. 4f, m).

In other cases, although minor deviations are repeated, the apparent viscosity decreases over almost the entire fg range, while the Lg graphs are nearly constant between 0.4 and 0.8. For example, two humps at 0.5 and 0.7 can be observed in both \(\mu_{{{\text{app}}}}\) and Ld graphs, indicating that these deviations are not random and are associated with changes in foam viscosity at 5% NaCl (Fig. 4d, l). Very fine foam texture with undistinguishable bubble size is observed at fg = 0.2 and 0.3 at both total flow rates while distinguishable bubbles appear at fg > 0.4.

Ld graph of 8% NaCl at 0.3 cm3/min is also near constant while the corresponding \(\mu_{{{\text{app}}}}\) graph decreases in the range of 0.5–0.8 (Fig. 4f, m).

Both \(\mu_{{{\text{app}}}}\) graphs of 10% NaCl decrease while the corresponding Ld graphs increase up to inflection points of 0.5 and remain nearly constant in the range of 0.6–0.9.

This is the opposite to what we have observed for 50 mD limestone. For 50 mD limestone, the apparent viscosity was constant in low-quality regime, but the Ld increased (Rudyk et al. 2019).

The explanation may be that the droplet volume occupies a small fraction of the pore volume in the higher permeability rock. The displacement of the increasing lengths of droplets due to the increase in fg does not significantly affect dP in low-quality regime. In contrast, droplet volume occupies a big portion of the pore volume in low permeability rock. Insignificant changes in the length of displaced droplets due to the increase in fg lead to a significant decrease in dP.

At 12% NaCl, \(\mu_{{{\text{app}}}}\) graphs and Ld graphs have close values from 0.2 to inflection points of 0.5. Fine foam texture is observed in the range of 0.2–0.5 while the foam consists of a garland of three big bubbles with some fine foam on the boundaries between bubbles at 0.6 and 0.7 and bigger bubbles at 0.8. Compared to the experiment with 50 mD limestone, gas breaks through starting at fg = 0.4 at salinity above 8% NaCl.

Longer foam droplets should indicate a lower foam viscosity at the outlet. For the exception of 1% NaCl, higher dP is accompanied by longer droplets at higher total flow rate of 0.3 cm3/min. However, longer droplets accompany lower apparent viscosity at 0.3 cm3/min for 5% and 8% NaCl, and at 0.2 cm3/min for 1% NaCl, as in the experiment with 50 mD limestone. This shows that the droplet length correctly indicates the apparent viscosity. For 10% and 12% NaCl, Ld at the two total flow rates are very close over at most of fg, which makes it difficult to capture the difference. In addition, the factor of high salinity and reduced permeability due to possible precipitation of salt can be important.

Foam texture

The changes of foam texture with fg are examined to study if the similarity in foam textures may explain the overlap of the dP or \(\mu_{{{\text{app}}}}\) curves at different salinities or total flow rates.

The visual inspection of the foam droplets reveals that the foam is finer at 0.3 cm3/min than at 0.2 cm3/min at the same fg and salinity. The example is shown for 8% NaCl at 0.2 cm3/min and 0.3 cm3/min in Fig. 7.

Fig. 7
figure 7

Photographs of the foam droplets exiting the system at increasing gas fraction at 8% NaCl and 0.2 and 0.3 cm3/min of total flow rate

Full size image

At 0.3 cm3/min, the foam textures of 5% NaCl and 8% NaCl are similar at a specific fg, which may explain their close length of droplets and overlap of apparent viscosity. However, irrespective the overlap of the corresponding apparent viscosity graphs, the foam is finer and the droplets are shorter for 5% NaCl, compared to 8% NaCl, at 0.2 cm3/min. In addition, the foam texture for 10 mD limestone at 8% NaCl is very different, compared to 50 mD limestone, regardless of the overlapping of the apparent viscosity graphs in Fig. 5d.

Meanwhile, foam textures are similar at the limiting salinities for 50 mD limestone (8% NaCl) and 10 mD limestone (12% NaCl), but the apparent viscosities are different.

Consequently, foam textures can indicate apparent viscosity when the same rock samples are compared, but different foam textures can produce the same dP/apparent viscosity values in different rock samples. Thus, apparent viscosity alone cannot reflect foam quality and texture.

Conclusions

  1. 1.

    Foam formation was observed up to 12% NaCl, while no foam is formed even at 9% NaCl through a 50 mD limestone core. Thus, a porous system with a lower permeability increases the limiting salinity at which foam can form. This expands the rock types and reservoir conditions in which the surfactants can be applied.

  2. 2.

    dP and apparent viscosity decrease over almost the entire gas fraction range at 1–10% NaCl, compared to an increase in \(\mu_{{{\text{app}}}}\) in highly permeable rocks. With an increase in the gas fraction, dP increases in accordance with the flow rates of injected liquid and gas, but the apparent viscosity depends on the magnitude of dP. Low dP is measured at 1% and 10% NaCl, and high dP is measured at 5%, 8% and 12% NaCl. Thus, at higher total flow rate, the dP is higher for all salinities, but the apparent viscosity is higher at 1 and 10% NaCl (low dP) and lower at 5%, 8%, and 12% NaCl (high dP).

  3. 3.

    Linear correlations found between apparent viscosity and liquid flow rate in high-quality regime allow predicting \(\mu_{{{\text{app}}}}\), which can be considered when simulating foam flow.

  4. 4.

    As the liquid flow rate increases, the apparent viscosity overlap based on salinity for cases exhibited low dP and based on total flow rate for the cases exhibiting high dP.

  5. 5.

    Changes in apparent viscosity are mimicked by changes in the length of the foam droplets, which also correspond to the dependence on the total flow rate. Apparent viscosity alone is not representative of foam texture, as different foam textures can generate similar apparent viscosities for different rocks and experimental conditions.