Abstract
Although gas-lift is an established technology for improving the performances of oil production wells, the simplicity, robustness and accuracy of gas-lift models remain to be fully resolved. As an improvement on the traditional practice, this paper proposes a new approach for modelling the performance of gas-lifted wells at steady-state conditions. The conceptual framework splits the wellbore into two segments. The segments are of unique characteristics, yet they are hydraulically connected. While one segment is controlled primarily by the upstream reservoir-sandface conditions, the dynamics of the second segment are dominated by the lift-gas. This work results in a new four-phase model and an accompanying workflow for analysing the steady-state performance of a gas-lifted well. Using examples from fields operating under diverse conditions in the Niger Delta and North Sea, the new model is validated against a commercial wellbore performance simulator and actual field results. The new model yields average absolute deviation (AAD) of 2.7 and 5.4% against the commercial simulator and field results, respectively. Notwithstanding its relative simplicity, the range of AAD recorded for the new model and workflow attests to its robustness and applicability in practice. In addition to its simple mathematical form, a competitive feature of the proposed model relative to the commercial simulator and most other models is that it accounts for the four phases (gas, oil, water and solid particulates) typically encountered in mature oil production wells and brown fields.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Gas-lift is a mature technique applied to assist production in oil fields. It entails the injection of compressed gas from the surface into the wellbore such that the injected gas mixes with the native (formation) fluids in the wellbore. It improves production rate of the native fluids by reducing the bulk density, and hence the hydrostatic head, in the wellbore. While the lift-gas reduces the hydrostatic head in the wellbore, the overall production optimization objective demands that this hydrostatic-related gain be balanced against the increased frictional effects caused by improved fluidity in the wellbore. Therefore, the overarching objective is to maintain the well performance curve, which relates the output (liquid production rate) and the input (gas-lift injection rate), at the optimum conditions. In a typical gas-lifted oil well, the lift-gas is injected into the tubing–casing annulus and it flows down to the injection valves, through which it enters the tubing.
Gas-lift is one of the most widely used artificial lift methods in the exploration and production industry. Its wide applicability and competitive advantage over other artificial lift methods are attributed to several factors. These factors include its versatility in terms of terrain, well trajectory, relatively low operating costs and the ease of valve replacement (BenAmara 2016; Bellarby 2009; Vázquez-Román and Palafox-Hernández 2005; Alarcón et al. 2002; Chia and Hussain 1999; Winkler 1987). Aside from its well-known applications in well clean-up, ramping up production and resuscitating dead wells, gas-lift can potentially be used to extend the stable production limit of an oil well, hence increasing its operating envelop and production lifetime as well as improving project economics (Yadua et al. 2020).
While the basic principles remain largely the same, gas-lift technology has evolved over the years. The evolution includes the transition from the injection of compressed air to the use of natural gas to aid well performance (Beckwith 2014; Robertson et al. 1987). Though it entails the cycling of associated gas in a closed system, gas-lifting applications partly reduce flaring and fugitive emissions, hence mitigating carbon footprints and other environmental concerns in many oil fields (Mousavi et al. 2020; Lawal et al. 2017). With increasing demands for the oil and gas industry to improve on environmental stewardship, one can expect gas-lift to remain a prominent artificial lift technique in the foreseeable future.
As an industrial production process within a delicate and capital-intensive system, gas-lifting requires proper modelling and simulations to aid decision-making. The primary objective of modelling the performance of a gas-lifted well is to establish a reliable well performance curve, which is then used to determine the optimum operating conditions for such wells. Reliable models facilitate system design and management. In this regard, there are two broad categories of single-well models for describing continuous gas-lift operations. These categories are (i) mechanistic and (ii) empirical models. Mechanistic models are generally applicable to all systems because they are based on first principles. On the other hand, empirical models are usually employed where process analysis proves too complicated and computationally expensive. Moreover, the usefulness of empirical models may be limited by the size of the problem as well as the accuracy of the empirical dataset underlying such models (Garrouch et al. 2020).
The traditional mechanistic models for gas-lifted oil wells employ nodal analysis, which combines an inflow performance relationship (IPR) and a vertical lift performance (VLP) model to determine the production rate at a given node in the system (Guo et al. 2007; Beggs 2003). Although the gas-lift process is quite simple, it is an irony that these conventional models are intricate, partly due to the complexities of both the established VLP models and their corresponding nodal analysis algorithms (Guo et al. 2007). Notwithstanding their varied sophistications, the age-long questions about the general robustness and consistency of the various VLP correlations remain valid. Departing from the nodal analysis method, Vázquez-Román and Palafox-Hernández (2005) proposed a mechanistic model that is based on mass, energy and momentum balances. Though this model is promising, its major drawbacks include (i) downplays the importance of the reservoir–well interaction (inflow performance), (ii) the challenging and impractical requirement to provide the molar fraction of each chemical species in the wellbore and (iii) its unrealistic assumption of a uniform temperature in the wellbore.
On the empirical models, Garrouch et al. (2020) highlighted some models which were developed with tools such as artificial intelligence, experimental design and dimensional analysis. While these models may seem reliable, it is worth noting that they bear the inherent limitations of empirical models; hence, they are limited in applicability beyond the underlying datasets used in their developments. For example, the Garrouch et al. (2020) model is based on a database of 388 gas-lifted vertical oil wells in the Middle East, and it only yields the technical optimum gas injection rate and the corresponding maximum oil rate. Consequently, it is inherently not suitable for deviated wells. Specifically, this model cannot support the prediction of the economic optimum injection rate, and it is incapable of evaluating other key factors, such as productivity index, that influence the performance of gas-lifted wells.
For simplicity, some researchers have approximated the complex multiphase flow in gas-lifted wells as single phase. While such appropriations may not be unreasonable at early stages of production when the well is producing at bubble flow regime, such approximations are obviously inappropriate for mid- to late lifetimes when water cut, sand cut and gas cap production complicate the flow behaviour. This limitation motivated some workers to consider two-phase approximation in the tubing (Hasan et al. 2010; Guet et al. 2005; Shi et al. 2005). Although they have yielded good performances in a number of cases, such approximations have not fully addressed the problem.
As a contribution to the existing body of works on the analysis and management of continuous gas-lift operations, this paper proposes a relatively simple and reliable mechanistic model. We take advantage of the recent work by Yadua et al. (2020) on the stabilized production rate of oil wells. For convenience, the wellbore is split into two segments that are connected hydraulically. The inflow behaviour is described by the productivity index, which is applicable under steady and semi-steady-state conditions. Rather than employing traditional empirical correlations to describe VLP, we defer to a first-principles approach to develop the VLP used in this work. The VLP model, which considers multiphasic (four phases) flow, is described as a function of wellbore geometry, fluid and other thermodynamic variables. For completeness, the proposed model accounts for the four phases of gas, oil, water and solid particulates in the production stream. The novelty of this paper is in the segmentation of the wellbore and the treatment of the multiphase VLP of a gas-lifted oil well.
This paper is segmented into three main sections. The first part describes the physical problem, the underlying principles and development of a new set of analytical models and solution procedure for analysing the performance of gas-lifted oil wells. The second part presents relevant theoretical and field examples, which are used to demonstrate the practicality of the proposed model and workflow. The results of validation against a commercial wellbore performance simulator as well as field data are discussed. Finally, relevant concluding remarks and scope for further work are articulated.
Model formulation
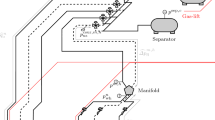
In a gas-lifted oil well (Fig. 1), the sandface-wellhead production flow path can be divided into two parts: (i) the part above the gas injection valve (segment A) and (ii) the part below the same valve (segment B). Because the injected (lift) gas is relatively light, it flows upward and mixes with the native fluids in segment A. Conversely, under normal operating conditions, the injected gas does not enter segment B because buoyancy inhibits its downward flow.
Given the foregoing description of the physical problem, we seek a simple mathematical model for evaluating the performance of a gas-lifted oil well under steady-state conditions. In particular, the focus is on the stability of the net oil flow as a result of the interactions between the upward flowing multiphase mixture from the reservoir and the lift-gas. For completeness, we account for the four phases often encountered in mature oil production wells. The four phases are oil, gas, water and solid (sand) phases. Although we have taken sand as the solid phase of interest in this work, the principles presented can readily be extended to account for other production-related solids such as wax, scales and asphaltene, if required.
The following are key assumptions underlying the proposed model (i) steady-state system, (ii) homogeneous and simple heterogenous flow, (iii) uniform tubing internal diameter across segments A and B, (iv) neither the native nor lift-gas is soluble in water and (v) one-dimensional flow.
The first assumption eliminates the complexity of rigorous modelling of the transients associated with gas-lifting (Mahdiani and Khamehchi 2015; Jahanshahi et al 2008). Rather, we focus on gaining insights into the key influence of the lift-gas on the overall flow stability. The second assumption, which involves a predominance of bubble flow in a turbulent regime, simplifies the formulation as it ignores slippage. The remaining assumptions further simplify the problem in terms of flow geometry and the treatment of phase equilibria.
Due to its higher gas fraction, which is partly caused by phase segregation, the bulk flow in segment A is expected to have a lower average mixture density than its counterpart in segment B. Therefore, for convenience, it is necessary to treat the hydraulics of these segments differently at first instance and then integrate both to understand the overall system hydraulics.
Accounting for frictional and hydrostatic losses across segments A and B, the bottomhole flowing pressure (BHFP) of the VLP relationship is given by
The definitions and units of the quantities in Eq. 1 and other equations in this paper are presented in the nomenclature section.
According to Yadua et al. (2020), the frictional and gravitation pressure loss terms are expressed as
On the other hand, the BHFP of the IPR is given by
At the operating (equilibrium) point of the system, the inflow and outflow performances are equal. Therefore, substituting Eqs. 2 and 3 in Eq. 1, while recognizing the independence of the applicable segments, and equating Eqs. 1 and 4 yield the following equation.
The resulting equilibrium equation (Eq. 5) is a quadratic, with the solution presented in Eq. 6. The positive root of this quadratic equation yields the “stabilized” (or equilibrium) liquid production rate, QLS at the prevailing conditions. The method and correlations used to estimate the average mixture density (ρm) are discussed in appendices A and B.
where
Solution procedure
Given the number of unknowns versus the number of mathematical equations, the problem is not well posed; hence, an iterative solution procedure is required. The problem is solved by reaching three (3) convergence conditions simultaneously. To aid the solution, we developed a simple tool that implements the following solution algorithm (Appendix C).
-
The value of lift-gas injection rate, Qgi, is required as an input
-
A guess of RiL is provided (RiL ≥ 0 SCF/STB); then, RiL is iterated until Eq. 10 is satisfied within a specified tolerance
-
This convergence condition ensures that the model reliably calculates (within prescribed tolerance) the RiL and QLS that characterize the prevailing state of the well–reservoir system
$${\text{ii}}{.}\quad P_{v} - \left( {P_{wh} + \Delta P_{fA} + \Delta P_{gA} } \right) = 0.$$(11) -
Pwh is an input. For practical purposes, it is considered as some target minimum Pwh that should be achieved for flow assurance downstream of the wellhead in an integrated production system
-
A guess of Pv is given (Pwh < Pv < Pr); then, Pv is iterated until Eq. 11 is satisfied within a prescribed tolerance
$${\text{iii}}{.}\quad P_{wf} - \left( {P_{v} + \Delta P_{fB} + \Delta P_{gB} } \right) = 0.$$(12) -
The Pv value in every iteration step (Eq. 11) is used in Eq. 12
-
A guess of Pwf is given (Pv < Pwf < Pr); then, Pwf is iterated until Eq. 12 is satisfied within a defined tolerance
-
Given the importance of fluid density on system performance (Eqs. 5 and 6) and the dependence of density on pressure (and temperature), the aim of the last two convergence conditions is to estimate the average in situ mixture densities in both segments of the well.
Assuming a simple linear sandface-wellhead temperature profile, the tubing temperature at the injection valve location is estimated as follows. Figure 2 illustrates the workflow for implementing this solution procedure in practice.
Model validation and results
The validity of the proposed model and the accompanying solution procedure is examined. For robustness, we consider both theoretical and field examples, covering different well profiles from different operating environments and basins. These examples demonstrate the applicability of the model as a predictive and diagnostic aid. Additionally, the examples provide results of some sensitivity tests conducted to gain insights into the key variables that control the performance of a gas-lift oil well at steady-state conditions.
Theoretical validation
This entails conducting various sensitivity tests using dataset for a hypothetical well A-1. As a benchmark, we compare the results of the proposed model against PIPESIM (version 2017.1), which is a commercial well performance simulator developed by Schlumberger.
Specifically, we evaluate sensitivities of the stabilized flow rate of a gas-lifted oil well to (i) injection (valve) depth, (ii) lift-gas injection rate, (iii) lift-gas specific gravity, (iv) wellhead flowing pressure (WHFP), (v) well length, (vi) liquid productivity index (PI) and (vii) solids content. For a given set of input data, these sensitivity tests were conducted with our proposed model and its complementary solution procedure.
Subsequently, the same set of sensitivity tests was repeated with PIPESIM. Afterwards, the results of both models were compared. The effects of the solids content (i.e. test vii) were not analysed using PIPESIM, because this commercial software ignores the presence of solids in the flow stream. However, insights were gained into the influence of solids concentration in the bulk flow on the equilibrium rate of a gas-lifted oil well at steady-state conditions using the new model. Table 1 outlines the input data for the various sensitivity tests. For each test, we consider the average absolute deviation (AAD) of the stabilized rates at different states to quantify the performance of the proposed model in relation to PIPESIM.
Four arbitrary injection points on the well path were tested. As shown in Fig. 3, although the stabilized flow rate exhibits a weak correlation with injection depth within the range covered in this example, the predictions of the new model are in excellent agreement with the corresponding results from PIPESIM. Specifically, relative to PIPESIM, the AAD of the new model is 2.3%.
With more details provided in Table 2, both models show that, below the injection depth LA = 5,029 ft, stabilized liquid rate increases (though weakly) with injection depth in this example. Conversely, at some point beyond this injection depth, liquid rate begins to decline. This behaviour, which supports the existence of an optimum injection depth for lift-gas, is attributed to the interplay between gravitational and frictional pressure losses. When gravity dominates friction, the stabilized production rate increases with deeper injection points. This appears to be the case in wells producing relatively dense fluid mixtures such as heavy oil and high water cut wells. The converse is the case when friction dominates gravity, as such scenario is characterized by the trend of stabilized production rate increasing with shallower injection points; hence, the optimum injection depth in such cases is expected to be shallower.
Evidently, the general notion that the maximum liquid production rate correlates with the deepest possible injection point is not always correct, especially for highly deviated wells such as A-1 in the current example (Nagoo and Vangolen 2020; Bellarby 2009; Guo et al. 2007; Beggs 2003). Based on these results, injection depth is considered an important parameter in a gas-lift system because it affects the hydraulics of segment A. By default, the injection depth also affects the tubing and injection pressures (Beggs 2003; Winkler 1987).
Depending on the field and the strategy of the operating company, the quantity of lift-gas available for injection may vary from zero to virtually unlimited. Against the foregoing background and based on our experience, the effects of lift-gas injection rates in the range of 0–8 MMSCF/d were investigated in this case study. Figure 4 displays the sensitivity of stabilized flow rate to the lift-gas rate for well A-1. Again, the results of PIPESIM and our model remain consistent, substantiated by an AAD of 2.6%.
As shown in Fig. 4, the aforementioned gravity–friction interplay also drives the influence of lift-gas injection rate on system performance. In this case, both PIPESIM and the new model indicate a technical optimum injection rate of about 4 MMSCF/d, under the prevailing conditions. It is worth noting that the technical optimum injection rate may not always yield maximum economic returns (Garrouch et al. 2020; Beggs 2003). However, because the new model accommodates a broad spectrum of injection rates, it can be used, in conjunction with an economic model and other considerations such as gas availability and well integrity, to estimate the overall optimum lift-gas injection rate on a case-by-case basis over time.
Every fluid in the well contributes to the average in situ mixture density, which impacts well performance. As a result, it is desirable to understand how sensitive the well is to lift-gas density. In this test, lift-gas specific gravity was varied between 0.55 and 0.75. Returning an AAD of 0.7%, the results obtained from PIPESIM and the new model exhibit excellent agreement (Fig. 5). The impact of lift-gas specific gravity is quite straightforward, but not so significant within the range investigated in this example. The negligible influence observed in this case study is attributed to the relatively low concentration of lift-gas in the bulk mixture; hence, its overall effect on bulk density is insignificant. This notwithstanding, the model suggests that a lighter lift-gas generally improves system performance. This understanding justifies the usual treatment of lift-gas streams to remove entrained liquids, such as water and oil droplets, prior to being employed for gas-lifting applications.
The WHFP is influenced by the prevailing choke size (opening) and well–manifold interactions. Hence, in the proposed model, the WHFP is a proxy for these two crucial factors. Based on our experiences in managing several oil fields, we consider a WHFP range of 50–1,050 psia reasonable for this simulation exercise. As expected, there is a strong inverse relationship between stabilized production rate and WHFP (Fig. 6). Again, the results of the new model are consistent with those of PIPESIM. In this case, the AAD is 2.9%.
Notwithstanding the insights gained from test i, the new model was tested with another hypothetical well. However, in this case, well A-1 is vertical. That is, the wellhead-sandface depths (L and h) of this hypothetical vertical well equal to the wellhead-sandface vertical depth (h) of A-1. Accordingly, the operating conditions of test i and a higher number of injection points were used for this test. As with test i, this test (v) demonstrates the efficacy of the proposed model (Fig. 7). In contrast to test i that has the well A-1 deviated, it is observed that the stabilized liquid rate of this test v vertical well generally increases with injection depth. This is because, at the same vertical depth in both wells, the longer flow length associated with the test i case makes the magnitude of friction in that case exceed what is obtainable in the test v case. Although these results suggest that the injection valve should be placed as deep as possible in a vertical well, one needs to be mindful that the injection depth may be constrained by gas compressor capacity, as higher injection pressure is required to overcome the increased backpressures at deeper injection points.
The PI encapsulates the rock, fluid and well properties that drive fluid flow from the reservoir to the wellbore. Thus, PI was used to examine how the new model responds to well inflow dynamics. Figure 8 shows that the performance of the new model is comparable to that of PIPESIM, yielding an AAD of 3.1%. Within the parameter space examined, the change in the stabilized production rate with respect to PI is dramatic when PI is below 50 STB/d/psi but becomes increasingly gentle as PI exceeds 50 STB/d/psi. These results imply that the impacts of permeability improvement operations such as hydraulic fracturing and skin removal interventions such as acid stimulation are more crucial to low-PI gas-lifted oil wells than their high-PI counterparts.
As earlier mentioned, an advantage of the new model over PIPESIM is that it accounts for solids content, whereas PIPESIM does not. Unlike the previous tests in which solids were absent in the inflow stream from the reservoir into the wellbore, this additional sensitivity test considers solids content in the range 0–20 lb/1,000 STB liquid, while assuming the solid phase strictly consists of sand particulates. As reflected in Table 3, sand contents below 20 lb/1,000 STB liquid have no material effect on production rate. This is due to the relatively low sand concentration in the bulk stream and hence negligible influence on the overall density of the bulk flow. To put things in context, there is ~ 298,000 lb of oil in 1,000 STB of liquid in this example.
One limitation of the proposed model is that it equates the mass of in situ solids with the mass of produced solids, implicitly assuming negligible accumulation of solids within the wellbore. However, in reality, mass of in situ solids is the sum of the masses of produced and accumulated solids. Hence, when solids accumulate in the well, the mass of in situ solids is greater than the mass of produced solids. In such scenario, the well is more burdened, and its production rate drops as a result of higher backpressure attributed to hydrostatic effects of increased solids concentration. Therefore, in the event of considerable solids accumulation in the well, the stabilized production rate estimated with the proposed model may be somewhat optimistic; hence, it may be necessary to apply some adjustment factors on the estimates of stabilized rates in such cases.
In all the sensitivities presented, both the PIPESIM and proposed models were built with an IPR that assumed the same, but constant PI in each of the simulation cases. However, their VLP relationships are dramatically different. The PIPESIM model incorporates the widely acclaimed Hagedorn and Brown (1965) VLP correlation, which is a relatively complex empirical separated-flow model. In contrast, the VLP relationship in the proposed model is a relatively simple analytical formulation. Despite the disparity in the underlying VLPs between PIPESIM and the new model in these examples, it is reassuring that their results are in good agreement as evident in an overall AAD of 2.7%. Some screenshots from PIPESIM and our tool are displayed in Appendix C. Given the similarity of their underlying IPRs, the consistency of the PIPESIM and the new model suggests that the simple VLP underpinning the latter is sufficiently robust and fit for purpose.
Parametric tests are helpful in identifying the main parameters to be considered for the surveillance and management of gas-lifted wells. Each parameter under surveillance should have a significant impact on performance and should easily be monitored and controlled. Based on the outcome of the various sensitivity tests conducted in this study, it can be deduced that the proper monitoring and control of lift-gas injection rate and WHFP (choke opening and downstream backpressure) as well as the management of PI are among the critical success factors for a gas-lifted oil production well.
Field examples
As a further check on the robustness of the proposed model, validation tests are conducted on some field examples. Specifically, the proposed model was tested against field data for a total of eight gas-lifted oil wells, spread between the Niger Delta (Nigeria) and North Sea (Norway) basins.
The Niger Delta wells in question are two vertical wells (X-1 and Y-2) and two deviated wells (X-2 and Y-1). Wells X-1 and X-2 are in field X, while Y-1 and Y-2 are in field Y. Both fields are onshore, are adjacent to each other and are in similar geologic setting. The crude oils produced by this group of wells are such that their gas solubility and formation volume factor (FVF) are well characterized by the Lasater (1958) and Glaso (1980) correlations, respectively.
The four North Sea wells are in an offshore terrain. These wells produced from the west segment of the Varg field, which comprises various isolated compartments. The well A-10T2 is horizontal, while the remaining wells A-03, A-09A and A-12BT2 are deviated. It is noteworthy that the solution gas–oil ratio and FVF of the oil in the Varg west segment are well described by the respective Standing (1947) correlations. The relevant field data for this set of validation tests are publicly available (Ibrahim 2007).
Tables 4 and 5 present the descriptions of the wells during their gas-lifting periods at reasonably steady-state conditions. The results of the validation tests are included in the same tables. Compared to the actual measurements, our model returns an AAD of 5.3 and 5.4% for the Niger Delta and North Sea examples, respectively. Based on these results, it can be concluded that the performance of the proposed model is satisfactory, hence supporting the conclusion reached from the theoretical validation. Nonetheless, it is worth stating that the proposed model is most suited to oil wells with high liquid flow rates and low gas–liquid ratios because such conditions most approximate homogenous flow. A potential improvement area is to direct future advancements of our new method to more complex flow regimes, which are often less homogenous.
The relatively higher AAD and absolute deviations obtained with the North Sea examples (especially well A-09A) are noteworthy. Apart from uncertainties in the actual measurements, the production tubings of the North Sea wells, unlike their Niger Delta counterparts, do not have uniform internal diameter (ID) throughout their lengths. As a result, we have invoked the concept of equivalent ID to approximate the changing tubing IDs in the relevant wells (Appendix D).
It is noteworthy that the field validation tests conducted with the proposed model were performed independent of the actual field results. In other words, the model simulations were executed without a recourse to the field results. In practice, one would have had to calibrate the simulation results against the field results and adjusting relevant (and less certain) model parameters until a reasonable match to the field results is obtained. Despite ignoring this important calibration step, it is reassuring that the performances of the proposed model are satisfactory for the theoretical and field validation cases examined.
Conclusion
A simple but robust analytical model is provided for the evaluation and optimisation of the performances of gas-lifted oil production wells. The VLP relationship employed in the model, which considers the four phases (i.e. gas, oil, water and solid particulates) often reported in a brown-field production stream, is described as a function of wellbore geometry, fluid and other thermodynamic variables. Validation tests of the new model against actual field measurements for gas-lifted oil wells in onshore Niger Delta and offshore North Sea gave AAD below 6%. In addition, validation tests against a commercial wellbore performance simulator yielded AAD below 3%.
The model confirms the strong inverse relationship between stabilized production rate and WHFP. It also affirms that a lighter lift-gas generally improves system performance. However, for the examples considered, it is found that sand contents lower than 20 lb/1,000 STB liquid have no significant effect on gas-lift performance.
The model assumes that the mass of in situ solids equals that of produced solids. However, the mass of in situ solids is the sum of the masses of produced and accumulated solids. Thus, a substantial accumulation of solids in a well increases the backpressure, and it may have significant impact on the performance of a gas-lifted well. For such cases, it may be necessary to apply an adjustment factor in the model to achieve more accurate evaluation of production performance. Such scenarios would have to be treated on a case-by-case basis. Other areas of improvement include extending this work to wells operating at unsteady-state conditions, including accounting for changing productivity index.
Availability of data and material
All the data pertaining to this study are available upon request.
Code availability
No. The underlying mathematical models are straightforward and can readily be coded.
Abbreviations
- a :
-
Numerical coefficient [psi/(STB/d)2]
- b :
-
Numerical coefficient [psi/(STB/d)]
- c :
-
Numerical coefficient (psi)
- \(\overline{{B_{g} }}\) :
-
Average gas formation volume factor (ft3/SCF)
- \(\overline{B}\) :
-
Average oil/water formation volume factor (bbl/STB)
- D :
-
Tubing inner diameter (ft)
- D eq :
-
Equivalent tubing inner diameter (ft)
- f w :
-
Water cut (fraction)
- h :
-
True vertical depth (wellhead to sandface) or over the interval of interest (ft)
- J L :
-
Liquid productivity index (STB/d/psi)
- L :
-
Measured depth (wellhead to sandface) or over the interval of interest (ft)
- m :
-
Mass of fluids and/or solids (lb)
- \(M^{\prime}\) :
-
Mass of fluids and/or solids associated with 1 STB of liquid (lb)
- M s*:
-
Solids content of produced liquid (lb/1000 STB liquid)
- \(\overline{P}_{r}\) :
-
Average reservoir pressure (psia)
- P v :
-
Tubing pressure at the injection depth (psia)
- P wf :
-
Bottomhole flowing pressure (psia)
- P wh :
-
Wellhead flowing pressure (psia)
- \(\overline{P}\) :
-
Average in situ pressure (psia),
- Q gi :
-
Lift-gas injection rate (MMSCF/d)
- Q LS :
-
Stabilized (equilibrium) liquid production rate (STB/d)
- R iL :
-
Injected lift-gas/liquid ratio (SCF/STB)
- R p :
-
Native produced (total) gas–oil ratio (SCF/STB)
- \(\overline{{R_{s} }}\) :
-
Average in situ solution gas–oil ratio (SCF/STB)
- T v :
-
Tubing temperature at the injection depth (°F)
- T wf :
-
Bottomhole flowing temperature (°F)
- T wh :
-
Wellhead flowing temperature (°F)
- \(\overline{T}\) :
-
Average in situ temperature (°F)
- V g :
-
Produced gas volume (SCF)
- V :
-
Produced oil and/or water volume (STB)
- \(\overline{V}\) :
-
Average in situ fluids and/or solids volume (ft3)
- \(\overline{V^{\prime}}\) :
-
Average in situ fluids and/or solids volume associated with 1 STB of liquid (ft3)
- \(\overline{z}\) :
-
Average in situ gas compressibility factor (dimensionless)
- ΔP f :
-
Frictional pressure loss (psi)
- ΔP g :
-
Gravitational pressure loss (psi)
- ρ :
-
Fluids/solids density at standard conditions (lb/SCF)
- \(\overline{{\rho_{m} }}\) :
-
Average in situ mixture density (lb/ft3)
- γ gi :
-
Lift-gas specific gravity (air = 1)
- γ gn :
-
Native gas specific gravity (air = 1)
- γ o :
-
Oil specific gravity (freshwater = 1)
- γ w :
-
Produced water specific gravity (freshwater = 1)
- a :
-
Air
- A :
-
Segment A
- B :
-
Segment B
- fw :
-
Freshwater
- g :
-
Gas
- i :
-
Injected
- j :
-
Tubing section counter
- m :
-
Mixture
- n :
-
Native
- o :
-
Oil
- s :
-
Solids
- S :
-
Stabilized
- w :
-
Water
References
Alarcón GA, Torres CF, Gómez LE (2002) Global optimization of gas allocation to a group of wells in artificial lift using nonlinear constrained programming. J Energy Resour Technol 124(4):262–268
Beckwith R (2014) Pumping oil: 155 years of artificial lift. J Petrol Technol 66(10):101–107
Beggs HD (2003) Artificial lift design. Production optimization using nodal analysis. OGCI and Petroskills Publication, Tulsa, pp 155–185
Bellarby J (2009) Artificial lift. In: Bellarby J (ed) Well completion design. Elsevier, Amsterdam, pp 303–367
Ben Amara A (2016) Gas lift—past and future. SPE paper 184221 presented at the SPE Middle East artificial lift conference and exhibition, Manama, 30 Nov–1 Dec
Chia YC, Hussain S (1999) Gas lift optimization efforts and challenges. SPE paper 57313 presented at the SPE Asia Pacific improved oil recovery conference, Kuala Lumpur, 25–26 Oct
Garrouch AA, Al-Dousari MM, Al-Sarraf Z (2020) A pragmatic approach for optimizing gas lift operations. J Petrol Explor Prod Technol 10:197–216
Glaso O (1980) Generalized pressure-volume-temperature correlations. J Petrol Technol 32(05):785–795
Guet S, Ooms G, Oliemans RVA (2005) Simplified two-fluid model for gas-lift efficiency predictions. AIChE J 51(7):1885–1896
Guo B, Lyons WC, Ghalambor A (2007) Petroleum production engineering. Gulf Professional Publishing, Burlington
Hagedorn AR, Brown KE (1965) Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits. J Pet Tech 17(4):475–478
Hasan AR, Kabir CS, Sayarpour M (2010) Simplified two-phase flow modelling in wellbores. J Pet Sci Eng 72(1–2):42–49
Ibrahim AT (2007) Optimization of gas lift system in Varg field. MSc thesis, University of Stavanger, Norway
Jahanshahi E, Salahshoor K, Kharrat R, Rahnema H (2008) Modeling and simulation of instabilities in gas-lifted oil wells. SPE paper 112108 presented at the SPE North Africa Technical Conference and Exhibition, Marrakech, 12–14 Mar
Lasater JA (1958) Bubble point pressure correlation. J Pet Tech 10(5):379–381
Lawal KA (2018) An analytic study on flowline hydraulics as an impairment mechanism of water injectors. SPE paper 193426 presented at the SPE Nigeria Annual International Conference and Exhibition, 6–8 August, Lagos
Lawal KA, Ovuru MI, Eyitayo SI, Matemilola S, Adeniyi AT (2017) Underground storage as a solution for stranded associated gas in oil fields. J Pet Sci Eng 150:366–375
Mahdiani MR, Khamehchi E (2015) Stabilizing gas lift optimization with different amounts of available lift gas. J Natl Gas Sci Eng 26:18–27
Mousavi SM, Lari M, Salehi G, Azad MT (2020) Technical, economic, and environmental assessment of flare gas recovery system: a case study. Energy Sour Part A Recover Util Environ Eff. https://doi.org/10.1080/15567036.2020.1737597
Nagoo AS, Vangolen BN (2020) Will gas lifting in the heel and lateral sections of horizontal wells improve lift performance? The multiphase flow view. SPE paper 201403 presented at the SPE Annual Technical Conference and Exhibition, Colorado, 26–29 Oct
Robertson JO, Chilingarian GV, Carter WG, Kumar S (1987) Gas lift. In: Chilingarian GV, Robertson JO, Kumar S (eds) Surface operations in petroleum production, I. Elsevier, Amsterdam, pp 415–465
Shi H, Holmes JA, Durlofsky LJ (2005) Drift-flux modelling of two-phase flow in wellbores. SPE J 10(1):24–33
Standing MB (1947) A pressure-volume-temperature correlation for mixtures of California oil and gases. Drill. & Prod. Prac., API
Vázquez-Román R, Palafox-Hernández P (2005) A new approach for continuous gas lift simulation and optimization. SPE paper 95949 presented at the SPE annual technical conference and exhibition, Dallas, 9–12 Oct
Winkler HW (1987) Gas lift. In: Bradley HB (ed) Petroleum engineering handbook. SPE, Texas
Yadua AU, Lawal KA, Okoh OM, Ovuru MI, Eyitayo SI, Matemilola S, Obi CC (2020) Stability and stable production limit of an oil production well. J Petrol Explor Prod Technol 10:3673–3687
Acknowledgements
The authors are grateful to Kenneth Guobadia and Mathilda Ovuru, who are FIRST E&P colleagues, for their support on some aspects of this work. We are equally grateful to the managements of NPDC, NAPIMS and FIRST E&P for the encouragement.
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Average mixture density in segment A
Mass of mixture associated with 1 STB liquid
The mixture mass is the sum of the individual masses of the four phases (oil, water, gas and solids). At steady state, we have
Since mass is conserved, it is convenient to calculate the mass at standard conditions.
Dead liquid (no solution gas)
The density of freshwater at standard conditions (60°F and 14.7 psia) is 62.43 lb/ft3 and 1 bbl is equivalent to 5.6146 ft3. Therefore, the mass of liquid (oil and water) associated with 1 STB liquid is:
Total gas
The total gas consists of the native gas and the injected gas. Therefore,
where
where RiL is the volumetric ratio of lift-gas injection rate to liquid production rate. In other words, lift-gas rate is a controllable variable, while liquid rate is an output variable.
Substituting Eqs. 20 and 21 into Eq. 19, and entering 0.0765 lb/ft3 as the density of air at standard conditions, we obtain
Therefore, the mass of gas associated with 1 STB liquid is:
Solids
With the assumption that there is no accumulation of solids in the well, the mass of solids associated with 1 STB liquid in the well is calculated directly from the solids content of the produced liquid.
Hence, the mass of mixture associated with 1 STB liquid in segment A is given by
Average in situ mixture volume associated with 1 STB liquid
The average in situ mixture volume is given by
Live liquid (with solution gas)
The average in situ volume of live liquid associated with 1 STB liquid is therefore
Free gas
It is assumed that the injected gas does not dissolve in the liquid. Therefore, the volume of free gas in the well is the sum of the volume of native free gas and the volume of injected gas. Accordingly, the in situ free gas volume is calculated as follows.
With the real gas equation, it can be shown that
Substituting Eq. 31 into Eq. 30 and entering 1 STB as the value of VL yield the average in situ volume of free gas associated with 1 STB liquid:
Solids
The volume of solids associated with 1 STB liquid is given by
The average in situ mixture volume associated with 1 STB liquid is obtained by adding Eqs. 29, 32 and 33.
For simplicity, the average oil formation volume factor, average solution gas–oil ratio and, by extension, the average mixture density in each segment are calculated using the average tubing temperature and pressure between its first and last nodes. The average water formation volume factor and the average gas compressibility factor in each segment were assumed to be 1 bbl/STB and 1, respectively. Sensitivity tests conducted using other values of water volume factor and gas compressibility factor within practical ranges did not have significant impacts on the results obtained with Bw = 1 bbl/STB and z = 1.
For all the sensitivity tests, estimates of Bo and Rs are obtained from the empirical correlations proposed by Standing (1947) and Lasater (1958), respectively.
For completeness, the average in situ mixture density of segment A can be estimated by combining Eqs. 25 and 34 as follows.
Appendix B: Average mixture density in segment B
Segment B differs from segment A in terms of the average temperature and pressure, as well as the absence of injected gas. Therefore, its mass of mixture associated with 1 STB liquid is given by
while its average in situ mixture volume associated with 1 STB liquid is calculated as follows
For completeness, the average in situ mixture density of segment B can be estimated by combining Eqs. 36 and 37 as follows.
Appendix C: Screenshots from the new tool and PIPESIM
Figure 9 shows the dashboard of the new accompanying tool, while each of Figs. 10, 11, 12, 13, 14, 15 displays a pair of corresponding results from PIPESIM (background) and the new tool (superimposed) developed from this study.
Appendix D: Equivalent tubing ID
For a tubing string with multiple sections of varying IDs, the pressure loss across the entire string is the sum of the pressure losses across the individual sections. In principle, there should be a single-ID tubing that will approximate the performance of its multi-ID counterpart. Therefore, provided acceleration is negligible, the pressure loss in the equivalent (single-ID) tubing string is given by
When the flow is incompressible and steady, the equivalent tubing ID can be expressed as (Lawal 2018).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yadua, A.U., Lawal, K.A., Eyitayo, S.I. et al. Performance of a gas-lifted oil production well at steady state. J Petrol Explor Prod Technol 11, 2805–2821 (2021). https://doi.org/10.1007/s13202-021-01188-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-021-01188-0