A pragmatic approach for optimizing gas lift operations

Abstract

The oil flow rate in a single vertical well undergoing gas lift operations is complicated by three factors: (1) The flow is driven by gas injection, in addition to the fluid flow potential gradient applied along the well, (2) the well is interfaced with a porous and permeable reservoir contributing with a fluid feed, and (3) the wellbore geometry may consist of concentric pipes of varying diameters and lengths, rather than a single-diameter pipe. Dimensional analysis is applied to this complex, highly nonlinear production problem, in order to develop empirical models for predicting the optimal gas injection rate and the maximum oil production rate that may be produced from continuous gas lift operations. Two pairs of coupled dimensionless groups are revealed. The first pair consists of a dimensionless pressure drop (π₁) adjusted to the complex wellbore geometry, and a dimensionless ratio of kinetic to viscous forces (π₂) which accounts for the porous medium feed. A constructed database for 388 vertical wells producing by continuous gas lift operations has been used to validate the dimensionless groups. A power-law relation is revealed between the dimensionless groups π₁ and π₂, allowing to construct an analytical model for predicting the maximum oil production rate that corresponds to the optimal gas injection rate. The second pair consists of two groups denoted χ₁ and χ₂. The group χ₁ is a dimensionless pressure drop with adjustment being augmented to account for the temperature effects on gas flow. Similar to π₂, the dimensionless group χ₂ is a ratio of kinetic to viscous forces, adjusted to account for the porous medium feed. However, χ₂ is a function of the injection rate, instead of the oil production rate. Likewise, a power-law relation is revealed between χ₁ and χ₂, allowing to construct an analytical model for predicting the optimal gas injection rate. All power-law relations yield high correlation coefficients when the validation data are segregated according to a discrete productivity index. The analytical models developed by applying dimensional analysis appear to capture the physical controls of gas lift operations. Intuitively, the optimal gas injection rate depends on the pressure gradient along the pipe, the wellbore geometry, the temperature conditions at the bottom of the well and in the stock-tank, the oil density, and on the productivity index. Similarly, the maximum oil production rate, corresponding to the optimal gas injection rate, depends on the pressure gradient along the pipe, the wellbore geometry, the oil density, the productivity index which is implicitly affected by the oil permeability, and viscosity. Unlike multivariate nonlinear regression analysis, the application of dimensional analysis for deriving the analytical models, presented in this study, does not require a presumed functional relationship. In retrospect, dimensional analysis evades the guessing process associated with nonlinear regression analysis.

Introduction

Continuous gas lift is a means of producing mature and depleted reservoirs, which can no longer produce under their natural energy. Besides, gas lift is often applied at start-up to commission production (de Souza et al. 2010). A continuous gas lift operation consists of injecting gas through the well annulus into the producing fluid column, reducing the hydrostatic pressure. The reduction in the mixture density by the intrusion of gas bubbles in the crude results in lowering the bottom hole pressure, causing an increase in drawdown and a boost in the oil production (Mahdiani and Khamehchi 2015). At relatively high gas injection rate, the frictional pressure losses become significant. As a consequence, the reduction in the hydrostatic head no longer translates into an increased oil production. Hence, the optimization of the gas lift operation consists of using an optimal gas injection rate that yields a maximum liquid production rate. Estimating these two parameters are among the main concerns dealt with in gas lift operations.

Gas injection has been used as early as 1864 for lifting oil wells (BenAmara 2016). It is applied both onshore and offshore. Its popularity derives from the fact that it is cost-effective compared to other artificial lift techniques. In retrospect, continuous gas lift offers the advantage of (1) producing sand-loaded fluids, (2) producing from deviated wells, and (3) producing high gas–liquid ratio wells which tend to be troublesome using other artificial lift methods like electrical submersible pumps (Chia and Hussain 1999).

In the long run, many oil wells require gas lift to enhance the production performance. Recent reports indicate that gas lift projects contribute to approximately 70% of the oil production in Brazil (Shao et al. 2016). Little innovation has been introduced in the gas lift completion since the development of side-pocket mandrel in 1951 (BenAmara 2016), with the exception of the recently developed digital mandrels. Typically, several slick-wire managed side-pocket mandrels are installed in the tubing string at various depth levels. The upper mandrels are equipped with unloading valves that unload the completion fluid from the well. As the completion fluid is unloaded, pressure-sensitive valves bellows allow gas to progress down to the lower levels in the tubing, until the final injection orifice is reached. The higher the available gas compression pressure is, the deeper the injection port can be, and the lesser the amount of gas is needed to achieve a particular bottom hole pressure (Beggs 2003). The maximum benefit from a continuous gas lift is, therefore, achieved by injecting gas at the deepest possible point in the well.

In the digital age, mandrels with up to six independent injection ports are electronically controlled from the surface (Beggs 2003). The use of various combinations of the injection orifices allows a large spectrum of injection rates. The digital mandrels with pressure and temperature sensors allow to collect vital data needed for gas lift design like flowing temperature and pressure. The digital remotely controlled mandrels provide a longevity advantage compared to the slick-wire managed mandrels. This adds a great flexibility in managing efficiently offshore and deep-water wells with dual completions (Khamehchi et al. 2009a, b).

Continuous gas lift optimization for single-well production has been attempted, in the past, using artificial intelligence tools like fuzzy logic, pattern recognition, and artificial neural network (Khamehchi et al. 2009a; Camponogara 2005; Ray and Sarkar 2007; Ranjan et al. 2015; Miresmaeili et al. 2015). Ranjan et al. (2015) developed a feed-forward back-propagation neural network for estimating simultaneously gas injection rate and the maximum oil production rate as a function of production variables. These input variables consist of the static bottom hole pressure, the flowing tubing head pressure, the flowing bottom hole pressure, the productivity index, the tubing diameter, the water cut percentage, the choke size, the separator temperature and pressure, and the solution gas–oil ratio. Ranjan et al. (2015) reported a reasonable value of the coefficient of determination of approximately 0.9 for predicting the optimal gas injection rate and the maximum oil production rate, using the testing data set. Behjoomanesh et al. (2015) developed a polynomial model for predicting the maximum oil rate as a function of the optimal gas injection rate, by applying the Box–Behnken experimental design technique. Even though, the model was developed to predict the liquid performance of a network of wells, it could be extrapolated to estimate the liquid performance of a single well. Behjoomanesh et al. (2015) model, however, requires advance knowledge of the gas injection rate and does not account for any reservoir, fluid, or tubing flow parameters.

As shown in Fig. 1, the optimization of the gas injection rate is achieved graphically using nodal analysis (Beggs 2003; Redden et al. 1974). In retrospect, the reservoir inflow performance, which is an expression of Darcy’s law giving the bottom hole flowing pressure (P_wf) as a function of the liquid volumetric flow rate, is intersected with the outflow performance which is equivalent to the mechanical energy equation applied to two-phase flow inside the well-tubing, at a fixed gas–liquid ratio (GLR). The solution of the liquid rate (q_L) for an arbitrary total gas–liquid ratio (GLR) is obtained from the intersection of the inflow and outflow performance curves. The required gas injection rate (q_inj) that needs to complement the solution gas ratio to reach the required GLR is then calculated, and a performance curve is constructed (Fig. 2). The performance curve of Fig. 2 gives the liquid production rate versus the injection gas rate. As shown in Fig. 2, the oil production rate increases as the gas injection rate increases, up to a certain optimal value. Beyond this, an excessive gas injection rate will increase the operation costs without providing an added value to the cumulative liquid production. This latter plot gives the graphical solution for the maximum liquid rate that can be obtained, and the corresponding optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$). Nevertheless, economic constraints may force the operator to select a gas injection rate smaller than the optimum, depending on the gas cost, the gas compression cost, the available gas, and the oil sales price.

Fig. 1

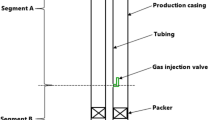
A schematic of gas lift well nodal analysis (Beggs 2003)

Fig. 2

A schematic showing the construction of a plot giving the optimum gas injection rate (Beggs 2003)

Nishikiori et al. (1998) presented a thorough literature survey of researchers who developed analytical models and artificial intelligence models for estimating the optimum gas injection rate, however, for a network of wells. The optimization process is subject to gas availability constraints and surface facility constraints and to the reservoir operational requirements associated with each well in the whole network (Djikpesse and Couet 2010; Fang and Lo 1996; Gutierrez et al. 2007; Lu and Fleming 2011). Empirical models for optimizing the injection rate and estimating the maximum oil rate of a single well subjected to natural gas lift are scarce in the literature. The development of general analytical models that account for the inherent complexity in gas lift design and allow to react to changing wellbore, reservoir, and surface equipment conditions becomes eminent.

The objective of this study consists of developing analytical models for optimizing the gas injection rate in continuous gas lift operation, and for predicting the maximum oil production. The continuous gas lift operations considered in this paper are for single producing vertical wells with unlimited amount of natural gas available for injection. The procedure consists of applying dimensional analysis for identifying dimensionless groups that control the physics of gas lift operations. Collected production data from many fields from the Middle East region are then used to validate these dimensionless groups and deduce the target analytical models. The validation data used in this study are described next.

Data description

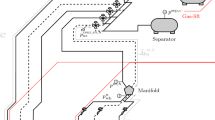
A database of 388 wells for continuous gas lift operations has been constructed by accumulating gas lift data for wells producing from various oil fields in the Middle East (Alsarraf 2019). Collected data correspond to vertical wells in which high-pressure gas is injected at the deepest point of injection in order to lighten the fluid column, allowing the reservoir pressure to lift oil from the bottom of the well to the surface. The injected gas is recovered at the surface with the reservoir crude and with the solution gas, through a low-pressure separation system which has sufficient gas separation capacity to handle the total produced gas. The constructed database is used in this study for model validation.

A typical gas lift system is illustrated in Fig. 3. High-pressure gas is injected at the gas manifold into the annulus, with injection rate being fixed by a variable orifice controller. Gas injection rate is measured using an orifice plate meter (Chia and Hussain 1999; Sutton 2008; Ojukwu and Edwards 2008). Well head flowing pressure is registered using a pressure recorder installed at the wellhead. The oil rate, the GLR, the water cut, the API gravity, and the oil formation volume factor have been determined using a track or skid mounted Portable Test (Oglesby et al. 2006; Camponogara et al. 2010).

Fig. 3

A schematic of an arbitrary well completion corresponding to the constructed database

Figure 4a–f shows histograms for the static bottom hole pressure, the flowing bottom hole pressure, the separator pressure, the flowing tubing head pressure, the bottom hole temperature, and the separator temperature. A list of these variables statistics is given in Table 1. The static bottom hole pressure appears to be normally distributed, varying from 1490 to 3837 psi. Likewise, the flowing bottom hole pressure appears to have a bimodal normal distribution. It is varying from 690 to 3191 psi. The separator pressure appears to be positively skewed, varying from 60 to 401 psi, with a mode at 3 psi. The flowing tubing head pressure appears to be positively skewed. It varies from 45 to 530 psi, with a mode of 90 psi. The separator temperature appears to be normally distributed, varying from 60 to 134 °F with a mode of 90 °F. The bottom hole temperature varies from 142 to 159 °F, with a mode of approximately 142 °F.

Fig. 4

a Histogram for the static bottom hole pressure data (Alsarraf 2019). b Histogram for the flowing bottom hole pressure data (Alsarraf 2019). c Histogram for the separator pressure data (Alsarraf 2019). d Histogram for the flowing tubing head pressure data (Alsarraf 2019). e Histogram for the separator temperature data (Alsarraf 2019). f Histogram for the bottom hole temperature data (Alsarraf 2019)

Table 1 Statistics for the whole data set of 388 wells

Figure 5a–f displays histograms for the API gravity, the productivity index, the oil rate, the gas injection rate, the gas–liquid ratio, and the water cut. A list of these variables statistics is also given in Table 1. The API gravity varies from 19 to 32.2, and appears to have a mode of approximately 32.2. The oil rate varies from 46.4 to 3913 STB/day and appears to be positively skewed with a mode at 611 STB/day. The gas injection rate varies from 0.0259 to 6.9 MMscf/day and appears to have a mode of approximately 2 MMscf/day. The total gas–liquid ratio (GLR) varies from approximately 48 scf/STB to 60,252 scf/day. The GLR appears to be positively skewed with a mode of approximately 322.5 scf/STB. The total gas–liquid ratio accounts for the solution gas and the gas injected. That explains some of the relatively high values observed. The water cut data for the 388 wells appear to be negatively skewed. The water cut varies from 0 to 98%, with a mode of 80%. In practice, gas lift operations have been applied to high, moderate, and low water-cut wells (Beggs 2003). The target productivity index varies from approximately 0.037 to 26.81 STB/day/psi and appears to have a positively skewed distribution, with a mode of approximately 3 STB/day/psi. The low values of productivity index (less than one) correspond to severely depleted reservoirs (Alsarraf 2019).

Fig. 5

a Histogram for the API gravity data(Alsarraf 2019). b Histogram for the productivity index data (Alsarraf 2019). c Histogram for the solution gas oil ratio (Alsarraf 2019). d Histogram for the oil rate data (Alsarraf 2019). e Histogram for the gas injection rate data (Alsarraf 2019). f Histogram for the water cut data (Alsarraf 2019)

A plot of maximum oil rate versus optimum gas injection rate (Fig. 6) appears to be fraught by a significant amount of scatter, with no clear trend between the two variables. Likewise, a plot of oil rate versus tubing pressure gradient features a sizeable amount of data scatter (Fig. 7). The correlation coefficient matrix (Table 2) shows weak correlations between all variables, with the exception of the equivalent radius which naturally decreases with depth. These facts summed together appear to suggest highly nonlinear relations between the optimal gas injection rate, the maximum oil rate, the equivalent wellbore radius, and fluid and reservoir properties. The next section attempts to define these relations using dimensional analysis.

Fig. 6

Maximum oil rate versus optimal gas injection rate, from database of 388 wells (Alsarraf 2019)

Fig. 7

Maximum oil rate versus tubing flowing pressure gradient, from database of 388 wells (Alsarraf 2019)

Table 2 Correlation coefficient matrix for the whole data set of 388 wells

Dimensional analysis

Dimensional analysis is a well-established mathematical approach for studying similar systems for which the defining equations may or may not be completely articulated (Zendehboudi et al. 2011; Al-Dousari and Garrouch 2013). It is useful to define general autonomous relationships, between dependent and independent variables, which are not affected by the scale dimension. Reynold’s empirical relationship between the dimensionless pressure drop (friction factor) and the ratio of the kinetic to viscous forces ratio (Reynold’s number) is perhaps among the pioneering applications of dimensional analysis that characterized steady-state flow of incompressible liquids in flow conduits (Munson et al. 2010). Recently, Garrouch and Al-Sultan (2019) applied dimensional analysis as a tool for developing a nonlinear empirical model giving the flow zone indicator (FZI) as a function of open-hole log measurements. A unique power-law relation has emerged between a dimensionless FZI group, and a dimensionless resistivity group, for distinct hydraulic flow units. The application of dimensional analysis in that particular study proved that petrotyping, using either the discrete rock type (DRT) approach, or the global hydraulic elements (GHE) approach, provides a credible framework for comparative hydraulic flow unit description. Garrouch (2018) applied dimensional analysis for characterizing the electrical double-layer polarization and the high-frequency electronic polarization, in porous and permeable reservoir rocks. An analytical model for estimating the cation exchange capacity of rocks from fast, reliable, and noninvasive complex impedance measurements has emanated, as a consequence (Garrouch 2018).

An MLT dimensional analysis for the dependence of the maximum oil rate (q_o), and the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$) on the production parameters, is performed next. The objective of this analysis is to develop empirical models for predicting $q_{\text{inj}}^{\text{opt}}$ and q_o as a function of reservoir and crude properties, as well as flow variables characterizing the gas lift operation. MLT stands for the fundamental dimensions of mass (M), length (L), and time (T).

Dimensional analysis for formulating the maximum oil production rate

Maximizing the oil production rate at the optimal gas injection rate is a challenging task, given the many interacting production system components and constraints involved. An MLT dimensional analysis for the dependence of the maximum oil production rate (q_o) corresponding to the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$) is illustrated in this section. The complexity of the problem arises from the dependence of the wellbore fluid flow on the feeding reservoir properties, the intricate wellbore geometry, the crude PVT properties, and the surface pressure and temperature conditions. It is postulated, here, that q_o associated with the optimal gas injection rate is a function of the equivalent radius (R_eq), the flowing pressure gradient inside the tubing (ΔP/L), the oil density (ρ_o), and the target productivity index (PI). The postulated relationship is expressed generically as follows:

$$q_{\text{o}} = f\left( {R_{\text{eq}} ,\frac{\Delta P}{{L_{t} }},\rho_{\text{o}} ,{\text{PI}}} \right)$$

(1)

In the above notation, the flowing pressure gradient inside the tubing is given as follows:

$$\frac{\Delta P}{{L_{t} }} = \left( {\frac{{P_{\text{wf}} - P_{\text{th}} }}{{L_{t} }}} \right),$$

(2)

where L_t is the total tubing length. Obviously, the flowing pressure gradient inside the tubing is the two-phase flow anchor variable affecting the oil flow rate given by Eq. (1).

As shown in Fig. 3, for a well completion that is composed of pipes of various radii (R₁, R₂,…, R_n) with corresponding lengths (L₁, L₂, …, L_n), the equivalent radius (R_eq) is obtained by equating the fluid flow potential difference to the sum of fluid flow potential differences through the various pipe sections (“Appendix A”). The resulting equivalent radius is given as follows:

$$R_{\text{eq}} = \left[ {\frac{{L_{t} }}{{\frac{{L_{1} }}{{R_{1}^{4} }} + \frac{{L_{2} }}{{R_{2}^{4} }} + \cdots + \frac{{L_{n} }}{{R_{n}^{4} }}}}} \right]^{{\frac{1}{4}}}$$

(3)

The PI is a unique function of the ratio of the flow capacity normalized with respect to crude viscosity, and with respect to the ratio of field geometry radii. For instance, for a penetrating well producing at steady-state with a constant flow rate, the productivity index may be expressed as a function of reservoir and crude properties as follows (Bedrikovetsky et al. 2003):

$${\text{PI}} = \frac{{2\pi k_{o} H}}{{\mu_{o} \ln \left( {\frac{{r_{\text{e}} }}{{r_{\text{w}} }}} \right)}}$$

(4)

In the above notation, H is the reservoir thickness, k_o is the reservoir permeability, μ_o is the crude viscosity, r_e is the reservoir radius, r_w is the wellbore radius.

The variables to the right-hand side of Eq. (1) do not bear any similarity, or dependence. This fact makes Eq. (1) suitable for further dimensional analysis. For the three fundamental dimensions (MLT) used in the analysis and the five total variables expressed in Eq. (1), the Buckingham pi theorem (Munson et al. 2010) depicts two related dimensionless groups (π₁ and π₂). The groups are products of unique repeating and non-repeating variables. The selection of the repeating and the non-repeating variables conforms to the following rules (Munson et al. 2010).

• 1. The repeating variable must appear in all dimensionless groups.

• 2. The repeating variables bear no resemblance and are dimensionally independent of each other.

• 3. The three fundamental dimensions M, L, and T should be embodied in the repeating variable set.

Taking PI, and ΔP/L as the non-repeating variables, and the parameters q_o, R_eq, and the oil density (ρ_o) as the repeating variables satisfy the above mentioned rules and allow to formulate the following two dimensionless groups:

$$\pi_{1} = \frac{{\Delta P_{{}} }}{{L_{t} }}\;\left[ {\;q_{\text{o}} } \right]^{a} \;\left[ {R_{\text{eq}} } \right]^{b} \;\left[ {\rho_{\text{o}} } \right]^{c}$$

(5)

$$\pi_{2} = {\text{PI}}\;\left[ {\;q_{\text{o}} } \right]^{a'} \;\left[ {R_{\text{eq}} } \right]^{b'} \;\left[ {\rho_{\text{o}} } \right]^{c'}$$

(6)

The variables of Eq. (5) are replaced by their MLT fundamental dimensions, as follows:

$$\begin{aligned} \pi_{1} \equiv \left[ {MT^{ - 2} L^{ - 2} } \right]\;\left[ {L^{3} \;T^{ - 1} } \right]^{a} \;\left[ {L^{{}} } \right]^{b} \;\left[ {ML^{ - 3} } \right]^{c} \hfill \\ \hfill \\ \end{aligned}$$

(7)

The exponent powers of each fundamental dimensions of Eq. (7) are summed up and are equated to zero, leading to the following system of equations:

$$\left\{ {\begin{array}{*{20}l} {1 + c = 0} \hfill \\ { - a - 2 = 0} \hfill \\ { - 2 + 3a + b - 3c = 0} \hfill \\ \end{array} } \right.$$

(8)

The coefficient values obtained from the above system of equations are substituted in Eq. (5). The first dimensionless group (π₁) is, therefore, formulated as follows:

$$\pi_{1} = \frac{{\Delta P_{{}} }}{{L_{\text{t}} }}\;\frac{{R_{\text{eq}}^{5} }}{{q_{\text{o}}^{2} \rho_{\text{o}} }}$$

(9)

Likewise, the variables of Eq. (6) are replaced by their MLT fundamental dimensions, as follows:

$$\begin{aligned} \pi_{2} \equiv \left[ {M^{ - 1} TL^{4} } \right]\;\left[ {L^{3} \;T^{ - 1} } \right]^{a'} \;\left[ {L^{{}} } \right]^{b'} \;\left[ {ML^{ - 3} } \right]^{c'} \hfill \\ \hfill \\ \end{aligned}$$

(10)

The exponent powers of each fundamental dimension of Eq. (10) are summed up and are equated to zero, leading to the following system of equations:

$$\left\{ {\begin{array}{*{20}l} { - 1 + c' = 0} \hfill \\ {1 - a' = 0} \hfill \\ {4 + 3a' + b' - 3c' = 0} \hfill \\ \end{array} } \right.$$

(11)

The coefficient values obtained from the above system of equations are substituted in Eq. (6). The second dimensionless group is, therefore, formulated as follows:

$$\pi_{2} = {\text{PI}}\frac{{q_{\text{o}}^{{}} \rho_{\text{o}} }}{{R_{\text{eq}}^{4} }}$$

(12)

In Eq. (9), π₁ is designated as a dimensionless pressure drop, or a friction factor adjusted for the complex wellbore geometry. In Eq. (12), π₂ is designated as the ratio of kinetic to viscous forces, adjusted for the effect of porous media feed (PI), and adjusted for the complex wellbore geometry (R_eq). For carefully defined variables contributing to the dimensionless groups, dimensional analysis is likely to lead to a general relation between the dimensional groups that might be applied for similar systems (Garrouch 2018; Garrouch and Al-Sultan 2019). This particular inference can only be confirmed with the gas lift production data, described earlier.

A plot of π₁ versus π₂ in a log–log paper, using the whole production data set collected in this study for 388 wells, shows no particular trend (Fig. 8). Nevertheless, when the data are segregated according to a discrete productivity index (DPI), the collected field data appear to yield a well-correlated power-law relation between the two dimensionless groups (Fig. 9). The discrete productivity index (DPI) is defined in this study as a function of the productivity index (PI) as follows:

Fig. 8

Friction factor versus ratio of kinetic to viscous forces for the whole data set, with math formulation pertinent to the maximum oil rate

Fig. 9

Friction factor versus ratio of kinetic to viscous forces, with math formulation pertinent to the maximum oil rate. Data are segregated according to DPI values (Alsarraf 2019)

$${\text{DPI}} = {\text{Round}}\left[ {2\ln \left( {\text{PI}} \right) + 10.6} \right]$$

(13)

These results appear to validate the dimensionless groups. Therefore, the physical relationship between the maximum flow rate q_o and the remaining variables given by Eq. (1), is contracted into a more succinct functional form given by

$$\pi_{1} = \alpha \pi_{2}^{\beta }$$

(14)

In the above notation, α and β are constants. Table 3 displays the values of α and β, as well as the coefficients of determination obtained for various DPI values. The reduced form of Eq. (14) illustrates the main utility of the dimensional analysis. The power-law relation between the derived dimensionless groups (Eq. (14)) confirms a high degree of nonlinearity between the maximum oil flow rate q_o and the relevant parameters of Eq. (1). By substituting Eqs. (9) and (12) in Eq. (14), the following expression for the maximum oil production rate corresponding to the optimal gas injection rate as a function of the relevant production parameters is obtained as follows:

Table 3 Coefficient and exponents for the analytical empirical models developed in this study

$$q_{\text{o}}^{{}} = \frac{1}{{{\text{PI}}^{{\frac{\beta }{2 + \beta }}} }}\left( {\frac{{\Delta P_{{}} }}{{\alpha L_{t} }}} \right)^{{\frac{1}{2 + \beta }}} \left( {\;\frac{{R_{\text{eq}}^{{\frac{5 + 4\beta }{2 + \beta }}} }}{{\rho_{\text{o}}^{{\frac{1 + \beta }{2 + \beta }}} }}} \right)$$

(15)

Figure 10 illustrates a comparison between the oil flow rate values obtained using the dimensional analysis analytical model with actual measured oil flow rates for the whole data set. Figure 11 shows the same comparison as in Fig. 10, but showing discrete productivity index (DPI) delineation. The agreement between predicted and measured flow rates appears to be satisfactory. The analytical model developed for estimating the maximum oil rate, by applying dimensional analysis, appears to capture the main physical controls of continuous gas lift operations. Intuitively, the maximum oil production rate depends on the pressure gradient along the pipe, the wellbore geometry, the oil density, the target productivity index which is implicitly affected by the oil permeability, and viscosity (Eq. (15)). It is implicit in Eq. (15) that the viscous pressure losses caused by two-phase flow are accounted for by the flowing pressure gradient inside the tubing.

Fig. 10

Estimated oil rate, using dimensional analysis analytical model, versus measured oil rate for the whole data set

Fig. 11

Estimated oil rate, using dimensional analysis analytical model, versus measured oil rate for distinct DPI values (Alsarraf 2019)

An error analysis applied on the volumetric flow rate allows to evaluate the uncertainty associated with the production schedule. An error analysis on the flow rate empirical model given by Eq. (15) can also be used to assess the error contribution of each independent variable on the overall relative error of the oil flow rate. Application of the Chain rule (Garrouch and Al-Sultan 2019) on the natural logarithm of the flow rate given by Eq. (15) leads to the following approximation for the maximum possible relative error in the oil flow rate as a function of the relative errors of the independent variables ΔP, ρ_o, R_eq, PI, and L_t:

$$\frac{{\Delta q_{\text{o}} }}{{q_{\text{o}} }} \approx \left[ {\frac{\beta }{2 + \beta }\frac{{\Delta {\text{PI}}}}{\text{PI}}} \right] + \left[ {\frac{1}{2 + \beta }\frac{\Delta \Delta P}{\Delta P}} \right] + \left[ {\frac{1}{2 + \beta }\frac{{\Delta L_{t} }}{{L_{t} }}} \right] + \left[ {\frac{5 + 4\beta }{2 + \beta }\frac{{\Delta R_{\text{eq}} }}{{R_{\text{eq}} }}} \right] + \left[ {\frac{1 + \beta }{2 + \beta }\frac{{\Delta \rho_{\text{o}} }}{{\rho_{\text{o}} }}} \right]$$

(16)

The components to the RHS of Eq. (16) give the contribution of each production variable into the total relative error of the flow rate. A plot of the individual relative error contributions, for the whole data set segregated according to the discrete productivity index value (DPI), is shown in Fig. 12. From Fig. 12, it appears that the relative error in the productivity index (PI) contributes by about 65% to the total relative error in the flow rate. The pressure drop (ΔP) comes second, with approximately 25% contribution in the overall error. The relative errors in the total length (L_t) and in the equivalent radius (R_eq) contribute by about 3, and 6%, respectively, in the overall relative error of q_o. The relative error in the density (ρ_o) has the least contribution in the overall error (approximately 1%). In conclusion, the productivity index and the pressure drop across the tubing appear to be the most influential variables on the flow rate accuracy.

Fig. 12

Individual production variables contributions to the relative error in the oil flow rate versus DPI

Dimensional analysis for formulating the optimal gas injection rate

A second dimensional analysis is conducted for the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$), as a function of relevant production parameters. This is done by adjusting Eq. (1) to account for the temperature conditions in the well and in the separator tank, as follows:

$$q_{\text{inj}}^{\text{opt}} = g\left( {\text{R}_{\text{eq}} ,\frac{\Delta P}{{L_{t} }} \cdot \left[ {\frac{{T_{\text{BH}} }}{{T_{\text{sep}} }}} \right]^{{m_{1} }} ,\rho_{\text{o}} ,{\text{PI}}} \right)$$

(17)

In the above notation, m₁ is an arbitrary constant. Similarly to the previous dimensional analysis, by taking PI, and $\frac{\Delta P}{{L_{t} }} \cdot \left[ {\frac{{T_{\text{BH}} }}{{T_{\text{sep}} }}} \right]^{{m_{1} }}$ as the non-repeating variables, and the parameters $q_{\text{inj}}^{\text{opt}}$, R_eq, and the oil density (ρ_o) as the repeating variables, the following non-dimensional groups are derived:

$$\chi_{1} = \frac{\Delta P}{{L_{t} }} \cdot \left[ {\frac{{T_{\text{BH}} }}{{T_{\text{sep}} }}} \right]^{{m_{1} }} \;\frac{{R_{\text{eq}}^{5} }}{{\left( {q_{\text{inj}}^{\text{opt}} } \right)^{2} \rho_{\text{o}} }}$$

(18)

$$\chi_{2} = {\text{PI}}\frac{{q_{\text{inj}}^{\text{opt}} \rho_{o} }}{{R_{\text{eq}}^{4} }}$$

(19)

In Eq. (18), χ₁ is designated as a dimensionless pressure drop, or a friction factor adjusted for the temperature conditions, and for the complex wellbore geometry. In Eq. (19), χ₂ is designated as the ratio of kinetic to viscous forces, adjusted for the effect of porous media feed by including the productivity index. For carefully defined variables contributing to the functional relation (Eq. (17)), a unique plot of χ₁ versus χ₂ is likely to lead to a general relation, between the groups, that might be applied for similar systems (Garrouch 2018; Garrouch and Al-Sultan 2019). This particular inference can only be confirmed with gas lift production data.

A plot of χ₁ versus χ₂ in a log–log paper (Fig. 13), using the whole data set collected in this study, shows no particular trend. However, when the data are segregated according to the DPI, an obvious trend is depicted (Fig. 14). The physical relationship between the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$) and the remaining variables given by Eq. (17), is contracted into a more succinct functional form given by the following expression:

Fig. 13

Friction factor versus ratio of kinetic to viscous forces for the whole data set, with math formulation pertinent to the gas injection rate

Fig. 14

Friction factor versus ratio of kinetic to viscous forces, with math formulation pertinent to the optimal gas injection rate. Data are segregated according to DPI values (Alsarraf 2019)

$$\chi_{1} = \delta \chi_{2}^{\varpi }$$

(20)

In the above notation, δ and $\varpi$ are constants. Table 3 displays the values of δ and $\varpi$, as well as the coefficients of determination obtained for various DPI values. The reduced form of Eq. (20) illustrates the main utility of the dimensional analysis. The fact that the collected field data for 388 wells appear to yield the power-law relation between the two dimensionless groups validates the dimensional analysis results. By substituting Eqs. (18) and (19) in Eq. (20), the following expression is obtained for the optimal gas injection rate as a function of the relevant parameters:

$$q_{\text{inj}}^{\text{opt}} \; = \frac{1}{{{\text{PI}}^{{\frac{\varpi }{2 + \varpi }}} }}\left( {\frac{{\Delta P_{{}} }}{{\delta L_{t} }}\left( {\frac{{T_{\text{BH}} }}{{T_{\text{sep}} }}} \right)^{{m_{1} }} } \right)^{{\frac{1}{2 + \beta }}} \left( {\;\frac{{R_{\text{eq}}^{{\frac{5 + 4\varpi }{2 + \varpi }}} }}{{\rho_{\text{o}}^{{\frac{1 + \varpi }{2 + \varpi }}} }}} \right)$$

(21)

Equation (21) confirms a high degree of nonlinearity between $q_{\text{inj}}^{\text{opt}}$ and the relevant reservoir, crude, and wellbore parameters affecting gas lift operations. Figure 15 illustrates a comparison between the optimal gas injection rate values obtained using the dimensional analysis analytical model with measured optimal gas injection rate values for the whole data set. Overall, the agreement between estimated and measured optimal gas injection rates seems to be satisfactory. Figure 16 shows a comparison between the optimal gas injection rate values obtained using the dimensional analysis analytical model with measured optimal gas injection rate values for distinct DPI values. Overall, the agreement between estimated and measured optimal gas injection rates seems to be satisfactory, except for DPI value that equals eight. Indeed, it is rather awkward to make any reasonable statistical inference out of 4 observations. The analytical model developed for predicting the optimal gas injection rate, by applying dimensional analysis, appears to capture the principal physical controls of gas lift operations. Intuitively, the optimal gas injection rate depends on the pressure gradient along the pipe, the wellbore geometry, the temperature conditions at the bottom of the well and in the stock-tank, the oil density, and the productivity index.

Fig. 15

Estimated gas injection rate, using dimensional analysis analytical model, versus measured gas injection rate for the whole data set

Fig. 16

Estimated gas injection rate, using dimensional analysis analytical model, versus measured gas injection rate for distinct DPI values (Alsarraf 2019)

The two proposed empirical models for the optimal gas injection rate and the corresponding maximum oil rate may be considered as quick and explicit performance prediction tools. The models evade the tedious efforts of characterizing the two-phase flow regime (Khabibullin and Burtzev 2015). They also evade the demanding efforts of accounting for the effects of composition changes of oil and gas on the pressure drop calculations (Sarabia and Fairuzov 2013).

The next section illustrates the development of an artificial neural network model, similar to that developed by Ranjan et al. (2015), for predicting simultaneously the maximum oil rate and the optimal gas injection rate. The subtle difference is that Ranjan et al. (2015) built a feed-forward back-propagation architecture whereas in this study a general regression network paradigm is constructed, instead. In addition, this study uses more or less the same input variables of Ranjan et al. model (2015) augmented by the crude API, and the equivalent pipe radii, in order to be able to mimic gas lift operations for wells that have complex wellbore geometry. The learning process of the neural network improved significantly when the API gravity was included as an input variable (Smaoui and Garrouch 1997; Garrouch and Smaoui 1996). The developed artificial neural network model is used in this study for performance comparison with the developed dimensional analysis analytical models.

GRNN model development

GRNN model algorithm

The general regression neural network (GRNN) is a single-pass learning algorithm, with a highly parallel structure, that falls in the category of probabilistic networks. The application of probabilistic neural networks is especially favored when the training data are relatively scarce. GRNN is an attractive nonlinear prediction method because of its fast learning capability and sturdiness in the presence of noise. Al-Omair and Garrouch (2015), Al-Dousari et al. (2016), and Garrouch (2018) give applications of GRNN for building predictive models of petrophysical properties for small datasets. GRNN establishes empirically the functional form between a dependent variable Y, and an independent variable X, based on the data using nonparametric estimators (Specht 1991). X in this study corresponds to an array that consists of 12 input parameters. These are the shut-in bottom hole pressure (SBHP), the flowing tubing head pressure (FTHP), the flowing bottom hole pressure (FBHP), the productivity index (PI), the water cut (WC), the separator temperature (TSEP), the separator pressure (PSEP), the choke size, the tubing length, the equivalent radius (R_eq), and the crude API. The random variable Y is a vector that assumes the values of two outputs, namely the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$) and the maximum oil production rate (q_o). The joint probability density function (pdf) between the input and output arrays is expressed by Dai et al. (Dai et al. 2010) as follows:

$$f(X,Y) = \frac{1}{{2\pi^{{\left( {\frac{p + 1}{2}} \right)}} \sigma^{{\left( {p + 1} \right)}} }} \cdot \frac{1}{n}\sum\limits_{i = 1}^{n} {\exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right) \cdot \exp \left[ { - \frac{{\left( {Y - Y^{i} } \right)^{2} }}{{2\sigma^{2} }}} \right]}$$

(22)

where σ stands for the smoothing factor, n denotes the number of training vectors, p represents the dimension of the vector X, Yⁱ designates the output target values for the ith training vector.

$D_{i}^{2}$ signifies the distance between X and the ith training sample X_i, and is given by the following expression:

$$D_{i}^{2} = \sum\limits_{i = 1}^{p} {\left( {X_{j} - X_{ij} } \right)^{2} }$$

(23)

The conditional mean ($\hat{Y}$) of the target output vector (Y), for a nonparametric estimator of the joint pdf $f\left( {x,y} \right)$, is estimated using the class of consistent estimators proposed by Parzen (1962) as follows:

$$\mathop { \, Y}\limits^{ \wedge } \left( X \right) = \frac{{\sum\nolimits_{i = 1}^{n} {Y_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}{{\sum\nolimits_{i = 1}^{n} {\exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}$$

(24)

In the above notation, the smoothing factor $\sigma$ indicates the width of the Gaussian curve for the calculated joint pdf (Antanasijevic et al. 2015). Indeed, the optimization of the smoothing factor $\sigma$ is believed to be among the prominent computing tasks of the GRNN development (Huang and Williamson 1994). The procedure for estimating an optimum value for $\sigma$ has been detailed by Al-Omair and Garrouch (2015), and by Al-Dousari et al. (2016).

For very large values of $n$, the cluster version of a general regression is expressed as follows:

$$\mathop { \, Y}\limits^{ \wedge } \left( X \right) = \frac{{\sum\nolimits_{i = 1}^{m} {A_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}{{\sum\nolimits_{i = 1}^{m} {B_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}$$

(25)

In the above notation, parameters A_i and B_i are given by the following expressions:

$$A_{i} \left( k \right) = A_{i} \left( {k - 1} \right) + Y_{j}$$

(26)

and

$$B_{i} \left( k \right) = B_{i} \left( {k - 1} \right) + 1$$

(27)

where $m$ stands for the number of clusters, $k$ stands for the number of observations

The GRNN algorithm based on Eqs. (22)–(27) has been applied in a parallel neural network architecture shown in Fig. 17. The paradigm consists of an input layer, a hidden layer, a summation layer, and an output layer. The number of neurons in the input layer is equal to the number of independent variables. Neurons of this layer are connected with the input vector X values. The input neurons are all connected with neurons of the hidden layer (Fig. 17). Each unit of the hidden layer embodies a training sample. The distance between the test sample X and a corresponding training sample X_i, given by Eq. (23), is calculated in this layer. The summation layer consists of two units that calculate the numerator and denominator of Eq. (25), respectively (Huang and Williamson 1994). The output layer executes the division of the summation layer unit and finally presents the predicted output.

Fig. 17

A schematic of the GRNN paradigm (Alsarraf 2019)

GRNN model training and testing

An input file, consisting of 388 vectors with 11 input variables and two output variables, has been downloaded into NeuroShell database (Al-Dousari and Garrouch 2013). The input variables consist of the shut-in bottom hole pressure (SBHP), the flowing tubing head pressure (FTHP), the flowing bottom hole pressure (FBHP), the productivity index (PI), the water cut (WC), the separator temperature (TSEP), the choke size, the total tubing length (L), the equivalent radius (R_eq), the crude API. The output variables consist of the optimal gas injection rate ($q_{\text{inj}}^{\text{opt}}$), and the maximum oil rate (q_o). Details of the database of the 388 wells for continuous gas lift operations used in this analysis have been given earlier in the Data Description section. All input and output variables were normalized so that they all varied from − 1 to +1. Originally, these variables span ranges that are different by several orders of magnitude. The normalization of these variables facilitates the network concurrence. The following transformation has been applied to normalize the input and output variables into standardized values (Al-Dousari and Garrouch 2013):

$$\overline{Z} = - 1 + 2\left[ {\frac{Z - \lambda }{\eta - \lambda }} \right]$$

(28)

In the above notation, $\overline{Z}$ stands for the normalized variable. Z is the variable value. λ stands for the minimum value of variable observed. η is the maximum value of the variable observed.

NeuroShell randomly splits the data file into a training data set that consists of 80% of the data (310 vectors) and a blind test data set consisting of the remaining 20% of the data (78 vectors), used for validation purposes. Figures 18 and 19 show the comparison of the estimated q_o and $q_{\text{inj}}^{\text{opt}}$ values using the GRNN model with their respective measured values, for the training data set. With the satisfactory agreement between network-estimated and measured values shown in Figs. 18 and 19, the network appears to mimic reasonably well the physical relationships between the two outputs ($q_{\text{inj}}^{\text{opt}}$ and q_o) and the remaining 11 input variables. However, this GRNN performance needs to be confirmed with a blind test data set. Figures 20 and 21 show the comparison of the network-estimated q_oand$q_{\text{inj}}^{\text{opt}}$ values with corresponding measured values for the blind test data set. The GRNN model prediction, using the test data set, appears to be fraught by some spread, yielding coefficients of determination of 0.75 and 0.78 for q_o and q_inj, respectively. As shown in Figs. 11 and 15, the dimensional analysis models appears to give more precise estimates of q_o and $q_{\text{inj}}^{\text{opt}}$. It is concluded, therefore, that the dimensional analysis analytical models outperformed the GRNN model.

Fig. 18

GRNN estimated oil rate versus actual oil rate (Alsarraf 2019), for the training data set (r² = 0.99)

Fig. 19

GRNN estimated injection gas rate versus actual gas injection rate (Alsarraf 2019), for the testing data set (r² = 0.99)

Fig. 20

GRNN estimated oil rate versus actual oil rate (Alsarraf 2019), for the testing data set (r² = 0.75)

Fig. 21

GRNN estimated injection gas rate versus actual gas injection rate (Alsarraf 2019), for the testing data set (r² = 0.78)

Conclusions

Reliable and precise estimates of the optimal gas injection rate and the corresponding maximum oil rate are some of the main challenges in gas lift operations. In these operations, injected gas from the annulus flows into the tubing through a gas lift valve placed in a mandrel. An increase in total gas–liquid ratio, caused by the optimal gas injection rate, inside the tubing decreases the oil column density, and reduces the flowing bottom hole pressure, as a consequence. As the gas injection rate increases beyond the optimal rate, the friction pressure losses start to increase, causing an undesirable increase in the flowing bottom hole pressure. Therefore, it is important to inject gas at an optimal rate in order to maximize the oil production rate.

This study derives empirical models, using dimensional analysis, for both the optimal gas injection rate and the maximum oil rate are proposed. These empirical models have been validated using collected production data for 388 wells undergoing gas lift operations, from various Middle East oil fields. These models are applicable for single vertical wells undergoing continuous gas lift operations. The developed empirical models are suitable for situations where the amount of available gas for injection exceeds the requirements.

Dimensional analysis reveals the critical factors that affect the design of continuous-flow gas lift operation. The optimum gas injection rate and the maximum oil rate appear to dependent upon the critical combination of a number of pertinent variables, including the equivalent production-tubing radius, the pressure gradient inside the well, the oil density, the productivity index, and the ratio of bottom hole temperature to separator temperature. The empirical models developed in this study owe their robust performance to the dimensional analysis ability to identify pertinent parameters that influence the physics of the gas lift operation.

The results are compared with those obtained from a general regression neural network (GRNN) model, also developed in this study to predict the optimal gas injection rate and the maximum oil rate. GRNN is a memory-based, fast-learned network that is easily tuned. The GRNN models prediction capability has been tested with a blind data set. The dimensional analysis models prediction of the maximum oil rate and the optimal gas injection rate were in general slightly more accurate that those obtained from the GRNN model. Moreover, the dimensional analysis models are favored since they are explicit, and do not require any trial-and-error procedure.

The two proposed empirical models of this study, for estimating the optimal gas injection rate and the corresponding maximum oil rate, may be used as a quick performance prediction tools. The models elude the demanding efforts of characterizing the two-phase flow regime. They also elude the tedious efforts of accounting for the effects of composition changes of oil and gas on the pressure drop calculations. The results from these empirical models may be used as an input in network models, in order to estimate the performance of a network of wells. The strength of dimensional analysis consists of eliminating the guessing process generally associated with developing highly nonlinear regression models.

Appendix

Equivalent radius derivation

The derivation of the equivalent radius is performed for a steady-state flow of incompressible fluid in a composite vertical pipe of many segments of length L_i and radius R_i. The fluid flow potential across the composite pipe is the sum of the flow potential drop across various pipe segments, given as follows:

$$\Delta \varPhi = \Delta \varPhi_{1} + \Delta \varPhi_{2} + \cdots + \Delta \varPhi_{n}$$

(29)

The fluid flow potential differences may be expressed from the Hagen–Poiseuille equation as follows:

$$\frac{8\mu qL}{{\pi R_{\text{eq}}^{4} }} = \frac{{8\mu qL_{1} }}{{\pi R_{1}^{4} }} + \frac{{8\mu qL_{2} }}{{\pi R_{2}^{4} }} + \cdots + \frac{{8\mu qL_{n} }}{{\pi R_{n}^{4} }}$$

(30)

Since the flow rate, the fluid viscosity are assumed constant, the above expression may be rearranged as follows:

$$R_{\text{eq}} = \left[ {\frac{L}{{\frac{{L_{1} }}{{R_{1}^{4} }} + \frac{{L_{2} }}{{R_{2}^{4} }} + \cdots + \frac{{L_{n} }}{{R_{n}^{4} }}}}} \right]^{{\frac{1}{4}}} .$$

(31)