A new technique for forecasting pore pressure in two oil wells in North Rumaila field based on specific energy concept

Abstract

Forecasting the pore or formation pressure is crucially significant in every well drilling operation to determine whether the pore pressure gradient is abnormal or subnormal. Abnormal pore pressure gradient means that the pore pressure gradient exceeds the gradient of the normal pressure, while when the opposite happens it means that the pore pressure is subnormal. Both cases required high care with special control of the mud weight to overcome the vital situation. Accurate pore pressure determination is rigorous in drilling engineering to plan for drilling hydrocarbon wells with appropriate mud program with less effort and cost. Precise forecasting of formation pore pressure prevents occurring various drilling hazards such as lost circulation, stuck pipe and well kick as a result of abnormal pore pressure. In the present work, a new technique was proposed to predict the pore or formation pressure from the specific energy. A new formula of specific energy was used involving the rock properties and the drilling parameters. The new specific energy formula is functioned later in Eaton’s equation to obtain a new suggested formula of pore pressure. There is a lack of researches in the literature that determine the real-time pore pressure without depending on well logs. Abnormal and subnormal pressure zones can be determined accordingly based on the fact that abnormal pressure intervals possess low effective stress and require less energy to drill than the intervals that have normal pressure at the same depth. The new proposed formula of pore pressure was tested in two oil wells in North Rumaila field (N14 and N15) in Basrah province south of Iraq. The obtained pore pressure from the new technique based on the suggested specific energy formula that involves the physical properties of the rock being excavated and the drill bit is compared with the actual (measured) pore pressure derived from other wells in North Rumaila field using measurements while drilling logs, drill stem test and real formation test. There was a good rapprochement between the predicted and the measured pore pressure. The present approach depends mainly on the value of the slope (m) which is determined and varied from one place to another. The new method could provide an alternative method for estimating the pore pressure especially for wells being planned to be drilled where the actual pore pressure is unknown and there is shortage in well logs and formation tests, where most of the previous articles in the literature depend mainly on well logs of adjacent wells in predicting the pore pressure of a specific well. The findings of this study can help for better understanding the prediction of formation or pore pressure that helps to choose the appropriate mud weight to control the well without collapsing and preventing well kick that might occur.

Introduction

Predicating the in situ pore pressure for a well being drilled is crucially significant to design the wellbore and to avoid any drilling problems. Drilling within hydrostatic pressure zones is considered in ideal conditions, although this case is not always occurred, especially when high-pressure formation is encountered since the first appearance of the methods for predicting the pore pressure from the main drilling parameters might cause mysterious analysis especially in conditions that are significant such as rate of penetration, drill bit hydraulics and the lithology of the rock formation. Formation pressure gradient depends mainly on various factors such as the concentration of salt dissolved in the formation water, temperature (Swarbrick et al. 1998). The normal formation pressure gradient differs between 0.433 and 0.515 psi/ft. The average normal formation pressure gradient in the North Sea is 0.45 psi/ft (Holm 1998). Drilling overpressure intervals could unexpectedly cause disastrous accidents such as well kicks or blowouts. In addition, it is likely that abnormal pressure causes high drilling cost and might lead to environment destruction, loss of properties and even loss in human lives, therefore, it is crucially important to detect abnormal pressure zones prior to excavating into them. Accordingly, the wellbore stability needs monitoring of formation pressure of the formation intervals being drilled in order to choose the most suitable drilling mud weight (Narciso 2014).

One of the ideal assessments of the abnormally pressured intervals is by comparing the in situ formation pressure taken from different sources such as well logs, drilling parameters since depending on any single approach could cause misinterpretations (Fertl and Timko 1971). Nearly, most if not all formation pressure forecasting approaches require the so-called normal compaction trend (NCT) of the shale properties to be installed, this (NCT) line represents the normal or hydrostatic pressure. Any inclination from the (NCT) trend is likely indicating the launch of overpressure. Formation pressure is determined in shale formations. The (NCT) trend should be instantaneously monitored because, it is sensitive to shale formations due to the remarkable variations in the petro-physical properties of shale with respect to formation pressure that will give prior warning of overpressure zones (Hottmann and Johnson 1965; Atashbari and Tingay 2012).

In the current study, an approach was introduced for forecasting the pore pressure by introducing a new modified formula of Eaton equation. The new formula is based on the specific energy which is manifested by the exponent or power (m) in the modified formula. The value of (m) is significant to be determined, where finally the pore pressure gradient could be calculated without the need of well logs or other formation tests. This method could help determining the formation pressure gradient for planned offset wells to be drilled in the same field.

Figure 1 shows the general sketch of the procedure being followed in the present study to forecast the pore pressure gradient.

Fig. 1

General sketch illustrates the main objectives of the current study and the parameters required to be determined

As shown in Fig. 1, the steps of the suggested work are started with collecting the main parameters to calculate the specific energy. Mainly, the specific energy is dependent on many factors. However, a new approach was introduced to determine the specific energy from the physical properties of the rock formation being damaged and the drill bit, i.e., the hardness. Then, collecting overburden and normal pressure gradients from offset wells. After that, Eaton’s formula was modified to include the specific energy in it. Next, a log–log plot is performed to obtain the value of the slope or exponent (m) in Eaton’s modified equation. Finally, the pore pressure gradient is computed from Eaton’s modified formula and compared with the in situ pore pressure gradient.

Area of study

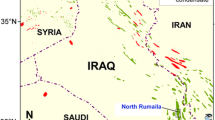
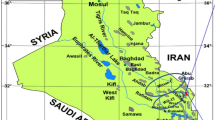
North Rumaila is one of the biggest oil fields in southern Iraq which produces about one-third of the total oil production of the country. It is situated about 50 km to the west of Basra province. Figure 2 demonstrates the location of this giant oil field among other producing oil fields in southern Iraq. The main producing formations in this field are Mishrif, Nahr Umr and Zubair.

Fig. 2

Map of Iraq illustrates the location of the specific oil field being studied (Al-Ameri et al. 2009)

Two oil-producing wells were studied in this field N14 and N15. Data for these two wells were collected from bit records, geological information and well logs besides the actual pore pressure gathered from repeated formation test (RFT) and drill stem test (DST).

Theoretical background

In the literature, many research works have been carried out in formation pressure prediction mainly by using the techniques of well logs, obtaining some empirical equations for formation pressure determination. Hottmann and Johnson studied the pore pressure prediction properties of shale taken from well logs (Hottmann and Johnson 1965). This technique depends on any deviation in the measured logs from its normal trend line. Later, many researchers have used well logs of resistivity, sonic, porosity and other well logs for formation pressure expectation. The majority of these researches are based on the hypothesis that any change in the petrophysical properties could lead to variation in the pore pressure. Therefore, the change of these parameters can help the interpretation and evaluation of formation pore pressure. Traditional techniques of the prediction of formation pressure are illustrated as follows:

Eaton approach

Historically, lots of methods were introduced for formation pressure determination in hydrocarbon wells (Eaton 1972). In 1975, Eaton introduced an empirical formula to determine the formation pressure from well logs such as resistivity, sonic and another empirical equation based on drilling parameters or (dc-exponent). The main assumption of his work is based on that the mechanism of disequilibrium compaction is the origin of abnormal generation (Eaton 1975).

Eaton (1975) suggested three quantitative equations of pore pressure dependent on sonic transit time, resistivity and dc-exponent calculated from drilling parameters as shown in (Eqs. (1)–(3), respectively). Eaton’s formulas still nowadays are widely used for the purpose of pore pressure quantification (Eaton 1975).

The suggested three sets of equations for the determination of pore pressure are shown as follows:

$${\text{Gpp}} = {\text{Gob}} - \left\{ {{\text{Gob}} - {\text{Gnp}}} \right\}*\left[ {\frac{{R_{{\text{o}}} }}{{R_{{\text{n}}} }}} \right]^{1.2}$$

(1)

$${\text{Gpp}} = {\text{Gob}} - \left\{ {{\text{Gob}} - {\text{Gnp}}} \right\}*\left[ {\frac{{\Delta t_{{\text{n}}} }}{{\Delta t_{{\text{o}}} }}} \right]^{3}$$

(2)

$${\text{Gpp}} = {\text{Gob}} - \left\{ {{\text{Gob}} - {\text{Gnp}}} \right\}*\left[ {\frac{{d_{{{\text{co}}}} }}{{d_{{{\text{cn}}}} }}} \right]^{1.2}$$

(3)

where R_o is the observed or measured resistivity (ohm m), R_n is the resistivity derived from the normal compaction trend (NCT), Δt_n is the acoustic time at the normal compaction line (μs/ft), Δt_o is the observed acoustic time (μs/ft), d_co is the observed or computed dc exponent values, and d_cn is the dc exponent values derived from the (NCT), Gpp is the formation pressure gradient (psi/ft), Gob is the overburden pressure gradient (psi/ft), Gnp is the hydrostatic or normal pressure gradient (psi/ft).

Estimation of pore pressure can be performed by using the concept of specific energy that based on the assumption that abnormal pressure intervals have low effective stress and require less energy to drill rather than the intervals that have normal (hydrostatic) pressure at the same depth. Oloruntobi et al. (2018), Oloruntobi and Butt (2019) proposed a new approach to determine the formation pressure using the so-called hydro-rotary specific energy (HRSE). The suggested new model was taken from the combination of the hydraulic and rotary energies along with the axial energy being neglected. The model suggests that while the depth of burial rises in normally compacted zones, the Hydro-Rotary Specific Energy (HRSE) needed to destruct and remove a unit volume of rock will also rise. Nevertheless, subsurface abnormal circumstances with lower effective stress need less energy to excavate than the normally compacted zones at the same depth that leads to the inverse trend of HRSE (Oloruntobi et al. 2018; Oloruntobi and Butt 2019).

Methodology

Anticipation of formation pressure by Eaton’s formula could be modified according to the concept of specific energy as the parameters used in previous Eaton’s equations can be replaced with specific energy as shown below:

$${\text{Gpp}} = {\text{Gob}} - \left\{ {{\text{Gob}} - {\text{Gnp}}} \right\}*\left[ {\frac{{{\text{SPE}}_{{\text{o}}} }}{{{\text{SPE}}_{{\text{n}}} }}} \right]^{m}$$

(4)

where the observed specific energy is referred to (SPE_o) (psi), the normal specific energy is denoted as (SPE_n) and m is the power that should be computed. After a series of mathematical operations shown in “Appendix,” the exponent (m) can be obtained.

It is worth mentioning that the normal compaction trend line must be formed. At normal or hydrostatic pressure intervals, specific energy increases with depth, whereas at overpressure zones, specific energy rises versus depth. Equation (4) is used to anticipate the formation pressure, where the specific energy must be computed firstly.

Many approaches were carried out for the quantification of the specific energy. Teale was one of the first researchers who studied the specific energy caused by the drill bit and its effect on rock destruction (Teale 1965). All previous methods for the determination of the specific energy depend mainly on drilling parameters regardless of the effect of the rock and the drill bit properties. Abbas (2017) suggested a new formula for specific energy based on the physical properties of the drill bit and the rock being excavated where the approach exhibited reasonable results. After series of simplifications and substitutions, Abbas came up with an equation as follows (Abbas 2017):

$${\text{SPE}} = \frac{{28{,}137.862 H_{W} }}{{ \left( {\frac{{H_{a} }}{{H_{W} }}} \right)^{2.5} }}$$

(5)

where SPE is the specific energy (lb/in²), H_W is the hardness of the rock being drilled (N/m²) and H_a is the hardness of the bit N/m².

Equation (5) depends mainly on the quantification of the hardness of the rock being drilled and the hardness of the material forming the drill bit, therefore, it is crucially significant to obtain these parameters first. The lithology of the formations being drilled was obtained from the adjacent wells and accordingly the corresponding rock type could be determined. Next, the hardness of the determined rock formations being excavated can be obtained from the literature, where the hardness of the material forming the tooth of the tri-cone bits are obtained from the work of Mouritz and Hutchings (1991) and Gokhale (2010) as illustrated in Table 1 (Mouritz and Hutchings 1991; Gokhale 2010).

Table 1 Rock formations being excavated in the studied area with the corresponding hardness (Mouritz and Hutchings 1991; Gokhale 2010)

The hardness of the inserts of Tungsten-Carbide (TC) bit is 15 GPa (Osipov et al. 2010), while the hardness of the milled bit which is made mainly from steel is approximately 12.95 GPa (Mouritz and Hutchings 1991).

Methodology of calculations

• 1. From the bit record, the hardness of the cutters of the drill bit should be determined after using bit classification chart to match the commercial bit type with the corresponded type of drill bit (IADC Classification Chart 2008).

• 2. Determine the hardness of the rock formation by the benefit of Table 1.

• 3. Calculate the observed real-time specific energy (SPE_o) values with depth using Eq. (5).

• 4. Plot the graph of specific energy (SPE) versus depth. The normal compaction trend line (NCL) should be established. This specific energy at (NCL) represents the normal specific energy (SPE_n) corresponded to hydrostatic or normal pore pressure, where any deviation from the (NCL) represents zones of abnormally high or low pressure.

• 5. Plot $\text{Log}\left[ {\frac{\text{Gob} - \hbox{Gpp}}{{\text{Gob} - \hbox{Gnp}}}} \right]$ versus $\text{Log}\left[ {\frac{{\text{SPE}_{\hbox{o}} }}{{\text{SPE}_{\hbox{n}} }}} \right]$, the slope (m) or the specific energy ratio exponent can be determined. The slope (m) is the most important parameter that affects the degree of convergence of the predicted pore pressure gradient with the actual one. The value of the slope (m) may vary from one region to another depending on many variable parameters (Oloruntobi et al. 2018; Oloruntobi and Butt 2019).

• 6. Calculate the formation pore pressure gradient by applying Eq. (4) and plot against depth.

• 7. Compare the anticipated pore pressure gradient with the actual pore pressure gradient obtained from real formation test (RFT) and well logs to verify the reliability of the suggested formula obtained from the current study. A statistical analysis could be useful to assist this comparison. Mean absolute error (M_E) formula is used as follows:

  $$M_{{\text{E}}} = \left[ {\frac{1}{N} \mathop \sum \limits_{i = 1}^{N} \left| {\frac{{Z\left( I \right)_{{\text{a}}} - Z\left( I \right)_{{\text{c}}} }}{{ Z\left( I \right)_{{\text{a}}} }}} \right|} \right]$$

  (6)

  where M_E is in (fraction or percentage), Z(I)_a is the actual values of a parameter, Z(I)_c is the calculated values for the same parameter, and N is the number of readings in a sample. This statistical analysis is useful for the purpose of comparison between the measured values for any model with the computed ones. The model that possesses the minimum value of M_E is the most closest to the actual and considered the most reliable (Huber 1964).

Results and discussion

Table 2 represents the most necessary data required for the computations in the current study. It was derived from the bit record report as well as from the geological information of North Rumaila field and particularly from well N14 in the south of Iraq. The actual formation pressure is collected from the real formation test (RFT) and well logs, while the hardness of the bit and the rock penetrated by it were obtained from the aforementioned Table 1.

Table 2 Data taken from the final report of bit record, logs and geological information for well # N14

As seen in Table 3, the values of the specific energy are obtained from Eq. (5) for both the observed and normal. As clearly observed from Eq. (5), the specific energy is affected mainly by two parameters: the hardness of the drill bit and the rock being penetrated by the drill bit. Hence, as mentioned previously, the normal values of (SPE) represent the values that lie on the normal compaction line (NCL). (SPE) is plotted against depth for wells N-14 and N15 as demonstrated in Fig. 1. The calculated specific energy values are given in Table 2.

Table 3 Obtained results of normal and observed specific energy for well #N14

Figure 3 illustrates the gradual rise of (SPE) needed to destroy a unit volume of a rock versus depth where the (NCT) line passes through the values that represents (SPE_n) also increases gradually as a result of increasing the compaction of the rock. The rock formations at such zones exhibit normal formation pressure or (hydrostatic).

Fig. 3

Plot of specific energy against depth (a well N14, b well N15)

It is worth mentioning that Fig. 3a shows at near depth (1600 m), the (SPE) curve starts to decrease until depth (1735 m) representing an overpressured zone, while for well # N15, similar drop in (SPE) values is observed at depth (1756 m) giving an indication that a zone of abnormal pressure is detected as shown in Fig. 3b. Afterward, the (SPE) resumes to increase for both wells and overturned the normal compaction trend line reaching depths (2190 m) and (2198 m) for wells N14 and N15, respectively. This sudden increase and passing of the (NCT) are attributed to the reduction in compaction of the rock formation resulting in a pressure below normal called subnormal pressure. Again the trend of (SPE) starts to drop for both wells reaching depths (2452 m) and (2561 m) for wells N14 and N15, respectively, but the drop was slight in well N15 explaining that another abnormal pressure zone is detected.

Now, in order to monitor the real-time pore pressure versus depth, therefore, the determination of formation pressure is highly required. As many previous research works relied mainly on well logs and geological information to estimate the pore pressure, the current technique does not need any well logs. However, to anticipate the formation pressure by the new suggested method requires the computation of the slope (m) in Eq. (4). To obtain the value of (m), a plot of ${\text{Log}}\left[ {\frac{{{\text{Gob}} - {\hbox{Gpp}}}}{{{\text{Gob}} - {\hbox{Gnp}}}}} \right]$ versus ${\text{Log}}\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]$ should be carried out. Figure 4 illustrates the plot of how the slope (m) is obtained. Figure 4 clarifies that the exponent (m) for well N14 was (0.2895), whereas, for well N15, the slope (m) was equal to (0.2781). It is shown that the value of (m) ranges from 0.2781 to 0.895.

Fig. 4

Plot of ${\text{Log}}\left[ {\frac{{{\text{Gob}} - {\hbox{Gpp}}}}{{{\text{Gob}} - {\hbox{Gnp}}}}} \right]$ versus ${\text{Log}}\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]$ in Eq. (4) (a well N14, b well N15)

To calculate the predicted pore pressure gradient from the new formula, Eq. (4) is applied. The results of the calculations along with the actual real-time formation pressure gradient are illustrated in Table 3 above. Figure 5 exhibits the graph of formation pore pressure estimated from the new formula (Eq. (4)). The predicted real-time pore pressure gradient and the actual pore pressure derived from real formation test (RFT), drill stem test (DST) and well logs were plotted together versus depth for wells N14 and N15 to examine the degree of rapprochement.

Fig. 5

Anticipated real-time formation pressure gradient from the suggested approach with the actual formation pressure gradient against depth (a well N14, b well N15)

Figure 5 shows the forecasted formation pressure compared with the actual pore pressure against depth where a good convergence was observed. As obtained previously that from Fig. 3, the values of (SPE) are nearly steady with depth, similar behavior was observed for the pore pressure gradient until reaching depth (1600 m) for well N14 and until depth (1986 m) for well N15, representing normal or hydrostatic formation pressure. The actual pore pressure gradient ranges from 0.457 to 0.46 psi/ft for well N14, while the anticipated pore pressure gradient ranges from 0.468 to 0.479 psi/ft, whereas for well N15, the actual formation pressure gradient ranges from 0.4571 to 0.4576 psi/ft, and the forecasted pore pressure gradient ranges from 0.455 to 0.478 psi/ft. It is worth mentioning that both ranges for the two wells are close to the normal density of water in Rumaila field (1.09 gm cc) or equals to (0.472 psi/ft) (Almalikee and Sen 2020). Afterward, for well N14, the actual formation pressure gradient increases slightly reaching (0.4804 psi/ft) at depth (1735 m) detecting a slight overpressure zone, while the forecasted pore pressure gradient reached (0.499 psi/ft) at the same depth. On the other hand, for well, N15 the actual pore pressure gradient elevates to a value of (0.4844 psi/ft) at depth (2148 m), whereas the predicted one was (0.511 psi/ft) at the same depth representing a slight abnormal pressure zone. This increase in the predicted and the actual formation pressure is attributed to the occurrence of shale layers that corresponded to Tanuma formation. This elevation in the actual and predicted formation pressure gradient for both wells within the mentioned interval indicates that the occurred shale layers which have low permeability were exposed to the phenomenon of under-compaction which happened in quick subsiding basins (Almalikee and Al-Najim 2018). At deeper depths, it is noticed that the predicted and the actual pore pressure gradient started to decrease for both studied wells.

For well N14, the actual formation pressure gradient decreased below the hydrostatic pressure gradient reaching a value of (0.34038 psi/ft) at depth (2190 m), while the anticipated pressure gradient also dropped to (0.4468 psi/ft) at the same depth. The corresponded formation at depth (2190 m) is Mishrif formation. This drop in pore pressure gradient is interpreted to the excessive production of oil from this formation a long time ago causing a considerable drop in the formation pressure.

For well N15, a similar behavior was observed. The actual and forecasted pore pressure gradient decreased to (0.33789 psi/ft) and (0.37079 psi/ft), respectively, at depth (2198 m) representing the entrance to Mishrif formation. Further down for both wells, the actual and anticipated formation pressure gradient recovered to the normal ranges which are near to the hydrostatic pressure gradient till the end. Overall, the new approach for forecasting the pore pressure gives a quick real-time prediction of the formation pressure, especially when well logs are unavailable.

It is worth mentioning that the obtained forecasted pore pressure gradient exhibits a similar trend with the actual one at most depth intervals for both studied wells. In addition, a good rapprochement was detected between the actual and predicted pressure gradient for both wells. Another interesting thing noticed from Fig. 5 is that the anticipated formation pressure gradient is slightly higher than the actual one for both wells. From the aforementioned results of the specific energy, i.e., Figure 3 and the obtained results of pore pressure gradient, i.e., Figure 5, the top of the abnormal and subnormal pressure zones could be determined as shown in Table 4:

Table 4 Top of overpressure and surpressure zones with the corresponded information for the studied wells

In order to analyze the comparison between the anticipated and the actual formation pressure gradient, a simple statistic formula was applied, i.e., mean absolute error (M_E) (Eq. 6). The resulted values of (M_E) were 5.083% and 3.446% for wells N14 and N15, respectively, as shown in Fig. 6 which are considered to be acceptable.

Fig. 6

Percentage of (M_E) for the studied wells in North Rumaila field

The current approach presented a new equation for quick and approximate pore pressure determination dependent on specific energy when other techniques, especially well logs, are unavailable. It is crucially important to denote that the current suggested approach depends on the actual formation pressure for the determination of the exponent (m) in Eq. (4). The actual pore pressure should be provided from many sources such as (RFT), (DST) or from well logs. However, when knowing the value of the power (m) in Eq. (4), the power pressure could be predicted. In the present work, the average value of the slope (m) is (0.2838) and it could be used later for the forecasting of formation pressure in any drilled well in the adjacent wells in North Rumaila field.

As previously shown, the main advantage of the current study is predicting the formation or pore pressure gradient for a hydrocarbon well being drilled or planned to be excavated without the need of well logs or well testing techniques. Another benefit of the current study is detecting the overpressure and underpressure zones which enables the drilling engineer to deal with this case with special care and interest. However, the main drawback that might appear in the present research is determining the real-time hardness of the rock formation being drilled for every interval not exceeding 10 m in order to give more accuracy of the determined specific energy and consequently the pore pressure gradient. In addition, overburden and normal pressure gradients are needed to be determined for the specific well in the field under study without calling these data from offset wells in the same field. This will also improve the precision of the obtained results.

The main limitation of the present work is that the forecasting of the pore pressure is for particular wells in a specific field is relied on the determined value of the exponent (m) in the modified equation of Eaton, whereas in other oil fields, the value of (m) might be varied and accordingly, the present study should be repeated for any other field to determine the new value of the slope (m) which governs the determination of the formation pore pressure.

Summary and conclusions

• The new proposed technique for pore pressure prediction is dependent on the specific energy which relied mainly on the hardness of the drill and the rock formation being spudded.

• The obtained results from the current approach is encouraging and it could be applied on other wells in the studied zone in order to give a quick and approximate pore pressure.

• By the benefit of the current approach, abnormal and subnormal pressure intervals can be detected, and accordingly, a special care should be carried out when dealing with overpressure, especially with the mud weight.

Appendix: Derivation of Eaton modified equation

$${\text{Gpp}} = {\text{Gob}} - \left\{ {{\text{Gob}} - {\hbox{Gnp}}} \right\}*\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]^{m}$$

(7)

$${\text{Gob}} - {\text{Gpp}} = \left[ {{\text{Gob}} - {\hbox{Gnp}}} \right]*\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]^{m}$$

(8)

$${\text{Log}}\left( {{\hbox{Gob}} - {\text{Gpp}}} \right) = {\text{Log}}\left[ {{\hbox{Gob}} - {\text{Gnp}}} \right] + m\log \left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]$$

(9)

$${\text{Log}}\left[ {\frac{{{\hbox{Gob}} - {\text{Gpp}}}}{{{\hbox{Gob}} - {\text{Gnp}}}}} \right] = m \cdot {\hbox{Log}}\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]$$

(10)

Hence, plotting ${\text{Log}}\left[ {\frac{{{\hbox{Gob}} - {\text{Gpp}}}}{{{\hbox{Gob}} - {\text{Gnp}}}}} \right]$ versus ${\hbox{Log}}\left[ {\frac{{{\text{SPE}}_{{\hbox{o}}} }}{{{\text{SPE}}_{{\hbox{n}}} }}} \right]$, where it is clearly seen that the slope m could be obtained and substituted in Eq. (7) to compute the pore pressure gradient.