Introduction

Subsurface pressure estimation is significant for both exploration and drilling projects. Optimizing well planning and drilling decisions in overpressure zones, where the geopressure is greater than the normal pressure (hydrostatic), is crucial to perform geopressure forecasts before drilling. Mud weight is the vital element to control the well stability depending on the pore pressure situation to prevent numerous drilling problems such as blowout, lost circulation, well kick, and reservoir destruction, which consequently leads to reducing the cost and an economic drilling, would be achieved.

Traditionally, there are various approaches to speculate subsurface pressure, especially from well logs that mainly depend on seismic velocity data. The well-known Eaton’s method commonly used for the geopressure speculation from sonic travel time data as well as from resistivity logs. Eaton’s formula may produce an error if the normal compaction trend line used for determining the normal hydrostatic pressure is not precisely drawn and accordingly corrections should take place (Chatterjee et al. 2012). Simulation approaches that depend on the seismic log data were carried out to obtain a reliable model for pore pressure determination where an encouraging results were obtained (Asedegbega et al. 2021). A recent study was performed for the goal of pore pressure determination using Artificial Neural Network (ANN) where this technique was successfully applied previously for the estimation of rate of penetration where reasonable results were produced (Markovic et al. 2021). Simulation approaches encourage further investigation for geopressure estimation as a successful alternative of actual pore pressure measurement. A recent study of using nanoparticles in drilling shows that the combination of nanoparticles and smart fluids could create a highly efficient sensor that can operate properly in extremely difficult drilling conditions and can provide precise measurements of temperature, geopressure, oil flow rate and tension in deep wells (Lastname 2018). Special nanoparticles (NPs) were added to the drilling mud can cause a drop in permeability and abnormal pressure. This novel finding could help dramatically the reduction in overpressure in the areas that suffer from the dilemma of high subsurface pressure (Saleh and Ibrahim 2019).

Abnormal formation pressure is one of the main drilling problems that should be dealt seriously to prevent the destruction consequences might be occurred; therefore, instantaneous monitoring of the pore pressure is indispensable along the excavation of any well. Many researches in the literature dealt with this issue (Fertl and Timko 1971; Holm 1998; Swarbrick et al. 1998). However, few researches were carried out on determining the subsurface pressure from the inception of Mechanical Specific Energy (MS), where the final obtained geopressure formula was applied on selected wells in Nigeria where good results were produced (Oloruntobi et al. 2018; Oloruntobi and Butt 2019).

All previous approaches available in the literature were targeting the determination of geopressure with fewer errors due to its crucial significance on overall drilling operation.

The main target of the current study is to suggest a new formula of subsurface pressure gradient that involves the main parameters of the penetrated rock along with the parameters of the drill bit itself, where there is shortage of covering this combination in the available literature.

Area of study

Three oil-producing wells were investigated in the current study, where the data were brought from geological reports, bit records, and well logs. The in situ actual geopressure was collected by the benefit of Repeated Formation Test (RFT) and Drill Stem Test (DST). The wells being investigated in the present research are Missan C, Zubair 171 and West Qurna 15 in south of Iraq.

Missan oil fields lie about 175 km north of Basrah province southern Iraq near to the border with Iran. Missan fields consist of Buzurgan, Abu Ghirab and Jabal Fauqi (Fakka) oil fields. The production of these fields reached 450.000 barrel/day, and the reserves is proved to be 2.5 billion barrels of oil. MS-C well was chosen to be involved the current study.

The second well included in the present study is Zubair-171 in Zubair supergiant oil field, which considered one of the largest hydrocarbon fields in the world. This field is located around 20 km west of Basrah city south of Iraq.

The last well being investigated in the current research is West Qurna-15 in West Qurna giant oil field that lies in north of Rumaila oil field, west of Basrah. West Qurna is believed to have a reserve of around 43 billion barrels.

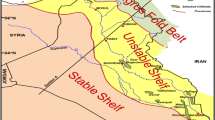
Figure 1 illustrates the location of three selected oil fields in southern Iraq that involves the three wells under study. The three studied wells are located in different geographical locations; consequently, various geological aspects are featured with each one, especially the stratigraphic columns.

Fig. 1
figure 1

Map or Iraq demonstrating the location of the particular oil wells being investigated (Abbas et al. 2020)

Full size image

Theoretical background and methodology

Formation pressure is predicted using several approaches mainly from Logging While Drilling (LWD), such as porosity, resistivity and sonic logs as well as where empirical formulas were obtained (Zhang 2011). The accuracy of these techniques was encouraging and consequently used for other calculations in well design. Other methods depend on seismic data for the forecasting of formation pressure based on (velocity and acoustic impedance), where also some empirical equations were developed with acceptable results were obtained (Pennebaker 1968). Drilling parameters could also be used for the speculation of pore pressure. The d-exponent approach was the oldest empirical formula for predicting the geopressure from drilling parameters (Rehm and Mcclendon 1971). Depending on just one approach could lead to misinterpretations; therefore, it is preferable to monitor the combination of the available data for instance, in cases of well caving, well logs might produce imprecise results, whereas drilling parameters might lead to better results. Furthermore, under severe bit conditions, well logs could provide more precise pore pressure estimation than the geopressure from drilling parameters. In the literature, the traditional Eaton formulas are implemented for the prediction of pore pressure from drilling parameters, i.e., dc exponent and from well logs (transit time and resistivity) as shown in Eqs. 1–3 as follows (Eaton 1975):

$$ Gpp = Gob - \{ Gob - Gnp\} *\left[ {\frac{dco}{{dcn}}} \right]^{1.2} $$
(1)
$$ Gpp = Gob - \{ Gob - Gnp\} *\left[ {\frac{\Delta tn}{{\Delta to}}} \right]^{3} $$
(2)
$$ Gpp = Gob - \{ Gob - Gnp\} *\left[ {\frac{Ro}{{Rn}}} \right]^{1.2} $$
(3)

where (dco) is the observed dc values (unitless), (dcn)is the (dc) values taken from the normal compaction trend line (dimensionless), (Δtn) is the transit time at the normal compaction trend line (μsec./ft), (Δto) is the observed transit time (μsec./ft), (Ro) is the measured resistivity (ohm.m), (Rn) is the resistivity taken from the normal trend line, (Gpp) is the geopressure gradient (psi/ft), (Gob) is the overburden pressure gradient (psi/ft), and (Gnp) is the normal or hydrostatic pressure gradient (psi/ft).

Determination of geopressure can be carried out by using the inception of mechanical specific energy (MS) based on the rule that overpressure intervals that possess low effective stress need less energy to excavate the rock formation rather than the intervals that have normal or hydrostatic pressure at the same depth according to the definition of the specific energy presented in Eq. (4a).

$$ {\text{Specific energy}} = \frac{{\text{Energy rate}}}{{\text{Volume rate of the rock being exavated}}} $$
(4a)

Oloruntobi et al. (2018), Oloruntobi and Butt (2019) suggested a new method to quantify the geopressure. The proposed new model was derived from the rotary and hydraulic energies. The new approach is based on the hydraulic specific energy which is the combination of axial, hydraulic and torsional energies (Oloruntobi et al. 2018; Oloruntobi and Butt 2019). However, the previous approaches obtained encouraging results and improvement should be done to include the effect of the rock formation hardness as well as the hardness of the drill bit. No references in the literature include this significant effect; therefore, an essential development of Eaton's formula was carried out.

$$ HMS = \frac{{\text{Axial Energy}}}{{\text{Rock Volume Excavated}}} + \frac{{\text{Hydraulic Energy}}}{{\text{Rock Volume Drilled}}} + \frac{{\text{Torosional Energy}}}{{\text{Rock Volume being drilled}}} $$
(4b)
$$ HMS = \frac{WOB}{{A_{b} }} + \frac{{1154*\Delta p_{b} }}{{A_{b} *ROP}} + \frac{120*\pi *N*T}{{A_{b} *ROP}} $$
(5)

where WOB is the weight on bit (lb), d is the bit diameter (in), N is the bit rotary speed (rpm), ROP is the penetration rate (ft/hr), T is the bit torque (ib.ft), Ab is the surface area of the bit (in2), ∆pb is the pressure drop at the bit (psi), and HMS is expressed in psi.

Quantification of geopressure gradient at any certain depth could be determined by modifying one of Eaton's equation sets (1–3) and replacing the hydraulic specific energy instead of the other parameters. The new proposed formula of geopressure gradient is presented in Eq. (6).

$$ Gpp = Gob - \{ Gob - Gnp\} *\left[ {\frac{{HMS_{o} }}{{HMS_{n} }}} \right]^{m} $$
(6)

where HMSo represents the observed hydraulic mechanical specific energy (psi), HMSn denotes the normal hydraulic mechanical specific energy, and (m) is the power that should be known. The power in Eq. (6) (m) varies from a specific region to another.

By the beneficial of Eq. (7), Abbas (2017) suggested a new formula for the determination of the mechanical specific energy instead of using Eq. (5), because in many cases the bit torque is not unavailable (Abbas 2017). The proposed formula in Eq. (7) is based on the drilling properties as well as the mechanical effects on the specific energy, especially the hardness of the rock and materials that form the drill bit. After a series of derivations shown in Appendix A, the new suggested formula of mechanical specific energy is as follows:

$$ MS = \frac{{K_{1} H_{W} }}{{ \left( {\frac{{H_{a} }}{{H_{W} }}} \right)^{2.5} }} $$
(7)

where MS is the mechanical specific energy (psi), HW is the hardness of the rock formation being excavated (N/m2), Ha is the hardness of the materials forming the bit (N/m2), and K1 is a constant for the conversion which equals to (28,137.862).

Substituting Eq. (7) into Eq. (6) leads to the following:

$$ Gpp = Gob - \{ Gob - Gnp\} *\left[ {\frac{{MS_{o} }}{{MS_{n} }}} \right]^{m} $$
(8)

The power (m) in Eq. (8) can be determined by the following simplification steps:

Taking Logarithm of both sides of Eq. (8) yields the following:

$$ \begin{gathered} Log(Gob - Gpp) = Log[Gob - Gnp] + m\log \left[ {\frac{MSo}{{MSn}}} \right] \hfill \\ Log\left[ {\frac{Gob - Gpp}{{Gob - Gnp}}} \right]{ = }m\;.\;Log\left[ {\frac{MSo}{{MSn}}} \right] \, \hfill \\ \end{gathered} $$

Sketching \(Log\left[ {\frac{Gob - Gpp}{{Gob - Gnp}}} \right]\) vs. \(Log\left[ {\frac{MSo}{{MSn}}} \right]\), the exponent (m) which represents the slope could be determined accordingly.

In the present research, the following procedure is followed to quantify the geopressure gradient as shown below:

  1. 1.

    By the benefit of bit record, all drill bits been used have commercial numbers that need to be identify their type (Tri-cone rotary, Insert or PDC bits). Bit classification charts are used for the purpose of determining the type of drill bit which corresponds to the commercial bit type. If the type of the drill bit is known, the hardness of the drill bit tooth will be known accordingly (IADC classification chart 2008).

  2. 2.

    From the geological reports as well as from the study of Almahdawi (2016) (Abbas 2017), the lithology of Missan oil field is prepared to extract the hardness value of the rock layer being drilled in the current study as shown in Fig. 2, whereas the lithologies for the other two wells were gathered from the geological reports relevant of the two wells. The hardness of the materials forming the bit according to its type is collected from Table 1 (Mouritz and Hutchings 1991; Gokhale 2010).

  3. 3.

    From the literature, the hardness of the roller tungsten carbide (TC) bit is 15 GPa, whereas the hardness of the roller milled bit is approximately 12.95 GPa (IADC classification chart 2008; Osipov et al. 2010); therefore, the values of the hardness of the bits are determined.

  4. 4.

    The observed mechanical specific energy values (MSo) from Eq. (7) are computed. Next, the (MS) values vs. depth are plotted.

  5. 5.

    The Mechanical Specific Energy (MS) vs. depth is sketched, where the values of the observed (MS) that lie in a normal increasing trend represent the normal compaction trend line that means the normal or hydrostatic geopressure zone. Any inclination from this normal trend line denotes abnormal pressure regions.

  6. 6.

    Plotting \(Log\left[ {\frac{Gob - Gpp}{{Gob - Gnp}}} \right]\) vs. \(Log\left[ {\frac{SEo}{{SEn}}} \right]\), in order to find the value of the exponent (m). The value of (m) is the most significant parameter that should be obtained in order to quantify the subsurface pressure gradient. It is worth mentioning that the value of (m) may differ from one area to another relying on several effective parameters.

  7. 7.

    After knowing the value of the exponent (m), the geopressure gradient can be computed by implementing Eq. (8). It is worthy to mention that the normal trend line of the pore pressure gradient should be created, where at high pressure intervals, the geopressure gradient rises from the hydrostatic or normal pressure gradient trend line with depth. It is crucially important to collect the information obtained from steps 1–6, as each step hence depends on the previous one; therefore, the quantification of the geopressure gradient from the current approach would not be useful if any step above was not performed successfully.

  8. 8.

    Then, the speculated values of the subsurface gradient with the in situ actual geopressure gradient are validated. A comparative study between the anticipated and the actual geopressure gradient is carried out to validate the proximity of each well with the actual subsurface pressure gradient. A statistical formula can be applied to enhance the validation. Statistical Mean Absolute Error (MAE) is used for this purpose. Furthermore, another statistical formula is used, i.e., Mean Squared Error (MSE) as follows:

    $$ MAE = \left[ {\frac{1}{N} \mathop \sum \limits_{i = 1}^{N} \left| {\frac{{V\left( I \right)_{a} - V\left( I \right)_{c} }}{{ V\left( I \right)_{a} }}} \right| } \right] $$
    (9)
    $$ MSE = \left[ {\frac{1}{N} \mathop \sum \limits_{i = 1}^{N} \left( {V\left( I \right)_{a} - V\left( I \right)_{c} } \right)^{2} } \right] $$
    (10)
Fig. 2
figure 2

Stratigraphic column of Missan oil field southern Iraq showing the rock formation being penetrated in the current study with depth (Almahdawi 2016)

Full size image
Table 1 Type of rock formations being drilled in the current work with their corresponding values of hardness [19.20]
Full size table

where MAE is in (percentage or fraction), V(I)a is the measured or (actual) values of a parameter, V(I)c is the computed (predicted) values for the same parameter, and N is the readings number for a sample. Thus, MAE is a useful indicator for the comparison between the actual values for any model with the predicted ones. The model that has the lowest value of MAE is the closest to the actual. MSE is also a good indicator for the validation between the predicted and the observed values. When MSE is close to zero, it means that the model is the closest to the observed values. (Huber 1964). Therefore, the two aforementioned statistical tests shown in Eqs. 9 and 10 were used to validate the anticipated geopressure gradient with the actual in-situ one.

It is concluded that the proposed formula of the mechanical specific energy depends mainly on the mechanical properties of the rock and the drill bit used to penetrate it. Furthermore, the suggested equation of geopressure relies mainly on the exponent (m) in Eq. (8) which affects vitally the intensity of the speculated subsurface pressure.

Results and discussion

The necessary data for completing the rest of calculations, aforementioned in the procedure steps above, are shown in Table 2 for well Missan C. The data were collected from geological and bit record reports and well logs for three hydrocarbon wells in southern Iraq: (Missan C, Zubair 171 and West Qurna 15). It should be noted that the in situ or actual pore pressure gradient is provided from Repeated Formation Test (RFT) and Drill Stem Test (DST).

Table 2 Sample of the data derived from well logs, geological reports, and bit records for well Missan C in south of Iraq showing the main parameters of the drill bit and the rock being penetrated
Full size table

The mechanical specific energy (MS) is determined from Eq. (7) and tabulated in Table 3 for well Missan C, where (MS) clearly relies mainly on the hardness of the rock and the drill bit that excavates the rock formations. Values of (MS) are plotted vs. depth, where the normal trend line (NL) should be established as demonstrated in Fig. 3. The normal trend line denotes the values of normal (hydrostatic) pressure. It is worthy to mention that, the mechanical specific energy at the normal compaction trend line denotes the normal mechanical specific energy (MSn) at hydrostatic or normal geopressure, where any inclination from the normal trend line represents regions of either surpressure or overpressure. Figure 3 shows how the mechanical specific energy (MS) increases gradually with depth for well # Missan C which represents the normal pore pressure zones until reaching depth (2020 m), where (MS) started to decrease sharply till the end of the well detecting an overpressure region as illustrated in Fig. 3a.

Table 3 Sample of the calculated values of the mechanical specific energy from Eq. (7), in situ actual and predicted geopressure for well Missan C, south of Iraq
Full size table
Fig. 3
figure 3

Plot of the calculated mechanical specific energy vs. depth for three wells southern Iraq (a Missan C, b West Qurna 15, and c Zubair 171)

Full size image

For well West Qurna 15, the mechanical specific energy increases slightly with depth until depth (3300 m) representing hydrostatic pressure region. Afterward, a sever reduction of (MS) values was observed clearly. This reduction illustrates the detection of three high overpressure zones, i.e. (3300–3910 m), (3910–4115 m) and (4115–4550 m) as illustrated in Fig. 3b. This abnormal pressure is attributed mainly to the existence of anhydrite and salt series that extends from Sulaiy to Najmah formations.

The behavior of specific energy for well Zubair 171 is quite different from the previous two wells as shown in Fig. 3c. The (MS) values rise normally with depth exhibiting normal pore pressure zone until depth (1938 m) where (MS) values dropped until depth (2088 m) encountering a slight overpressure zone. Afterward, (MS) shows a dramatic rise until depth (2280 m) denoting a slight surpressure (below hydrostatic pressure). The values of (MS) after depth (2280 m) exhibiting a sharp reduction until reaching depth (2330 m) demonstrating the recovery of the subsurface pressure to its normal trend.

Next step is the surveillance of the anticipated geopressure with depth. For this purpose, the value of the power (m) in Eq. (8) should be determined in order to quantify the subsurface pressure gradient. Therefore, a sketch of \(Log\left[ {\frac{Gob - Gpp}{{Gob - Gnp}}} \right]\) vs. \(Log\left[ {\frac{SEo}{{SEn}}} \right]\) must be achieved. Figure 4 exhibits the determination of the power (m) in Eq. (8) for wells Missan C, West Qurna 15, and Zubair 171).

Fig. 4
figure 4

Determination of the slope (m) in Eq. (8) a Missan C, b West Qurna 15, and c Zubair 171)

Full size image

From Fig. 4, it is shown that the power (m) for wells Missan C, West Qurna, and Zubiar 171were (0.6896), (0.5617), and (0.1626), respectively. Surprisingly, the values of the slope (m) are increased in the upward direction as the well Zubair 171 located at the south of the rest two investigated wells and the well Missan C is lied on the north of the rest two wells. Figure 1 shows the geographical locations of the three wells.

The most significant step now is to determine the subsurface pressure gradient from the suggested formula, i.e. Equation (8). The computations of the predicted formation pressure gradient is tabulated in the last column of Table 3 for well Missan C. The anticipated pore pressure gradient from the proposed formula along with the in situ (actual) geopressure gradient taken from well logs, DST, and RFT is plotted vs. depth for the three wells as illustrated in Fig. 5. The plot shows the rapprochement between the forecasted and the actual geopressure gradient.

Fig. 5
figure 5

Forecasted geopressure gradient from the proposed formula of Eq. 8 along with the in-situ actual geopressure pressure gradient vs. depth (a well Missan C, b well West Qurna 15, and c Zubair 171)

Full size image

Figure 5 demonstrates the behavior of the anticipated geopressure gradient along with the in situ or actual subsurface pressure gradient where good rapprochement was noticed.

For well Missan C, the forecasted formation pressure exhibits a normal geopressure gradient from the beginning until nearly depth (2020 m), where the subsurface pressure gradient started to elevate dramatically showing an overpressure zone which extends till the end of the well as shown in Fig. 5a. The value of the pore pressure gradient at this overpressure zone ranged (0.51–0.781 psi/ft). The existence of overpressure in the wells of Missan field is most probably attributed to the multiple cap rocks originated from the beds uncompacted shale interceded with anhydrite, dolomite and salt beds. Salt rocks behave as seals for entrapment of salt water causing abnormal pressure (Al-Rubaiee 1987).

For well West Qurna 15, the abnormal formation pressure gradient encountered at three intervals (3300- 3910 m), (3910- 4115 m) and (4115–4550 m) showing geopressure gradients (0.5–0.752 psi/ft), (0.752–0.789 psi/ft), and (0.789–0.99 psift) which is approximately compatible with the actual geopressure gradient as illustrated in Fig. 5b. The predicted pore pressure gradient declined slightly from the highest abnormal to about (0.92 psi/ft) at depth 4526 ft. It is believed that the main cause of high subsurface pressure at the wells in West Qurna field is due to the influence of impermeable beds of Gotnia salt series that encountered in the Arabian gulf which extend to the south of Iraq (Fertl 1976).

The comportment of well Zubair 171 is unlike the previous wells, where the anticipated subsurface pressure gradient is normal until near depth (1939 m). Afterward, a slight abnormal pressure gradient is observed at depth range (1939–2088 m), where the predicted geopressure gradient increases from 0.42 to 0.449n psi/ft. It is worthy to mention that the average normal geopressure gradient in Rumaila field (south of Iraq) which is adjacent to the selected well being investigated is equal to (0.472 psi/ft) (Almalikee and Sen 2020).

This rise in formation pressure is corresponded to Tanuma Shale formation indicating that the encountered shale that have low permeability were exposed to geological under-compaction that occurred in rapid subsiding basins Then, the predicted geopressure gradient is declined until depth (2280 m) exhibiting a value of (0.396 psi/ft) referring to a slight subnormal pressure gradient that is corresponded to Mishrif formation. This decline in geopressure gradient is attributed to the excrescent production of hydrocarbon from this layer a long time ago resulting a considerable decrease in the geopressure pressure gradient (Almalikee and Sen 2020). After depth (2280 m), the subsurface pressure gradient started to return to its normal behavior as clearly seen in Fig. 5c.

Statistical analysis should take place to validate the predicted values of geopressure gradient with the in situ actual ones. Two statistical analysis methods were used in the present work to give robustness for the proposed approach of geopressure prediction: Statistical Mean Absolute Percentage Error (MAE) and Mean Squared Error (MSE).

Statistical Mean Absolute Percentage Error (MAE) is applied for the three wells to verify the rapprochement between the anticipated and the actual geopressure gradient. For this purpose, Eq. (9) is used as mentioned previously. The obtained results of (MAE) were (4.8865%), (3.905%) and (1.7242%) for wells Missan C, West Qurna 15, and Zubair 171, respectively, as demonstrated in Fig. 6. Mean Absolute Percentage Error (MAE) values for the three investigated wells were acceptable. Mean Squared Error (MSE) is also applied as shown in Eq. (10) to enhance the previous analysis where also encouraging results were obtained i.e. (0.00129), (0.00149) and (0.00009) for wells Missan C, West Qurna 15, and Zubair 171, respectively, as illustrated in Fig. 7.

Fig. 6
figure 6

Percentages of the statistical Mean Absolute Error (MAE) for the studied wells

Full size image
Fig. 7
figure 7

Values of the statistical Mean Squared Error (MSE) for wells Missan C, West Qurna 15, and Zubair 171

Full size image

According to the above statistical analysis, the present study gave a quick forecasting of the formation pressure gradient without the need for further use of well logs and other special tests such RFT and DST. However, the current study is limited for the fields that the wells are within them. Other fields in other areas require a similar study, but in general the exponent value (m) in Eq. (8) is the most significant affecting parameter in the determination of the subsurface pressure.

After the validation, it is concluded that the present approach could be applied successfully to the offset wells in the specific fields. The current technique gives an instant approximation of the subsurface pressure gradient, especially when the absence of the expensive tests (RFT and (DST).

Conclusions

From the obtained results, it is concluded that overpressure zones could be detected successfully from the new proposed method as well as anticipating the subsurface pressure gradient. The value of the slope (m) in Eq. (8) has a vital effect on the geopressure formula, where it varies from field to another depending on the rock type being penetrated as well as the kind of materials that the drill bit consists of. It was concluded that the slope value (m) increased in the upward direction according to the geographical location of the studied wells. The current approach found to be useful for instant prediction of geopressure gradient, especially when the costly and time consuming tests for actual pore pressure measurement especially (RFT) are unavailable. In addition, the present proposed method gives a continuous speculation of the subsurface pressure gradient with depth. The presented new technique could be implemented on other new wells, but adjacent to the investigated wells in the present research to determine the geopressure gradient, and thus all relevant considerations should be taken into account to avoid drilling problems that might be caused due to unwise prediction of geopressure. The present study could be expanded in scope to include more wells in various regions in order to establish a map of the distribution of the values of the exponent (m) and the resulted formation pressure gradient.