Rotary steerable systems: mathematical modeling and their case study

Abstract

Directional drilling is a common and essential procedure of major extended reach drilling operations. With the development of directional drilling technologies, the percentage of recoverable oil production has increased. However, its challenges, like real-time bit steering, directional drilling tools selection and control, are main barriers leading to low drilling efficiency and high nonproductive time. The fact inspires this study. Our work aims to contribute to the better understanding of directional drilling, more specifically regarding rotary steerable system (RSS) technology. For instance, finding the solutions of the technological challenges involved in RSSs, such as bit steering control, bit position calculation and bit speed estimation, is the main considerations of our study. Classical definitions from fundamental physics including Newton’s third law, beam bending analysis, bit force analysis, rate of penetration (ROP) modeling are employed to estimate bit position and then conduct RSS control to steer the bit accordingly. The results are illustrated in case study with the consideration of the 2D and 3D wellbore scenarios.

Introduction

Directional drilling has been bringing a lot of innovations and increased the efficiency of hydrocarbons extraction, especially in these past decades. Compared to vertical drilling, directional drilling is extremely useful when a wellbore needs to reach a target or a number of targets that are located at a horizontal distance of thousands meters from the well site, among other advantages Mitchell and Miska (2011). The directional drilling techniques can be summarized into two mains: point-the-bit (POB) and push-the-bit (PUB). The first one involves bending of the bottom hole assembly (BHA) into the direction of the desired curvature, while the second one pushes the bit in the directional perpendicular to the axis of the drill string, achieving a curved well.

Downhole mud motors and bent subs have been used for many years, since they are effective, reliable and a cheap solution of creating a deviated well. The drill string is oriented in a toolface direction and only the drill bit is rotated due to the hydraulic power of the mud motor, located several meters behind the bit, while the rest of the drill string stays without rotation Wiktorski et al. (2017). One of the main drawbacks of mud motors is the necessity of stop the rotation of the drill string once the toolface is pointed to the desired direction. It can create potential problems like pipe sticking or pack-off of tools, since the cuttings are not being rotated and could create a bed of cuttings easier.

On the other hand, the principal element to create a deviation of a well using the PUB technique is rotary steerable system (RSS) Schaaf et al. (2007); Warren (2006). It requires a special BHA component to direct the well path toward the desired direction, so-called rotary steering device Ruszka (2003). The tool accomplishes the tasks varying from simple gravity-based to more complex internal driveshafts of the BHA by the application of side forces from pads against the borehole wall. Some RSSs also employ automatic drilling modes where a well path is automatically steered using a programmed closed-loop control system (Ruszka 2003; Hansen et al. 2020).

The use of the RSS in the past years has proved that the RSS is more stable, less prone to sticking, facilitates the hole cleaning and increases the rate of penetration (ROP) compared with mud motor systems Hossain and Al-Mejed (2015); Stump (2019). The RSS has the ability to provide directional drilling control while allowing continuous rotation of the drill string. The RSS includes two main components: the control platform and the biasing mechanism. The control platform is the “brain” of the rotary guidance system and controls the direction of the biasing mechanism. The biasing mechanism is the “actuator” for the RSS Li et al. (2020). This steering is made with the use of an actuator which eccentrically displaces the center line of the drilling system away from the center line of the hole by a controllable offset Elshafei et al. (2015). Typically, the RSS actuator is a 3-pad tool which pushes one pad against the formation to direct the bit in the opposite direction. The pads are rotating along with the rest of the drill string, but when one pad aligns with the toolface, it is activated to push the tool. Once the pad is no longer aligned with the toolface, it starts deactivating gradually until it is totally deactivated while the next pad is being activated gradually.

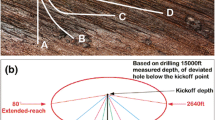
There are still several challenges and technical issues of RSSs that desirably need to be resolved or improved. For instance, directional drilling systems need to continuously monitor the bit dynamics and bit position to steer the bit following the planed path through the RSS control. Today, most commonly information is sent from the near bit area of drill strings via mud pulse telemetry. The signal rate for this form of telemetry is quite low, nominally 5–20 bits/second. There are several drawbacks with this form of data transmission in addition to low data rate; communication is essentially only in one direction; it is difficult to send signal down to the bit; communication is unavailable under tripping/connection; data quality is poor; and the number of downhole sensors is limited. The limited downhole information is a source of difficulties for the RSS control and resulting in more nonproductive time. To accurately and continuously estimate bit position and to precisely steer the bit to target positions are demanding and essential for the RSS technology’s improvements and developments. Due to the limited downhole measurements, mathematical modeling based on physics conservation laws becomes important for better solving such above-mentioned technological challenges. Therefore, the objective of this work is to develop mathematical models for RSSs to calculate the forces applying on the bit, bit position and bit speed in vertical and horizontal plane, and then continuously estimate bit path steered by the RSSs. These models are derived and explained through natural displacement caused by the formation, ROP compositions in 2D and 3D coordinates, bit force analysis by beam bending physics and the behavior of the RSS controllers. Case study illustrates that having such models enriches the performance of the RSSs in terms of real-time bit steering and control. This work provides high opportunities for better real-time well path control and optimization, and drilling automation related to the automatic RSS control.

RSS equipment

New technologies of RSSs have been developed with hybrid concepts of POB and PUB Rønnau et al. (2005); Alvord et al. (2007). The first commercially deployed RSSs contain three pads that guide the system [13]. The three pads are installed at the same distance from the drill bit around the body of the RSS tool. The entire system including drill bit, RSS tool and drill string rotates from the surface. At the kickoff point (KOP), the activation of the pads occurs. A hypothetical situation proposes a target location in the south direction. For an RSS tool, one pad faces the north direction, a second pad faces the southeast direction and a third pad faces the southwest direction. In this situation, the only pad that is creating a force against the formation is the pad facing the north direction. This pad pushes the formation and a reaction force is applied to the RSS tool toward the south direction. This reaction force is transferred to the bit and the entire system goes to the south direction.

Fig. 1

RSS work principle

Even though the most of the RSSs work with a 3 steering pads, one innovative BHA tool, called “OrientXpress® RSS” [14], has a cylindrical actuator that dislocates from the BHA to create an offset which pushes the bit along the opposite direction, see Fig. 1. One of the advantages of this tool is that the actuator can dislocate its center and push the formation in any direction with less moving parts than the three pads. The actuator activation is controlled by electric motors. Such actuator works with an electric and self-powered mud turbine generator and it also has shock, vibration and stick–slip sensors, which are very close to the bit. As a result, the control of the well path can be more accurate and reliable based on the real-time measured data. Additional advantages are versatile operational conditions, best buildup rates and closest sensors to the bit, see more details in [14].

In Fig. 1, such system has two eccentric cylindrical parts when drilling vertically (offset $0\%$), where the actuator (red cylinder) functions similarly as the pads. Once the inclination/azimuth is anticipated, the actuator starts dislocating and pushing formations. In Fig. 1, with the actuator being active (offset $100\%$), the entire system is being pushed to the desired direction. For RSS control, the actuator dislocates and pushes the formation gradually. In turn, the reaction force from the formation bends the RSS tool and transfers the force to the bit. The essential of this process is to control and adjust the degree of the RSS tool bending. In Sect. 3, the natural displacement representing the impact on the bending of the tool is modeled and calculated.

Mathematical models

Bit force

The total bit force ($F_{bit}$) shows how the applied and reaction forces are present on the bit. Here $F_{bit}$ is calculated using a beam bending logic. The idea here is to model how the actuator applies the force on the bit and how the natural displacement of the bending of the RSS tool generated by the curvature of the well impacts the bit force. The total bit force is considered here having two elements:

$$\begin{aligned} F_{bit}=F_O +F_H, \end{aligned}$$

(1)

where $F_O$ is the force caused by the RSS actuator and $F_H$ is the force caused by natural displacement due to the bending of the RSS. The force $F_H$ depends on the wellbore geometry and the natural displacement ($H_n$). Here the natural displacement, $H_n$, represents how much the tool has been bent along the well path, caused by the well path curvature formation. The force $F_O$ is mainly controlled by the offset displacement ($H_o$), which represents the effect of the offset controller. In general, the force $F_H$/$F_O$ is dependent on the displacement, $H_n$/$H_o$ and bending properties of the RSS tools. It can be expressed using a general nonlinear function $f(\cdot )$ or

$$\begin{aligned} F_{H(O)}=f(H_{n(o)}, bending ~properties). \end{aligned}$$

(2)

In our study, the beam bending analysis is conducted to derive an explicit mathematical correlation of (2) to calculate $F_H$ and $F_O$. In the beam bending scenarios, the behavior of a bar/pipe regarding its material, geometry and its length is modeled depending on the loads and the contact point of these loads that exactly represents the reality of the RSS operations using this specific tool. The forces on the beam are generated by the actuator and the curvature formation. The beam bending situation, in which the application and transmission of forces from the RSS body to the bit are best described, is shown in Fig. 2. The contact points of the beam bending schematic are the stabilizer, the offset and the bit Oberg et al. (2004). In general cases, the deflection at load (H) caused by the force W is calculated by

$$\begin{aligned} H=\frac{Wa^2b^2}{3EIl}, \end{aligned}$$

(3)

where E is the elasticity modulus, I represents the inertia, a is the distance between the drill bit and the actuator location, b is the distance between the actuator location and the upper stabilizer and $l=a+b$ is the length of the beam.

Fig. 2

Beam bending analysis

From (3), it is easy to back-calculate the force on the bit F, or

$$\begin{aligned} F=\frac{Wb}{l}=3\frac{HEI}{a^2b}. \end{aligned}$$

(4)

Therefore, considering the forces $F_H$ and $F_O$, once $H_n$ and $H_o$ are known, according to (4), they could be calculated as

$$\begin{aligned} F_{H}=3\frac{H_{n}EI}{a^2b},~F_{O}=3\frac{H_{o}EI}{a^2b}. \end{aligned}$$

(5)

For the different RSSs, the ways to calculate $H_n$ and $H_o$ might be distinct. For this OrientXpress${\circledR }$ RSS, the details of the derivation of $H_n$ are given in Appendix A. Moreover, the way of controlling $H_o$ is given in Appendix B.

Fig. 3

2D and 3D cases for well path visualization

When considering 3D wellbore trajectory, it aims to steer the bit to reach the target azimuth and inclination. Compared with the 2D case, the actuator creates the offset displacements considering in the 3D coordinates, where $H_o^i$ represents the offset displacement projected on the true vertical depth (TVD) and horizontal displacement (HD) coordinate, and $H_o^i$ represents the offset displacement projected on the north and east quadrant. Similarly, the natural displacements in the 3D coordinates could be also considered by two displacements: $H_n^i$ and $H_n^a$. Figure 3 shows how these displacements look like in the 2D coordinates and the 3D coordinates, respectively. The approach to calculate the displacements in the 3D case is quite similar as the one in the 2D case. Due to the limited space there, the displacement calculations in the 3D case are not discussed here, but more details are available in Saramago (2020). Now the bit force is considered with respective to the azimuth and inclination, using $F_{bit}^i$ for the inclination and $F_{bit}^a$ for the azimuth. Then we have the force causing the azimuth shown as:

$$\begin{aligned} F_{bit}^a=F_H^a+F_O^a, \end{aligned}$$

(6)

and the force causing the inclination shown as

$$\begin{aligned} F_{bit}^i=F_H^i+F_O^i. \end{aligned}$$

(7)

To specify the forces $F_H^a$ and $F_H^i$, following the 2D model, we have

$$\begin{aligned} F_{H}^a=3\frac{H_{n}^aEI}{a^2b},~F_{H}^i=3\frac{H_{n}^iEI}{a^2b}. \end{aligned}$$

(8)

Following the same way, the forces $F_O^a$ and $F_O^i$ can be calculated by

$$\begin{aligned} F_{O}^a=3\frac{H_{o}^aEI}{a^2b},~F_{O}^i=3\frac{H_{o}^iEI}{a^2b}. \end{aligned}$$

(9)

ROP modeling

In the 2D scenario, the model considers the inclination variation, see Fig. 3, that generates the HD and the TVD. The ROP axial model represents the rate of penetration in the vertical direction, $ROP_v$. Here a generic nonlinear function $f_v(\cdot )$ is considered as a mathematical ROP axial model, or:

$$\begin{aligned} ROP_v=f_v(N, WOB, \alpha ), \end{aligned}$$

(10)

where N is the rotary speed of the drill string, WOB is the weight on bit and $\alpha$ is the model parameter representing the factors like rock properties, flow dynamics, bit type and size and others. Similarly, the ROP normal model ($f_h(\cdot )$) represents the rate of penetration with 90 degrees to the axial direction, or

$$\begin{aligned} ROP_h=f_h(N,F_{bit}, \beta ), \end{aligned}$$

(11)

where $F_{bit}$ is the total bit force calculated by (1) applied by the RSS and the formation, and $\beta$ is the model parameter representing the factors like well path geometry, rock properties and so on. In the literature, there are several ROP models to calculate $ROP_v$ Eren (2011); Bataee et al. (2010), for instance like Bingham model Bingham (1964), Teale model (Teale 2015) and Bourgoyne model (Bourgoyne et al. 1986). In this study, Teale’s model is used, given by

$$\begin{aligned} ROP_v=\frac{13.33\mu N}{D(\frac{Es}{WOB}-\frac{1}{A_b})}, \end{aligned}$$

(12)

where $\mu$ is the friction coefficient, D is the bit diameter, $A_b$ is the wellbore area and $E_s$ is the specific energy of the rock. For the $ROP_h$, to the best of authors’ knowledge, few models have been proposed to calculate it. For the calculation of the $ROP_h$, here the equation modified based on the Teale’s model is considered, given below as:

$$\begin{aligned} ROP_h=\frac{\mu N}{D\left(\frac{Es}{F_{bit}}-\frac{1}{A_b}\right)}\phi (\gamma ) \end{aligned}$$

(13)

where $\phi (\cdot )$ is the calibrating function and $\gamma$ plays a role to calibrate such ROP model in order to make the output $ROP_h$ close to real measurement, tied mostly to drill bit steerability. It is possible to considerate different types of calibrating function $\phi (\cdot )$, like polynomial function, linear function, power function or exponential function. Considering the practical use, it would be highly recommended to model $f_v(\cdot )$ and $f_h(\cdot )$ based on field measurements, for instance using machine learning technologies (Hegde et al. 2019; Esmaeli et al. 2012; Tunkiel et al. 2020; Soares and Gray 2020). Since the goal of the work is to analyze RSSs, the light focus was made to improve the ROP models. If extra efforts were added to the ROP mathematical modeling, the more reliable outputs from the RSS models can be obtained.

Considering the 3D system, the azimuth is not constant any more. It means that the HD will deviate in different directions, see Fig. 3. The variation of the inclination and the azimuth happens simultaneously after the kickoff point. This generates the necessity of defining an additional coordinate plane. In terms of 3D modeling, two ROPs besides $ROP_v$ are considered. The one is defined as $ROP_h^i$ that represents the velocity dynamics causing the inclination variation and the other is defined as $ROP_h^a$ showing the performance leading to the azimuth change. The differences among the ROP calculations in the 2D and the 3D cases are shown in Fig. 4.

Fig. 4

2D and 3D ROP cases

Similar as the model presented in the 2D case, the chosen ROP model in the study is the Teale model Teale (2015), but the other considerations of the ROP models are also possible. The $ROP_h^a$ is then calculated by

$$\begin{aligned} ROP_{h}^a=\frac{\mu N}{D(\frac{Es}{F_{bit}^a}-\frac{1}{A_b})}\phi (\gamma ^a) \end{aligned}$$

(14)

and the $ROP_h^i$ is calculated by

$$\begin{aligned} ROP_{h}^i=\frac{\mu N}{D(\frac{Es}{F_{bit}^i}-\frac{1}{A_b})}\phi (\gamma ^i), \end{aligned}$$

(15)

where $F_{bit}^a$ and $F_{bit}^i$ are calculated from (6) and (7), respectively, and $\gamma ^a$ and $\gamma ^i$ are the model parameters. They may, but don’t have to be equal. Having the ROP values from the above calculations, we could further calculate the bit position, see the following discussions.

Well path calculations

In the 2D case, based on the simple geometry, the change of the inclination is then calculated based on the $ROP_h$ and the $ROP_v$, or

$$\begin{aligned} \Delta \theta =\arctan (\frac{ROP_h}{ROP_v})\Delta t, \end{aligned}$$

(16)

where $\theta$ is the inclination and $\Delta t$ is the sampling time interval. Therefore, the change of the measured depth (MD) can be calculated as

$$\begin{aligned} \Delta MD=\sqrt{ROP_h^2+ROP_v^2}\Delta t. \end{aligned}$$

(17)

Then the change of the TVD can be easily obtained by

$$\begin{aligned} \Delta TVD=\Delta MD\cos (\theta (t))\Delta t, \end{aligned}$$

(18)

where $\theta (t)=\theta (t-1) +\Delta \theta$ with $\theta (t)$ being the inclination at time t. The dogleg severity (DLS) reflects the angular variance on the angle for each meter drilled that can be easily calculated by

$$\begin{aligned} DLS=\frac{180^o\Delta \theta }{\pi \Delta MD}. \end{aligned}$$

(19)

Similar as the 2D case, when we calculate the change of the inclination in the 3D case, it is given by

$$\begin{aligned} \Delta \theta =\arctan (\frac{ROP_{h}^i}{ROP_v})\Delta t. \end{aligned}$$

(20)

Similarly, the change of the azimuth can be calculated as

$$\begin{aligned} \Delta Az=\arctan (\frac{ROP_{h}^a}{ROP_v})\Delta t. \end{aligned}$$

(21)

Following it, the change of the MD can be calculated as

$$\begin{aligned} \Delta MD=\sqrt{(ROP_{h}^i)^2+(ROP_{h}^a)^2+ROP_v^2}\Delta t. \end{aligned}$$

(22)

The DLS is calculated as

$$\begin{aligned} DLS=\frac{180^o\arccos (\cos (\theta (t))\cos (\theta (t-1))+\sin (\theta (t))\sin (\theta (t-1))\cos (\Delta Az))}{\pi \Delta MD}. \end{aligned}$$

(23)

The other difference between the azimuth and the inclination is the projection coordinates. The azimuth is projected on the north and east quadrant while the inclination is projected on the TVD and the HD quadrant. The equations of the TVD and the HD were already given; therefore, the definitions of displacements in the north and east directions are easily obtained, where the change of north displacement is

$$\begin{aligned} \Delta North=\cos (Az(t))\cos (\theta (t))\Delta MD. \end{aligned}$$

(24)

and the change of Ease displacement is

$$\begin{aligned} \Delta East=\sin (Az(t))\cos (\theta (t))\Delta MD. \end{aligned}$$

(25)

Model schematics

Fig. 5

Workflow of the RSS

The schematic of the work is shown in Fig. 5. The first step is to define a target point. This is done by a well planner. For the 2D wellbore path, the target point requires two parameters: the target inclination and the location of the kickoff point. For the 3D path, additional information is the target azimuth. Once the kickoff point is reached, the offset displacement from the RSS and natural displacement are calculated and updated dynamically. Resultant forces on the bit will be calculated accordingly and in turn $ROP_v$ and $ROP_h$ will be calculated. Based on the ROP composition created, the outputs of the system are then continuously calculated at each time step, such as HD, TVD, azimuth, inclination, DLS, and north and east coordinates. For the 2D case, some characteristics of the process are considered:

• The development considers a constant azimuth, a target inclination and a kickoff point.

• The model is divided into two behaviors—vertical well path and inclined well path.

• The model is built per time step to calculate its respective outputs.

The detailed flowchart for the 2D calculations is shown in Fig. 6.

Fig. 6

Flowchart for the 2D case

Fig. 7

Flowchart for the 3D case

The 3D model controls the bit to reach the target azimuth and the target inclination. The resultant offset of the tool is defined by the actuator controller depending on the actuator limitations of the RSS, the target inclination and azimuth, and the current location of the bit, see more discussions on actuator control in Appendix B. Based on the beam bending analysis, the forces ($F_{bit}^i$ and $F_{bit}^a$) generated by the offset and natural displacements are then calculated. Based on them, the corresponding $ROP_h^i$ and $ROP_h^a$ are then calculated. The outputs from the 3D RSS models are shown in Fig. 7. As the 3D model was developed based on the 2D model, there are a lot of similarities. The characteristics that differ from the 3D model to the 2D model are mainly the following:

• Azimuth is not constant, and it varies according to the time.

• The actuator controller must be able to define the best direction to set the offset, considering the azimuth and inclination target at the same time.

Case study

2D case

Fig. 8

2D case, trajectory profile

For this simulation, it is assumed that the RSS has received the following orders:

• 1) After 100 ft MD, the target inclination is 50 degree;

• 2) After 2000 ft MD, the target inclination is 90 degree;

• 3) After 4000 ft MD, the target inclination is 110 degree.

Results

The results from the simulations are presented in the following figures. Figure 8 shows the 2D profile of the well, which simulates the 3 KOP at different measured depths. The actuator activation is a crucial mechanism that has the influence on the rest of the parameters during the drilling simulation. The model uses an on/off mechanism of the activation of the offset. In other words, the offset is activated with 100% of its haul when there is necessity of increasing or decreasing the angle of the well, and then, it is deactivated or use 0% of its haul when the well needs to maintain its angle (see Fig. 9a).

Fig. 9

2D case, simulation results

When the offset is activated, the bit will start to experiment forces acting against its surface (Fig. 9b) and the behavior follows the same as the offset, since one of the main sources of forces on the bit is the reaction force created when the actuator is pushing against one of the borehole walls. In the same way, the inclination increments (Fig. 9c) represent the same behavior of the offset activation. When the offset is applied, the inclination changes, see Fig. 9c.

Validations

The process of validation for the 2D simulation is based on the differences between the planned well path (PWP) and the simulation path (Sim), in other words, how close the simulation results are to the planned trajectory for that specific well. In Fig. 10a, the red line and blue line represent the PWP and the simulation trajectory, respectively. It is evident that both lines are very close to each other, which means that the simulator follows the planned trajectory in a reliable way. Even though the inclinations of the hold sections are very similar to the planned inclinations, there are some differences regarding the coordinates (HD, TVD) of the planned and the simulated trajectories (Fig. 10b). The buildup sections are the main source of error that creates a little gap between the planned and the simulated drilling after these points.

Fig. 10

2D case, PWP and simulation trajectories comparison

The principal reason for this error in the curved sections is that the simulator is not achieving the same aggressiveness of the PWP. As a result, the curvature simulated is softer and it takes more distance to achieve the final inclination after a certain buildup section. Furthermore, the data set used in the PWP is shown in Fig. 15 in Appendix and the input parameters used in the simulation are given in Table 3 in Appendix.¹

The standard deviation (SD) has been calculated for the TVD and HD from both, the PWP and the simulated path, in order to verify whether a similar value is obtained. In the same way, the coefficient of determination has been implemented. The TVD and HD from the PWP have been compared with the TVD and HD from the simulation, respectively. The results of both calculations are given in Table 1. The results from the last table indicate that the 2D RSS model follows the planned trajectory path very accurately in this study case. However, there are some differences in the curved sections that could be corrected with a better offset control of the actuator in the future.

Table 1 Standard deviation and $R^2$ of the 2D model

3D case

Fig. 11

3D case, trajectory profile

A similar scenario was chosen for the 3D modeling. For this simulation, we assume that the RSS has received the following orders:

• 1) After 1000 ft MD:

  • The target azimuth is 120 degree;

  • The target inclination is 25 degree;

• 2) After 2000 ft MD:

  • The target azimuth is 90 degree;

  • The target inclination is 120 degree;

• 3) After 4000 ft MD:

  • The target azimuth is 50 degree;

  • The target inclination is 80 degrees.

Results

Unlike the case before, this simulation considers a decreasing of the inclination angle after the third KOP, as it can be appreciated in the 2D well profile (Fig. 11a). For the 3D case, it is also mandatory to calculate the direction or azimuth of the well in the transverse plane, as it is shown in Fig. 11b, where the 3 different directions of the simulation are evident. With both planes, the lateral and transverse planes, it is possible to form a 3-axis projection of the simulated well (Fig. 11c). In this figure, it is possible to observe the complexity of the well and the different shapes that the drill bit must follow.

The offset activation is, again, one of the most important parameters that controls the resultant deviation of the well. As was explained before, the behavior of the offset follows an on/off execution, see Fig. 12a. It is important to mention that Fig. 12a is the total offset. In the 3D case the offset is not only applied to one direction. As a result, the offset is decomposed into 2 directions or planes: One of the directions is related to the offset that deviate the inclination, and the other is related to the offset that varies the azimuth.

The inclination of the of the well path presents 2 sections where it rises and 1 section that goes downwards, following the 3 target inclinations ordered at the beginning of the simulation (Fig. 12b). Around 2400 ft of measured depth, there is a small change of slope in the inclination where it becomes higher. This phenomenon is related to the ROP inclination and ROP azimuth that will be explained later. Moreover, the DLS follows a similar behavior of the offset, but there is a main difference around 2000 ft and 2400 ft of MD (Fig. 12c). As it was said before, this difference is related to the ROPs.

Fig. 12

3D case, simulation results

Figure 12d and 12e shows the results calculated with the models for the ROP inclination and ROP azimuth, respectively. In Fig. 12d, there is a peculiarity along the 2000 ft and 2400 ft of measured depth. This is caused by the ROP azimuth, if we appreciate Fig. 12e, the ROP azimuth has negative values (decreasing the azimuth) exactly in the same MD range. Therefore, when both ROPs are being executed at the same time, the forces are distributed or divided between these two directions. As soon as the one of the targets (inclination or azimuth) has been reached, the other ROP will have the total force and will increase its value. The same phenomenon has happened around the 4500 ft of MD, but now the ROP azimuth is the one which is having a greater (more negative) value suddenly, which is shown in Fig. 12e. Casually, the target azimuth is reached a little later than the target inclination after the third KOP, so the difference of values is not as well appreciated as Fig. 12d, where the target azimuth is achieved sooner than the target inclination. The concept of the ROP decomposition has shown that works really well since it can simulate the position of the next survey of the bit, and it even shows which direction (inclination or azimuth) will have more influence over the deviation of the well, in case both are performed at the same time.

Validations

The validation process for the 3D RSS Model is based on the same principle as the 2D model. Figure 13 presents both 3D trajectories, the blue line is the PWP, while the red line is the simulated trajectory. It is clear that there is certain matching between the behavior of the PWP and the simulated trajectory. However, again, the curvature sections show a bigger gap than the hold sections.

Fig. 13

3D case, trajectory comparison

The gap is caused by the offset control of the 3D RSS Model. It is turning the well slower and softer than the PWP for the curvature section, before reaching the target inclination and azimuth. As a result, the hold section that is drilled after the curvature is going to be a parallel line to the PWP hold sections, since the last point of the curvature (either buildup or drop) will be placed in different coordinates than the same point in the curvature of the PWP. The validation calculations are performed in the same way for the 2D RSS Model, where the PWP and the simulation results are compared using the SD and the $R^2$. But, in the 3D case, the parameters to compare are TVD, east and north. Besides, the initial data used for generated the PWP and the initial data for running the simulation are presented in Table 4 in Appendix.

The differences in the SD and the R2 between the mentioned parameters, from the PWP and the simulation results, show the following results in Table 2. For this case of study, the simulation represents very close the drilling path proposed in the PWP. Even though the result for this study case is acceptable, the curvature sections are an important area to focus for future improvements. Consequently, the offset control should be using another approach or combine the actual one with more restrictions and algorithms.

Table 2 Standard deviation and $R^2$ of the 3D model

Discussions

Assumptions and limitations

Some assumptions are considered when developing the mathematical models:

• Only two forces are considered for bit force estimation: $F_O$ and $F_H$;

• No sensor lag is considered;

• No data quantity and measurement uncertainty are considered;

• No model uncertainty is considered;

• No complex geometry of the BHA and bit is considered;

• No advanced offset control is considered.

The system does not consider the effect of gravity. The gravity affects the beam bending scheme and interferes with the resultant force on the bit. Including the weight of the tool as a dispersed force across the beam bending calculation is probably a good improvement.

As the formula of inclination, the calculation considers the bit location. Typically, sensors that measure the inclination are behind of the bit, but on the BHA. This could cause some divergences between the model calculations and the inclination and azimuth measurements from downhole sensors. In the future work, it would be nice to consider the sensor lag issues for inclination and azimuth calculations.

The input variables, see Figures 6 or 7, must be accurate and reliable. If an input variable is set to be a constant even though a variation of this variable is expected, the outputs from the system carry the errors. As the focus of this study is the development of the RSS, the inputs of the ROP equations are not evaluated in this work. Downhole drilling data communication and poor data quality issues are specific data challenges. The input variables need to be filtered and further processed in order to improve the accuracy of the calculations.

The ROP model used in the case study is modified from the model presented in Teale (2015) that possibly has the deviations from real measurement. So the ROP model uncertainties can be introduced and transmitted to other calculations. Therefore, the ROP calculations need to be further improved and validated. Since our goal is to use a ROP model that represents the conditions of the formation, the bending resultant force on the bit and the effect of offset controller, so that the ROP approximations presented in this study achieve it, but validations are necessary in the further development.

For the geometry calculation, it would be recommended to consider the expansion of the drill string due to thermal conditions. It is an example that would impact the calculated displacements.

RSS challenges and improvements

From the analysis of simulation results, the offset can be identified like the most relevant parameter. It will lead the behavior of the rest of the parameters and consequently the shape of the well path. Nevertheless, the offset algorithm is basic that is currently used in the industrial that is need to be improved in the future in order to avoid having an on/off performance. Instead a linear function should be achieved, which shows a gradual progression of the activation and deactivation of the offset or actuator of the tool.

Moreover, variations in the offset follow the time interval between two defined time steps. In other words, the offset can be changed from time t to time $t+\Delta t$. The simulation time interval $\Delta t$ is with a recommended value of 5 seconds. The actual activation time depends on its mechanics and the drilling speed, $ROP_h$. In the simulations, the activation time interval could be freely selected without the evaluation on the speeding $ROP_h$. It might lead to potential damages if there is an abrupt change of the offset in high values of $ROP_h$.

Another possible improvement is to consider the geometry of the upper stabilizer and the gauge of the bit. These factors were not considered in this paper and for the sake of simplicity, where it is assumed that their diameters are the same as the bit diameter.

Other RSS models

There are a number of other published models targeting rotary steerable systems. A recently published paper Wang et al. (2020) presents a similar model to the one presented here, admittedly taking into account additional effects, such as leverage effect, that method presented here does not take into account. However, the method presented here is presented with full well drilling simulation, while paper Wang et al. (2020) focuses purely on analyzing forces, and not a dynamic system.

An older paper Li and Li (2008) uses similar approach to presented here, implementing the beam bending model through differential equations, additionally implementing the right walking force and dropping force. A short section of the well is predicted, spanning 32 meters, consisting of constant drilling parameter; those results are then compared to the actual measurements. As with the previously compared work, no full well simulation is performed, and no results are presented where dynamic behavior of the model can be observed. Method presented in this paper is analyzed in terms of both full well drilled and evaluation of the inclination and azimuth control system. Overall, our paper presents model similar to previously published, exploiting the same physical models, and is expanded to a full simulation where model can respond to well bore that it drilled. Lastly, work presented here will be published as open-source implementation, which other publications lack. It must be noted that RSS models are not always transferable between one product to another. There are multiple designs in existence, and if a tool steers by pointing, instead of pushing the bit Schaaf et al. (2007), then the model presented in this paper is not compatible with it.

Conclusion

The main goal of this study is to enhance the knowledge of the RSSs by developing mathematical models. In this work, the new concepts were developed, e.g., defining ROP components in different planes, calculating the displacements caused by the formation curvature on the bending of the tools and offset displacements, and defining an offset controller behavior. Such calculations and models enrich the knowledge from the RSSs and open doors for future improvements. The developed work is also adaptable for different RSS tools. It can be used by RSS designing engineers to evaluate the impact of possible design changes of tools under planning or construction phase. With using the mathematical models, it is possible to simulate changes on the geometry of the RSS tool and evaluate its behavior and performance before manufacturing the actual tool.

The work had access to mechanical design details necessary for deep analysis, testing logs to evaluate real-life performance and design of the control system of RSS tools. The achieved results show that the calculations fit the performances of RSSs used in the industry. Certainly, improvements are possible, e.g., developing more complex beam bending calculations, improving the actuator control and considering additional forces applied to the bit. For instance, the well profile, pipe materials and weight, frictional forces. mainly govern mechanical stretch. The thermal expansion of the drill string components and assembly govern the change in length of drill string due to temperature. It would be the next step of our work to compensate for these effects through a series of mathematical algorithms to identify the mechanical condition of the drill string, BHA and RSS in different scenarios. These possible improvements are promising avenues for future research.

Although the RSS model still needs some mathematical improvements, verification and validation process to be considered as the applicable model, the potential that it has is encouraging for its future since more upgrades can be made in order to reduce its execution time, improve the accuracy, evolve its offset control or add new compatible features. The advantages of the RSS model can still be explored since it allows to perform other studies, for instance: sensitivity analysis of the incidence of the position of the actuator along the BHA, experiments on the steerability over the direction of the well or comparing different alternatives of well planning in order to select the most efficient and profitable. The work will inspire further developments regarding directional drilling technology.

Appendix

Appendix A—natural displacement

The bending that happens on the space from the bit until the upper stabilizer of the RSS will generate a natural displacement and in turn an additional force on the drill bit. In order to get the natural displacement, some coordinates are required, as given in Fig. 14. These coordinates come from the HD and TVD of the bit, actuator and stabilizer; with them, it is possible to generate two straight line equations that are used to determine the distance between one of their ends.

The “short line” represents the lineal distance between the bit and the actuator, while the “long line” is the lineal distance between the bit and the stabilizer. Using the length from the “short line” superposed over the “long line,” it will create a new coordinate ($x_{p~long}$, $y_{p~long}$). The distance between the coordinate of the actuator ($x_{p~short}$, $y_{p~short}$) and the new coordinate will form the natural displacement ($H_n$). The calculation of the distance $H_n$ is given as

$$\begin{aligned} H_n=\sqrt{(x_{p~short}-x_{p~long})^2+(y_{p~short}-y_{p~long})^2}. \end{aligned}$$

(26)

Fig. 14

Natural displacement calculation

Appendix B—offset displacement

The inputs consist of the “maxoff” and the target inclination for every point of the planned well trajectory. The maxoff represents the value of the maximum offset desired by the planner. The value of the maxoff can vary from zero until one. It represents a percentage of the maximum offset that the tool is capable. If the percentage is decreased, the dogleg severity decreases as well. The second input is the target inclination. This target inclination is defined by the well planner of the trajectory. After the target inclination is achieved, the tool is programmed to hold the inclination until further orders. If there is some external force or any natural fracture on the formation that generates a force on the bit that dislocates the bit from its target inclination, the offset will be automatically activated to hold the target and correct its inclination. The calculation of the $H_o$ updated constantly. It takes into account the target inclination and the current inclination of the bit on every simulated step.

There are two main behaviors of the designed offset controller. If the target inclination is considerably far from the current inclination, the offset of the tool will be equal to the maximum allowed offset. When the bit achieves current inclinations closer to the target inclination, the offset will reduce its value gradually to achieve the target inclination as smooth as possible. It is described below:

• If the target inclination minus current inclination is bigger than $\epsilon$:

  $$\begin{aligned} H_o=\pm 100\%\times maxoff(upwards~ or~ downwards) \end{aligned}$$

  (27)

• If the target inclination minus current inclination is smaller than $\epsilon$:

  $$\begin{aligned} H_o=\pm (target~inclination -current~inclination)*\delta *maxoff, \end{aligned}$$

  (28)

where maxoff is the maximum allowed offset and $\delta$ is the coefficient to determine the variation rate of $H_o$ and is the threshold. In the case study, the point of the transition between the two behaviors is chosen to be $\epsilon =0.65$ degrees. In other words, if the current inclination of the bit is more than 0.65 degrees further from the target inclination, the offset is automatically defined as $100\%$ of the maximum offset. Afterward, as the current inclination becomes closer to the target inclination, the offset will decrease gradually until the value of the offset is equal to zero and the tool maintains its target inclination. The gradual decrease of the offset is ruled by the difference in inclinations. If the distance of the current inclination to the target inclination is less than 0.65 the absolute offset value will be defined as $\delta$ times the maximum offset times the distance from the target inclination to the current inclination. As the distance becomes smaller over time, the offset also gets smaller and reduces its value gradually. If the target inclination is greater than the current inclination, it will take positive sign; otherwise, it will take negative sign.

Appendix C—data for case study

The planned path for 2D case is shown in Fig. 15; the input data for 2D case are shown in Table 3 and the input data for 3D case are shown in Table 4.

Fig. 15

2D case: planed trajectory data

Table 3 2D RSS simulation input parameters

Table 4 3D RSS simulation input parameters