Introduction

When the natural energy of the reservoir is not able to transfer the fluid to surface and to overcome the weight of the fluid column in the well, one of the artificial lift techniques should be used to produce the fluid in an economically efficient way. Artificial lift techniques reduce the pressure from the fluid column in the well and, as a result, reduce the pressure at the well bottom, causing a large pressure difference between the reservoir and the well bottom, resulting in the transfer of the fluid produced to the surface. One of the most commonly used artificial lift techniques is the gas lift process. In this method, the pressured gas is injected in the bottom of the tubing, and the oil is produced through two mechanisms of pushing through the expansion of the gas and reducing the hydrostatic pressure of the fluid column inside the well. However, the excessive increase in the amount of gas injected leads to the increased frictional pressure drop and, consequently, a decrease in the production increase due to the reduction in hydrostatic pressure (Economides et al. 2013). Therefore, determining the optimal amount of injected gas between network of production wells is one of the main gas lift challenges and is referred to as the gas lift allocation problem (Miresmaeili et al. 2015).

Gas lift allocation optimization

In general, the gas lift allocation optimization is discussed in two scenarios: (1) optimizing the allocation of gas between wells to maximize oil production in conditions where a limited amount of gas is available (Hamedi et al. 2011) and (2) optimizing the allocation of gas between wells and minimizing gas injections in a situation where a certain amount of oil production is pre-planned. All studies conducted so far on gas lift allocation optimization have focused on the first case and explored it from different perspectives (Hamedi et al. 2011; Miresmaeili et al. 2015; Mahdiani and Khamehchi 2015; Miresmaeili et al. 2019). However, gas lift allocation optimization using the second technique is not studied yet and addressed for the first time in the present study. The objective function typically used when a limited amount of gas is available to maximize the oil production level (scenario 1) is expressed as follows (Hamedi et al. 2011):

$$\hbox{max} \mathop \sum \limits_{1}^{n} Q_{\text{oi}} = f\left( {Q_{g1} , Q_{g2} , \ldots ,Q_{\text{gi}} } \right),\quad i = 1, 2, \ldots , n$$
(1)

in which the total amount of injected gas to the wells must be equal to or less than the amount of available gas and is expressed as a linear inequality constraint (Hamedi et al. 2011):

$$\mathop \sum \limits_{1}^{n} Q_{\text{gi}} \le A$$
(2)

where n represents the number of wells, \(Q_{\text{oi}}\) is the amount of oil produced per well, \(Q_{\text{gi}}\) is the amount of gas injected per well and A is the amount of available gas (Hamedi et al. 2011). In the second scenario which aims to minimize the amount of gas injected into wells to produce a predetermined quantity of oil, the objective function is expressed as follows:

$$\hbox{min} \mathop \sum \limits_{1}^{n} Q_{\text{gi}} , \quad i = 1, 2, \ldots , n$$
(3)

in which the total oil produced from the well is equal to a predetermined amount and expressed as follows:

$$\mathop \sum \limits_{1}^{n} Q_{\text{oi}} = f\left( {Q_{g1} , Q_{g2} , \ldots ,Q_{\text{gi}} } \right) = B$$
(4)

where B is the predetermined oil quantity for production. The important point is that in the second scenario the problem constraint turns into a nonlinear equality constraint compared to the first case with a linear inequality constraint, since the production of each well is itself a nonlinear function of the amount of gas injection, resulting in a nonlinear function of the amount of gas injected. Therefore, in the second scenario, handling the problem constraints will be more complicated.

In addition, an initial gas injection is required in some wells in order to start the production of oil, and there is also an optimum performance point in the gas lift performance curve (GLPC) beyond which the gas injection further increases the frictional pressure gradient and decreases the production level. Therefore, in both scenarios, the following constraints are expressed in addition to the constraints specific to each state (Hamedi et al. 2011):

$$Q_{\text{gi}} \ge Q_{{{\text{gi}} - { \hbox{min} }}}$$
(5)
$$Q_{\text{gi}} \le Q_{{{\text{gi}} - { \hbox{max} }}}$$
(6)

where \(Q_{{{\text{gi}} - { \hbox{max} }}}\) is the minimum amount of gas injection required to start the oil production and \(Q_{{{\text{gi}} - { \hbox{max} }}}\) is the amount of gas injected in the peak of gas lift performance curve (optimum performance point).

Literature review

Considering the importance of gas allocation optimization, many studies have been conducted to explore it. For instance, Kanu et al. (1981) used the equal slope method to properly distribute gas rates between wells. Later, Nishikiori et al. (1995) used the nonlinear constrained formulation with a stochastic quasi-Newton method to find optimal solutions. Fang and Lo (1996) departed from the nonlinear programming process and proposed the piecewise linearization of the well performance curves and thus changed the problem into a linear programming problem. Afterward, Buitrago et al. (1996) combined stochastic search and heuristic descent direction and called their method Ex-In. Alarcon et al. (2002) improved the method proposed by Nishikiori et al. (1995) by replacing the quasi-Newton algorithm with sequential quadratic programming (SQP). Wang et al. (2002) proposed a mixed-integer nonlinear programming (MINLP) techniques for integrating the previous methods. Their model included the allocation of gas rates, the production rate of wells and equipment constraints. Nakashima and Camponogara (2006) developed the recursive algorithm for gas rate allocation. They were the first to study the discontinuity of the well performance curve in detail. Ray and Sarker (2006) used the piecewise linearization method and genetic algorithm (GA) to optimize the gas allocation rate. Camponogara and Conto (2009) improved the piecewise linearization formulation that was previously developed. Zerafat et al. (2009) solved the gas rate distribution using two genetic and ant colony (ACO) algorithms. Hamedi et al. (2011) used the particle swarm optimization algorithm (PSO) to optimize the gas rate allocation in the wells of an Iranian oil field. Sharma and Glemmestad (2013) used the generalized reduced gradient (GRG) technique, self-optimizing control structure and multi-start technique to optimize gas allocation in the gas lift process. Ghaedi et al. (2014) employed the continuous ant colony (CACO) algorithm to explore gas allocation optimization and compared their results with previous studies. Ghassemzadeh and Pourafshary (2015) proposed a new method for considering the time factor in optimizing the gas allocation process. They used a piecewise cubic hermite function for modeling the gas lift performance and genetic algorithm for optimization. Miresmaeili et al. (2015) used a multi-objective optimization algorithm, Gaussian Bayesian networks and Gaussian kernels to solve the gas allocation problem in the gas lift process. Mahdiani and Khamehchi (2015) used the genetic algorithm to investigate instability in the gas allocation optimization problem. Tavakoli et al. (2017) used the artificial neural networks (ANNs) to the gas lift modeling and then studied the gas allocation optimization using the genetic algorithm. Also, Miresmaeili et al. (2019) employed the artificial neural networks and used Levenberg–Marquardt (LM) and Bayesian regularization (BR) algorithms to model gas lift operation and then used the teaching–learning-based optimization (TLBO) algorithm to optimize gas allocation. Moreover, Namdar and Shahmohammadi (2019), with the help of a simple method without programming, optimized the gas allocation by the excel solver optimization tool.

In this study, in order to increase the speed and accuracy of solving gas lift allocation optimization problems, at the first a new correlation was proposed for modeling the gas lift process and GLPC curve fitting. The modeling results were compared with those obtained through other modeling techniques. In order to improve the optimization performance, a water cycle optimization algorithm (WCA) was used and the results of its implementation were compared with the results obtained from previous studies on TLBO, CACO, GA and PSO algorithms for solving the five-well Nishikiori (1989) index problem. Also, given the effect of the gas lift process modeling on the optimization results, and since previous studies have used various modeling techniques, we compared the performance of the water cycle optimization algorithm with the two well-known PSO and GA algorithms in terms of convergence rate, non-capture at local optimum points and repeatability with the same correlation for modeling gas lift and with equal number of iterations in order to evaluate the performance of the algorithm itself individually and eliminate the modeling accuracy effects. Finally, given that the optimization problem of scenario 2 has not been investigated so far, this study attempted to optimize the gas allocation between the wells of one of the heavy oil fields in the southwest of Iran with predetermined quantities of oil production. In this scenario, the optimization goal was to obtain the minimum amount of gas required to produce the predetermined oil levels using the water cycle optimization algorithm.

Water cycle algorithm

This new meta-heuristic algorithm has been inspired by the behavior of the water cycle in nature (Fig. 1) and has not yet been used in the field of petroleum engineering. Similar to other meta-heuristic algorithms, the water cycle algorithm begins with the initial population of so-called streams created after rain. To simulate this process, initially, a primitive population Npop is created randomly, each stream having Nvar design variables (Sadollah et al. 2015).

Fig. 1
figure 1

Schematic diagram of water cycle in the nature (Sadollah et al. 2015)

Full size image

Then, the value of the objective function of each stream is calculated and the best solution is selected as the sea. Afterward, some of the streams that are best after the sea are chosen as rivers, and the remaining streams are remained as streams and flow to the rivers or directly to the sea. NSR is a parameter whose value is determined by the user and the number of rivers, and a sea is determined through Eq. 7. As a result, the number of streams (NStreams), which is the remainder of the population, is calculated from Eq. 8 (Sadollah et al. 2015):

(7)
$$N_{\text{Stream}} = N_{\text{pop}} - N_{\text{SR}}$$
(8)

Thereafter, the number of streams flowing into specific rivers or the sea is determined. The allocation of streams is based on the intensity of the flow of rivers and the sea (or the values of their objective functions) through Eqs. 9 and 10 (Sadollah et al. 2015):

$$C_{n} = {\text{Cost}}_{n} - {\text{Cost}}_{{N_{\text{SR}} + 1}} , n = 1, 2, 3, \ldots , N_{\text{SR}}$$
(9)
$${\text{NS}}_{n} = {\text{round}}\left\{ {\left| {\frac{{C_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{\text{SR}} }} {\text{Cost}}_{i} }}} \right| \times N_{\text{Stream}} } \right\}, n = 1, 2, 3, \ldots , N_{\text{SR}}$$
(10)

where \({\text{NS}}_{n}\) is the number of streams that flow into specific rivers or the sea. After that, the surface movement of streams and rivers to the sea or the movement of streams to the rivers and their new positions are determined. The movement of the streams directly flowing into the sea is calculated by Eq. 11, the movement of the streams joining the rivers is determined through Eq. 12 and the movement of the rivers to the sea is estimated through Eq. 13 (Sadollah et al. 2015):

$$\vec{X}_{\text{Stream}}^{i} \left( {t + 1} \right) = \vec{X}_{\text{Stream}}^{i} \left( t \right) + {\text{rand}} \times C \times \left( {\vec{X}_{\text{Sea}}^{i} \left( t \right) - \vec{X}_{\text{Stream}}^{i} \left( t \right)} \right), \quad i = 1, 2, \ldots , N_{\text{Stream}}$$
(11)
$$\vec{X}_{\text{Stream}}^{i} \left( {t + 1} \right) = \vec{X}_{\text{Stream}}^{i} \left( t \right) + rand \times C \times \left( {\vec{X}_{\text{River}}^{i} \left( t \right) - \vec{X}_{\text{Stream}}^{i} \left( t \right)} \right),\quad i = 1, 2, \ldots , N_{\text{Stream}}$$
(12)
$$\vec{X}_{\text{River}}^{i} \left( {t + 1} \right) = \vec{X}_{\text{River}}^{t} \left( t \right) + {\text{rand}} \times C \times \left( {\vec{X}_{\text{Sea}}^{i} \left( t \right) - \vec{X}_{\text{River}}^{i} \left( t \right)} \right),\quad i = 1, 2, \ldots , (N_{\text{SR}} - 1)$$
(13)

where t is the iteration number, and C is a constant whose value varies from 1 to 2 and its best value equals two. Also, rand is a uniformly distributed random number ranging from zero to one. These equations act as exploration at the initial stages and as exploitations at the final stages (Sadollah et al. 2015).

If the solution presented by a river is more effective than that of the sea, then the position of the river and the sea is exchanged (that is, the sea changes into the river and the river into the sea). This exchange can also occur for the streams and the sea as well as the streams and the rivers (Sadollah et al. 2015).

In order to prevent the rapid convergence of the algorithms (immature convergence) and increase the exploration ability of the algorithms, a new chance commensurate with the distance of the rivers and streams from the sea is given to them. This concept in the WCA algorithm is applied under evaporation condition and raining process. If the Euclidean distance of the rivers and streams from the sea is less than a predetermined insignificant value (near zero) (\(d_{ \hbox{max} }\)), the conditions for evaporation from the sea are fulfilled and the raining process starts, and the rivers and streams are reformed (Sadollah et al. 2015).

The conditions for evaporation from the sea for rivers and streams are expressed by pseudo-codes 14 and 15, respectively (Sadollah et al. 2015):

(14)
(15)

where \(d_{ \hbox{max} }\) sets the intensity of the search around the sea and decreases by Eq. 16 in each step (Sadollah et al. 2015):

$$d_{ \hbox{max} } \left( {t + 1} \right) = d_{ \hbox{max} } \left( t \right) - \frac{{d_{ \hbox{max} } \left( t \right)}}{{\hbox{max} \;{\text{Iteration}}}} ,\quad t = 1, 2, 3, \ldots , {\text{Max Iteration}}$$
(16)

If a condition for evaporation is fulfilled, new streams are formed randomly in the search space due to raining, and the new location of these streams is determined by the following equation (Sadollah et al. 2015):

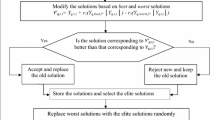
$$\vec{X}_{\text{Stream}}^{\text{New}} = \overrightarrow {\text{LB}} + {\text{rand}} \times \left( {\overrightarrow {\text{UB}} - \overrightarrow {\text{LB}} } \right)$$
(17)

where UB and LB are upper and lower bound vectors that are defined by the problem. Figure 2 shows the developed WCA optimization process. The circles, stars and the diamond refer to streams, rivers and sea, respectively, and the white circles and stars mark the new positions of streams and rivers, respectively.

Fig. 2
figure 2

Schematic view of the used methods in the WCA (Sadollah et al. 2015)

Full size image

The application of constraints

Usually, in gas lift allocation optimization problems, a penalty function is used to address the constraints of the problem and prevent violation of them (Sukarno et al. 2009; Rashid 2010; Hamedi et al. 2011). The main problem with this method is that the coefficient of the penalty function itself needs to be optimized and if it is not selected properly, the slightest violation of the constraints may result in a large penalty for the objective function. In order to apply the constraints and to reach feasible solutions, Deb (2000) approach was used in this study. This approach is based on the penalty function, with the difference that there is no need for the coefficient of the penalty function and its optimization. This method is used for the genetic algorithm by Deb (2000) and is used in this study for use in the water cycle algorithm. The rules used in this method (for the minimization problem) are as follows:

  1. 1.

    Of two feasible solutions, the solution whose objective function has a lower value is selected.

  2. 2.

    Of a feasible solution and a non-feasible solution, the feasible solution is preferred.

  3. 3.

    Of the two non-feasible solutions, a solution that has the slightest violation of the constraints is selected as the feasible solution.

Methodology

The increased speed and accuracy in solving optimization problems of gas allocation in the gas lift process are of high importance. Solving gas allocation optimization problems generally involve two steps:

  1. 1.

    Modeling the gas lift process and fitting the oil production data against gas injections by one of the correlations presented.

  2. 2.

    Implementation of the objective function of the gas allocation optimization problem and its constraints and solving it by one of the optimization algorithms.

Therefore, in order to increase the speed and accuracy of solving gas allocation optimization problems, each of these steps needs to be improved individually. In order to increase the accuracy of the first stage, first, a new correlation was proposed to model the gas lift process, and then the results of modeling with it were compared with the results obtained from other methods for different wells. In order to improve the performance of the second stage of the optimization process, an optimization algorithm was used and the results of this algorithm were compared with the results obtained from previous studies on TLBO, CACO, GA and PSO algorithms for solving the five-well Nishikiori (1989) index problem. Also, given the effect of the gas lift process modeling on the optimization results, we compared the performance of the water cycle optimization algorithm with the two well-known PSO and GA algorithms in terms of convergence rate, non-capture at local optimum points and repeatability with the same correlation for modeling gas injections and with equal number of iterations in order to evaluate the performance of the algorithm itself individually and eliminate the modeling accuracy effects. Finally, this study attempted to optimize the gas allocation between the wells of one of the heavy oil fields in the southwest of Iran with predetermined quantities of oil production. In this scenario, the optimization goal was to obtain the minimum amount of gas required to produce the predetermined oil levels using the water cycle optimization algorithm. In other words, the aim was to divide the oil production among the wells in a way that it requires the minimum gas rate for injection into the wells. Figure 3 shows the proposed procedure used in this study to solve the gas lift optimization problems.

Fig. 3
figure 3

Graphical demonstration of the procedure used in this study to solve the gas lift optimization problems

Full size image

Results and discussion

Gas lift modeling process

The formation of the gas lift performance curve (GLPC) is the first step in modeling the gas lift process. Obtaining an accurate GLPC has a significant effect on optimizing the allocation of injected gas into wells because if the curves are not sufficiently accurate, despite the high performance of the optimization algorithm, the optimization results will not be accurate and the produced oil overestimated or underestimated. So far, many methods have been used to model the gas lift process and the fitting of GLPCs. In general, these methods can be divided into two groups: modeling methods by fitting through correlation and modeling methods based on artificial neural networks. To date, various correlations have been proposed for GLPC fitting. The quadratic polynomial model is one of these models (Nishikiori 1989).

However, since most of the GLPCs are not symmetrical, the model does not have a high efficiency for modeling. In order to increase the accuracy of the quadratic polynomial model, Alarcon et al. (2002) added a logarithmic term to it and proposed the following model:

$$Q_{o} = a + b \times Q_{g} + c \times Q_{g}^{2} + d \times Ln(Q_{g} + 1)$$
(18)

By replacing the quadratic term of the quadratic polynomial model with a squared term, Hamedi et al. (2011) proposed the following model:

$$Q_{o} = a + b \times \sqrt {Q_{g} } + c \times Q_{g}$$
(19)

With the linear combination of the previously proposed models, Behjoomanesh et al. (2015) developed a model as follows:

$$Q_{o} = a + b \times Q_{g} + c \times Q_{g}^{2} + d \times Ln\left( {Q_{g} + 1} \right) + e \times \sqrt {Q_{g} } + f \times \exp \left( {Q_{g} } \right)$$
(20)

In addition to the previously proposed models, the author developed the following model fitting the operational data of oil production against gas injection by adjusting the numbers in the previously proposed correlations and removing some of the less important terms:

$$Q_{o} = a + b \times Q_{g} + c \times Q_{g}^{0.7} + d \times Ln\left( {Q_{g} + 0.9} \right) + e \times \exp \left( { - Q_{g}^{0.6} } \right)$$
(21)

where a, b, c, d, e and f are constant coefficients of correlations, \(Q_{g}\) is the injected gas flow rate and \(Q_{o}\) is the produced oil flow rate. Among the previous correlations proposed for modeling the gas lift process, the correlation proposed by Behjoomanesh et al. (2015), despite the high accuracy in fitting, has some basic problems, which reduces its generalizability to be used for all wells. Therefore, it has been tried to solve these problems in the model proposed by the author, while maintaining the accuracy of the model proposed by Behjoomanesh et al. (2015). The fitting of operational oil production data against gas injection becomes convergent for some wells in the model proposed by Behjoomanesh et al. (2015), and it is necessary to limit the range of variations of the coefficients of this model. For example, operational data on oil production versus gas injections presented in studies conducted by Nishikiori (1989) and Jung and Lim (2016) cannot be fitted by this equation for the mentioned reasons. Also, the operational data fitting using the model proposed by Behjoomanesh et al. (2015) would result in overestimating or underestimating the oil production in some wells. Figure 4 shows a comparison of the fitting of the operational data for six wells studied by Kanu et al. (1981) using the model developed by the author of the present study and the model proposed by Behjoomanesh et al. (2015).

Fig. 4
figure 4

Comparison of operational data fitting for wells studied by Kanu et al. (1981) using the author’s model and the Behjoomanesh et al.’s (2015) model

Full size image

As it can be seen, the GLPC fitting curve trend in the model proposed by Behjoomanesh et al. (2015) is in a way that leads to the overestimation or underestimation of oil production in some parts of the fitting curve. Generally, the GLPC curve should follow a downward trend on the right side, while, as shown in Fig. 4, in wells 2, 3 and 5, the model proposed by Behjoomanesh et al. (2015) moves upward in the right. Also, however, the downward trend of the curve for well 6 is suddenly bulged and these behaviors generally invalidate the oil production values estimated by this model.

In order to assess the accuracy of the proposed models and to select the best one for modeling the gas lift process, the fitting of operational data for oil production versus gas injection of wells in the previous studies was calculated and the results were compared with the results of the model proposed in this study. In order to evaluate the accuracy of the models, the indices of correlation factor (R2) and the root-mean-square error (RMSE) were used for fitting the operational data. The correlation factor (R2) shows the correlation between the model and the data and the closer values to one are more optimal. This coefficient can be defined as follows (MATLAB Manual 2018):

$$R^{2} = 1 - \frac{{\text{SSE}}}{{\text{TSS}}}$$
(22)

where SSE is the sum of squared errors and is estimated as follows:

$${\text{SSE}} = \mathop \sum \limits_{i = 1}^{n} w_{i} \left( {y_{i} - \hat{y}_{i} } \right)^{2}$$
(23)

where n is the number of observation data, \(y_{i}\) is the ith observed value, \(\hat{y}_{i}\) is the estimated value of \(y_{i}\) from fit and \(w_{i}\) is the weight used for each data point, which is usually 1. TSS is the total sum of squares and is calculated as follows:

$${\text{TSS}} = \mathop \sum \limits_{i = 1}^{n} w_{i} \left( {y_{i} - \bar{y}_{ii} } \right)^{2}$$
(24)

As before, n is the number of observation data, \(y_{i}\) is the ith observed value, \(\bar{y}_{i}\) is the mean of all observed data and \(w_{i}\) is the weight used for each data point, which is usually 1.

Root-mean-square error (RMSE) represents the average difference between the values predicted by the model and the actual values, and the closer the value to zero, the model fit is more accurate. This index is defined as follows (MATLAB Manual 2018):

$${\text{RMSE}} = \sqrt {\text{MSE}}$$
(25)

MSE is the mean squared error and is calculated as follows:

$${\text{MSE}} = \frac{1}{n}{\text{SSE}}$$
(26)

Table 1 shows the accuracy of the proposed model by author and the models presented by Hamedi et al. (2011) and Alarcon et al. (2002) in terms of fitting the operational data in the studies conducted by Nishikiori (1989) and Jung and Lim (2016). As shown in Table 1, the proposed model by author yields better results than the other two models.

Table 1 Results of author’s model, Alarcon et al.’s (2002) model and Hamedi et al.’s (2011) model for fitting operational data from Nishikiori (1989) and Jung and Lim (2016)
Full size table

Table 2 also shows the results of the fitting of the operational data in the studies of Vieira (2015) by the proposed model by author and the models presented by Behjoomanesh et al. (2015), Hamedi et al. (2011) and Alarcon et al. (2002). As shown in Table 2, the proposed model by author has higher R2 values and lower RMSE, thus having more accurate fitting results than the other three models.

Table 2 Results of author’s model, Behjoomanesh et al.’s (2015) model, Hamedi et al.’s (2011) model and Alarcon et al.’s (2002) model for fitting operational data from Vieira (2015)
Full size table

As shown in Table 2, although the proposed model has one constant less than the model proposed by Behjoomanesh et al. (2015), it has higher R2 values and lower RMSE than the other three models and thus provides more accurate results in terms of the operational data fitting. The lower number of constants while maintaining the fitting accuracy makes it possible to reduce the time of computation by maintaining accuracy in cases where it is necessary to optimize the gas allocation between a large numbers of wells.

In addition, Tavakoli et al. (2017) fitted the operational data with artificial neural networks and compared their results with models presented by Hamedi et al. (2011) and Alarcon et al. (2002) in terms of R2 values. Table 3 shows the results of fitting the data in the study conducted by Tavakoli et al. (2017) using the proposed model, in comparison with the artificial neural network and the models proposed by Hamedi et al. (2011) and Alarcon et al. (2002).

Table 3 Results of author’s model, ANN method, Hamedi et al.’s (2011) model and Alarcon et al.’s (2002) model for fitting operational data from Tavakoli et al. (2017)
Full size table

As it is shown, the accuracy of the model proposed in the present study is within the limits of the artificial neural network approach. Accordingly, it can be suggested that the proposed model possesses a high accuracy in terms of the operational data fitting. In the following section, the proposed model is used for the gas lift performance curve (GLPC) fitting.

Performance evaluation of the water cycle algorithm

In order to assess and validate the performance of the water cycle algorithm, it was attempted to optimize the five-well Nishikiori (1989) index problem using the water cycle algorithm and the obtained results were compared with the results obtained from previous studies. The five-well Nishikiori (1989) index problem is a gas allocation optimization problem of scenario 1 and has been optimized for the available gas quantities of 4600 MMSCF/D by the TLBO (Miresmaeili et al. 2019), CACO (Ghaedi et al. 2014) and GA (Ghassemzadeh and Pourafshary 2015) algorithms and 3000 MMSCF/D by PSO algorithm (Hamedi et al. 2011). Table 4 illustrates the optimization results for the five-well Nishikiori (1989) index problem by using the water cycle optimization algorithm and compares them with the TLBO, CACO, GA and PSO algorithms. As shown in Table 4, only the oil rates generated by the TLBO algorithm are more than the values obtained by the WCA algorithm, but a thorough examination of the data obtained for the gas allocation among the wells by the TLBO algorithm shows that the oil production rate by this algorithm has been overestimated. An investigation of initial operational data for oil production versus gas injection for well no. 1 in Nishikiori (1989) studies indicates that only 490.2 MSCF/D gas is required to produce 367.5 STB/D oil. However, the amount of gas required to produce 367.4 STB/D oil is estimated by the TLBO algorithm to be 394.3 MSCF/D. In other words, the amount of oil producible by this amount of gas is overestimated.

Table 4 Comparison of the optimization results for the five-well Nishikiori (1989) index problem by using the TLBO, CACO, GA and PSO algorithms
Full size table

Also investigation of initial operational data for oil production versus gas injection for well no. 5 in Nishikiori (1989) studies indicates that by injecting 1667.3 MSCF/D gas into the well no. 5, the oil production rate will be 813.6 STB/D. Therefore, in order to produce 839.3 STB/D oil, over 1667.3 MSCF/D gas needs to be injected into the well. However, the required amount of the injected gas to produce the same amount of oil as estimated by this algorithm is less than 1667.3 MSCF/D (1447.7 MSCF/D). Therefore, it can be said that the oil production rate is overestimated by the TLBO algorithm, while the results obtained by the WCA algorithm are more reasonable than the initial operational data of the Nishikiori’s (1989) study.

Also, given the effect of the gas lift process modeling on the optimization results, and since previous studies have used various modeling techniques for solving the five-well Nishikiori (1989) index problem, the performance of the water cycle optimization algorithm was compared with the two well-known PSO and GA algorithms in terms of convergence rate, non-capture at local optimum points and repeatability with the same correlation for modeling gas lift process and with equal number of iterations in order to evaluate the performance of the algorithm itself individually and eliminate the modeling accuracy effects. For this purpose, in all three algorithms, the correlation proposed by the author was used in the present study for gas lift fitting and modeling. Also, following previous studies for solving Nishikiori (1989) index problem (Miresmaeili et al. 2019, Ghaedi et al. 2014, Hamedi et al. 2011), the number of iterations was considered equal to 100 in all three algorithms.

The WCA, PSO and GA algorithms are all three population-based algorithms, in which the population in these three algorithms is expressed in terms of the number of streams, chromosomes and particles. Figure 5 shows optimized oil production rates in different populations using the three WCA, PSO and GA algorithms.

Fig. 5
figure 5

Optimized oil production rate in different populations as estimated by WCA, PSO and GA algorithms

Full size image

As it is shown Fig. 5, the exploration and exploitation phase in the search space in the genetic algorithm is highly dependent on the population and in the lower population, the algorithm is trapped in the local optimum points, while the PSO and WCA algorithms have a more powerful, exploration and extraction phase in the search space and, therefore, are not so dependent on the population and are not trapped in the local optimum points. In addition, the PSO and WCA algorithms have high repeatability in the obtained results.

Figure 6 shows the optimization run time by the three algorithms studied in different populations. As it is shown, the PSO optimization algorithm has a better performance than the GA algorithm in terms of speed because the PSO algorithm converges to the optimal point at 24.81 s with a population of 50, while the GA algorithm converges to the optimal point at 85.85 s with a population of 650. In contrast, the WCA algorithm has a much better performance in terms of speed than the PSO algorithm, so that it converges to the optimal point at lower populations and at higher speeds. However, as shown in Fig. 6, the PSO algorithm has a lower performance at high populations in terms of speed. The WCA algorithm converges to an optimal point in 0.56 s with a population of 50. Therefore, it can be said that the WCA algorithm has a better performance in the optimization problems than GA and PSO algorithms in terms of convergence speed, non-capture in local optimum points and repeatability.

Fig. 6
figure 6

Optimization CPU run time at different populations for WCA, PSO and GA algorithms

Full size image

Case study (Scenario 2)

All studies on gas lift allocation optimization have assumed that if a limited amount of gas is available, then the gas should be distributed between the wells in a manner that it would be possible to produce the maximum amount of oil. However, an issue of interest not investigated in the previous studies is if the goal is to produce a predetermined amount of oil from the reservoir, then how this predetermined amount of oil should be distributed between the wells to require the minimum amount of gas injection in the gas lift operation? This section addresses this problem in one of the heavy oil fields of southwest Iran using the water cycle algorithm. The field in question contains four wells, of which the well no. 2 is closed because of the high water cut. Table 5 shows the specifications of the three productive wells in the field. The normal production of the field is 3728 STB/D without any gas lift operation. Table 6 also shows the data of oil production against gas injection in the wells in gas lift operation, which were obtained by using wells modeling in Prosper software.

Table 5 Specifications of the three productive wells in the field
Full size table
Table 6 Data of oil production versus gas injection in wells of the field
Full size table

To solve the optimization problems, it is necessary to have a correlation to calculate the amount of oil produced for different amounts of injected gas. Therefore, to find the best correlation, we calculated the fitting of the data presented in Table 6 by using different correlations. Table 7 shows the correlation factor (R2) and root-mean-square error (RMSE) for the GLPC fitting calculated through different correlations. As it was expected, the model proposed in this study produces better fitting results than other models presented in the literature. Therefore, the proposed model was used to investigate gas allocation optimization.

Table 7 Error indices values of GLPC fitting through different correlations
Full size table

Table 8 shows the values of the constants obtained from the GLPC fitting by the proposed model. The GLPCs for different wells suggest that the injection of 8.718, 10.017 and 10.13 MMSCF/D in the wells 1, 3 and 4 results in the production of maximum oil production, i.e., 1937.257 STB/D. Four oil production targets (12500, 15000, 17500 and 19737.257 STB/D) were set for the oil field under analysis. Following these targets, the gas allocation between the wells was optimized in such a way that the minimum amount of gas is required for the production of the targeted oil production rates. Furthermore, to show the effect of optimization, the worst possible gas injection scenario with the maximum amount of gas used to produce the predetermined oil production was calculated.

Table 8 Constants of the proposed model obtained from the GLPC fitting
Full size table

Table 9 shows the results for the gas allocation optimization for different wells of the oil field at different oil flow rates. The Qo/Qg ratio in the table indicates the number of standard barrels of oil produced per injection of every one million cubic feet of the standard gas. As it was expected, in the optimal scenario (the minimum required gas), a higher number of standard barrels of oil can be produced per injection of every one million cubic feet of gas than the worst scenario (the maximum required gas). Figure 7 also shows the surplus oil rate produced in the optimal scenario (the minimum required gas) compared to the worst possible scenario (the maximum required gas). As it can be seen, the closer the targeted oil production rates to the maximum oil production rate in the gas lift process (1937.257 STB/D), the surplus oil producible through the optimization can be reduced. Therefore, it can be suggested that in lower oil production targets, the optimization is more important and generates more extra oil.

Table 9 Gas allocation optimization for wells of the field at different oil flow rates
Full size table
Fig. 7
figure 7

Surplus oil rate produced in the optimal scenario (the minimum required gas) compared to the worst possible scenario (the maximum required gas)

Full size image

In addition to the gas lift, the method used in this paper can be used in improving steam allocation management in thermal enhanced oil recovery methods such as SAGD. One of the challenges in these methods is excessive water production which is due to an improper steam injection plan. Thus, for a given volume of steam, steam allocation between wells should be managed in a manner to delay the water breakthrough in producer wells and, as a result, improves sweep efficiency and increases the oil recovery.

Conclusion

  1. 1.

    In the gas lift process modeling, the correlation proposed by Behjoomanesh et al. (2015), despite the high precision, cannot be applied to all wells because firstly, in some wells, convergence requires limiting the variations of constant coefficients, and secondly, the oil production rates in some oil wells are overestimated or underestimated

  2. 2.

    The model proposed in this study, despite the reduction of a constant compared to the model presented by Behjoomanesh et al. (2015), has a higher fitting accuracy and is also free from the limitations of the mentioned model. Reducing a constant coefficient in this model will increase the speed of optimization. Also, the correlation proposed in this study is more accurate than the Hamedi et al. (2011) and Alarcon et al. (2002).correlations.

  3. 3.

    The GA algorithm is highly dependent on population and is trapped in low populations at local optimum points, while the water cycle and PSO algorithms are not so population dependent and have good repeatability.

  4. 4.

    In terms of the convergence rate, the water cycle algorithm has a much better performance than the PSO and GA algorithms. In high populations, the performance of the PSO and GA algorithms is reduced significantly in terms of speed. The PSO algorithm converges to the optimal response faster than the GA algorithm in a smaller population and more rapidly.

  5. 5.

    In optimization problems that aim to produce a predetermined amount of oil, the closer the targeted oil production rates to the maximum oil production rate in the gas lift process, the surplus oil producible through the optimization can be reduced. As a result, in lower oil production targets, the optimization is more important and generates more extra oil.