Optimization of operating conditions of CO₂-enhanced gas recovery and carbon sequestration

Abstract

Currently, the climate changes are the big issue due to increasing in amount of CO₂ foot print over the time. One of the most effective solutions to reduce CO₂ emissions is to inject CO₂ into the earth as known as carbon sequestration. CO₂ injection has two advantages for CO₂ gas storage and increases gas production in depleted reservoir or known as enhanced gas recovery (EGR). Although many studies of EGR model and characterization have been done and the results show that the application of EGR has potentially increased gas production and CO₂ storage; however, EGR has not been applied in the field. The obstacle remaining in application of EGR is the significant cost related to EGR technology starting from CO₂ procurement cost, transportation and operational cost. The operational costs of CO₂ injection depend on the operating conditions of CO₂ injection which is mass flow rate, pressure and temperature of CO₂ injection. In this research, CO₂ EGR and carbon sequestration processes were modeled by dividing into three parts, i.e., injection well, reservoir and production well. Pressure gradient in injection and production well was modeled using Beggs–Brill, while in reservoir by using Darcy equation. Temperature gradient for each part was modeled using mass and energy balances equations. The fluid properties were predicted using Peng–Robinson vapor–liquid equilibrium under commercial software HYSYS. Validation of injection and production well models was compared with PIPESIM, and the average mean deviations are 1.919% and 1.578%, respectively. Meanwhile, the validation of pressure and temperature gradient model compared to COMSOL Multiphysics software simulation in reservoir shows the average mean deviation of 0.2003% and 0.0002%, respectively. Based on the sensitivity analysis of the model, the profit will increase proportionally if mass flow rate and temperature increase; otherwise, it will decrease if CO₂ injection pressure increases. Before optimization, the presence of CO₂ injection in depleted gas reservoir with normal operating conditions can produce gas recovery of about 90.09% in which the profit generated is 6175.6 USD/day. EGR optimization has been performed using several recent stochastic algorithms, and the best optimization result was obtained by using Killer Whale Algorithm, duelist algorithm and Rain Water Algorithm. The optimization results show an increase in profit from 4453.8 USD/day to 12,331.9 USD/day or about 276.9% higher than the initial condition of the injection or without optimization. By using injection parameters that have been optimized, the CO₂ that can be stored is 1486.01 tons.

Introduction

Recently, the utilization of hydrocarbon fuels to serve human life increases over the time. On the other hand, it will increase CO₂ concentration in the Earth’s atmosphere. In the last 250 years, CO₂ concentrations have increased from 270 ppm to more than 370 ppm (Cakici 2003). Increased CO₂ emissions cause climate changes which already have many adverse effects on the environment. People have been trying to reduce the carbon foot print by using renewable energy; however, nowadays this way is considered less effective. One of the most effective solutions to reduce CO₂ emissions is by injecting back CO₂ into the earth or better known as carbon sequestration (CS) (Clemens and Wit 2002). CO₂ from stationary sources such as power plants and petrochemical industries is collected and then transferred to a hydrocarbon reservoir such as gas or oil reservoir to be stored for long periods (Faiz et al. 2007).

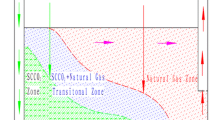
Natural gas reservoir has several advantages compared to oil reservoirs mainly in terms of CO₂ storage requirements. In a comparison, the gas and oil reservoir with the same initial hydrocarbon pore volume and then the declined natural gas reservoir (mainly containing methane) can save more CO₂ than the oil reservoir. It happened due to two reasons: First is ultimate gas recovery that is valued at an average of around 65% of initial gas in place, almost two times more than ultimate oil recovery, which ranges from an average of 35% from the initial oil in place. Second, gas is about 30 times more compressible compared to oil or water. At isothermal pressure of 13.8 MPa, compressibility of natural gas is around 72.5 × 10⁻⁶/kPa compared to oil and water, namely 2.2 × 10⁻⁶/kPa and 0.4 × 10⁻⁶/kPa (Turta and Cucuiat 1982). In addition, because of the density of CO₂ higher than the density of natural gas (2–6 times depending on reservoir conditions), hence it will separate automatically. CO₂ has lower mobility compared to natural gas because of the greater viscosity which will result in high natural gas transfer efficiency in the enhanced gas recovery (EGR) process (Turta et al. 2007).

Based on the results of previous research, CO₂ injection into gas reservoir not only gives advantage for CO₂ gas storage but also can increase gas production in depleted reservoir or known as enhanced gas recovery (EGR). The concept of EGR is not much different from enhanced oil recovery (EOR). CO₂ EOR has been proven technically and economically successful for over 40 years (Oldenburg et al. 2004). However, CO₂ injection has not been applied for EGR and carbon sequestration. Several simulation and experiment works have been conducted to prove the feasibility of CO₂ injection in the EGR process. Laboratory test showed that injection of 33% CO₂ and 67% CH₄ mixtures into a water-porous medium at pressure of 15 MPa and temperature of 40 °C yielded 23% of CH₄ gas and 40% of CO₂ trapped in the media (Cucuiat et al. 1983; Turta and Cucuiat 1982). In addition, simulation work has also been conducted. The production of gas from the initial condition of the simulation is 320 million m³, and after EGR the production of gas became 700 million m³ (Clemens and Wit 2002). Therefore, the presence of CO₂ injections can improve gas recovery (Turta et al. 2007).

Although many studies of EGR model and characterization have been done and the results show that the application of EGR has potentially increased gas production and CO₂ storage, however, EGR has not been applied in the field. Currently, there are only a few natural decline gas reservoirs that utilized EGR due to many considerations, for example, in Budafa Szinfeletti Field, Hungary (Beggs and Brill 1973). There are several aspects to take in consideration starting from the technical side to the economic aspect. From a technical point of view, excessive mixing of CO₂ and CH4 will cause CO₂ breakthrough. CO₂ breakthrough is a condition when CO₂ is brought to the production well. This condition will cause a decrease in natural gas production so that the EGR and carbon sequestration processes cannot be optimized (Srichai 2006). However, this can be overcome by utilizing a much larger ratio of CO₂ density compared to CH4 (Wang and Economodies 2009). It can be performed by selecting the appropriate reservoir and injecting CO₂ at the deepest point of the reservoir (Srichai 2006). While in economic aspects, large enough costs are needed to use EGR technology starting from the cost of procuring CO₂, transportation to operational costs. The operational cost of CO₂ injection depends on the pressure and flow rate requirements so that the injected CO₂ meets the reservoir criteria. If the pressure and CO₂ flow rate are excessive, it will increase operating costs, whereas if less, the natural gas produced and CO₂ storage are less than optimal; hence, the optimization of operating condition is needed.

In this study, optimization of CO₂ EGR and carbon sequestration was carried out by optimizing the injection operation conditions and considering costs. Optimized variables include flow rate, temperature and CO₂ pressure that are injected into the natural gas reservoir through injection wells. The aim of this study is optimizing the operating conditions to minimize EGR production costs and finally generate maximum profit from natural gas production and CO₂ storage.

Approach/methodology

Determination of operating condition range of CO₂ EGR and reservoir formation properties

The case study for operation condition of CO₂ EGR and carbon sequestration in this research uses the data from Morrow County, Ohio, USA (Fukai and Mishra 2016). Pressure, temperature and mass flow rate injection conditions are 7.38 MPa, 31 °C and 0.30443 kg/s, respectively, while the natural gas reservoir condition used as case study in this research is based on field condition data of Cooperstown, Venango, and Crawford County Gas Field, Pennsylvania, USA, from the U.S. Geological Survey. From these data, it is known that reservoir has grimsby rock formation type with porosity of 10.35% and at depth 1706 m below ground level. The reservoir has permeability of 27.1 mD and water saturation value of 12%. The reservoir pressure and temperature conditions were 13.51 MPa and 48.33 °C, respectively (Castle and Brynes 2005). In this research, reservoir is assumed in the cylindrical shape and isolated along the length of 100 m of the reservoir (from injection well to production well).

The natural gas composition used is based on the conditions of the natural gas content of the Brown gas well located in the state of Pennsylvania where it has the same geological formation, porosity, and depth characteristics with the Cooperstown gas field. The data obtained from the U.S. Geological Survey state that the reservoir contains natural gas with condensate gas (Burruss and Ryder 2014) (Table 1).

Table 1 Natural gas composition

Pressure and Temperature Gradient Model of CO₂ EGR and Carbon Sequestration

Injected CO₂ will encounter changes in temperature and pressure. Thus, it is necessary to derive the empirical equations to know the changes and impact through the fluid. In this research, Beggs–Brill equation is used to model pressure drop in injection well and production well, whereas Darcy equation is used to model pressure drop in reservoir. Temperature gradient for each part is modeled using mass and energy balances equations. The fluid properties were predicted using Peng–Robinson vapor–liquid equilibrium under commercial software HYSYS. (Banete 2014; Beggs and Brill 1973; Srichai 2006). Validation of the model is performed by comparing the model results with simulation results using PIPESIM software for injection well and production well and COMSOL Multiphysics for reservoir.

Calculation of Natural Gas Production Rate and Profit of CO₂ EGR

Natural gas production rate is calculated through additional recovery, cumulative production, mass flow rate and duration of CO₂ EGR injection time. In addition, the amount of the original gas in place or the amount of gas contained in the reservoir are considered in the calculation of the natural gas production rate. The revenue of CO₂ EGR process can be obtained by multiplying the natural gas production rate and the price of natural gas (Wang and Economodies 2009) (Table 2).

Table 2 Parameter for NP value

$$P_{\text{t}} = V_{\text{pd}} \times P_{\text{o}}$$

(1)

$$V_{\text{pd}} = \frac{\text{Gp}}{t}$$

(2)

$$Gp = G \times \left( {1 - \frac{p/z}{{p_{i} /z_{i} }}} \right)$$

(3)

$$G = \frac{{Ah \phi S_{\text{gi}} }}{{B_{\text{gi}} }}$$

(4)

$$B_{\text{gi}} = 0.028793 \times \frac{p/z}{{p_{i} /z_{i} }}$$

(5)

$$S_{\text{gi}} = - 0.0000005 \times f_{\text{g}}^{5} + 0.00004 \times f_{\text{g}}^{4} - 0.001 \times f_{\text{g}}^{3} + 0.0071 \times f_{\text{g}}^{2} + 0.0521 \times f_{\text{g}} + 0.2623$$

(6)

$$f_{\text{g}} = \frac{1}{{\left( {1 + M} \right)}}$$

(7)

$$M = \frac{{\mu_{\text{ng}} }}{{\mu_{\text{mix}} }}$$

(8)

In all industrial business, profit is the main goal to be achieved. In CO₂ EGR, profit can be obtained if there is a gain between revenue and production cost of CO₂ EGR. Hence, the revenue must be obtained as much as possible; otherwise, the cost production must be reduced.

$${\text{NP}} = R - {\text{CC}} - {\text{RC}} - {\text{PC}}$$

(9)

where

$$R = {\text{PR}} \times {\text{Pr}}_{\text{NG}}$$

(10)

$${\text{CC}} = m_{{{\text{CO}}_{2} }} \times {\text{Pr}}_{{{\text{CO}}_{2} }}$$

(11)

$${\text{RC}} = m_{{{\text{CO}}_{2} }} \times {\text{Pr}}_{\text{R}}$$

(12)

$${\text{PC}} = W \times t \times { \Pr }_{\text{E}}$$

(13)

The amount of CO₂ stored in the reservoir during a certain time interval can be determined from the ratio between the amount of CO₂ carried to the production line and the amount of CO₂ injected into the reservoir. The formula can be seen in Eq. 14.

$$F_{{{\text{CO}}_{2} }} = \frac{{Q_{{{\text{prodCO}}_{2} }} }}{{Q_{{{\text{injCO}}_{2} }} }}$$

(14)

If all of the CO₂ injected is stored in the reservoir, $F_{{{\text{CO}}_{2} }}$ = 0, whereas if all CO₂ is brought to the production line, $F_{{{\text{CO}}_{2} }}$ = 1.

Optimization techniques

Optimization is performed to provide the optimum profit by regulating the CO₂ EGR operating conditions. The operating condition variables are pressure, mass flow rate and temperature of CO₂ injection. The recent stochastic algorithms have been utilized, i.e., Killer Whale Algorithm (KWA) (Biyanto et al. 2017a, b, 2018a), duelist algorithm (DA) (Biyanto et al. 2016a, 2017c, 2018b), particle swarm optimization (PSO) (Biyanto and Dina 2016), Rain Water Algorithm (RWA) (Biyanto et al. 2018c, d) and genetic algorithm (GA) (Biyanto et al. 2016b, c). The rest of discussion will discuss regarding the best results from the optimization algorithms.

Results and discussions

Pressure and temperature gradient model in injection and production well

Pressure drop in injection and production wells is modeled using the Beggs–Brill method, while the temperature gradient is modeled using mass and heat transfer equation. Injection inlet conditions for modeling are taken based on real natural gas field conditions in the Cooperstown gas field, USA.

Pressure and temperature gradients models in injection and production wells for each 50 m depth are validated using PIPESIM software. Model validation is performed by varying the inlet mass flow rate of CO₂ injection, injection pressure and steam quality in some ranges of operating conditions and comparing the outlet of model and PIPESIM. Mean deviation of the pressure and temperature gradient model in injection well is 3.03642% and 1.76961%, respectively, while in production well, mean deviation is 0.80225% for pressure and 1.38729% for temperature. Pressure and temperature gradients models and PIPESIM simulation results in injection and production wells are shown in Figs. 1 and 2.

Fig. 1

Injection well pressure (a) and temperature gradient (b) model and PIPESIM simulation results

Fig. 2

Production well pressure (a) and temperature gradient (b) model and PIPESIM simulation results

Pressure and temperature gradient model in reservoir

The pressure and temperature gradients in the reservoir are modeled using the Darcy equation and mass and heat transfer equations. The reservoir characteristics used as input for the Darcy equation are shown in Table 3.

Table 3 Input parameters for pressure and temperature gradient modeling

The fluid properties are estimated using Peng–Robinson vapor–liquid equilibrium under HYSYS commercial software. The inlet of reservoir model is the outlet of injection well model, and the outlet of reservoir model is the inlet of production well model. The outlet of production well will be represented as produced gas associated with CO₂ at surface facilities. Furthermore, the CO₂ will be recovered and recycled to the injection well. Mean deviation of model and COMSOL Multiphysics simulation results is 0.2003% for pressure and 0.0002% for temperature. The pressure and temperature gradient of the model and COMSOL simulation is shown in Fig. 3 (Table 4).

Fig. 3

Reservoir pressure (a) and temperature gradient (b) model and COMSOL simulation results

Table 4 Input parameters for reservoir model

Natural gas production rate and profit of CO₂ EGR

The stored natural gas volume in the reservoir or original gas in place (OGIP) is estimated using Eq. 4, OGIP obtained using the parameters according to the initial condition of the reservoir which is 5757.919 m³ or 0.2 MMCF natural gas. By using Eq. 3, the value of gas recovery is 90.909% of OGIP; hence, the cumulative production is equal to 5234.472 m³ or 0.185 MMCF natural gas.

The presence of CO₂ injection with normal operating conditions can provide natural gas production rate of about 40.798 m³/day, where the natural gas fraction consists of 68.29% CH₄ and 31.71% gas condensate. Hence, the production rate of CH₄ and condensate gas are 27.861 m³/day and 12.937 m³/day, respectively, or 0.985 MMBtu/day and 76.082 bbl/day. These production rates yield the CO₂ EGR of about 4454.189 USD/day. Total injection time in this model is 128 days.

CO₂ EGR costs according to NP parameters and Eqs. 9–13, the CO₂ purchase cost is 408.789 USD/day, recycling cost to recover CO₂ is 99.188 USD/day, and pumping cost is 221.367 USD/day. The calculation of profit can be determined using the revenue and costs. Details of profit are shown in Table 5.

Table 5 Profit detail calculation of CO₂ EGR and carbon sequestration

Sensitivity analysis

Sensitivity analysis is used to determine the effect of variation on the operation condition parameter (pressure, temperature and mass flow rate of CO₂ injection) to the profit value. Figure 4 shows the curve of sensitivity analysis of CO₂ injection pressure related to profit. The increase in CO₂ injection mass flow rate with constant temperature and pressure will increase EGR and carbon sequestration CO₂ profits proportionally. This is because the greater CO₂ injected into the reservoir will increase the produced natural gas even though the purchase cost, recycling and pumping cost will also increase.

Fig. 4

Sensitivity analysis curve of changes in mass flow rate

Sensitivity analysis for changes in CO₂ injection pressure with constant mass flow rate and CO2 injection temperature is shown in Fig. 5. The curve shows that the increase in value of CO₂ injection pressure will reduce the profit. It is because the increase in injection pressure will actually reduce the production of natural gas while pump operational costs increase.

Fig. 5

Sensitivity analysis curve of changes in pressure

While sensitivity analysis of changes in CO₂ injection temperature with constant mass flow rate and pressure will increase profit as shown in Fig. 6, increasing the injection temperature will increase the natural gas produced and also decrease the pump operational cost.

Fig. 6

Sensitivity analysis curve of changes in temperature

From the sensitivity results, it can be concluded that a high mass flow rate and temperature will increase profit. In order to obtain a high mass flow rate, it is required high CO₂ injection pressure. Meanwhile, high injection pressure will reduce profits due to lower natural gas production rate and also increase the cost of pump during operation. Hence, it is necessary to determine the combination of operation condition parameter (mass flow rate, temperature and pressure of CO₂ injection) to obtain optimum profit.

Optimization of operating conditions of CO₂ EGR and CS

As mentioned before, optimization objective function is to find the maximum profit by adjusting the optimum operating condition or optimization variable of EGR and CS processes which are pressure, temperature and mass flow rate of CO₂ injection. Profit is the amount of revenue or income subtracted from operating costs for EGR CO₂ injection and CS which includes the cost of procuring and separating CO₂ and pump operating costs. The constraints used in this optimization are production well head pressure more than 7.38 MPa, CO₂ injection temperature range between 30 and 40 °C and CO₂ injection mass flow rate range between 0.3044 and 0.625 kg/s. The optimization technique in this study uses stochastic algorithms optimization technique due to their capability to find the global optimum. The stochastic algorithms optimization technique used in this research consists of Killer Whale Algorithm (KWA), duelist algorithm (DA), genetic algorithm (GA), Rain Water Algorithm (RWA) and particle swarm optimization (PSO). The results of the optimization and the best results of each optimization techniques are shown in Table 6. The mass flow rate will be the same value at all places; however, pressure and temperature decrease due to thermal and hydraulic loses as shown in Figs. 8, 9 and 10.

Table 6 Optimum variable resulted from optimization

There are three optimization techniques that produced the same optimum variable, i.e., KWA, DA and RWA. The details of income, CO₂ procurement costs, CO₂ separation costs, pump operational costs and net profit on each optimization techniques are tabulated in Table 7.

Table 7 Profit detail calculation after optimization

Table 6 shows the profit of each optimization techniques having three different values. The best optimization results were provided by KWA, DA and RWA that produce the same objective function value and same optimum optimization variables. These techniques generate profits of 12,334.7 USD/day or profit increase of 276.9%. compared to before optimization profit of 4453.9 USD/day. Meanwhile, GA and PSO optimization produces a lower profit value with an increase of 266.1% for GA and 266.5% for PSO.

The typical iterations of objective function during optimization for KWA, DA and RWA optimization algorithms are shown in Fig. 7. The objective function has low value at the early of iteration and increases over the iterations and reached global optimum at about 20th iteration.

Fig. 7

Increase in objective function during iterations

Comparing before (Figs. 1, 2, 3) and after (Figs. 8, 9, 10) optimization by using the same model and optimized variables according to Table 6 (mass balances), the graphical presentation to prove effectiveness of optimization method in searching best pressure and temperature variables of CO₂ EGR and carbon sequestration are shown in Figs. 8,9 and 10. BY similar simulation way before and after optimization, CO₂ is injected into injection well using optimized mass flow rate, pressure and temperature variables (refer to Table 6).

Fig. 8

Injection well pressure (a) and temperature (b) gradient optimization results

Fig. 9

Reservoir pressure (a) and temperature gradient (b) optimization results

Fig. 10

Production well pressure (a) and temperature gradient (b) optimization results

Comparison of Figs. 1 and 8 shows the degradation of temperature and pressure with slight difference. However, in injection wells, the temperature of CO₂ is higher than the temperature of the rock outside the tubing, hence the CO₂ temperature decreased along 100 m of injection well and it heats up again after temperature equilibrium. Meanwhile, the pressure on CO₂ increases continuously due to the gravitational force. In addition, the influence of temperature on supercritical CO₂ pressure has no significant effect. Gravitational force and pressure drop are influenced by the density of CO₂. Therefore, the injection well model using Beggs–Brill method can capture the nonlinearity of injection well tube and rock.

Figures 9a and 3a show that the degradation of pressure is slightly different due to the pressure difference before and after optimization quite similar. Meanwhile, in Figs. 9b and 3b, the inlet temperature of reservoir as a representation of outlet temperature of injection well is different. Hence, the nonlinearity effect due to range of temperature is a main cause. It can be concluded that the reservoir model using Darcy and mass energy balances method can capture the nonlinearity of reservoir rock accurately.

The natural gas conditions in production well before and after optimization are similar operating conditions (Figs. 2, 10). The pressure and temperature will decrease with the increase in distance from the reservoir. Production well outlet pressure after optimization will decrease due to lower reservoir pressure.

Conclusion

CO₂ EGR and carbon sequestration (CS) can be modeled by dividing into three parts, i.e., injection well, reservoir and production well. Injection pressure drop model in injection and production wells uses Beggs–Brill method, while in reservoir by using Darcy equation. Temperature gradient modeling uses mass and heat transfer equations. The average deviation of pressure drops and temperature gradient model in injection well compared to PIPESIM software simulation were 3.03642% and 1.76961%, respectively. Meanwhile, validation at reservoir pressure drop model and temperature gradient compared to COMSOL Multiphysics software simulation has mean deviation of about 0.2003% and 0.0002%, respectively. The average deviation of pressure drops model and temperature gradient in production well have average deviation of 0.80225% and 1.38729% for pressure drop and temperature, respectively. More importantly, it can be concluded that the reservoir model using Darcy and mass energy balances method, and injection and production wells model using Beggs–Brill method can capture the nonlinearity of wellbore accurately. Based on the sensitivity analysis, the profit will increase when mass flow rate and temperature increase; otherwise, it will decrease when CO₂ injection pressure increases. The best results of optimization were provided by using Killer Whale Algorithm (KWA), duelist algorithm (DA) and Rain Water Algorithm (RWA). The optimization results show an increase in profit from 4454.189 USD/day to 12,334.685 USD/day or 276.9% higher than the initial condition of the injection without optimization. By using injection parameters that have been optimized, the CO₂ that can be stored is 1486.01 tons.