Introduction

Thermal recovery is a common method for exploiting heavy oil and bitumen resources. Although it is energy intensive, it remains the most successful method for the in situ development of these vast petroleum resources. However, heat losses to adjoining geologic formations are well-documented challenges in such applications (Zargar and Farouq Ali 2017, 2018; Yee and Stroich 2004; Doan et al. 1999; Vinsome and Westerveld 1980). The heating of the surroundings and unwanted volumes of a reservoir is non-productive, undermining the techno-economic and environmental performances of thermal floods (Doan et al. 2019; Farouq Ali 2018; Valbuena et al. 2009; Law et al. 2003a, b; Jones 1992).

Although thermal losses to the adjoining geologic systems are virtually inevitable, a proper evaluation of their magnitude and potential impacts is important for the design, analysis and management of thermal floods. Such understanding is required for effective mitigation of related project risks and value erosion. Consequently, the development of a robust, yet simple, approach to modelling thermal losses to the adjacent formations has always attracted considerable interests among generations of researchers (Zargar and Farouq Ali 2017, 2018; LaForce et al. 2014; Muradov and Davies 2012; Pruess and Zhang 2005; Pruess and Narasimhan 1988; Vinsome and Westerveld 1980; Weinstein 1972, 1974; Chase and O’Dell 1973).

From the viewpoint of thermal losses to the surroundings, the heat sinks of a petroleum reservoir can be internal or external. The internal sinks are gas and water zones enclosed within the same cap and base rocks as the oil zone of interest. Conversely, the external sinks can be gas-, oil- or water-bearing formations immediately overlying or underlying, as well as on the sides of the subject reservoir (Austin-Adigio et al. 2017; Roche 2008; Law et al. 2003a, b). Unlike the internal sinks that are hydraulically connected to the subject oil zone, there is negligible mass exchange between the oil zone and the external sinks. Depending on their geometry, nature of saturating fluids and bulk thermal properties, one would expect any adjoining heat sink (internal or external) to have some impacts on the thermal efficiency, hence the overall performance of a thermal flood. Accordingly, it is imperative that the formulation and assessment of boundary thermal losses reflect and explicitly account for the relevant properties of both internal and external sinks.

Typically, the detailed treatment of this problem requires a numerical method (Cho et al. 2015; Hansamuit et al. 1992; Lewis et al. 1985). The overburden and underburden are described explicitly by grid blocks, extending far above and below the reservoir in question. In most thermal simulators, a large fraction of the grid blocks is defined as inactive for fluid flow, while these same blocks remain active to describe heat flow within the formation. Accordingly, the focus is an “accurate” characterisation of the semi-infinite boundaries adjacent to the subject petroleum reservoir. At “infinite” ends of the boundaries, the reservoir is assumed to be in thermodynamic equilibrium with the “ultimate” sinks. Although this treatment yields high accuracy, the incremental computational costs are not always worthwhile (Satman 2011; Satman et al. 1984; Vinsome and Westerveld 1980).

The analytical treatment of boundary thermal losses has generally taken either a conductive or a convective heat-transport form. Notwithstanding its popularity, one of the limitations of the conductive approach is that it makes the problem more complex as a result of the increased dimensions of the associated heat-balance equation (LaForce et al. 2013, 2014; Satman 2011; Pruess and Zhang 2005; Satman et al. 1984). For example, coupling a conductive thermal loss model to the one-dimensional (1D) flow equation yields a 2D heat-balance equation. Conversely, the convective treatment of boundary thermal losses does not complicate the original dimensions of the heat-balance equation (Satman 2011; Satman et al. 1984).

On the assumption that the overburden and underburden are impermeable, hence governed by conductive heat transport, Marx and Langenheim (1959) derived an expression for quantifying the rate of boundary thermal losses in reservoirs. Although their final expression relates heat loss rate to the growth rate of the heated area, its drawbacks include the relative complexity of the expression and the underlying assumption of an ideal step temperature profile for the heated and unheated zones. Furthermore, the assumption that the rates of heat loss to the overburden and underburden are equal is limiting.

To simplify the dimensions of the conductive thermal loss equation and thereby improve computational efficiency, semi-analytic techniques have been developed. Using the 1D conductive equation, these approximate methods describe the reservoir boundary as a semi-infinite heat conductor. In 1D applications, some arbitrary “fitting” functions are employed to model the temperature profile into the cap or base rock. The parameters of the fitting function are updated every timestep. As would be expected, different fitting functions have been used in practice. These applications highlighted the sensitivity of the predicted thermal losses to the fitting function utilised (Pruess and Zhang 2005; Pruess and Narasimhan 1988; Vinsome and Westerveld 1980; Weinstein 1972, 1974; Chase and O’Dell 1973).

In the process of solving a steam-flood problem, Hansamuit et al. (1992) appraised four different methods typically used in thermal simulators to estimate the rate of thermal losses to surroundings. They reported that, though it offers the highest computational efficiency, the semi-analytical method is the least accurate among the four methods investigated. On the other hand, the accuracy and performance of the full numerical gridding method were found to be sensitive to the grid size utilised in discretising the contiguous overburden and underburden systems. More importantly, it was concluded that the analytical–numerical method, which is a numerical approximation of the exact analytical solution, was the most robust in terms of accuracy and computational efficiency. The sensitivity of numerical thermal simulations to grid size has been reported by other workers (Cho et al. 2015).

The modelling of laboratory-scale experiments is inherently challenging to both the full-discretisation and semi-analytic approximation methods. Because laboratory physical models have relatively thin boundary walls (typically, in centimetres), the concept of “infinitely” long boundary with a temperature profile that decays smoothly towards its end is not quite applicable. The limited wall thickness makes the wall-ambient interface a point of sharp temperature discontinuity. In applying the full-discretisation method, one needs to think critically about how to discretise the surroundings, which consist of convecting air layers in an infinite medium, as against the idea of stationary and conducting continuous solid body underpinning the full-discretisation and semi-analytic methods. Joshi and Castanier (1993), based on results obtained from their experimental and numerical simulation studies on a steam flood, highlighted the robustness of a convective heat-loss model over a conductive semi-analytic approximation.

Notwithstanding their popularity, the semi-analytic methods have some major shortcomings. These include (1) not accounting for the thickness and thermal properties of the “wall” separating the reservoir and the external sink in the direction of heat flow; (2) dependency of results on the fitting function (and number of parameters) used; (3) lack of a clear procedure to assess, in advance, the appropriateness or otherwise of adiabatic assumption or other boundary conditions; and (4) lack of clear insights into how the fluids contained in the adjacent formations affect thermal flooding in the reservoir of interest.

Similar to its conductive heat-loss counterpart, the convective treatment of boundary thermal losses has received some attention. Most convective treatments for thermal floods applied overall heat-transfer coefficient (U), in which both constant and time-variant forms have been proposed (Satman et al. 1979, 1984; Zolotukhin 1979). In principle, U is a function of the thermal properties of the heating (reservoir) medium, heated medium (adjacent strata), as well as the interface between the two media (Bird et al. 2001). However, the existing convective treatments of boundary thermal losses do not reflect the thermal properties of the reservoir-boundary interfaces (walls) in their estimation of U required for the execution of the convective treatment (Satman et al. 1979, 1984; Zolotukhin 1979). Similarly, the previous convective techniques do not provide explicitly for the saturating fluids and local heat-transfer coefficients of the adjoining sinks in their estimation of U (Satman 2011; Satman et al. 1979, 1984; Zolotukhin 1979).

Considering the drawbacks of the existing methods, this paper explores a different approach. The principle of heat exchanger is invoked to model the boundary-sink system. This treats the boundary as a conductive “wall” through which the reservoir and adjoining formations, which are at different temperatures, exchange heat but not mass. Considering that our primary interest is in the thermal resistance of the wall, as against an accurate characterisation of the temperature distribution across the wall, the proposed approach eliminates the need for a predetermined temperature fitting function. Because it is premised on a convective treatment, our proposal does not increase the dimensions and complexity of the original heat equation.

As noted earlier, the proposed use of a convective model to describe boundary thermal losses is not new. However, as an improvement over existing treatments, the current approach explicitly accounts for key interface (reservoir overburden and reservoir underburden) properties such as thermal conductivity, thickness and heat capacity. Furthermore, our approach explicitly considers the relevant thermal properties of the adjacent formations and, through the corresponding local convective heat-transfer coefficients, provides insights into how the fluids contained in the adjoining porous media can potentially influence the efficiency of a thermal flood in the reservoir of interest. In essence, as against a lumped approach, we explicitly consider the layered thermal resistances of the reservoir-overburden interface wall, the reservoir-underburden wall as well as the overburden and underburden systems.

Model formulation and solution

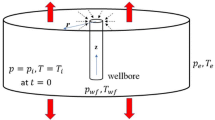
Figure 1 shows a schematic of the problem. It represents steam-assisted gravity drainage (SAGD) and electrical heating processes (Zargar and Farouq Ali 2017; Lawal 2011; McGee and Vermeulen 2007). On a production timescale, the cap and base rocks are rock layers (walls) that prevent mass flow, while dampening heat flow from the reservoir to the overlying (top external sink) and underlying (bottom external sink) formations. Although they thwart convective heat flow, they still allow conductive heat exchange between the reservoir and its adjoining formations. Depending on the depositional environment, such walls are usually shale, siltstone or evaporite.

Fig. 1
figure 1

Model reservoir and its adjoining heat sinks in 1D (Lawal 2011)

Full size image

Taking the injector as the heat source and assuming no production, heat transport in this 1D reservoir is described by Closmann and Smith (1983):

$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} = \frac{\partial T}{\partial t},$$
(1)

where the quantities α, T, z and t are the bulk thermal diffusivity, temperature, vertical distance from injector and elapsed time, respectively.

Heat transport through the boundaries

The system of reservoir and adjacent formations is conceptualised as a heat exchanger. Typical heat exchangers consist of two fluid bodies, isolated by a conducting wall. When a temperature difference exists, the fluids exchange heat through the non-permeable wall, but no mass transfer occurs between the fluids. The present model has the reservoir, boundary and adjacent formations being analogous to the hotter fluid, wall and colder fluid, respectively. The following are the key assumptions underpinning subsequent derivations:

  • The cap and base rocks are in contact with sinks of infinite volumes. The temperatures of these sinks remain constant at their initial conditions.

  • In the direction of heat flow (normal to reservoir dip), thermal resistances act in series; hence, they are additive.

  • Thermophysical properties of cap/base rocks and sinks are temperature independent.

The first assumption suggests that the timescale for heating the reservoir is negligible in comparison with the adjoining sinks. Considering that the overburden and underburden are of infinite volumes relative to the reservoir, it is not unreasonable to anticipate that any heat received from the reservoir would be absorbed instantly by the external sinks, without causing significant changes to the average bulk temperatures of these sinks over a production lifetime. Satman (2011) also assumed constant temperatures in the overburden and underburden formations. Although this assumption would exaggerate thermal losses in the vertical direction, any overestimation partly compensates for lateral losses neglected in this 1D model.

At the cap and base rocks, the heat-transport model (Eq. 1) becomes (to avoid confusion, we use the notation Δz instead of dz):

$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} - \frac{{Q_{\text{loss}} }}{{\rho c_{\text{p}} A\Delta z}} = \frac{\partial T}{\partial t},$$
(2)

where Qloss is the net heat exchanged with the adjacent formations, i.e. Qcap and Qbase for the cap and base rock, respectively. ρ, cp and A are bulk density, specific heat capacity and cross-sectional area of the reservoir-boundary interface, respectively. For all other layers except the cap and base layers, \(Q_{\text{loss}} = 0\). Specifically, the quantities \({{Q_{\text{cap}} } \mathord{\left/ {\vphantom {{Q_{\text{cap}} } {A\Delta z}}} \right. \kern-0pt} {A\Delta z}}\) and \({{Q_{\text{base}} } \mathord{\left/ {\vphantom {{Q_{\text{base}} } {A\Delta z}}} \right. \kern-0pt} {A\Delta z}}\) are the rates of boundary heat losses per unit volume of the differential element of thickness Δz.

For a reservoir of thickness H (above injector), and gross volume AH, Eq. 2 becomes:

$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} - \frac{{Q_{\text{loss}} }}{{\rho c_{\text{p}} AH}} = \frac{\partial T}{\partial t} .$$
(3)

With the description of the reservoir–cap rock–top sink and reservoir–base rock–bottom sink as heat exchangers, Qcap and Qbase are given by:

$$Q_{\text{cap}} = U_{\text{c}} A\left( {T_{\text{c}} - T_{\text{a}} } \right),$$
(4)
$$Q_{\text{base}} = U_{\text{b}} A\left( {T_{\text{b}} - T_{\text{a}} } \right) ,$$
(5)

where Uc and Ub are overall heat-transfer coefficients of reservoir–cap rock–sink and reservoir–base rock–sink systems, respectively, Ta is the temperature of the infinite surrounding and Tc and Tb are instantaneous temperatures of cap and base rocks (boundaries), respectively.

From Eqs. 3–5, the following are the partial differential equations (PDE) at other layers in the reservoir, cap and base layers, respectively:

$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} = \frac{\partial T}{\partial t},$$
(6)
$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} - \frac{{U_{\text{c}} \left( {T_{\text{c}} - T_{\text{a}} } \right)}}{{\rho c_{\text{p}} H}} = \frac{\partial T}{\partial t},$$
(7)
$$\alpha \frac{{\partial^{2} T}}{{\partial z^{2} }} - \frac{{U_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)}}{{\rho c_{\text{p}} H}} = \frac{\partial T}{\partial t}.$$
(8)

In the case where the cap, base or both layers are considered to have sufficient thermal insulation capacity, the engineer simply sets \(U_{\text{b}} = 0\), \(U_{\text{c}} = 0\) or \(U_{\text{b}} = U_{\text{c}} = 0\) as appropriate. From the standpoint of thermal losses to the surroundings, these scenarios describe an adiabatic behaviour, which approximates well-insulated laboratory experiments.

Overall heat-transfer coefficients

The following expressions yield the overall heat-transfer coefficients for the top and bottom boundaries. Through the thermal conductivities and convective coefficients, temperature-induced changes to Uc and Ub can readily be captured. However, for simplicity, the current study ignores these changes throughout the operating lifetime.

$$U_{\text{c}} = \left[ {\frac{1}{{h_{{{\text{i}}\,{\text{c}}}} }} + \frac{{Z_{\text{c}} }}{{\kappa_{\text{c}} }} + \frac{1}{{h_{\text{sc}} }}} \right]^{ - 1} ,$$
(9)
$$U_{\text{b}} = \left[ {\frac{1}{{h_{\text{ib}} }} + \frac{{Z_{\text{b}} }}{{\kappa_{\text{b}} }} + \frac{1}{{h_{\text{sb}} }}} \right]^{ - 1} .$$
(10)

where hic and hsc are the heat-transfer coefficients of the layers immediately below and above the cap rock, respectively and κc and Zc are thermal conductivity and thickness of the cap rock, respectively. Similar notations apply to the base rock, i.e. hib and hsb refer to the layer just before (within reservoir) and below (sink) the base rock, respectively.

Numerical solution

A finite-difference scheme is employed to solve the resulting system of equations. For simplicity, a standard implicit scheme is utilised; hence, the procedure for discretisation is typical (Smith 1985). Considering a uniform grid spacing h and timestep k, while assuming central and forward difference formulae for \({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0pt} {\partial z}}\) and \({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-0pt} {\partial t}}\), the heating of the reservoir is described by the following numerical scheme. This is a discretisation of the PDE for an intermediate grid (e.g. Eq. 7), which provides for heat exchange with a boundary:

$$\begin{aligned} & - \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i - 1,j + 1} + \left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right)T_{i,j + 1} - \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i + 1,j + 1} \\ & \quad \approx \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i - 1,j} - \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right)T_{i,j} + \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i + 1,j} \\ &\quad\quad- \frac{{U\left( {T_{\text{boundary}}^{j} - T_{\text{a}} } \right)}}{{\rho c_{\text{p}} H}}. \\ \end{aligned}$$
(11)

At the intermediate grids, \(U = 0\), but the cap rock has \(U = U_{\text{c}}\) and \(T_{\text{boundary}}^{j} = T_{\text{c}}^{j}\). Corresponding expressions at the base are \(U = U_{\text{b}}\) and \(T_{\text{boundary}}^{j} = T_{\text{b}}^{j}\). The terms \(T_{\text{c}}^{j}\) and \(T_{\text{b}}^{j}\) are evaluated at the preceding timestep, j.

Boundary conditions

Ignoring heat storage in the cap and base rocks (interface layers), the following are the boundary conditions. For simplicity, we assume no production, hence no convective losses through the production well:

$$T\left( {z,0} \right) = T_{\text{i}} \quad t \, < \, 0,$$
(12)
$$T\left( {0,t} \right) = T_{\text{s}} \quad t \, \ge \, 0,$$
(13)
$$z = H;\quad - \kappa_{\text{R}} \frac{{{\text{d}}T}}{{{\text{d}}z}} = q(t)\quad t \, \ge \, 0,$$
(14)

where κR is the reservoir thermal conductivity, while Ti and Ts are the initial and heating temperatures, respectively.

Based on the heat-exchanger concept and the definition of the flux \(q\left( t \right)\), while ensuring energy conservation at the boundary, Eq. 14 becomes:

$$- \kappa_{\text{R}} \frac{{{\text{d}}T}}{{{\text{d}}z}} = - U_{\text{c}} \left( {T - T_{\text{a}} } \right) .$$
(15)

Through the overall heat-transfer coefficients, this form of boundary conditions accounts for the effects of both the geometry and thermophysical properties of the physical boundaries, whether at field or laboratory scale. Additionally, it captures the characteristics of the adjacent formations, providing insights into how these can potentially influence the performance of a thermal flood. To complete our mathematical description of the current problem, the boundary conditions are integrated into the numerical scheme of Eq. 11.

Integration of the cap rock boundary condition warrants a “fictitious” grid \(\left( {N_{z + 2} } \right)\) from the cap rock into the sink. Following an application of the central-difference formula to Eq. 15 at the cap rock (\(i = N_{z + 1}\)) and subsequent elimination of the “fictitious” grid, the cap rock is described by:

$$\begin{aligned} & - \kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }}} \right)T_{{N_{z} ,j + 1}} + \left\{ {\kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right) + U_{\text{c}} \left( {\frac{\alpha }{h}} \right)} \right\}T_{{N_{z + 1} ,j + 1}} \\ & \quad \approx \kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }}} \right)T_{{N_{z} ,j}} - \left\{ {\kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right) + U_{\text{c}} \left( {\frac{\alpha }{h}} \right)} \right\}T_{{N_{z + 1} ,j}} \\ & \quad + 2U_{\text{c}} T_{\text{a}} \left( {\frac{\alpha }{h}} \right) - \frac{{\kappa_{\text{R}} }}{{\rho c_{\text{p}} H}}\left\{ {U_{\text{c}} \left( {T_{{N_{z + 1} ,j}} - T_{\text{a}} } \right)} \right\}. \\ \end{aligned} .$$
(16)

Applying Eq. 11 at the injection plane, while noting that this must always be at temperature Ts, we have the following equation with two unknowns T2 and T3 at next timestep (j + 1):

$$\begin{aligned} &\left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right)T_{2,j + 1} - \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{3,j + 1} \approx \left( {\frac{\alpha }{{h^{2} }}} \right)T_{\text{s}} \\ &\quad- \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right)T_{2,j} + \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{3,j} - \frac{{U_{\text{b}} \left( {T_{\text{b}}^{j} - T_{\text{a}} } \right)}}{{\rho c_{\text{p}} H}} . \end{aligned}$$
(17)

Solution of PDE under conducting boundaries

To generate the temperature profiles in a reservoir exposed to conduction-dominated heating, Eqs. 11, 16 and 17 have to be solved simultaneously at every timestep. For illustration, we derive the relevant system of algebraic equations for a reservoir discretised into Nz grids on the z-axis. The injection plane and cap rock are represented by grids i = 1 and i = Nz+1, respectively. For conductive heating, the following equations are applicable at the injection plane (i = 1), intermediate grids \(\left( {i = 2,3, \ldots ,N_{z} } \right)\) and cap rock (i = Nz+1), respectively:

$$\begin{aligned} &\left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right)T_{2,j + 1} - \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{3,j + 1} \\&\quad\approx \left( {\frac{\alpha }{{h^{2} }}} \right)T_{\text{s}} - \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right)T_{2,j} + \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{3,j} \\&\qquad- \frac{{U_{\text{b}} \left( {T_{\text{b}}^{j} - T_{\text{a}} } \right)}}{{\rho c_{\text{p}} H}} . \end{aligned}$$
(18)
$$\begin{aligned} &- \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i - 1,j + 1} + \left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right)T_{i,j + 1} - \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i + 1,j + 1} \\ &\quad\approx \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i - 1,j} - \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right)T_{i,j} + \left( {\frac{\alpha }{{2h^{2} }}} \right)T_{i + 1,j} . \end{aligned}$$
(19)
$$\begin{aligned} & - \kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }}} \right)T_{{N_{z} ,j + 1}} + \left\{ {\kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }} + \frac{1}{k}} \right) + U_{\text{c}} \left( {\frac{\alpha }{h}} \right)} \right\}T_{{N_{z + 1} ,j + 1}} \\&\quad\approx \kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }}} \right)T_{{N_{z} ,j}} \\ & - \left\{ {\kappa_{\text{R}} \left( {\frac{\alpha }{{h^{2} }} - \frac{1}{k}} \right) + U_{\text{c}} \left( {\frac{\alpha }{h}} \right)} \right\}T_{{N_{z + 1} ,j}} + 2U_{\text{c}} T_{\text{a}} \left( {\frac{\alpha }{h}} \right) \\ &\quad- \frac{{\kappa_{\text{R}} }}{{\rho c_{\text{p}} H}}\left\{ {U_{\text{c}} \left( {T_{{N_{z + 1} ,j}} - T_{\text{a}} } \right)} \right\}. \\ \end{aligned}$$
(20)

These expressions suggest that every timestep is characterised by Nz algebraic equations in Nz unknown temperature points. This well-posed system of simultaneous equations submits to ready solution with a simple computer program.

An example

The applicability of the proposed formulations is tested with a case of conductive heating of an example heavy-oil reservoir. Table 1 presents simulation input data for a typical oil sand (Lawal 2011; Lawal and Vesovic 2010; Li and Chalaturnyk 2009; Law et al. 2003b). To evaluate non-adiabatic (\(U_{\text{b}} \ne 0\),\(U_{\text{c}} \ne 0\)) behaviour of the reservoir system, independent cases of gas- and liquid-saturated contiguous formations are considered (Table 2). For benchmarking, the limiting cases of adiabatic, isothermal (cap rock kept at initial temperature) and semi-infinite boundaries are included. This example investigates the nature of sink saturants (fluids saturating the sinks) as the primary driver of thermal losses.

Table 1 Input data for simulations
Full size table
Table 2 Effects of sink saturants and boundary conditions (G = gas saturated, L = liquid saturated)
Full size table

We recognise that it is rare to encounter a natural gas column underlying an oil sand within the same continuous reservoir. Notwithstanding, the following scenarios are fair approximations of such occurrence: (1) leakage of gas from an underlying gas-bearing formation into the reservoir in question; (2) accumulation of live steam, flashed condensate and/or vapourised oil in the vicinity of the producer. In contrast to the rarity of encountering a natural gas column underlying an oil sand within the same reservoir, cases of a water zone overlying an oil sand in the same formation are fairly common, especially in Canada (Austin-Adigio et al. 2017). Therefore, the cases in Table 2 cover the full range of possible combinations of saturating fluids at the boundaries and adjacent formations.

In this example, the convective heat-transfer coefficients of gas- and liquid-filled porous media are assumed constant at 12 and 500 W m−2 K−1, respectively. Although such data are not readily available for petroleum reservoirs, these estimates are comparable to the 3–24 and 100–1200 W m−2 K−1, which generally characterise free convection of gas and liquid in industrial systems, respectively (Jiji 2006; Bird et al. 2001). For simplicity, the assumed convective heat-transfer coefficients are aggregates of both free and forced convections. Furthermore, the present example does not account for potential temporal variations of Ub and Uc as the flood matures. Nevertheless, if required, such variations can readily be captured through temperature-induced changes to thermal conductivities and convective coefficients as the thermal flood progresses.

In principle, the adjoining sinks may be viewed as some natural controllers that aim to maintain the reservoir temperature at its pre-heating value (steady state). For the present analysis, we use steady-state temperature (Tss) and steady-state deviation (δ) to quantify the impacts of boundary conditions and combination of sink saturants on the conductive heating of the example petroleum reservoir. By definition, Tss is the average temperature ultimately reached in the heated reservoir, while δ is the percentage deviation of Tss from the source temperature Ts.

Results and discussion

The predicted ultimate average temperature and deviation are presented in Table 2 for the five runs. Regardless of the combination of sink saturants, all the non-isothermal boundary conditions show sharp variations from the reference adiabatic case (run 5). However, at ca. 48% deviation, the case of isothermal boundaries (run 3) yields the most pessimistic heating in this example. As would be expected, the scenario of a semi-infinite reservoir (run 4 in Table 2) provides the next most optimistic heating performance. Considering the magnitude of steady-state temperature deviations in Table 2, it is deduced that the adiabatic assumption is not a good approximation for both isothermal and non-adiabatic operations for the specific case examined in the present study.

To facilitate the analysis of heating performances, the quantity “thermal-flood maturity” is introduced to describe the fraction of the formation penetrated by heat conduction after an elapsed time. Reckoning that this is a conduction-dominated process, the present application defines thermal-flood maturity as \(t_{\text{m}} = {{\sqrt {\alpha t} } \mathord{\left/ {\vphantom {{\sqrt {\alpha t} } H}} \right. \kern-0pt} H}\). Beyond the penetration depth \(\sqrt {\alpha t}\), it is considered that the temperature has not changed significantly from its initial state.

For the same set of fluid fill in the contiguous geologic systems and boundary conditions, the instantaneous temperature profiles of the subject reservoir are displayed in Fig. 2 after 1000 days of continuous heating. At this instant, the temperature distributions within the first 50% of the reservoir column are largely insensitive to the boundary conditions, and the nature of the adjoining strata. This observation is in contrast to the remaining part of the reservoir, where sensitivity of the temperature profile to the boundary conditions is evident.

Fig. 2
figure 2

Temperature profiles for various boundary saturants/conditions (t = 1000 days)

Full size image

Owing to the relative immaturity (tm = 0.37) of the thermal flood at 1000 days, the temperature profiles in the vicinity of the boundaries do not exhibit significant differences at this time. It is interesting to see the case of liquid-saturated sinks behaving as if the reservoir were a semi-infinite system. Therefore, except for the isothermal case, the temperature profile in a relatively thick formation may not be very sensitive to the characteristics of the adjacent media and boundary conditions at early times when the flood is still immature.

The flood is characterised by tm = 0.73 after some 4000 days of heating. For the various boundary conditions of interest, Fig. 3 displays the instantaneous temperature profiles. At this instant, the effects of the boundaries are more pronounced, not just in the vicinity of the boundaries but most parts of the reservoir. Because of the full retention of injected heat, the adiabatic case shows a sharp departure from the other cases at this time. More importantly, due to the higher maturity attained by the flood at this time, the sensitivity of temperature distribution to boundary condition is pronounced in more than 80% of the reservoir interval. Therefore, as a thermal flood becomes more mature, the impacts of the adjacent strata and the bounding interface layers increase, and the justification to reflect appropriate boundary conditions and fluid fills becomes stronger.

Fig. 3
figure 3

Temperature profiles for various boundary saturants/conditions (t = 4000 days)

Full size image

After 10,000 days of heating, the flood reaches tm = 1.16, suggesting that the thermal diffusion length is beyond the reservoir, thus a very mature flood. From the results illustrated in Fig. 4, it is evident that the effects of adjacent porous media and boundary conditions are significant in most parts of the reservoir. The divergence of profiles becomes increasingly significant away from the heat source. These results reinforce the prior observations that the effects of the adjacent strata and bounding beds on heating performance become more pronounced as the flood matures.

Fig. 4
figure 4

Temperature profiles for various boundary saturants/conditions (t = 10,000 days)

Full size image

It is instructive to note the relative closeness of the semi-infinite and adiabatic results over time. This observation suggests that as a thermal flood matures, the semi-infinite assumption approaches an adiabatic scenario, with the tendency to overestimate the performance of a thermal flood in a number of practical applications. By the same argument, we recommend that some caution be exercised with the common practice of using the semi-infinite model to estimate the thermal losses while heating a petroleum reservoir (Pruess and Zhang 2005; Vinsome and Westerveld 1980).

Comparing Figs. 3 and 4, it is evident that all the non-adiabatic responses have reached their respective stabilised states after about 4000 days of continuous conductive heating. This notwithstanding, it is clear that the case of gas-saturated boundaries offer superior heating performance compared to its liquid-saturated counterpart. The better thermal efficiency of the former is attributed to the lower heat-transport capacity, hence higher insulating capacity, of gas compared to liquid.

The simulation results provide additional insights. As evident in the progressive widening of the difference between the adiabatic and non-adiabatic solutions, the non-productive heating of the adjoining geologic systems increases over time. This observation is a consequence of the continuous expansion of the heated zone, which consistently increases the temperature differences between the reservoir boundaries and the neighbouring sinks. This is one of the reasons that thermal floods generally become less efficient as they mature. The drive to optimise the energy and environmental performances of mature floods has necessitated a number of variants to the conventional thermal recovery techniques. These variants include the wind-down processes that entail either a partial or full substitution of steam with cheaper agents such as CO2, nitrogen, flue or natural gas at late life (Yee and Stroich 2004; Jiang et al. 2000). Besides the possibility of forming some thermally insulating blankets in the vicinity of the boundaries, when compared to steam, the lower heat-carrying capacities of these agents inhibit heat losses to the adjacent formations.

Model validation

We compare the performance of the proposed model against using the following expression of overall heat-transfer coefficient introduced by Zolotukhin (1979). Equation 21 assumes that the overburden and underburden have the same characteristics, hence the factor 2:

$$U = 2\sqrt {\frac{{\left( {\kappa \rho c_{\text{p}} } \right)_{\text{adj}} }}{pt}} ,$$
(21)

where the quantity \(\left( {\kappa \rho c_{\text{p}} } \right)_{\text{adj}}\) refers to the adjacent formation, while p and t are injection pressure and elapsed time, respectively.

For the validation, we consider run 1 in Table 2, while assuming that the overburden and underburden have the same thermal properties as suggested by the original authors of Eq. 21. To implement Eq. 21 in the numerical scheme (Eqs. 18–20), the heating fluid is taken as saturated steam. Hence, at the steam temperature of 250 °C, the corresponding injection pressure is approximately 3.973 × 106 Pa.

For the case of 1000 days of continuous heating, Fig. 5 shows that the results of the proposed model and that using the overall heat-transfer coefficient from Zolotukhin (1979) are comparable. The difference between the two profiles towards the boundary is attributed to the non-inclusion of thermal resistance across the reservoir-boundary walls in the evaluation of the quantity U with the Zolotukhin (1979) model. This point is reinforced with the same run, but reducing the thickness of both interface walls to 0.3 m, thus reducing the thermal resistances of the walls by an order of magnitude. As shown in Fig. 6, the proposed model yields a lower reservoir temperature profile in response to reduced thermal resistances of the walls. But, contrary to expectation, the results of Zolotukhin (1979) remain unchanged between Figs. 5 and 6. The insensitivity of Zolotukhin (1979) to this perturbation is not surprising, considering that Eq. 21 is inherently devoid of the resistance (thickness and conductivity) of the walls.

Fig. 5
figure 5

Proposed versus Zolotukhin (1979) models for run 1 (t = 1000 days; zb = zc = 3 m)

Full size image
Fig. 6
figure 6

Proposed versus Zolotukhin (1979) models for run 1 (t = 1000 days; zb = zc = 0.3 m)

Full size image

The implication of this comparative evaluation is that in immature floods, in which the thermal front is still very much distant from the reservoir boundaries, the proposed and Zolotukhin (1979) models would yield similar temperature profiles. However, as the flood matures in terms of the thermal front reaching the boundaries, the results of the two models would exhibit increasing divergence. Therefore, in the formulation and simulation of realistic thermal floods, it is imperative to ensure appropriate description of the thermal resistances associated with the boundary layers and adjoining formations. As evident in this work, the overall heat-transfer coefficient offers a reasonable approach to capture and integrate the relevant boundary, overburden and underburden thermal resistances in the formulation and solution of thermal-flood problems.

Conclusion

To improve the description of thermal losses through the cap and base rocks, convective heat-loss equation has been applied to the 1D modelling of heat transport in petroleum reservoirs. This application covers the non-isothermal conditions of adiabatic and non-adiabatic behaviours, as well as isothermal boundaries. Numerical solutions of the resulting system of PDEs are provided for all these possible conditions.

This modelling approach takes advantage of the well-established theory of heat exchangers. The proposed method explicitly accounts for the effects of the fluids saturating the adjoining geologic systems, as well as the characteristics of the boundary layers (walls separating the reservoir from the cap and base rocks) on the rate of reservoir heating. It offers insights into the relative impacts of these variables on the performance of a thermal flood. Comparison of the proposed method with another analytical model shows satisfactory performance and highlights the relative advantage of the former.

From detailed sensitivity tests performed on different combinations of saturating fluids in the adjacent geologic systems, it is concluded that thermal floods are sensitive to heat losses through the boundaries and the prevailing boundary conditions, which are largely influenced by the adjacent formations. More importantly, apart from the early times when the heated volume is relatively limited, the simulation results indicate that neither an adiabatic nor a semi-infinite reservoir assumption is a good approximation for most realistic thermal floods. Otherwise, there is a high chance that reservoir performance and project value would be grossly overestimated, hence putting large investments at risk. In addition, there is the associated risk that the potential environmental impacts of a thermal flood will be under-estimated, which may further jeopardise the project.