Introduction

Streamline numerical simulation is widely used as an important means to characterize fluid flow paths and describe the intensity of the flow field during the development of an oil field. By establishing the pressure equation on the grid and quadrature of the streamline, we can get the corresponding pressure equipotential surface and establish a natural migration network. The fluid moves along the streamline, so as to track the migration of oil, gas, and water in the reservoir. Compared with the traditional finite difference numerical simulation method, modern reservoir streamline simulation in many aspects has achieved great breakthroughs, such as the Pollock streamline tracing method (Jackson et al. 1988), data transfer method between the network and grid (Batycky et al. 1997), and the history matching method based on streamline simulation (Wang 2002). Thiele and Batycky (2003) established water injection optimization model by streamline numerical simulation technology. Cheng et al. (2007) established the historical fitting method of streamline field numerical simulation through three-dimensional three-phase reservoir streamline simulation. Zhao et al. (2016) predicted the connectivity between oil and water wells based on the interwell connectivity inversion model. Wang et al. (2017) characterized the water drive flow field through the water drive characteristic curve and the interwell connectivity model. However, the current streamline field simulation can only qualitatively judge the distribution of the current flow field by the streamline density in each area of the reservoir; it cannot quantitatively evaluate the streamline field. Therefore, we need to explore a method for quantitative evaluation of reservoir streamline field.

Clustering analysis is an important statistical method in research on classification; one clustering method classifies the data through unsupervised ways and tests the similarity and difference between data. In the end, classification results of the large similarity in each cluster and large differences between clusters are formed (Agarwal et al. 1999). With the development of data mining technology, clustering methods have been used to analyze data sets with multiple attributes and complex distribution structures (Grabmeier and Rudolph 2002). In recent years, quantum clustering, spectral clustering, granularity clustering, probabilistic graph clustering, and synchronous clustering have also become popular. Aminzadeh et al. (2013) used tomographic inversion, fuzzy clustering, and shear wave splitting to obtain reliable characteristics about fractured areas; it can be used to optimize drilling targets or stimulation jobs to reduce costs and maximize production. Tan et al. (2016) introduced the application of data miming to petroleum exploration and development to obtain high-performance predictive models and optimal classifications of geology, reservoirs, reservoir beds, and fluid properties. Aliyarov and Ramazanov (2016) used fuzzy clustering to predict reservoir rock properties. However, under the influence of the difficulty in extracting the streamline data of the reservoir, there is no relevant literature to introduce the clustering evaluation method of streamline field based on reservoir numerical simulation at present. How to extract and cluster streamline data and determine the optimal number of clusters is the focus of this study.

In this paper, the data of the streamline field were extracted, and the streamline field was evaluated by the peak density clustering algorithm. An evaluation coefficient was used to evaluate the clustering effect of different streamline cluster numbers, and ultimately we achieved the purpose of streamline grading optimization. The results show that, for the current streamline field of the Nm3-4-1 layer in the Gang dong oil field, when the evaluation coefficient we specified is the minimum, the clustering result is the best. The grading results clearly show the distribution of displacing efficiency at the present time of reservoir streamline field. The new method provides a way to regulate the streamline field and enhance oil recovery.

The establishment of the peak density algorithm model

Rodriguez and Laio (2014) published “Machine learning. Clustering by fast search and find of density peaks” in the magazine “Science”. Their peak density algorithm provided a new way for clustering evaluation. They considered that the cluster centers should have the characteristics of high density and far away from the data point that is larger than it is. The difference between density-based and distance-based clustering algorithms is that the density-based clustering algorithm determines clusters of arbitrary shapes, while the distance-based clustering algorithm determines a spherical cluster. This plays an important role in the evaluation of data sets with noise points and density differences.

The calculation flow of the peak density algorithm is shown in Fig. 1. The basic principle is to measure sample density based on the number of similar samples. Select the maximum density sample of the local area as the clustering center, and ensure that the distance between the sample and other samples with a larger density is large enough.

Fig. 1
figure 1

Calculation flow chart of peak density algorithm

Full size image

The specific steps for the peak density algorithm are:

  1. 1.

    Standardize data sets to eliminate the effects of different data units.

  2. 2.

    Determine the local density and separation distance of each sample separately.

  3. 3.

    The product of local density and separation distance is used as the evaluation value, and the sample evaluation values are arranged in descending order. The samples with the top rank are selected as the clustering centers.

  4. 4.

    Assign the remaining points to the higher density clusters that are adjacent to it.

In the calculation process, the formula for calculating the local density of item i is:

$${\rho _i}=\mathop \sum \limits_{j} ({d_{ij}} - {d_{\text{c}}})\quad i=1,2,3 \ldots n,$$
(1)

where \({\rho _i}\) is the local density of sample i, \(~{d_{ij}}\) is the distance between sample i and sample j, \(~{d_{\text{c}}}\) is the cut-off distance, and n is the total sample size.

To ensure a large separation distance between sample i and larger density samples, we need to evaluate the separation distance of the sample. The expression is:

$${\delta _{{q_i}}}=\mathop {\hbox{min} }\limits_{{{q_j},j<i}} {d_{{q_i}{q_j}}},$$
(2)

where \({\delta _{{q_i}}}\) is the separation distance of samples and \({d_{{q_i}{q_j}}}\) is the distance between sample \({q_i}\) and sample \({q_j}\).

For a cluster center, it should have two attributes with larger local density in its own interior and larger separation distance from other cluster centers. Therefore, the cluster center evaluation formula for the samples i can be determined as follows:

$$~{\gamma _i}={\rho _i} \cdot {\delta _{{q_i}}},$$
(3)

where \({\text{~}}{\gamma _i}\) is the cluster center evaluation value of samples i.

Assume that the total data are divided into n group of cluster center, we can descend the \(\gamma\) calculated by all the data, and the former n sample point is the cluster center point; then the cluster can be determined according to the control range which the user set up at the density center point.

The peak density algorithm has strong ability to distinguish data sets. When the reservoir reaches the high water cut stage, the distribution of streamline field is complex, the streamline attributes are different in density, and so we choose the peak density algorithm to evaluate the streamline field on the basis of density distribution difference.

Determination of evaluation index for clustering effect

The peak density algorithm is used to classify the reservoir streamline field, which can quickly determine the collection of the same kind of streamline. However, the quality of the clustering effect can directly affect the evaluation result. Too many or too few streamline clusters are meaningless; it is necessary to evaluate the effectiveness of the clustering results. Many scholars put forward different algorithms to evaluate the clustering effect from the compactness and separation degree of the cluster. Compactness is a measure of whether a set of samples is compact enough through the average distance, variance, and other parameters of the cluster center, while the degree of separation is to measure whether the distance between one cluster and another cluster is far enough.

Calinski determined the effectiveness of the clustering effect by evaluating the square sum coefficient between different clusters in 1974. When Calinski–Harabasz index reaches the maximum, clustering is the best (Caliński and Harabasz 1974). Its expression is:

$${\text{Calinski}}-{\text{Harabasz}}\,{\text{index}}:\frac{{\mathop \sum \nolimits_{i} {n_i}{d^2}({c_i},c)/({\text{NC}} - 1)}}{{\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{{x \in {C_i}}} {d^2}(x,{c_i})/(n - {\text{NC}})}}.$$
(4)

In the above expressions, \({n_i}\) is the number of objects in \({C_i}\); d(x, y): distance between x and y; \(~{c_i}\) is the center of \({C_i}\); NC is the clusters number; n is the number of objects in sample set; \(~{C_i}\) is the i-th cluster; i is the code for different cluster clusters.

Dunn (1974) used the minimum distance between different clusters as the evaluation of the internal separation degree, and the maximum diameter between different clusters was used to evaluate the compactness of the cluster. When Dunn index reaches the maximum, clustering is the best. The specific expression is as follows:

$${\text{Dunn}}\,{\text{index}}:{\text{mi}}{{\text{n}}_i}\left\{ {{\text{mi}}{{\text{n}}_j}\left( {\frac{{{\text{mi}}{{\text{n}}_{x \in {C_i},y \in {C_j}d\left( {x,y} \right)}}}}{{{\text{ma}}{{\text{x}}_k}\left\{ {{\text{ma}}{{\text{x}}_{x,y \in {C_k}}}d\left( {x,y} \right)} \right\}}}} \right)} \right\},$$
(5)

where j is the code for different cluster clusters.

In 1985, Hubert proposed to evaluate the clustering effect by calculating the inconsistencies between different cluster data. The Modified Hubert coefficients corresponding to different clusters are numerically plotted; when the inflection point appears in the curve, the corresponding number of clusters is the best (Hubert and Arabie 1985). The expression is:

$${\text{Modified}}\,{\text{Hubert}}\,{\text{coefficient}}:\frac{2}{{n(n - 1)}}\mathop \sum \limits_{{x \in D}} \mathop \sum \limits_{{y \in D}} d(x,y)~~{d_x} \in {C_i},{d_y} \in {C_j}({c_i},{c_j}),$$
(6)

where D is the data sets; n is the number of objects in D; \(~{c_i},{c_j}\) is the center of \({\text{~}}{C_i},{C_j}\), respectively.

Rousseeuw and Sihouettes (1987) defined the contour coefficient, which is based on the distance difference between and within the cluster to evaluate the clustering effect. When the contour coefficient value is the largest, the corresponding number of clusters is the best.

$${\text{Contour}}\,{\text{coefficient}}:\frac{1}{{{\text{NC}}}}\mathop \sum \limits_{i} \left\{ {\frac{1}{{{n_i}}}\mathop \sum \limits_{{x \in {C_i}}} \frac{{b(x) - a(x)}}{{\hbox{max} \left[ {b(x),a(x)} \right]}}} \right\},$$
(7)

where \(a(x)=\frac{1}{{{n_i} - 1}}\mathop \sum \nolimits_{{y \in {C_i},y \ne x}} d(x,y)\) and \(b(x)={\hbox{min} _{j,j \ne i}}\left[ {\frac{1}{{{n_j}}}\mathop \sum \nolimits_{{y \in {C_j}}} d(x,y)} \right].\)

In 1996, Mark Marcucci proposed the method of root-mean-square standard deviation to evaluate the clustering effect. It mainly measured the uniformity of the cluster. When the curve formed by the numerical connection of different clustering numbers occurs at inflection point, the corresponding clustering number is the best (Marcucci 1996). The expression is:

$${\text{Root-mean-square}}\,{\text{standard}}\;{\text{deviation}}:{\left\{ {{{\mathop \sum \limits_{i} \mathop \sum \limits_{{x \in {C_i}}} x - {c_i}^{2}} \mathord{\left/ {\vphantom {{\mathop \sum \limits_{i} \mathop \sum \limits_{{x \in {C_i}}} x - {c_i}^{2}} {\left[ {P\mathop \sum \limits_{i} ({n_i} - 1)} \right]}}} \right. \kern-0pt} {\left[ {P\mathop \sum \limits_{i} ({n_i} - 1)} \right]}}} \right\}^{\frac{1}{2}}}.$$
(8)

In the above expressions, P is the attributes number of D (in this streamline clustering evaluation process, the value of P is 4, including centers X and Y, and oil/water phase velocities).

The SD index method is based on the concept of the average scattering and the total separation of the clusters. The concept of average scattering is based on variance clustering of an object to calculate the compactness, while the total separation is calculated according to the distance between different cluster centers. The value of SD index is the summation of these two terms. When the index reaches minimum, the corresponding cluster number is the best (Halkidi et al. 2000), and the expression is:

$${\text{SD}}\;{\text{index}}:{\text{Dis}}({\text{N}}{{\text{C}}_{\hbox{max} }}){\text{Scat}}({\text{NC}})+{\text{Dis}}({\text{NC}}),$$
(9)

where \({\text{Scat}}({\text{NC}})=\frac{1}{{{\text{NC}}}}\mathop \sum \limits_{i} \sigma ({C_i})/\sigma (D)\) and \({\text{Dis}}({\text{NC}})=\frac{{{{\hbox{max} }_{i,j}}d({c_i},{c_j})}}{{{{\hbox{min} }_{i,j}}d({c_i},{c_j})}}\mathop \sum \limits_{i} {\left( {\mathop \sum \limits_{j} d({c_i},{c_j})} \right)^{ - 1}}\).

In the above expressions, \(~\sigma ({C_i})\) is the variance vector of \({C_i}\); \(\sigma (D)\) is the variance vector of \(D\); \({\text{N}}{{\text{C}}_{\hbox{max} }}\) is the maximum clustering number.

The R-squared index is the ratio of the sum of squares between clusters to the total sum of squares of the whole data set. It is used to measure the degree of difference between clusters. When the index is the largest, the number of clusters corresponding to it is the best. Its expression is:

$${\text{R-squared}}\;{\text{index}}:\mathop \sum \limits_{{x \in D}} x - {c^2} - \mathop \sum \limits_{i} \mathop \sum \limits_{{x \in {c_i}}} x - {c_i}^{2}/\mathop \sum \limits_{{x \in D}} x - {c^2}.$$
(10)

The basic idea of the S_Dbw coefficient is that there is at least one point in all cluster centers whose density is larger than the density of their midpoint. Then, the SD algorithm is used to determine the clustering effect (Halkidi et al. 2000). When the S_Dbw coefficient is the smallest, the number of clusters corresponding to it is the best. The expression of the S_Dbw coefficient is:Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

$${\text{S}}\_{\text{Dbw}}\;{\text{coefficient}}:{\text{Scat}}({\text{NC}})+{\text{Dens}}\_{\text{bw}}({\text{NC}}),$$
(11)

where \({\text{Dens}}\_{\text{bw}}({\text{NC}})=\frac{1}{{{\text{NC}}(1 - {\text{NC}})}}\mathop \sum \nolimits_{i} \left[ {\mathop \sum \limits_{{j,j \ne i}} \frac{{\mathop \sum \nolimits_{{x \in {C_i}\mathop \cup \nolimits^{} {C_j}}} d(x,{u_{i,j}})}}{{{\text{max}}\left\{ {\mathop \sum \nolimits_{{x \in {C_i}}} d\left( {x,{c_i}} \right),\mathop \sum \nolimits_{{x \in {C_j}}} d(x,{c_j})} \right\}}}} \right].\)

Maulik defined I index in 2002 to determine the best number of clusters. It represents the degree of separation by the maximum distance between cluster centers; when I index reaches the minimum, the number of clusters corresponding to it is the best (Maulik and Bandyopadhyay 2002). The expression is as follows:

$${\text{I}}\;{\text{index}}:{\left( {\frac{1}{{{\text{NC}}}} \cdot \frac{{\mathop \sum \nolimits_{{x \in D}} d(x,c)}}{{\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{{x \in {C_i}}} d(x,{c_i})}} \cdot {\text{ma}}{{\text{x}}_{i,j}}d({c_i},{c_j})} \right)^P}.$$
(12)

In the high water cut stage, the distribution of streamline field is complex, and the data are greatly influenced by streamline density. Different clustering validation algorithms may lead to differences in prediction accuracy.

The peak density algorithm was applied to two-dimensional data sets as shown in Figs. 2, 3, 4, 5, 6, 7 and 8; clusters were formed respectively. The effectiveness of different clustering groups was evaluated by the above clustering validation method. As we can see, judging by the naked eye, the data set can be roughly divided into three clusters, and the density of each cluster is different, which will also result in different verifying results from different verification methods. Through the above verification method, the clustering effects of different cluster numbers were evaluated as shown in Table 1. The data in bold font in each line were the best number of clusters for each verification method. We can see that the various verification methods are different in determining the optimal number of clusters. The conclusions obtained by several validation methods are inaccurate. The verification methods that can get the correct conclusions are Calinski–Harabasz index, Dunn index, contour coefficient, SD index and S_Dbw coefficient. The S_Dbw coefficient considers the density factor of the data set as the evaluation criterion of the clustering separation degree, and the evaluation is accurate. Therefore, the S_Dbw coefficient was used as the criterion to evaluate the number of clusters in the streamline field.

Fig. 2
figure 2

2-D sample data set

Full size image
Table 1 Comparison of clustering effect verification methods under different numbers of clusters
Full size table

The procedure of applying artificial intelligence algorithm to analyze the streamline field

The current commercial numerical simulation software can only determine the streamline field intensity of the reservoir by the density of the streamlines in the various regions, and the corresponding oil–water saturation attribute and flow velocity attribute on the streamline cannot be classified; these can all lead to the failure to evaluate the streamline field quantitatively. Making full use of the spatial position of each streamline coordinate point and its corresponding oil and water attribute parameters, we used the peak density algorithm to classify the rank of the streamline cluster and determined the optimal number of clusters by the S_Dbw coefficient. The basic process is shown in Fig. 3. Based on the peak density algorithm and the S_Dbw coefficient evaluation method, the reservoir streamline field evaluation software was developed. The Petrel_RE-based streamline field evaluation plug-in was formed. The software can effectively access the software of the commercial reservoir numerical simulation and provide technical support for the analysis of the streamline field of the reservoir by the peak density clustering algorithm. Here we described the following key steps in the whole evaluation process.

Fig. 3
figure 3

Application of the peak density clustering algorithm to evaluate the streamline field

Full size image

Data optimization and extraction of reservoir streamline field

The extraction of streamline data is mainly to obtain the spatial coordinates of the streamline data and their corresponding attribute data, thus applying these data to the cluster analysis. Because the commercial numerical simulation software cannot directly derive the relevant parameters of the streamline, this study has developed the relevant software through the ocean platform of the Schlumberger Company. The X and Y spatial coordinates and corresponding water phase flow velocity and oil phase flow velocity data were extracted from the target block streamlines. The spatial coordinate data were to reflect streamline clusters with similar positions in space, and the water phase and oil phase flow velocities were to ensure that the streamline clusters obtained by clustering not only had similar positions, but also had similar flow capacity.

Standardization of the streamline data

Because all kinds of streamline attributes have different data ranges, if they are not standardized, the weight of some attributes will be reduced or increased, which will affect the clustering results. After standardization of streamline coordinates and attributes, the distribution of various parameters can be reflected reasonably. In this study, the location of the X and Y coordinates at the middle point, the oil phase flow velocity and the water phase flow velocity of one single streamline were obtained, and the standard deviation was used to standardize the data. The method of obtaining each parameter is shown as follows:

X coordinates of the middle point position of the streamline:

$$~{X_a}=\mathop \sum \limits_{1}^{{{n_a}}} {x_i}/{n_a}.$$
(13)

Y coordinates of the middle point position of the streamline:

$${Y_a}=\mathop \sum \limits_{1}^{{{n_a}}} {y_i}/{n_a}.$$
(14)

Average water phase flow velocity on a streamline:

$${V_o}=\mathop \sum \limits_{1}^{{{n_a}}} {v_{oi}}/{n_a}.$$
(15)

Average oil phase flow velocity on a streamline:

$${V_w}=\mathop \sum \limits_{1}^{{{n_a}}} {v_{wi}}/{n_a}.$$
(16)

In all the above expressions, \({X_a}\) is the X-axis coordinates of the middle point position of a single streamline. \(~{x_i}\) is the x coordinates of a single coordinate point on a streamline. \(~{n_a}\) is the total number of data points on a single streamline. \({Y_a}\) is the Y-axis coordinates of the middle point position of a single streamline. \(~{y_i}\) is the y coordinates of a single coordinate point on a streamline.\({\text{~}}{V_o}\) is the average oil phase velocity of a single streamline. \(~{v_{oi}}\) is the oil phase velocity of a single coordinate point on a streamline. \({\text{~}}{V_w}\) is the average water phase velocity of a single streamline.\(~{v_{wi}}\) is the water phase velocity of a single coordinate point on a streamline.

Cluster evaluation of reservoir streamline field

We can evaluate the spatial coordinates and the oil–water flow ratio of the streamline field through the peak density algorithm mentioned in “The establishment of the peak density algorithm model”. The optimal streamline clustering number is determined by the S_Dbw coefficient mentioned in “Determination of evaluation index for clustering effect”. On the basis of characteristic analysis of clustering results, the reservoir streamline gradational evaluation map is formed. The core content of this study is how to extract the effective information of the streamline field and form the best method of clustering and evaluation.

Example application

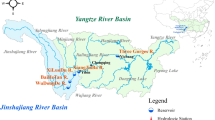
The Gang Dong oil field, as shown in Fig. 4, is located in the middle part of the Huang Hua depression. Its main oil-bearing formations are Minghua formation and Guantao formation. The average permeability is 800 \(\times\) 10− 3 μm2, which corresponds to a typical medium high-permeability reservoir. To date, the comprehensive water cut has reached 95.68%, and the recovery degree has reached 43.18%. At present, there are serious problems such as invalid reservoir water circulation and difficulty in subsequent development. The distribution of streamline field is complex, and it is hard to improve oil recovery. In this paper, the applicability of the gradational optimization of the streamline field was discussed through the example of the Nm3-4-1 layer of the Gang Dong oil field.

Fig. 4
figure 4

Location map of study area in Gang dong oil field, China

Full size image

Analysis of the distribution of the streamline field in the Nm3-4-1 layer

According to the streamline field corresponding to the oil saturation property of Fig. 5, it can be seen that the overall oil saturation of the Nm3-4-1 layer is close to the residual oil saturation. Only the edge of the reservoir has some areas with high oil saturation. For such low-potential reservoirs with high water cut, an important reason for the difficulty of tapping is that the distribution of the streamline field is complex and unclear. Therefore, it is necessary to apply the method of peak density clustering to optimize the streamline field of the reservoir.

Fig. 5
figure 5

Streamline distribution of the Nm3-4-1 layer in the Gang Dong oil field

Full size image

Extraction and evaluation of the reservoir streamline field

Extracting the spatial coordinates, and the oil and water flow ratio of each position point in the Nm3-4-1 layer of the Gang Dong oil field as the parameters of the cluster analysis, after standardization, the parameters were evaluated by the peak density clustering method, and 4–20 groups of streamline cluster number were formed. The S_Dbw coefficient was used to evaluate the clustering effect of different streamline cluster number, as shown in Fig. 6. With the increase of the streamline cluster number, the S_Dbw coefficient first decreased, indicating that the effect of clustering was gradually changed. When the number of cluster was 14, the S_Dbw coefficient was the smallest, and its value was 0.04, then the S_Dbw coefficient began to increase. So the best number of streamline cluster was 14 and we chose to divide the current streamline field of the Nm3-4-1 layer into 14 sets of streamline cluster.

Fig. 6
figure 6

Re between cluster number of streamline cluster and S_Dbw coefficient

Full size image

Analysis of clustering characteristics of the streamline field

The Nm3-4-1 layer streamline field was divided into 14 types using the peak density clustering algorithm, as shown in Fig. 7. Different classifications represent the rank of streamline clusters, of which the first type of streamline clusters indicates that the oil–water flow ratio of the group is the largest and the development potential is the maximum. In contrast, the 14th class of streamline clusters represents the minimum oil–water flow ratio and the least development potential. Sorting the different streamline cluster regions, the smallest oil–water flow ratio area is distributed between Lq7-8 and Lq8-8 wells. In contrast, the largest oil–water flow ratio area is located near the northern Lq2-15 well area. The grade of streamline in the middle of the oil reservoir is obviously higher than the streamline at the edge of the reservoir.

Fig. 7
figure 7

Gradational evaluation of Nm3-4-1 layer streamline field in the Gang Dong oil field

Full size image

Comparison of the different types of streamline attributes in the 14 clusters is shown in Table 2. In the first types of streamline clusters, the average oil saturation, the flow rate of oil phase fluid, and the oil–water flow ratio are much higher than that of the 14th type of streamline cluster. The above parameters decrease with the increase of streamline classification. The average water saturation and the flow rate of water phase fluid in different streamline clusters increase with the increase of streamline classification. We can accurately determine the optimal number of streamline clusters using the S_Dbw coefficient. Meanwhile, the streamline field evaluation by the peak density clustering algorithm can well reflect the current development status of the reservoir.

Table 2 Streamline attribute statistics with different levels
Full size table

When a medium–high-permeability reservoir reaches the high water cut stage, the potential of residual oil in the layer is small, but this does not mean that there is no potential in the target layer. Through the evaluation of the streamline field, we can get the fluid flow path at the current time. At the same time, based on the streamline attribute clustering method, we can classify the streamlines on different flow trajectories, which can reflect the current flow state of the reservoir and determine the potential of different regions. All these provide the basis for the adjustment of the streamline field in the high water cut period.

Optimization of the reservoir streamline field

According to the current streamline field distribution of the Nm3-4-1 layer, the streamline field was adjusted to weaken the flow intensity between Lq7-8 and Lq8-8 wells, and enhance the flow intensity in the Lq2-15 well area. The other areas were adjusted according to the level of different streamline clusters. We varied the production and injection rates in each well and the equilibrium displacement was achieved according to the classification of the streamline field. The streamline field distribution of the adjustment scheme was predicted after 10 years, and the cluster evaluation and effectiveness verification were carried out again. The new streamline field was formed as shown in Fig. 8. After adjustment, the optimal clustering number for the streamline field was seven groups. Compared with 14 groups of streamline clusters before adjustment, the reduction of the number of new streamline clusters after adjustment meant that the internal differences of the whole streamline field were weakened after the new cluster evaluation and effect verification, and the displacement energy in each region was more balanced. By comparing the development indicators before and after adjustment in Table 3, the variation coefficient of oil–water mobility ratio was reduced by 0.33, the water cut was reduced by 3.8%, the cumulative oil production was increased by 95,000 tons, the remaining oil saturation changed from 0.42 before adjustment to 0.35 after adjustment, and the development effect was improved significantly.

Fig. 8
figure 8

Gang Dong oilfield Nm3-4-1 layer streamline field gradational evaluation after adjustment

Full size image
Table 3 Comparison of parameters before and after adjustment of the Nm3-4-1 layer streamline field
Full size table

Conclusions

We used the peak density clustering algorithm to classify the streamline field and determined the best streamline cluster number by the S_Dbw coefficient. These methods take full account of the internal attributes of streamline data, reduce the human factors of qualitative evaluation of reservoir streamline field and determine the direction for remaining oil potential in the high water cut stage. The new streamline field grading method classifies the displacement energy according to the streamline spatial coordinates and the oil and water flow ratio, and clearly indicates the distribution position of the weak drive streamline and the strong drive streamline, making the streamline numerical simulation not only relying on the streamline density to determine the flow intensity qualitatively, but can reach the quantitative evaluation. The Nm3-4-1 layer of the Gang Dong oilfield is in the late stage of high water cut development. The distribution of the streamline field is complex. By adjusting the streamline field in time, the flow strength between Lq7-8 and Lq8-8 wells is decreased. The streamline field distribution is more uniform, and the development effect is improved.