Introduction

The transport of fluid (liquid, gas and their mixture) in porous medium is so called percolation or seepage. Study on the characteristics of porous flow and fluid mechanics is of vital significance in oil and gas field development. We have surveyed a lot of literatures aiming at the stress sensitivity of porous media, which is generated from the effective stress of rock skeleton increasing and the pore pressure decreasing.

In tight rocks, the existence of stress sensitivity is widely confirmed. Numerous efforts have been made to investigate the stress-sensitivity mechanism via laboratory experiments or physical modeling (Dormieux et al. 2011; Zhao et al. 2013; Liu et al. 2015; Tian et al. 2015). Wang et al. (2015) established the relationship between overburden pressure and effective stress considering stress arching effect in Sulige gas field and proved that the stress sensitivity of permeability greatly depends on stress arching ratio. Tan et al. (2015a, b) developed the predictive models for permeability of porous media considering stress sensitivity based on the fractal theory and mechanics of materials. Xiao et al. (2016) proposed a stress-sensitivity evaluation standard considering experiment data and rock micro-structural features, on the basis of analysis of the empirical models and theoretical models on the relationships between permeability and effective stress. Through the conventional measurement of the core plug samples from carbonate formation, Hamid et al. (2016) developed a relationship between permeability, porosity, velocity and effective horizontal stress for carbonate reservoirs using both core and field data. Luo et al. (2017) proposed a model using microseismic data to calculate fracturing network parameters for tight oil reservoirs. Xu et al. (2018) carried out an experimental study on porosity and permeability stress-sensitive behavior of sandstone, including characteristics, mechanisms and controlling factors.

Pressure transient analysis considering specific factors (such as stress sensitivity) is always a hot and difficult problem in the field of seepage theory (Guo et al. 2015a, b; Zhao et al. 2014; Zhang et al. 2017; Abbas et al. 2017). For the pressure transient analysis of tight rocks related to the stress-sensitive permeability, some scholars chose an exponential model in their mathematical derivation. Zhang et al. (2011) presented a well test model for stress-sensitive composite dual-porosity reservoirs based on the concept of permeability modulus, which is the key parameter in permeability exponential model. Yao et al. (2013) presented a semi-analytical model to facilitate transient pressure analysis with stress-dependent hydraulic fracture conductivities for both hydraulically fractured vertical wells and multi-stage fractured horizontal wells. They pointed out the effect of stress-sensitive conductivities on transient pressure behavior results in a hump on the pressure derivative curves. Qanbari and Clarkson (2014) provided a new method for analysis of transient linear flow in stress-sensitive tight oil reservoirs, in which a correction factor is taken into account. The results indicated that the correction factor becomes more important for higher values of permeability modulus and pressure drawdown. Dou et al. (2015) introduced a new procedure to quantify the permeability stress sensitivity by applying the traditional straight-line analysis method. They determined the permeability modulus and the formation parameters based on the corrected pseudo-parameters and the concept of cut-and-trial. Guo et al. (2015a, b) presented the pressure transient analysis (PTA) and rate decline analysis (RDA) on the hydraulic fractured vertical wells with finite conductivity in shale gas reservoirs considering multiple flow mechanisms. Bahrami et al. (2015) proposed a practical methodology and workflow for characterizing the SRV parameters in multi-fractured wells in unconventional oil and gas reservoirs using well test and rate transient data analysis based on diffusivity equation solution for linear and elliptical flow regimes integrated with numerical reservoir simulation. Lei et al. (2016) proposed a comprehensive hybrid grid model and performance analysis workflow to study the impact of reservoir and hydraulic fracturing parameters on production performance of tight oil reservoir. Yao et al. (2016) developed a semi-analytical composite model for multi-stage fractured horizontal wells (MFHWs) in heterogeneous reservoirs. The model was better prepared for not only incorporating pressure-dependent heterogeneous reservoir properties, but also investigating the different production behavior at different fracture stages in complex heterogeneous reservoirs. Huang et al. (2018) also established a new analytical model based on the permeability exponential model in tight oil reservoirs for pressure transient analysis.

To sum up, many researches on the pressure transient analysis have been performed, while the rate transient analysis about reservoirs with stress-sensitive property is rarely discussed, which acts as the motivation of this work. This study develops a seepage model of multi-fractured horizontal well incorporating stress-sensitive permeability based on source/sink function method. The model is semi-analytically solved by fracture discretization, Pedrosa’s transformation, perturbation theory, and integration transformation method. Not only pressure transient analysis, but also rate transient analysis is separately performed with relevant parameters. The model presented here can provide some insights into well dynamic forecasting during exploiting such reservoirs.

Line-sink model considering stress sensitivity

Due to the difficulty of describing the multiple fractures inner boundary condition with a direct mathematical formula, the model of a continuous line-sink in stress-sensitive porous medium is first addressed here. The system of units and symbols adopted in this paper is listed in nomenclature for the convenience of comprehending the coefficients in the formulas.

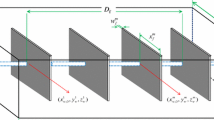
Figure 1 illustrates the physical model of a continuous line-sink throughout the top and bottom boundaries. The mass conservation equation for single-phase fluid is written as

Fig. 1
figure 1

A line-sink of natural gas in stress-sensitive porous medium

Full size image
$$\nabla \cdot \left( {\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} } \right)+\frac{{\partial \left( {\rho \phi } \right)}}{{\partial t}}=0.$$
(1)

Like a vertical well, gas only flows along the radial r direction from the porous medium into the line-sink. Therefore, the equation of motion is expressed by

$$\vec {v}={v_{\text{r}}}\vec {r}= - \;3.6\frac{K}{\mu }\frac{{\partial p}}{{\partial r}}.$$
(2)

Considering the permeability is affected by the stress sensitivity of the porous medium, which is resulted from the decreasing of pore pressure and the increasing of effective stress during the production process, the permeability modulus \(\gamma\) is introduced by

$$\gamma =\frac{1}{K}\frac{{{\text{d}}K}}{{{\text{d}}p}}.$$
(3)

Solving Eq. (3), we obtain:

$$K={K_{\text{i}}}{{\text{e}}^{ - \gamma ({p_{\text{i}}} - p)}}.$$
(4)

Substituting (4) into (2) yields the equation of motion:

$${v_{\text{r}}}= - \;3.6\frac{{{K_{\text{i}}}}}{\mu }{{\text{e}}^{ - \gamma ({p_{\text{i}}} - p)}}\frac{{\partial p}}{{\partial r}}.$$
(5)

The rock-state equation:

$$\phi ={\phi _0}[1+{C_\phi }(p - {p_0})].$$
(6)

The gas-state equation:

$$\rho ={\rho _0}[1+{C_\rho }(p - {p_0})],$$
(7)
$$\rho =\frac{{Mp}}{{RTZ}}.$$
(8)

Substituting Eqs. (5)–(8) into Eq. (1) yields the governing equation that accounts for the stress sensitivity:

$$\frac{{{K_{\text{i}}}}}{r}\frac{\partial }{{\partial r}}\left[ {r\frac{p}{{\mu Z}}{{\text{e}}^{ - \gamma ({p_{\text{i}}} - p)}}\frac{{\partial p}}{{\partial r}}} \right]=\frac{{\phi \mu {C_{\text{t}}}}}{{3.6}}\frac{p}{{\mu Z}}\frac{{\partial p}}{{\partial t}},$$
(9)

where the total compressibility coefficient \({C_t}={C_\rho }+{C_\phi }\), MPa−1.

Define the pseudo pressure and pseudo permeability modulus as the following expressions:

$$m(p)=\int_{{{p_0}}}^{p} {\frac{{2p}}{{\mu Z}}{\text{d}}p} ,$$
(10)
$$K={K_{\text{i}}}{{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}},$$
(11)

where p0 is the reference pressure and can be variable, and γm is introduced according to the pseudo pressure. Therefore:

$$\frac{{\partial m}}{{\partial r}}=\frac{{2p}}{{\mu Z}}\frac{{\partial p}}{{\partial r}},$$
(12)
$$\frac{{\partial m}}{{\partial t}}=\frac{{2p}}{{\mu Z}}\frac{{\partial p}}{{\partial t}}.$$
(13)

Combining Eqs. (11)–(13) into Eq. (9) and multiplying both sides by \(\frac{2}{{{K_{\text{i}}}}}\), we obtain:

$$\frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}}\frac{{\partial m}}{{\partial r}}} \right]=\frac{{\phi \mu {C_{\text{t}}}}}{{3.6{K_{\text{i}}}}}\frac{{\partial m}}{{\partial t}}.$$
(14)

The left-hand term of Eq. (14) can be written as

$$\begin{aligned} & \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{\text{e}}^{ - {\gamma _m}({m_{\text{i}}} - m)}}\frac{{\partial m}}{{\partial r}}} \right] \\ & \quad =\frac{1}{r}\left[ {{{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}}\frac{{\partial m}}{{\partial r}}+r{{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}}{\gamma _{\text{m}}}\left( {\frac{{\partial m}}{{\partial r}}} \right)+r{{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}}\frac{{{\partial ^2}m}}{{\partial {r^2}}}} \right] \\ & \quad ={{\text{e}}^{ - {\gamma _{\text{m}}}({m_{\text{i}}} - m)}}\left[ {\frac{{{\partial ^2}m}}{{\partial r2}}+\frac{1}{r}\frac{{\partial m}}{{\partial r}}+{\gamma _{\text{m}}}{{\left( {\frac{{\partial m}}{{\partial r}}} \right)}^2}} \right]. \\ \end{aligned}$$
(15)

Therefore, Eq. (14) is rewritten as

$$\frac{{{\partial ^2}m}}{{\partial {r^2}}}+\frac{1}{r}\frac{{\partial m}}{{\partial r}}+{\gamma _{\text{m}}}{\left( {\frac{{\partial m}}{{\partial r}}} \right)^2}={{\text{e}}^{{\gamma _{\text{m}}}({m_{\text{i}}} - m)}}\frac{{\phi \mu {C_{\text{t}}}}}{{3.6{K_{\text{i}}}}}\frac{{\partial m}}{{\partial t}}.$$
(16)

Based on the dimensionless definitions listed in Table 1, the dimensionless governing flow equation, converted from Eq. (16), can be obtained as

Table 1 Definitions of the dimensionless variables
Full size table
$$\frac{{{\partial ^2}{m_{\text{D}}}}}{{\partial r_{{\text{D}}}^{2}}}+\frac{1}{{{r_{\text{D}}}}}\frac{{\partial {m_{\text{D}}}}}{{\partial {r_{\text{D}}}}} - {\gamma _{{\text{mD}}}}{\left( {\frac{{\partial {m_{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)^2}={{\text{e}}^{{\gamma _{{\text{mD}}}}{m_{\text{D}}}}}\frac{{\partial {m_{\text{D}}}}}{{\partial {t_{\text{D}}}}}.$$
(17)

Initial condition:

$${m_{\text{D}}}\left| {_{{{t_{\text{D}}}=0}}} \right.=0.$$
(18)

Inner boundary condition:

$$\mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} \left( {{r_{\text{D}}}{{\text{e}}^{ - {\gamma _{{\text{mD}}}}{m_{\text{D}}}}}\frac{{\partial {m_{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)= - \;1.$$
(19)

Infinite lateral boundary condition:

$${m_{\text{D}}}\left| {_{{{r_{\text{D}}} \to \infty }}} \right.=0.$$
(20)

Equations (17)–(20) compose the mathematical model for a continuous link-sink in stress-sensitive porous medium.

According to Pedrosa (1986), introduce the variable substitution to alleviate the nonlinearity of Eqs. (17) and (19):

$${m_{\text{D}}}\left( {{r_{\text{D}}},{t_{\text{D}}}} \right)= - \frac{1}{{{\gamma _{{\text{mD}}}}}}\ln \left[ {1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}\left( {{r_{\text{D}}},{t_{\text{D}}}} \right)} \right],$$
(21)

where \({\eta _{\text{D}}}\left( {{r_{\text{D}}},{t_{\text{D}}}} \right)\) is an intermediate variable which is also called the perturbation deformation function.

The following formulas can be derived from Eq. (21):

$$\left\{ \begin{gathered} {{\text{e}}^{ - {m_{\text{D}}}{\gamma _{{\text{mD}}}}}}=1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}} \hfill \\ \frac{{\partial {m_{\text{D}}}}}{{\partial {r_{\text{D}}}}}=\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}\frac{{\partial {\eta _{\text{D}}}}}{{\partial {r_{\text{D}}}}} \hfill \\ \frac{{{\partial ^2}{m_{\text{D}}}}}{{\partial {r_{\text{D}}}^{2}}}=\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}\frac{{{\partial ^2}{\eta _{\text{D}}}}}{{\partial {r_{\text{D}}}^{2}}}+\frac{{{\gamma _{{\text{mD}}}}}}{{{{\left( {1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}} \right)}^2}}}{\left( {\frac{{\partial {\eta _{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)^2} \hfill \\ \frac{{\partial {m_{\text{D}}}}}{{\partial {t_{\text{D}}}}}=\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}\frac{{\partial {\eta _{\text{D}}}}}{{\partial {t_{\text{D}}}}} \hfill \\ \end{gathered} \right..$$
(22)

Substituting (21) and (22) into the model (17)–(20) yields:

$$\left\{ \begin{gathered} \frac{1}{{{r_{\text{D}}}}}\frac{\partial }{{\partial {r_{\text{D}}}}}\left( {{r_{\text{D}}}\frac{{\partial {\eta _{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)=\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}\frac{{\partial {\eta _{\text{D}}}}}{{\partial {t_{\text{D}}}}} \hfill \\ {\eta _{\text{D}}}\left| {_{{{t_{\text{D}}}=0}}} \right.=0 \hfill \\ \mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} \left( {{r_{\text{D}}}\frac{{\partial {\eta _{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)= - 1 \hfill \\ {\eta _{\text{D}}}\left| {_{{{r_{\text{D}}} \to \infty }}} \right.=0 \hfill \\ \end{gathered} \right..$$
(23)

According to the regular perturbation theory, the terms \({\eta _{\text{D}}}\), \(\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}\), and \(- \frac{1}{{{\gamma _{{\text{mD}}}}}}\ln \left( {1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}} \right)\) in (23) can be expanded as power series in dimensionless permeability modulus, which are:

$${\eta _{\text{D}}}={\eta _{{\text{D0}}}}+{\gamma _{{\text{mD}}}}{\eta _{{\text{D1}}}}+\gamma _{{{\text{mD}}}}^{2}{\eta _{{\text{D2}}}}+ \cdots ,$$
(24)
$$\frac{1}{{1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}}}=1+{\gamma _{{\text{mD}}}}{\eta _{\text{D}}}+{\gamma _{{\text{mD}}}}^{2}{\eta _{\text{D}}}^{2}+ \cdots ,$$
(25)
$$- \frac{1}{{{\gamma _{{\text{mD}}}}}}\ln \left( {1 - {\gamma _{{\text{mD}}}}{\eta _{\text{D}}}} \right)={\eta _{\text{D}}}+\frac{1}{2}{\gamma _{{\text{mD}}}}{\eta _{\text{D}}}^{2}+ \cdots$$
(26)

The zero-order approximate solution can meet the requirements of engineering precision because the dimensionless permeability modulus is usually small (\({\gamma _{{\text{mD}}}} \ll 1\)), so the model (23) becomes:

$$\left\{ \begin{gathered} \frac{1}{{{r_{\text{D}}}}}\frac{\partial }{{\partial {r_{\text{D}}}}}\left( {{r_{\text{D}}}\frac{{\partial {\eta _{{\text{D0}}}}}}{{\partial {r_{\text{D}}}}}} \right)=\frac{{\partial {\eta _{{\text{D0}}}}}}{{\partial {t_{\text{D}}}}} \hfill \\ {\eta _{{\text{D0}}}}\left| {_{{{t_{\text{D}}}=0}}} \right.=0 \hfill \\ \mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} \left( {{r_{\text{D}}}\frac{{\partial {\eta _{{\text{D0}}}}}}{{\partial {r_{\text{D}}}}}} \right)= - 1 \hfill \\ {\eta _{{\text{D0}}}}\left| {_{{{r_{\text{D}}} \to \infty }}} \right.=0 \hfill \\ \end{gathered} \right..$$
(27)

Equation (27) is the linearized line-sink model in stress-sensitive porous medium.

Applying Laplace transformation, the model (27) becomes:

$$\left\{ \begin{gathered} \frac{1}{{{r_{\text{D}}}}}\frac{\partial }{{\partial {r_{\text{D}}}}}\left( {{r_{\text{D}}}\frac{{\partial {{\bar {\eta }}_{{\text{D0}}}}}}{{\partial {r_{\text{D}}}}}} \right)=s{{\bar {\eta }}_{{\text{D0}}}} \hfill \\ \mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} \left( {{r_{\text{D}}}\frac{{\partial {{\bar {\eta }}_{{\text{D0}}}}}}{{\partial {r_{\text{D}}}}}} \right)= - \frac{1}{s} \hfill \\ \hfill \\ {{\bar {\eta }}_{{\text{D0}}}}\left| {_{{{r_{\text{D}}} \to \infty }}} \right.=0 \hfill \\ \end{gathered} \right.,$$
(28)

where s is the Laplace transformation variable.

The general solution of (28) can be easily obtained as follows:

$${\bar {\eta }_{{\text{D0}}}}=A{I_0}\left( {{r_{\text{D}}}\sqrt s } \right)+B{K_0}\left( {{r_{\text{D}}}\sqrt s } \right),$$
(29)

where I0 is the first kind of zero-order-modified Bessel function, K0 is the second kind of zero-order-modified Bessel function, and A and B are constants.

Substitution of Eq. (29) into the inner boundary condition yields:

$$\mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} {r_{\text{D}}}\frac{{\partial {{\bar {\eta }}_{{\text{D0}}}}}}{{\partial {r_{\text{D}}}}}=\mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} {r_{\text{D}}}\sqrt s \left[ {A{I_1}\left( {{r_{\text{D}}}\sqrt s } \right) - B{K_1}\left( {{r_{\text{D}}}\sqrt s } \right)} \right]= - \frac{1}{s}.$$
(30)

According to the properties of Bessel’s function, which are \({\lim _{x \to 0}}x{I_1}(x) \to 0\), and \({\lim _{x \to 0}}x{K_1}(x) \to 1\), Eq. (28) becomes:

$$B=\frac{1}{s}.$$
(31)

Likewise, with the outer boundary condition given in (28) and the properties of Bessel’s function, \({\lim _{x \to \infty }}{I_0}(x) \to \infty\) and \({\lim _{x \to \infty }}{K_0}(x) \to 0\), and the coefficient in (29), A, should satisfy the following equation:

$$A=0.$$
(32)

With (31) and (32), we can get the final form of (29) as follows:

$${\bar {\eta }_{{\text{D0}}}}=\frac{1}{s}{K_0}\left( {{r_{\text{D}}}\sqrt s } \right).$$
(33)

As mentioned above, zero-order perturbation solution is enough to approximate the exact solution of Eq. (23), that is:

$${\bar {\eta }_{\text{D}}} \approx {\bar {\eta }_{{\text{D0}}}}=\frac{1}{s}{K_0}\left( {{r_{\text{D}}}\sqrt s } \right),$$
(34)

where \(r_{{\text{D}}}^{2}={\left( {{x_{\text{D}}} - {x_{{\text{wD}}}}} \right)^2}+{\left( {{y_{\text{D}}} - {y_{{\text{wD}}}}} \right)^2}\).

Equation (44) is the basic line-sink solution in Laplace domain for stress-sensitive porous medium. Employing the superposition principle, the pressure response of a multi-fractured horizontal well will be derived in the next section.

Model illustration and solution for multi-fractured horizontal well

Physical model

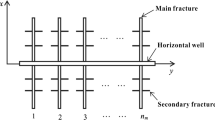
Given that a horizontal well with multiple hydraulic fractures is producing in stress-sensitive porous medium at a constant surface flow rate qsc (see Fig. 2), such assumptions of physical model are outlined as follows:

Fig. 2
figure 2

Schematic of a multi-fractured horizontal well

Full size image
  1. 1.

    The thickness of the formation is h, the lateral boundary is infinite, and the top and bottom boundaries are assumed to be penetrated completely by each fracture (a total of M). The initial permeability of porous medium is Ki under the initial formation pressure pi.

  2. 2.

    The horizontal wellbore is parallel to the top and bottom boundaries. Fractures are evenly spaced. At each fracture, the height is h, the width is neglected, and the half-length is Xf.

  3. 3.

    Gas flow obeys Darcy rule, while the permeability is considered stress sensitive to the impact of effective stress increasing and pore pressure decreasing during production.

  4. 4.

    Both the horizontal wellbore and the fractures have infinite conductivity. Each fracture has the different flow rate.

  5. 5.

    Consider single-phase isothermal flow and negligible gravity and capillary effects.

Pressure solution of producing at a constant production rate

Based the basic line-sink solution, we applied the fracture discretization and superposition principle to obtain the solution for a multi-fractured horizontal well.

Figure 3 shows the top view of the multi-fractured horizontal well and described the fracture discrete segments. The coordinate origin is set to the turning point of horizontal well. M fractures are evenly distributed along the y-axis (horizontal wellbore) with the spacing of Δy. The cross point of the ith (i = 1, 2,…, M) fracture and the y-axis is represented by (0, yi). Along the x-axis direction, each fracture is divided into 2N segments, which will generate a total of 2N midpoints and 2N + 1 endpoints. For jth segment on the ith fracture (j = 1, 2,…,2N), the midpoint is denoted by (Xi,j, Yi,j) and the corresponding endpoints are (xi,j, yi,j) and (xi,j+1, yi,j+1).

Fig. 3
figure 3

Description of fracture discrete segments

Full size image

The flow rate of each fracture is different and the flux strength is also different along the fracture length. Nevertheless, for the single discrete segment (i, j), the flux strength is considered as constant, and the flux density per unit length is represented by \({\tilde {q}_{i,j}}\). Therefore, the dimensionless pressure response at any point of porous medium (x, y), caused by the segment (i, j), can be calculated by integrating the basic line-sink along the segment length:

$${\bar {\eta }_{{\text{D}}i,j}}\left( {{x_{\text{D}}},{y_{\text{D}}}} \right)={\bar {q}_{{\text{D}}i,j}}\int_{{{x_{{\text{D}}i,j}}}}^{{{x_{{\text{D}}i,j+1}}}} {{K_0}\left( {\sqrt s \sqrt {{{\left( {x{}_{{\text{D}}} - x{}_{{{\text{wD}}}}} \right)}^2}+{{\left( {y{}_{{\text{D}}} - y{}_{{{\text{wD}}}}} \right)}^2}} } \right){\text{d}}{x_{{\text{wD}}}}} ,$$
(35)

where \({y_{{\text{wD}}}}={y_{{\text{D}}i}}\), \({x_{{\text{D}}i,j}}=\frac{{{x_{i,j}}}}{{{X_{\text{f}}}}}\), \({y_{{\text{D}}i,j}}=\frac{{{y_{i,j}}}}{{{X_{\text{f}}}}}\), and \({q_{{\text{D}}i,j}}=\frac{{{{\tilde {q}}_{{\text{D}}i,j}}{X_{\text{f}}}}}{{{q_{{\text{sc}}}}}}\).

Applying the superposition principle over all discrete fracture segments, the dimensionless pressure response at (x, y) caused by a total of (M × 2N) discrete segments can be written as

$${\bar {\eta }_{\text{D}}}\left( {{x_{\text{D}}},{y_{\text{D}}}} \right)=\sum\limits_{{i=1}}^{M} {\sum\limits_{{j=1}}^{{2N}} {{{\bar {\eta }}_{{\text{D}}i,j}}\left( {{x_{\text{D}}},{y_{\text{D}}}} \right)} } .$$
(36)

Set the point (x, y) to the midpoint of the segment (k, v), i.e. (Xk,v,Yk,v), Eq. (36) is changed into:

$${\bar {\eta }_{\text{D}}}\left( {{X_{{\text{D}}k,v}},{Y_{{\text{D}}k,v}}} \right)=\sum\limits_{{i=1}}^{M} {\sum\limits_{{j=1}}^{{2N}} {{{\bar {\eta }}_{{\text{D}}i,j}}\left( {{X_{{\text{D}}k,v}},{Y_{{\text{D}}k,v}}} \right)} } .$$
(37)

Since the infinite conductive fractures and wellbore reveal that the pressure in hydraulic fractures is equal to the bottom-hole pressure, we have:

$${\bar {\eta }_{{\text{wDN}}}}=\sum\limits_{{i=1}}^{M} {\sum\limits_{{j=1}}^{{2N}} {{{\bar {\eta }}_{{\text{D}}i,j}}\left( {{X_{{\text{D}}k,v}},{Y_{{\text{D}}k,v}}} \right)} } .$$
(38)

Letting k = 1,2,…, M and v = 1,2,…, 2N, i.e. writing (38) for all discrete segments, we can get M × 2N equations, which are including (M × 2N + 1) unknowns. The flow constraint condition is given as follows:

$$\sum\limits_{{i=1}}^{M} {\sum\limits_{{j=1}}^{{2N}} {\left[ {\left( {{x_{{\text{D}}i,j+1}} - {x_{{\text{D}}i,j}}} \right) \cdot {q_{{\text{D}}i,j}}} \right]} } =1.$$
(39)

In the Laplace domain Eq. (39) is written as

$$\sum\limits_{{i=1}}^{M} {\sum\limits_{{j=1}}^{{2N}} {\left[ {\left( {{x_{{\text{D}}i,j+1}} - {x_{{\text{D}}i,j}}} \right) \cdot {{\bar {q}}_{{\text{D}}i,j}}} \right]} } =\frac{1}{s}.$$
(40)

There are (M × 2N + 1) equations when composing Eq. (38) at each segment together with Eq. (40), which can solve the (M × 2N + 1) unknowns of \({\bar {\eta }_{{\text{wDN}}}}\) and \({\bar {q}_{{\text{D}}i,j}}\)(i = 1,2,…, M; j = 1,2,…, 2N). The matrix expression is:

$$\left[ {\begin{array}{*{20}{c}} {{A_{1.1}}}& \cdots &{{A_{1,v}}}& \cdots &{{A_{1,2N}}}&{ - 1} \\ \vdots &{}& \vdots &{}&{ \vdots }& \vdots \\ {{A_{k,1}}}& \cdots &{{A_{k,v}}}& \cdots &{{A_{k,2N}}}&{ - 1} \\ \vdots &{}& \vdots &{}&{ \vdots }& \vdots \\ {{A_{M,1}}}& \cdots &{{A_{M,v}}}& \cdots &{{A_{M,2N}}}&{ - 1} \\ {\left( {{x_{{\text{D}}1,2}} - {x_{{\text{D}}1,1}}} \right)}& \cdots &{\left( {{x_{{\text{D}}k{\text{,v}}+{\text{1}}}} - {x_{{\text{D}}k,v}}} \right)}& \cdots &{\left( {{x_{{\text{D}}M,2N+1}} - {x_{{\text{D}}M,2N}}} \right)}&0 \end{array}} \right] \times \left[ \begin{gathered} {{\bar {q}}_{{\text{D}}1,1}} \hfill \\ \vdots \hfill \\ {{\bar {q}}_{{\text{D}}k,v}} \hfill \\ \vdots \hfill \\ {{\bar {q}}_{{\text{D}}M,2N}} \hfill \\ {{\bar {\eta }}_{{\text{wDN}}}} \hfill \\ \end{gathered} \right]=\left[ \begin{gathered} 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ 1/s \hfill \\ \end{gathered} \right].$$
(41)

Employing Duhamel’s theorem to incorporate wellbore storage coefficient and skin factor into well response, the pseudo pressure solution is:

$${\bar {\eta }_{{\text{wD}}}}=\frac{{s{{\bar {\eta }}_{{\text{wDN}}}}+S}}{{s+{C_{\text{D}}}{s^2}(s{{\bar {\eta }}_{{\text{wDN}}}}+S)}}.$$
(42)

\({\bar {\eta }_{{\text{wD}}}}\) in (42) is the bottom-hole pressure response in the Laplace domain, and by Stehfest numerical inversion algorithm we can calculate the pressure responses \({\eta _{{\text{wD}}}}({t_{\text{D}}})\) in real-time domain. Then, with (43), we can obtain the bottom-hole pressure response for the multi-fractured horizontal wells in stress-sensitive porous media:

$${m_{\text{D}}}= - \frac{1}{{{\gamma _{{\text{mD}}}}}}\ln \left( {1 - {\gamma _{{\text{mD}}}}{\eta _{{\text{wD}}}}} \right).$$
(43)

According to Stehfest (1970), the expression of the pressure response in the real domain is written as

$${m_{\text{D}}}= - \frac{1}{{{\gamma _{{\text{mD}}}}}}\ln \left[ {1 - \frac{{{\gamma _{{\text{mD}}}}\ln 2}}{{{t_{\text{D}}}}}\sum\limits_{{i=1}}^{N} {{V_i}} \frac{{{s_i}{{\bar {\eta }}_{{\text{wDN}}}}+S}}{{{s_i}+{C_{\text{D}}}s_{i}^{2}\left( {{s_i}{{\bar {\eta }}_{{\text{wDN}}}}+S} \right)}}} \right],$$
(44)

where N is an even number and \({s_i}=\frac{{\ln 2}}{{{t_{\text{D}}}}}i\). The weight coefficient \({V_i}\) is given by

$${{\text{V}}_{\text{i}}}={( - 1)^{\frac{{\text{N}}}{2}+{\text{i}}}}\sum\limits_{{{\text{k=}}\frac{{{\text{i+}}1}}{2}}}^{{\hbox{min} \left( {{\text{i}},\frac{{\text{N}}}{2}} \right)}} {\frac{{{{\text{k}}^{\frac{{\text{N}}}{2}}}(2{\text{k+}}1)!}}{{({\text{k}}+1)!{\text{k}}!(\frac{{\text{N}}}{2} - {\text{k+}}1)!({\text{i}} - {\text{k+}}1)!(2{\text{k}} - {\text{i+}}1)!}}} .$$
(45)

Equation (44) is the semi-analytical solution of transient pressure response for a multi-fractured horizontal well in stress-sensitive porous medium.

Production solution of producing at a constant bottom-hole pressure

The dimensionless flowrate equation for the constant-pressure production case can be determined by the relationship between the dimensionless pressure and the rate in the Laplace space (Van Everdingen and Hurst 1949):

$${\bar {q}_{\text{D}}}(s)=\frac{1}{{{s^2}{{\bar {m}}_{\text{D}}}(s)}}.$$
(46)

Therefore, taking Lapace transformation over the values of \({m_{\text{D}}}\) in Eq. (44) into \({\bar {m}_{\text{D}}}\), and substituting \({\bar {m}_{\text{D}}}\) into Eq. (46), we can determine the dimensionless production rate in the Laplace domain. Furthermore, the production rate in real space can be calculated by Stehfest numerical inversion and expressed as

$${q_{\text{D}}}=\frac{{\ln 2}}{{{t_{\text{D}}}}}\sum\limits_{{i=1}}^{N} {{V_i}} \frac{{ - {\gamma _{{\text{mD}}}}}}{{{s_i}\ln \left[ {1 - \frac{{{\gamma _{{\text{mD}}}}\ln 2}}{{{t_{\text{D}}}}}\sum\limits_{{i=1}}^{N} {{V_i}} \frac{{{s_i}{{\bar {\eta }}_{{\text{wDN}}}}+S}}{{{s_i}+{C_{\text{D}}}s_{i}^{2}\left( {{s_i}{{\bar {\eta }}_{{\text{wDN}}}}+S} \right)}}} \right].}}$$
(47)

Equation (47) is the semi-analytical solution of transient production rate for a multi-fractured horizontal well in stress-sensitive porous medium.

Results and analysis

As one of the applications of the above mathematical and mechanics derivation, the flow characteristic investigation of a multi-fractured horizontal well in stress-sensitive porous medium is performed in this section. We plotted the double-logarithmic type curves of transient pressure response and transient rate decline through the Matlab programming.

Pressure transient analysis of producing at a constant production rate

Figure 4 shows the transient pressure curves affected by different permeability modulus, which can be classified into six seepage stages as follows.

Fig. 4
figure 4

Effect of permeability modulus on transient pressure curves

Full size image

Stage 1, pure wellbore storage effect flow. Both pressure curve and derivative curve exhibit unit slope on the log–log plots. Stage 2, skin effect transition flow. The pressure derivative curve acts out like a “hump” representing the effect of skin. Stage 3, early linear flow perpendicular to hydraulic fractures. The pressure derivative curve manifests as an upward straight line with a slope of “1/2”. Stage 4, mid-time pseudo-radial flow around each fracture. The pressure derivative curve exerts a horizontal level with a value of “1/2M”, where M is the number of hydraulic fractures. Stage 5, linear flow of whole system perpendicular to horizontal wellbore. Another straight line with a slope of “1/2” can be observed in the derivative curve. Stage 6, late-time pseudo-radial flow of whole system. The pressure derivative curve behaves as a horizontal line with the value of “0.5” on the y-axis.

Permeability modulus γmD reflects the extent of the stress sensitive effect. From Fig. 4, we can see γmD starts to take effect from stage 2, i.e. the first period of gas flow in the underground formation. With the increase of the value of γmD, the derivative curves turn upward gradually and deviate from the 0.5 level line, which means the stronger stress sensitivity is, the more serious damage of permeability is, the more difficult of fluid flow, and the larger drawdown pressure is needed.

Figure 5 represents the effect of fracture number (M) on transient pressure curves. The derivative curve gradually declines with the increasing of fracture number, but this phenomenon is not so obvious in wellbore storage period (stage 1) and late-time pseudo-radial flow period (stage 6). Because the bigger of M, the more flow channels for natural gas, the better of the formation connectivity, and thus the smaller drawdown pressure is needed.

Fig. 5
figure 5

Effect of fracture number on transient pressure curves

Full size image

Figure 6 indicates the effect of fracture spacing Δyi on transient pressure curves. It can be observed that Δyi mainly affects the mid-time pseudo-radial flow of fracture system (stage 4) and the subsequent linear flow of whole system (stage 5). The larger the fracture spacing, the longer the duration of the mid-time pseudo-radial flow of fracture system, and the later the occurrence of the linear flow of whole system.

Fig. 6
figure 6

Effect of fracture spacing on transient pressure curves

Full size image

Figure 7 illustrates the effect of fracture half-length Xf on transient pressure curves. As we can see, with the increase of fracture length, the early linear flow perpendicular to hydraulic fractures (stage 3) will last longer with lower position of pressure derivative curves, and the mid-time pseudo-radial flow around each fracture (stage 4) occurs later with shorter duration. When Xf continues to increase, the horizontal line on the pressure derivative curves reflecting stage 4 will be gradually concealed.

Fig. 7
figure 7

Effect of fracture half-length on transient pressure curves

Full size image

Rate transient analysis of producing at a constant bottom-hole pressure

Figure 8 reflects the effect of permeability modulus γmD on rate decline curves. The greater of γmD, the stronger of the stress sensitivity, i.e. the more serious of permeability damage, so the worse the reservoir property is, and the lower the production rate under constant pressure will be, resulting in a steeper downwarping of the production decline curve and a more obvious upwarping of the derivative curve.

Fig. 8
figure 8

Effect of permeability modulus on rate decline curves

Full size image

Figures 9, 10 and 11 successively reveal the rate decline curves affected by fracture number (M), fracture spacing (Δyi) and fracture half-length (Xf). The bigger the M, the better the reservoir connectivity, so that driving pressure differential of fluid flow is smaller, and the production rate is higher (see Fig. 9). The smaller the Δyi, the more serious the fracture interference, and the lower the production rate. Correspondingly, on the rate derivative curve, the shorter the duration of the mid-time pseudo-radial flow around each fracture, even to be covered (see Fig. 10), the larger the Xf, the greater the drainage area, and the higher position of production rate curves. Meanwhile, the early linear flow perpendicular to hydraulic fractures will last longer with lower position of rate derivative curves (see Fig. 11).

Fig. 9
figure 9

Effect of fracture number on rate decline curves

Full size image
Fig. 10
figure 10

Effect of fracture spacing on rate decline curves

Full size image
Fig. 11
figure 11

Effect of fracture half-length on rate decline curves

Full size image

Concluding remarks

This study mainly deduced a semi-analytical model of gas transient transport from the stress-sensitive porous medium to a multi-fractured horizontal well. Based on the semi-analytical solution, a series of transient flow dynamic curves (including pressure response and rate decline) were plotted. The following conclusions can be summarized:

  1. 1.

    A semi-analytical solution of multi-fractured horizontal well is developed by orderly employing Pedrosa’s linearization, perturbation technique, Laplace transformation, fractures discretization and superposition principle.

  2. 2.

    The stress-sensitivity indicates the permeability damage of formation and results in larger pressure drawdown during intermediate and late flow regimes, which are reflected by upward tendencies in both pressure and rate derivative curves.

  3. 3.

    The major factors (mainly related to the geometry and placement of hydraulic fractures including fracture number, fracture spacing and fracture half-length) influence on the transient flow behavior is analyzed to better understand the gas transport characteristics.

  4. 4.

    The proposed model is better prepared for not only well test interpretation but also rate transient analysis, which contributes to evaluating underground fluid transport in stress-sensitive formations efficiently and accurately.