The study on calculating flow pressure for tight oil well

Abstract

This paper presents a new method to calculate flow pressure for tight oil well with partial penetration fracture. The solution to the diffusivity equation can be obtained using dimensionless transformation, Laplace transformation, Fourier cosine transformation and other mathematical methods. The calculation results of relative simple system are in good agreement with Kuchuk and Brighan’s analytical solution, suggesting that this method in this paper is accurate. The pressure dynamic flow curve can be divided into four stages: transient flow, first linear flow, first radial flow, and boundary dominated flow. The effect of parameters including fracture orientation, fracture length, the degree of penetration, reservoir boundary anisotropy, reservoir boundary conditions and reservoir width on the pressure and pressure derivative was fully investigated in detail. The fracture length mainly affects the early linear flow, and permeability anisotropy mainly affects the mid-radial flow, and the degree of penetration in the reservoir and fracture orientation mainly affect the late spherical flow, and the boundary conditions and reservoir border width mainly affect the control flow. The method can be used to determine the optimal degree of opening shot, vertical permeability and other useful parameters.

Introduction

The exploration and development of tight oil in China started relatively late. China was one of the first countries in the world to discover tight oil. Early in 1907, tight oil was discovered in the Triassic strata by the Well Yan 1 in the Ordos Basin and in 1989, a giant tight oil field of Jingbian was found in the Carboniferous–Permian strata in this basin. From then on, tight oil fields were successively explored in various basins such as Sichuan, Junggar, Songliao, Bohai Bay, etc. In conclusion, tight oil is abundantly stored in multiple formations and layers in large or medium-sized basins all over China, of which tight oil reserves were estimated to be 28–30 billion tons.

Tight sandstone reservoirs generally have the characteristics of large thickness and natural fractures. It is well known that the perforation completion is used in well completion, and the hydraulic fracturing is used to increase the well production. However, the degree of perforation is relatively small (a few meters), which can affect the wellbore pressure transmission and productivity (Al Rbeawi and Tiab 2012, 2013; Alpheus and Tiab 2008). Therefore, it is crucial to analyze the seepage pressure of the fractured straight well in tight sandstone reservoirs.

There are many methods to calculate the seepage pressure, such as conformal transformation method (Ramey and Gringarten 1974; Buhidmal and Raghavan 1980; Kuchuk and Kirwan 1987; Hegeman and Abbaszaqdeh 1990), equivalent seepage resistance method (Raghavan and Ozkan 1991; Onur and Satman 1993; Bui et al. 2000; Valko and Amini 2007), split flow field method (Lin and Zhu 2012; Feng and; Wenguang 1985), numerical simulation method (Li and Liu 1997; Liu et al. 2001) and physical simulation method (Wang et al. 2007; Zhao et al. 2016, 2017). The above methods mainly have the following shortcomings:

• 1. The seepage model uses special functions.

• 2. The derivation and calculation are cumbersome.

• 3. The well pattern evaluation method is more suitable for the small well group, which is inconsistent with the actual well pattern.

• 4. The various modeling methods are relatively independent, and the formula expansion is poor.

What’s more, the hydraulic fractures are assumed to be fully penetrating the formation in the previous studies. Limited efforts have been made to investigate the effects of partially penetrating fracture orientation on the performance of wells. In practice, fully penetrating fractures may lead to an early or immediate water or gas breakthrough in a reservoir with bottom water or gas cap in contact, whereas partially penetrating fractures provide a better way to prevent the early breakthrough. Most of the existing methods are based on Gringarten and Ramey’s point source solution and Green function, whereas the original physical model established by Gringarten and Ramey only considered the upper and lower bounds, limiting the scope of the application. Therefore, it is necessary to study flow pressure for tight oil well with partial penetration fracture.

Here, the physical model of the non-homogeneous reservoir is established, and then the mathematical model of the unstable seepage flow in the three-dimensional anisotropic rectangular reservoir is built under several certain conditions. The mathematical model of unstable seepage flow is solved by means of dimensionless transformation, Laplace transformation, Fourier cosine transformation and separation variable method. The numerical solution of the real field is obtained through the Stevenson numerical inversion method and the pressure dynamic curve is drawn for well test analysis. The advantages of Laplace domain solution is that it can make it easy to incorporate storage coefficient and skin factor, and it can also reduce the amount of computation.

Model establishing

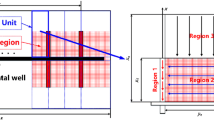
As shown in Fig. 1, a reservoir formation is fractured by hydraulic fracturing. After hydraulic fracturing, the half-length and height of the fracture constitute the fracture surface. Combining with the distance between the fractures, the one-dimensional diffusion volume of the reservoir fluid was built. The diffusion volume affects the flow rate of the reservoir fluid in the longitudinal direction. The fracture width and the fracture surface confine the range of the linear flow in the fractures, which affects the whole straight well production. The influence of the fracture parameters on the seepage pressure can be analyzed according to the coupling model of the reservoir–fracture–wellbore, and through sensitivity analyzing, artificial fracture parameter combination can be obtained, which forms the optimal fracture grid to achieve yield optimization. Therefore, to study the seepage pressure of fractured straight well, the seepage pressure of single fracture needs to be studied at first, as shown in Fig. 2. Using the superposition principle, the multi-fracture seepage pressure can be obtained. To simplify the physical model, the following assumptions are made:

Fig. 1

The schematic of multi-stage fracturing wells

Fig. 2

Single fracture schematic of section penetration

• 1. The oil production is constant, and the formation of the reservoir is bounded and non-homogeneous, with equal thickness.

• 2. The reservoir pressure is equal to the original formation pressure.

• 3. The reservoir fluid is micro-compressible.

• 4. The inter-fracture interference is ignored, and the fluid flow in the fracture obeys the Darcy’s law.

• 5. The gravity and capillary force are ignored, and the porosity and fluid viscosity are constant;

• 6. The fracture partially penetrates the formation, and the reservoir fluid flows to the wellbore in a limited range.

• 7. Crossflow between the fracture and the matrix is ignored.

The center of one fracture is located at (x₀, y₀, z₀). Based on the above assumptions, the mathematical model of the fracture is established as the following:

$$\frac{{{k_x}}}{{\phi \mu {c_{\text{t}}}}}\frac{{{\partial ^2}P}}{{\partial {x^2}}}+\frac{{{k_y}}}{{\phi \mu {c_{\text{t}}}}}\frac{{{\partial ^2}P}}{{\partial {y^2}}}+\frac{{{k_z}}}{{\phi \mu {c_{\text{t}}}}}\frac{{{\partial ^2}P}}{{\partial {z^2}}}+\frac{{8q{w_x}{w_y}{w_z}}}{{\phi \mu {c_{\text{t}}}}}f(x,y,z)=\frac{{\partial P}}{{\partial t}},$$

(1)

where k_x, k_y, k_z are the permeabilities in the x, y and z directions. c_t is total compressibility, $\phi$ is porosity, p is reservoir pressure, t is the time, B is formation volume factor, q is the flow rate of per unit area flowing through the fracture.

f(x,y,z) is the position of the source (sink) phase, and its expression is

$$f(x,y,z)=\frac{1}{{8{w_x}{w_y}{w_z}}}\iiint\limits_{v} {\delta [(x - {x_0})}(y - {y_0})(z - {z_0})]{\text{d}}v,$$

(2)

$$({x_0} - {w_x})({y_0} - {w_y})({z_0} - {w_z}) \leqslant v \leqslant ({x_0}+{w_x})({y_0}+{w_y})({z_0}+{w_z}),$$

(3)

where δ is Dirac delta function.

The initial conditions are

$$p(x,y,z,0)={p_i}.$$

(4)

The inner boundary condition is

$$\mathop {\lim }\limits_{{r \to {r_{\text{w}}}}} \left( {r\frac{{\partial p}}{{\partial r}}} \right)=\frac{{Bq\mu }}{{2\pi kh}}\quad r =\sqrt {{{(x - {x_0})}^2}+{{(y - {y_0})}^2}+{{(z - {z_0})}^2}} .$$

(5)

The outer boundary condition is

$$\frac{{\partial p}}{{\partial x}}\left| {_{{x=0,a}}} \right.=0\quad\frac{{\partial p}}{{\partial y}}\left| {_{{y=0,b}}} \right.=0\quad\frac{{\partial p}}{{\partial z}}\left| {_{{z=0,h}}} \right.=0.$$

(6)

Model solving

Solution research

According to the literature survey, there are mainly three methods to solve Eq. (1). First, by ignoring the pressure propagation time and using the Green’s function method, the analytical solution of the Lagrangian space to Eq. (1) can be obtained (Valko and Amini 2007; Lin and Zhu 2012; Wang et al. 2007). Secondly, on the condition that the boundary extension is regarded as the function of time, using steady-state successive replacement method and differential discretization method, the numerical solution to Eq. (1) can be obtained (Li and Liu 1997; Zhao et al. 2016, 2017). Thirdly, using numerical approximation method and series expansion method, the correlation between the leading edge of the pressure propagation and the time can be solved. However, these three methods have made some assumptions to solve Eq. (1), which may affect the accuracy of equation solving. To improve the accuracy of equation solving, this paper presents a new way to solve Eq. (1), which is by means of mathematical methods such as dimensionless transformation, Laplace transform, Fourier cosine transformation and separation variable method, Eq. (1) can be solved.

Dimensionless transformation

Dimensionless transformation is a method of converting the seepage equation into a conventional mathematical equation. By dimensionless transformation, the number of comparisons can be greatly reduced, which makes the mathematical physics equation simple, neat, easy to analyze and solve (Wang 2006). The following dimensionless transformation is introduced in this paper:

$$N=\sqrt {\frac{{abh}}{L}} ,$$

(7)

$${P_{\text{D}}}=\frac{{2\pi kN({p_i} - p)}}{{QB\mu }}\,{t_{\text{D}}}=\frac{k}{{\phi \mu {c_t}{N^2}}}t,$$

(8)

$${x_{\text{D}}}=\sqrt {\frac{k}{{{k_x}}}} \frac{x}{N}\quad{y_{\text{D}}}=\sqrt {\frac{k}{{{k_x}}}} \frac{y}{N}\quad{z_{\text{D}}}=\sqrt {\frac{k}{{{k_x}}}} \frac{z}{N},$$

(9)

$${a_{\text{D}}}=\frac{a}{N}\quad{b_{\text{D}}}=\frac{b}{N}\quad{h_{\text{D}}}=\frac{h}{N},$$

(10)

$${w_{x{\text{D}}}}=\frac{{{w_x}}}{N}\quad{w_{y{\text{D}}}}=\frac{{{w_y}}}{N}\quad{w_{z{\text{D}}}}=\frac{{{w_z}}}{N},$$

(11)

$${x_{0{\text{D}}}}=\frac{{{x_0}}}{r}\,{y_{0{\text{D}}}}=\frac{{{y_0}}}{r}\,{z_{0{\text{D}}}}=\frac{{{z_0}}}{r},$$

(12)

where L is the length of the firing reservoir (m).

So Eq. (1) can be written as:

$$\frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial x_{{\text{D}}}^{2}}}+\frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial y_{{\text{D}}}^{2}}}+\frac{{{\partial ^2}{P_{\text{D}}}}}{{\partial z_{{\text{D}}}^{2}}}+\frac{{4\pi }}{{{N^2}}}f({x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}})=\frac{{\partial {P_{\text{D}}}}}{{\partial {t_{\text{D}}}}},$$

(13)

where f(x_D,y_D,z_D) is:

$$f({x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}})=\frac{1}{{8{w_{x{\text{D}}}}{w_{y{\text{D}}}}{w_{z{\text{D}}}}}}\iiint\limits_{{{v_{\text{D}}}}} {\delta [({x_{\text{D}}} - {x_{0{\text{D}}}})}({y_{\text{D}}} - {y_{0{\text{D}}}})({z_{\text{D}}} - {z_{0{\text{D}}}})]{\text{d}}{v_{\text{D}}},$$

(14)

$$({x_{0{\text{D}}}} - {w_{x{\text{D}}}})({y_{0{\text{D}}}} - {w_{y{\text{D}}}})({z_{0{\text{D}}}} - {w_{z{\text{D}}}}) \leqslant {v_{\text{D}}} \leqslant ({x_{0{\text{D}}}}+{w_{x{\text{D}}}})({y_{0{\text{D}}}}+{w_{y{\text{D}}}})({z_{0{\text{D}}}}+{w_{z{\text{D}}}}).$$

(15)

Initial conditions:

$${p_{\text{D}}}({x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}},0)=0.$$

(16)

Inner boundary conditions:

$$\mathop {\lim }\limits_{{{r_{\text{D}}} \to 1}} \left( {{r_{\text{D}}}\frac{{\partial {p_{\text{D}}}}}{{\partial {r_{\text{D}}}}}} \right)= - 1\quad{r_{\text{D}}}=\frac{r}{N}.$$

(17)

Outer boundary conditions:

$$\frac{{\partial {p_{\text{D}}}}}{{\partial {x_{\text{D}}}}}\left| {_{{{x_{\text{D}}}=0,{a_{\text{D}}}}}} \right.=0\quad\frac{{\partial {p_{\text{D}}}}}{{\partial {y_{\text{D}}}}}\left| {_{{{y_{\text{D}}}=0,{b_{\text{D}}}}}} \right.=0\quad\frac{{\partial {p_{\text{D}}}}}{{\partial {z_{\text{D}}}}}\left| {_{{{z_{\text{D}}}=0,{h_{\text{D}}}}}} \right.=0.$$

(18)

Equation solving

Laplace transform can eliminate the partial derivative of time from the unstable seepage equation, and has been widely used to solve the problem of unstable seepage (Wang 2006). Using Laplace transformation, Eq. (13) can be written as:

$$\frac{{{\partial ^2}{{\tilde {p}}_{\text{D}}}}}{{\partial x_{{\text{D}}}^{2}}}+\frac{{{\partial ^2}{{\tilde {p}}_{\text{D}}}}}{{\partial y_{{\text{D}}}^{2}}}+\frac{{{\partial ^2}{{\tilde {p}}_{\text{D}}}}}{{\partial z_{{\text{D}}}^{2}}}+\frac{{4\pi }}{{s{N^2}}}f({x_{\text{D}}},{y_{\text{D}}},{z_{\text{D}}})=s{\tilde {p}_{\text{D}}}.$$

(19)

Using Fourier cosine transformation of x_D, y_D and z_D, Eq. (19) can be written as:

$${\bar {\bar {\bar {\tilde {p}}}}_{\text{D}}}=\frac{1}{{u_{m}^{2}+v_{n}^{2}+w_{p}^{2}+s}}\frac{{4\pi }}{{s{N^2}}}f({u_m},{v_n},{w_p}),$$

(20)

where u_m, v_n and w_p is the solution of the following equations.

$$\left\{ \begin{gathered} {u_m}\tan {u_m} - {a_{\text{D}}}=0 \hfill \\ {v_n}\tan {v_n} - {b_{\text{D}}}=0 \hfill \\ {w_p}\tan {w_p} - {h_{\text{D}}}=0, \hfill \\ \end{gathered} \right.$$

(21)

$$f({u_m},{v_n},{w_p})={F_1} \times {F_2}{\kern 1pt} \times {F_3},$$

(22)

$${F_1}=\frac{{\left\{ {\sin \left[ {{u_m}({x_{0{\text{D}}}}+{w_{x{\text{D}}}})} \right] - \sin \left[ {{u_m}({x_{0{\text{D}}}} - {w_{x{\text{D}}}})} \right]} \right\}}}{{2{u_m}{w_{x{\text{D}}}}}},$$

(23)

$${F_2}=\frac{{\left\{ {\sin \left[ {{v_n}({y_{0{\text{D}}}}+{w_{y{\text{D}}}})} \right] - \sin \left[ {{v_n}({y_{0{\text{D}}}} - {w_{y{\text{D}}}})} \right]} \right\}}}{{2{v_n}{w_{y{\text{D}}}}}},$$

(24)

$${F_3}=\frac{{\left\{ {\sin \left[ {{w_p}({z_{0{\text{D}}}}+{w_{z{\text{D}}}})} \right] - \sin \left[ {{w_p}({z_{0{\text{D}}}} - {w_{z{\text{D}}}})} \right]} \right\}}}{{2{w_p}{w_{z{\text{D}}}}}}.$$

(25)

The Laplace space solution is obtained using Fourier cosine inverse transformation. The Fourier cosine inverse transformation can be written as:

$${P_{\text{D}}}({x_{\text{D}}})=\sum\limits_{{m=1}} {\frac{{\cos ({u_m}{x_{\text{D}}})}}{{N(n)}}{{\bar {P}}_{\text{D}}}({u_m})} ,$$

(26)

where $N(n)$ is the norm, and its expression is:

$$N(n)=\frac{1}{2}\left( {1+\frac{{\sin {u_n}\cos {u_n}}}{{{u_n}}}} \right).$$

(27)

Using Fourier cosine inverse transformation of z_D, y_D and x_D, Eq. (20) can be written as:

$$\begin{aligned} s{{\tilde {p}}_{\text{D}}} & =\frac{{4\pi }}{{{a_{\text{D}}}{b_{\text{D}}}{h_{\text{D}}}}}\Big\{ {\frac{1}{s}} +2\sum\limits_{{m=1}}^{{}} {\cos ({u_m}{x_{\text{D}}})} \frac{{{F_1}}}{{(s+u_{m}^{2})}}+2\sum\limits_{{n=1}}^{{}} {\cos ({v_n}{y_{\text{D}}})} \frac{{{F_2}}}{{(s+v_{n}^{2})}} \\ & \quad +4\sum\limits_{{n=1}}^{{}} {\sum\limits_{{m=1}}^{{}} {\cos ({v_n}{y_{\text{D}}})\cos ({u_m}{x_{\text{D}}})} } \frac{{{F_1}{F_2}}}{{(s+u_{m}^{2}+v_{n}^{2})}}+2\sum\limits_{{p=1}}^{{}} {\cos ({w_p}{z_{\text{D}}})} \frac{{{F_3}}}{{(s+w_{p}^{2})}} \\ & \quad +4\sum\limits_{{m=1}}^{{}} {\sum\limits_{{p=1}}^{{}} {\cos ({w_p}{z_{\text{D}}})} \cos ({u_m}{x_{\text{D}}})} \frac{{{F_1}{F_3}}}{{(s+u_{m}^{2}+w_{p}^{2})}} \\ & \quad +4\sum\limits_{{n=1}}^{{}} {\sum\limits_{{p=1}}^{{}} {\cos ({v_n}{y_{\text{D}}})\cos ({w_p}{z_{\text{D}}})} } \frac{{{F_2}{F_3}}}{{(s+v_{n}^{2}+w_{p}^{2})}} \\ & \quad +8\sum\limits_{{m=1}}^{{}} {\sum\limits_{{n=1}}^{{}} {\sum\limits_{{p=1}}^{{}} {\cos ({v_n}{y_{\text{D}}})\cos ({w_p}{z_{\text{D}}})} } \cos ({u_m}{x_{\text{D}}})} {\frac{{{F_1}{F_2}{F_3}}}{{(s+u_{m}^{2}+v_{n}^{2}+w_{p}^{2})}}} \Big\}. \\ \end{aligned}$$

(28)

By introducing two equations:

$$2\cos (\alpha \beta )\cos (\alpha \gamma )=\cos [\alpha (\beta +\gamma )]+\cos [\alpha (\beta - \gamma )],$$

(29)

$$\sum\limits_{{k=1}}^{{}} {\frac{{\cos kx}}{{{k^2}+{\alpha ^2}}}} =\frac{\pi }{{2\alpha }}\frac{{\cosh \alpha (\pi - x)}}{{\sinh \alpha \pi }} - \frac{1}{{2{\alpha ^2}}},$$

(30)

Eq. (28) can be written as:

$$\begin{aligned} s{{\tilde {p}}_{\text{D}}} & =\frac{{2\pi }}{{{a_{\text{D}}}{b_{\text{D}}}{h_{\text{D}}}}}\Big\{ {\frac{{[\cos h\sqrt s ({b_{\text{D}}} - {y_{\text{D}}}+{y_{0{\text{D}}}})+\cos h\sqrt s ({b_{\text{D}}} - {y_{\text{D}}} - {y_{0{\text{D}}}})]}}{{\sqrt s \sin h\sqrt s {b_{\text{D}}}}}} \\ & \quad +2\sum\limits_{{m=1}}^{{}} {\cos ({u_m}{x_{\text{D}}})} \frac{{\cos ({u_m}{x_{0{\text{D}}}})\sin ({u_m}{w_{x{\text{D}}}})}}{{{u_m}{w_{x{\text{D}}}}}} \\ & \quad \times \frac{{\cos h{\tau _m}[({b_{\text{D}}} - ({y_{\text{D}}} - {y_{0{\text{D}}}})]+\cos h{\tau _m}[{b_{\text{D}}} - ({y_{\text{D}}}+{y_{0{\text{D}}}})]}}{{{\tau _m}\sin h{\tau _m}{b_{\text{D}}}}} \\ & \quad +2\sum\limits_{{p=1}}^{{}} {\cos ({w_p}{z_{\text{D}}})} \frac{{\cos ({w_p}{y_{0{\text{D}}}})\sin ({w_p}{w_{z{\text{D}}}})}}{{{w_p}{w_{z{\text{D}}}}}} \\ & \quad \times \frac{{\cos h{\tau _p}[({b_{\text{D}}} - ({y_{\text{D}}} - {y_{0{\text{D}}}})]+\cos h{\tau _p}[{b_{\text{D}}} - ({y_{\text{D}}}+{y_{0{\text{D}}}})]}}{{{\tau _p}\sin h{\tau _p}{b_{\text{D}}}}} \\ & \quad +4\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{p=1}}^{\infty } {\cos ({u_m}{x_{\text{D}}})\cos ({w_p}{z_{\text{D}}})} } \frac{{\cos ({u_m}{x_{0{\text{D}}}})\sin ({u_m}{w_{x{\text{D}}}})}}{{{u_m}{w_{x{\text{D}}}}}}\frac{{\cos ({w_p}{z_{0{\text{D}}}})\sin ({w_p}{w_{z{\text{D}}}})}}{{{w_p}{w_{z{\text{D}}}}}} \\ & \quad \times {\frac{{\cos h{\tau _{mp}}[({b_{\text{D}}} - ({y_{\text{D}}} - {y_{0{\text{D}}}})]+\cos h{\tau _{mp}}[{b_{\text{D}}} - ({y_{\text{D}}}+{y_{0{\text{D}}}})]}}{{{\tau _{mp}}\sin h{\tau _{mp}}{b_{\text{D}}}}}} \Big\}, \\ \end{aligned}$$

(31)

where

$${\tau _m}=\sqrt {s+u_{m}^{2}} \quad{\tau _p}=\sqrt {s+w_{p}^{2}} \quad{\tau _{mp}}=\sqrt {s+u_{m}^{2}+w_{p}^{2}} .$$

(32)

Equation (31) is an analytical solution model under Laplacian space. Its applicable conditions are anisotropic homogeneous rectangular reservoir with impermeable region and outer boundary by fracturing. Using Stehfest numerical inversion method (Stehfest 1970), a numerical solution of the seepage pressure can be obtained. By changing the center of the fracture, the seepage pressure of the fracture at different locations can be obtained.

From Fig. 3, we can get that it takes only 21.282 s to run the program of seepage pressure of the fracture at different locations, when the computer’s processor model is Intel(R) Core(TM) i7-6700 CPU @3.4 GHz 3.4 GHz, which shows that this method in this paper is simple and it can compute efficiently and reduce the amount of computation.

Fig. 3

Running time of productivity prediction program

Model validation

Kuchuk and Brighan (1979) presented an analytical solution of infinite-conductivity vertically fractured wells. This published analytical solution is suitable to a well with a constant rate or pressure in an anisotropic and elliptically shaped reservoirs. There is some difference between Kuchuk and this paper in terms of derivation of the equations. For the Kuchuk and Brighan model, as the seepage equation is linear, it is not necessary to do the dimensionless transformation. What need to do is separation of variables and stepping integration. It is much easier to solve Kuchuk and Brighan model. However, the model in this paper, the seepage equation is not linear, and we must linearize the equation through dimensionless transformation. As the seepage flow is unsteady state, it is necessary to introduce Laplace transformation and Fourier transformation to reduce the number of unknown variables, and then solve the equation.

To validate this work in this paper, a special case that the fracture is fully penetration is used. From the literature of Kuchuk and Brighan, some data are obtained. The required parameters for these two methods are shown in Table 1, and the results of the above two methods for the fully penetrating infinite-conductivity isotropic case are shown in Fig. 4. From Fig. 4, it can be seen that this work solution and the Kuchuk and Brighan solution match very well, suggesting that this method in this paper is reliable.

Table 1 Basic data of the system

Fig. 4

Calculating results of this work and literature results

Flow period division

The fracture center is located in the center of the well, and the partially penetrating degree is 50%. Moreover, ${k_x}={k_y}$, and ${{{k_x}} \mathord{\left/ {\vphantom {{{k_x}} {{k_z}}}} \right. \kern-0pt} {{k_z}}}=100$. There is only one fracture in the center of the reservoir. The flow division schematic of partial penetration fractured vertical wells is drawn, as shown in Fig. 5. The partially penetrating fracturing straight well seepage pressure (pressure derivative) model curve can be divided into four flow periods: transient flow, first linear flow, first radial flow, and boundary dominated flow. The transient flow is affected by epidermal effect and wellbore storage effect, and in the stage of the transient flow, the slope of the pressure derivative curve is about 1, and the reservoir fluid is continuously flowing to the wellbore, and then the reservoir fluid enters the first linear flow. The higher the degree of partially penetrating is, the longer the first linear flow is. With the pressure gradually spreading out, before the pressure transmits to the boundary, it is mainly the first radial flow, and the pressure derivative gradient becomes smaller until it tends to be stable. When the pressure propagates to the boundary, the boundary dominated flow occurs, and the pressure derivative value changes faster. Finally, the reservoir fluid flows to the wellbore in the form of quasi-steady flow.

Fig. 5

The flow division schematic of partial penetration fractured vertical wells

Sensitivity analysis

Basing on the controlling variable method, parameters affecting pressure and pressure derivative (template curve), including fracture orientation, fracture scale, the degree of penetration in the reservoir, permeability anisotropy, reservoir boundary condition and reservoir scale were analyzed with the parameters in Table 1.

Fracture orientation

The orientation of fractures is divided into two aspects, namely, in the reservoir center (as shown in Fig. 6a) and not in the reservoir center (Fig. 6b). By setting the coordinates of different fractures, the relationships between the reciprocal pressure, the reciprocal of pressure and the producing time are shown in Fig. 7.

Fig. 6

Schematic diagram of fracture orientation

Fig. 7

The effect of fracture orientation on template curves

Figure 7 shows that the fracture orientation mainly affects the first radial flow stage of the template curve. When the fracture is located in the reservoir center, the pressure is easier to propagate outwards. In the first radial flow stage, the reservoir fluid flows to the wellbore in the form of linear flow. The fractures of hydraulic fracturing are the “flow network” established in the reservoir, and connect the seepage channel of the reservoir, which increases the seepage area.

The performance of fluid flow and pressure transmission improve with the increasing of fractural symmetry and the decreasing of the complexity of flow channel.

Fracture length

With different fracturing scales, the length of the fractures is not the same, leading to the diverse seepage area in the reservoir. Thus, the pressure transmission trends are different. Figure 8 shows that the length of the fracture mainly affects the early linear and first linear flow, especially the first linear flow. At the same producing time, as the length of the fracture increases, the pressure drop rate decreases, and the pressure propagation becomes faster. In the transient flow stage, small fractures tend to produce more pressure drop, which can be explained by the positive correlation between fractures size and seepage area. Larger seepage area indicates stronger fluid supply capacity, therefore the transient flow stage is longer. When the fracture length is the same, the pressure drop tends to be consistent, so the fracture length only affects the duration of the transient flow, and its effect on the pressure drop is not obvious. Using the progressive analysis method, we can see that the slope of the straight line in this stage is 0.5.

Fig. 8

The effect of fracture length on template curves

The degree of penetration in the reservoir

The usage of reasonable degree of penetration can not only save the cost of perforation, but also get the maximum production. The effect of the degree of penetration on fluid pressure is significant, as shown in Fig. 9. The degree of penetration affects the end of the first radial flow and the beginning of the boundary dominated flow. When the height of the reservoir increases, the first radial flow becomes shorter, and the fluid seepage enters the boundary dominated flow stage earlier. When the reservoir is completely penetrated, the fluid flows into the boundary dominated flow stage without going through the spherical flow stage.

Fig. 9

The effect of opening shot degree on template curves

Reservoir anisotropy

Since the permeability varies little in the horizontal direction, the permeability in the x and y direction is considered as the same value. Figure 10 shows that the permeability of the vertical anisotropy mainly affects the first linear flow stage. It is probably because that in the actual formation, the fluid flow in the fractures increases with the increasing of vertical permeability. Therefore, when the ratio of horizontal permeability to vertical permeability increases, the first linear flow becomes longer, because that when the horizontal permeability plays a dominant role, the reservoir fluid mainly flows to the wellbore from the horizontal direction.

Fig. 10

The effect of reservoir anisotropy on template curves

Reservoir boundary conditions

The combination of different reservoir boundary conditions has different effects on the template curve. Figure 11 shows that the boundary condition mainly affects the boundary dominated flow stage. For the closed boundary condition, the value of the pressure drop tends to be stable, and the pressure derivative is about 0.01. For the constant pressure boundary condition, the pressure is continuously propagating and the pressure derivative is gradually reducing due to the sufficient supply of external energy until the pressure equals to the boundary pressure, and the pressure derivative slope is about 1, and the reservoir fluid develops quasi-steady state seepage. When the upper (lower) boundary is closed, and the pressure of lower (upper) boundary is constant, then the pressure change is between the above two cases. In this situation, only the pressure derivative slope is not a constant.

Fig. 11

The effect of reservoir boundary conditions on template curves

Reservoir width

Figure 12 shows that the reservoir width mainly affects the time when the fluid enters the boundary dominated flow stage and the speed of the pressure derivative curve decreasing at this stage. With the reservoir width decreasing, the seepage pressure enters the boundary dominated flow stage more quickly, and the pressure drop is smaller. When the width of the reservoir decreases, the pressure tends to spread quickly to the boundary under the condition of constant production. The earlier the seepage pressure is into the boundary dominated flow stage, the earlier and faster the pressure increases.

Fig. 12

The effect of reservoir width on template curves

Conclusion

A new way to solve the analytical solution of flow pressure for tight oil well with partial penetration fracture is presented in a detailed step-by-step manner. The calculation results of relative simple system are in good agreement with Kuchuk and Brighan’s analytical solution, which proved the correctness of the method.

The pressure dynamic flow curve can be divided into four stages: transient flow, first linear flow, first radial flow, and boundary dominated flow. The fracture length mainly affects the early linear flow, and permeability anisotropy mainly affects the mid-radial flow, and the degree of penetration in the reservoir and fracture orientation mainly affect the late spherical flow, and the boundary conditions and reservoir border width mainly affect the control flow. The method can be used to determine the optimal degree of opening shot, vertical permeability and other useful parameters.

The advantage of the solution is that it can compute efficiently and reduce the amount of computation. This method can be used to determine the parameters such as optimal degree of penetration and vertical permeability, providing theoretical guidance for reservoir engineering analysis and fracturing process design.