Abstract
Deterministic modeling lonely provides a unique boundary layout, depending on the geological interpretation or interpolation from the hard available data. Changing the interpreter’s attitude or interpolation parameters leads to displacing the location of these borders. In contrary, probabilistic modeling of geological domains such as lithofacies is a critical aspect to providing information to take proper decision in the case of evaluation of oil reservoirs parameters, that is, applicable for quantification of uncertainty along the boundaries. These stochastic modeling manifests itself dramatically beyond this occasion. Conventional approaches of probabilistic modeling (object and pixel-based) mostly suffers from consideration of contact knowledge on the simulated domains. Plurigaussian simulation algorithm, in contrast, allows reproducing the complex transitions among the lithofacies domains and has found wide acceptance for modeling petroleum reservoirs. Stationary assumption for this framework has implications on the homogeneous characterization of the lithofacies. In this case, the proportion is assumed constant and the covariance function as a typical feature of spatial continuity depends only on the Euclidean distances between two points. But, whenever there exists a heterogeneity phenomenon in the region, this assumption does not urge model to generate the desired variability of the underlying proportion of facies over the domain. Geophysical attributes as a secondary variable in this place, plays an important role for generation of the realistic contact relationship between the simulated categories. In this paper, a hierarchical plurigaussian simulation approach is used to construct multiple realizations of lithofacies by incorporating the acoustic impedance as soft data through an oil reservoir in Iran.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Geological modeling has been widely used in different disciplines of numerical reservoir modeling (Walker 1992; Shakiba et al. 2015; Nazeri et al. 2016). Different characteristics of petrophysical properties such as porosity, permeability, and saturation are significantly controlled by lithofacies features (Pyrcz and Deutsch 2014). Following this concept, it justifies the need to model the layout of lithofacies prior to any modeling of those continuous variables (Journel and Huijbregts 1978).
Deterministic modeling of the lithofacies provides only one unique boundary between two adjacent geo-domains. This usually can be done based on expert judgment or interpolating form inadequate available surrounding data (Madani and Emery 2015). Stochastic algorithms, as an alternative, are extensively utilized for constructing multiple realizations that honoring the conditional data and lead to quantify the uncertainty of the lithofacies at unsampled locations. These geostatistical simulation methods are mostly classified to two main families: multi-point statistics and two-point statistics. The first family relies on the training image (Strebelle 2002). The most challenging issue for this method is constructing a representative training image, which is still experiencing with ongoing research (Emery and Lantuéjoul 2014). The later family corresponds to pixel-based methods, which offer more flexible framework to infer the statistical parameters (Deutsch 2006). For instance, sequential indicator simulation (Journel 1983; Journel and Isaaks 1984; Alabert 1987; Journel and Alabert 1988) and transition probability-based indicator simulation (Carle and Fogg 1996) are such an indicator-based algorithms, which present acceptable results under some circumstances. The realizations are often susceptible to not well reproducing the low proportion of the facies in the region (Deutsch 2006; Emery 2004). Moreover, the contact relationship in this approach cannot be imposed into the process of modeling. Truncated Gaussian simulation (Matheron et al. 1987, 1988; Galli et al. 1994) as an alternative is suitable where an ordering sequence can be confirmed through the geological settings (e.g., strata in sedimentary deposits). Plurigaussian simulation as an extension of the truncated Gaussian simulation is more capable of handling the complex contacts relationship among the lithofacies. In this context, the allowed and forbidden contacts can be injected into the modeling process. In a nutshell, it has found wide acceptance between the practitioners for modeling the petroleum reservoirs (Armstrong et al. 2011). However, conventional method of Plurigaussian simulation (Emery 2007) mostly is limited to a few number of facies (no more than five) and the Gaussian random fields (no more than three). Madani and Emery, (2015) presented an extension of the former Plurigaussian simulation, to increase the number of underlying Gaussian random fields, that is, applicable for the geological settings such that younger geo-domains cross-cut the older ones and the contact knowledge can be organized respecting to their chronology. In this case, all the facies should be in touch altogether and such a forbidden contact is not allowed. Maleki et al. (2016) presented another application of this technique, in which the geo-domains are, in the same way, ordered hierarchically, but the forbidden contacts play an important role. All these approaches are based on stationary phenomena (i.e., homogenous variability). However, in the case of heterogonous variability, things get more complicated and one requires updating the stationary assumptions (Madani and Emery 2017) or applies secondary information for reproducing the trend. This available information can be seismic data. In this paper, the proposed methodology (hierarchical simulation approach) is integrated with seismic information (acoustic impedance) to contribute the heterogeneity and homogeneity modeling of the lithofacies in an Iranian oil field.
Methodology
Plurigaussian simulation
Truncated Gaussian simulation was first coined by Matheron et al. (1987) to simulate the Geo-domains with sequential ordering in a domain. One application in reservoir modeling can be found in Liu et al. (2016) for stochastic modeling of eight lithofacies in an oilfield. Beucher and Renard (2016) also explained precisely how this methodology is incorporated for digital modeling of geological phenomena. The basic idea of this approach is to define one Gaussian random variable whose spatial continuity is defined by indicator variograms. This regionalized variable then will be divided into discrete classes corresponding to each lithofacies. Following this mechanism, the threshold values are inspired from proportion of each of these lithofacies (Armstrong et al. 2011). For instance, in a sedimentary geological setting, there may exist a usual ordering between lithofacies. Figure 1 as an example shows how one realization (a) can be generated according the sequential ordering through five different types of lithofacies in a siliciclastic platform after truncation of an underlying Gaussian random field (b & c). In this case, Sand touches the Shale sand and Shale sand is in direct contact with Shale, in which Shale has a unique border with Limestone. The Limestone manifests itself via an explicit border with Argillite limestone. The underlying thresholds for separating the classes are arbitrary defined: − 1.987, − 0.487, 0.865, and 1.924.
In some sort of cases, truncated Gaussian is too restrictive to be applicable. For example, if there is no natural sequence or one can distinguish a forbidden contact between the lithofacies. To come up with this problem, Plurigaussian simulation (Galli et al. 1994) is an alternative method designed to adapt to a wider range of complicated types of geological contacts. In particular it has been widely applied to the modeling of petroleum reservoirs (Zagayevskiy and Deutsch 2016; Beucher and Renard 2016; Martinious et al 2017; Cahutru et al. 2015; Almeida 2010). The bottom line of the plurigaussian simulation is to extension of one Gaussian random field into two or more ones and using a truncation rule to convert the Gaussian data into lithofacies acting. Generally speaking, the practical implementation of the model can be summarized as the follow (Armstrong et al. 2011):
Definition of model parameter
Truncation rule consists in splitting a space into sub-classes, which associates the values of the Gaussian random fields with the geological domains. (Armstrong et al. 2011; Lantuéjoul 2002; Le Loc’h et al. 1994). Figure 2 shows the same siliciclastic platform (as mentioned in Fig. 1) with more complex contact relationship. In this case, the sequential ordering is not anymore represented between whole lithofacies and as can be seen from the truncation rule (Fig. 2c), the Shale is in contact with both Limestone and Argillite limestone simultaneously (Fig. 2a). So, the two Gaussian random fields (Fig. 2d, b) should be simulated and truncated considering the truncation thresholds. Let us suppose that \(N\) is underlying Gaussian random fields, grouped into a vector random field \(Z=\{ Z\left( x \right);x \in {R^d}\}\) with \(N\) components, \(M\) lithofacies domains and \(g(.)\) is the joint probability density function of the Gaussian random fields. To calculate the probability of occurrence of the ith lithofacies domain at a given location \(x\), one needs to solve the following equation analytically or numerically (Armstrong et al. 2011):
Covariances or variograms of the underlying Gaussian random fields characterize the spatial continuity of these fields, and the geological domains can be obtained after applying the truncation rule. For any separation vector h, the indicator cross variogram between two geological domains (with indices \(i\) and \(j\)) is derived from the corresponding non-centered covariance (Armstrong et al. 2011):
with
If \({D_i}\) and \({D_j}\) are rectangular parallelepipeds of \({{\mathbb{R}}^N}\) and the components of the vector random field \({\varvec{Z}}\) are independent, the second member of Eq. (3) is a function of the direct covariances or variograms of the components of \({\varvec{Z}}\) and can be calculated by numerical integration (Dowd et al. 2003) or using the expansions into Hermite polynomials (Emery 2007). This establishes a link between the variograms of the underlying Gaussian random fields and the indicator variograms, which are accessible experimentally from the observed geological domains at sampling locations. The former can, therefore, be determined according to the fitting of the latter, quiet often, through a trial-and error procedure (Le Loc’h and Galli 1997; Emery 2007; Armstrong et al. 2011).
Conditional simulation
The simulation can be performed in three main steps after definition of model parameters (Lantuéjoul 2002; Emery 2007; Dowd, 2003; Armstrong et al. 2011). The first step is converting the categorical data into Gaussian random fields that can be realized by an iterative algorithm known as the Gibbs Sampler (German and German 1984; Casella and George 1992). The second step consist in simulation of Gaussian random fields at target locations, conditionally to the values obtained from the Gibbs sampler. This step can be implemented by any algorithm for simulating stationary Gaussian random fields: Cholesky decomposition of the covariance matrix (Davis 1987), sequential Gaussian simulation (Ripley 1987; Deutsch and Journel 1992; Gomez-Hernandez and; Journel 1993), discrete spectral simulation (Chiles and Delfiner 1997), continuous spectral simulation (Shinozuka 1971; Mejia and Rodrigues-Iturbe 1974; Lantuéjoul 2002), and turning bands simulation (Matheron 1973; Lantuejoul 1994; Emery and Lantuéjoul 2006), to name a few (see also Chiles and Delfiner 2012 and reference therein). The third step is truncating the Gaussian random variables according to the truncation rule and obtain the simulated domains.
Hierarchical simulation
Two-dimensional truncation rule allows intuitively interpreting the contact relationship among lithofacies in the region. However, it restricts the process of modeling whenever there exists more than four or five lithofacies with complex contact relationship. To overcome this impediment, following Xu et al. (2006) and Emery (2007); Madani and Emery (2015) increased the number of Gaussian random fields to permit whole geological domains to be in contact together for modeling seven rock units in the copper Rio-Blanco deposit located in Chile. In this study, the hierarchical approach is based on the geo-chronology of the rock units. Maleki et al. 2016 also applied the hierarchical simulation for modeling ten rock types in an iron ore deposit with more complicated relationship including some forbidden contacts. This technique is more flexible and is a particular case of plurigaussian simulation based on iteratively truncation of several Gaussian random fields. The proposed approach splits the region into sublayers. For example, in the previous siliciclastic platform, based on this concept, the first layer is Sand, Shale sand, and Shale and its complement, while the second layer only conveys Limestone and Argillite limestone (Fig. 3). The truncation threshold and variogram analysis remain unchanged and one can define the underlying lithofacies at location \({\varvec{x}}\) for such a case, corresponding to two Gaussian random fields \(\left\{ {{Z_1},{Z_2}} \right\}\) and four truncation threshold \(\left\{ {{t_1},{t_2},{t_3},{t_4}} \right\}\) as below:
Heterogeneous hierarchical modeling
The domain is not always stationary and homogenous. For example, in some petroleum reservoirs, due to the sedimentary sequences and cyclic changes during deposition, the lithofacies vary vertically and laterally which make the reservoir heterogeneous. Figure 4 shows how the same siliciclastic platform may show heterogeneous behavior through the region of interest. As can be seen, the Sand is deposited in one part without any replications through other parts (model nos. 1 & 2). In model number three as another example of heterogeneous phenomena, the Limestone is formed in north section of the region with no any combination with other lithofacies. Stochastic modeling of these kind of geological layout by conventional hierarchical approaches proves to be too restrictive. To account for these changes, some approaches such as vertical proportion curves (Matheron et al. 1987; Ravenne et al. 2002) have been designed to estimate the domain proportions as a function of depth. Beucher et al. (2006) constructed a 3D matrix of proportion curves to model the evolution in the proportions both vertically and laterally. The proportions were first calculated locally, in sampled areas, then interpolated (by kriging) over a regular grid covering the region of interest. Inferring regionalized proportions can also account for secondary data, such as geophysical information (Moulière et al. 1997; Moulière 1998). Actually, static reservoir modeling of an oilfield most often suffers from lack of adequate information obtained from well data and the idea is how to model such a reservoir with those few data. In contrary, seismic information such as acoustic impedance (AI) plays a beneficial role for modeling the heterogeneous lithofacies as the secondary variable. Abundant information of this kind of data contributes to the lithofacies variations characteristics. Therefore, to providing this information to modeling the lithofacies, the first step is to calibrate the seismic data to the lithofacies proportions at well locations. The interested reader for considering the method of calibration is referred to Pyrcz and Deutsch (2014). The calibrated proportion then can be estimated by any linear interpolation methods such as kriging. Indeed, the produced maps for each lithofacies demonstrate the region of that lithofacies in high and low probability varying gradually between 0 and 1, respectively, in which they mimic valuable secondary information within each pixel. In this case, after inferring the local proportions, the truncation rule is as the same as presented previously, but the thresholds vary locally instead of global proportion assumption, honoring these generated maps of calibrated proportion.
Geophysical attribute
Acoustic impedance (AI) is a layer-based property of the earth that could be retrieved from seismic data using inversion techniques. This technique is considered as the reverse process of forward modeling which involves creating a synthetic seismic section based on an earth model. Based on the type of input seismic data for inversion techniques, there are two main seismic inversion approaches known as pre-stack and post-stack inversions. The data set considered in this paper as secondary value of the modeling, is prepared based on post-stack inversion that provide acoustic Impedance (AI) property volume. AI is a layer property and closely related to rock/reservoir and fluid property such as lithology, porosity and pore fluid which then could be suitable for lithofacies and seismic stratigraphic studies. AI data consist more information compared to the seismic data, since it is integrating several sources of data; typically seismic information, well logs and seismic velocity information. Seismic inversion technique increases the resolution of seismic data by reducing the effects of wavelet tuning and attenuating the random noise.
Sonic and density well logs are essential to generate synthetic seismogram required for AI inversion. There could be some problems in well logs data, such as wellbore washout, casing point, and different loggings run. To compensate these errors, all suspicious values of logs are corrected or omitted and then the intervals with no logs data, are estimated from other logs, based on artificial neural network approach. Investigation of the seismic data and interpreted horizons revealed the suitable quality of these data as input of AI inversion.
After quality control of the input data, the well to seismic correlation and wavelet extraction from post-stack seismic data can be performed. In this study, one wavelet extracted using five wells. Finally after generation of low-frequency model and determination of inversion parameters, constrained sparse spike inversion (CSSI) process was utilized on the seismic data. Figure 5 shows an example of AI inversion section as an instance.
Geological setting
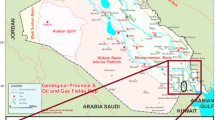
The study area is located at the junction of the Arabian Shield and Iranian continental block that belong to two different lithospheric plates (Arabian and Eurasian). Collision of these plates at the Mesozoic/Cenozoic boundary produced the Zagros Fold Belt and the large Mesopotamian Foredeep, which is a member of the Persian Gulf Basin. The area is located in the northwest Persian Gulf (Fig. 6) and the geologic time of the studied rocks is Albian. Albian stage occupies one of the most important places in the Mesozoic stratigraphy of the Persian Gulf with high-frequency tectonic changes. A rapid sea level drop in early Albian initiated deposition of Kazhdumi and Burgan over the Dariyan and Shuaiba carbonates. In the deeper part of the basin where break in sedimentation is documented between Dariyan carbonates, and the Kazhdumi, deposition may have commenced in the Late Aptian (Ghazban 2007). During this time, the Arabian Shield became the source for the clastic sediments in that area. From the Arabian Shield to the Iranian coast, these clastics pass into the neritic argillaceous limestone and organic-rich shales (Fig. 6) of the Kazhdumi formation (Konyuhov and Maleki 2006). Thickness of the formation increases toward northwest and east of Persian Gulf and decreases on the middle part.
Lithofacies distribution of the Lower Cretaceous (Aptian-Albian) in the Persian Gulf (after Konyuhov and Maleki 2006)
There is an interval of clastic sediments (claystone, siltstone, and sandstone) in the lower part of the Kazhdumi formation. This unit was deposited during the transgression on post Aptian unconformity surface in a deltaic environment. The sandy part of this unit is hydrocarbon reservoir in some part of north of Persian Gulf. However, strong facies changes of the layer on one hand and poorly distributed data on other hand are the main challenge for modeling this reservoir.
The Kazhdumi formation is time equivalent of three stratigraphic units in the western Persian Gulf countries. These three formations are Nahr Umr, Dair, and Burgan, which are, respectively, equivalent to the Upper, Middle, and Lower Kazhdumi Formation. This formation reaches a thickness of 230 m at the type section in northwest Zagros but thins to 40–50 m in southern Persian Gulf. But In this work, to handle Kazhdumi Facies estimation, it was divided into five zones, Kz-1 to Kz-5, based on well data. These five zones are equivalent to three previously known stratigraphic parts of the formation. Kz-1 and Kz-2 are equivalent to the upper and middle Kazhdumi, respectively, but Kz-3, Kz-4, and Kz-5 zones are all equivalent to the lower Kazhdumi (Burgan) formation. These three zones have different distributions in the study area. However, target of the study is stochastic lithofacies modeling for the Kz-4 in the area.
Presentation of the data set
The dataset is composed of 11 well data upscaled into two meters located in layer no. 261 of Kazhdomi-4 formation. This layer mainly consists of siltstone (50%), sandstone (30%) and marl (20%). Although, it consists of sandstone (70%) and shale (30%) in southern part, pure sandstone in the southwest, and moderately shale (50%) and sandstone (50%) in the middle part of the study area. The location map can be seen in Fig. 7 to intuitively considering well distribution in the region. As a typical act in oil reservoirs, we are dealing with a few conditioning information and the majority of wells are located far enough, in some case, it reaches to 5 km. For instance, some lithofacies are presented only one time in a well. To save the space through the paper, all the lithofacies are coded into the numbers as presented in Table 1.
Because of irregularity of the sampling mesh and preventing any bias in the calculation process, the proportion of each lithofacies is determined before and after declustering. As can be inspired form declustered proportion, the most covered lithofacies in the region is Sand, Sh (70, 30) and the least one is the sand located in western part of the region. According to the geological interpretation, the lithofacies 116 and 113 should be at the left side of the region and the right side, the lithofacies 83 and 106 are more dominated. This consideration is a key to validate the results.
Model parameters
Truncation rule
The contact relationship according to the geological consideration is defined as: alrgLst, Sh (70, 30) is in contact with Sh. ShSand, argLst (50, 30, 20) and this lithofacies itself then is in contact with other lithofacies [Sh, Sand, ShSand (50, 40, 10), SandSh, ShSand, MI (50, 30, 20), Sand and Sand, Sh (70, 30)]. Therefore, it is supposed that there should not be any geological relationship between the first lithofacies (code: 83) and (code: 107, 108, 113, and 116). As mentioned earlier, in the case of complex contact relationship, the hierarchical plurigaussian simulation provides such a flexibility to handle the process of modeling. So, one can see the conceptual hierarchical relationship of the underlying lithofacies in Fig. 8. So, four sublayers can, therefore, be concluded as follow:
-
1.
First layer: lithofacies 83 is in direct relationship with lithofacies 106 and the former one is in contact with its complement.
-
2.
Second layer: lithofacies 107 is in direct relationship with its lithofacies complements (106, 108, 113, and 116) except lithofacies 83.
-
3.
Third layer: lithofacies 108 is in direct relationship with its lithofacies complements (106, 107, 113, and 116) except lithofacies 83.
-
4.
Fourth layer: lithofacies 113 is in direct relationship with its complement (106, 107, 108, and 116) except lithofacies 83.
As four layers are considerable in this case, consequently, four Gaussian random fields are recognized and therefore, the hierarchical relationship of the lithofacies requires to be described through the following system representing a four-dimensional flag:
Truncation thresholds
Such a hierarchical contact based on the explained truncation rule involves five truncation thresholds, which can be defined corresponding to the declustered proportion (Armstrong et al. 2011). To calculation of the proportions, it is required to transfer the categorical data (in this place, lithofacies) to indicator data defined by 0, 1 or unknown values, where the indicators can be defined thanks to the above system (5) (Table 2). Hence, Proportion of the first lithofacies threshold according to the Eq. (1) equals \({G^{ - 1}}\left( {{P_{83}}} \right)= - 2.063\), where \(G\) stands for the cumulative distribution function of a normal standard distribution \(N(0,~\;1)\). As \({t_1}\) and \({t_2}\) are independent in one Gaussian random field, the second threshold can be defined as \(\left[ {1 - {G^{ - 1}}\left( {{P_{83}}} \right)} \right] \times {G^{ - 1}}\left( {{P_{106}}} \right)= - 1.095\), the same procedure can be applied for the remaining thresholds.
Variogram analysis
To derive variograms for the four Gaussian random fields \(\left\{ {{Y_1},{Y_2},{Y_3},{Y_4}} \right\}\), experimental indicator variograms are calculated over the indicator variables (Table 2) along the three specified main anisotropy direction: maximum continuity \(\left( {150^\circ } \right)\), minimum continuity \(\left( {60^\circ } \right)\), and vertical. Indeed, the approximate anisotropy directions are inferred from two source of information: the seismic map of geophysical attribute and the nearest neighborhood interpolation map of the well data. Although the deterministic techniques such as nearest neighborhood cannot quantify the uncertainty at unsampled locations and provides just one exact boundary among two adjacent lithofacies, but they produce some intuitively useful consideration about the approximate layout of the lithofacies.
The next step is to fit theoretical variograms to the experimental variograms. However, the experimental indicator variograms calculated from well data resulted in a very patchy sort of experimental points in the variogram graph and one cannot fit a proper model. This problem emerged due to the lack of adequate lithofacies data at well location. An idea is to use the seismic information instead, owing to the fact that it conveys abundant knowledge through the entire region (Pyrcz and Deutsch 2014). As mentioned earlier, calibrated proportions by seismic information could propose the maps showing the probability for each lithofacies. Based on the most probable plot obtained from these probability maps, one can generate a categorical map (Fig. 9). This map bears a resemblance to the nearest neighborhood map and could also provide visual favorable information. The experimental indicator variograms are derived again, but this time from the most probable map so obtained. Figure 10 shows that the experimental variograms are reasonable to fit a model. The fitting process is a type of semi-automated algorithm presented by (Emery 2010). It is worth mentioning that the fitted model of variogram, which is cubic, getting an impact from the smoothness of the contact lines between the lithofacies. This type of variogram leads to regular boundaries (Lantuejoul 2002).
Plurigaussian simulation
Provided with the inferencing the model parameters (truncation rule, truncation thresholds, and variogram analysis), to consideration whether the geophysical information has an impact on the probabilistic modeling of lithofacies domains, the geostatistical simulation of lithofacies has been implemented over three following cases:
Case I
In this case, 100 realizations have been generated, using a procedure applied by (Maleki et al. 2016) conditionally to the well data regardless of any geophysical considerations. In truncation rule, the declustered global proportions have been inserted to infer the truncation thresholds.
Case II
In this case, following Madani and Emery (2015), 100 realizations have been generated conditionally to the well data, but the local calibrated proportions acquired from seismic information “Model parameters” section are used for truncation threshold, instead of declustered global proportions. The truncation rule and variogram analysis remain also unchanged.
Case III
In this case, 100 realizations have been generated conditionally to the well data, but for truncation thresholds, the declustered global proportions have been used for lithofacies 83, 106, 107, 108, and for lithofacies 113 and 116, the calibrated proportions have been used which acquired from seismic information. It should be noted that the proportions are then rescaled to sum to 1.
Figures 11 and 12 depict two different realizations in a same plan view obtained from three above methodologies. In case I, the truncation rule is favorably recognized (hierarchical relationship between lithofacies (Figs. 11, 12a), but according to the the assumption of non-stationary for some lithofacies such as 113, the heterogeneity for this lithofacies is not honored. For instance, realization no. 20 displays that an extension of this lithofacies can be found in north-east of the region. This phenomenon according to the geological consideration cannot be interpreted. In case II, both realizations could not meet the truncation rule (Figs. 11, 12b) and all the lithofacies are in contact altogether. This problem arises in the interest of equal weighting thresholds from calibrated proportions in truncation rule. The heterogeneity for lithofacies 113 somewhat is honored, but the realizations lack realism from the contact relationship point of view. But in case III, the results are more interesting, one can see from Figs. 11 and 12c that the heterogeneity for the lithofacies 113 is honored and the expected contact relationship is in complete agreement with truncation rule. Furthermore, the extension of lithofacies 83 and 106 as were expected agreed the geological understanding. Therefore, as mentioned earlier, the anticipation from geological consideration which met in this case is that, firstly, the lithofacies 83 should not have any relationship with others and, secondly, should demonstrate an extended region from north-east to south-east, sheltered by lithofacies 106. Attention must be taken in this place that all the realization are in complete compatibility with well data locations (Fig. 7).
Probabilistic modeling of facies domains
These realizations obtained from each case can then be post processed to calculate the uncertainty in the lithofacies at a local scale (within the blocks), by means of probability maps. These maps present a hint for the risk of finding a lithofacies at unsampled and sampled locations (Fig. 13). The frequency of occurrence of each lithofacies can be calculated for each block in complement of geological interpretation. The blue areas are those with high uncertainty and a low probability for a given lithofacies. In contrast, the red areas showing low uncertainty and high probability for finding that type of lithofacies. For saving the space, the probability maps of the third case are presented. As was attended, lithofacies 83 and 106 are in complete agreement with the geological interpretations.
Conclusion
Deterministic modeling of lithofacies is not able to provide the uncertainty through the layout of the boundaries. However, stochastic modeling has ability to manage the uncertainty at unsampled locations. In this paper, one stochastic approach known as hierarchical plurigaussian simulation has been applied of considering proportion for the truncation rule. Conventional approach of plurigaussian simulation approach based on stationary assumption uses the global proportion (declustered) which is insecure to reproduce the geological heterogeneity behavior of the Geo-domain. The second method which acknowledges the local proportion acquired from calibrated proportion of lithofacies with seismic information also fails to reproduce the desired contact relationship, although the special interpretation of some lithofacies is granted. The third case is more appealing. It represents more flexibility to work with calibrated local and declustered global proportions at the same time. The lithofacies with non-stationary behavior can be quantified with this local proportion acquired from the geophysical information. According to the geological interpretation and sedimentary evolution, lithofacies 113 & 116 can just be found in the east part of the region. Hence, the third case is in complete agreement with this interpretation and can be visually validated.
References
Alabert FG (1987) Stochastic imaging of spatial distributions using hard and soft information. Master’s Thesis, Stanford University, Stanford, CA
Armstrong M, Galli A, Beucher H, Le Loc’h G, Renard D, Doligez B, Eschard R, Geffroy F (2011) Plurigaussian simulations in geosciences. Springer, Berlin
Beucher, Renard (2016) Truncated Gaussian and derived methods. Computes Rendus Geosci 348:510–519
Beucher H, Doligez B, Yarus JM (2006) Modeling complex reservoirs with multiple conditional techniques: a practical approach to reservoir characterization. In: Coburn TC, Yarus JM, Chambers RL (eds) Stochastic modeling and Geostatistics: principles, methods, and case studies, volume II: AAPG Computer Applications in Geology, Oklahoma City pp. 289–299
Carle SF, Fogg GE (1996) Transition probability-based indicator geostatistics. Math Geol 28(4):453–476
Casella G, George EI (1992) Explaining the Gibbs sampler. Am Stat 46(3):167–174
Chautru JM, Meunier R, Binet H, Bourges M (2015) Geobodies stochastic analysis for geological model parameter inference. Pet Geostat 23:293–297
Chilès JP, Delfiner P (1997) Discrete exact simulation by the Fourier method. In: Baafi EY, Schofield NA (eds) Geostatistics Wollongong’ 96. Kluwer, Dordrecht, pp 258–269
Chilès JP, Delfiner P (2012) Geostatistics: modeling spatial uncertainty. Wiley, New York
Davis M (1987) Production of conditional simulations via the LU triangular decomposition of the covariance matrix. Math Geol 19(2):91–98
De Almeida JA (2010) Stochastic simulation methods for characterization of lithoclasses in carbonate reservoirs. Earth Sci Rev 101:250–270
Deutsch C (2006) A sequential indicator simulation program for categorical variables with point and block data: BlockSIS. Comput Geosci Vol 32:1669–1681
Deutsch CV, Journel AG (1992) GSLIB: Geostatistical software library and user’s guide. Oxford University Press, New York, p 340
Dowd PA, Pardo-Iguzquiza E, Xu C (2003) Plurigau: a computer program for simulating spatial facies using the truncated plurigaussian method. Comput Geosci 29(2):123–141
Emery X (2004) Properties and limitations of sequential indicator simulation. Stoch Env Res Risk Assess 18(6):414–424
Emery X (2007) Simulation of geological domains using the plurigaussian model: new developments and computer programs. Comput Geosci 33(9):1189–1201
Emery X (2010) Iterative algorithms for fitting a linear model of coregionalization. Comput Geosci 36(9):1150–1160
Emery X, Lantuéjoul C (2006) TBSIM: a computer program for conditional simulation of three-dimensional Gaussian random fields via the turning bands method. Comput Geosci 32(10):1615–1628
Emery X, Lantuéjoul C (2014) Can a training image be a substitute for a random field model? Math Geosci Vol 46(2):133–147
Galli A, Beucher H, Le Loc’h G, Doligez B (1994) The pros and cons of the truncated Gaussian method. In: Armstrong M, Dowd PA (eds) Geostatistical simulations. Kluwer, Dordrecht, pp 217–233
Geman S, Geman D (1984) Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell 6:721–741
Ghazban (2007) Petroleum geology of Persian Gulf. University of Tehran Publication, Tehran
Gómez–Hernández J, Journel AG (1993) Joint sequential simulation of multigaussian fields. In: Soares A (ed) Geostatistics Troia’92. Kluwer Academic, Dordrecht, pp 85–94
Journel AG (1983) Nonparametric estimation of spatial distribution. Math Geol 15(3):445–468
Journel AG, Alabert FG (1988) Focusing on spatial connectivity of extreme valued attributes: stochastic indicator models of reservoir heterogeneities, SPE Paper 18324
Journel AG, Huijbregts CJ (1978) Mining Geostatistics. Academic Press, London
Journel AG, Isaaks EH (1984) Conditional indicator simulation: application to a saskatchewan uranium deposit. Math Geol 16(7):685–718
Konyuhov AI, Maleki B (2006) The persian gulf basin: geological history, sedimentary formations, and petroleum potential. Lithol Min Resour 41:344–361
Lantuéjoul C (1994) Non conditional simulation of stationary isotropic multigaussian random functions. In: Armstrong M, Dowd PA (eds) Geostatistical simulations. Kluwer, Dordrecht, pp 147–177
Lantuéjoul C (2002) Geostatistical simulation, models and algorithms. Springer, Berlin
Le Loc’h G, Galli A (1997) Truncated plurigaussian method: theoretical and practical points of view. In: Baafi EY, Schofield NA (eds) Geostatistics Wollongong’96. Kluwer Academic, Dordrecht, pp 211–222
Le Loc’h G, Beucher H, Galli A, Doligez B (1994) Improvement in the truncated Gaussian method: combining several Gaussian functions. In: ECMOR IV, Fourth European Conference on the Mathematics of Oil Recovery. Røros, Norway
Liu L, Zhang J, Wang R et al (2016) Facies architectural analysis and three-dimensional modeling of Wen79 fault block, Wenliu oilfield, Dongpu depression, China. Arab J Geosci 9:714. https://doi.org/10.1007/s12517-016-2749-3
Madani N, Emery X (2015) Simulation of geo-domains accounting for chronology and contact relationships: application to the Rio Blanco copper deposit. Stoch Environ Res Risk Assess 29:2173–2191
Madani N, Emery X (2017) Plurigaussian modeling of geological domains based on the truncation of non-stationary Gaussian random fields. Stoch Environ Res Risk Assess 31:893–913
Maleki M, Emery X, Caceres A, Ribeiro D, Cunha E (2016) Quantifying the uncertainty in the spatial layout of rock types in an iron ore deposit. Comput Geosci 20:1013–1028
Martinius AW, Fustic M, Garner DL, Jablonski BVL, Strobl RS, MacEachern JA, Dashtgard SE (2017) Reservoir characterization and multiscale heterogeneity modeling of inclined heterolithic strata for bitumen-production forecasting, McMurray Formation, Corner, Alberta, Canada. Mar Pet Geol 82:336–361
Matheron G (1973) The intrinsic random functions and their applications. Adv Appl Probab 5(3):439–468
Matheron G, Beucher H, de Fouquet C, Galli A, Guerillot D, Ravenne C (1987) Conditional simulation of the geometry of fluvio deltaic reservoirs. In: SPE 1987 annual technical conference and exhibition, Dallas, Texas, pp 591–599. SPE
Matheron G, Beucher H, de Fouquet C, Galli A, Ravenne C (1988) Simulation conditionnelle à trois facies d’une falaise de la formation du Brent. Sciences de la Terre. Série Inform Géol 28:213–249
Mejia JM, Rodríguez-Iturbe I (1974) On the synthesis of random field sampling from the spectrum: an application to the generation of hydrologic spatial processes. Water Resour Res 10(4):705–711
Moulière D (1998) Intégration d’information sismiques pour la simulation de reservoirs. Thèse de Docteur de l’Ecole des Mines de Paris, pp. 182
Moulière D, Beucher H, Hu LY, Fournier F, Terdich P, Melchiori F, Griffi G (1997) Integration of seismic derived information in reservoir stochastic modeling using the truncated Gaussian approach. In: Baafi E, Schofield NA (eds) Geostatistics Wollongong’96. Kluwer Academic, Dordrecht, pp 374–385
Nazeri M, Asghari O, Emery X, Azizzadeh M, Khoshbakht F (2016) Fracture network modeling using Petrophysical data, an approach based on geostatistical concepts. J Nat Gas Sci Eng 31:758–768
Pyrcz MJ, Deutsch CV (2014) Geostatistical reservoir modeling. Oxford University Press, New York
Ravenne C, Galli A, Doligez B, Beucher H, Eschard R (2002) Quantification of facies relationships via proportion curves. In: Armstrong M, Bettini C, Champigny N, Galli A, Remacre A (eds) Geostatistics Rio 2000. Kluwer Academic, Dordrecht, pp 19–40
Ripley BD (1987) Stochastic simulation. Wiley, New York
Shakiba S, Asghari O, Keshavarz N, Sarallah S, Tokhmechi. B (2015) Fault and non-fault detection based on seismic data through min/max autocorrelation factors and fuzzy classification. J Nat Gas Sci Eng 26:51–60
Shinozuka M (1971) Simulation of multivariate and multidimensional random processes. J Acoust Soc Am 49(1B):357–367
Strebelle S (2002) Conditional simulation of complex geological structures using multiple-point statistics. Math Geol 34(1):1–22
Walker RG (1992) Facies, facies models and modern stratigraphic concepts. Geological Association of Canada, Canada, pp 1–14
Xu C, Dowd PA, Mardia KV, Fowell RJ (2006) A flexible true plurigaussian code for spatial facies simulations. Comput Geosci 32(10):1629–1645
Zagayevskiy Y, Deutsch CV (2016) Grid-free petroleum reservoir characterization with truncated pluri-Gaussian simulation: Hekla case study. Pet Geosci 22:241–256
Acknowledgements
This research was funded by the National Elites Foundation of Iran in collaboration with Research Institute Petroleum of Industry in Iran under the project number of 9265005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Madani, N., Biranvand, B., Naderi, A. et al. Lithofacies uncertainty modeling in a siliciclastic reservoir setting by incorporating geological contacts and seismic information. J Petrol Explor Prod Technol 9, 1–16 (2019). https://doi.org/10.1007/s13202-018-0531-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-018-0531-7