Design of safe well on the top of Atharamura anticline, Tripura, India, on the basis of predicted pore pressure from seismic velocity data

Abstract

Pore pressure prediction is an essential part of wildcat well planning. In India, Tripura sub-basin is characterised by huge anticlines, normal faults and abnormally pressured formations. These factors push the wildcat well planning in this area into wide margin of uncertainty. Pore pressures were predicted from seismic velocities by using modified Eaton’s method over the synclinal and flank part of Atharamura to understand the pressure succession towards the anticline. These predicted pore pressures on the flank part lead to a reasonable match when plotted with offset well-measured pore pressures. To reduce the uncertainty, fracture pressures were established by various methods such as Hubbert and Willis method and Matthews and Kelly method from predicted pore pressures. But the fracture pressures were predicted with available horizontal stress correlations due to lack of Poisson’s ratio curve for the study area. The mud pressure required to drill the well is calculated using median line principle, and hence drilling mud window is established by assuming virtual tight conditions. The plot of equivalent circulation density versus depth suggests that well can be drilled with two casing policy. But it is found that adding one more casing pipe will ensure the safety of well. Casing pipes were designed on the basis of collapse pressure, burst pressure and tensile load. Finally, a well plan which includes pore pressure, fracture pressure, drilling mud policy, casing policy and kick tolerance graph were proposed to give clear picture on well planning on the top of the anticline in pore pressure point of view.

Introduction

The systematic study of the fluid characteristics of subsurface formations is a critical importance in the well planning and formation evaluation. Pore pressure prediction plays a very important role in studying the hydrocarbon trap seals, mapping of hydrocarbon migration pathways, analysing trap configurations and basin geometry and providing calibrations for basin modelling. With the help of pore pressure prediction, an appropriate mud weight to be selected and drilling casing program to be optimised, safe and economic subsurface drilling can be designed. Nowadays, the prediction of pore pressure formed an integral part of prospect evaluation and well planning. The main objective of this study is to plan a safe well over Atharamura anticline to explore and exploit hydrocarbons. Planning an exploratory well from seismic velocities aims to produce: pore pressure prediction, establishing drilling mud window, target depth selection, optimal mud policy, kick tolerance guidelines and general guidelines for drillers. The main challenges in this area are there is no seismic velocity data available on the top of the Atharamura anticline. So, it is decided to take a model-based seismic velocity data which are developed by the operating company from offset seismic data. As the data are issued by the operating company, seismic velocity model-related details are not discussed here.

Hydrostatic pressure is defined as the pressure exerted by a column of water at any given point in that column, when the water at rest. It is the pressure due to the density and vertical height of the fluid column exerts force in all directions perpendicular to the contacting surfaces (Bourgoyne et al. 1991).

Pressure exerted on the fluids trapped inside pore spaces of rocks is called pore pressure or formation pressure. In normally pressured formations, pore pressure will be equal to the hydrostatic pressure to the corresponding depth, when exceeds or lags the hydrostatic pressure gradient, over-pressure or sub-pressure develops (Chillingar et al. 1995).

Terzaghi et al. (1948) developed the basic relation that the pore pressure at any depth in the formation will be the difference between overburden pressure (vertical stress) and grain pressure (effective vertical stress). At any depth, overburden pressure will be the summation of weight of the sediments and fluids in it. When the fluid in pore starts supporting the weight of the overlying sediments, over-pressure occurs.

The main causes of abnormal pore pressure or over-pressure are under-compaction, fluid volume increase, fluid migration and buoyancy, tectonics (Swarbick et al. 1999). The role of vertical effective stress at different subsurface conditions is illustrated in Fig. 1.

Fig. 1

Effect of vertical effective stress to different subsurface conditions

Compaction is the process associated with the sedimentation. When the deposition occurs, grain supports the weight of overlying sediments due to point-to-point contact between the grains. As deposition proceeds, fluid trapped in the pore spaces escapes and porosity reduces to balance the overburden weight so as to maintain the normal hydrostatic pore pressure. Even this equilibrium (pore water expulsion) is distributed by the rapid sedimentation (Rubey 1927) of absence of permeable pore networks, abnormal or over-pressure occurs. This change in normal compaction trend is called under-compaction or compaction disequilibrium. This is the dominant over-pressure causing mechanisms shallow depth.

Expansion of pore fluids at deeper depths is the main over-pressure causing mechanism as fluid volume increases under the temperature conditions (Bowers 1995). If pore volume remains constant with burial and temperature increase, the thermal expansion of water can cause extremely rapid pore pressure increase. But the integrity of the seal supporting over-pressure should strong enough to encounter the pressure increase.

Digenesis is defined as the physical, chemical or biological alteration of sediments into the sedimentary rock at relatively low temperature and pressure that can result in changes to the rock’s original mineralogy and texture. It includes compaction, cementation, re-crystallization and replacement. Clay contains water in the form of free water and bound water. Bound water having higher density becomes free water during digenesis and undergoes volume expansion. If the free water is not allowed to escape due to rapid sedimentation, it will lead to increase in pore pressure. Mostly, pronounced over-pressure causing mechanism digenesis occurs at the bottomhole temperature of 200 °F. Clay digenesis is the main over-pressure causing mechanism in shale.

Kerogen maturates into oil and gas, results in excess fluid and oil cracking into gas, again resulting in excess fluid. Under good sealing and low-permeability conditions, this phenomenon can cause over-pressure (Huffman and Bowers 2002). This cause has been postulated as a possible cause of high (17 ppg) pore pressure recorded in the high-pressure/high-temperature (HP/TP) reservoirs in the deep Jurassic clay stones and sandstones of the central North Sea.

Tectonic plays main role in the over-pressure development as the validity of over-pressure depends on the seal integrity which can be offered by tectonics. The additional horizontal tectonic stress created by folding can compact the clays latterly. For the formation to remain normally pressured, the increased compaction must be balanced by pore water expulsion. If the formation water can’t escape, abnormal pressure will result. A very dangerous form of unloading occurs when sediments are uplifted by tectonic activity. Uplifted sediments alone will not cause unloading if the overburden load is not changed, but when the overburden is reduced during uplift either by sync—depositional tectonic process—or by erosion, the accompanying reduction in overburden results in the original in situ pore pressure being contained by a much lower overburden, which results in a reduction in the effective stress and unloading.

In this paper, our main objective is to plan a safe well over Atharamura anticline to explore and exploit hydrocarbons. Two seismic sections are considered for the purpose one at flank part and another at syncline part of the Atharamura anticline as shown in Fig. 2. Pore pressures were predicted from these two seismic sections using modified Eaton’s method and fracture gradients were predicted as well. The fracture pressures were predicted using various methods such as Hubbert and Willis method, Matthews and Kelly method for the better accuracy due to the highly geological complexity of the study area. Tectonic correction is very essential for such type of geologically complex area to get the accuracy of fracture pressure. Here, the fracture pressures predicted by modified Eaton’s method and tectonic corrected were considered for the well planning. Planning an exploratory well from seismic velocities aims to produce pore and fracture pressure, drilling mud window, optimal mud policy selection, propose safe casing policy and kick tolerance guidelines.

Fig. 2

(Reproduced with permission from Ganguly 1993)

Anticlines and synclines in and round Atharamura, Baramur and Tulamura anticlines. Map depicts the structural position of the study area

Study area

The Tripura region is situated in the north-eastern sector of India and is surrounded by the territories of Bangladesh and Burma, except in the north-eastern part, which is bordered by the Indian states Assam and Manipur.

Geographically, it is bounded by the latitudes 22°00′N–24°30′N and longitudes 91°10′E–93°30′E.

Geomorphologically, this region is characterised by an alternating succession of ridges and valleys of roughly north–south trend. The general elevation of the region rises eastward from a few tens of metres in the area adjoin Bangladesh (Baghwan 1999) plains in western Tripura to about 1800 metres in eastern Mizoram bordering the Chin Hills of Burma.

Beyond the geological boundaries, the sub-basins of Tripura and Bangladesh form a single geological entity representing a part of the basinal facies of Assam–Arakan basin which came into existence during the late Cretaceous collision and concomitant subduction of the Indian plate margin below Burmese plate. This combined geological unit can be subdivided into three broad elements: Sylhet through the north, Tripura–Chittagong fold belt to the east and south-east and Patuakhali depression to the south. A series of long and narrow anticlines with N–S treading axial traces separated by broad intervening synclines are present in Tripura FTB. Some of these anticlines show an echelon offsets (Fig. 2).

The sedimentation in this basin probably started with a break-up of the Gondwana land in Jurassic and Cretaceous and had been almost continuous since then. The Palaeocene Eocene Disang formation forms the base overlain by rocks of the Barail Group which is divided into Lower Linsang followed by Jenam and Renji formation. The overlain Miocene Surma Group is made up of Lower, Middle and Upper Bhuban formations with Bokabil formation occupying the topmost part. The Tipam, Dupitila, Disang formations constitute the Upper Neogene units (Fig. 3). The oldest rock exposed in the core of many of the anticlines belongs to Bhuban formation. As of now, most of well drilled on the anticlines where Middle Bhuban is covered by Tipam, Bokabil formations. Unlike other anticlines, Middle Bhuban is exposed to the surface on the Atharamura anticline where overlying sediments were eroded and offer less sediment thickness for drilling. So, super-pressure is expected to start at shallow depth on Atharamura anticline, where drilling is highly challengeable due to the well control problems.

Fig. 3

Stratigraphy and petroleum system of Tripura, Assam–Arakan basin (the red intervals highlighted above reflect the gross intervals within which multiple pays are producing). The range of pays varies between 40 and 80 m. (After Akram et al. 2004). The gross thickness of gas pools is shown with red rectangles

Theory

From the literature available, it’s clear that Bower’s approach is more promising in predicting the pore pressure, but needs offset well data, effective stress data and extensive calibration to the graphical constants. On concerning the study area which starves of exploration, availability of data is the main constraint in selecting the prediction method. Presently, seismic velocity data at synclinal and flank part of the Atharamura are available. The Eaton’s method is used to predict pore pressure, and certain corrections are made to reduce the uncertainty in the estimation of the pore pressure. The general approach is to develop normal compaction curve for the formation of interest and comparing it with actual compaction curve and over-pressure is calculated in terms of deviation from normal trend. The development of normal compaction parameters plays a vital role in determining the reliability of the pore pressure prediction.

Pore pressure

Eaton’s method (1975) approximates the effective vertical stress with ratio of sonic log velocities and resistivity values. The modified Eaton’s equation for variable overburden gradient is

$$P_{\text{p}} = \sigma_{\text{ob}} - \left( {\sigma_{\text{ob}} - P_{{{\text{p}}\;{\text{normal}}}} } \right)\left( {\frac{{V_{\text{observed}} }}{{V_{\text{normal}} }}} \right)^{3} ,$$

$$P_{\text{p}} = \sigma_{\text{ob}} - \left( {\sigma_{\text{ob}} - P_{{{\text{p}}\;{\text{normal}}}} } \right)\left( {\frac{{R_{\text{observed}} }}{{R_{\text{normal}} }}} \right)^{1.2} ,$$

where $V_{\text{observed}}$ is observed values of interval velocity at the depth of interest, $R_{\text{observed }}$ observed values of resistivity at the depth of interest, $V_{\text{normal }}$ values of interval velocity if the formation would have been compacted normally at the same depth, $R_{\text{normal }}$ values of resistivity if the formation would have been compacted at the same depth, $\sigma_{\text{ob}}$ overburden stress, $P_{{{\text{p}}\;{\text{normal}}}}$ normal pore pressure, and $P_{\text{p}}$ predicted pore pressure.

Fracture pressure

Using accepted engineering theory, Hubbert and Willis (1957) showed that a surface stress regime is such that, when the normal faults occur (60° to the horizontal), the minimum horizontal compressive stress is of the order of one-third to one-half of the maximum vertical compressive stress and proposed the following relationship:

$$\frac{{P_{\text{f}} }}{D} = \left( {\frac{{P_{\text{ov}} }}{D} - \frac{{P_{\text{p}} }}{D}} \right)\left( {\frac{\vartheta }{1 - \vartheta }} \right) + \frac{{P_{\text{p}} }}{D}.$$

On assuming unit overburden gradient and $\vartheta = 0.25$, above equation reduces to as follows which is known as Hubbert–Willis equation:

$$\frac{{P_{\text{f}} }}{D} = \frac{1}{3}\left( {\frac{{P_{\text{ov}} }}{D}} \right) + \frac{2}{3}\left( {\frac{{P_{\text{p}} }}{D}} \right),$$

where $\frac{{ P_{\text{f}} }}{D}$ is fracture gradient (psi/ft), $\frac{{P_{\text{ov}} }}{D}$ overburden gradient (psi/ft), and $\frac{{P_{\text{p}} }}{D}$ pore pressure gradient (psi/ft).

Matthews and Kelly (1967) presented a fracture gradient equation similar to Hubbert’s. However, they introduced the concept of a variable horizontal-to-vertical stress ratio instead of constant 0.33.

$$\frac{{P_{\text{f}} }}{D} = k_{\text{i}} \left( {\frac{{\sigma_{\text{v}} }}{D}} \right) + \frac{{P_{\text{p}} }}{D},$$

where $k_{\text{i}}$ is stress ratio and $\frac{{\sigma_{\text{v}} }}{D}$ compaction or effective stress gradient (psi/ft).

However, both methods hold good only in relaxed formations (normal faults) which is rarely encountered in drilling. Assumption of unit overburden gradient is also not correct and leads to wrong estimation of fracture pressure.

Eaton (1969) further improved the Hubbert’s equation by introducing the variable Poisson’s ratio and variable overburden gradient. Eaton defined Poisson’s ratio as the ratio of the lateral unit strain to the longitudinal strain in a body that has been stressed longitudinally within its elastic limit. Eaton’s relationship to find the fracture gradient is given below:

$$\frac{{P_{\text{f}} }}{D} = \left( {\frac{{P_{\text{ov}} }}{D} - \frac{{P_{\text{p}} }}{D}} \right)\left( {\frac{\vartheta }{1 - \vartheta }} \right) + \frac{{P_{\text{p}} }}{D}.$$

Eaton’s Poisson’s ratio is not a function of the rock but of the regional stress field, the horizontal-to-vertical stress ratio. Thus, since Hubbert and Willis assumed that the minimum horizontal stress is approximately one-third, it corresponds to a Poisson’s ratio of 0.25 through the above relationship. Eaton presented empirical curves for Poisson’s ratio versus depth calculated from Gulf coast data (Fig. 4). These curves are independent of rock type. Thus, it is found that Poisson’s ratio varies from 0.25 to 0.5.

Fig. 4

Eaton’s Poisson’s ratio curve for Gulf of Mexico region

Modified Eaton’s method is very important to calculate fracture pressure gradient at geologically challenged area (Daines 1982). This method includes one more parameter known as superposed horizontal tectonic stress $\left( {\sigma_{\text{t}} } \right)$. Tectonic stress correction is not required in this method.

$$\frac{{P_{\text{f}} }}{D} = \frac{{\sigma_{\text{t}} }}{D} + \left( {\frac{{P_{\text{ov}} }}{D} - \frac{{P_{\text{p}} }}{D}} \right)\left( {\frac{\vartheta }{1 - \vartheta }} \right) + \frac{{P_{\text{p}} }}{D},$$

$$\sigma_{\text{t}} = \left( {P_{\text{ov}} - P_{\text{p}} } \right) \times {\text{Horizontal}}\;{\text{stress}}\;{\text{ratio}} .$$

Another empirical method was published by Anderson (1972). The aim was to derive all necessary parameters to estimate fracture pressures from electric logs. Utilising Biot’s stress/strain relationships for porous media, they developed the following relationship:

$$\frac{{P_{f} }}{D} = \left( {\frac{2\vartheta }{1 - \vartheta }} \right)\frac{{P_{ov} }}{D} + \left( {\frac{1 - 3\vartheta }{1 - \vartheta }} \right)\frac{{\alpha P_{p} }}{D},$$

where $\alpha = 1 - \frac{{c_{\text{r}} }}{{C_{\text{b}} }};$ $c_{\text{r}}$ is compressibility of the rock matrix, $c_{\text{b}}$ is compressibility of the rock skeleton. $\alpha = 1 - \left( {1 - \varphi } \right)^{n}$: $\varphi$ = porosity.

Terzaghi et al. (1948) experimentally found that α = 1 and Poisson’s ratio can be found from sonic velocities as follows:

$$\vartheta = \frac{{1 - 2\left( {\frac{{V_{\text{s}} }}{{V_{\text{c}} }}} \right)^{2} }}{{2\left( {1 - \frac{{V_{\text{s}} }}{{V_{\text{c}} }}} \right)^{2} }},$$

where $V_{\text{s}}$ is shear wave velocity (µs/ft) and $V_{\text{c}}$ compressional wave velocity (µs/ft)

But differentiation of shear wave from compression wave is difficult. Anderson made the broad assumption that ‘Poisson’s ratio is a function of the shaliness of the sand since the shale would act essential as a plastic bonding agent’. The estimation of the shale content of the sand from sonic and density logs was accomplished using a shale index:

$$I_{\text{sh}} = \frac{{\emptyset_{\text{s}} - \emptyset_{\text{D}} }}{{\emptyset_{\text{s}} }},$$

where $\emptyset_{\text{s}}$ is sonic log porosity and $\emptyset_{\text{D}}$ density log porosity.

Optimal mud weight selection: median line principle

Selection of the mud weight can be done by many ways. One way is to blindly assume certain amount of fixed overbalance (normally 200–500 psi) to account for the surge and swab pressures. But it will be more reasonable if the mud weight selection is based on the borehole geomechanics, because borehole geomechanics reduces the possible borehole failures by accounting in situ stresses.

Normally, stresses acting on the borehole well are vertical stress, radial stress and tangential stress which are equal to overburden pressure, pore pressure and hoop stress, respectively.

When the borehole pressure is lesser than the formation pressure, shear stress will appear due to the difference between radial stress and tangential stress and lead to borehole collapse. When the borehole pressure is higher, tangential stress goes into tension. As rocks are weak in tension, it results in tensile failure in the form of axial fracture. So it is clear that higher and lower mud weight produces abnormal stresses and pushes the borehole into failure state. So, the mud weight has to be selected in such a way that there is no abnormal stress induced or in other words mud weight should be equal to the in situ horizontal stresses.

In borehole, fracture occurs when the effective hoop stress of effective tangential stress becomes zero. At that point, borehole pressure will be equal to the fracture pressure and it can be expressed as:

$$\sigma_{\varphi } - P_{\text{p}} = 0 \Rightarrow 2\sigma_{{{\text{H}},\;{\text{Avg}}}} - P_{\text{w}} - P_{\text{f}} = 0 \Rightarrow \sigma_{{{\text{H}},\;{\text{Avg}}}} = \frac{1}{2}\left( {P_{\text{w}} + P_{\text{f}} } \right),$$

where $\sigma_{\varphi } = 2\sigma_{{{\text{H}},\;{\text{Avg}}}} - P_{\text{w}}$ is tangential stress, $P_{\text{w}}$ wellbore pressure, and $\sigma_{{{\text{H}},\;{\text{Avg}}}}$ average horizontal stress.

As the mud weight should be average pressure between pore and fracture pressure of the formation to balance the in situ horizontal stresses, this mud weight selection method keeps the borehole in shape. As the fracture pressure is corrected for tectonic stress, the median line principle can be used to calculate the required mud weight.

Collapse pressure

Collapse will occur only when external pressure outside the casing exceeds the fluid pressure inside the casing. So in designing it is assumed that there is no fluid inside the casing. This kind of situation will occur only when there is lost circulation zone encountered near casing shoe. Though the complete evacuation of fluid inside the casing is not possible it is assumed so. Collapse occurs mainly due to the hydrostatic pressure caused by the mud in the annulus. For collapse pressure the factor of safety (FOS) here is 1.125.

$${\text{Collapse}}\;{\text{Pressure}}\;\left( {\text{psi}} \right) = {\text{Maximum}}\;{\text{Mud}}\;{\text{Pressure}} \; \times \; 1.125$$

Burst pressure

Burst will occur when the fluid pressure inside the casing exceeds the external pressure. In burst pressure calculations, it is assumed that there is no fluid in the casing annulus. Again, this complete evacuation of fluid in the annulus will never occur, but during kick the gas will enter into the annulus and prevents the drilling mud. Here, factor of safety (FOS) of burst pressure is 1.1.

$${\text{Burst}}\;{\text{Pressure }}\left( {\text{psi}} \right) = {\text{maximum}}\;{\text{Mud}}\;{\text{Pressure}}\; \times \; 1.1.$$

Tensile load

Tensile load for the casing is the maximum at the top of the casing joint which is caused by the weight of the casing. For all the calculations assumed that there is bouncy force is acting on the casing. Here, factor of safety (FOS) of tensile load is 1.8.

$${\text{Tensile}}\;{\text{ Load }}\left( {\text{lbf}} \right) = {\text{Length}}\;{\text{of}}\;{\text{the}}\;{\text{casing }}\left( {\text{ft}} \right) \; \times \;{\text{Nominal}}\;{\text{weight}}\;\left( {{\text{lb}}/{\text{ft}}} \right)\; \times \;1.8.$$

Kick tolerance

After a leak-off test and prior to drilling ahead, the kick tolerance should be calculated at intervals through the borehole section to be drilled at the expected mud weight. Input details required to calculate the kick tolerance are: pore pressure from next target depth (TD), maximum mud weight to be used in the next open hole section (P_m), fracture gradient at current casing shoe (FG) and design influx volume that can be safely circulated out (V_k). The influx volume can be calculated as:

$$\begin{aligned} {\text{Influx}}\;{\text{volume}}\;{\text{at}}\;{\text{the}}\;{\text{shoe }}\left( {V_{\text{ks}} } \right) = {\text{Hole}}\;{\text{cross sectional}}\;{\text{ area }}\left( A \right) \hfill \\ \quad \times\,{\text{Maximum}}\;{\text{height}}\;{\text{of}}\;{\text{the}}\;{\text{gas}}\;{\text{bubble }}\left( H \right), \hfill \\ \end{aligned}$$

$${\text{Hole}}\;{\text{cross}}\;{\text{sectional}}\;{\text{area }}\left( A \right) = \frac{\pi }{4}\left( {d_{1}^{2} - d_{2}^{2} } \right),$$

${\text{Maximum}}\;{\text{height}}\;{\text{of}}\;{\text{the}}\;{\text{gas}}\;{\text{bubble}} \left( H \right) = \frac{{0.052 \times P_{\text{m}} \left( {{\text{TD}} - {\text{CSD}}} \right) + \left( {{\text{FG}} \times {\text{CSD}} \times 0.052 - P_{\text{p}} } \right)}}{{0.052 \times P_{\text{m}} - G}}.$

Once the influx volume at the shoe is calculated at the target depth has to be calculated by using the ideal has law:

$$\frac{{P_{\text{fs}} \times V_{\text{ks}} }}{{T_{\text{s}} }} = \frac{{P_{{{\text{p}},\;{\text{TD}}}} \times V_{{{\text{k,}}\;{\text{TD}}}} }}{{T_{\text{TD}} }}.$$

Kick tolerance can be expressed in terms of additional mud weight (ppg) = (FG–P_m).

Also, it can be expressed in terms of drill pipe shut-in pressure (DPSIP), psi = (FG–P_m) × CSD × 0.052.where FG is fracture gradient at the shoe (ppg), CSD casing seat depth (ft), G gas gradient (vary from 0.05 to 0.15) (psi/ft), P_fs, P_p,TD fracture pressure at shoe, maximum pore pressure at the target depth, respectively, V_ks, V_k,TD influx volume at shoe and at target depth (bbl), T_s, T_TD temperature at the shoe and at target depth, in Rankine.

Methodologies

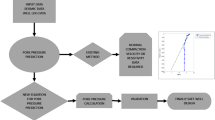
Two seismic sections named ‘A’ and ‘B’ located in the synclinal (A) and flank (B) part of the Atharamura anticline are taken. Both seismic sections are oriented in the directions of west-east, and input data contain corrected values two-way travel time and average (normal) velocity values for various common depth points (CDP). The details of pore pressure and fracture pressure predictions are explained in details in Fig. 5 (flow chart).

Fig. 5

Flow chart for pore and fracture pressures prediction

From the stratigraphy (Fig. 3), it is found that Middle Bhuban encountered around 3000 m depth. Though the Middle Bhuban is exposed on the Atharamura anticline, it is decided to select the target depth 3800 m as the pore pressure accelerates to higher magnitude at these depths which may be due to the hydrocarbon presence. Also, it is better to design an exploratory well for deeper depths not only to explore hydrocarbons, but also to obtain safe casing policy. So the target depth for the well on the top of the anticline is selected as 4000 m (approximately 12,500 ft).

Result and discussions

Pore pressure prediction

The over-pressure is starting at the depth 1482 m in synclinal (Section A) and 2630 m in the flank (Section B) part of the Atharamura (Figs. 6, 7).

Fig. 6

(Reproduced with permission from Brahma 2013)

Rokhia structure—RO1-measured pore pressures vs predicted pore pressures

Fig. 7

(Reproduced with permission from Brahma 2013)

Tichna structure—TI1-measured pore pressures vs predicted pore pressures

Pressure predicted from seismic velocities shows the over-pressure existence up to the depth 10,000 m, which indicates over-pressured zones exist also in the Lower Bhuban and continues up to basement rocks which are meaningless as basement doesn’t have pore. So the depth of reliability for predicted pore pressure is taken as 6000 m, as basement rocks are encountered below that depth. The reason behind this depth validity is that our entire pore pressure calculation is based on the assumption that V_rms = V_avg, which is true only in shallow depths (6000 m).

To estimate the reliability and to understand the subsurface fluid flow, the predicted pressure values at CDPs are compared with pore pressure measured by RFT (repeat formation tester) from drilled offset wells. In this comparison study, total number of 14 well’s RFT data were taken and out of these 8 wells had over-pressures.

On comparing the RFT data with predicted pore pressure from seismic data, interestingly some CDP–Eaton’s method-derived pressures matched with measured RFT pressures drilled wells, and the observations are summarised in Table 1.

Table 1 Predicted pore pressures match with measured pore pressures from offset wells

The offset wells which show the pressure match were located 50–60 km away from the Atharamura and located in different tectonic environments. It is also observed that most of the wells which show the pressure match have been located in the western side of the Atharamura.

On combining these observations, it is interpreted that Tripura region is characterised by single pressure source and distributed evenly in all the anticlines in this region. As the anticline becomes steeper from west to east, the over-pressure measured in the top of anticlines in the western part matched with predicted pressure from anticline in eastern part (Atharamura). This increasing steep from west to east is the main reason for the depth migration of over-pressures.

Fracture pressure prediction

To reduce the uncertainty, fracture pressure was established by various methods such as Hubbert and Willis method and Matthews and Kelly method and modified Eaton’s method (Daines 1982) from predicted pore pressures. Using the constant Poisson’s ratio of 0.25 as recommended by the operating company, Hubbert and Willis fracture pressure equations were implemented to calculate fracture pressures. Hubbert’s equations have the lowest fracture pressure values comparing to Matthews; moreover, Hubbert’s equation works well in the relaxed basins such as Atharamura where the normal faults are frequent. Normally, it is believed that horizontal stress acts in equal magnitude in all directions in the relaxed basins. But in actual scenario this is not true. As the Atharamura structure itself an anticline which undergone folding and then normal faulting, there should be a certain amount of tectonic stress in particular horizontal direction which can form the stress anisotropy. So it is necessary to correct the fracture pressure for tectonic stress in calculations. Bradley developed an equation in which stress anisotropy due to horizontal stress variation can be modelled (Brandley 1979). Quantifying horizontal tectonic stress for wildcat well location is almost impossible without P-wave and S-wave velocity data or leak-off test data. Aadnoy suggested that using the relation of $\sigma_{{{\text{H}},{\text{Min}}}} = 0.8\sigma_{{{\text{H}},{\text{Max}}}}$ (Aadnoy 2010) holds good for most of the areas. In India, minimum horizontal varies between 0.77 and 0.8 maximum horizontal effective stresses (Rahman and Sharma 2009). By taking minimum Poisson’s ratio value of 0.25, fracture pressures (Hubbert and Willis 1957) can be back-calculated by using the horizontal stress ratio relation. The modified Eaton’s method has given almost same result as tectonic-corrected results of other two methods. For tectonically challenged area such as Atharamura anticline, Hubbert and Willis and Matthews and Kelly methods are not recommended without tectonic corrections. Comparatively modified Eaton’s method is more suitable for this study area due to very complex geological structure. The comparative fracture pressures on the top of the anticline are shown in Table 2.

Table 2 Predicted fracture pressure on the Atharamura anticline top

Establishing drilling mud window

Drilling mud window establishment is the basic information for the petroleum engineers to plan the well. Drilling mud window shows the pressure boundaries in terms of drilling mud weight within which the well can be drilled without inviting blowout and fracturing the fraction. The available drilling mud window at the top of the Atharamura anticline is shown in the left side figure. From Fig. 8, it is obvious that inclusion of tectonic stress reduces the fracture resistance which indicates that the tectonic stress acts in the maximum horizontal direction.

Fig. 8

Drilling mud window on the Atharamura anticline top

Optimal mud weight selection: median line principle

As the fracture pressure is corrected for tectonic stress, median line principle can be used to calculate the required mud weight. Median line principle precisely calculates the mud weight required to balance the in-situ stresses to keep the borehole in shape. So it is necessary to add the surge and swab margin to reduce the pressure fluctuations during making and breaking the connections. Once all these corrections have been made, mud weight required to drill the well can be plotted against depth as shown in Fig. 9.

Fig. 9

Selected mud weight on the top of Atharamura anticline—median line principle

Casing seat selection policy

Casing policy proposal needs two essential parameters namely casing seat dept selection and number of casing string and its dimensions required to drill the well. Precise knowledge about pore pressure, fracture pressure and optimal selection of mud weight is key factor in selecting the casing seats which are tabulated in Table 3. Casing seat selection determines the depth at which the casing seat should be landed, so that the next open borehole section can be drilled out without fracturing the previous casing seat.

Table 3 Selected mud weight on the top of Atharamura anticline—median line principle

Eaton (1970) proposed a systematic simple procedure to find casing seat depths by plotting pore, fracture, drilling mud weight gradients against depth. At Atharamura anticline top, it is found that well can be drilled with two casing strings namely intermediate and production casings (Fig. 10). But the important fact is that the pressures predicted in this region are from seismic velocities. So the first velocity data are obtained at the depth of 400 m (from the first reflector). In other words, from surface up to 400 m we have no knowledge about the geo-pressures. So it is safe to include the conductor casing for the first 400 m where risky gas bearing formation may be encountered. The inclusion of casing string can increase the well cost but offers safe drilling environment. So the well is planned to complete with three casing strings at casing seat depths of 1320, 8500, 12,500 ft, respectively.

Fig. 10

Casing seat selection on the top of Atharamura anticline

Once the number of casing strings has been determined, then it is necessary to determine the dimensions of the borehole and casing diameters and grades. To make this process simple, borehole dimension normally used in oil industry (Adam 1985) was taken.

The selected borehole dimensions are standard and accounts for the effective hole cleaning by offering more annular area. Casing diameters and nominal weights were designed on the basis of collapse pressure, burst pressure and tensional load. In brief, the casing policy is shown in Table 4. From the available casing data (Gabolde 1999), the casing pipes which satisfy Table 4 design requirement are selected and shown in Table 5.

Table 4 Calculated designed requirement for the casing pipes

Table 5 Properties of selected casing pipes

Kick tolerance graph

Kick tolerance may be defined as the maximum kick size which can be tolerated without fracturing the previous casing shoe. Kick tolerance may also be defined in terms of the maximum allowable pore pressure at the next target depth (TD) or maximum allowable mud weight which can be tolerated without fracturing the previous casing shoe. Thus, finding the kick tolerance for the casing seat is crucial factor for this study area where the possibilities of abnormal pressure kicks are frequent.

Kick tolerance calculation gives some handy information to encounter the abnormal kick situation such as maximum kick volume which can be circulated out without fracturing the previous casing shoe, maximum drill pipe shut-in pressure (DPSIP), additional mud weight required to counter the kick.

Kick tolerance can be shown in terms of plotting the kick volume against maximum DPSIP. The straight line which joins the drill pipe shut-in pressure to the corresponding kick volume is called kick tolerance graph.

All points to the top and right of the line represent internal blowout, but lost circulation conditions. Points below the line represent safe conditions and give kick tolerance for any combination of kick size and drill pipe shut-in pressure. Kick tolerance graph for the Atharamura anticline is shown in Fig. 11 and detailed values are tabulated in Table 6. In final well plan, the entire details that needed to plan well are summarised. The diagrammatic well plan is summarised in Fig. 12.

Fig. 11

Kick tolerance graph for conductor and intermediate casing on the top of Atharamura anticline

Table 6 Calculated kick tolerance parameters

Fig. 12

Proposed casing policy on the top of Atharamura anticline

Conclusions

From the predicted pore pressure, it is obvious that over-pressured formation encountered at shallow depths itself with relatively less magnitude in shallow depth. The higher magnitude of over-pressured formations is encountered after 400 m. As the depth validity for the Eaton-predicted pore pressure is 6000 m, these over-pressures are not wrong. This may be due to the presence of shale having good sealing potential at these depths.

Circulating out any volume of kicks during drilling should be within the safety limits as shown in the kick tolerance graph.

Mud weight calculated from median line principle increased by 0.6 ppg to account for surge and swab margin. So, further addition of surge and swab margin may lead to formation damage.

Three types of casing pipe have been recommended for safe drilling namely conductor, intermediate and production with casing seat depth at 1320, 8500 and 12500 ft, respectively.