Introduction

Naturally fractured reservoirs are widely distributed around the world. A considerable number of natural gas reservoirs, both conventional and unconventional, are naturally fractured. As a result of the recent rapid development of unconventional resources, naturally fractured reservoirs are supplying increasing amount of oil and gas to the world markets. Natural fractures result from various reasons such as tectonic movement, lithostatic pressure changes, thermal stress, and high fluid pressure. The fractures are either connected or discrete. Good interconnectivity between fractures yields fracture network dividing matrix into individual blocks, which is found in many reservoirs. Fluid flow in fractures is treated as Darcy flow in these models. The fractures have large flow capacity, but small storage capacity. On the contrary, matrix is characterized by small flow capacity, but large storage capacity. In such a system, flow throughout the reservoir occurs in fracture system, and matrix blocks act as source of fluids. Barenblatt et al. (1960) first proposed a dual-porosity model for liquid flow in naturally fractured reservoirs. Warren and Root (1963) subsequently applied Barenblatt’s et al. (1960) theory to well testing using a pseudo-steady-state interporosity flow equation, given as follows:

$$\frac{{\partial \left( {\phi_{\text{m}} \rho_{\text{m}} } \right)}}{\partial t} = \rho_{\text{m}} \frac{{\alpha k_{\text{m}} }}{\mu }\left( {p_{\text{f}} - p_{\text{m}} } \right)$$
(1)

where ϕ m is matrix porosity, ρ m is fluid density in the matrix, α is the shape factor, k m is matrix permeability, μ is liquid viscosity, p m is matrix fluid pressure, and p f is fracture fluid pressure. In this interporosity equation, α is a constant in Warren and Root’s model, but differs with the changes in matrix blocks’ shapes. Zimmerman et al. (1993) demonstrated the rigorous derivation of Eq. 1 and the shape factor for a slab-like matrix blocks. Lim and Aziz (1995) used the same approach to generate shape factors for different matrix shapes.

Equation 1 assumes liquid flow, i.e., a fluid with constant viscosity and constant compressibility, in its development. Yet due to the drastic pressure changes that occur as fluid flows from the matrix to the fractures, Eq. 1 can prove to be inadequate for modeling interporosity gas flow in naturally fractured gas systems. A rigorous interporosity flow equation for gas needs to be in place for the reliable production data analysis in such systems. Though Eq. 1 does not account for viscosity–compressibility changes in the fluid, it remains widely applied. For example, a number of reservoir simulators utilize this equation for reservoir modeling with viscosity and compressibility evaluated at the pressure of the upstream one between matrix and fracture when modeling dual-porosity gas systems.

Azom and Javadpour (2012) used a modified pseudo-pressure approach and obtained an adequate matrix–fracture shape factor for interporosity gas flow. They presented a two-dimensional implicit dual-continuum reservoir simulator for naturally fractured reservoirs with single-phase compositional setting. However, implementing the model required implementing a numerical simulation. Sureshjani et al. (2012) derived explicit rate-time solution of single-phase interporosity gas flow assuming quasi-steady-state flow for dual-porosity system. In the derivation, they approximated pseudo-time to time when integrating outflow from matrix block, and moreover, \(\frac{{\mu_{\text{i}} c_{\text{i}} }}{\mu c} \approx {{\left( {\frac{p}{Z}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{p}{Z}} \right)} {\left( {\frac{p}{Z}} \right)_{\text{i}} }}} \right. \kern-0pt} {\left( {\frac{p}{Z}} \right)_{\text{i}} }}\) is assumed. Ranjbar and Hassanzadeh (2011) developed semi-analytical solutions for nonlinear diffusion equation in gas-bearing reservoir before back-calculating matrix–fracture shape factor with the developed solution. However, the solutions contain two unknown parameters determined by matching data generated by numerical simulator for corresponding matrix and fluid type.

Incorporation of the aforementioned interporosity equation for gas in decline curve analysis needs to be investigated more thoroughly. State-of-the-art methodologies of decline curve analysis for naturally fractured gas reservoirs have been using the liquid-form interporosity flow equation for development or validation purposes. Spivey and Semmelbeck (1995), for example, combined transient radial model, adjusted pressure, and desorption term together and developed a production-prediction method for shale gas and dewatered coal seams producing at constant bottom-hole pressure. Adjusted pseudo-time and adjusted pseudo-pressure were used instead of real time and real pressure in the analytical solution for Warren and Root’s model. This approach produces error less than 10 % when \(\xi r_{\text{eD}} \ge 1\) with a slab-like dual-porosity model. The study did not specify details on the interporosity flow equation implemented in the simulator. In addition, a direct substitution of pseudo-pressure and pseudo-time into the liquid analytical solution seems not to be supported by the governing equations.

Gerami et al. (2007) applied pseudo-time and pseudo-pressure to dual-porosity reservoirs, and, without derivation, they proposed a pseudo-pressure-based interporosity flow equation for gas. However, their model verification did not use a numerical simulator that accounted for an appropriate gas interporosity flow equation. As a result, their prediction error increased with increased production when their semi-analytical results were compared against results from a commercial simulator.

In this study, a pseudo-steady-state interporosity flow equation for single-phase gas is rigorously derived. Application of the new model is found to enable pseudo-functions-based decline curve analysis in dual-porosity gas systems. For the case of single-porosity systems, Ye and Ayala (2012, 2013), and Ayala and Ye (2012, 2013) had proposed a density-based approach for decline curve analysis. With depletion-driven dimensionless variables λ and β, Ye and Ayala (2012) was able to rescale dimensionless gas rate solution under constant bottom-hole pressure from their liquid counterparts, which thereupon facilitates the decline curve analysis based on density. Zhang and Ayala (2014a) provided rigorous derivation for the density-based approach and improved the methods for analyzing data at variable pressure drawdown/rate at decline stage (Ayala and Zhang 2013; Zhang and Ayala 2014b). In our study, the applicability of the density-based approach to naturally fractured systems is investigated and a match is found between density-based prediction and gas numerical responses with the application of gas interporosity flow equation.

Pseudo-steady-state interporosity flow equation for gas

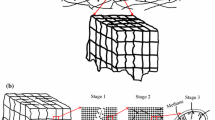
The interporosity flow equation in Barenblatt et al. (1960) and Warren and Root (1963) was proposed for pseudo-steady-state liquid flow from matrix blocks to fracture system. Starting from physical principles, Zimmerman et al. (1993) derived this interporosity flow equation for liquid using a spherical matrix shape. The development procedure assumes the quasi-steady-state approximation, which treats fracture pressure on the outer boundary, p f, as constant throughout the derivation. Developed for liquid flow, the interporosity equation can prove largely inadequate for gas flow. Since gas compressibility and viscosity are pressure-dependent, the gas flow out of the matrix gridlock experiences large changes in pressure-dependent properties and presents a markedly different behavior from that of liquid flow. This difference could be drastic as the contrast between fracture pressure and matrix pressure increases. In this study, we develop a different interporosity equation for gas with quasi-steady-state assumption. Following Zimmerman et al. (1993), a spherical matrix block is assumed throughout the derivation, as illustrated in Fig. 1.

Fig. 1
figure 1

Schematics of a spherical matrix block

Full size image

Pressure on the surface of the sphere is fracture fluid pressure, p f, and pressure inside the sphere is denoted by p m, which is a function of the radius and time. The sphere’s radius is a m. Initial pressure throughout the sphere is denoted as initial reservoir pressure, p i. The diffusivity equation of gas flow in the matrix block is as follows:

$$- \nabla \cdot \left( {\rho_{\text{m}} u_{\text{m}} } \right) = \frac{{\partial \left( {\phi_{{{\text{m}} }} \rho_{\text{m}} } \right)}}{\partial t}$$
(2)

where u m is the Darcy velocity of fluid flow. Substituting Darcy’s law into Eq. 2 gives:

$$\nabla \cdot \left( {\rho_{\text{m}} \frac{{k_{\text{m}} }}{{\mu_{\text{gm}} }}\nabla p_{\text{m}} } \right) = \frac{{\partial \left( {\phi_{{{\text{m}} }} \rho_{\text{m}} } \right)}}{\partial t}$$
(3)

Assuming an incompressible matrix rock, multiplying both sides by θ, adding the term \(\mu_{\text{gm}} c_{\text{gm}} /(\mu_{\text{gm}} c_{\text{gm}} )\) on the RHS and substituting \({\text{d}}m(p_{\text{m}} ) = 2\theta {\text{d}}\rho_{\text{m}} /(\mu_{\text{gm}} c_{\text{gm}} )\) gives:

$$\nabla \cdot \left( {k_{\text{m}} \nabla m\left( {p_{\text{m}} } \right)} \right) = \phi_{\text{m}} \mu_{\text{gm}} c_{\text{gm}} \frac{{\partial m\left( {p_{\text{m}} } \right)}}{\partial t}$$
(4)

For a homogeneous and isotropic matrix (constant \(k_{\text{m}}\)), dividing both sides by ϕ m μ gm c gm, and substituting \(\lambda_{\text{m}}^{*} = \mu_{\text{gi}} c_{\text{gi}} /(\mu_{\text{gm}} c_{\text{gm}} )\) into Eq. 4 gives:

$$\frac{{\partial m(p_{\text{m}} )}}{{\lambda_{\text{m}}^{*} \partial t}} = \frac{{k_{\text{m}} }}{{\phi_{\text{m}} \mu_{\text{gi}} c_{\text{gi}} }}\nabla^{2} m(p_{\text{m}} )$$
(5)

Denoting \(\bar{\lambda }_{\text{m}}^{*}\) as the \(\lambda_{\text{m}}^{*}\) evaluated average pressure in the matrix block and substitute \(\beta_{\text{m}}^{*} = \smallint \bar{\lambda }_{\text{m}}^{*} {\text{d}}t/t\) into Eq. 5. This yields:

$$\frac{{\partial m(p_{\text{m}} )}}{{\partial \left( {\beta_{\text{m}}^{*} t} \right)}} = \frac{{k_{\text{m}} }}{{\phi_{\text{m}} \mu_{\text{gi}} c_{\text{gi}} }}\nabla^{2} m(p_{\text{m}} )$$
(6)

where \(\beta_{\text{m}}^{*} t\) is a term equivalent to normalized pseudo-time. For gas reservoirs, the average reservoir pressure is utilized to evaluate pseudo-time, which has been proven to work well during boundary dominated period. Expanding Eq. 6 to spherical coordinates and taking u (r, t) = m (p m) r gives:

$$\frac{\partial u}{{\partial \left( {\beta_{\text{m}}^{*} t} \right)}} = \frac{{k_{\text{m}} }}{{\phi_{\text{m}} \mu_{\text{gi}} c_{\text{gi}} }}\frac{{\partial^{2} u}}{{\partial r^{2} }}$$
(7)

We then take the spherical matrix shape with radius a m. With the fracture surrounding the matrix, the pressure at the matrix surface is the same as the fracture pressure. The boundary conditions are written as:

$$u\left( {0,\beta_{\text{m}}^{*} t} \right) = 0$$
(8)
$$u\left( {a_{\text{m}} ,\beta_{\text{m}}^{*} t} \right) = a_{\text{m}} m(p_{\text{f}} )$$
(9)
$$u(r,0) = rm(p_{\text{i}} )$$
(10)

Solving Eqs. 8–10 for \(m(p_{\text{m}} )\) distribution and calculating the average pseudo-pressure gives (Crank 1975):

$$\frac{{m_{\text{avg}} (p_{\text{m}} ) - m(p_{\text{i}} )}}{{m(p_{\text{f}} ) - m(p_{\text{i}} )}} = 1 - \frac{6}{{\pi^{2} }}\sum\limits_{n = 1}^{\infty } {\frac{1}{{n^{2} }}{ \exp }\left( { - \frac{{\pi^{2} k_{\text{m}} n^{2} \beta_{\text{m}}^{*} t}}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}} \right)}$$
(11)

where m avg(p m) is the average pseudo-pressure throughout the matrix block. The long-term approximation truncates to the first term of the infinite series, giving:

$$\frac{{m_{\text{avg}} \left( {p_{\text{m}} } \right) - m\left( {p_{\text{i}} } \right)}}{{m\left( {p_{\text{f}} } \right) - m\left( {p_{\text{i}} } \right)}} = 1 - \frac{6}{{\pi^{2} }}{ \exp }\left( { - \frac{{\pi^{2} k_{\text{m}} \beta_{\text{m}}^{*} t}}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}} \right)$$
(12)

Lim and Aziz (1995) validated the long-term approximation in their derivation for a liquid system. This approximation is accurate for \(\pi^{2} k_{\text{m}} \beta_{\text{m}}^{*} t/\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{m}^{2} > 0.5\) as shown in Fig. 8 of their work. For a wide variety of cases, the approximation is valid at the decline stage. Rearranging terms in Eq. 12 gives:

$$\frac{6}{{\pi^{2} }}\exp \left( { - \frac{{\pi^{2} k_{\text{m}} \beta_{\text{m}}^{*} t}}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}} \right) = \frac{{m(p_{\text{f}} ) - m_{\text{avg}} (p_{\text{m}} )}}{{m(p_{\text{f}} ) - m(p_{\text{i}} )}}$$
(13)

Taking the derivatives of Eq. 13 with respect to \(\beta_{\text{m}}^{*} t\) gives:

$$\frac{1}{{m(p_{\text{f}} ) - m(p_{\text{i}} )}}\frac{{d(m_{\text{avg}} (p_{\text{m}} ))}}{{d\left( {\beta_{\text{m}}^{*} t} \right)}} = \frac{6}{{\pi^{2} }}\exp \left( { - \frac{{\pi^{2} k_{\text{m}} \beta_{\text{m}}^{*} t}}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}} \right)\frac{{\pi^{2} k_{\text{m}} }}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}$$
(14)

Writing \({\text{d}}(m_{\text{avg}} (p_{\text{m}} ))/{\text{d}}\left( {\beta_{\text{m}}^{*} t} \right)\) in Eq. 14 as \(\frac{{{\text{d}}(m_{\text{avg}} (p_{\text{m}} ))}}{{{\text{d}}t}} \frac{{{\text{d}}t}}{{{\text{d}}\left( {\beta_{\text{m}}^{*} t} \right)}}\) and substituting \(d\left( {\beta_{\text{m}}^{*} t} \right) = \bar{\lambda }_{\text{m}}^{*} {\text{d}}t\) into the resulting equation gives:

$$\frac{1}{{m(p_{\text{f}} ) - m\left( {p_{\text{i}} } \right)}}\frac{{d\left( {m_{\text{avg}} \left( {p_{\text{m}} } \right)} \right)}}{{{\text{d}}t}} = \frac{6}{{\pi^{2} }}\exp \left( { - \frac{{\pi^{2} k_{\text{m}} \beta_{\text{m}}^{*} t}}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}} \right)\frac{{\pi^{2} k_{\text{m}} }}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }} \bar{\lambda }_{\text{m}}^{*}$$
(15)

Substituting Eq. 13 into Eq. 15 gives:

$$\frac{{d(m_{\text{avg}} (p_{\text{m}} ))}}{{\bar{\lambda }_{\text{m}}^{*} {\text{d}}t}} = \frac{{\pi^{2} k_{\text{m}} }}{{\mu_{\text{gi}} c_{\text{gi}} \phi_{\text{m}} a_{\text{m}}^{2} }}(m(p_{\text{f}} ) - m_{\text{avg}} (p_{\text{m}} ))$$
(16)

\(\frac{{\pi^{2} }}{{a_{\text{m}}^{2} }}\) is a constant known as shape factor, α, that changes with the geometry of matrix. Moreover, replacing average pseudo-pressure in matrix volume, m avg(p m), with point-specific matrix pseudo-pressure and substituting \(\bar{\lambda }_{\text{m}}^{*}\) with \(\lambda_{\text{m}}^{*}\) since matrix is point-specific as represented by the governing equations gives:

$$\phi_{\text{m}} \frac{{d(m(p_{\text{m}} ))}}{{\lambda_{\text{m}}^{*} {\text{d}}t}} = \frac{{\alpha k_{\text{m}} }}{{\mu_{\text{gi}} c_{\text{gi}} }}\left( {m\left( {p_{\text{f}} } \right) - m\left( {p_{\text{m}} } \right)} \right)$$
(17)

The application of the definition of \(\lambda_{\text{m}}^{*}\) and \(d (m(p_{\text{m}} ) )= 2\theta d\rho_{\text{m}} /\mu_{\text{gm}} c_{\text{gm}}\) to Eq. 17 gives:

$$\phi_{\text{m}} \frac{{{\text{d}}\rho_{\text{m}} }}{{{\text{d}}t}} = \frac{{\alpha k_{\text{m}} }}{2\theta }(m(p_{\text{f}} ) - m(p_{\text{m}} ))$$
(18)

This interporosity flow equation is rigorously derived for gas, incorporating the viscosity–compressibility effects. An important characteristic of this model is the same shape factor as that in Lim and Aziz (1995) for Warren and Root’s model. For the slab-like matrix, the shape factor is \(\pi^{2} /4L^{2}\), where L denotes fracture half-spacing. Equation 18 is in the same form as the interporosity flow equation written by Gerami et al. (2007) without derivation—Footnote 1 if we consider an incompressible matrix and fracture and no connate water. Sureshjani et al. (2012) proposed the same interporosity flow equation in a different form with a different approach utilizing two approximations in a different derivation:

$$\frac{{\mu_{\text{gi}} c_{\text{gi}} }}{{\mu_{\text{g}} c_{\text{g}} }} \approx \frac{p/Z}{{(p/Z)_{\text{i}} }}$$
(19)
$$\quad\quad t \approx t_{\text{a}}$$
(20)

This study shows that this pseudo-steady-state interporosity flow equation is valid without invoking such approximations. Sureshjani et al. (2012) built a fine grid single-porosity numerical simulator to model flow between slab-shaped matrix and fracture. Both the matrix and the fracture are represented by fine gridblocks. The shape factor is back-calculated and compared against \(\pi^{2} /4L^{2}\), demonstrating a close match at the decline stage. The results of the comparison validate the pseudo-steady-state interporosity flow equation for gas. The back calculation is thus rewritten as follows:

$$\alpha = \frac{{2\theta \phi_{\text{m}} }}{{k_{\text{m}} \left( {m\left( {p_{\text{f}} } \right) - m\left( {p_{\text{m}} } \right)} \right)}}\frac{{{\text{d}}\rho_{\text{m}} }}{{{\text{d}}t}}$$
(21)

Substituting \({\text{d}}m\left( {p_{\text{m}} } \right) = 2\theta {\text{d}}\rho_{\text{m}} /\mu_{\text{gm}} c_{\text{gm}}\) into Eq. 18 and canceling 2θ, Eq. 18 can be rewritten as:

$$\phi_{m} \frac{{{\text{d}}\rho_{\text{m}} }}{{{\text{d}}t}} = \alpha k_{\text{m}} \left( {\mathop \int \limits_{0}^{{\rho_{\text{f}} }} \frac{1}{{\mu_{\text{gf}} c_{\text{gf}} }}{\text{d}}\rho_{\text{f}} - \mathop \int \limits_{0}^{{\rho_{\text{m}} }} \frac{1}{{\mu_{\text{gm}} c_{\text{gm}} }}{\text{d}}\rho_{\text{m}} } \right)$$
(22)

If a constant viscosity and compressibility is assumed, Eq. 22 would collapse to the interporosity flow equation in the Warren and Root’s model, which was developed for liquid. Replacing μ gf c gf and μ gm c gm with the constant μc in Eq. 22 gives:

$$\phi_{\text{m}} \frac{{{\text{d}}\rho_{\text{m}} }}{{{\text{d}}t}} = \frac{{\alpha k_{\text{m}} }}{\mu c}(\rho_{\text{f}} - \rho_{\text{m}} )$$
(23)

The liquid systems have similar ρ f and ρ m due to small compressibility. Thus, by substituting \(p_{\text{f}} - p_{\text{m}} = { \ln }\left( {\rho_{\text{f}} /\rho_{\text{m}} } \right)/c_{\text{l}}\) and \({\text{ln(}}\rho_{\text{f}} /\rho_{\text{m}} )\approx (\rho_{\text{f}} - \rho_{\text{m}} )/\rho_{\text{m}}\) into Eq. 22, the interporosity flow equation in Warren and Root’s model is produced:

$$\phi_{\text{m}} \frac{1}{{\rho_{\text{m}} }}\frac{{\partial \rho_{\text{m}} }}{\partial t} = \frac{{\alpha k_{\text{m}} }}{\mu }\left( {p_{\text{f}} - p_{\text{m}} } \right)$$
(24)

The biggest obstacle to using the Warren and Root’s model in gas scenarios is the difference between viscosity and compressibility in the fracture systems and the matrix systems for gas. The derived interporosity flow equation for gas incorporates effects of pressure-dependent properties by invoking pseudo-functions. The development embraces pseudo-steady-state interporosity flow and long-term approximation that requires π 2 k m β *m t/μ gi c gi ϕ m a 2m  > 0.5 for the spherical matrix block.

Rate-time forecast of naturally fractured gas reservoirs

An in-house dual-porosity reservoir simulator, in-house simulator 1, was developed for modeling dual-porosity gas reservoirs using the appropriate pseudo-steady-state interporosity flow equation for gas derived above. This is an important undertaking because commercial simulators use the liquid-form interporosity flow equation in Warren and Root’s model with fluid properties evaluated at the pressure of the upstream one between fracture and matrix instead. As shown above, such liquid-version of the interporosity equation is written as follows:

$$\phi_{\text{m}} \frac{{\partial (p_{\text{m}} )}}{\partial t} = \frac{{\alpha k_{\text{m}} }}{{c_{t} \mu_{\text{g}} }}(p_{\text{f}} - p_{\text{m}} )$$
(25)

For comparison purposes, this study also developed the ‘in-house simulator 2’, which solves all the dual-porosity gas reservoir equations but forces the use of the liquid-version of the interporosity equation above—as done by commercial simulators. Our numerical simulator implementation follows Abou-Kassem et al. (2006). A circular reservoir is considered with a well fully penetrating with no skin at the center. The reservoir is homogeneous and isotropic. Logarithmic discretization is taken owing to its radial nature. Equation discretization is implicit, and simple-iteration method (SIM) acts as pressure advancing algorithm. Viscosity is calculated with method by Lee et al. (1966). The Abou-Kassem et al. (1990) is used for determining compressibility, and compressibility factor calculation follows Dranchuk and Abou-Kassem (1975). For testing purposes, a synthetic case was analyzed as described in Tables 1 and 2. The specific gravity of natural gas, r g, is 0.55. Matrix porosity and fracture porosity are taken as 0.15 and 0.01, respectively. The permeability values in the matrix and fractures are changed to 0.005 and 50 md, respectively, to guarantee apparent dual-porosity behavior. The shape factor is assumed to be \(9.98959 \times 10^{ - 05} \;1/{\text{ft}}^{2}\). A summary of the relevant properties is provided in Table 1. Three scenarios with different reservoir sizes are used for generating production data and are presented in Table 2.

Table 1 Reservoir and fluid properties
Full size table
Table 2 Reservoir Size and OGIP for three Scenarios
Full size table

When it comes to a dual-porosity reservoirs, two systems—the fracture system and the matrix system—overlap with each other, and the two systems communicate through an interporosity flow described by the interporosity flow equation. The behavior of production rate, when producing from a dual-porosity system at constant bottom-hole pressure, is different from that in a single-porosity system. As has been pointed out by Moench (1984), in the first decline stage, the production is primarily from fracture storage, and matrix storage does not begin to significantly contribute to production until the end of this stage. At the end of the first decline stage, fluids originally in the fracture system are depleted compared to those in the matrix system. Therefore, with decreasing fracture fluid pressure, interporosity flow develops and becomes dominant in the second decline stage. That is, flow out of the matrix into the fracture makes the dominant contribution to gas production. The matrix blocks are therefore treated as the only storage sites at the second decline stage, and the matrix blocks’ pressures are representative pressure in the reservoir for evaluating pressure-dependent effects.

For decline analysis of single-porosity gas reservoirs, Ye and Ayala (2012, 2013) and Ayala and Ye (2012, 2013) proposed a density-based approach. Using depletion-driven dimensionless variables λ and β, they successfully decoupled pressure-dependent effects from pressure depletion. Ye and Ayala (2012) were accordingly able to show that the dimensionless gas rate solutions under constant bottom-hole pressure can be rescaled from their liquid counterparts with depletion-driven dimensionless variables λ and β. Zhang and Ayala (2014a) subsequently provided rigorous derivation for the rescaling approach. The relationship is written by Zhang and Ayala (2014a) as follows:

$$q_{\text{D}}^{\text{gas}} \left( {t_{\text{D}} } \right) = \bar{\lambda } \cdot q_{\text{D}}^{\text{liq}} \left( {\bar{\beta }t_{\text{D}} } \right)$$
(26)

where \(q_{\text{D}}^{\text{gas}}\) is the dimensionless gas flow rate, \(q_{\text{D}}^{\text{liq}}\) is the liquid counterpart, and \(\bar{\lambda }\) and \(\bar{\beta }\) are depletion-driven dimensionless variables defined as follows:

$$\bar{\lambda } = \frac{{\mu_{\text{gi}} c_{\text{gi}} }}{{\frac{{2\theta \left( {\bar{\rho } - \rho_{\text{wf}} } \right)}}{{\bar{m}\left( p \right) - m\left( {p_{\text{wf}} } \right)}}}}$$
(27)

where \(\bar{\rho }\) is the average reservoir gas density, ρ wf is the gas density at the bottom-hole condition, \(\bar{m}(p)\) is the average pseudo-pressure of reservoir fluids, m(p wf) is the pseudo-pressure of gas at the bottom-hole condition, μ gi and c gi are the initial gas viscosity and initial gas compressibility, θ = RT/MW, T is temperature, and MW is molecular weight.

$$\beta = \frac{{\int\nolimits_{0}^{t} \lambda {\text{d}}t}}{t}$$
(28)

\(\bar{\rho }\) could be obtained from a material balance equation assuming a tank model for the reservoir, \(\bar{m}\left( p \right)\) is evaluated at the pressure corresponding to \(\bar{\rho }\). It was demonstrated that \(\bar{\lambda }\) and \(\bar{\beta }\) are able to capture the effects of pressure-sensitive properties on a single-porosity system’s behavior.

For dual-porosity reservoirs, following Moench (1984), it would be reasonable to speculate that \(\bar{\lambda }\) and \(\bar{\beta }\) could capture the response of a dual-porosity system in the second decline stage since the pressure-sensitive effects are controlled by matrix pressure only. From this perspective, the \(\bar{\lambda }\) and \(\bar{\beta }\) for a dual-porosity systems could be written as \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\). Considering that matrix fluids account for the vast majority of reservoir fluids, the fracture pressure’s influence on the average reservoir pressure is negligible. Thus, a simple material balance equation for a single-porosity system is able to predict the average pressure, from which \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\) are then calculated.

The proposed \(\bar{\lambda }\) and \(\bar{\beta }\) rescaling approach can be validated for a variety of scenarios that exhibit dual-porosity behaviors. First, we test the rescaling approach against the three scenarios described by Tables 1 and 2. The in-house simulator 1 is used to generate production data. The rate-time production data are then transformed into a dimensionless form and compared against rescaled dimensionless gas production rates from analytical dimensionless liquid flow rates.

The dimensionless flow rate produced at constant bottom-hole pressure in a bounded circular reservoir in Laplace space is given as follows (Da Prat et al. 1981):

$$\tilde{q}_{\text{D}} = \frac{{\sqrt {{\text{sf}}\left( s \right)} \left( {I_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} r_{\text{eD}} } \right)K_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} } \right) - K_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} r_{\text{eD}} } \right)I_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} } \right)} \right)}}{{s\left( {I_{0} \left( {\sqrt {{\text{sf}}\left( s \right)} } \right)K_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} r_{\text{eD}} } \right) + K_{0} \left( {\sqrt {{\text{sf}}\left( s \right)} } \right)I_{1} \left( {\sqrt {{\text{sf}}\left( s \right)} r_{\text{eD}} } \right)} \right)}}$$
(29)

By numerical inversion such as the Stehfest algorithm (Stehfest 1970) from Laplace space to real space, the dimensionless liquid flow rate is obtained. Similar to its counterpart in a single-porosity system (Ye and Ayala 2012), the definition of \(q_{\text{D}}^{\text{gas}}\) is:

$$q_{\text{D}}^{\text{gas}} = \frac{{\rho_{\text{sc}} \mu_{\text{gi}} c_{\text{gi}} q_{\text{gsc}} }}{{2\pi k_{\text{f}} h\left( {\rho_{\text{i}} - \rho_{\text{wf}} } \right)}}$$
(30)

where ρ sc is gas density under standard conditions and k f is fracture permeability.

Figure 2 presents the well-known constant-pressure liquid solutions of a dual-porosity system in terms of \(q_{\text{D}} = q_{\text{D}} (r_{\text{D}} , t_{\text{D}} )\) with Eq. 29 for the three different reservoir sizes under consideration in Tables 1 and 2 and the rescaled liquid solutions using \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\). The curves and the dots are dimensionless liquid rates and rescaled dimensionless liquid rates, respectively. Figure 3 presents a comparison between rescaled dimensionless liquid production rates and dimensionless production rates using data generated by the in-house simulator 1. The curves and the dots are rescaled dimensionless liquid rates and dimensionless gas rates using results from the in-house simulator 1, respectively.

Fig. 2
figure 2

Proposed density-based approximation versus dual-porosity liquid analytical solution for scenarios 1, 2, and 3

Full size image
Fig. 3
figure 3

Proposed density-based approximation from dual-porosity liquid solution versus numerically generated profile for scenarios 1, 2, and 3

Full size image

Figures 2 and 3 reveal that a liquid analytical solution for a dual-porosity reservoir can be used to accurately predict the long-term behavior of the corresponding dual-porosity gas reservoirs by rescaling from the dual-porosity liquid solution using \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\). A close match between the rescaled q liqD and q gasD from the in-house simulator leads to the conclusion that the depletion-driven dimensionless variables λ and β could successfully decouple pressure-dependent effects from pressure/density depletion for a dual-porosity system at the second decline stage. The liquid analytical solution for a dual-porosity system as described by Eq. 29 could be readily used to accurately predict the corresponding natural gas reservoir analytical responses by transforming the liquid traces based on the depletion-driven dimensionless parameters \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\). This implies the possible applicability of the production data analysis developed previously by Zhang and Ayala (2014b) based on density.

Spivey and Semmelbeck (1995) and Gerami et al. (2007) studied the applicability of pseudo-pressure and pseudo-time in dual-porosity systems, but their results show deviations, which are extreme in certain cases, between proposed methods and gas numerical responses. Spivey and Semmelbeck (1995) used the liquid-form interporosity flow equation, and Gerami et al. (2007) proposed the gas interporosity flow equation but did not implement it in the numerical model. We reexamine the applicability of pseudo-pressure and pseudo-time using the in-house simulator, which uses the derived gas interporosity flow equation. Three scenarios, as described by Tables 1 and 2, are used for validation purposes. Figure 4 plots the gas numerical response in terms of \(q_{\text{D}} = q_{\text{D}} (r_{\text{D}} , t_{\text{D}} )\) for the three scenarios as described by Tables 1 and 2. Figure 4 presents the comparisons between such numerical gas responses and the gas response using Gerami et al.’s (2007) method, both in dimensionless terms. \(\bar{\omega }\) is a constant in this case, and no iteration for an analytical solution is needed.

Fig. 4
figure 4

Dimensionless gas rate from in-house simulator 1 versus dimensionless gas rate generated using Gerami’s et al.’s (2007) approach

Full size image

Figure 4 demonstrates that pseudo-time and pseudo-pressure could effectively linearize the governing equations of dual-porosity gas systems, especially in the second decline stage during the production period. Therefore, applying pseudo-time and pseudo-pressure, the liquid analytical solution to a dual-porosity system could accurately describe the behavior of its gas counterpart at the second decline stage. The pseudo-time evaluated at average reservoir pressure successfully linearizes the governing equations, provided that the proposed interporosity gas flow equation is applied to modeling fluid transfer between the matrix and fracture. However, production profiles generated using λ and β rescaling approach and pseudo-function approach fail to strike match with production data from the in-house simulator 2 which utilizes the liquid-form interporosity flow equation, as demonstrated in Figs. 5 and 6. The deviation decreases and then increases, which ranges from 0 percent to 100 percent based on results from Gerami’s method and the rescaled dimensionless rates throughout the second decline stage. Modeling interporosity flow in naturally fractured gas reservoirs using the liquid-form interporosity flow with fluid properties evaluated at the pressure of the upstream one between matrix and fracture bring should be replaced with more appropriate interporosity flow model such as the derived gas interporosity flow equation.

Fig. 5
figure 5

Proposed density-based approximation from dual-porosity liquid solution versus numerically generated profile for scenarios 1, 2, and 3 from in-house simulator 2

Full size image
Fig. 6
figure 6

Dimensionless gas rate from simulation using in-house simulator 2 versus dimensionless gas rate generated using Gerami’s et al.’s (2007) approach

Full size image

It is reiterated that commercial simulators (CMG-IMEX in this case study, for example) utilize the liquid-form interporosity flow equation with gas viscosity and compressibility evaluated at matrix pressure or fracture pressure depending on which is upstream. Therefore, the production profiles behave the same as the in-house simulator 2 utilizing the liquid-form interporosity flow equation, which can significantly deviate from the production behavior of the in-house simulator utilizing gas interporosity flow equation. We illustrate the relationship among three production profiles by plotting the gas numerical profiles from the two in-house simulators and production profiles from CMG-IMEX. Figure 7 shows, for instance, Scenario 1’s gas numerical responses in terms of q sc versus t from the three simulators under the consideration in Tables 1 and 2. No difference is observed among three production profiles at the first decline stage in Fig. 7 as the production is primarily from fracture storage at this stage.

Fig. 7
figure 7

Comparison of production behaviors between CMG-IMEX and the two in-house simulators for scenario 1

Full size image

Figures 8, 9, 10 plot gas numerical responses in terms of q sc versus t from the two in-house simulators and CMG-IMEX in Scenarios 1, 2, and 3, as described in Tables 1 and 2, respectively. They show, more clearly, the difference in q sc versus t brought about by applying different interporosity flow equations by looking at the second decline stages in the three scenarios. The solid curve represents results from CMG-IMEX; the dashed line corresponds to results from the in-house simulator 1; and the red circles represent results from the in-house simulator 2. The comparisons shown in Figs. 8, 9, 10 demonstrate that the in-house simulator 2, which employs the liquid-form interporosity flow equation, and CMG-IMEX show similar production behaviors for the same scenarios. On the other hand, the in-house simulator 1, which uses the gas interporosity flow equation, demonstrates very different production behaviors from CMG-IMEX at the second stage. The major difference between our gas interporosity flow equation and the liquid-form equation in Warren and Root’s model is that we have considered the viscosity–compressibility change as gas flows from matrix to fracture. Behaviors of the two systems are similar when interporosity flow is not significant in its contribution to production. With the depletion of the fracture system, however, interporosity flow becomes dominant in its contribution to the gas production rate and the consideration of viscosity–compressibility change from matrix to fracture in the interporosity flow equation brings about a major change. The relative difference between production rates of the two systems becomes apparent at the end of the first decline stage at which point the production rate from in-house simulator 2 higher than that from the in-house simulator 1. The difference increases and then decreases before the two production rates meet each other early in the second decline stage. Late in the second decline stage, production rate from the in-house simulator 1 surpasses that of the in-house simulator 2, and the relative difference grows with time. Notably, the gas production rates from the in-house simulator 1 may increase to nearly twice those of the in-house simulator 2 during the late stage. The interporosity flow equation in the in-house simulator 2 is derived only for liquid and assumes constant viscosity and compressibility in the derivation thereby misrepresents gas flow from matrix blocks to fracture. The gas interporosity flow equation, derived rigorously based on physical principles as shown above, is a better representation for the flow exchange between matrix and fracture system for the gas case. Using the liquid-form interporosity flow equation in Warren and Root’s model can thus lead to significant error and distort the production behavior. Thus, using the liquid-form interporosity flow equation for dual-porosity gas systems is not recommended.

Fig. 8
figure 8

Comparison of production behaviors between CMG-IMEX and the in-house simulators at the second decline stage for scenario 1

Full size image
Fig. 9
figure 9

Comparison of production behaviors between CMG-IMEX and the in-house simulators at the second decline stage for scenario 2

Full size image
Fig. 10
figure 10

Comparison of production behaviors between CMG-IMEX and the in-house simulators at the second decline stage for scenario 3

Full size image

Reserve prediction for naturally fractured gas reservoirs

Zhang and Ayala (2014a, b) and Ayala and Zhang (2013) demonstrated that single-porosity gas reservoirs can be analyzed using straight-line analysis and harmonic decline equations for the prediction of original gas in place (G i). The two methods are based on the same principles but are written in different forms. The governing equation for the straight-line analysis is:

$$\bar{\lambda }\frac{{r_{\rho } }}{{q_{\text{gsc}} }} = \frac{1}{\text{OGIP}}\bar{\lambda }\frac{{G_{\text{p}} }}{{q_{\text{gsc}} }} + \frac{1}{{q_{\text{gi}}^{\text{e}} }}$$
(31)

where \(r_{\rho } = 1 - \frac{{\rho_{\text{wf}} }}{{\rho_{\text{i}} }}\), G p is cumulative gas production, and \(q_{\text{gi}}^{\text{e}}\) is a constant defined as follows:

$$q_{\text{gi}}^{\text{e}} = \frac{{2\pi \rho_{\text{i}} {\text{kh}}}}{{b_{{{\text{D}},{\text{PSS}}}} \rho_{\text{sc}} \mu_{\text{gi}} c_{\text{gi}} }}$$
(32)

The method originates from a gas rate equation essential for the rigorous proof of λ and β rescaling. Therefore, it is reasonable to speculate, based on the results discussed in the preceding section, that dual-porosity systems should satisfy a similar equation at the second decline stage, in which case \(\bar{\lambda }_{\text{m}}\) would replace \(\bar{\lambda }\). In such a case, the same steps for G i prediction for a single-porosity system utilizing Eq. 31 would need to be taken except for replacing \(\bar{\lambda }\) with \(\bar{\lambda }_{\text{m}}\). Steps are detailed in Zhang and Ayala (2014b).

Data provided in Scenarios 1 through 3 have been used for validating the G i prediction methods for dual-porosity reservoirs. With G i derived by plotting \(r_{\rho } /q_{\text{gsc}}\) versus \(G_{\text{p}} /q_{\text{gsc}}\), we here plot \(\bar{\lambda }_{\text{m}} r_{\rho } /q_{\text{gsc}}\) versus \(\bar{\lambda}_{\text{m}} G_{\text{p}} /q_{\text{gsc}}\) and obtain the best-fit straight line through the points in the second decline stage, thereby revealing the gradient 1/G i hence G i. If the difference is large, we replot \(\bar{\lambda }_{\text{m}} r_{\rho } /q_{\text{gsc}}\) versus \(\bar{\lambda}_{\text{m}} G_{\text{p}} /q_{\text{gsc}}\) with the new G i. The resulting plot after four iterations of G i prediction is shown in Figs. 11-13 corresponding to the three scenarios. For Scenario 1, the fitted straight lines for the second decline stage yield a slope of \(8.2214 \times 10^{ - 7} \;{\text{Mscf}}^{ - 1}\), which corresponds to a G i estimation of 1.2162 Bscf with a relative error of 1.430 % with respect to the actual G i. The slope of the straight line for Scenarios 2 and 3 is \(2.0567 \times 10^{ - 7} \;{\text{Mscf}}^{ - 1}\) and \(5.1415 \times 10^{ - 8} \;{\text{Mscf}}^{ - 1}\), respectively, yielding G i estimation of 4.8621 and 19.458 Bscf with relative errors of 1.380 and 1.384 %, respectively. The intercepts for Figs. 11, 12, 13 are \(1.4101 \times 10^{ - 6} \left( {\frac{\text{Mscf}}{\text{D}}} \right)^{ - 1}\), \(4.96 \times 10^{ - 7} \left( {\frac{\text{Mscf}}{\text{D}}} \right)^{ - 1}\), and \(2.7862 \times 10^{ - 7} \; \left( {\frac{\text{Mscf}}{\text{D}}} \right)^{ - 1}\), respectively.

Fig. 11
figure 11

\(\frac{{\bar{\lambda }_{\text{m}} r_{\rho } }}{{q_{\text{gsc}} }}\) versus \(\frac{{\bar{\lambda }_{\text{m}} G_{\text{p}} }}{{q_{\text{gsc}} }}\) straight-line analysis for scenario 1

Full size image
Fig. 12
figure 12

\(\frac{{\bar{\lambda }_{\text{m}} r_{\rho } }}{{q_{\text{gsc}} }}\) versus \(\frac{{\bar{\lambda }_{\text{m}} G_{\text{p}} }}{{q_{\text{gsc}} }}\) straight-line analysis for scenario 2

Full size image
Fig. 13
figure 13

\(\frac{{\bar{\lambda }_{\text{m}} r_{\rho } }}{{q_{\text{gsc}} }}\) versus \(\frac{{\bar{\lambda }_{\text{m}} G_{\text{p}} }}{{q_{\text{gsc}} }}\) straight-line analysis for scenario 3

Full size image

A notable feature of Figs. 11, 12, 13 is how readily the production data fall along a straight line. We also observe negligible deviation between the derived G i and the actual G i in the three scenarios after four rounds of iterations. This observation implies that the gas production from the dual-porosity system at the second decline stage is as follows:

$$\bar{\lambda }_{\text{m}} \frac{{r_{\rho } }}{{q_{\text{gsc}} }} = \frac{1}{\text{OGIP}}\bar{\lambda }_{\text{m}} \frac{{G_{\text{p}} }}{{q_{\text{gsc}} }} + \frac{1}{{q_{\text{gi}}^{{{\text{e}}*}} }}$$
(33)

where \(q_{\text{gi}}^{{{\text{e}}*}}\) is constant. \(q_{\text{gi}}^{\text{e}}\) is not used because the theoretical \(q_{\text{gi}}^{\text{e}}\) is different from the inverse of the intercepts, which could be due to fitting errors. Significantly, this correlation could be readily used for predicting the G i of dual-porosity systems without any calculation of pseudo-pressure or pseudo-time variables. Moreover, with predicted G i and \(q_{\text{gi}}^{{{\text{e}}*}}\) known from the intercept, the production rate at the second decline stage can then be predicted based on Eq. 33 following the procedure below:

  1. 1.

    Knowing \(\bar{\lambda }_{\text{m}} G_{\text{p}} /q_{\text{gsc}}\) at the last time step, increase \(\bar{\lambda }_{\text{m}} G_{\text{p}} /q_{\text{gsc}}\) by a small value and calculate the corresponding \(\bar{\lambda }_{\text{m}} r_{\rho } /q_{\text{gsc}}\).

  2. 2.

    Calculate r ρ/G p with \(\bar{\lambda }_{\text{m}} \frac{{r_{\rho } }}{{q_{\text{gsc}} }}/\bar{\lambda }_{\text{m}} \frac{{G_{\text{p}} }}{{q_{\text{gsc}} }}\) and then calculate G p knowing r ρ . \(\frac{{\bar{p}}}{{\bar{Z}}}\) is then calculated using material balance equation:

    $$\frac{{\bar{p}}}{{\bar{Z}}} = \frac{{p_{\text{i}} }}{{Z_{\text{i}} }}\left( {1 - \frac{{G_{\text{p}} }}{\text{OGIP}}} \right)$$
    (34)
  3. 3.

    Calculate the pressure corresponding to \(\bar{p}/\bar{Z}\) at each time point by interpolating \(\bar{p}/\bar{Z}\) in the \(\bar{p}/\bar{Z}\) versus \(\bar{p}\) table. Then we calculate \(\bar{\lambda }_{\text{m}}\) and q gsc knowing \(\bar{\lambda }_{\text{m}} r_{\rho } /q_{\text{gsc}}\) and r ρ .

  4. 4.

    Calculate time using

    $$\left( t \right)^{\text{i}} = \left( t \right)^{{{\text{i}} - 1}} + \,2\frac{{\left( {G_{\text{p}} } \right)^{\text{i}}\, -\, \left( {G_{\text{p}} } \right)^{{{\text{i}} - 1}} }}{{\left( {q_{\text{gsc}} } \right)^{\text{i}}\, +\, \left( {q_{\text{gsc}} } \right)^{{{\text{i}} - 1}} }}$$
    (35)

    where i denotes time level.

  5. 5.

    Repeat steps 1 to 4 until final target time is attained.

Concluding remarks

This study presents the derivation of the appropriate pseudo-steady-state interporosity flow equation for single-phase gas starting from physical principles. The resultant model incorporates viscosity–compressibility changes as fluids flow from matrix to fracture compared to its counterpart in Warren and Root’s model (1963) that holds liquid assumptions (constant viscosity and fluid compressibility). We show that the liquid-form interporosity flow model employed by Warren and Root is a special case of the new interporosity flow equation to be used when liquid assumptions hold. Comparisons between production behaviors from two simulators with the gas interporosity flow equation and the liquid-form interporosity flow equation reveal significant differences at the second decline stage, which suggests the impropriety of using the liquid-form interporosity flow equation for naturally fractured gas reservoirs. The gas interporosity flow equation encompasses the pressure-dependent effects of gas, which is a more reasonable approximation. Investigation of a density-based approach found it applicable to dual-porosity systems, provided that the gas interporosity flow equation is implemented. Shifting the liquid traces with the depletion-driven dimensionless parameters \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\), the liquid analytical solution could rigorously predict the responses of natural gas reservoirs at the second decline stage. Notably, \(\bar{\lambda }_{\text{m}}\) and \(\bar{\beta }_{\text{m}}\), two depletion-driven parameters, are simply dependent on average pressure and bottom-hole pressure and do not require pseudo-time, making this method easier to implement than the pseudo-functions-based approach. Furthermore, density-based decline curve analysis, which was originally derived for the single-porosity systems, is able to accurately predict the G i of dual-porosity systems. The applicability of pseudo-pressure and pseudo-time for decline curve analysis with the simulator using the gas interporosity flow equation is found successful. Applying the pseudo-functions to the liquid analytical solution captures the behavior of its gas counterpart at the second decline stage. Importantly, this linearization is contingent on the gas interporosity flow equation. A reason for the deviation in the constant-pressure production in Gerami et al. (2007) is due to the use of data generated by CMG-IMEX that applies the liquid-form interporosity flow equation. Our results thus prove successful in extending the density-based method and the pseudo-functions-based linearization of governing equations to dual-porosity gas systems.