Pore-scale numerical modeling of relative permeability curves for CO₂–oil fluid system with an application in immiscible CO₂ flooding

Abstract

CO₂ injection is considered as one of the proven EOR methods and is being widely used nowadays in many EOR projects all over the globe. The process of in situ displacement of oil with CO₂ gas is implemented in both miscible and immiscible modes of operation. In some oil reservoirs, CO₂ miscibility will not be attained due to fluid composition characteristics as well as in situ pressure and temperature conditions. Laboratory determination of gas–oil relative permeability curves is usually performed with air, nitrogen, or helium gases, and the results are then implemented for both natural depletion processes (especially in reservoirs with “solution gas” or “gas cap” drive mechanisms) and gas injection processes. For the gas injection processes, it is therefore necessary to find out how selection of the gas phase would affect the relative permeability curves when the intention of developing the curves is to use them for immiscible CO₂ displacement. In this study, a reservoir simulator was first used to quantitatively analyze the effect of variation in relative permeability data (due to the use of different gas phases) on production performance of a reservoir. Then, computational analysis was performed on changes in relative permeability curves upon using different gas phases with the aid of pore-scale modeling using statistical methods. To predict gas–oil relative permeability curves, a Shan–Chen-type multi-component multiphase Lattice Boltzmann pore-scale model for two-phase flow in a 2D porous medium was developed. Fully periodic and “full-way” bounce-back boundary conditions were applied in the model to get infinite domain of fluid with nonslip solid nodes. Incorporation of an external body force was performed by Guo scheme, and the influence of pore structure and capillary number on relative permeability curves was also studied for CO₂–oil as well as N₂–oil fluid pairs. The modeled relative permeability curves were then compared with experimental results for both these fluid pairs.

Introduction

Rock and fluid properties are the two essential input data in any reservoir simulation study. Among the rock properties, capillary effects and relative permeability have great importance on flow performance of different fluid phases in porous structure. Laboratory determination of relative permeability curves is usually performed with air, nitrogen, or helium gas in terms of a base relative permeability measurement, and the results are then implemented for both natural depletion and injection processes. At present, CO₂ injection is widely used for many enhanced oil recovery (EOR) applications. There are some important reasons that motivate the operators to use CO₂ flooding such as small bi-nodal curve in the ternary diagram and hence low miscibility pressure associated with CO₂ which manifests itself in the form of vaporizing-gas multiple contact miscibility, lower price, and also safety in application (Mathiassen 2003). However, CO₂ miscibility is not attainable in all reservoirs. Generally, the required reservoir depth should be greater than 800 m. CO₂ miscibility pressure is inversely proportional to API gravity of oil in a sense that in situ oil with gravity of 27° API or less is not a good candidate for CO₂ miscible displacement (Khan 2009). The immiscible displacement scheme of gas flooding should then be followed when miscibility conditions are not fulfilled based on operating conditions, reservoir conditions, and thermodynamic properties of the in situ oil. The concept of relative permeability comes into the play when miscibility criteria are not met which should be studied accurately using appropriate fluid pairs and operating conditions.

Ghoodjani and Bolouri (2011) performed an experimental study with an ultimate aim to obtain relative permeability data associated with CO₂–oil fluid pair. In their study, a methodology was proposed to calculate the CO₂–oil relative permeability from base N₂–oil relative permeability data by computing some fluid properties such as interfacial tension, viscosity, and swelling factor when porous media properties and operating conditions were unchanged. However, it was highlighted that more experiments are needed to validate and modify the proposed method for different fluid pairs. In a literature review performed on injectivity issues in the WAG process, it was mentioned that use of base relative permeability data for CO₂–oil systems without proper adjustments for IFT, oil swelling effect, etc., could lead to significant errors in performance prediction of CO₂-based WAG process (Rogers and Grigg 2001). This is due to the significantly lower CO₂ relative permeability under three-phase conditions compared to the base gases typically used in relative permeability measurements. In our opinion, an alternative approach of pore-scale modeling using numerical methods and statistical approaches can also be used for the same purpose. Use of the pore-scale modeling has another added value of enabling us to sensitively analyze the effect of pore structure properties (i.e., total surface area and wettability) and flow and fluid properties (i.e., viscosity ratio, IFT, and capillary number) on gas–oil relative permeability data. Of particular interest and capability is the pore-scale modeling using Lattice Boltzmann method.

Several studies focused on the use of Lattice Boltzmann modeling were published in the literature, targeting multiphase flow through porous media, such as “color method” by Gunstensen et al. (1991), “potential method” by Shan and Chen (1993), “free-energy model” by Swift et al. (1995), and “incompressible-indexed model”’ by He et al. (1999). Validity verification of relative permeability data, originated from Darcy’s law, was one of the subjects of application of multiphase lattice gas and Lattice Boltzmann modeling for multi-component oil–water systems (Sukop and Or 2004). Yiotis et al. (2007) used Lattice Boltzmann modeling to study viscous coupling effects in immiscible two-phase flow in porous media based on the single-component multiphase model of He et al. (1999), assuming that the pressure of non-ideal fluids is described by Carnahan–Starling equation of state (EOS). Viscous coupling effects for two-phase flow in porous media were also studied by Huang et al. (2008) by the use of Shan–Chen-type multiphase Lattice Boltzmann. The same modeling approach of Shan–Chen-type multiphase Lattice Boltzmann was also used by Huang and Lu (2009) to study relative permeabilities and coupling effects in steady-state gas–liquid flow in porous media. In both of these two last studies, single-component multiphase model was used along with R–K EOS to model vapor liquid systems with high density ratio.

In the current study, multi-component multiphase Shan–Chen-type Lattice Boltzmann model was used to study apparent relative permeabilities of gas–liquid systems. This type of modeling is suitable for flow simulation of different fluid pairs such as CO₂ and oil with essentially different kinematic viscosity values. In addition, Guo scheme was used for representation of body force which is proved to be one of the best representatives of continuity and momentum equations at the macroscopic scale (Guo et al. 2002). In addition to this pore-scale modeling methodology, numerical simulation analysis was also performed to investigate the effect of relative permeability variation on reservoir performance in terms of cumulative oil produced as well as to quantify the difference between relative permeability curves of a few fluid flow systems containing different gas phases.

In this paper, first, the quantitative analysis of the effect of variation in relative permeability on reservoir performance is presented by the use of a numerical simulator. After a brief review of the theory of the Lattice Boltzmann method, gas–liquid relative permeability curves were calculated as a function of wetting fluid saturation, M, and for a specific capillary number, Ca. The predicted relative permeability data were then corrected for the effect of pore structure and capillary number. The predicted relative permeability curves were then compared with experimental results.

Sensitivity analysis of the production performance with respect to relative permeability curves: use of appropriate relative permeability data

To demonstrate how sensitive production performance data are with respect to relative permeability curves, a simple 3D simulation model was constructed and solved using Eclipse 300 software package. In the compositional model, the fluids system was maintained above the bubble point and below the miscibility pressure to ensure the secondary flood. Compositional simulation considers the dynamic effects of contact between the desired gas and the specified oil. The model consisted of a cubical geometry with Cartesian grid dimensions of 50 × 10 × 30 grid blocks which can be considered as a quarter of a five-spot pattern. The grid block properties and dimensional characteristics are presented in Table 1. Three scenarios were investigated to sensitively analyze the dependency of production performance on relative permeability data under similar operating conditions and in situ oil properties: N₂ injection with N₂–oil relative permeability data, CO₂ injection with N₂–oil relative permeability data, and CO₂ injection with experimentally obtained CO₂–oil relative permeability curves, borrowed from Ghoodjani and Bolouri (2011). In our simulation study, an oil sample from one of the Southern Iranian oil fields was selected with physical properties (i.e., saturation pressure, density, and viscosity) very close to the ones used in Ghoodjani and Bolouri (2011) experimental work. The original and lumped oil compositions are given in Table 2, and the tuning parameters are presented in Table 3. The oil phase had density of 0.73 g/cc, viscosity of 1.13 cp, and average interfacial tension of 7 dyne/cm with displacing CO₂ at bubble point pressure and temperature of 1845 psia and 255 °F, respectively. The fluid modeling and tuning process was performed by three-parameter Peng Robinson EOS and Lohrenz–Bray–Clark (LBC) viscosity correlation. The bubble point pressure and minimum miscibility pressure for the lumped composition was calculated as 1862 and 5530 psia, respectively.

Table 1 Simulation model properties

Table 2 Original and lumped oil compositions

Table 3 Tuning parameters for lumped oil sample

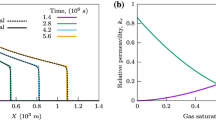
Local gas saturation as well as relative permeability history values were plotted and then compared across the reservoir boundaries for different simulation cases. For instance in Figs. 1 and 2, gas saturation and relative permeability versus time are plotted for three simulation cases in a particular coordinate in the grid system. It is apparent that use of different relative permeability curves results in different gas saturation histories. It is also found that regardless of the type of gas phase injected, the mobility and hence saturation history of the gas phase is more affected by the type of relative permeability curves employed for flow simulation (Fig. 1).

Fig. 1

Comparison of gas saturation history for three simulation cases with different relative permeability curves in a particular location in the reservoir

Fig. 2

Comparison of gas relative permeability history for three simulation cases with different relative permeability curves in a particular location in the reservoir

The field-scale performance of each of these three simulation scenarios can be studied by plotting the history of gas saturation, oil saturation, and total field oil production (Figs. 3, 4, 5). The N₂ injection simulation case resulted in the greatest field-average gas saturation which manifested itself in achieving the minimum field-average oil saturation. Of particular importance is the very similar trend observed in the field-scale oil and gas saturation histories for the CO₂ injection cases with two different relative permeability datasets during the early life as well as the midlife of the displacement process. However, for the late life of the simulation time, CO₂ injection with experimentally obtained relative permeability curves exhibits greater field-scale gas saturation (i.e., less field-scale oil saturation) due to less gas mobility (i.e., greater oil mobility) originated from using the more appropriate relative permeability curves. The CO₂ injection cases, with both employed relative permeability curves, exhibit more field-total oil production, especially during the late production stages, compared to the N₂ injection case, with more oil produced for the case in which the experimentally obtained relative permeability curves were used (i.e., less mobility of the gas phase). This is likely due to swelling effects originated from the nature of the CO₂–oil fluid interaction which is not seen for any other gas type, including N₂.

Fig. 3

Comparison of the field-average gas saturation history for three simulation cases with different relative permeability curves

Fig. 4

Comparison of the field-average oil saturation history for three simulation cases with different relative permeability curves

Fig. 5

Comparison of the field-total cumulative oil production for three simulation cases with different relative permeability curves

Lattice Boltzmann method: theory, background, and model setup

In pore-scale modeling of fluid flow through 2D models with the aid of Lattice Boltzmann method, the geometrical domain is divided into regular lattices with similar spacing in both x- and y-directions. A distribution function of $f_{m}^{\sigma } \left( { \, x \, , \, y, \, t} \right)$ is defined at each lattice site that denotes the number of fluid particles, σ, at site (x, y) in the direction of m with velocity of e _m and reduced to eight directions (D2Q9). During each time step, streaming and collisions of these particles are governed by Boltzmann equation which is presented below for a discrete domain (Sukop and Thorne 2007):

$$f_{\alpha } \left( {x + e_{\alpha }\Delta t,t +\Delta t} \right) = f_{\alpha } \left( {x,t} \right) - \frac{{f_{\alpha } \left( {x,t} \right) - f_{\alpha }^{\text{eq}} (x,t)}}{\tau }$$

(1)

$$\begin{aligned} f_{\alpha }^{\text{eq}} \left( x \right) & = w_{\alpha } \rho \left( x \right)\left[ {1 + 3c_{\alpha } \cdot u^{\text{eq}} + 9\left( {c_{\alpha } \cdot u^{\text{eq}} } \right)^{2} - 3u^{\text{eq2}} /2} \right] \\ w_{1} & = 4/9;\quad w_{2345} = 1/9;\quad w_{6789} = 1/36 \\ \end{aligned}$$

(2)

in which f _α is directional density (local distribution function), f ^eq _α is local equilibrium distribution function, w _α is directional weighting multiplier, ρ is average density, c _α is directional basic lattice speed of particles, u ^eq is equilibrium macroscopic velocity.

τ is the relaxation time which in single relaxation time Bhatnagar–Gross–Krook model (i.e., BGK model) relaxes the distribution function toward local equilibrium (i.e., f ^eq). The fluid kinematic viscosity is also defined as:

$$\nu = \frac{1}{3}\left( {\tau - 0.5} \right)$$

(3)

ρ is the macroscopic fluid density which is defined as the summation of directional densities:

$$\rho = \mathop \sum \limits_{\alpha = 1}^{9} f_{\alpha }$$

(4)

The macroscopic velocity, u, is an average of the microscopic velocities e _m weighted by the directional densities f _m :

$$u = \frac{1}{\rho }\mathop \sum \limits_{\alpha = 1}^{9} f_{\alpha } e_{\alpha }$$

(5)

Based on Newton’s second law, when there is an external body force (F), the macroscopic equilibrium velocity is computed as:

$$u^{\text{eq}} = u +\Delta u = u + \tau \cdot F/\rho$$

(6)

To simulate multiphase systems, forces between two different phases including fluid–fluid and fluid–solid forces should be incorporated in the model. By introducing the second species in the model in the form of a multi-component multiphase model, previous equations should be slightly modified. In such a case, equilibrium velocity for fluid phase σ is defined as:

$$u_{\sigma }^{\text{eq}} = u^{'} + \frac{{\tau_{\sigma } F}}{{\rho_{\sigma } }}$$

(7)

In Eq. 7, F and u′ are the total force and composite velocity, respectively, defined in the form of:

$$F = F_{\text{cohesion}} + F_{\text{adsorption}} + F_{\text{external}}$$

(8)

$$u^{'} = \left( {\sum\limits_{\sigma } {\sum\limits_{\alpha = 1}^{9} {f_{\alpha }^{\sigma } e_{\alpha } /\tau_{\sigma } } } } \right)\Big/\left( {\sum\limits_{\sigma } {\rho_{\sigma } /\tau_{\sigma } } } \right)$$

(9)

in which F_cohesion is cohesion force, F_adsorption is adsorption force, F_external is external body force, and e _α is microscopic velocity.

The composite velocity is a measure of the whole fluid velocity which can be computed as (Shan and Doolen 1996):

$$u = u^{'} + F/(2\rho )$$

(10)

with

$$\rho = \mathop \sum \limits_{\sigma } \rho_{\sigma }$$

(11)

Cohesion and adsorption interaction forces can be calculated based on the nearest neighboring nodes with the following form presented by Sukop and Thorne (2007):

$$F_{c} \left( {x,t} \right) = - G_{c} \psi_{\sigma } (x,t)\mathop \sum \limits_{\alpha = 1}^{9} w_{\alpha } \psi_{{\overline{\sigma } }} \left( {x + e_{\alpha }\Delta t,t} \right)e_{\alpha }$$

(12)

$$F_{\text{ads}} \left( {x,t} \right) = - G_{\text{ads}} \psi (x,t)\mathop \sum \limits_{\alpha = 1}^{9} w_{\alpha } S\left( {x + e_{\alpha }\Delta t} \right)e_{\alpha }$$

(13)

in which σ and $\overline{\sigma }$ denote two different fluids, and G _c and G _ads are used to control the IFT and the contact angle, respectively. The latter two parameters are determined using bubble and contact angle tests, respectively. Depending on the nature of the interaction between two fluids, smaller values of G _c lead to diffused interfaces, whereas larger values associated with this parameter lead to sharp interfaces and more pure components. However, the simulation will suffer from numerical instability after some critical values when larger values of G _c are used. The sign of these two parameters (i.e., G _c and G _ads) indicates the repulsion or attraction nature of the forces. Their absolute values can be adjusted to model the desired IFT and contact angle values. In the above equations, ψ and S are potential functions, indicating solid sites (1) or pore sites (0), respectively (Sukop and Thorne 2007). We found that the potential function ψ, proposed by Shan and Chen (1993) for the EOS, is the best choice for conducting multi-component and multiphase flow behavior suited with high viscosity ratio:

$$\psi (\rho ) = \rho_{0} \left[ {1 - \exp \left( { - \frac{\rho }{{\rho_{0} }}} \right)} \right]$$

(14)

in which ρ ₀ is an arbitrary initial fluid density, here taken as 1.2 mu/lu².

To incorporate an external body force, we implemented the Guo scheme. According to Guo et al. (2002), the best procedure to accommodate Lattice Boltzmann modeling with continuity and momentum equations (i.e., Navier–Stokes equation) at the macroscopic scale is in the following form:

$$F_{i} = w_{i} \left( {1 - \frac{1}{2\tau }} \right)\left[ {3(e_{i} - u) + 9e_{i} \left( {e_{i} \cdot u} \right)} \right] \cdot F$$

(15)

Guo examined the common procedures in inclusion of external body force in Lattice Boltzmann modeling. Through Chapman–Enskog expansion of Boltzmann discrete equation (i.e., Eq. 1), he showed that none of those procedures could produce the exact Navier–Stokes equation. The above method, in which both the discrete lattice effect and the contribution of body force to the momentum flux are considered, should assist in developing Lattice Boltzmann models with external/internal body forces. This external body force term needs to be added to the collision operator. The velocity term should also be shifted as: $u^{\text{eq}} = u + F/2\rho$.

The “full-way” bounce-back scheme and fully periodic boundaries were applied at the solid and non-solid boundaries of the domain, respectively, to get an infinite fluid domain. The “bounce-back” method is applied to simulate the nonslip boundaries at the solid nodes, whereas in periodic boundary condition, nodes on the opposite boundary are simply considered as the neighboring points of the boundary nodes.

To verify the validity of Lattice Boltzmann model, it should pass through the primary bubble and contact angle tests, followed by more validation on predicting the Poiseuille flow pattern using simulation of multiphase flow in a channel. In bubble test, the interfacial tension is adjusted, and the model’s ability in relating the pressure difference, radius of curvature, and interfacial tension when a bubble of a fluid is immersed in other fluid is checked. Through the contact angle test, one can check the model’s ability to predict different wetting behavior, controlled by the parameter G _ads, and verify the assumption of direct relationship between cohesion and adsorption parameters and the interfacial tension values in Young’s equation. Out of the mentioned conventional validation processes for the Lattice Boltzmann model, only modeling of two-phase flow in a 2D channel is presented in this paper.

Two-phase flow in a 2D channel

After constructing the model, the problem of two-phase flow in a 2D channel was considered to be investigated to check model’s ability to simulate multiphase flow problems. To reduce the computational cost as well as the effect of somewhat thick interface (i.e., 6–8 lu) on San–Chen model and also considering the periodicity advantage in Lattice Boltzmann model, a 121 × 11 lu² domain was used. Using analytical solution of Poiseuille flow geometry in a 2D channel, the corresponding relative permeability expressions for wetting and non-wetting phases are expressed as (Yiotis et al. 2007):

$$k_{r,w} = \frac{1}{2}S_{w}^{2} \left( {3 - S_{w} } \right)$$

(16)

$$k_{{r,{\text{nw}}}} = S_{\text{nw}} \left[ {\frac{3}{2}M + S_{\text{nw}}^{2} \left( {1 - \frac{3}{2}M} \right)} \right]$$

(17)

in which wetting phase saturation, S _w , is defined as S _w  = 1 − a/b with 2b and a being the channel width and location of the fluids interface relative to the central line of the channel, respectively. The viscosity ratio, M, was defined as: M = μ _nw/μ _w  = ν _nw ρ _nw/(ν _w ρ _w ). Calculation of the relative permeabilities using Lattice Boltzmann modeling was performed at the outlet face of the medium and was defined as the cumulative flux of one particular fluid divided by the total cumulative fluid flux when only that fluid exists in the domain. This method is applicable when Darcy’s law conditions are satisfied which implies that small Reynolds number and steady-state (i.e., constant saturation) conditions are reached. To obtain numerical values of τ, G _c, G _ads, and θ parameters, the bubble test was conducted by placement of various initial radii bubbles of less viscous fluid in a domain of size 150 × 150 lu². The pressure difference versus radius of curvature was plotted with the slope being the interfacial tension. In contact angle tests, a droplet of 30 lu diameter of wetting fluid was placed in a domain of size 120 × 150 lu² surrounded by non-wetting fluid. The equations in Huang et al. (2007) were applied to compute the contact angle of a drop on a surface with the parameters R _d , L _d , and H _d being the drop radius, drop base, and drop height, respectively. τ, G _c, and G _ads parameters were then adjusted such that various viscosity ratios for different fluid pairs with the desired IFT and θ data could be achieved. These simulations were performed with tau values of 0.75 and 1.17, G _c = 3 and G _ads = 1.5. The IFT and contact angle values were calculated as σ = 0.042 and θ = 9°, respectively.

Capillary number, Ca, is regarded as the ratio of the body forces to the interfacial forces (Rothman and Keller 1988). The numerical values of body force in the literature range from 10⁻⁴ to 10⁻⁸ mu/(lu.ts²), depending on the problem at hand and the desired or required value of capillary number. In this section, a typical value of 10⁻⁴ mu/(lu.ts²) was assigned to the uniform steady body force, F _ext, which resulted in Ca = 10⁻⁴/0.042 = 2.4 × 10⁻³. The Reynolds number was also maintained small to ensure the applicability of Darcy’s law; the maximum lattice velocity of 0.00014 lu/ts with kinematic viscosity of 0.167 lu²/ts and 20 lu pore diameter resulted in $\text{Re} = Ud/\nu = 0.017$.

Figure 6 shows the analytical and simulation results for the relative permeability curves, obtained based on Poiseuille flow geometry and Lattice Boltzmann modeling, respectively. In a situation where the more viscous fluid is the wetting phase, the relative permeability of wetting and non-wetting fluids obeys the conventional pattern in which the non-wetting relative permeability is greater in magnitude. It is also obtained that there is a very good agreement between the relative permeability data predicted by Lattice Boltzmann model and those obtained analytically based on Poiseuille equation for all the ranges of mobility ratio. Since the wetting fluid relative permeability is not a function of viscosity ratio, wetting fluid relative permeability curve does not change when the wetting phase viscosity is less than that of the non-wetting phase; however, the non-wetting fluid phase experiences a lubricating effect during the flow, hence shows a relative permeability greater than unity. The velocity profile at a particular time frame, obtained using both analytical approach and Lattice Boltzmann model, is shown in Fig. 7. Although it seems that Lattice Boltzmann model underestimates the maximum experienced velocity at the half-way width of the channel with respect to the analytical approach, the difference between these two predictions fades away in greater time steps.

Fig. 6

Comparison of Lattice Boltzmann modeling results and analytical solution for variation in wetting- and non-wetting phase relative permeabilities versus wetting phase saturation in two-phase Poiseuille flow

Fig. 7

Velocity profile in the channel, obtained using Lattice Boltzmann modeling and analytical solution of Poiseuille flow, after 30,000 time step

Two-phase flow through porous media

In this section, model setup and initialization is discussed followed by the details on the sensitivity analysis of the modeling results with respect to the effect of pore structure and capillary number.

Model setup and initialization

To represent the porous medium, a symmetric image relative to x–y-axes of a micromodel pore structure pattern was reproduced. This piece, which has the size of 569 µm × 891 µm, was extracted from a micromodel which was constructed using a thin section of a 3D Berea sandstone rock sample with 22 % porosity (Boek and Venturoli 2010). The true porosity value of the micromodel was reported to be 33 %. Following this procedure, a more simplified image, as presented in Fig. 8, was derived from the symmetric image. This simplified image can be compared with the ideal sphere pack model, presented in Fig. 9, with respect to porosity and total pattern area.

Fig. 8

Simplified pore structure, 264 × 502 lu², 38 % porosity

Fig. 9

Ideal sphere pack, 262 × 484 lu², 38 % porosity

When it comes to simulation of multiphase flow in porous structure using Lattice Boltzmann modeling, the typical porosity values are somewhat greater than 50 % in magnitude to achieve percolating system in all directions as well as to reduce the effect of interface thickness and that of the pore structure on the simulation results. Another alternate is to increase the resolution of the medium by reducing μm/lu in which μm represents length scale in physical porous structure and lu represents the unit length in simulated lattice structure. The latter solution results in an obvious drawback of increased computational cost or in other words high-performance computing hardware requirements. In addition, having a porous network with small porosity value induces a limit on threshold capillary number, i.e., the smaller the porosity, the greater should be the Ca to acquire a full percolating system.

Using a MATLAB code, numerical simulation of a 200 × 200 lu² domain with 47 % porosity for up to 40,000 ts simulation time using Lattice Boltzmann modeling approach took about 1 h to complete. This simulation run was conducted using a Personal Computer with a 3 GHz Intel processor and 1 GB RAM. Considering the huge number of simulation runs needed to optimize the tuning parameters of G _c, G _ads, and τ for the purpose of obtaining relative permeability curves at different saturations, a number of alternatives and assumptions were made: First, it was decided to implement a 150 × 150 lu² geometrical domain with porosity value of about 60 %. Note that the typical geometrical domain in the literature is 200 × 200 lu². Second, a simplified symmetrical pore structure was used to reduce numerical instability even though the real pore structures are more complex. Third, the capillary number was adjusted in the range of 10⁻³–10⁻⁴ to reduce the computational cost by speeding up the simulation as well as to achieve a full percolating system. Forth, it is assumed that use of the simple periodic boundary condition easily compensated for the small domain size by repeating the domain at each time step. In the event of having other boundary conditions, using extensively large domains is necessary to acquire meaningful results. The simulation runs could be initialized considering two alternatives for initial saturation distribution along the domain, namely as a random distribution and an injection-like initial saturation. The first initial saturation distribution is suitable for a pair of fluids with large density difference to gain stability, whereas the second distribution is more realistic to simulate the injection processes. Utilizing the mentioned boundary condition and initial condition of injecting the less viscous fluid into the medium, the relative permeabilities were calculated at different cross sections to obtain an average value. In all simulation runs, the initial constant saturation throughout the medium was attained after 10,000 ts; however, it was assumed that the steady-state condition prevails after 30,000 ts.

Effect of pore structure

In experimental measurement of relative permeability during immiscible displacement process in a strongly wetted porous medium, it is customary to neglect the effect of gravity and capillary forces in the viscous-dominated displacement process (Archer and Wall 1986). In such measurements, capillary pressure can only be considered to set the initial saturation condition while the results are independent of bond number. It is expected that in such conditions, the relative permeability data depend only on the pore structure and capillary number. In this section, effect of the pore structure on relative permeability data is discussed for gas–oil immiscible displacement. Details for these two simulation runs are provided in Table 4. The predicted relative permeability curves for both wetting and non-wetting fluid phases are presented in Figs. 10 and 11 for the two simulation runs at constant level of capillary number. In these two figures, Index 1 delineates the simplified pore structure captured from the micromodel pattern, presented in Fig. 8, whereas Index 2 identifies the ideal sphere pack model as the pore structure which is presented in Fig. 9. It is noted that the results are independent of porosity value associated with these two pore structures considering 38 % equivalent porosity for both these pore networks. Due to the reduced particle size and increased number density of particles embedded in porous structure 2 compared to 1, the total surface area associated with the former network is larger than that of the latter one. As illustrated in Figs. 10 and 11, an increase in pore-scale surface area slightly reduces the non-wetting phase relative permeability especially at smaller wetting phase saturation but almost does not alter the wetting phase relative permeability.

Table 4 Fluid and model properties in studying the influence of pore structure on predicted relative permeability data

Fig. 10

Effect of pore structure on predicted relative permeability curves using Lattice Boltzmann modeling at constant Ca value (M = 0.065, σ = 0.021 mu.lu/ts², Index 1 indicates pore structure originates from micromodel, whereas Index 2 represents the homogeneous sphere pack pore pattern)

Fig. 11

Effect of pore structure on predicted relative permeability curves using Lattice Boltzmann modeling at constant Ca value (M = 0.021, σ = 0.048 mu.lu/ts², Index 1 indicates pore structure originates from micromodel, whereas Index 2 represents the homogeneous sphere pack pore pattern)

Effect of capillary number

Four simulation trials with two different fluid sets and two capillary number values were conducted to investigate the influence of capillary number on relative permeability curves. The details of these simulation runs for two different sets of fluids are provided in Table 5. In all these trials, similar pore structure of ideal sphere pack with porosity of 57 % was utilized to obtain higher precision and also less dependency on the pore structure. For each fluid type set, two capillary number values of the order of 10⁻³ were used (Figs. 12, 13).

Table 5 Fluid and model properties in studying the influence of capillary number on predicted relative permeability data using Lattice Boltzmann modeling

Fig. 12

Effect of capillary number on predicted relative permeability curves for N₂–oil fluid system using Lattice Boltzmann modeling at fixed pore structure

Fig. 13

Effect of capillary number on predicted relative permeability curves for CO₂–oil fluid system using Lattice Boltzmann modeling at fixed pore structure

It was obtained that although the capillary number has a minor effect on residual saturations, it noticeably affects the wetting phase relative permeability at wetting phase saturations of 0.3 or greater as well as that of the non-wetting phase at corresponding non-wetting phase saturations of 0.5 or greater (Figs. 12, 13). The smaller the capillary number, the smaller is the predicted relative permeability value (for both phases) at each particular wetting phase saturation. These results are in agreement with the general trend observed in the literature on the effect of capillary number on the relative permeability curves.

Gas–oil system

The Lattice Boltzmann model developed in “Model setup and initialization” section and fine-tuned in “Effect of pore structure” section and “Effect of capillary number” section was used in this section to simulate immiscible displacement of oil with gas (CO₂ and N₂ in this study) in a two-phase flow system where gravity force was neglected. The purpose was to manipulate the model parameters so that the experimental conditions of Ghoodjani and Bolouri (2011) will be achieved. The simulation job is supposed to represent the experimental conditions of Ghoodjani and Bolouri (2011) in which the relative permeability curves of CO₂–oil and N₂–oil fluid pairs were obtained with the aid of coreflooding tests using a sandstone core sample and two carbonate ones. They used the unsteady-state method to calculate the two-phase relative permeability values using Jones and Roszelle (1978) procedure (Table 6). The experimental procedure used by Ghoodjani and Bolouri (2011) is as follows: The cleaned core samples were evacuated and then saturated with brine at the beginning of each experiment. To ensure complete saturation, several pore volumes of brine were cycled through, after which the absolute permeability to water was measured. The next step was to flood the samples with oil until reaching the irreducible water saturation state. In gas injection tests, the gas rate was sustained at 0.3 cc/h. After injection of 4 pore volumes, the injection was continued with higher rate until the oil production ceased. For comparison of relative permeability curves in full range of saturation, the Corey’s model was used to normalize saturation and relative permeability values to fit the experimental data. To develop a methodology for calculation of CO₂–oil relative permeability from base N₂–oil relative permeability data, the authors computed some properties of fluids (i.e., interfacial tension, viscosity, and swelling factor) using a commercial fluid analysis software to study how the use of CO₂ and N₂ will affect them. Since the comparisons were performed using similar porous media properties, pressure, and temperature, the computed values are independent of operating conditions and porous media properties, i.e., the type of gas is the only parameter influencing the computed fluid properties.

Table 6 Fluid and model properties and experimental conditions of the relative permeability measurement tests extracted from Ghoodjani and Bolouri (2011)

As stated above, gravity force was neglected which is in agreement with most of the laboratory-scale immiscible displacement studies using 1D coreflood as well as 2D micromodel tests. The properties of the Lattice Boltzmann model used in this section are presented in Table 5. In such an immiscible displacement process, role of the gravity force in the overall body force should be minimal so that the viscosity ratio parameter and capillary number would affect the value of the body force the most. This also minimizes the numerical instability which would be caused by the presence of small values associated with both viscosity ratio as well as density ratio parameters. The objective of such a simulation is to correct the relative permeability curves used in our Lattice Boltzmann model previously in the last three sections by providing model properties very similar to those of the real experimental conditions. Of particular importance among model parameters that should be modified are the pore structure, which shows itself in terms of the porosity value, and capillary number.

An almost 50 % increase in the surface area of the pore structure was required to reduce the porosity associated with the 2D model presented in “Effect of pore structure” and “Effect of capillary number” section (i.e., 57 %) to the 15 % value reported in Table 6. The capillary number was also corrected from the initial value of 4.7 × 10⁻³ to the values reported in Table 6 for each particular immiscible flood. By matching the production data associated with each particular immiscible flood, the relative permeability curves for each test were simulated and are presented in Figs. 14 and 15. According to these two figures, it is clear that both the wetting and non-wetting relative permeability curves associated with these two immiscible floods are not interchangeable; therefore, it is not a valid decision to implement other fluid pairs’ relative permeability data for particular displacement processes including CO₂ flood.

Fig. 14

Corrected oil relative permeability curves for the N₂ and CO₂ floods

Fig. 15

Corrected gas relative permeability curves for the N₂ and CO₂ floods

Now that the developed Lattice Boltzmann model is tuned and corrected, one can apply real experimental conditions involving CO₂–oil system and adjust model parameters to obtain model predictions and then compare them against those measured experimentally using coreflood tests. Although the implied domain in our pore-scale modeling does not truly represent the physical core plug(s) in which CO₂–oil relative permeability data were measured by Ghoodjani and Bolouri (2011), we believe the proposed procedure is capable of predicting acceptable and realistic behavior. The predicted CO₂–oil relative permeability data using pore-scale modeling approach are compared against the experimental data obtained from Ghoodjani and Bolouri (2011) in Fig. 16; a satisfactory and realistic behavior of predicted data is observed in this figure that matches those of the experimental data.

Fig. 16

Comparison between the CO₂–oil relative permeability predictions and the experimental data obtained from Ghoodjani and Bolouri (2011)

Conclusions

In this study, computational methods were used to analyze the relative permeability curves in immiscible displacement process using Lattice Boltzmann pore-scale modeling. Quantitative analysis of the effect of relative permeability curves on production performance of immiscible displacement at reservoir-scale was also performed. A multi-component multiphase Shan–Chen-type Lattice Boltzmann model was developed and implemented to study the two-phase flow in porous media with focus on relative permeability curves of different involving gas phases. The relative permeability curves were calculated as a function of wetting phase saturation for different viscosity ratios, capillary numbers, and pore structures.

An increase in the surface area associated with particular pore structures resulted in reduction in the non-wetting phase relative permeability values but almost did not affect the wetting phase relative permeability values. The capillary number had a direct impact on the relative permeability values for both the wetting and non-wetting phases at constant pore structure condition. The developed Lattice Boltzmann model was then tuned in terms of porosity and capillary number to represent the true experimental conditions presented by Ghoodjani and Bolouri (2011). The production performance reported by Ghoodjani and Bolouri (2011) was matched by Lattice Boltzmann model to compute the relative permeability values for each particular involving fluid phase. It was concluded that the wetting and non-wetting phase relative permeability curves associated with two immiscible floods are not interchangeable; therefore, it is required to measure the relative permeability data for each particular fluid pair of interest targeted for immiscible displacement studies.

The outcome of this study is a model capable of dealing with high viscosity ratio fluid pairs to reproduce the gas–liquid relative permeability curves through contribution of Guo scheme and proper selection of potential function. It can be attributed to any gas type by proper tuning procedure. This model is also capable of considering any pore structure, either sandstone or carbonate, provided that appropriate lattice resolution is assigned.