Introduction

As hydrocarbon demand stays high and its production from the field is declining, in the future, the hydrocarbon demand will outrun the world's hydrocarbon production1. Therefore, the significance of using new techniques to produce more hydrocarbon is very important1. Different enhanced oil recovery (EOR) techniques can be used for the production of more hydrocarbon, one of the commonly used EOR methods is gas injection, especially for light oil reservoir1,2,3. Poor injectivity and sensitivity issues are known as limitations in water flooding, which can be overcome in the gas injection process4. As most of injection gases are greenhouse gas, this technique is known as an environmentally friendly method4. Both natural and non-natural gas can be injected to enhance the production of oil in mature fields. Carbon dioxide (CO2), associated gas, air, and nitrogen (N2) are the most used gases in gas flooding4,5. Because of its physical properties, viscosity reduction and oil swelling can be made well with CO2. In addition, the existence of CO2 in some formations can result in the dissolution of limestone minerals and subsequently increase formation injectivity6,7,8,9. Accessibility and low cost of air caused this gas to become one of the interesting injection fluids in gas flooding10. The main issue in air injection is its oxygen content, as it can create a threat to the safety of the operation process11. The main feature of associated gas is its high solubility in reservoir fluid. Hence, it can generate a miscible flooding process, but due to its high cost, it will be injected with other natural gas12. The performance of flue gas in the reservoirs that contain heavy crude oil and have thin-pay is acceptable13. Because of the physical properties of flue gas, it is unlikely to form miscible phase with reservoir fluid; therefore, massive amount of injected gas remains as a free gas13. Gas can be injected in miscible, immiscible, and near miscible conditions, which depends on the reservoir temperature and pressure, hydrocarbon components of reservoir, and type of injection gas. High reservoir pressure and gas with low minimum miscibility pressure (MMP) resulted in miscible conditions, and injected fluid and reservoir fluid created a single phase. In this process, the viscosity of the oil will be reduced, and oil swelling will be occurred14. In an immiscible process, the oil displacement is controlled by capillary pressure and relative permeability14. Unlike the miscible process, in immiscible injection, only part of the gas will be dissolved in the reservoir oil14.

As the gas injection is known as an interesting EOR technique, researchers have studied this method experimentally as well as numerically. Karimaie et al.15 investigated the process of gas injection in a fractured reservoir. They showed that CO2 resulted in more oil production than N2 at high pressure and temperature. Chukwudeme and Hamouda16 conducted a series of experiments to study miscible CO2 flooding. Based on their experiments, compared with asphaltenic oil, CO2 flooding resulted in more oil recovery for non-asphaltenic oil. The performance of CO2 in tight reservoirs was studied by Arshad et al.17. Oil recoveries of 87–97% were achieved in their experiments. In 2014, Bhoendie et al.18 conducted a series of core flooding tests to investigate the potential of some N2 and CO2 injections. They showed that both CO2 and N2 WAG caused the highest oil recovery. Injection of N2 after water flooding had a higher recovery than CO2 flooding after water injection. In the other hand, in gas injection phase CO2 had higher oil production compared with N2. In order to investigate immiscible N2 flooding, Janssen et al.19 conducted five series of experiments: continuous N2 injection at increasing backpressures, continuous N2 injection at 5 and 10 bar backpressure, continuous N2 injection after water flooding, and water alternative gas20 injection. Their experiments illustrated that WAG injection resulted in more oil recovery, among other schemes. Huang et al.4 investigated the performance of CO2, deoxygenated air, associated gas, and fuel gas in the tertiary recovery process. Based on their experiments, the performance of continuous gas injection was better than WAG injection. In addition, among the above-mentioned gas and in continuous gas injection, associated gas has better performance in oil recovery. They showed that in the WAG process, the performance of CO2 is much better than the three other gases. The experimental study was conducted by Khather et al.7 to study the impact of CO2 injection on both oil recovery and petrophysics. They reported that the injection of CO2 after water flooding resulted in higher oil recovery. Based on their experiment, a reduction in permeability of samples occurred after the CO2 injection. Different mechanisms such as mineral precipitation/dissolution, resin precipitation, compaction, and asphaltene precipitation can be the reasons for this reduction7. The performance of associate gas huff-n-puff in organic-rich shale core was evaluated by Shilov et al.21. Based on their observation in non-miscible conditions, oil recovery increased from 29 to 79.55%. While in the near miscible condition, the oil recovery was improved from 41 to 88.4%.

Besides extensive experimental study in the gas injection process, there is various numerical study. Hoteit and Firoozabadi22 developed a numerical model for the gas injection process in the fractured reservoir that considers the physical diffusion of the multicomponent mixture. Based on their results, away from miscibility pressure, the effect of diffusion on the recovery was high. They also investigated their model for fractured gas condensate and showed that diffusion affected the condensate recovery. Alfarge et al.23 investigated the numerical simulation study on miscible EOR techniques for enhancing oil recovery in shale oil reservoirs. Their simulation results showed the significance of molecular diffusion in a gas injection on EOR for the studied reservoirs. Zhong et al.24 studied a numerical simulation of the WAG process for optimizing carbon storage and EOR. Their results showed that injection of WAG caused the mobility ratio of water and oil to decrease and swept coefficient to increase, the total recovery of the reservoir after WAG injection increased. In terms of CO2 storage, a low WAG time ratio was better. However, in terms of oil recovery, a high WAG time ratio was acceptable. They also showed that higher oil recovery could be achieved because of the higher injection rate of CO2. Shilov et al.21 investigated the performance of associated gas huff-n puff and validated their observation with numerical study. Based on their numerical study, injection pressure influenced the oil recovery, especially in near miscible and miscible conditions.

As there is a high demand for oil, unconventional reservoir, such as shale oil, tight oil, coal seam gas/coal bed-methane, shale gas, basin-center gas, gas hydrates, tight gas, chalk, and tar sand, have become main source of oil production. There is some substantial differences between conventional and unconventional reservoirs. Large volume of formations that charged with hydrocarbon are exist in unconventional reservoirs. Buoyancy and gravity of reservoir fluids do not affect the production of these type of reservoirs. Reservoir and source rock in unconventional reservoirs are coexist, while in conventional reservoir they are separated form each other. In this regard, special methods was employed to produce for these type of reservoirs25. According to important role of unconventional reservoir in energy production, several researchers investigated the performance of different EOR method in theses reservoirs. As well as conventional reservoirs, gas injection is one of interesting EOR method in unconventional reservoirs. Therefore, many experimental and numerical investigations have been conducted to study gas injection technique in unconventional reservoirs26,27,28,29,30,31,32,33,34. The potential of cyclic CO2 injection for oil recovery in shale reservoirs was investigated experimentally by Gamadi et al.32. They showed that miscible CO2 affected the oil recovery more than immiscible CO2 injection. In addition, based on their experiment, the injection of CO2 at MMP did not have a strong effect on the final oil recovery. Meng et al.26 proposed a huff-n-puff gas injection for improving recovery from shale gas-condensate reservoirs. Based on their experiments, they introduced huff-n-puff gas injection as a suitable technique for enhancing gas condensate recovery in shale gas reservoirs. An experimental study to investigate the potential of the huff-n-puff gas injection method for recovery in shale gas-condensate reservoirs was conducted by Meng et al.27. Then to verify their experimental results, the numerical model was developed. Based on their results, the huff-n-puff technique is a suitable method for recovery in shale gas-condensate reservoirs. In order to study the mechanism of CO2 EOR in the unconventional reservoirs, a numerical study was conducted by Zhang et al.28. Their study indicated that higher oil production is achieved as a result of CO2 injection in these types of reservoirs via hydraulic fractures. Based on their results, among different gas mechanisms, diffusion played a minimal role, while multi-contact miscibility was a dominant mechanism.

As shown in the literature review, the process of gas injection is one of the interesting methods. Therefore, in the present study the effect and performance of these gases was investigated. New developed code can investigate the effect of each rich gases on IFT of system, the fractional flow, gas saturation profile and relative permeability of gas and oil and based on these output can be achieved comprehensive information about the performance of these gases. In addition, based on considered crude oil and developed code in the present study, sensitivity analysis can be conducted on GOR, and injection pressure, and suitable injection rich gas, GOR, and injection pressure for introduced crude oil can be suggested. It is worth noting to mention that developed code considered the effect of porous media. In order to develop aforementioned code, first methane has been riched in Naphtha, LPG, and NGL and the composition of rich gases was determined, then developed codes was validated with available experimental and numerical data. Our developed code includes the estimation of compressibility factor, gas-oil ratio, and formation volume factor. Then based on empirical correlation, the IFT of the system was predicted. After modification of the relative permeability and viscosity of each fluid, the modified Buckley-Leverett equation was used to determine the saturation profile and fractional flow of gas. After that, the results of the simulation are presented and discussed. In the end, the conclusions of this work are presented.

Method of work

Mathematical model

This study contains four steps: (1) mixing of methane with LPG, NGL, and Naphtha and generation of rich gas, (2) calculation of interfacial tension (IFT) of rich gas-oil system, (3) modification of relative permeability and viscosity of rich gas and oil, (4) determination of the model output, i.e., relative permeability, rich gas saturation and fractional flow of rich gas (Fig. 1).

Figure 1
figure 1

The Flow chart of the present simulation.

Full size image

At the first step, NGL, LPG, and Naphtha were mixed with methane at three different GORs of 1.25, 2.5, and 5 MSCF/STB. Tables 1, 2 and 3 presented the final composition of rich gases.

Table 1 The composition of rich gas with LPG.
Full size table
Table 2 The composition of rich gas with NGL.
Full size table
Table 3 The composition of rich gas with Naphtha.
Full size table

In the second step, the IFT of rich gas-oil must be determined. There are several methods for calculation of the IFT of the system. Ramey's correlation35 was used for the IFT of the system:

$${\sigma }_{go}^{1/4}={P}_{o}\left({x}_{o}\frac{{\rho }_{o}}{{M}_{og}}-{y}_{o}\frac{{\rho }_{g}}{{M}_{go}}\right)-{P}_{g}\left({x}_{g}\frac{{\rho }_{o}}{{M}_{og}}-{y}_{g}\frac{{\rho }_{g}}{{M}_{go}}\right).$$
(1)

In above equation, \({\sigma }_{go}\) is the IFT of gas-oil system. \({x}_{g}\), \({x}_{o}\), \({y}_{g}\), and \({y}_{o}\) present mole fraction of components in the oil and gas phase, respectively. The density of gas and oil is shown by \({\rho }_{g}\) and \({\rho }_{o}\), respectively. \({M}_{go}\) and \({M}_{og}\) show the average molecular weight of the gas and oil phase, respectively. In addition, Parachor equation for gas and oil phase is presented by \({P}_{g}\) and \({P}_{o}\), respectively. Equations (2)–(13) was used to calculated considered parameters for Ramey's correlation:

$${M}_{g}=28.97\times {\gamma }_{g},$$
(2)
$${M}_{o}=6084/({\gamma }_{API}-5.9),$$
(3)
$${P}_{g}=25.2+2.86{M}_{g},$$
(4)
$${P}_{o}=\left(2.376+0.0102{\gamma }_{API}\right){M}_{o},$$
(5)
$${x}_{o}={[1+\frac{7.521\times {10}^{-6}{R}_{s}{M}_{o}}{{\gamma }_{o}}]}^{-1},$$
(6)
$${x}_{g}=1-{x}_{o},$$
(7)
$${y}_{o}={[1+\frac{7.521\times {10}^{-6}{M}_{o}}{{\gamma }_{o}{r}_{v}}]}^{-1},$$
(8)
$${y}_{g}=1-{y}_{o},$$
(9)
$${\rho }_{g}=9.3184\times {10}^{-2}\frac{P{M}_{go}}{62.4*ZT},$$
(10)
$${\rho }_{o}=\frac{{\gamma }_{o}+2.179\times {10}^{-4}{\gamma }_{g}{R}_{s}}{{B}_{o}},$$
(11)
$${M}_{go}={y}_{o}{M}_{o}+{y}_{g}{M}_{g},$$
(12)
$${M}_{og}={x}_{o}{M}_{o}+{x}_{g}{M}_{g},$$
(13)

where \({M}_{o}\) and \({M}_{g}\) show molecular weight of oil and gas phase. Compressibility factor and solution gas-oil ratio are denoted by \(Z\), and \({R}_{s}\). Vaporized oil in the gas phase which considered 0 in the present study is shown by \({r}_{v}\).

In order to determine the IFT of the system, critical pressure and temperature, solution gas-oil ratio, formation volume factor, and compressibility factor must be determined. To this end, Sutton's correlation36 for critical temperature and pressure, Brill and Beggs' correlation37 for compressibility factor, and Standing's correlation38 for solution gas-oil ratio and oil formation volume factor were used.

$${T}_{pc}=169.2+349.5\times {\gamma }_{g}-74\times {\gamma }_{g}^{2},$$
(14)
$${T}_{pr}=\frac{T}{{T}_{pc}},$$
(15)
$$tpr=\frac{1}{{T}_{pr}},$$
(16)
$${P}_{pc}=756.8-131.07\times {\gamma }_{g}-3.6\times {\gamma }_{g}^{2},$$
(17)
$${P}_{pr}=\frac{P}{{P}_{pc}},$$
(18)
$$A=1.39{({T}_{pr}-0.92)}^{0.5}-0.36{T}_{pr}-0.10,$$
(19)
$$B=\left(0.62-0.23{T}_{pr}\right){P}_{pr}+\left(\frac{0.066}{{T}_{pr}-0.86}-0.037\right){P}_{pr}^{2}+\frac{0.32{P}_{pr}^{2}}{{10}^{E}},$$
(20)
$$C=0.132-0.32\mathrm{log}\left({T}_{pr}\right),$$
(21)
$$D={10}^{F},$$
(22)
$$E=9\left({T}_{pr}-1\right),$$
(23)
$$F=0.3106-0.49{T}_{pr}+0.1824{T}_{pr}^{2},$$
(24)
$$Z=A+\frac{1-A}{{e}^{B}}+C{p}_{pr}^{D},$$
(25)
$$a=0.00091\left(T-460\right)-0.0125{\gamma }_{API},$$
(26)
$${R}_{s}={\gamma }_{g}{[(\frac{p}{18.2}+1.4){10}^{a}]}^{1.2048},$$
(27)
$${B}_{o}=0.9759+0.000120{[{R}_{s}{\left(\frac{{\gamma }_{g}}{{\gamma }_{o}}\right)}^{0.5}+1.25(T-460)]}^{1.2}.$$
(28)

Pseudocritical temperature and pressure are shown by \({T}_{pc}\) and \({P}_{pc}\). In addition, pseudoreduced pressure and temperature are illustrated by \({P}_{pr}\) and \({T}_{pr}\). \({\gamma }_{g}\) and \({\gamma }_{o}\) show the specific gravity of gas and oil, respectively. \({\gamma }_{o}\) and \({\gamma }_{API}\) can be related to each other through \({\gamma }_{API}=\frac{141.5}{{\gamma }_{o}}-131.5\). Oil formation volume factor is denoted by \({B}_{o}\), respectively. In the above equation, temperature and pressure are shown by \(T\) and \(P\), respectively. In addition, A-F are the constants for Brill and Beggs' correlation.

One of the main parts of this numerical study is the modification of relative permeability. There are several methods for modification of relative permeability. However, the method introduced by Coats39 is known as a suitable method and used in the present study. In this method, the effect of IFT was involved in the modification of relative permeability. The effect of IFT was considered through the relative permeability interpolation parameter, \({F}_{k}\):

$${F}_{K}=min\left[1,{\left(\frac{\sigma }{{\sigma }_{0}}\right)}^{N}\right],$$
(29)
$$N=\frac{1}{{n}_{l}}.$$
(30)

Now by using the Corey–Brook correlation40, the relative permeability of each phase was determined as follows:

$${S}_{gi}={F}_{K}\times {S}_{gi}^{imm},$$
(31)
$${S}_{or}={F}_{K}\times {S}_{or}^{imm},$$
(32)
$${S}_{gn}=\frac{{S}_{g}-{S}_{gi}}{1-{S}_{gi}-{S}_{or}},$$
(33)
$${K}_{rg}^{imm}={K}_{rg}\times {S}_{gn}^{ng},$$
(34)
$${K}_{ro}^{imm}={K}_{ro}\times {\left(1-{S}_{gn}\right)}^{{n}_{o}},$$
(35)
$${K}_{rg}^{mis}={S}_{gn}^{{n}_{m}},$$
(36)
$${K}_{ro}^{mis}={(1-{S}_{gn})}^{{n}_{m}}.$$
(37)

Then by using the \({F}_{k}\), the miscible and immiscible relative permeability of each phase was measured.

$${K}_{RG}={\left(1-{F}_{K}\right)\times {K}_{rg}^{mis}+F}_{K}\times {K}_{rg}^{imm},$$
(38)
$${K}_{RO}={\left(1-{F}_{K}\right)\times {K}_{ro}^{mis}+ F}_{K}\times {K}_{ro}^{imm},$$
(39)

where \({K}_{RO}\), and \({K}_{RG}\) show modified oil and gas relative permeability, respectively. In above equations, the immiscible and miscible oil relative permeability is presented by \({K}_{ro}^{imm}\) and \({K}_{ro}^{mis}\), respectively. In addition, \({K}_{rg}^{imm}\), and \({K}_{rg}^{mis}\) are immiscible and miscible gas relative permeability, respectively. \({\sigma }_{0}\), \(\sigma\), and \({n}_{l}\) illustrate the IFT at MMP, IFT at intended pressure, and read in exponent, respectively. \({S}_{or}\), \({S}_{or}^{imm}\), \({S}_{g}\), \({S}_{gi}\), and \({S}_{gi}^{imm}\) show modified residual oil saturation, residual oil saturation at immiscible conditions, gas saturation, modified irreducible gas saturation, and irreducible gas saturation at immiscible conditions. \({K}_{ro}\) and \({K}_{rg}\) illustrated the relative permeability of oil and gas at irreducible gas and residual oil saturation, respectively. In addition, gas and oil exponent for Brooks–Corey functions is shown by \({n}_{g}\) and \({n}_{o}\), respectively. \({n}_{m}\) is relative permeability index and in the present study is considered 1.1.

Modification of viscosity is another step of this study. For this purpose, Todd–Longstaff41 model was used:

$${\mu }_{geff}={\mu }_{g}^{1-\omega }\times {\mu }_{m}^{\omega },$$
(40)
$${\mu }_{oeff}={\mu }_{o}^{1-\omega }\times {\mu }_{m}^{\omega },$$
(41)
$${(\frac{1}{{\mu }_{m}})}^\frac{1}{4}=\frac{{S}_{g}^{^{\prime}}}{{S}_{n}^{^{\prime}}}{(\frac{1}{{\mu }_{g}})}^\frac{1}{4}+\frac{{S}_{o}^{^{\prime}}}{{S}_{n}^{^{\prime}}}{(\frac{1}{{\mu }_{o}})}^\frac{1}{4},$$
(42)
$${S}_{g}^{^{\prime}}={S}_{g}-{S}_{gi},$$
(43)
$${S}_{o}^{^{\prime}}={S}_{o}-{S}_{or},$$
(44)
$${S}_{n}^{^{\prime}}={S}_{o}^{^{\prime}}-{S}_{g}^{^{\prime}}.$$
(45)

In this study, the mixing factor of viscosity (\(\omega\)) is 1/3. \({\mu }_{geff}\), \({\mu }_{oeff}\), and \({\mu }_{m}\) show gas and oil effective viscosity, and mixing viscosity, respectively.

In order to study the process of gas injection and determine the output of the model, the Buckley–Leverett model was used 42:

$${f}_{g}=\frac{{S}_{g}^{2}}{{S}_{g}^{2}+{(1-{S}_{g})}^{2}VR}.$$
(46)

In Eq. (46), \(V\) shows the viscosity ratio and fractional flow for the gas phase are presented by \({f}_{g}\). Derivative of the fractional flow of gas phase to gas saturation is determined through the following equation:

$$\frac{{df}_{g}}{{dS}_{g}}=\frac{2V({S}_{g}-1){S}_{g}}{{(V{\left({S}_{g}-1\right)}^{2}+{S}_{g}^{2})}^{2}}.$$
(47)

Dimensionless pore volume and distance transferred by a specific \({S}_{g}\) contour are measured through the following equations:

$$PVI=\frac{{q}_{t}t}{L\phi Area},$$
(48)
$${x}_{{S}_{g}}=PVI\times L{\left(\frac{{df}_{g}}{{dS}_{g}}\right)}_{{S}_{g}}.$$
(49)

In the above equation, dimensionless pore volume, porosity, length of the domain, cross-section area, total injection rate, injection time, and moving distance by a specific \({S}_{g}\) contour are shown by \(PVI\), \(\phi\), \(L\), \(Area\), \({q}_{t}\), \(t\), and \({x}_{{S}_{g}}\), respectively.

Results and discussion

Numerical simulation

Simulation parameter that used in the present study is shown in Table 4:

Table 4 Parameters for simulation of IFT and gas injection.
Full size table

Some numerical and experimental study was used to investigate the performance of correlations used in the present study. As shown in Figs. 2 and 3, the correlations had acceptable performance.

Figure 2
figure 2

Comparison of the simulated value solution gas-oil ratio, oil formation volume factor, oil density, and relative gas and oil permeability.

Full size image
Figure 3
figure 3

Comparison of simulated value of fractional flow at gas viscosity of 0.035 mPa s three injection pressures of 30, 22, and 14 MPa with the results of Mu et al.43.

Full size image

Effect of injected rich gas on the output of the model

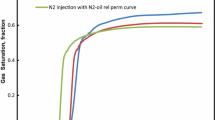
Three rich gas was used as an injection fluid in the present study. The effect on the relative permeability, saturation profile, and fractional flow was investigated in this section. Figure 4 shows the IFT of the rich gas-oil system at different GOR.

Figure 4
figure 4

IFT of rich gas-oil system for three GORs of 1.25, 2.5, and 5 Mscf/STB.

Full size image

As shown in Fig. 4, when injected gas was rich gas with NGL and LPG, the IFT of the system was more than the condition that injected gas was a rich gas with Naphtha. The main reason for this phenomenon was that Naphtha is a heavy gas; therefore, lower IFT for the oil-rich gas systems was achieved. The percentage of methane in the composition of LPG and NGL was higher than other components; hence, as shown in Fig. 5, the IFT of rich gas-oil system for rich gas with NGL and LPG was closed to the IFT of methane-oil system.

Figure 5
figure 5

Comparison of IFT of methane-oil system and each rich gas-oil system at different GOR.

Full size image

Effect of gas-oil ratio

As previously mentioned, rich gas were made with different GORs. The effect of GOR on the relative permeability, saturation profile, and fractional flow for each rich gas was investigated in this section. Figures 6 and 7 show the effect of GOR at two injection pressures of 500 and 3115 psi on the output of the model once gas-rich with LPG was used as an injection gas. When LPG was used for rich gas, the final composition of gas was not severely changed. Therefore, the GOR cannot affect the output of the model, as shown in Figs. 6 and 7.

Figure 6
figure 6

Effect of GOR of LPG on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 500 psi.

Full size image
Figure 7
figure 7

Effect of GOR of LPG on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 3115 psi.

Full size image

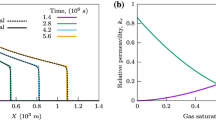
In the second scenario, a gas was riched in Naphtha was injected. In this scenario, three-injection pressure of 500, 1500, and 2000 psi was used. As shown in Fig. 8, at low injection pressure, GOR cannot affect the relative permeability curve, saturation profile curve, and fractional flow curve. However, by increasing the injection pressure, the effect of GOR appeared. At injection pressure of 1500 psi, higher GOR, 5 MSCF/STB, resulted in shifting the relative permeability of oil to the left side, increase, and relative permeability of gas to the right side, decrease (Fig. 9). In addition, lower GOR, 1.25 MSCF/STB, caused gas to move faster in the domain (Fig. 9), and the effect of GOR on the fractional flow curve was evident in Fig. 9. Higher GOR resulted in higher fractional flow of gas and consequently lower oil production will be expected. The main reason for this phenomenon was that at lower GOR, the amount of methane in the gas composition was higher than in other GORs. Therefore, the gas moved faster in the domain, shifting the relative permeability of oil to the right side and the relative permeability of gas to the left side. In other words, at high GOR the gas became heavy and its relative permeability will be decrease, therefore it moved with lower velocity in the domain and breakthrough will not be occurred and more oil will be produced. The same results were observed at higher injection pressure, 2000 psi (Fig. 10).

Figure 8
figure 8

Effect of GOR of Naphtha on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 500 psi.

Full size image
Figure 9
figure 9

Effect of GOR of Naphtha on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 1500 psi.

Full size image
Figure 10
figure 10

Effect of GOR of Naphtha on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 2000 psi.

Full size image

The third injection gas was rich with NGL. The effect of GOR at two injection pressure of 500 and 3000 psi was investigated. The same as LPG, the effect of GOR on the output of the model at two injection pressures were not observed (Figs. 11, 12).

Figure 11
figure 11

Effect of GOR of NGL on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 500 psi.

Full size image
Figure 12
figure 12

Effect of GOR of NGL on relative permeability, saturation profile, and fractional flow curve at an injection pressure of 3000 psi.

Full size image

Effect of injection pressure

In this section, the effect of injection pressure on the performance of each rich gas was investigated. The effect of injection pressure on the performance of rich gas with LPG and NGL was the same as the effect of GOR. Both injection pressures did not have any influence on the output of the model (Figs. 13, 14). However, when gas was rich in Naphtha, the effect of injection pressure was clear. Higher injection pressure shifted the relative permeability of oil and gas to the right and left sides, respectively (Fig. 15). In addition, when the injection pressure was high, 2000 psi, gas moved faster in the medium, and the breakthrough occurred, while at two other injection pressures, 500 and 1500 psi, the breakthrough was not observed (Fig. 15). As shown in Fig. 15, the effect of injection pressure on the fractional flow curve was obvious. Higher injection pressure resulted in lower fractional flow of gas and consequently more oil will be produced.

Figure 13
figure 13

Effect of injection pressure of LPG on relative permeability, saturation profile, and fractional flow curve at GOR 2.5 MSCF/STB.

Full size image
Figure 14
figure 14

Effect of injection pressure of NGL on the (a) relative permeability, (b) saturation profile, and (c) fractional flow curve at GOR 2.5 MSCF/STB.

Full size image
Figure 15
figure 15

Effect of injection pressure of Naphtha on the (a) relative permeability, (b) saturation profile, and (c) fractional flow curve at GOR 2.5 MSCF/STB.

Full size image

Conclusions

In this work, a new numerical simulation was developed to simulate the process of gas injection with rich gases, which can simulate the process in the three conditions: miscible, near miscible and immiscible. Effect of injection of rich gases, GOR of mixing process, and injection pressure on the output of the model were investigated. The main conclusions are summarized as follows:

  1. 1.

    Gas that is rich in Naphtha has lower IFT than two other rich gases because Naphtha is heavier than the two other ones.

  2. 2.

    As the main component of LPG and NGL is methane, the percentage of methane in these two rich gas was high; the IFT of LPG-oil and NGL-oil systems was close to IFT of methane-oil.

  3. 3.

    The GOR did not affect the performance of rich gas with LPG and NGL. Therefore, if LPG or NGL want to be used as an injection fluid for the reservoir that contains introduced crude oil, as GOR did not affected relative permeability of fluids, fractional flow, and saturation profile of gas, lower GOR was suggested.

  4. 4.

    In contrast to LPG and NGL, GOR affected the performance of naphtha. Decreasing the GOR shifted the relative permeability of oil to the right side and the relative permeability of gas to the left side. In addition, by decreasing GOR, gas moved fast in the domain. Therefore, for introduced oil, when naphtha was used as an injection fluid, in term of EOR, higher GOR of naphtha was resulted in better performance.

  5. 5.

    The same as GOR, injection pressure did not affect the performance of rich gas with NGL and LPG. While higher injection pressure resulted in faster movement of riched gas with Naphtha. Hence, lower injection pressure was suggested for injection fluid when naphtha was used as an injection fluid.