Integration of static and dynamic reservoir data to optimize the generation of subsurface fracture map

Abstract

This paper presents a new three-dimensional fully coupled poroelastic numerical model to simulate pressure transient response of naturally fractured reservoirs. One of the main applications of the new approach is to improve the reservoir characterization by decreasing the uncertainties associated with subsurface fracture map and to understand the interaction between fracture and matrix. The model is based on a hybrid methodology to simulate fluid flow by combining a single continuum and discrete fracture network approaches. To decrease the uncertainty associated with subsurface fracture map, a different realizations of the discrete fracture systems are generated based on image logs, seismic, geological features and the tectonic history of the studied reservoir. An iterative loops have been used between the reservoir static model and dynamic well-test data to optimize the generation of subsurface fracture maps. At each loop, a new discrete fracture system is used and the simulated pressure transient data are compared with the available field data. The process is repeated till the matching between the simulated and the measured pressure transient data is achieved using the most appropriate fracture realization. The numerical model is validated against an analytical pressure transient solution for dual-porosity system, and then applied to a real case taken from fractured basement reservoir in offshore Southern Vietnam. The developed hybrid methodology used to simulate fluid flow and rock deformation to improve the characterization of the fractured basement by simulating the pressure transient testing. The results predicted by the presented model are in a good agreement with field data; also the model was able to predict the fractures network distribution and fractures inherent properties around the tested well.

Introduction

Flow transport in fractured medium differs from that in porous medium, an intergranular porous medium. In naturally fractured reservoirs, the matrix provides the main storage for fluids, while flow transport takes place through fracture network system. The first step in fluid flow simulation is to characterize the fracture network, therefore the length, geometry and orientation of fractures. Characterization of fracture system has been carried out by integrating information from two different sources; static data (seismic, well logs, core description, borehole images, tectonic history, geological structures, etc.) and dynamic data (well-test data and well production history). Readers can be referred to the publication by “Gholizadeh Doonechaly and Rahman (2012)” for interpretation of static data and generation of subsurface fracture map using various techniques. The dynamic data, on the other hand, have been used to further improve subsurface fracture properties. To date the fractured medium, however, is represented by bulk macroscopic values of averaged point-to-point variations of relevant properties over a representative elementary volume (REV) instead of discrete fractures.

Currently three major approaches have been used to simulate fluid flow in a fractured reservoir which includes single continuum, dual-porosity and discrete fracture network.

In the single continuum approach, the reservoir is divided into a number of blocks and the fracture properties in each block are averaged by using a representative effective permeability tensor. Estimation of the effective permeability tensor for regular fracture pattern of simple geometries was first proposed by Lough (Lough et al. 1997). The approach was further improved by Teimoori et al. (2005) to simulate fluid flow in arbitrary oriented and intersected fracture system (Teimoori et al. 2005). Despite the improved computational efficiency of the single continuum approach, it does not adequately address the flow behaviour of fractures (Tarahhom et al. 2009).

In the dual continuum approach, the reservoir is divided into two major parts: fractures and matrix. According to Warren and Root (1963), a fractured reservoir comprises a series of sugar cubes with evenly spaced fractures, as shown in Fig. 1. In this approach, fractures provide the main flow paths, while the matrix acts as a source of fluid. The fluid transfer between the fractures and the matrix is defined based on the specific transfer functions. Lee (1977), Pruess (1985) and Kazemi (1969) introduced a range of different matrix/fracture transfer functions to simulate the fluid flow in large scales. Following these works, a significant number of studies have been carried out in both analytical and numerical frameworks (Pride and Berryman 2003, Gong et al. 2008).

Fig. 1

Dual-porosity model description of a naturally fractured reservoir: a actual reservoir and b sugar cube reservoir model

The limitations of dual-porosity/permeability approach are as follow: (1) the fluid distribution within the matrix blocks remains constant during the simulation period, (2) the model cannot be applied to disconnected and discrete fratured (oriented fractures) media and (3) a small number of large-scale fractures can be considered for flow simulation. Therefore, the developed numerical model presented in this paper overcomes all above mentiond limitations by considering fluid flows through matrix porous media and discrete fractures.

The discrete fracture approach, on the other hand, has been proposed as an explicit means of considering the fluid flow and transport inside individual fractures (Karimi-Fard et al. 2004).

The transmissivity of individual fractures and their effect on fluid flow have been studied by considering fracture properties, namely orientation, size and location into the flow calculation. This approach was first introduced for single phase flow. Among of the earliest authors that represent the fracture as 1D entity in 2D fractured porous system were Noorishad et al. (1984) and Baca et al. (1984). Further studies were done by Wei et al. (1998), Karimi-Fard et al. (2004), Rogers et al. (2007) and Watanabe et al. (2010). The main difficulty of discrete fracture approach is the need for extensive computation involved in reservoir scale flow simulation.

Wei et al. (1998) developed a 3D numerical model in order to simulate pressure transient through fracture/matrix system. The results indicated that the simulated pressure derivative showed a different behaviour for each fracture pattern configuration. Also authors showed that dual-porosity model failed to describe the behaviour of fluid flow through fractured system in many cases. Carlson (2003) was using specific transfer functions to simulate the flow transfer from fractures to matrix. It was assumed that the fractures provide the main flow conduit and matrix acts as a source/sink to the fractures.

Basquet et al. (2005) used a homogenization method to simulate pressure transient through fractured system. The idea is to simplify discrete fracture network approach by reducing number of generated fracture nodes. This approach keeps the actual fracture network geometry and also the hydraulic properties of the whole system. Casabianca et al. (2007) presented a discrete fracture network model by using an integrated interpretation methodology to improve the characterization of a fractured chalk reservoir.

Recently, there are many studies on using pressure transient data for naturally fractured reservoir modelling. Morton (2012) presented two new techniques used to calibrate numerical-based fracture model with well-test data by integrating a reservoir model inversion technique and boundary element method for determining the pressure transient behaviour of the reservoir with arbitrary distributed vertical fractures. Kuchuk and Biryukov (2012) presented semi-analytical solution in order to understand pressure behaviour of continuously and discretely fractured reservoirs. This solution used to interpret well-test data of formation containing network of discrete conductive fractures. The author showed that Warren and Root's (1963) dual-porosity model is not adequate for pressure transient well-test interpretation as it does not capture the behaviour of these reservoirs.

In this study, a hybrid methodology—combining the single continuum and the discrete fracture approaches—is utilized to increase the efficiency of the fluid flow simulation. The reservoir domain is discretized using tetrahedral elements, and fluid flow is then simulated in these elements by using the single continuum approach. In the proposed methodology, a threshold value for fracture radius is defined. Fractures, with the radius smaller than the threshold value, are used to generate the grid-based permeability tensor. Fractures, with radius longer than the threshold value, are explicitly discretized in the domain by using the triangular elements, and the fluid flow is modelled using the discrete fracture approach.

Model validation

To validate the presented numerical model, a sugar cube reservoir is created using in house 3D mesh generator code with two sets of orthogonal vertical fractures having the same dip angle (90°) and different azimuth angles (0°, 90°). An equal fracture spacing of 250 m is assumed with a vertical well at the centre of the model penetrating the whole reservoir thickness (see Fig. 2). Horizontal fractures are ignored as usually not observed below moderate depth, and only vertical fractures are considered (Tankersley et al. 2013). Properties of the fractures, matrix and stresses values are presented in Table 1. A single phase draw down test is performed for 3500 days at constant production rate of 4500 STB/day simulated numerically using a discrete fracture network approach. The pressure response at the wellbore was compared against analytical pressure transient solution introduced by Warren and Root (1963) for dual-porosity model.

Fig. 2

Stressed sugar cube model with two sets of orthogonal vertical fractures, a vertical well penetrating the model from top to the bottom

Table 1 Input data for a sugar cube model used in a numerical simulation validation process

Figure 3 shows that the simulated response of discrete fracture model matched well with the analytical solution. The derivative behaviour looks like a bell between 20 and 1000 h. This behaviour indicates that within the transition flow period the matrix starts to feed the fractures network. During this flow period, the oil production at the wellbore is very low and pressure starts to drop slowly. The dip of this bell-shaped behaviour is controlled by the value of matrix storativity ratio (ω). As the (ω) gets smaller, the dip gets deeper and starts earlier.

Fig. 3

log–log plot of pressure drop and pressure derivative of a drawdown test for a dual-porosity model with a vertical well using Discrete Fracture Model

The horizontal portion of the pressure derivative curve from 1000 to 40,000 h indicates the ending of transition period and starting of the composite system flow. This flow period is controlled by the value of interporosity flow coefficient (λ).

The unit slope of pressure derivative curve between 10,000 and 100,000 h indicates pseudo-steady-state condition for the entire reservoir volume. By using this flow period, a reservoir volume and shape can be calculated.

At early-time response for idealized dual-porosity transient behaviour with a very low wellbore storage effects, a first radial flow regime is expected to appear before starting of transition flow period. This radial flow regime is governed by the flow only inside the fractures network. The simulation result does not show that, as the response of discrete fracture network model before 10 h is not clear and the presented simulation model ignored the wellbore storage effect.

Case study

The test case is taken from granitic oil-bearing formation in southern offshore Vietnam (Farag et al. 2010). The formation is highly fractured with fractures having short lengths identified from image logs and forming the storage capacity of the reservoir. Geological interpretation showed that the reservoir has very low matrix porosity and permeability. Pore space in the rock is formed through the fractures network and digenetic processes. A Drill Stem Test (DST) was conducted in this formation with controlled flow periods before shutting to understand the extent of the reservoir from the wellbore, prove the possibility of the hydrocarbon existence, and evaluate well deliverability and reservoir performance.

Farag et al. (2010) used a simple model of parallel vertical fractures with a vertical well to simulate main build-up period of DST test by ignoring the actual distribution of fracture network around the tested well.

The aim of this study is to generate a subsurface fracture map using available field data, and to use the presented model to simulate the main build-up period of the DST test to calibrate logs permeability values in the area under study.

Generation of discrete fracture map of a typical basement reservoir

The author used an innovative methodology to generate the 3D subsurface fracture map of the studied reservoir by integrating field data, such as wellbore images and conventional well logs. In this approach, an object-based conditional global optimization technique is used to generate the subsurface fracture map of the reservoir which combines the following: (1) statistical analysis of different sources of data (as mentioned above); (2) finite element-based modelling of tectonic history of the reservoir structure to generate probabilistic fracture attributes; (3) development of complex relationship between different sources of data (data sources mentioned in (1) and the data generated in (2)) using back propagation neural network; (4) sequential Gaussian stochastic simulation to generate object-based 3D subsurface fracture map and (5) simulated annealing optimization technique to generate an optimum subsurface fracture map. In object-based model, each single fracture is treated as a single object with its specific properties such as location (centre point), dip, azimuth and size (radius). Each object possesses a variety of rules for behaviour in space such as shift, rotate, grow, shrink, multiply or disappear. The optimization process involves a series of trial and errors utilizing the nominated rules to minimize the objective function which is the difference between each fracture system realization and the target. The procedure is detailed in Gholizadeh Doonechaly and Rahman (2012).

Figure 4 shows the generated subsurface fracture map around the tested well. Figure 5 shows the DST history data. Reservoir input data used for numerical simulation model are presented in Table 2.

Fig. 4

Three-dimensional generated fracture map (a), three-dimensional mesh (tetrahedral elements for matrix and triangle elements for fractures) used in the simulation process (b) distribution of applied stresses in the generated mesh

Fig. 5

DST history used to test the applicability of the current numerical simulation model in improving reservoir characterization process (Farag et al. 2010)

Table 2 Reservoir inputs parameters for numerical simulation model

The hybrid approach

Single phase fluid flow in a typical fractured basement reservoir is simulated by coupling 3D permeability tensors (heterogamous permeability, see Fig. 6) with flow through discrete fractures. Long fractures (l ≥ 40 m) along with their original properties (orientations and locations) are discretized explicitly within the reservoir domain.

Fig. 6

Description of how the reservoir domain is discretized for hybrid methodology: a the reservoir domain is divided into a number of grid blocks without considering of long fractures; b 3D block-based permeability tensor for short to medium fractures; c the block-based permeability tensors are distributed to the corresponding tetrahedral elements (matrix porous media) and long fractures are discretized explicitly

The well path has been divided into number of segments and each segment has a different flux which depends on the element size intersected by each one. Figure 7 shows how the wellbore intersected with blocks of lower fracture density.

Fig. 7

Close view of fracture intensity map around the wellbore. The producing well partially penetrates the formation thickness and intersects with blocks that have a low fracture intensity value. Fracture block intensities less than 0.165 m⁻¹ are removed from the fracture intensity map

Firstly, different subsurface fracture maps have been generated using the available field data. The number of fractures that have been created is 4000 fractures. The fractures with length <40 m were used to estimate the block-based permeability tensor, and long fracture with length >40 m were discretized explicitly in the reservoir domain. The fracture aperture has been assumed of 0.04 mm which is equal to the maximum value shown in the image logs. Due to the lack of information about far field stresses, the horizontal stresses are estimated based on overburden stress (Zoback 2007). Results of simulated as well as measured data from field test are presented in Fig. 8.

Fig. 8

Shut in pressure plot of build-up test for measured and simulated data using two different values of fracture aperture 0.04 mm and 0.004 mm

As shown in Fig. 8, a poor matching occurred between build-up history and simulated data at first trial using fracture aperture = 0.04 mm using the best generated fracture realization. In addition, the figure (see Fig. 8) shows the simulated pressure curve is higher than measured one. This behaviour is obtained due to the use of a large fracture aperture that enables pressure to build up quickly around the wellbore.

Since the simulated results were moving in the direction as expected as it has almost the same trend of the history data, the decision is taken by keeping the fracture realization that has been predicted using the iteration process as described before, and further trials were continued by changing fracture aperture.

After several trials, the simulated data are matched with the history data by using fracture aperture of 0.004 mm. The early-time response is truncated from gauge data after 20 min from the beginning of the test by using Horner plot (Aguilera 1980); wellbore storage effect has been neglected. The numerical model was able to match the build-up test reasonably well for about 52 h.

Figure 9 presents a log–log plot between (P _ws − P _wf) versus ∆t _e (equivalent time), where

$$\Delta t_{e} = \frac{\Delta t}{{\frac{{t_{p} + \Delta t}}{\Delta t}}}.$$

(1)

Fig. 9

Log–Log plot of build-up test for a vertical partially penetrated well in a highly fractured system

Figure 9 shows a good match between measured and simulated pressure change using fracture aperture = 0.004 mm. The simulated and measured data before 0.1 h does not show the effect of wellbore storage (slope of plotted data before 0.1 h is not a unit slope).

Figure 10 shows a log–log plot of pressure derivatives of measured and simulated data vs time (∆t)._. By using this plot most of flow regimes can be defined. The first flow regime as expected is a spherical flow which occurs due to partially penetrated well used in the numerical model and is seen in the derivative plot as a negative slope trend. The second flow regime is a radial flow which appears in the derivative curve as a flat line with zero slope (m = 0). The third flow regime is a linear flow recognized as a positive half-slope trend caused by the fractures network.

Fig. 10

Log–Log plot for measured and simulated pressure derivative data

The build-up period was simulated successfully using the generated subsurface fracture map around the area under study. The new model was able to characterize the area around the tested well and also the fracture aperture value has been predicted.

Conclusion

A new numerical simulation model is developed using a hybrid technique of single continuum and Discrete Fracture Network approaches to simulate well pressure transient response for improving reservoir static model by decreasing uncertainties in reservoir characterization process. The new model used a permeability tensor concept to replace fractures with a short length by an equivalent tensor in a three-dimensional space using a finite element technique. A discrete fracture network approach used to simulate fluid flow inside long fractures to observe the effect of these fractures on the pressure response at the tested well.

A model was validated against analytical solution of Warren and Root using dual-porosity reservoir to test its robustness and accuracy, and then the applicability of the model on how to simulate actual build-up test is performed. The model is able to characterize the simulated area around the studied well by predicting the proper fractures network distribution and also the fractures network inherent parameters.

Appendices

Appendix 1: Calculations of 3D permeability tensors

Three-dimensional flow equations used for permeability tensor calculations are given by Darcy’s law and continuity equations as follow:

$$\left[ {\begin{array}{*{20}c} {v_{x} } \\ {v{}_{y}} \\ {v_{z} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {k_{xx} } & {k_{xy} } & {k_{xz} } \\ {k_{yx} } & {k_{yy} } & {k_{yz} } \\ {k_{zx} } & {k_{zy} } & {k_{zz} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial p}{\partial x}} \\ {\frac{\partial p}{\partial y}} \\ {\frac{\partial p}{\partial z}} \\ \end{array} } \right] = \vec{\vec{k}}.\nabla p$$

(2)

$$\nabla .v = 0,$$

(3)

where v is the fluid velocity vector, $\overrightarrow {{\vec{k}}}$ is the permeability tensor and $\nabla p$ is the local pressure gradient. The grid-based permeability tensors for short to medium fractures are calculated by using finite element technique. Each fracture is represented as a sandwiched element (triangular element) between three-dimensional tetrahedral elements representing the matrix porous media as shown in Fig. 11. Single phase fluid flow governing equation through matrix porous medium can be written as follows:

$$\nabla .\left( {\frac{{\overrightarrow {{\overrightarrow {k} }} }}{\mu }.\nabla p} \right) + Q_{\text{H}} = 0$$

(4)

$$v = - \left( {\frac{{\overrightarrow {{\overrightarrow {k} }} }}{\mu }.\nabla p} \right),$$

(5)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {k} }}$ is a full permeability tensor, μ is the fluid viscosity, $Q_{\text{H}}$ is fluid source/sink term which represents the fluid exchange betweenmatrix and fracture or fluid extraction (injection) from the wellbore.

Fig. 11

Formulation of a full matrix in 3D space. Fracture is represented as sandwich elements and matrix elements (Elements 1 & 2) assembled to be used during the simulation process

Single phase fluid flow governing equation through discrete fractures can be expresses as

$$\nabla \left( {\frac{{k_{\text{f}} }}{\mu }.\nabla p_{\text{f}} } \right) + q^{ + } + q^{ - } = 0.0,$$

(6)

where ${\text{q}}^{ + } {\text{and }}q^{ - }$ are the leakage fluxes across the boundary interfaces, $\bar{\nabla }$ is the divergence operator in local coordinates system (Watanabe et al. 2011), and P_f is the pressure inside the fracture. The permeability of the fracture can be expressed by a parallel plate concept (cubic law) as shown in Eq. (7). It has been assumed that the fracture surfaces are parallel and the fluid flow through a single discrete fracture is laminar (Snow 1969).

$$k_{\text{f}} = \frac{{b^{2} }}{12},$$

(7)

where b is the fracture aperture, and $k_{\text{f}}$ is the fracture permeability. As a result of superimposing fracture/matrix system, the fracture/matrix interface is directly treated by using the finite element technique (see Fig. 11). The fracture aperture is uniform at the beginning of simulation process and then it will be changed as a function of stresses changes.

Finite element method formulation

The weighted-residual method is used to derive the weak formulation of the governing equation of fluid flow through a fractured system. Standard Galerkin method is applied to discretize the weak forms with appropriate boundary conditions (Zimmerman and Bodvarsson 1996).

Equations (4) and (6) are written separately for matrix porous medium and discrete fractures in finite element formulation. The matrix is discretized using 3D tetrahedral elements and fractures are discretized by using 2D triangle elements. If ${\text{FEQ}}$ represents the flow equation, the integral form can be written as follow:

$$\int {\int_{\varOmega } {{\text{FEQ d}}\varOmega } } = \int {\int_{{\varOmega_{\text{m}} }} {{\text{FEQ d}}\varOmega_{\text{m}} } } + \int {\int_{{\varOmega_{f} }} {{\text{FEQ}} {\text{d}}\bar{\varOmega }_{f} } },$$

(8)

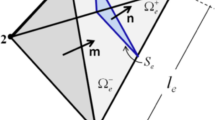
where $\bar{\varOmega }_{\text{f}}$ represents the fracture part of the domain as a 2D entity, $\varOmega_{\text{m}}$ represents matrix domain and $\varOmega$ is the entire domain. 2D integral fracture equation is multiplied by the fracture aperture b for consistency of the integral form.

The formulation of the governing equation for hydraulic process through matrix porous medium can be written as

$$\nabla \left( {\frac{{\vec{\vec{k}}}}{\mu }.\nabla p} \right) + Q_{\text{H}} = 0.0.$$

(9)

Introducing weak formulation, Eq. (9) is expanded as follow:

$$\int\limits_{\varOmega } {w \times } \left( {\begin{array}{*{20}l} {\frac{\partial }{\partial x}\left( {\frac{{k_{xx} }}{\mu }\frac{\partial p}{\partial x} + \frac{{k_{xy} }}{\mu }\frac{\partial p}{\partial y} + \frac{{k_{xz} }}{\mu }\frac{\partial p}{\partial z}} \right)} \hfill & +\,\,{\frac{\partial }{\partial y}\left( {\frac{{k_{yx} }}{\mu }\frac{\partial p}{\partial x} + \frac{{k_{yy} }}{\mu }\frac{\partial p}{\partial y} + \frac{{k_{yz} }}{\mu }\frac{\partial p}{\partial z}} \right)} \hfill \\ +\,\,{\frac{\partial }{\partial z}\left( {\frac{{k_{zx} }}{\mu }\frac{\partial p}{\partial x} + \frac{{k_{zy} }}{\mu }\frac{\partial p}{\partial y} + \frac{{k_{zz} }}{\mu }\frac{\partial p}{\partial z}} \right)} \hfill & {} \hfill \\ \end{array} } \right) + \int\limits_{\varGamma } {w^{T} q{\text{d}}\varGamma } = 0.0,$$

(10)

where (w = w(x, y, z)) is a trial function. The weak formulation for discrete fractures of Eq. (10) is expanded as follow:

$$\int\limits_{{\varOmega {}_{\text{f}}}} {\nabla w} \times \left( {\frac{{k_{\text{f}} }}{\mu }.\nabla p_{\text{f}} } \right) + \int\limits_{{\varGamma_{\text{f}} }} {w \times q^{ + } {\text{d}}\varGamma } + \int\limits_{{\varGamma_{\text{f}} }} {w \times q^{ - } } {\text{d}}\varGamma = 0.0.$$

(11)

Galerkin finite element method

Three basic steps in finite element approximation are (1) domain discretization by finite elements, (2) discretization of integral (weak) formulation and (3) shape functions generation of field variables unknowns. Galerkin finite element method is used to discretize the integral weak forms of Eqs. (10) and (11). Unknown variables are approximated by using appropriate shape functions.

$$p = N{}_{p} \times \overline{p},$$

(12)

where $N{}_{p}$ the pressure is shape function and $\overline{p}$ is the vector of nodal values of the unknown variable.

Finite element formulation of the governing equation for hydraulic process for matrix and fracture system can be written in a matrix form:

$$\overrightarrow {{\overrightarrow {M} }} \Delta \overrightarrow {p} = \overrightarrow {f}$$

(13)

$$\overrightarrow {{\overrightarrow {M} }} = \overrightarrow {{\overrightarrow {{M_{f} }} }} + \overrightarrow {{\overrightarrow {M} }}_{m}$$

(14)

$$\overrightarrow {{\overrightarrow {M} }} = \int\limits_{\varOmega } {\nabla N_{p}^{{m^{T} }} \frac{{\overrightarrow {{\overrightarrow {k} }} }}{\mu }\nabla N_{p}^{m} } {\text{d}}\varOmega + \int\limits_{\varGamma } {\nabla N_{p}^{{f^{T} }} \frac{{k_{\text{f}} \times b}}{\mu }\nabla N_{p}^{f} } {\text{d}}\varGamma$$

(15)

$$\overrightarrow {f} = - \int\limits_{\varGamma } {N_{p}^{{m^{T} }} Q_{\text{H}} } {\text{d}}\varGamma - \overrightarrow {{\overrightarrow {{M_{\text{f}} }} }} \times \overrightarrow {p}^{{i - 1^{\text{f}} }} - \overrightarrow {{\overrightarrow {{M_{\text{m}} }} }} \times \overrightarrow {p}^{{i - 1^{\text{m}} }},$$

(16)

where m is referring to matrix porous medium and f to fracture network.

Boundary conditions

Pressure and flux boundary conditions that have been presented by Durlofsky (1991) are used for calculations of permeability tensor in fractured porous medium. These conditions are listed in Eqs. (17) to (22) and Fig. 12.

$$p\left( {y,x = 0,z} \right) = p\left( {y,x = 1,z} \right) - G\quad {\text{on}}\quad \partial D_{3} \quad {\text{and}}\quad \partial D_{4}$$

(17)

$$u\left( {y,x = 0,z} \right).\overrightarrow {{n_{3} }} = - u\left( {y,x = 1,z} \right).\overrightarrow {n}_{4} \quad {\text{on}}\quad \partial D_{3} \quad {\text{and}}\quad \partial D_{4}$$

(18)

$$p\left( {y = 0,x,z} \right) = p\left( {y = 1,x,z} \right) - G\quad {\text{on}}\quad \partial D_{1} \quad {\text{and}}\quad \partial D_{2}$$

(19)

$$u\left( {y = 0,x,z} \right).\overrightarrow {{n_{1} }} = - u\left( {y = 1,x,z} \right).\overrightarrow {n}_{2} \quad {\text{on}}\quad \partial D_{1} \quad {\text{and}}\quad \partial D_{2}$$

(20)

$$p\left( {y,x,z = 0} \right) = p\left( {y,x,z = 1} \right) - G\quad {\text{on}}\quad \partial D_{5} \quad {\text{and}}\quad \partial D_{6}$$

(21)

$$u\left( {y,x,z = 0} \right).\overrightarrow {{n_{5} }} = - u\left( {y,x,z = 1} \right).\overrightarrow {n}_{6} \quad {\text{on}}\quad \partial D_{5} \quad {\text{and}}\quad \partial D_{6},$$

(22)

where n is the outward normal vector at the boundaries, ∂D is the grid block boundary and G is the pressure gradient. Specifying a zero pressure gradient along the y-, z-faces ($\frac{\partial p}{\partial y} = 0$, and $\frac{\partial p}{\partial z} = 0$) and solving Eq. (13) using the abovementioned periodic boundary conditions, the average velocity along x-, y- and z- directions can be calculated as follow:

$$\left\langle {v_{x} } \right\rangle = - \int\limits_{{\partial D_{3} }} {v.\overrightarrow {n3} \,} {\text{d}}x{\text{d}}z$$

(23)

$$\left\langle {v_{y} } \right\rangle = - \int\limits_{{\partial D_{1} }} {v.\overrightarrow {{n_{1} }} }\,{\text{d}}y{\text{d}}z$$

(24)

$$\left\langle {v_{z} } \right\rangle = - \int\limits_{{\partial D_{5} }} {v.\overrightarrow {{n_{5} }} }\,{\text{d}}x{\text{d}}y.$$

(25)

Fig. 12

Periodic boundary conditions used for over a grid block

Equation (2) can be expressed in an explicit form as follow:

$$v_{x} = - k_{xx} \frac{\partial p}{\partial x} - k_{xy} \frac{\partial p}{\partial y} - k_{xz} \frac{\partial p}{\partial z}$$

(26)

$$v_{y} = - k_{yx} \frac{\partial p}{\partial x} - k_{yy} \frac{\partial p}{\partial y} - k_{yz} \frac{\partial p}{\partial z}$$

(27)

$$v_{z} = - k_{zx} \frac{\partial p}{\partial x} - k_{zy} \frac{\partial p}{\partial y} - k_{zz} \frac{\partial p}{\partial z},$$

(28)

where $v_{x}$, $v_{y}$ and $v_{z}$ are velocities in x-, y- and z-directions, respectively. Since pressure gradient through x-direction is assumed and $v_{x}$, $v_{y}$ and $v_{z}$ are known, then $k_{xx}$, $k_{xy}$ and $k_{xz}$ are easily determined. The rest of permeability tensor elements can be calculated by using the same boundary conditions as abovementioned but in other directions.

Appendix 2: Implementation of finite element method (FEM) for governing equations of poroelasticity for single phase fluid flow

This appendix details the FEM formulation of the Poroelastic problem.

Assuming off-diagonal components of permeability tensor are zero,

$$\begin{aligned} \mathop {{\text{ }}k}\limits^{{\mathop \to \limits^{ \to } }} &= \left( {\begin{array}{*{20}l} {k_{{xx}} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {k_{{yy}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {k_{{zz}} } \hfill \\ \end{array} } \right) \hfill \\ \phi c_{t} \frac{{\partial p}}{{\partial t}} - \alpha \frac{\partial }{{\partial t}}\left( {\frac{\partial }{{\partial x}}\frac{\partial }{{\partial y}}\frac{\partial }{{\partial z}}} \right)\vec{u} &= \frac{\partial }{{\partial x}}\left( {\frac{{k_{x} }}{\mu }\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{k_{y} }}{\mu }\frac{{\partial p}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{k_{z} }}{\mu }\frac{{\partial p}}{{\partial z}}} \right) \hfill \\ \end{aligned}.$$

(29)

Multiplying both sides of Eq. 54 by a trial function, w, and integrating over the domain, Ω yields

$$\int\limits_{\varOmega } {\left( {wc_{t} \phi \frac{\partial p}{\partial t}} \right)} {\text{d}}\varOmega - \int\limits_{\varOmega } {\left[ {w\alpha \frac{\partial }{\partial t}\left( {\frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z}} \right)\mathop u\limits^{ \to } } \right]} {\text{d}}\varOmega = \int\limits_{\varOmega } {w\left( {\frac{\partial }{\partial x}\left( {\frac{{k_{x} }}{\mu }\frac{\partial p}{\partial x}} \right) + \left( {\frac{{k_{y} }}{\mu }\frac{\partial }{\partial y}} \right) + \left( {\frac{{k_{z} }}{\mu }\frac{\partial }{\partial z}} \right)} \right)} {\text{d}}\varOmega.$$

(30)

Using the Green formulae, Eq. 30 becomes

$$\begin{aligned} & \int\limits_{\varOmega } {\left( {wc_{t} \phi \frac{\partial p}{\partial t}} \right)} {\text{d}}\varOmega + \int\limits_{\varOmega } {\frac{\partial w}{\partial x}\left( {\frac{{k_{x} }}{\mu }\frac{\partial p}{\partial x}} \right)} {\text{d}}\varOmega \\ &\qquad +\int\limits_{\varOmega } {\frac{\partial w}{\partial y}\left( {\frac{{k_{y} }}{\mu }\frac{\partial p}{\partial y}} \right)} {\text{d}}\varOmega \int\limits_{\varOmega } {\frac{\partial w}{\partial z}} \left( {\frac{{k_{z} }}{\mu }\frac{\partial p}{\partial z}} \right){\text{d}}\varOmega\\ &\quad = \oint\limits_{r} w \left( {\frac{{k_{x} }}{\mu }\frac{\partial p}{\partial x}n_{x} + \frac{{k_{y} }}{\mu }\frac{\partial p}{\partial y}n_{y} + \frac{{k_{z} }}{\mu }\frac{\partial p}{\partial z}n_{z} } \right){\text{d}}\varGamma \\ & \qquad+ \int\limits_{\varOmega } {\left[ {w\alpha \frac{\partial }{\partial t}\left( {\frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z}} \right)\mathop u\limits^{ \to } } \right]} {\text{d}}\varOmega \\ \end{aligned},$$

(31)

where ‘Γ’ is the boundary and ‘n’ is the outward normal to the boundary. Finite difference method is used to discretize the terms including differentiation with respect to time. Permeability and porosity remain constant with change in time. After rearranging, Eq. 31 becomes

$$\begin{aligned} & \int\limits_{\varOmega } {\left( {wc_{t}^{i - 1} \phi^{i - 1} \frac{{p^{i} - p^{i - 1} }}{{\Delta t^{i} }}} \right)} {\text{d}}\varOmega + \int\limits_{\varOmega } {\frac{\partial w}{\partial x}\left( {\frac{{k_{x}^{i - 1} }}{\mu }\frac{{\partial p^{i} }}{\partial x}} \right)} {\text{d}}\varOmega \\ & + \int\limits_{\varOmega } {\frac{\partial w}{\partial y}\left( {\frac{{k_{y}^{i - 1} }}{\mu }\frac{{\partial p^{i} }}{{\partial_{y} }}} \right)} {\text{d}}\varOmega + \int\limits_{\varOmega } {\frac{\partial w}{\partial z}\left( {\frac{{k_{z}^{i - 1} }}{\mu }\frac{{\partial p^{i} }}{\partial z}} \right)} {\text{d}}\varOmega = \int\limits_{\varOmega } {\left[ {w\alpha \left( {\frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z}} \right)\frac{{\overrightarrow {u}^{i} - \overrightarrow {u}^{i - 1} }}{{\Delta t^{i} }}} \right]} {\text{d}}\varOmega \\ \end{aligned}.$$

(32)

In which ‘i’ and ‘i − 1’ are current and previous times, respectively. Using Galerkin approach (Zienkiewicz and Taylor 2000), Eq. 32 becomes

$$\begin{aligned} & \left[ {\int\limits_{\varOmega } {c_{t} \phi^{i} } \vec{N}_{p}^{T} \vec{N}_{p} d\varOmega } \right]\frac{{\overrightarrow {P}^{i} - \overrightarrow {P}^{i - 1} }}{{\Delta t^{i} }} + \left[ {\int\limits_{\varOmega } {\left( {\frac{{k_{x}^{i - 1} }}{{\mu^{i - 1} }}\frac{{\partial \overrightarrow {N}_{p}^{T} }}{\partial x}\frac{{\partial \overrightarrow {N} {}_{p}}}{\partial x} + \frac{{k_{y}^{i - 1} }}{{\mu^{i - 1} }}\frac{{\partial \overrightarrow {N}_{p}^{T} }}{\partial y}\frac{{\partial \overrightarrow {N} {}_{p}}}{\partial y} + \frac{{k_{z}^{i - 1} }}{{\mu^{i - 1} }}\frac{{\partial \overrightarrow {N}_{p}^{T} }}{\partial z}\frac{{\partial \overrightarrow {N} {}_{p}}}{\partial z}} \right)} {\text{d}}\varOmega } \right]\overrightarrow {P}^{i} \\ & \left( {\int\limits_{\varOmega } {\vec{N}_{p}^{T} \alpha \left( {\frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z}} \right)} {\text{d}}\varOmega } \right)\frac{{\overrightarrow {U}^{i} - \overrightarrow {U}^{i - 1} }}{{\Delta t^{i} }} = 0 \\ \end{aligned},$$

(33)

where

$$\overrightarrow {P}^{T} = \left( {p_{1} p_{2} \cdots p_{n} } \right)$$

(34)

$$\overrightarrow {N}_{p}^{T} = \left( {N_{1} N_{2} \cdots Nn} \right)$$

(35)

$$\overrightarrow {N}_{u} = \left[ {\begin{array}{*{20}l} {N_{1} } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ 0 \hfill & {N_{1} } \hfill & \cdots \hfill & {N_{n} } \hfill \\ \end{array} } \right]$$

(36)

$$\overrightarrow {U}^{T} = \left( {u_{x1} u_{y1} u_{z1} u_{x2} \cdots u_{yn} } \right),$$

(37)

where ‘n’ is the total number of nodes. After rearrangement, Eq. 37 can be written as

$$\overrightarrow {{\overrightarrow {L} }} \left( {\overrightarrow {p}^{i} - p^{i - 1} } \right) + \Delta t^{i} \overrightarrow {{\overrightarrow {H} }} \overrightarrow {p}^{i} - \overrightarrow {{\overrightarrow {Q} }} \left( {\overrightarrow {U}^{i} - U^{i - 1} } \right) = \overrightarrow {0},$$

(38)

where

$$\overrightarrow {{\overrightarrow {L} }} = \sum\limits_{e = 1}^{\text{ne}} {\overrightarrow {{\overrightarrow {{L^{e} }} }} }$$

(39)

in which ‘e’ denotes element, ‘ne’ the number of elements and

$$\overrightarrow {{\overrightarrow {{L^{e} }} }} = \int\limits_{\varOmega } {\left( {c_{t}^{i - 1} \phi^{{e^{i - 1} }} \overrightarrow {N}_{p}^{T} \overrightarrow {N}_{p} } \right)} {\text{d}}\varOmega.$$

(40)

In which

$$\overrightarrow {{\overrightarrow {H} }} = \mathop \sum \limits_{e = 1}^{ne} \overrightarrow {{\overrightarrow {{H^{e} }} }}$$

(41)

$$\overrightarrow {{\overrightarrow {{H^{e} }} }} = \int\limits_{{\varOmega^{e} }} {\left( {\frac{{k_{x}^{{e^{i - 1} }} }}{{\mu^{{e^{i - 1} }} }}\frac{{\partial \overrightarrow {{N^{e} }}_{p}^{T} }}{\partial x}\frac{{\partial \overrightarrow {{N_{p}^{e} }} }}{\partial x} + \frac{{k_{y}^{{e^{i - 1} }} }}{{\mu^{{e^{i - 1} }} }}\frac{{\partial \overrightarrow {{N^{e} }}_{p}^{T} }}{\partial y}\frac{{\partial \overrightarrow {{N_{p}^{e} }} }}{\partial y} + \frac{{k_{z}^{{e^{i - 1} }} }}{{\mu^{{e^{i - 1} }} }}\frac{{\partial \overrightarrow {{N^{e} }}_{p}^{T} }}{\partial z}\frac{{\partial \overrightarrow {{N_{p}^{e} }} }}{\partial z}} \right)} {\text{d}}\varOmega$$

(42)

$$\overrightarrow {{\overrightarrow {Q} }} = \sum\limits_{e = 1}^{\text{ne}} {\overrightarrow {{\overrightarrow {{Q^{e} }} }} },$$

(43)

where

$$Qe = \alpha \int\limits_{{\varOmega^{e} }} {\overrightarrow {N}_{P}^{{e^{T} }} \left( {\frac{{\partial N^{e}_{u} }}{\partial x} + \frac{{\partial N^{e}_{u} }}{\partial x}} \right)} {\text{d}}\varOmega.$$

(44)

Equation 36 in an incremental form can be written as

$$(\overrightarrow {{\overrightarrow {L} }} + \Delta t^{i} \overrightarrow {{\overrightarrow {H} }} )\Delta P^{i} - \overrightarrow {{\overrightarrow {Q} }} \overrightarrow {{\Delta U^{i} }} = \overrightarrow {{f_{1} }}$$

(45)

$$\begin{array}{*{20}l} {\text{where}} \hfill \\ {\overrightarrow {\Delta P} = \overrightarrow {{P^{i} }} - \overrightarrow {{P^{i - 1} }} ,\quad \overrightarrow {\Delta U} = \overrightarrow {{U^{i} }} - \overrightarrow {{U^{i - 1} }} {\text{and}}:} \hfill \\ {\overrightarrow {f}_{1}^{e} = - \Delta t^{i} \overrightarrow {{\overrightarrow {H} }} \overrightarrow {{P^{i - 1} }} } \hfill \\ \end{array}$$

(46)

Gaussian quadrature is applied for integration, and one gets

$$\int\limits_{\varOmega } {\left( {\overrightarrow {W}^{T} \overrightarrow {{\overrightarrow {{S^{T} }} }} \overrightarrow {\Delta \sigma } } \right)} {\text{d}}\varOmega = \overrightarrow {0},$$

(47)

where

$$\overrightarrow {W} = \left[ {_{\begin{subarray}{l} W_{2} (x,y,z) \\ W_{3} (x,y,z) \end{subarray} }^{{W_{1} (x,y,z)}} } \right].$$

(48)

And w ₁ and w ₂ are trial functions. Using Green’s identity, one obtains

$$\int\limits_{\varGamma } {\left( {\overrightarrow {W}^{T} \overrightarrow {{\overrightarrow {M} }}^{T} \overrightarrow {\Delta \sigma } } \right){\text{d}}\varGamma - \int\limits_{\varOmega } {\overrightarrow {\Delta \sigma }^{T} } } \left( {\overrightarrow {{\overrightarrow {S} }} \overrightarrow {W} } \right){\text{d}}\varOmega = \overrightarrow {0},$$

(49)

where

$$\overrightarrow {{\overrightarrow {{M^{T} }} }} = \left[ {\begin{array}{lllll} {n_{x} } & 0 & {n_{y} } & 0& {n_{z} }\\ 0& {n_{y} } & {n_{x} } & 0 & {n_{z} }\end{array} } \right].$$

(50)

Rearrange Eq. B.46, one gets

$$\int\limits_{\varOmega } {\left( {\overrightarrow {{\overrightarrow {S} }} \overrightarrow {W} } \right)}^{T} \overrightarrow {{\overrightarrow {D} }}_{e} \overrightarrow {{\overrightarrow {S} }} \overrightarrow {\Delta U}^{i} {\text{d}}\varOmega + \alpha \int\limits_{\varOmega } {\left( {\overrightarrow {{\overrightarrow {S} }} \overrightarrow {W} } \right)} \overrightarrow {\Delta P}^{i} {\text{d}}\varOmega = \int\limits_{\varGamma } {\left( {W^{T} \overrightarrow {{\overrightarrow {{M^{T} }} }} \overrightarrow {\Delta \sigma }^{i} } \right)} {\text{d}}\varGamma.$$

(51)

Using Galerkin method, Eq. B.48 yields

$$\left( {\int\limits_{\varOmega } {\left( {\overrightarrow {{\overrightarrow {S} }} \overrightarrow {N}_{u} } \right)^{T} \overrightarrow {{\overrightarrow {D} }}_{e} \overrightarrow {{\overrightarrow {S} }} } \overrightarrow {N}_{u} {\text{d}}\varOmega } \right)\overrightarrow {\Delta U}^{i} + \alpha \left( {\int\limits_{\varOmega } {\left( {\left( {\frac{{\partial \overrightarrow {N}_{u} }}{\partial X}\frac{{\partial \overrightarrow {N}_{u} }}{\partial X}} \right)\overrightarrow {N}_{P} } \right)}^{T} {\text{d}}\varOmega } \right)\overrightarrow {\Delta P}^{i} = \int\limits_{\varGamma } {\left( {\overrightarrow {N}_{u} {}^{T}\overrightarrow {{\overrightarrow {M} }}^{T} \overrightarrow {\Delta \sigma }^{i} } \right)} {\text{d}}\varGamma.$$

(52)

Or in a compact form as follow:

$$\overrightarrow {{\overrightarrow {K} }} \Delta \overrightarrow {U} + \overrightarrow {{\overrightarrow {{Q_{{}}^{T} }} }} \Delta \overrightarrow {P} = \overrightarrow {{f_{2} }}$$

(53)

$$\overrightarrow {{\overrightarrow {K} }} = \sum\limits_{e = 1}^{ne} {\overrightarrow {{\overrightarrow {{K^{e} }} }} }^{{}}$$

(54)

$$\overrightarrow {{\overrightarrow {{K^{e} }} }} = \int\limits_{{\varOmega^{e} }} {\left( {\overrightarrow {{\overrightarrow {S} }} \overrightarrow {N}_{u}^{e} } \right)^{T} } \overrightarrow {{\overrightarrow {{D_{e} }} }} \overrightarrow {{\overrightarrow {S} }} \overrightarrow {N}_{u}^{e} {\text{d}}\varOmega$$

(55)

$$\overrightarrow {f}_{2} = \sum\limits_{e = 1}^{ne} {\overrightarrow {f}_{2}^{e} }$$

(56)

$$\overrightarrow {f}_{2} = \int\limits_{{\varGamma^{e} }} {\left( {\overrightarrow {N}_{u} \overrightarrow {{\overrightarrow {{M^{T} }} }} \overrightarrow {\Delta \sigma }^{i} } \right)} {\text{d}}\varGamma.$$

(57)

Equations 48 and 56 are the final finite element equations to be simultaneously solved as a system of linear equations which is as follows:

$$\left[ {\begin{array}{*{20}c} {\overrightarrow {{\overrightarrow {L} }} + \Delta t\overrightarrow {{\overrightarrow {H} }} - } \\ {\overrightarrow {{\overrightarrow {{Q^{T} }} }} } \\ \end{array} \begin{array}{*{20}c} {\overrightarrow {{\overrightarrow {Q} }} } \\ {\overrightarrow {{\overrightarrow {K} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \overrightarrow {P}^{i} } \\ {\Delta \overrightarrow {U}^{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\overrightarrow {{f_{1} }} } \\ {\overrightarrow {{f_{2} }} } \\ \end{array} } \right].$$

(58)