Introduction

Fuzzy theory was proposed by cybernetic professor L. A. Zadeh in University of California in 1965 (Gao 2004) and has been widely used in the natural sciences and social sciences fields in the following 50 years. Fuzzy clustering analysis is a branch of fuzzy mathematics, and its range of applications involves time series prediction (Ryoke et al. 1995), neural networks training (Karayiannies and Mi 1997), nonlinear system identification (Runkler et al. 1996), parameter estimation (Gath and Geva 1989), medical diagnosis (Bezdek and Fordon 1979), weather forecast (Newton 1992), food classification (Windham 1985), and water quality analysis (Mukherjee 1995).

The limitations of traditional fuzzy clustering analysis are several controlling factors, such as the choice of initial cluster centers, the correlation between samples, the trade-off between iteration times, and solutions accuracy. To solve these problems, many researchers had proposed many modified algorithms, such as K-means clustering, C-means clustering, fuzzy clustering neural network, and fuzzy clustering genetic.

Overview of worldwide, the workers had made many researches about the lithology identification of CCSD-MH; however, the database of CCSD-MH core data was still incomplete and inaccurate. Xu et al. (2006) analyzed magnetic susceptibility and density of different rocks from CCSD-MH in the depth Section 0–2000 miles, identified the lithology with SPSS statistical software. Jing et al. (2007) summed up 11 kinds of eclogites into 6 kinds based on multivariate statistic methods. Gu et al. (2009) constructed the lithology recognition model combining the logging response and several well logs of different rocks with the method of cluster analysis and stepwise discriminant analysis. Luo and Pan (2010) used core-log correlation and cross-plotting methods, and the results allowed the authors to conclude that the lithology is mainly comprised orthogneiss, paragneiss, eclogite, amphibolite, and ultramafic rocks. Bosch et al. (2013) used fuzzy logic for lithology prediction from well log data of the German Continental Deep Drilling Program (KTB). Results showed that this fuzzy logic-based method was suited for rapidly and reasonably suggesting a lithology column from KTB well log data. The above authors heavily focused on approaches such as visual inspection, cross-plotting technology, and discriminate function analysis, and not formed a method that can neatly identify the main units and refine the classification of the CCSD-MH whole well.

Reservoir evaluation needs the data of many kinds of rocks, which have a much more different porosity and permeability. The well logs have varieties of responses based on different kinds of rocks’ characteristic. And the lithology data is mainly carried out by cores recovery in lab which is very expensive and its interpretation is time consuming, so accurate identification of lithology from geophysical well log data plays a significant role in reservoir evaluation.

In this study, a fast and practical K-means clustering algorithm was proposed in order to better deal with lithology recognition of CCSD-MH from geophysical log data. Based on the traditional K-means clustering algorithm, Euclidean distance was replaced by Mahalanobis distance, and the initial cluster centers were acquired from the average of characteristic values, in addition, added weight value in each characteristic value of the objective function. The model was applied to classify CCSD-MH metamorphic rocks and get the cluster centers of each class. The cluster centers, as well as weight values, were used to calculate the hamming approach degree, which can neatly identify the main units and refine the classification of the CCSD-MH whole well.

Modified K-means clustering

Cluster center

Let us choose m objects, and each object has n characteristic values that may be classified into z classes. According to the fuzzy theory, the fuzzy matrix involving the above objects can be constructed as \(X = [x_{ij} ]\), (\(i = 1, \, 2, \ldots ,\;m\); \(j = 1, \, 2, \ldots ,\;n\)). The cluster center matrix is defined as \(C = [c_{kj} ]\), and \(k\) (\(k = 1, \, 2,\; \ldots ,\;z\)), \(j\) (\(j = 1, \, 2, \ldots ,\;n\)). And \(m \ge z\). The two matrixes and their compositions are as follows:

$$\;X = \{ X_{1} ,X_{2} , \ldots ,X_{n} \} \;{\text{and}}{\quad{X_{i} = \{ x_{i1} ,x_{i2} , \ldots ,x_{in} \}}}$$
(1)
$$\;C = \{ C_{1} ,C_{2} , \ldots ,C_{z} \} \quad{\text{and}}{\quad{C_{k} = \{ c_{k1} ,c_{k2} , \ldots ,c_{kn} \}}} .$$
(2)

The traditional K-means algorithm will increase iteration times if initial cluster centers selected inappropriately, and may easily fall into local optimums. In order to alleviate this problem, we acquired the initial cluster centers from the average of characteristics values in matrix \(X\) based on the theory of cluster center (Liao 2013).

Therefore, any elements \(C_{k} = \{ c_{k1} ,c_{k2} , \ldots ,c_{kn} \}\) of matrix \(C\) can be defined as follows:

$$\;\;c_{k1} = \frac{k}{z}\frac{1}{n}\sum\limits_{j = 1}^{n} {x_{j1} } \,c_{k2} = \frac{k}{z}\frac{1}{n}\sum\limits_{j = 1}^{n} {x_{j2} } , \ldots ,c_{kn} = \frac{k}{z}\frac{1}{n}\sum\limits_{j = 1}^{n} {x_{jn} } .$$
(3)

The weight value

Traditional K-clustering takes the same contribution for cluster results by different characteristic values, which will be susceptible to noise data resulting in the inaccuracy of cluster result. However, the contribution of each characteristic value to the cluster result is different. Therefore, a weighted value scheme is proposed to deal with the relationship between various samples data and cluster centers in the objective function. The weight value of each characteristic in fuzzy matrix \(X\) can be obtained as follows:

Firstly, we introduce a standard to evaluate the comparison of every two groups of characteristic values:

$$b_{ij} = \frac{{x_{ij} - x_{\hbox{min} } }}{{x_{\hbox{max} } - x_{\hbox{min} } }} ,$$
(4)

where \(x_{\hbox{min} }\) and \(x_{\hbox{max} }\) refer to the maximum and minimum of the given each group of characteristic values.

Secondly, the weight \(w_{j}\) is defined as information entropy for the jth group characteristic value, which can be evaluated by (Feng et al. 2010; Zhang et al. 2010)

$$H_{j} = - \frac{1}{\ln m}\left(\sum\limits_{i = 1}^{m} {f_{ij} \ln f_{ij} } \right) ,$$
(5)

where \(f_{ij}\) is the weight of the jth index for the ith sample in all samples which can be estimated using normalized judgment matrix elements \(b_{ij}\), giving (Zhang et al. 2010)

$$f_{ij} = \frac{{1 + b_{ij} }}{{\sum\limits_{i = 1}^{m} {(1 + b_{ij} )} }} .$$
(6)

Finally, the weight \(w_{j}\) can evaluate the contribution of each characteristic value to the lithology classification results, which is given by (Feng et al. 2010; Zhang et al. 2010)

$$w_{j} = \frac{{1 - H_{j} }}{{n - \sum\limits_{j = 1}^{n} {H_{j} } }}\;,{\text{ and}}\quad \sum\limits_{j = 1}^{n} {w_{j} = 1} .$$
(7)

Objective function

Based on the traditional K-means clustering algorithm, Euclidean distance is replaced by Mahalanobis distance, in addition, added different weight values in each characteristic value. The weight is given a higher value if the contribution of its corresponding characteristic value has quite a higher influence to the lithology recognition, while the redundant characteristic values are given much smaller values. Therefore, the objective function of modified K-means cluster algorithm can be defined as

$$F(X,C) = \hbox{min} \left( {\sum\limits_{k = 1}^{z} {\sum\limits_{i = 1}^{m} {\sqrt {w_{1} (x_{i1} - c_{k1} )\sum^{ - 1} (x_{i1} - c_{k1} )^{T} + \cdot \cdot \cdot + w_{n} (x_{in} - c_{kn} )\sum^{ - 1} (x_{in} - c_{kn} )^{T} } } } } \right) ,$$
(8)

where ∑ is the covariance matrix and \(w_{j}\) is the weight of each characteristic value.

If the \(\sum\) was a singular matrix, \(\sum\) can be written as the product of three pieces, \(\sum = A^{T} GA\). The pseudo-inverse of \(\sum\) can be solved through the inverse of \(G\) (Wu et al. 2011). Uniquely to Euclidean distance, Mahalanobis distance takes the correlation of every two groups of characteristic values into account and solves the repetitive information reused that leads to the clustering results inaccuracy. The weigh value of each characteristic value is taken as the parameter for reflect the different contributions of every group of characteristic value to the clustering results, and thus the calculated clustering center can be much closer to the actual results.

The modified K-means clustering follows

  1. (1)

    Given the maximum iteration times \(T\) or threshold value \(\varepsilon\), and the cluster center number z. The initial iterative value \(t = 1\).

  2. (2)

    Calculating the cluster centers and weight values with Eqs. (3) and (7), respectively, and the covariance matrix.

  3. (3)

    Calculating the distances between the undetermined samples and every cluster centers with Eq. (8), and assigning the sample to the class, whose cluster center is the nearest to this sample.

  4. (4)

    Calculating the new cluster centers of every new class.

  5. (5)

    According to Eq. (8), calculating the objective function \(J(X,C)\). It will not stop operating until \(\left| {J(X,C)^{(t)} - J(X,C)^{(t - 1)} } \right| \le \varepsilon\) or \(T \le t\). If so, output the cluster centers of each class; otherwise, make \(t = t + 1\), backward to step 3, and go on iterating.

Method application

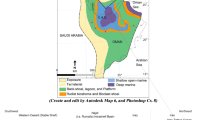
The drill site of the CCSD is located near Maobei village (N34°25′, E118°40′), about 17 km southwest of Donghai in the southern segment of the Sulu UHP terrane (Wang et al. 2013), as shown in Fig. 1. Major goals of the CCSD, as outlined by Xu et al. (1998), include (1) to reveal the crustal structure of convergent plate boundaries, (2) to provide constraints on crust-mantle interactions and mantle behavior during deep subduction of continental crust, and (3) to investigate fluid evolution during UHP metamorphism. The CCSD-MH was completed at its final depth of 5158 m in March 2005.

Fig. 1
figure 1

Simplified geological location of CCSD-MH by a star symbol (Ni et al. 2013; Zhang et al. 2006)

Full size image

The lithology types have been confirmed by core recovery of 112 drill hole samples in laboratory from 220 to 4000 miles, are mainly eclogite, paragneiss, orthogneiss, amphibolites, serpentinite, and granite (Zhang et al. 2000, 2003; Ya et al. 2000; Liu et al. 2004, 2005).

In this paper, we chose several well logs and core recovery materials of CCSD-MH from the depth Section 100–2000 miles for method development, which will identify the lithology of the whole well from the depth 100–5118.2 miles. In order to demonstrate the method capacity in identifying lithology, we selected 9 kinds of rocks that almost distribute in the whole well based on the log representations and core recovery materials. There are seven well logs that are selected by analyzing the corresponding relationship between the logs and lithology; they are deep induction resistivity (RILD), compensated neutron (CNL), interval transit time (AC), compensated density (DEN), natural gamma (GR), uranium (U), and thorium (TH).

The fuzzy matrix mentioned above contains 45 samples, 9 kinds of lithology, and each lithology has five samples. We identified the lithologies both using the traditional K-means cluster and modified K-means algorithms, and output the cluster centers of each lithology (Table 1 and Table 2).

Table 1 Cluster centers of each lithology using traditional K- means cluster algorithm
Full size table
Table 2 Cluster centers of each lithology using modified K-means cluster algorithm
Full size table

The parameter setting of traditional K-means cluster algorithm is as follows: input 45 samples, threshold ε = 0.001, and cluster numbers z = 9. The initial cluster centers are selected randomly and were the former z samples. The classification accuracy of 45 samples was 77.78 %. Output the cluster centers of each lithology (Table 1).

The parameter setting of modified K-means algorithm is as follows: input 45 samples, threshold ε = 0.001, and cluster numbers z = 9. In order to make a comparison, the modified K-means cluster algorithm tested the same samples with the traditional K-means cluster algorithm, and the classification accuracy was 88.89 %. Compared with the traditional K-means clustering, the accurate rate of the modified K-means clustering in lithologic identification has improved, raised 11.11 %. Output the cluster centers of each lithology (Table 2).

Results and discussion

Verification of method prediction

According to the modified K-means cluster algorithm, 9 cluster centers were acquired from the 45 samples. The information entropy used to evaluate the contribution of each well logs on identifying the CCSD-MH lithology was calculated with Eq. (7). After that, calculating the hamming approach degree between the undetermined samples and 9 cluster centers, which is to determine the class of the samples. The computation of the hamming approach degree is as follows (Zhang et al. 2010):

$$H = 1 - \sum\limits_{j = 1}^{n} {w_{j} \left| {x_{j} - c_{k} } \right|} \;\quad k = 1, \, 2, \ldots ,{\text{ z}} ,$$
(9)

where \(H\) was the hamming approach degree of the undetermined samples and one cluster center. \(x_{j}\) represents the undetermined sample, and \(c_{k}\) represents the cluster center of one class. \(w_{j}\) is the weight of jth well log.

Hamming approach degree is defined to the similar degree between the undetermined samples and standard samples, and the greater its value indicates that the undetermined samples are closer to the standard samples, that is to say, the undetermined samples and the standard samples are owned to the same class. In this paper, 27 undetermined samples are selected in the depth Section 100.0–5118.2 miles (the whole well).

As shown in Fig. 2a, it is the hamming approach degree curve of 27 undetermined samples and cluster center 4 (Table 2); the hamming approach degrees of number 10, number 11, and number 12 undetermined samples are the biggest, 0.984, 0.985, and 0.976, respectively, almost 1. We can conclude that the three samples belong to the class 4 and are paragneiss. Figure 2b shows the curve of 27 undetermined samples and cluster center 7; and number 19, number 20, and number 21 undetermined samples’ hamming approach degree are the biggest, 0.981, 0.979 and 0.979, respectively. These three samples belong to the class 7, and are serpentinite.

Fig. 2
figure 2

Hamming approach degree curve of 27 samples and cluster center 4 and cluster 7

Full size image

Through the classification of the former 6 samples, it can be concluded that number 1, number 2, and number 3 are rutile eclogite; number 4, number 5, and number 6 are phengite; number 7, number 8, and number 9 are retrograded eclogite; number 13, number 14, and number 15 are orthogneiss; number 16, number 17, and number 18 are amphibolites; number 22, number 23, and number 24 are chlorite amphibolites; and number 25, number 26, and number 27 are moyite. According to hamming approach degree curves, we determine the lithology of 27 samples, as shown in Table 3. The predicted results and the core recovery are exactly the same by comparison.

Table 3 The undetermined samples and corresponding lithology
Full size table

As shown in Fig. 2, the curves of different lithologies have sudden changes; the reason would be both the theoretical model and logging data. In addition, the approach degree of the same lithology also exits slight differences. However, the model could meet the needs of lithology identification for the overall prediction results. Therefore, the cluster centers acquired from the modified K-means clustering algorithm, as well as the hamming approach degree can identify CCSD-MH lithology effectively and accurately, which could also be made applied to other areas.

Well logging graphic of lithology

The lithology analysis figure resulted from the traditional K-means clustering and modified K-means clustering for visual identification of CCSD-MH lithology, as shown in Figs. 3 and 4. With these two figures, the lithology of CCSD-MH can be easily distinguished.

Fig. 3
figure 3

Well logging graphic of CCSD-MH lithology analysis in the depth Section 1600.0–1640.7 m. 1 Rutile eclogite, 2 phengite eclogite, 3 retrograded eclogite, 4 paragneiss, 5-orthogneiss, 6 amphibolites, 7 serpentinite, 8 chlorite amphibolites, 9 moyite and 10 fracture zone

Full size image
Fig. 4
figure 4

Well logging graphic of CCSD-MH lithology analysis in the depth Sect. 1700.0 ~ 1750.0 m. 1 Rutile eclogite, 2 phengite eclogite, 3 retrograded eclogite, 4 paragneiss, 5 orthogneiss, 6 amphibolites, 7 serpentinite, 8 chlorite amphibolites, 9 moyite and 10 fracture zone

Full size image

As shown in Fig. 3, the section of CCSD-MH was divided into 15 parts from the core recovery, while the section could be divided into 11 and 13 parts based on the traditional and modified K-means clustering, respectively.

According to the core recovery, there are five kinds of lithology, and two fracture zones. There are also five kinds of lithology, and no fracture zone displayed based on the identification methods of the traditional K-means cluster and modified K-means cluster. The great error section is from 1600.0 to 1616.7 miles which corresponds to chlorite amphibolites, and there is no fracture zone from the two fuzzy clusters. According to the traditional K-means cluster, there are no chlorite amphibolites between the depth of 1601.52 and 1614.40 miles, and all is phengite eclogite, while the modified K-means cluster has good correspondence with the core recovery and presents the same lithology at the same depth position. At the end depth of the phengite eclogite from the core recovery, there is a short section of orthogneiss, while the corresponding position of the traditional K-means cluster and modified K-means cluster is amphibolites. Several small errors exist between the depth 1615.4 and 1640.7 miles at the transition of two layers from the traditional K-means cluster and the core recovery, while the modified K-means cluster has a good correspondence with the core recovery, except that a fracture zone presents from the core recovery.

Three kinds of lithology and five fracture zones are shown in Fig.4 from the depth 1700.0 to 1750.0 miles based on the core recovery. According to the modified K-means clustering, the section could be divided into nine parts, and this section was divided into eight parts based on the traditional K-means clustering, one phengite eclogite layer is neglected.

The great error section is from 1705.2 to 1716.5 miles, there are two thin phengite eclogite layers and one fracture zone, while there is no phengite eclogite presented with the two methods in the corresponding depth. Because of the thin layer, the well logging response of phengite eclogite was affected by the surrounding rocks and did not present the characteristic of phengite eclogite layers, so they were not properly identified. In general, the lithology of fracture zones is the same with the surrounding rocks. The density of fracture zone is about 1.55–1.67 g/cm3 which is so low that the entropy information is small; thus its contribution to the lithology recognition is low. The phengite eclogite layer was not identified with the method of traditional K-means clustering in the depth Section 1728.3–1730.7 miles, and there were several slight depth errors in the rock transition section. Therefore, the modified K-means cluster has better correspondence with the core recovery than the traditional K-means cluster.

Clustering analysis

In order to verify the striking effect that modified K-means cluster algorithm has brought about, the same 45 samples were used by the traditional K- means cluster algorithm to identify the lithology of CCSD-MH. The iteration times, the threshold value, and the cluster numbers were given as \(T = 1250\), \(\varepsilon = 0.001\), and \(z = 9\), respectively. The results are shown in Table 4.

Table 4 Performance comparison of clustering analysis
Full size table

As shown in Table 4, the accuracy of modified K-means cluster algorithm is higher than traditional K-means cluster algorithm. This is mainly because of the cluster centers that the modified K-means cluster algorithm calculated used Eq. (3), which reduces the iteration times and avoids falling into local optimums. Moreover, the algorithm takes the weight values into account, which distinguishes the contributions of different well logs to lithology identification. For the same accuracy, the modified K-means cluster algorithm would take less iteration times and time than the traditional K-means cluster algorithm. Therefore, the identification result showed that the modified K-means cluster algorithm has high identification accuracy and improve practicability.

Conclusions

Reservoir lithology is one of the most important data to evaluate rock formation; it mainly carried out by core recovery in laboratory which is very expensive, and its interpretation is time consuming. Accurate identification of lithology from geophysical log data plays a significant role in reservoir evaluation.

In this study, a fast and practical K-means clustering algorithm was proposed based on the shortcoming of the traditional K-means clustering algorithm. Euclidean distance was replaced by Mahalanobis distance, and the initial cluster centers are acquired from the average of characteristic values in matrix but not selected randomly, in addition, adding weight value in each characteristic value of the objective function. For the same 45 rock samples of CCSD-MH, the accuracy rate of traditional K-means clustering algorithm is 77.78 %, while modified K-means clustering algorithm is 88.89 %, which shows that our modified algorithm is applicable.

According to the modified K-means cluster algorithm, 45 samples can be classified into 9 classes and get 9 cluster centers. The classes of 27 undetermined samples were identified by analyzing the hamming approach degree curves. The predicted results and core recovery are exactly the same by comparison.

In conclusion, the modified K-means clustering algorithm gives better accuracy of CCSD-MH lithology classification than traditional K-means clustering. The hamming approach degree, as well as the cluster centers identified the whole well of CCSD-MH lithology effectively and accurately. Since its flexibility and capability in identifying the lithology, the model can be served as an effective approach in evaluating rock reservoirs when it lacks of core recovery materials. Further, the model may be useful in other fields.