Introduction

Conservation of water supplies became very important while water loss due to seepage from open channels represents one of the major components of water loss. Lining irrigation canals is considered one of the most efficient ways of ameliorating water-conveying systems (Awan 2017). It improves the flow characteristics, reduces seepage losses, controls the weeds growing along the canal bed and sides, and reduces the maintenance cost for the canals (Abd-Elaty et al. 2022). Moreover, it aims to avoid the potential water logging risk of adjacent low agricultural lands due to seepage (Abd-Elziz et al. 2022). For lined canals, high velocities are permitted, which leads to saving in the canal cross-sectional area and the required expropriation width, thereby minimizing total construction cost (Eltarabily et al. 2020).

To reduce seepage discharges, canals can be lined using various materials like concrete, asphaltic concrete, flexible membranes, compacted earth, and soil cement mixture (Waller and Yitayew 2015). The amount of seeping water depends on many factors, such as soil hydraulic conductivity, canal shape, wetted perimeter and side slopes, and the suspended solids in water (Mutema and Dhavu 2022). However, the amount of seepage under different lining materials should be studied and quantified to precisely select the suitable lining material (Elkamhawy et al. 2021). Seepage discharges can be measured in situ using inflow–outflow, ponding, and double-ring infiltration methods. Due to the difficulties of measuring seepage discharges in the field, analytical methods can be used (Eshetu and Alamirew 2018). However, analytical methods can be implemented to a limited extent due to assumptions rarely being met in the field (Eltarabily and Negm 2015).

Based on knowledge of the hydraulic characteristics of a canal (e.g., discharge, velocity), canal geometry, and soil hydraulic properties, engineers such as Davis Wilson, Moritz, Molesworth, Yennidumia, and Ingham developed empirical formulas that are easy and simple to use (Kraatz and Mahajan 1982). Due to a wide range of constant coefficients, these empirical relationships are insufficient. These equations' coefficients are usually defined for local conditions and must be calibrated for another. Using soil hydraulic conductivity makes a constant coefficient unnecessary for empirical relationships.

Over the past few years, numerical methods have been widely used to estimate seepage losses from irrigation canals. These methods were flexible, rapid, and non-laborious and had fewer inputs than physical models and field measurements (Rocscience 2002). The finite element model was used to estimate seepage losses from trapezoidal unlined and concrete-lined irrigation canals (Solomon & Ekolu 2014). They studied different hydraulic parameters and lining materials. The Slide2 model was utilized to estimate seepage losses under a hydraulic structure (Kathem Taeh Alnealy, 2015). SEEP/W model was employed to investigate the effect of compacted earth lining on seepage losses. They stated that seepage losses could be reduced by 99.80% if the soil is highly compacted (El-Molla and El-Molla 2021).

Recently, researchers in many fields of science and engineering have been interested in the ANN model. However, ANN can connect enormous and complex data sets without knowing how they are connected. The first use of ANN modeling was in civil engineering at the beginning of the 1980s to improve the efficiency of construction tasks (Flood and Kartam 1994). Later, applications of ANN extend to water resources engineering, hydraulics, hydrology, and environmental engineering (e.g., El-Din and Smith 2002; Shayya and Sablani 1998). Gokmen et al. (2005) used an ANN model to predict seepage losses through the Jeziorsko Dam (earth-fill type) in Poland with R2 = 0.96. El-kiki (2008) developed an ANN model for predicting the scour parameters downstream of the skew siphon pipes with R2 = 0.997. Although ANN was broadly applied in water resources and hydraulic fields, ANN has not been widely applied for estimating seepage losses from irrigation canals, even lined or unlined, so far.

Based on the above, the main aim of this research is to investigate the effect of lining on seepage losses from lined trapezoidal irrigation canals with different geometric and hydraulic parameters. Moreover, it develops an accurate model for calculating seepage losses from trapezoidal lined irrigation canals. We believe our findings will give clear insights regarding seepage losses under different lining materials and how to effortlessly estimate it without requiring further field measurements. These insights will be helpful for water resources specialists and decision-makers in Egypt and other countries with similar conditions to select the suitable lining material that can be used for lining irrigation canals and to manage the agricultural water budget precisely.

Materials and methods

The methodological approach used in the current study can be described as shown in Fig. 1. The Slide2 model was first validated using measured field data. It was used to conduct a parametric study to calculate seepage losses from lined trapezoidal irrigation canals with different geometric and hydraulic parameters and investigate the effect of lining on seepage losses. In addition, SPSS was used to develop three models; NLR, MLP-ANN, and RBF-ANN models based on Slide2 results. Then, the developed models’ results were compared by the seepage losses estimated from the Slide2 model by the statistical parameters. Moreover, MATLAB software was used to write script code for the ANNs.

Fig. 1
figure 1

Flow chart of methodological approach

Full size image

Slide2 numerical model

Model description

In the current study, the Slide2 model was used to estimate the seepage losses from lined trapezoidal irrigation canals. Furthermore, to investigate the combined effect of canal geometry and lining type on seepage losses. The Slide2 model can simulate water flow through a porous medium using a built-in finite element groundwater seepage analysis (Rocscience 2002). Confined and unconfined flow can also be simulated using this model. Equation 1 is the governing equation in the Slide2 model and was given by (Mahmud 1996):

$$\frac{\partial }{\partial x}\left({K}_{xx}\frac{\partial H}{\partial x}+{K}_{xy}\frac{\partial H}{\partial y}\right)+\frac{\partial }{\partial y}\left({K}_{yy}\frac{\partial H}{\partial y}+{K}_{yx}\frac{\partial H}{\partial x}\right)=0$$
(1)

where H is the total head and K is soil hydraulic conductivity.

Model setup

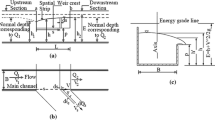
Seepage flow was assumed to move vertically downwards, and no influence of groundwater on seepage was considered during the simulation (Rocscience 2002). To capture any slight change in fluxes within the simulation domain, mesh refinement was used during the discretization of the simulation domain. Three thousand mesh elements of 3-noded triangles element were used to build the simulation domain. Figure 2a shows canal geometry and the parameters affecting the seepage per canal unit length. Figure 2b shows the simulation domain and the imposed boundary conditions (BCs). A discharge section was drawn at the bottom of the domain to estimate the seepage flux (i.e., seepage losses (q)).

Fig. 2
figure 2

a Canal geometry and effective parameters, b Simulation domain and the imposed boundary conditions

Full size image

Effective parameters

The following parameters affect the seepage losses from lined trapezoidal canals. They are q seepage losses per canal unit length, water depth (y), bed width (b), the canal side slope (z), the thickness of lining material (tL), hydraulic conductivity of lining material (KL), and the soil hydraulic conductivity (K) under the canal.

By using dimensional analysis, the following expression (Eq. 2) can be written as:

$$f\left(q,z,b,y,{K}_{{\text{L}}},K,{t}_{{\text{L}}}\right)=0$$
(2)

By the application of Buckingham's \(\pi\) theorem (Hanche-Olsen 2004), the \(\pi\) terms functional relation can be written as shown in Eq. (3):

$$\left(\frac{q}{Ky},\frac{b}{y},z,\frac{{K}_{{\text{L}}}}{K},\frac{{t}_{{\text{L}}}}{y}\right)=0$$
(3)

where \(\left(\frac{q}{Ky}\right)={q}^{*}(\mathrm{dependent variable}); \left(\frac{b}{y}\right)={b}^{*},\left(\frac{{K}_{{\text{L}}}}{K}\right)={K}^{*},\mathrm{ and }\left(\frac{{t}_{{\text{L}}}}{y}\right)={t}^{*}(\) independent variables).

Model validation

To verify the accuracy of seepage losses obtained from the Slide2 model, the model results were compared to measured field values of a branch canal located in North Al-Hussainiya Plain, Sharqia Governorate, Egypt (MWRI 2021). Figure 3 shows the canal location between latitudes 30° 58′ 33.7″ and 31° 00′ 42.6″ N and longitudes between 32° 04′ 32.7″ and 32° 05′ 23.2″ E. The measured field and Slide2 model values of seepage losses in the unlined and lined sections of the branch canal are shown in Table 1. Results showed that Slide2 model results were similar to the measured field values and thus ensured the accuracy of the Slide2 model regardless of the existence of calculated seepage losses by the model in the lined section that was mere to vanish (near to zero) as the field measured value.

Fig. 3
figure 3

Location of investigated branch canal

Full size image
Table 1 Comparison between the seepage losses measured in the field and Slide2 model
Full size table

Simulation scenarios

After the validation process, a parametric study was conducted to calculate seepage losses from lined trapezoidal irrigation canals with different geometric and hydraulic parameters. Six hundred simulation scenarios were performed using the Slide2 model. The scenarios included different geometric and hydraulic ratios for a trapezoidal irrigation canal. Table 2 shows the ratios of the modeled scenarios.

Table 2 The range of the studied geometric and hydraulic parameters
Full size table

Statistical analysis

Based on the results of the simulated scenarios (i.e., q*), SPSS was used to develop three models for estimating seepage losses from lined trapezoidal irrigation canals based on the results of the Slide2 model. They were NLR, MLP-ANN, and RBF-ANN models, as described later in "Statistical analysis" section. These models were built to investigate their ability to reduce seepage losses estimation for lined trapezoidal irrigation canals. NLR model was chosen to achieve higher accuracy than the linear regression model (Hosseinzadeh Asl et al. 2020; Salmasi and Abraham 2020). The determination coefficient (R2), root mean square error (RMSE), mean average error (MAE), and index of agreement (d) were the statistical parameters used to quantitatively analyze the NLR and ANNs performance. Moreover, MATLAB (R2019a) and its neural modeling application (Neural Network Toolbox; Demuth and Beale 1992) were used to write script code for the ANNs. The following are the expressions (Eqs. 4, 5, 6 and 7) for the statistical parameters mentioned above:

$${R}^{2}=1-\frac{\sum {\left({y}_{i} - \widehat{y}\right)}^{2}}{\sum {\left({y}_{i} - \overline{y}\right)}^{2}}$$
(4)
$${\text{RMSE}}=\sqrt{\frac{1}{N}\times \sum_{i=1}^{N}{\left({y}_{i}-\widehat{y}\right)}^{2}}$$
(5)
$${\text{MAE}}=\frac{1}{N}\times \sum_{i=1}^{N}\left|{y}_{i}-\widehat{y}\right|$$
(6)
$$d=1-\frac{\sum_{i=1}^{N}{\left({y}_{i}-\widehat{y}\right)}^{2}}{\sum_{i=1}^{N}{\left(\left|\widehat{y} - \overline{y}\right|+\left|{y}_{i} - \overline{y}\right|\right)}^{2}}$$
(7)

where \({y}_{i}\) are the estimated values of seepage losses by Slide2 model; \(\widehat{y}\) are the predicted values of the seepage losses by the proposed models, and \(\overline{y}\) is the mean value of the Slide2 model scenarios.

Nonlinear regression model (NLR)

Nonlinear models are simple, interpretable, and predictive (Archontoulis and Miguez 2015; Hosseinzadeh Asl et al. 2020). These models can accommodate a wide variety of mean functions. However, they can be less flexible than linear models (i.e., polynomials) regarding the data they can describe. However, nonlinear models appropriate for a given application can be more parsimonious (i.e., have fewer parameters) and more interpretable. Interpretability comes from associating parameters with a biologically meaningful process (Salmasi and Abraham 2020).

The following steps were used to develop the NLR model. They are (1) q* term was defined as the dependent variable, (2) propose NLR equation, which is a function of the independent variables (i.e., \({b}^{*}, z, {K}^{*},\mathrm{ and }\;{t}^{*}\)), (3) enter the estimation parameters of the proposed NLR equation by assuming the starting value; Levenberg–Marquardt was the used estimation method, (4) Finally, the nonlinear regression analysis was started, and the model results were shown in the output log. By trial and error, the best form of the nonlinear equation developed by the nonlinear regression analysis for the dependent variable \({q}^{*}\) was obtained. Equation 8 was proposed as follows:

$${q}^{*}={\left({b}^{*}\right)}^{a}\times {\left(z\right)}^{b}\times {\left({K}^{*}\right)}^{c}\times {\left({t}^{*}\right)}^{d}\times e$$
(8)

where a, b, c, d, and e are constant parameters. The equation was calibrated using 70% of the scenarios and verified by the remaining 30%.

ANN models

ANN is an Artificial Intelligence machine learning tool that mimics human brain function. ANN can model both linear and nonlinear systems without the implicit assumptions made by most conventional statistical techniques. It has been utilized in numerous scientific and engineering disciplines (Chantasut et al. 2004). ANN is a powerful mathematical modeling tool that can process complex input–output relationships like the human brain. When presented with data patterns, sets of historical input and output data describing the problem are modeled. ANN can map the cause and build relationships between the model input and output data. This mapping of input and output relationships in the ANN model architecture allows engineers to predict the value of the model output parameter with satisfactory accuracy if any reasonable combination of model input data is given. However, the success of an ANN application depends on the quality and quantity of the available data (Haykin et al. 2012).

ANN model has seven major components, collectively known as the ANN architecture. These components are (1) processing units or neurons, (2) a state of activation, (3) an output function for each neuron, (4) a pattern of connectivity or weights between units, (5) a propagation rule for propagating patterns of activities by the weights, (6) an activation function for combining the inputs impinging on a unit with the current state of that unit to produce a new level of activation for that unit, and (7) a learning rule whereby weights are modified by experience (Shayya and Sablani 1998).

Depending on the ANN software employed, the model developer may adjust or modify some of these components. In ANN applications, three stages are considered: training, validation, and testing. The purpose of training a network is to minimize the error between the outputs of the network and target values. Training of the algorithm reduces the error by adjusting the weights and biases of the network. In the training stage, input values are multiplied by respective connection weights, and biases are added. The exact process is repeated for the output layer, where the output of the hidden layer is used as an input for the output layer. In the validation stage, the model performance is evaluated. In contrast, in the test stage, the model is tested to optimize its overall performance.

This study used Multi-Layer Perceptron (MLP) and Radial Basis Function (RBF) neural networks. MLP and RBF networks are the most common feed-forward network type and consist of three layers, namely, input, output, and hidden layers as shown in Fig. 4a and b; (Ghorbani et al. 2016). In the input layer of MLP, neurons only function as buffers for transmitting input signals to neurons in the hidden layer. In RBF, the input layer has neurons with an activation function that feeds the input signals to the hidden layer. Moreover, the connections between the input and hidden layer are not weighted. In the hidden layer of MLP, it computes its output as a function of the sum of its input signals after weighting them with the strengths of their respective connections from the input layer.

Fig. 4
figure 4

a MLP-ANN and b RBF-ANN (Ghorbani et al. 2016)

Full size image

In contrast, in the RBF, the hidden neurons are the processing units that perform the RBF. Similarly, the output of neurons in the output layer of MLP is computed, while in RBF, the output neuron is a summing unit to produce the output as a weighted sum of the hidden layer outputs. The most widely used MLP training algorithm is the Levenberg–Marquardt back-propagation algorithm, which gives the weight of a connection between neurons (Haykin et al. 2012; Jayawardena et al. 1998).

Results and discussions

In this section, the Slide2 model results were demonstrated, the effect of the hydraulic parameters on seepage losses was explored, and the ANNs investigated the importance of each parameter. In addition, the developed nonlinear equation was compared to other proposed models (i.e., MLP-ANN and RBF-ANN). Moreover, MATLAB was used to write down the script code of the ANNs.

Effect of the hydraulic parameters on seepage losses

Lining hydraulic conductivity (K*)

Eight ratios of K* were considered while keeping the t* constant and equal to 0.20. The Slide2 model results showed that the hydraulic conductivity positively correlates with the seepage losses. Figure 5 shows the q* values under different K* and b* ratios when t* = 0.20 and z = 1. Seepage loss reduction percentages due to different K* and b* ratios when t* = 0.20 and z = 1 are shown in Fig. 6. To save space, only the results of z = 1 were presented as the same trend was obtained under other side slopes. Figures show that the lining process becomes useless after a specific hydraulic conductivity (K*) value of the lining material. For instance, a lining layer of (t* = 0.20) can lower seepage losses by a mean percentage of 8.9, 20.4, 67.9, 82.6, 96.2, 97.4, 99.4, and 99.7% for the ratios of K* = 0.5, 0.3, 0.1, 0.05, 0.01, 0.005, 0.001, and 0.0005, respectively. Figure 6 showed that regardless of the canal's inner side slope value, seepage losses were reduced for all b* ratios when the (K*) ratio decreased.

Fig. 5
figure 5

The q* values under different K* and b* ratios when (t* = 0.20) and z = 1

Full size image
Fig. 6
figure 6

Seepage losses reduction under different K* and b* ratios when (t* = 0.20) and z = 1

Full size image

Lining thickness (t*)

To investigate how different lining thicknesses affect seepage losses, five different t* ratios were considered while keeping K* constant and equal to 0.1. The K* value of 0.1 was chosen because it is neither too low nor too high within the investigated range. At K* = 1, seepage losses are mitigated using lining material. Meanwhile, seepage losses nearly vanished at a low K* ratio (i.e., K* = 0.01 or less). Hence, to evaluate the effect of lining thickness on seepage, K* = 0.1 was chosen. Lining thickness negatively correlates to the seepage losses for all investigated b* ratios at z = 1. Figure 7 shows that as t* increases, seepage losses decrease. The percentages of seepage loss reduction corresponding to different t* ratios for all investigated b* ratios are shown in Fig. 8. At K* = 0.1 and z = 1, the average percentage of seepage losses was reduced by 10.6, 22.7, 42.0, 63.4, and 68.5% for t* = 0.02, 0.05, 0.1, 0.15, and 0.2. At every 0.05 increase in the lining layer thickness ratio (t*), seepage losses will decrease by around 15% regardless of the canal's inner side slope. That occurred because water seeps from the same wetted perimeter in each ratio.

Fig. 7
figure 7

The q* values under different t* and b* ratios when (K* = 0.10) and z = 1

Full size image
Fig. 8
figure 8

Seepage losses reduction percentage under different t* and b* ratios when (K* = 0.1) at z = 1

Full size image

Canal inner side slope (z)

Figure 9 shows the average seepage reduction at each K* ratio corresponding to z values. It can be noted that as the canal's inner side slope increases, the seepage losses term q* increase. At t* = 0.20, with every increase in the value of z by 0.5, the mean percentage of seepage losses can be reduced by 12.1, 23.3, 67.8, 84.5, 96.1, 97.3, 99.3, and 99.7% for the ratios of K* = 0.5, 0.3, 0.1, 0.05, 0.01, 0.005, 0.001, and 0.0005, respectively. Figure 10 shows the average seepage reduction at each t* ratio corresponding to different z values. At K* = 0.10, with every increase in the value of z by 0.5, the mean seepage losses reduction percentages are 9.93, 22.6, 41.4, 61.1, and 67.8% for the case of tL/y = 0.02, 0.05, 0.1, 0.15, and 0.2, respectively. Regardless of the b* ratio, as the K* ratio gets lower and the t* ratio gets higher, the seepage losses decrease at all z values. However, when the side slopes are flat, there is more seepage than the steep side slopes. That happens because flattening the side slopes creates a long-wetted perimeter.

Fig. 9
figure 9

Seepage losses reduction percentage under different K* ratios and z values when (t* = 0.20)

Full size image
Fig. 10
figure 10

Seepage losses reduction percentage under different t* ratios and z values when (K* = 0.10)

Full size image

Statistical models

NLR model

To ensure the best fit to the Slide2 model results in seepage losses estimation from trapezoidal lined irrigation canals, the multi-variable nonlinear regression model (NLR) developed a nonlinear equation and estimated the values of the proposed parameters (i.e., a, b, c, d, and e), and by substitution in Eq. (8), the developed nonlinear equation (Eq. 9) can be written as follows:

$${q}^{*}={4.791\times \left({b}^{*}\right)}^{0.423}\times {\left(z\right)}^{0.265}\times {\left({K}^{*}\right)}^{0.422}\times {\left({t}^{*}\right)}^{-0.166}$$
(9)

MLP-ANN model

In this model, the scenarios were divided randomly in the training, validation, and testing stages as 79.3, 9.5, and 11.2%, respectively. By trial and error, four hidden neurons were used. The hyperbolic tangent and linear functions were used as activation functions in the hidden and output layers, respectively, to obtain the best MLP-ANN of architecture (21-4-1).

RBF-ANN model

In this model, the scenarios were divided randomly in the training, validation, and testing stages as 91.2, 5.2, and 3.8%, respectively. By trial and error, forty-three hidden neurons were used. The SoftMax and linear functions were used as activation functions in the hidden and output layers, respectively, to obtain the best RBF-ANN of architecture (21-45-1).

Importance of the investigated parameters by ANNs

Figure 11 showed the importance of each independent variable was investigated by ANNs that the dependent variable (i.e., q*) was affected by the independent variables (i.e., b*, z, K*, and t*) values by 27.8, 7.9, 100.0, 26.1%, respectively. ANN's results showed that seepage was highly affected by the lining's hydraulic conductivity but was lightly affected by canal geometry and lining thickness. However, the side slope was the least important to the seepage loss estimation. Thus, the results agree with the results of the Slide2 model.

Fig. 11
figure 11

Importance percentage of each input

Full size image

Performance of models

In this section, the comparison between the proposed models was investigated to obtain the best model. Table 3 shows the calculated statistics parameters for each model. Figure 12a–c showed the correlation between the Slide2 numerical model and the three proposed models (i.e., NLR, MLP-ANN, and RBF-ANN), respectively. Results indicated that MLP-ANN and RBF-ANN were the best models for estimating seepage discharges in lined trapezoidal canals with different geometric and hydraulic parameters. That happened because ANNs had the highest R2 and d with the least RMSE and MAE. However, the NLR model can be applied in seepage estimation for trapezoidal lined irrigation canals as an alternative technique with a considerable difference in the seepage loss values.

Table 3 Statistical parameters of the proposed models
Full size table
Fig. 12
figure 12

a q*(NLR) vs q* (Slide2), b q*(MLP-ANN) vs q* (Slide2), c q*(RBF-ANN) vs q* (Slide2)

Full size image

ANN developing via MATLAB

Figure 13 shows the programming procedure of ANN and the generated script code was developed. However, the following steps were applied sequentially:

  • Defining data in matrix form as (x = “Input'” and t = “Output'”).

  • Choosing a training function; (trainFcn = 'trainlm'; LM = 'trainlm'; %Levenberg–Marquardt).

  • Creating a fitting network by defining hidden layer size;

  • (hiddenLayerSize; net = fitnet(hiddenLayerSize,trainFcn)

  • Setting up the division of data for training, validation, and testing stages (net.divideParam.trainRatio; net.divideParam.valRatio; net.divideParam.testRatio)

  • Training the network; [net,tr] = train(net,t,y)

  • Testing the network; y = net(x); e = gsubtract(t,y); performance = perform(net,t,y)

  • Viewing the developed network; view(net)

Fig. 13
figure 13

Flow chart of ANN programming

Full size image

Conclusions and recommendations

In this study, the applicability of three models (NLR, MLP-ANN, and RBF-ANN) in estimating seepage losses from lined trapezoidal irrigation canals was investigated based on the scenarios conducted by the Slide2 numerical model. Consequently, the models’ results were compared with the Slide2 model results to obtain the best model.

Based on the results, the following conclusions can be drawn:

  • The Slide2 model was reliable in estimating seepage losses from unlined and lined trapezoidal irrigation canals compared to measured field data.

  • The ability of the lining to reduce seepage from the canal is affected by its hydraulic conductivity and thickness, in which the seepage losses were highly increased as the lining's hydraulic conductivity increased. In contrast, the lining thickness causes a noticeable reduction in seepage losses. Nevertheless, the canal's side slope had a low impact on the seepage.

  • The NLR, MLP-ANN, and RBF-ANN models can all be used to estimate seepage losses from lined trapezoidal irrigation canals.

  • The MLP-ANN and RBF-ANN models performed better than the NLR model with R2 of 0.996 and 0.965; RMSE of 1.172 and 0.699; MAE of 0.139 and 0.528; d of 0.999 and 0.991, respectively.

  • The NLR model can be applied in seepage estimation for lined trapezoidal irrigation canals as an alternative technique with a significant difference in the seepage losses with R2 of 0.906, RMSE of 1.198, MAE of 0.942, and d of 0.971.

  • ANNs models are recommended as a robust and rapid tool for estimating seepage losses from trapezoidal irrigation canals with different geometries and lining materials.

Further research is recommended to develop an ANN model to estimate seepage losses for lined canals with different shapes. Moreover, to investigate the effect of shallow groundwater tables on seepage losses for unlined and lined irrigation canals.