Introduction

The water crisis in many countries is one of the main concerns for future communities. Iran is located in an arid desert belt (Zamani et al. 2019), and water resources are wasted due to the lack of use of advanced technologies. Many experts believe that water management in Iran is not good enough and causes a severe reduction in water and some areas under agricultural cultivation.

Estimating reference crop evapotranspiration (ET0) is one of the most critical issues in irrigation planning, water budgeting, crop planning, and integrated management of agricultural systems (Pooralibaba and Shiri 2012). The water requirement of plants is determined in two ways: directly and indirectly. In the direct method, the crop is planted in a box or lysimeter, and its water requirement is measured by weight or water balance method. Due to the difficulty and cost of direct measurement, the indirect method is usually used. In this method, presented by the World Food and Agriculture Organization (FAO), the water requirement or evapotranspiration of the plant is determined in two stages.

The FAO standard defines reference crop evapotranspiration as the amount of water required by the surface area covered by the reference crop over a specific time period. A hypothetical grass with an assumed height of 0.12 m, a set surface resistance of 70 s/m, and an albedo of 0.23 serves as the reference surface. The plants will be protected from water stress during the growing season if the amount of ET0 is known and this amount of water is provided. Evapotranspiration is affected by various variables, including air temperature, wind speed, and solar radiation. In other words, transpiration from a wide surface was covered with green grass or alfalfa with a uniform height of about 12 cm and active growth, with full shading on the ground, without facing water shortage (Faqih 2015).

The quantity of meteorological parameters needed is the fundamental distinction between the many models that have been suggested to predict evapotranspiration. These models range from equations requiring only the air temperature component, such as Torrit White and Blaney–Criddle, to more intricate equations, like FAO Penman–Monteith, which also need relative humidity, wind speed, and solar radiation. These equations need to be calibrated and evaluated for use in different climatic conditions. According to research using the FAO Penman–Monteith, two elements—temperature and solar radiation—play a significant impact on evapotranspiration in dry areas, whereas other aspects are of secondary significance (Gorji and Raeini-Sarjaz 2016). Almorox et al. (2018) conducted work that demonstrates that a Penman–Monteith temperature formula may be used when only recorded maximum and minimum air temperature data exist, which is useful when all the meteorological data required for calculating the ET0 are not accessible.

Kovoor and Nandagiri (2018) used Monte Carlo (MC) simulations to assess the sensitivity of the FAO-56 Penman–Monteith reference evapotranspiration (ET0) model to the climatic variables used in its application. The analysis resulted in the sensitivity of the ET0 values to the various input parameters. Except for the humid station, where net radiation (Rn) was shown to be critical, wind speed was found to be the essential input variable at all other stations. This study’s findings provide information for estimating the consequences of forthcoming climate changes.

In recent years, an adaptive neural-fuzzy inference system model has been created to handle several difficulties connected to the mathematical modeling of phenomena such as water and soil. Artificial intelligence systems have found many applications in various water engineering issues where there is no clear relationship and pattern between the factors affecting the occurrence of a phenomenon. Artificial neural networks (ANN) and adaptive neuro-fuzzy inference systems (ANFIS) were used to calculate reference crop evapotranspiration. Also, hybrid models are designed to combine the strengths of different models and improve their overall performance. Elbeltagi et al. (2022) conducted research comparing the performance of five AI-based models for estimating reference evapotranspiration (ET0) and evaluated the best-yielding algorithms at three different stations in India. Based on the study’s results, AI-based hybrid meta-heuristics algorithms are promising approaches for estimating ET0.

Artificial intelligence (ANN) and (ANFIS) systems, along with experimental equations, were used by Karimi et al. (2013) to examine daily reference crop evapotranspiration estimates. The findings show that neural-fuzzy models are highly accurate at predicting the reference crop’s daily evapotranspiration (water need), with RMSE values ranging from 0.276 to 0.437 mm. Additionally, compared to experimental equations, artificial neural network models with RMSE values between 0.298 and 12.5 mm performed better. Feng et al. (2017) presented two models in their study for daily ET0 calculation: generalized regression neural networks (GRNN) and random forests (RF). Meteorological data between 2009 and 2014 from two sites in southwest China were used to train and test RF and GRNN models. This included minimum and maximum temperature, relative humidity, wind speed, and solar radiation data. Two input combinations were used: entire data and just temperature and extraterrestrial radiation (Ra) data. The findings suggest that temperature-based RF and GRNN models can accurately estimate daily ET0 in southwest China. Ghorbani et al. (2016) evaluated the performance of three models (multilayer perceptron, feedforward neural network, and minimum error neural network) to estimate the evapotranspiration of a reference crop at the Ahvaz station. Data that had not been utilized in the network’s testing and training were used to assess the models’ capacity to predict the reference crop’s evapotranspiration. It was discovered during the investigations that using the average daily temperature parameter as an input made it merely possible to predict the reference crop evapotranspiration using three different types of models with a respectable level of accuracy.

Additionally, it was discovered that FF and MLP models with higher R2 are more accurate than MNN in determining the reference crop evapotranspiration by comparing the outcomes of the three models with statistical testing. The effectiveness of hybrid wavelet-ANN and wavelet-ANFIS models for approximating daily ET0 was examined by Patil and Deka (2017). The study was conducted in an arid region. Based on R = 0.96 and RMSE = 0.632 mm/day, the W-ANN2 model was shown to be the most accurate for estimating daily ET0. The second-level db3 wavelet-decomposed subseries of temperature and the values of the previous day’s evapotranspiration were the inputs used in the suggested W-ANN2 model.

Given the importance of estimating the ET0 and the limited data, this paper investigates the ET0 using an artificial intelligence model in arid climates such as Iran with the help of an adjacent station. This study aims to compare three machine learning models, ANN, ANFIS, and the novel hybrid model of ANN-GWO, for estimating ET0 in an arid region while incorporating extrinsic data to improve the accuracy of the models. Also, specific combinations and data sources have been chosen to study the aspect of the limited dataset.

Materials and methods

The study area

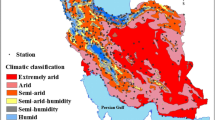
Monthly data on climatic conditions were gathered from two locations in Iran: Kerman, with a latitude of 30°15′N and a longitude of 56°58′E, and Sirjan, with a latitude of 29°28′N and a longitude of 55°41′E. The approximate location of the study site is shown on the map of Iran (Fig. 1). The dataset included geographic information such as latitude, longitude, and altitude for each station, as well as meteorological data including minimum and maximum temperature (Tmin and Tmax), dew point or relative humidity temperature, wind speed (U2), and radiation hours (Rs). The dataset covered the period from 1987 to 2017.

Fig. 1
figure 1

a Shows the location of Iran in the Middle East. Iran is located between latitude 25.05°N and 39.78°N and longitude 44.03°E and 63.34°E. b Shows the location of the studied stations in the Kerman province

Full size image

According to the UNEP index (1), both Kerman and Sirjan synoptic stations are in an arid climate.

$$R = \frac{P}{{{\text{ETP}}}}$$
(1)

Arid and semiarid regions’ general characteristics are low rainfall, high temperatures, and hence high evaporation (Buol 1977). Sirjan and Kerman stations, as shown in Table 1, have a maximum of 39 °C and 38 °C, respectively, and ET0 of 9 mm/day. The statistical properties were calculated for each climatic parameter (Tmin, Tmax, U2, Rs, and ET0), and the results are shown in Table 1.

Table 1 An overview of the statistical characteristics
Full size table

Max, Min, Mean, Cv, and Csx in Table 1 represent each parameter’s maximum, minimum, mean, variation coefficient, and skewness. The results show that Sirjan and Kerman have similar statistical properties, so it is proper to use these two stations. This may be due to the weather stations’ proximity (about 65 km apart). Also, ET0 is most correlated with minimum temperature for both stations, followed by maximum temperature and solar radiation.

The FAO Penman–Monteith method

A procedure prescribed in FAO-56 chapter 3 was followed to calculate all data needed to calculate weekly ET0 (Allen et al. 1998). The FAO Penman–Monteith equation has been proposed as the only standard method for calculating reference crop evapotranspiration as well as for evaluating other methods. This equation is as follows.

$${\text{ET}}_{0} = \frac{{0.408\Delta \left( {R_{{\text{n}}} - G} \right) + \gamma \frac{900}{{T + 273}}u_{2} \left( {e_{{\text{s}}} - e_{{\text{a}}} } \right)}}{{\Delta + \gamma \left( {1 + 0.34u_{2} } \right)}}$$
(2)

These results are placed as training goals for modeling using artificial neural network (ANN) and fuzzy neural adaptive inference system (ANFIS) and comparing with the classic Hargreaves–Samani method.

Hargreaves–Samani method

The ET0 was computed by the HS equation (Hargreaves and Samani 1985) (3). The method is frequently applied for computing ET0 (mm/unit time) and requires only temperature (minimum and maximum) and extraterrestrial radiations that might be found in very metrological stations (Ali Shah 2022).

$${\text{ET}}_{0} = C \times R_{{\text{a}}} \times \left( {T_{{{\text{mean}}}} + a} \right) \times \left( {T_{\max } - T_{\min } } \right)^{{\text{m}}}$$
(3)

In this relation, m, a, and c are coefficients with the amount of 0.0023, 17.8, and 0.5, respectively. Ra is extraterrestrial radiation (mm/day). Tmean is the average air temperature (degrees Celsius). Tmin and Tmax are, respectively, maximum and minimum air temperature (°C), and ET0 is the evaporation and transpiration potential of the reference plant (mm/d).

Artificial neural network (ANN)

A neural network is an adaptable system that consists of multiple basic processing units modeled after the neural network of the brain. The processing components, or neurons, work together to form a processing pathway. These processing elements are usually arranged in layers with regular patterns so that there are complete or random connections between the layers. The input layer functions as a processor, delivering processed input data to the network. The input layer is not a computational neural layer because its nodes have neither an input weight nor an activation function. The last layer is the output layer, which shows the network’s output in response to a specific input. The other layer is called the hidden layer or the middle layer. This layer is called hidden because there is no connection between it and the output layer (Karbasi 2016).

The majority of artificial neural network models (which are computational methods) employ a mathematical model of a nerve cell known as a neuron or perception, and the neuron is the neural network’s smallest building unit. Several neurons are coupled via weighted connections inside each of the layers. In this definition, layers stand for three layers that every network is made up of. These three layers are input layer, output layer, and one or more intermediate (hidden) layers. When the training of the network begins, recognizing the intrinsic relationships between data tries to provide a mapping between the input space (input layer) and the desired space (output layer), and the weights sequentially change in order to find the lowest error (Faghih 2015; Sabzi Parvar and Bayat Varkashi 2011).

Artificial nerves or neurons are the main components of a neural network (4). The input pattern to a node is similar to a biological cell, which can be represented by vectorization of the M component as X = (x1, x2, …, xm). The scalar variable S represents the total of the inputs multiplied by their weights.

$$S = \mathop \sum \limits_{m = 1}^{M} w_{m} x_{m} = W^{T} X$$
(4)

In the above equation, W = (w1, w2,…, wm) is the weight vector of neurons. The quantity s is then fed into a nonlinear function f to produce the output.

In this study, the dataset is divided into 90% for training, 5% for testing, and 5% for validation. The training of the artificial neural network is to change the weights in such a way that the error is minimized and the difference between the target value and the output is reduced.

Fuzzy neural adaptive inference system (ANFIS)

Fuzzy neural models were developed by Jang in 1993, combining fuzzy logic with artificial neural networks to aid in learning and adaptability. In reality, an adaptive network is employed in fuzzy-neural models to handle the challenge of identifying the parameters of the fuzzy inference system, which is the general state of the multilayer leading neural network.

The model can build a decent link between input and output variables due to the training capabilities of artificial neural networks. As a consequence, the adaptive neural-fuzzy inference system is introduced as a strong tool for forecasting results using current numerical data by combining the usage of a fuzzy inference system with the artificial neural network. ANFIS creates a nonlinear mapping between input space and output space using neural network methods and fuzzy logic.

Hybrid ANN-gray wolf optimizer algorithm (ANN-GWO)

Optimizing the weights and biases is crucial in training an artificial neural network (ANN). The weights and biases are typically randomly adjusted within the range of [− 1, 1]. After applying activation functions in the hidden and output layers, the weight of each neuron is computed for the next iteration. The output is then calculated using the following formula (Tikhamarine et al. 2019):

$${\text{ET}}_{0} = F_{o} \left[ {\mathop \sum \limits_{i = 1}^{m} W_{kj} \times F_{h} \left( {\mathop \sum \limits_{i = 1}^{n} W_{ji} X_{i} + b_{jo} } \right) + b_{ko} } \right]$$
(5)

Here, ET0 signifies the reference evapotranspiration estimation. Fo and Fh stand for the activation functions of the output and hidden layers, respectively. i, j, and k are representative of the input, hidden, and output layers, in that order. Wkj and Wji, respectively, symbolize the weights in the output and hidden layer connections. Xi denotes the input variables, while bjo and bko indicate the biases for the hidden and output layers, respectively. Additionally, the number of inputs and hidden neurons is represented by n and m, respectively. Figure 2 illustrates the flow architecture of the ANN-GWO model.

Fig. 2
figure 2

Social hierarchy of wolves in GWO

Full size image

Preparation of dataset

The input data comprise meteorological data from the meteorological station, and the output data include data from the Penman–Monteith technique. Eighty percent of each station’s total data is utilized for network training (1987–2011), while the remaining data (2011–2017) are also used for network testing. Using these data, reference crop evapotranspiration is estimated using the FAO’s standard Penman–Monteith technique. These control variables will be used to validate other models’ correctness (Feng et al. 2017).

Because acquiring all of the meteorological data required to compute FAO-PM can be costly, it is common practice to operate with restricted datasets (Althoff and Rodrigues 2022). For testing the models in the optimal conditions, the dataset that is most common in different stations and also more accessible has been chosen.

To model the methods based on artificial intelligence, using MATLAB software, different input combinations that are shown in Table 2 are performed for each station by artificial neural network (ANN), fuzzy neural adaptive inference system (ANFIS), and ANN-gray wolf optimization (ANN-GWO) methods, to identify the best models in the condition of limited data.

Table 2 Model inputs were classified into three combinations
Full size table

In the combination shown in Table 2Tmin and Tmax are assumed to be the most common and accessible climatic data, and in the condition of limited data in one station, getting help from an adjacent station is chosen to be tested in this study (although as shown in Table 1, Sirjan and Kerman have similar statistical properties).

Criteria for evaluating the accuracy of artificial intelligence models

Indicators that evaluate the performance of each network and its ability to accurately predict include roots mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (R2). The more (RMSE) and (MAE) to zero and (R2) to one desire, the better answer will be created for the model (Gharekhani et al. 2017).

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {vul_{i} - v\overline{u}l_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {vul_{i} - \overline{{vul_{i} }} } \right)^{2} }}$$
(6)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{\left( {vul_{i} - v\overline{u}l_{i} } \right)^{2} }}{{v\overline{u}l}}} \right)}$$
(7)

Results and discussion

The present study evaluated the ability of ANN, ANFIS, and the performance of novel hybrid models of ANN-GWO to estimate the reference crop evapotranspiration rate for Kerman Station as the current station with a limited dataset, and Sirjan was the adjacent station. In the end, although all three methods have acceptable results, as shown in Table 3, the ANFIS method can estimate the evapotranspiration rate better than the other two.

Table 3 The performance of the models in the presence of insufficient data for the Kerman station
Full size table

Between combinations, by using the external data, models have better results (Table 3). It will have better results when the minimum temperature and maximum temperature of the current station are used together with the ET0 of the adjacent station. Then in the second, the use of wind speed data of the current station with the ET0 of the adjacent station has the better result. In the last, the use of the air temperature station is suggested.

The process repeated for Sirjan station as a current station with a limited dataset (Table 4).

Table 4 The performance of the models in the presence of insufficient data for the Sirjan station
Full size table

Sirjan station has the same result as the Kerman station. ANFIS method showed better performance, and combination 2 was the suggested dataset (Table 3).

The findings presented in Tables 3 and 4 emphasize that the incorporation of external data has the capacity to enhance the outcomes across all test cases.

RMSE of combination 1 (without external data) in ANN, ANFIS, and ANN-GWO in both stations is approximately near 0.5, which is high in comparison with the other two combinations. The lower the RMSE, the better a given model is able to fit a dataset, and in contrast, when the RMSE is high, it shows that the data are overfitted and so have little predictive value when tested out of the sample. However, it is imperative to note that all three models yield outcomes that are deemed acceptable.

Also, as shown in Tables 3 and 4, the ANFIS method has higher accuracy than the ANN method in estimates in case of limited climatic data in all three cases of input data. The ANFIS method with combination 2 (Tmin, Tmax of the current station and ET0 of the adjacent station) in both stations of Kerman and Sirjan, respectively, with errors of 0.112 and 0.127 has the best results (Figs. 3 and 4).

Fig. 3
figure 3

Regression of the ANFIS method with combination 2 in Kerman station

Full size image
Fig. 4
figure 4

Regression of the ANFIS method with combination 2 in Sirjan station

Full size image

As shown in Figs. 3 and 4, models have a good result in the chart of test data in both Kerman and Sirjan stations with the R of 0.97 and 0.96, respectively.

Lastly, the findings were compared to the standard Hargreaves–Samani technique, as shown in Figs. 5 and 6

Fig. 5
figure 5

Experimental Hargreaves–Samani method with Kerman’s climatic data

Full size image
Fig. 6
figure 6

Experimental Hargreaves–Samani method with Sirjan’s climatic data

Full size image

Since Hargreaves–Samani is frequently used when there is only a need for temperature (minimum and maximum), and extraterrestrial radiation, its results also get compared in the end. With R of 0.88 for Kerman (Fig. 5) and R of 0.81 for Sirjan (Fig. 6), the results have been acceptable.

In comparison with three combinations, combination 2 (Tmin, Tmax of the current station and ET0 of the adjacent station) had the best results, which is why it is only discussed in Table 5.

Table 5 Final results of the three methods for each station for the combination 2
Full size table

According to Table 5, under limited data conditions, the ANFIS method provides more accurate results for estimating ET0 compared to ANN. Regarding the ANN-GWO hybrid model, although it aims to combine the strengths of different models and enhance their overall performance, the success of a hybrid model depends on the specific problem being addressed and the compatibility of the combined models. In this case, the ANN and ANFIS models already exhibited close-to-optimal performance, and the addition of the GWO optimization algorithm did not significantly improve their performance. Additionally, a study conducted by Seifi and Soroush (2020) in different climates of Iran, specifically Isfahan, an arid region similar to Kerman, demonstrated that in the comparative evaluation of ANN and ANN-GWO, ANN exhibited superior performance. Therefore, it can be inferred that in arid regions, although the ANN-GWO model produces acceptable results (as shown in Table 5), its performance is weaker compared to that of ANN and ANFIS.

It is important to emphasize that the novel hybrid model, the ANN-GWO method, may not be applicable in all scenarios. The findings of this study suggest that the ANN-GWO method may not consistently outperform other modeling approaches, emphasizing the necessity for ongoing evaluation and optimization.

Conclusion

In this study, an attempt was made to assess the effectiveness of modeling the process of estimating reference evapotranspiration (ET0) using an extreme learning machine. The viability of incorporating ET0 data from an external synoptic station as additional inputs to enhance the accuracy of evapotranspiration modeling was explored. Emphasis was placed on evaluating the statistical comparability between stations to ensure the reliability of the findings. The investigation revealed insights, particularly regarding input parameter selection. Among the various permutations evaluated, it became evident that the most accurate results were obtained when the ANFIS model utilized both the minimum and maximum temperature parameters from the present station, in combination with the ET0 data from a nearby station (combination 2). This finding underscores the value of merging intrinsic and extrinsic data sources to enhance the precision of modeling endeavors.

The study found that using the minimum and maximum temperatures, which are relatively easier to measure, in both ANFIS and ANN methods in both stations responded better to the empirical Hargreaves equation method. Additionally, the use of external data such as wind speed and ET0 of the adjacent station improved the accuracy of the models. The ANFIS method was found to have higher accuracy than ANN in all three cases of input data. The ANFIS method with the minimum and maximum temperatures and ET0 of the adjacent station in both stations of Kerman and Sirjan, respectively, with RMSE of 0.33 and 0.36, had the best results.

The integration of external data into the models not only demonstrates its viability but also emphasizes its potential utility, particularly in regions where limited weather station coverage is a challenge. Developing nations, often facing issues with sparse weather station networks capable of directly measuring ET0, can potentially derive significant benefits from these enhanced models, offering an alternative means of estimating this crucial parameter. However, it is imperative to acknowledge the ongoing evolution of scientific inquiry. While the findings present a promising avenue, the journey toward refining and fully harnessing the potential of these hybrid models is only in its nascent stages. Further investigations could delve more deeply into the intricacies of data fusion, model calibration, and validation techniques. Additionally, careful consideration is warranted regarding the models’ sensitivity to variations in geographic and climatic conditions to ensure robust applicability.

Overall, the passage highlights the importance of estimating ET0 for water resources management and crop growth control, especially in areas with limited climatic data. The study demonstrates the effectiveness of using minimal input data and ANFIS and ANN models to estimate ET0, with the ANFIS method being more accurate. The findings of the study have implications for improving water management and crop production in arid regions.