Introduction

A variety of compounds are slowly becoming prominent as contaminants that enter aquatic bodies through municipal and industrial wastewater (Gondi et al. 2022). These include pesticides, disinfectant byproducts, and antibiotics (Pirsaheb et al. 2013; Esmaili et al. 2023). According to the World Health Organization, 25% of water pollution is attributed to pharmaceutical products. With the rapid growth of the population and the development of agriculture, various types of antibiotics have been produced (Weidner et al. 2021). The widespread use of antibiotics can lead to allergic reactions, adverse effects, and the development of antibiotic-resistant microorganisms (Li et al. 2022). Antibiotics exist in surface water, groundwater, sewage, drinking water, and food products (Juela 2021). Even at low concentrations, these pollutants have a negative effect on the environment, ecosystem, human health, and drinking water quality (Hena et al. 2020). Certainly, antibiotics have revolutionized modern medicine and are effective in treating bacterial infections. However, they can also have negative effects on health. One of the most significant concerns regarding antibiotics is the emergence of antibiotic resistance. Overusing antibiotics can result in the development of antibiotic-resistant bacteria that are difficult to treat and can quickly spread. This can lead to serious infections that are difficult to treat and may even be life-threatening (Esmaili et al. 2023). Antibiotics can disrupt the natural balance of bacteria in the gut. The gut harbors a complex ecosystem of microorganisms that play a crucial role in digestion and overall health. Antibiotics can disrupt the delicate balance of microorganisms in the gut, potentially leading to digestive problems such as diarrhea, as well as other health issues. Some individuals may also develop allergic reactions to specific antibiotics (Zahmatkesh Anbarani et al. 2023). MDZ is an antibiotic used for treating infections (Sepehr et al. 2017). Due to its high solubility and poor biodegradability, this antibiotic is commonly found in water bodies (Fang et al. 2011).

Common treatment methods are ineffective in removing antibiotics from urban and industrial wastewaters. Therefore, these pollutants enter the water environment in large quantities (Berges et al. 2021). Today, researchers are exploring new techniques to eliminate emerging pollutants and mitigate their toxic effects on aquatic environments (Ighalo et al. 2020). Various techniques have been employed to remove different antibiotics, including ion exchange resin (Wang et al. 2017), electrocoagulation (Zhou et al. 2022), ozonation (Nasuhoglu et al. 2012), advanced oxidation processes (Lima et al. 2020), membrane technology (Nasrollahi et al. 2022), and ultrafiltration (Li et al. 2022). Adsorption-based processes are more interesting compared to other techniques because of their advantages, such as high efficiency, low cost, availability, profitability, and ease of operation (Gu et al. 2019). These processes are typically effective in eliminating various pollutants from water-based solutions (Juela 2021). RM generally consists of oxides and hydroxides of aluminum, silica, iron, calcium, and titanium (Wang et al. 2005). RM has been used to remove various environmental pollutants (Tor et al. 2006). Tandekar et al. (2021) effectively removed several anions, including phosphate, chromate, and fluoride ions, using a combination of red mud and chitosan (Tandekar et al. 2021). In previous studies, RM has been utilized to eliminate phenol (Tor et al. 2009), copper (Nadaroglu et al. 2010), and trace elements (da Conceição et al. 2021). RM is a mixture of metal oxides that acquires a positive charge through hydroxylation in aqueous environments (Aydin et al. 2019). Given the abundance of red mud and the valuable materials it contains, the primary objective of this research is to explore the use of red mud as an efficient and cost-effective adsorbent for removing MDZ from water environments. The research findings were analyzed using Langmuir, Freundlich, and Temkin isotherms, as well as pseudo-first-order, pseudo-second-order, and intraparticle diffusion kinetics. The study investigated the impact of various factors, such as pH, contact time, adsorbent dose, and initial MDZ concentration, on the removal efficiency.

Materials and methods

Materials

Metronidazole with a purity of 99% was purchased from Dana Pharmaceutical Company in Iran. RM was purchased from Alumina Company in Iran. All chemicals were obtained from Merck in Germany. Double-distilled water was used to prepare all solutions.

Preparation of red mud

Initially, RM was treated with 1N nitric acid for 24 h. The modified RM was then washed with distilled water to remove any excess acid, dried at 150 °C for 4 h, and sifted through a 100 mesh sieve (Shirzad-Siboni et al. 2014).

Characteristics The characteristics of MRM particles were investigated by FTIR, FESEM, EDX, DLS, and zeta potential tests.

Preparation of reaction mixtures

MDZ removal was performed under different laboratory conditions. To prepare for laboratory experiments, we first created a stock solution of MDZ at a concentration of 100 mg/L. This was achieved by dissolving 0.1 g of MDZ powder in 1000 mL of distilled water. The main laboratory factors, including contact time (10–60 min), pH (4–10), initial MDZ concentration (5–80 mg/L), and MRM dose (0.1–0.7 g/L), were investigated. Sodium hydroxide solution and sulfuric acid were used to adjust the pH of the samples. Table 1 displays the range of primary parameters utilized for MDZ removal. The samples were stirred using a shaker at a speed of 300 rpm. After completing the tests, 10 cc samples were collected from the laboratory solutions. These samples were then centrifuged for 10 min at 5000 rpm to separate the adsorbent from the suspension. The resulting supernatant was filtered through a 0.22 µm filter. Finally, the concentration of MDZ in suspension was measured using a spectrophotometer at λmax of 320 nm. The MDZ removal rate can be calculated using the formula (Zambrano et al. 2021; Mpelane et al. 2022):

$$\text{MDZ removal }(\mathrm{\%}) =\frac{\left({\mathrm{C}}_{0}-\mathrm{Ce}\right)\times 100}{{\mathrm{C}}_{0}}$$
(1)

where C0 represents the initial concentration of MDZ (mg/L) and Ce represents the concentration of MDZ in the treated solution after a specified period of time.

Table 1 Range of key parameters for MDZ removal
Full size table
$${\mathrm{q}}_{\mathrm{e}}=\frac{{(\mathrm{C}}_{0}-{\mathrm{C}}_{\mathrm{e}})}{\mathrm{m}}\times \mathrm{V}$$
(2)

The equation is as follows: W/V = mass of red mud (in grams) divided by the volume of the reaction mixture (in liters).

Adsorption kinetic and isotherm studies

Adsorption kinetics can be used to investigate the reaction rate, the variables that affect the reaction rate, and the transport behavior of the particles of the adsorbed substance. To achieve this goal, a reaction mixture was prepared with a concentration of 20–80 mg/L of MDZ, a contact time of 5–60 min, a pH of 5, and an MRM dose of 2.5 g/L. After conducting the tests, the removal rate of MDZ was assessed. Kinetic equations, such as the pseudo-first-order, pseudo-second-order, and intraparticle diffusion models, were calculated (Bonyadi et al. 2023). In the next step, adsorption isotherms were measured to describe how the amount of solute affects the adsorbent. For this purpose, the study results were evaluated using Langmuir, Freundlich, and Temkin adsorption isotherms (Bonyadi et al. 2022a, b).

Langmuir isotherm

Langmuir's isotherm is applicable when the surface is monolayer and homogeneous adsorption occurs. The Langmuir isotherm is as follows (Bonyadi et al. 2022a, b).:

$$\frac{Ce}{{Qe}} = \frac{1}{{b \times Q_{Max} }} + \frac{Ce}{{Q_{Max} }}$$
(3)

In this formula, Qmax is the maximum sorption capacity (mg/g), Qe is the equilibrium sorption capacity, and b is the Langmuir constant (L/mg) (Bonyadi et al. 2022a, b).

Freundlich isotherm

The effects of several variables, including the heterogeneity and energies of active sites following an exponential distribution, are assumed through an experimental model (Yoosefian et al. 2017). Freund The Freundlich isotherm is as follows:

$$lnq_{e} = lnk + \frac{1}{n}lnCe$$
(4)

In this formula, qe represents the adsorption capacity at equilibrium (mg/g), while kf denotes the Freundlich constant (L/g) (Nasoudari et al. 2021).

Results and discussion

Characterization

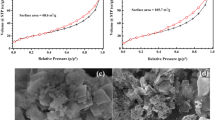
FESEM FESEM analysis was used to evaluate the morphology and surface characteristics of the adsorbent. Figure 1a–b indicates FESEM images of RM and MRM. The FESEM image displays RM particles with an agglomerated and slightly rough surface (Fig. 2a). After modifying the red mud with acid (Fig. 2b), the porosity and pores on the adsorbent surface are significantly increased. This modification enhances the adsorption capacity of the material, allowing it to effectively capture more MDZ antibiotic.

Fig. 1
figure 1

FESEM images of mud red (a) and modified mud red (b)

Full size image
Fig. 2
figure 2

FTIR spectrum of before (mud red a and modified mud red b) and after c adsorption

Full size image

FTIR FTIR was used to analyze and identify the functional groups present on the surface of the adsorbent. The results of the FTIR analysis are shown in Fig. 2. Focusing on Fig. 2a, we can see that the FTIR spectrum comprises various bands. The following bands are observed at the corresponding wavenumbers: 432 cm−1, 571 cm−1, 686 cm−1, 878 cm−1, 998 cm−1, 1119 cm−1, 1433 cm−1, 1629 cm−1, 1797 cm−1, 3433 cm−1, and 3530 cm−1. The band observed in the range of 3433–3530 cm-1 is associated with O–H groups. The peaks observed at 998 cm−1, 443 cm−1, and 1433 cm−1 correspond to Si(Al)–O, Fe–O, and carbonate groups, respectively (Smičiklas et al. 2013). After the acidic modification of RM, a strong band at 1415 cm−1 was observed due to the stretching of the C=O bond. However, this band was reduced by the dissolution of CaCO3 caused by the addition of acid to RM (Deihimi et al. 2018). The spectrum of RM showed the absence of Al–O and Fe–O bonds, possibly due to the dissolution of Fe and Al oxides/hydroxides (Fig. 2b). After the removal of MDZ, the C=C bond shifted to 1570 cm−1 as shown in Fig. 3C. (Theamwong et al. 2021).

Fig. 3
figure 3

EDX spectrum of modified mud red

Full size image

EDX, DLS, and zeta potential

EDX, DLS, and zeta potential analyses were used to determine the main elements, the size of adsorbent, and the effective electric charge on the adsorbent surface. Figure 3 shows the EDX analysis of MRM. According to the EDX image (Fig. 3), the composition of MRM was found to be 49.03% carbon, 32.13% oxygen, and 15.33% nitrogen. Table 2 displays DLS and zeta potential data for RM and MRM. According to Table 2, the average diameter of RM and MRM was found to be 1182 nm and 1202.9 nm, respectively.

Table 2 DLS and zeta potential for both for red mud and modified red mud
Full size table
Fig. 4
figure 4

Distribution of experimental vs. predicted removal for MDZ adsorption onto RM

Full size image

The zeta potential shows the mechanism of electrostatic dispersion and the stability of the adsorbent particles relative to each other. If the adsorbent particles have a significant positive or negative zeta potential (ζ >  + 30 mV and ζ < − 30 mV), it can be concluded that the particles repel each other. There is dispersion stability. However, in the case of the minimal zeta potential (− 30 mV < ζ <  + 30 mV), there may be no significant force preventing aggregation of particles and instability of dispersion (Neolaka et al. 2022). From Table 2, the value of zeta potential for RM and MRM was − 31.3 mV and − 33.3 mV, respectively. Therefore, there is a stable dispersion between the adsorbent (Tor et al. 2009).

Modeling of MDZ removal rate

The effect of main parameters, such as MRM dose, the initial MDZ concentration, the pH and the contact time on MDZ removal rate was investigated. The findings of MDZ removal by RM are exhibited in Table 3.

Table 3 BBD matrix for MDZ removal using MRM
Full size table

From Table 3, the removal efficiency of MDZ ranged from 26.25 to 69.87%. Table 4 exhibits the statistical adequacy assessment of models. Table 5 shows the coefficients of the quadratic model of MDZ removal.

Table 4 Statistical adequacy evaluation of models
Full size table
Table 5 The coefficients of the quadratic model of MDZ removal
Full size table

According to Table 5, the quadratic model of MDZ elimination is displayed based on the parameters coded in Eq. 5:

$$\begin{aligned} {\text{R}} = & \, + {67}.0{4}-{ 5}.{\text{77 A }} + { 3}.{\text{82 B }} + { 1}.{\text{98 C }}{-}{ 2}.{\text{45 D }} + { 8}.{\text{21 AB }} + 0.{\text{7 AC }} + \, 0.{\text{94 AD }} \\ & {-}{ 1}.{\text{88 BC }} + { 4}.{\text{91 BD }} + { 2}.{\text{11 CD }}{-}{ 18}.{\text{18 A}}^{{2}} {-}{ 6}.{\text{94 B}}^{{2}} {-}{ 5}.{\text{74 C}}^{{2}} {-}{ 11}.{\text{24 D}}^{{2}} \\ \end{aligned}$$
(5)

In this equation, each model has two variable and fixed sections. Accordingly, the removal rate was predicted to be 67.04%. The coded factors of A, B, C and D had the coefficients of − 5.77, 3.82, 1.98 and − 2.45 respectively. The factor of A with a coefficient of − 5.77 had the maximum effect of MDZ removal. AB had the maximum interaction, and A2 was the greatest square effect of the factors (Mazloomi et al. 2021).

Table 6 indicates analysis of variance (ANOVA) for quadratic model of MDZ removal using MRM. Overall, the findings of Table 6 was significant (P-value < 0.05). The values of R2, predicted R2, adjusted R2 and adequacy precision were acquired to be 0.87, 0.27, 0.74 and 9.62, respectively.

Table 6 ANOVA for quadratic model of MDZ removal by MRM
Full size table

From Table 6, MDZ removal rate is statistically significant. Figure 4 exhibits actual versus predicted removal. Based on Figure 4, the adequacy of the model to state a perfect prediction for MDZ removal is evident.

The effect of main parameters on MZD removal

Figure 5a–b demonstrates the relationship between the removal efficiency and the main parameters, including initial MDZ concentration, contact time, pH and MRM dose.

Initial antibiotic concentration and its effect

As can be seen from Fig. 5a, with increasing antibiotic concentration, the removal efficiency decreases (P-value < 0.05). The gradual decrease in removal efficiency may be attributed to the saturation of active sites on the adsorbent surface with metronidazole molecules at high pollutant concentrations, leaving no available sites for additional molecules to bind. At low concentrations, numerous active sites exist on the surface of RM. The presence of metronidazole molecules attached to them results in a high removal efficiency (Fang et al. 2011). Fang et al. (2011) obtained similar results (Fang et al. 2011).

Fig. 5
figure 5

Response surface plot about the effects of (a) Conc. vs. time, (b) Dose vs. pH

Full size image

Contact time and its effect

The results of Fig. 5a showed that the antibiotic removal efficiency increases with increasing contact time (P-value < 0.05). This indicates that as the contact time increases, more MDZ molecules are gradually adsorbed on the active sites. This type of adsorption behavior is not uncommon and can be attributed to factors such as the surface area, pore size, and chemical properties of the adsorbent. When MDZ molecules come into contact with the active sites on the surface of the adsorbent, they undergo a physical or chemical interaction, which leads to adsorption. The gradual increase in adsorption over time can be explained by the fact that as more MDZ molecules are adsorbed onto the active sites, fewer sites become available for further adsorption. As the number of available sites decreases, the adsorption rate also decreases. This results in a slower but continuous adsorption of the remaining MDZ molecules. Overall, these findings indicate that the adsorption process is effective in removing MDZ molecules from the solution. Increasing the contact time can lead to higher removal efficiency (Mohebbrad et al. 2019).

The pH effect study

In the adsorption process, the pH of the solution can affect the functional groups in the adsorbent, the degree of ionization and the removal efficiency. Figure 5b shows that the MDZ removal rate was highest at a pH ranging from 5.5 to 8 (P-value > 0.05). At pH above 8 and below 5.5, the removal efficiency of MDZ decreased. On the other hand, MDZ decreased in acidic pH due to the electrostatic repulsion between the adsorbent surface and MDZ-H+. At a pH higher than 8, the negative charge of the adsorbent surface and MDZ molecules led to a decreasing removal efficiency due to the repulsive electrostatic interactions. Therefore, the highest MDZ removal was expected at a pH around neutral or close to the point of zero charge of the adsorbent (Bonyadi et al. 2021).

Adsorbent dose effect

Based on the results of Fig. 5b, at the high dose of adsorbent, the maximum amount of MDZ removal was. In fact, with increasing adsorbent dose, the removal percentage increases (P-value > 0.05). The reason is that by increasing the adsorbent dose, a large accessible surface is provided for the surface adsorption process, and as a result, more molecules are attracted to the adsorbent surface. These finding are consistent with the study of Ahmadfazeli et al. (2021).

Isotherm and kinetic models

Kinetic equations are used to explain the transfer behavior of absorbed substance molecules per unit of time or to test the variables affecting the reaction rate (Movasaghi et al. 2019). In this research, pseudo-first-order, pseudo-second-order, and intraparticle diffusion kinetics were used to investigate the factors affecting reaction rate. Kinetic and isotherm parameters for MDZ removal are shown in Table 7. To know the application of kinetic and isotherm model, the correlation coefficient (R2) was analyzed.

Table 7 The kinetic and isotherm parameters fitted for MDZ removal by MRM
Full size table

The values of the kinetic parameters of the Adsorption process of MDZ shows that the correlation coefficient (R2) for the pseudo-first-order kinetics, pseudo-second-order kinetics, and intraparticle diffusion kinetics are R2 = 0.87, R2 = 0.99 and R2 = 0.96, respectively. Based on this, the pseudo-second order equation with the correlation coefficient (R2) is dominantly effective on the adsorption process. (Bonyadi et al. 2022a, b).

Adsorption isotherm models and equations are used to describe the properties of the adsorbent surface, providing useful information about the mechanism of the absorption process. Adsorption isotherms are important factors in designing the adsorption system and describing the relationship between the concentration of adsorbed substances and the adsorption capacity of an adsorbent (Bonyadi et al. 2022a, b). Experimental equilibrium data was analyzed using isotherm models, including Langmuir, Freundlich and Temkin.

The results of this research had more consistent with the Langmuir isotherm (R2 = 0.99) than the Freundlich and Tomkin isotherms. Following the adsorption process from the Langmuir model shows that MDZ is uniform and single-layered on MRM and all adsorbent surfaces have the same energy in the adsorption process (Sepehr et al. 2017).

Table 8 shows the adsorption capacity of RM and other adsorbents used for MDZ removal. The data in Table 8 indicate that RM has a good potential to remove MDZ from aqueous solutions.

Table 8 Comparison of Langmuir adsorption capacities of different adsorbents for MDZ
Full size table

Conclusion

In the present study, MRM was used to remove MDZ from aqueous environment. MRM was recognized as an effective, inexpensive and available absorbent. Analysis of the adsorbent using FESEM, FTIR, EDX, DLS, and zeta potential provided valuable insights into its morphology, surface characteristics, functional groups, size, and electrical charge. Acid modification of red mud increased the porosity and number of pores on the adsorbent surface, thereby enhancing its ability to adsorb the MDZ antibiotic. The FTIR spectrum displays various bands corresponding to different functional groups, such as O–H, si(Al)–O, Fe–O and carbonate groups. EDX analysis revealed that the composition of MRM includes carbon, oxygen, and nitrogen elements. The DLS and zeta potential data demonstrate the impact of particle size and electric charge of the adsorbent on the removal of MDZ. The optimization of MDZ removal was achieved using the Box–Benken model. The highest removal rate of MDZ was achieved under optimized parameters, including a pH of 7, a contact time of 35 min, an adsorbent dose of 0.4 g/L, and an initial MDZ concentration of 42.5 mg/L, resulting in a removal rate of 69.87%. The removal of MDZ followed the pseudo-second-order and Langmuir models. The maximum adsorption capacity for MDZ was 6.04 mg/g. The results showed that MRM significantly removes MDZ from aqueous solutions.