Introduction

Population growth and the rapid increase in human activities, including urbanization, industrial growth, and other agricultural and economic activities, especially in underdeveloped and developing countries, have led to a reduction in water resources and other land resources. This causes significant damage to the physical environment, including the destruction and depletion of natural resources and the unsustainable use of water and other resources.

One of the negative effects of indiscriminate extraction of groundwater resources is the creation of subsidence and sinkholes in critical aquifers, in addition to a sharp decrease in the groundwater level. Many studies have been done on the causes and the structure of aquifer subsidence, as well as the structure of sinkholes (Karimi and Taheri 2010; Khanlari et al. 2012; Taheri et al. 2015, 2019). The drop in the groundwater level in some aquifers has changed the hydrochemical parameters of the groundwater resources (Jalali 2009).

Also, the impact of climate change on the ecosystem and rising temperatures has accelerated the reduction of existing water resources (Acharyya 2014). The adverse impact of this phenomenon on water resources in arid and semi-arid regions, which are mainly from developing countries, is particularly significant (Kumar and Singh 2015). Groundwater is the largest supplier of freshwater in the world, which plays an important role in preserving the ecosystem. The strategic importance of groundwater for global food and water security is not hidden from anyone, and the effect of climate change with the intensification of droughts and floods, as well as changes in rainfall, soil moisture and surface water has led to increasing discharge and depletion of groundwater. The effect of climate change on groundwater resources through natural and man-made processes as well as groundwater-based feedback on the climate system can be evaluated (Taylor et al. 2012). Changes in temperature and precipitation in the future will affect the aquifer recharge. The response of unconfined aquifers to changes in temperature and precipitation parameters is in the form of changes in groundwater level (Zektser and Loaiciga 1993; Changnon et al. 1988). Mathematical models are used to study the fluctuations of groundwater resources, balance changes and management of aquifer operation (Kersic 1997).

Mathematical models GMS and MODFLOW are the most complete models that have been used in many new researches to predict the temporal and spatial fluctuations of the groundwater level (Zeinali et al. 2020a, b; Kamkar et al. 2021; Malekzadeh et al. 2019a, b; Poursaeid et al. 2020, 2021, 2022 Azizpour et al. 2021, 2022; Yosefvand and Shabanlou 2020; Alizadeh et al. 2021; Goorani and Shabanlou 2021). Forecasting the groundwater level without using mathematical models is usually a averages series of groundwater level and does not provide a distribution map for the plain (Guzman et al. 2019; Nadiri et al. 2019; Azari et al. 2021).

The best tool for studying and generating climate scenarios and the impact of greenhouse gases on the Earth's atmosphere on a regional scale is the use of the General Atmospheric Circulation Model (AOGCM) (Wilby and Harris 2006). In climate change studies, various uncertainties affect the final results and by ignoring them, the validity of the results is reduced (IPCC 2014). To reduce the uncertainty of models in climate change studies, a general circulation model should not be enough. We should try to use the results of several models and scenarios to create a wide range for analysis and minimize uncertainty in the production of future climate data (New and Hulme 2000; Ansari et al. 2014).

Climate change and its consequences are one of the major problems in the management of surface and groundwater resources, and an accurate estimation of it in the future is necessary. Many studies on this subject have been done in recent years. Karamouz et al. (2011) evaluated the effect of climate change and meteorological elements on groundwater resources in the Rafsanjan plain using the LARS-WG and PMWIN models. Ansari et al. (2016) investigated the effect of climate change on groundwater recharge in the Sefid Plain based on the HADCM3 model under two scenarios A2 and B1. Crosbie et al. (2013) have investigated the potential effects of climate change on groundwater recharge in the highland aquifer of the United States. In this study, 16 global climate models (GCM) and three scenarios were used to examine changes in groundwater recharge rates in 2050 compared to 1990. The results included increased recharge in the northern high plains (% + 8), a slight decrease in the central high plain (% − 3) and a greater decrease in the southern high plains (%− 10).

Lemieuxet al. (2015) in the Magdalen Islands of Quebec, Canada, examined the effects of climate change on water resources. The simulation results show an increase in the sea level, a decrease in groundwater level and an increase in coastal erosion. Over a period of 28 years, the combination of these effects will cause the intrusion of saline seawater towards groundwater. Shrestha et al. (2016) based on the CMIP5 models, studied the effects of climate change on groundwater resources in the Mekong Delta in Vietnam. The results showed that the average annual temperature under the RCP4.5 scenario would increase by 1.5 °C and in the RCP8.5 scenario by 4.5 °C. Also, the amount of rainfall would increase in wet seasons and decrease in dry seasons, leading to reduce the groundwater level. Gulacha et al. (2017) used the SDSM model for statistical microscaling and conversion of atmospheric general circulation (GCM) models to local scale in the Wami-Ruvu River Basin, Tanzania. Finally, their research showed that in the Wami-Ruvu River Basin, the potential for floods and droughts is very high in climate change conditions.

The conducted research shows the undeniable effect of climate change on groundwater resources and the effect of choosing a climate model and the proposed emission scenario on the results. Therefore, the purpose of this study is to investigate the effect of uncertainty of climate models and emission scenarios on the prediction of groundwater level under the influence of climate change. Another goal of this research is to evaluate the efficiency of the developed method using probability levels to apply the uncertainty of climate scenarios. Using the method of probability levels instead of the weighting method of climate change models to check the uncertainty of these models and also to separate the contribution of the effect of human factors and climate change on the groundwater level is one of the innovations of this research.

Materials and methods

Study area

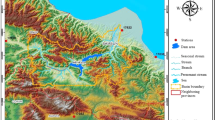
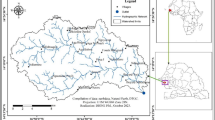
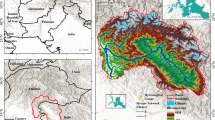
The study area is the Razan plain with an area of 1553 square kilometers located in Hamadan province. This plain is located in the area between the cities of Famenin, Razan and Hamedan. The number of extraction wells in this plain is about 1817. Rivers and streams of the region flow north to south in this plain. The Razan plain has faced a drop in groundwater level in recent years, and climate change will exacerbate the crisis in the region. Due to sinkholes that has occurred in this plain and its surroundings, studies in this field are of special importance. The position of this plain is shown in Fig. 1.

Fig. 1
figure 1

Location of the study area, meteorological stations and rivers

Full size image

Establishing models and scenarios

General circulation models and scenarios to investigate the effects of climate change

Statistics and data of the Famenin synoptic station were used to extract rainfall data, minimum and maximum temperatures and sundials. To extract rainfall and temperature data in climate change conditions, the CMIP5 series models of the Fifth Report of the International Board (AR5) were used. The CMIP5 model series includes 39 models from the Fifth Report of the International Climate Change Board (AR5), which is available via the database at: https://esgf-node.llnl.gov/search/cmip5/

They can be selected and downloaded. These models have the ability to produce precipitation, minimum temperature, maximum temperature and the average temperature in the form of historical data from 1950 to 2005 and future prediction data in the form of the emission scenarios RCP2.6, RCP4.5, RCP6.0, RCP8. 5 from 2006 to 2100. Also, the spatial separation capability of the CMIP5 series compared to the CMIP4 series from the fourth report and the CMIP3 series from the third report has been enhanced from about 2.5 by 2.5 degrees to about 0.5 by 0.5 degrees, which is a great improvement (IPCC 2014). In this study, six models BCC-CSM1-1, CCSM4, GFDL-CM3, IPSL-CM5A-LR, MIROC-ESM and HadGEM2-ES, which have complete information of three scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 are chosen to extract climate change data.

Reference scenario

In order to separate the effects of human activities and climate change on groundwater drawdown, another scenario was defined as the reference scenario. The reference scenario was developed assuming the continuation of the existing well operation conditions and no change in climatic conditions in the coming years (from 2018 to 2045). Therefore, this scenario examines exactly the effect of human factors without changing the climatic conditions. In this scenario, it is assumed that the withdrawal pattern from the wells will not change in the next 27 years and will be similar to the past 27 years (1991 to 2018) and the climate parameters such as temperature and precipitation will also be similar to the past. So it is assumed that the amount of withdrawal from the wells and the changes in rainfall and temperature are similar to the last 27 years. Other climate change scenarios described in the previous section (Rcp 2.6، Rcp 4.5، Rcp 8.5) examine the combined effect of human factors and climate change (temperature and precipitation) in comparison to the reference scenario. Finally, the results of these scenarios were compared with the reference scenario and the effects of climate change on groundwater drawdown were separated.

Delta microscaling method or change factor

The Delta method or Change Factor method is used for statistical microscaling.

To calculate the value of the change factor or delta related to precipitation in each of the 12 months of the year, the average precipitation of each future climate month (Pf) must be divided by the historical average precipitation in the same month in the present climate (Ph), thus 12 change factors or delta is obtained for the grade in which the station is located. In this case, Eq. (1) is used to obtain rainfall in each of the climatic scenarios.

$${P}_{f}={C}_{f}\times {P}_{h}$$
(1)

In the case of temperature data, the microscaling method using the change factor or delta method is similar to precipitation, except that Eq. (2) is used to predict the temperature under climatic scenarios. To calculate the value of the change factor or delta related to the temperature of each of the 12 months of the year, the average temperature of each future climate month must be subtracted from the average temperature of the same month in the present climate. In this way, 12 change factors or delta are obtained for the desired grade or station.

$$T_{f} = T_{h } + C_{f}$$
(2)

Given that the output of atmospheric circulation models can produce precipitation, average temperature, minimum and maximum temperatures as historical data from 1950 to 2005 and future forecast data in the form of the emission scenarios RCP2.6, RCP4.5, RCP8 5 from 2006 to 2100, in this study, to calculate the change factor change or delta, the historical period of 30 years leading to 2005 is used and future data on precipitation, average temperature, maximum and minimum are utilized to predict and analyze the future status of the study area in two stages. Then, the groundwater level simulation is performed based on climate change data related to the periods 2018 to 2045 and 2045 to 2072.

Calculation of probabilities

In order to reduce the inter-model turbulences of the AOGCM model in calculations and to increase the accuracy of the existing climate change rates, the average period of these data is usually used instead of the direct use of the AOGCM data in the climate change calculations. To calculate the climate change scenario in each AOGCM model, the values of the temperature difference and the ratio of rainfall between the average annual long-term temperature in the future periods (2018–2045), (2045–2072) and the simulated base period (1991–2018) are computed by the same model for each cell of the computational network as follows (Wilby and Harris 2006; Sadat Ashofte and Bozorg Hadad 2014):

$$\Delta Ti \, = \left( {\overline{T}AOGCM, \, fut_{i} - \, \overline{T}AOGCM, \, base_{i} } \right)$$
(3)
$$\Delta Pi \, = \, (\overline{P}AOGCM, \, fut_{i} /\overline{P}AOGCM, \, base_{i} )$$
(4)

In the above relations, ∆Ti and ∆ Pi respectively represent the climate change scenario related to temperature and rainfall for the long-term average of each month (12 ≤ i ≤ 1), T̅AOGCM, futi and P̅AOGCM, futi, respectively denote average long-term temperature and precipitation simulated by AOGM in the next period for each month, T̅AOGCM, basei and P̅AOGCM, basei are the average long-term temperatures and precipitation simulated by AOGCM in the period similar with the observed period for each month.

It is simply not possible to consider all sources of uncertainty in climate change studies (Ruiz-Ramos and Minguez 2010). Therefore, in this study, the most important source of uncertainty, i.e. uncertainty of the AOGCM models, is investigated. To produce monthly climate and rainfall scenarios, considering the uncertainty of the AOGCM models, the values of ∆T and ∆P (Eqs. 3 and 4) are computed for each AOGCM model and each scenario including RCP2.6, RCP4.5, RCP8.5 are calculated for each month. In other words, to produce a probabilistic climate scenario in each future period, for each month, from 6 AOGCM models and 3 climate scenarios, a total of 18 ∆T and ∆P are calculated. Then, using the Easy Fit software, the best distribution function (Beta distribution function) is fitted to the values of ∆T and ∆P, and for each month, a beta distribution function is obtained for ∆T and ∆P of the same month. Then, the probabilistic cumulative distribution function (CDF) of ∆T and ∆Ps for each month is determined from the corresponding beta distribution function. Finally, ∆T and ∆P values are extracted from the respective CDF at 4 probability levels of 0.30, 0.50, 0.70 and 0.90 under three scenarios (including RCP2.6, RCP4.5 and RCP8.5). Using the extracted ∆T and ∆Ps selected for two levels of probability of 0.5 and 0.9, monthly temperature and precipitation scenarios are generated for the next period using Eqs. 3 and 4. In the next step, time series for temperature and precipitation are generated at the probability levels of 0.9 and 0.5, and temperature and precipitation values are predicted for these probabilistic scenarios. As an example, the values of ∆P for different months in the period 2045–2018 are given in the Fig. 2.

Fig. 2
figure 2

∆ P values for different months in the period 2045–2018

Full size image

Performance index and evaluation of models

To validate and evaluate the prediction accuracy of general circulation models and data fitting, goodness-of-fit tests including root mean square error (RMSE), mean absolute error (MAE) and Nash–Sutcliffe coefficient (NS) are used. Using these indices, the prediction accuracy of the models can be evaluated (Hosseinikhah et al. 2014; Sadat Ashofte and Bozorg Hadad 2014), which are presented in formulas (5) to (7).

$${\mathrm{RMSE}=\left[\sum_{i=1}^{N}\frac{{\left({O}_{i}-{C}_{i}\right)}^{2}}{n}\right]}^\frac{1}{2}$$
(5)
$$\mathrm{MAE}=\frac{\sum_{i=1}^{N}\left|{O}_{i}-{C}_{i}\right|}{n}$$
(6)
$$\mathrm{NS}=1- \frac{\sum_{i=1}^{N}{({O}_{i}{-C}_{i})}^{2}}{\sum_{i=1}^{N}{({O}_{i}-\overline{O })}^{2}}$$
(7)

In the above equations, O represents the observed value, Ō is the mean value of observed data, C is the value calculated by the models, and N is the number of observed data.

The best predictions occur once the RMSE and MAE quantities are their lowest state and the Nash – Sutcliffe coefficient is close to 1 (Kamal and Massahbavani 2012).

Table 1 shows that the MIROC model with coefficients of 0.54, 0.41 and 0.7 for precipitation and the HadGEM model with coefficients of 1.7, 1.47 and 0.96 for temperature, respectively have the lowest rate in RMSE and MAE, and highest rate in NS compared to other models and have the highest accuracy and efficiency for predicting precipitation and temperature quantities (Figs. 3, 4).

Table 1 Coefficients of performance indices of AOGCM models compared to the observed period for climatic parameters of temperature and precipitation
Full size table
Fig. 3
figure 3

Long-term average temperature prediction using Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in the period 2018–2045 compared to the base period of 1991–2018

Full size image
Fig. 4
figure 4

Long-term average temperature prediction using Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in 2046–2072 compared to the base period of 1991–1998

Full size image

Prediction of temperature and precipitation parameters in future periods

As mentioned, first, the microscaling data of the BCC-CSM1-1, CCSM4, GFDL-CM3, IPSL-CM5A-LR, MIROC-ESM and HadGEM2-ES models that have complete information of three scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 are generated using the Delta method. The results of forecasting climatic variables for the scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 and two levels of probability of 90 and 50%, respectively, changes for the long-term mean temperature of + 0.65, + 0.653, + 0.653, /04 -0 and + 6.6° C and changes in the long-term average rainfall of − 0.15, − 0.6, + 2.25, − 30.2 and − 0.095 percent during the period 2018–2045 In the same way, for long-term mean temperature changes of + 2, + 2.2, + 1.55, + 0.98 and + 3.3 °C and changes in long-term mean precipitation by − 17.7 They show − 23, − 18.3, − 46 and 13.8% during the statistical period of 2046–2072.

The results of forecasting climatic variables for the scenarios of Rcp 2.6, Rcp 4.5, Rcp 8.5 and two levels of probability of 90 and 50%, respectively, show changes for the long-term mean temperature of + 0.65, + 0.653, + 0.653, -0.04 and + 0.6 °C and changes in the long-term average rainfall of − 0.15, − 0.6, + 2.25, − 30.2 and − 0.095 percent during the period 2018–2045 and in the same way, for long-term mean temperature changes of + 2, + 2.2, + 1.55, + 0.98 and + 2.3 °C and changes in long-term mean precipitation by -17, -23.7, -18.3, -46 and 13.8% during the statistical period of 2046–2072.

As can be seen in the above Figs. 5 and 6, the highest increase in temperature for the period 2018–2045 occurs in September and May and for the period 2046–2072 in July and the highest decrease in temperature for the period 2018–2045 and the lowest increase in temperature in the period 2046–2072 are obtained in January and February (Figs. 7, 8).

Fig. 5
figure 5

Long-term temperature difference in various months for Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in the period 2018–2045 compared to the base period of 1991–2018

Full size image
Fig. 6
figure 6

Long-term temperature difference in various months for Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in the period 2046–2072 compared to the base period of 1991–1998

Full size image
Fig. 7
figure 7

Long-term average rainfall prediction using Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in the period 2018–2045 compared to the base period of 1991–2018

Full size image
Fig. 8
figure 8

Prediction of long-term average rainfall using Rcp 2.6, Rcp 4.5, Rcp 8.5 scenarios and 90 and 50% probability levels in the period 2046–2072 compared to the base period of 1991–1998

Full size image

As can be seen in Figs. 9 and 10, the highest increase in precipitation occurs in September and October for the scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 in both periods and the highest decrease in temperature the period 2018–2045 and the lowest temperature increase in the period 2046–2072 occur in January and February. Winter has the highest share of rainfall among other seasons and summer's share of rainfall is very small, so changes in the percentage of rainfall in this season have little effect on annual rainfall variation.

Fig. 9
figure 9

Percentage of precipitation variations in different months, the scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 and probability levels of 90 and 50% in the period 2018–2045 compared to the base period of 1991–1998

Full size image
Fig. 10
figure 10

Percentage of precipitation changes in different months, the scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5 and probability levels of 90 and 50% in the period 2046–2072 compared to the base period of 1991–1998

Full size image

GMS groundwater model

In this research, the GMS (Groundwater Modeling System) model is used to simulate the aquifer behavior in climate change conditions. The GMS numerical model is based on solving three-dimensional equations governing groundwater flow, which is presented in both steady and transient state conditions according to the flow conditions. Due to the fact that the Razan plain aquifer is of free type, the equation governing the groundwater flow, which is known as the Boussinesq nonlinear equation, is defined as follows.

$$\frac{\partial }{\partial x}\left( {k_{x} h\frac{\partial h}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {k_{y} h\frac{\partial h}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {k_{z} h\frac{\partial h}{{\partial z}}} \right) = S_{y} \frac{\partial h}{{\partial t}} \pm w$$
(8)

where \(K_{x} ,K_{y}\) and \(K_{z}\) are hydraulic conductivity in different directions, \(w\) denotes the recharge or discharge of groundwater, \(h\) represents the potential head (hydraulic head), \({S}_{y}\) represents the specific yield and \(t\) is time. Equation (8) is solved by applying the initial and boundary conditions and based on the finite difference method.

The structure of the conceptual model of the Razan plain aquifer includes modeling and initial distribution of the hydrogeological parameters (hydraulic conductivity and specific yield), discharge of extraction wells and their return water, observation wells, water exchange between river and aquifer, recharge rate from the surface to the aquifer and the boundary conditions of the aquifer. In this research, modeling has been done for a single-layer groundwater system and the modeling domain corresponds to the groundwater water budget. In order to estimate the initial hydraulic load and topography of the plain surface and bedrock, the interpolated groundwater level map obtained from piezometers of the region (level map of the month before the start of the simulation period), the digital elevation map of the region (DEM) and existing drilling points are utilezd, respectively. The inflows to the aquifer are also calculated by the values of the head in the General Head Boundary (GHB) cells based on the topography map. The initial values of hydraulic conductivity and specific yield are considered according to the grain size of the saturation layer (logs of wells) and their final values are obtained after calibration and validation of the model. To prepare the initial map of the recharge from the surface, soil maps, land use as well as rainfall status in the area are implemented. Also, the flow rates of the rivers in the tributaries are estimated from the hydrometric stations. All data required for aquifer modeling were obtained from Hamedan regional water company.

Considering the depth of the groundwater level in the region, which is more than 4 m, evaporation does not play a role in the groundwater balance in the region. Therefore, in the stages of preparing the conceptual model as well as the numerical model, the evaporation package is not considered.

To clarify the research steps, a flowchart that briefly shows the research steps is shown in Fig. 11.

Fig. 11
figure 11

Flowchart of the research steps

Full size image

Results and discussion

Calibration and validation of groundwater model

To adapt and proper performance of the model simulation, the model calibration is conducted for an 18-month period (October 2008 to March 2009). During the calibration phase, the input parameters of the model, including hydraulic and hydrodynamic data, are adjusted to an acceptable agreement between the observed groundwater level in the piezometers and the groundwater level calculated by the model. The model is calibrated in two states comprising steady and transient. In the steady state, one month with a steady groundwater level is selected and the model is calibrated in this state (Fig. 12). The inflows to the aquifer are calculated via the values of the head in the boundary cells (GHB) based on the topography map and imported to the model.

Fig. 12
figure 12

Position of calibrated piezometers in the steady state

Full size image

In the steady state, the hydraulic conductivity (K) and recharge, and in addition, in the transient state, the specific yield parameter (Sy) of the aquifer are entered into the model to in the form of zoning for by manual trial and error method to calibrate the model. In the transient state, the monthly variations of the aquifer are examined and the output of the model in the steady state (hydraulic conductivity) is set as the basis of the transient state. The specific yield and recharge parameters are calibrated at 103 piezometers for 18 months and the final simulation error values are obtained at the location of each piezometer. For both steady and transient states, the error rate of the RMSE and MAE indices is obtained. Figures 13 and 14 show the acceptable adaptation of the level simulation results in the groundwater model to the field data in the calibration and validation steps.

Fig. 13
figure 13

Values of ME, MAE and RMSE indices in the 18-month calibration period

Full size image
Fig. 14
figure 14

Values of ME, MAE and RMSE indices in the 18-month validation period

Full size image

The error rate in the steady state after the calibration of the model is in the acceptable range. For the transient state, the error values in different time steps (18 months) after the calibration of the model are seen in Fig. 13 and are in the acceptable range in all months, which indicates the proper performance of the model. To confirm the performance of the model, the model is validated for a period of 18 months (September 2011-April 2010), and the values of the obtained RMSE and MAE indices (Fig. 14) indicate the reasonable accuracy of the simulation model.

Error values in different time steps (18 months) during the validation of the model are seen in Fig. 14 and are in the acceptable range in all months, indicating the appropriate adaptation of the simulated model to the natural conditions of the aquifer.

Groundwater change trends

Human factors of declining groundwater level can be divided into two parts. The first part includes the production and increase of greenhouse gases and the consequences of climate change such as changes in temperature and rainfall and the second part includes increasing groundwater extraction such as increasing the area under cultivation (increasing water demand), increasing withdrawal from pumping wells, etc. The effects of these changes can also be extended to the groundwater of the Razan plain, which in this study the effect of climate change on fluctuations in groundwater resources of this plain are evaluated. The trend of changes in the groundwater level of the Razan plain, as seen in Fig. 15, shows a decrease of 4.5 m during the historical observational period. Also, in Fig. 15, the bar graph of monthly rainfall changes in millimeters was shown, which indicates a decreasing trend of monthly rainfall, especially in recent years.

Fig. 15
figure 15

Unit hydrograph of Razan plain, the trend of groundwater level change and monthly rainfall changes (mm) during the historical observational period

Full size image

The effects of climatic variables on the groundwater level of the region in future periods

As mentioned, the reference scenario was implemented to separate the effects of human activities and climate change on groundwater drawdown. The reference scenario was developed assuming the continuation of the existing well operation conditions and no change in climatic conditions in the coming years (from 2018 to 2045). This scenario examines exactly the effect of human factors without changing the climatic conditions.

Considering the fact that the hydrodynamic coefficients of the aquifer change with the change of the aquifer conditions in the far future (2045 to 2072), therefore, it is a little difficult to generalize the aquifer conditions for the future period of 2045 to 2072. Therefore, this period was excluded from the comparisons and only the groundwater drawdown in the future period (2018 to 2045) was compared under the reference scenario and different climate change scenarios so that the results are more realistic. Based on this, after simulating the system using the GMS model, a three-dimensional map of the groundwater level was drawn in the reference scenario at the end of the selected period (Sep, 2045), which is shown in Fig. 16.

Fig. 16
figure 16

The three-dimensional map of the groundwater level for Sep 2045 in the reference scenario

Full size image

According to Fig. 16, the average drop of the groundwater level in the northern, central and southern parts of the plain is 3.5, 15.7 and 5.5 m, respectively. Therefore, the largest amount of drawdown is in the central areas of the plain and near the sinkholes. In some central areas and in the vicinity of sinkholes, the maximum groundwater drawdown reaches 56 m. Considering the entire area of the plain, the average drawdown in the whole plain in the reference scenario was 8.5 m.

In the next step, the future status of the aquifer for future climate change scenarios in the next period, i.e. 2018–2045 was forecasted using the GMS model.

For this purpose, using the climate change scenarios Rcp2.6, Rcp 4.5, Rcp 8.5 and two probability levels of 90 and 50%, the aquifer is evaluated and its fluctuations are calculated. To this end, after applying changes in various parameters that have been affected by rainfall and temperature, including aquifer recharge, river flow rate and extraction from aquifer by wells, the conceptual model is re-run and the simulation was conducted for upcoming period.

The output of the results indicates that the fluctuations of the groundwater level caused by climate change under the scenarios.

The groundwater level under the climatic scenarios Rcp2.6, Rcp4.5, Rcp8.5 and two probability levels of 90 and 50% in different months for the period 2018–2045 compared to the reference scenario (Fig. 17).

Fig. 17
figure 17

Groundwater level fluctuations in climate change scenarios in different months for the period 2018–2045 compared to the reference scenario

Full size image

As shown in Fig. 17, in the six months of October to March (autumn and winter) the groundwater level drop has a soft decreasing trend and the reason is less change in rainfall in future periods and even increased rainfall for three scenarios Rcp 2.6, Rcp 4.5, Rcp 8.5. So, there is a slight increase in temperature in these six months and even in some scenarios, a decrease in temperature is observed. The groundwater level in the six months of April to September (spring and summer) have a greater decrease than the previous six months (autumn and winter). Rising temperatures and declining rainfall are the main reasons for the increase of groundwater level drop in this months. The highest drop in groundwater occurs in August and the lowest amount in January.

As mentioned in the definition of scenarios section, the reference scenario examines the effect of human factors assuming no change in climate conditions in the future. Other climate change scenarios including emission scenarios (Rcp 2.6, Rcp 4.5, Rcp 8.5) as well as scenarios with probability levels of 50% and 90% examine the combined effect of human factors and climate change (temperature and precipitation) compared to the reference scenario. In these scenarios, the changes in the groundwater level were simulated using the GMS model for the period of 2018–2045, and then by comparing with the reference scenario, the contribution of climate change in reducing the groundwater level during this period was separated. The results of the separation of the contribution of climate change and human factors in reducing the groundwater level are shown in Table 2.

Table 2 Separating the contribution of climate change and human factors in average groundwater drawdown (m) in the emission scenarios compared to the reference scenario (2018–2045)
Full size table

This table shows that in all scenarios, climatic factors have a lesser contribution in reducing the groundwater level in the plain, and the largest contribution is related to human factors and excessive withdrawal from the aquifer. According to Table 2, the contribution of climate change in the reduction of the groundwater level in probability scenarios of 0.9 and 0.5 and emission scenarios Rcp8.5, Rcp4.5 and Rcp2.6 is about 40.8, 24.3, 32.3, 27.6 and 22.2 percent respectively. In the probability scenario of 0.9, which is considered the upper limit of probability, the contribution of climate change in reducing the water level is significant, which is due to the sharp decrease of rainfall in the future period (2045–2018) in this scenario. After that, in the Rcp8.5 scenario, which is considered a pessimistically scenario, the contribution of climate change in lowering the groundwater level is finally 32%, and human factors and improper management of the aquifer are about 68% effective. Based on these results, the first priority for aquifer planning and management should be focused on human activities and controlling the amount of withdrawal from the aquifer. These results clearly show that the main cause of creating sinkholes and the sharp reduction of the groundwater level in the region is the excessive extraction of groundwater resources as a result of human activities, including agriculture and industrial demands, and not climate change.

Conclusion

The combined role of human factors and climate change in intensifying on the groundwater drawdown and separating the role of each on the reduction of groundwater reserves is one of the basic issues in water resources management and its estimation is very necessary in the proper management of the aquifer in the future. In this study to predict temperature and precipitation in the future, a general circulation model called " AOGCM" was utilized. To validate and evaluate the accuracy of general circulation models and data fitting, the RMSE, MAE and NS indices were used. In the uncertainty evaluation, one model is not enough to validate and increase the accuracy of the prediction results. So six general circulation models including BCC-CSM1-1, CCSM4, GFDL-CM3, IPSL-CM5A-LR and MIROC ESM and HadGEM2-ES were used for the emission scenarios Rcp2.6, Rcp 4.5, Rcp 8.5 and two probability levels of 90 and 50% of the output of six models and three scenarios. Also, in order to separate the effects of human activities and climate change on the amount of groundwater drawdown, the reference scenario was developed, assuming the continuation of the existing conditions of the exploitation of wells and without changing the climatic conditions in the coming years (from 2018 to 2045). The contribution of climate change in the reduction of the groundwater level in probability scenarios of 0.9 and 0.5 and emission scenarios Rcp8.5, Rcp4.5 and Rcp2.6 is about 40.8%, 24.3%, 32.3%, 27.6% and 22.2% respectively. Based on these results, the first priority for aquifer planning and management should be focused on human activities and controlling the amount of withdrawal from the aquifer. These results clearly show that the main cause of creating sinkholes and the sharp reduction of the groundwater level in the region is the excessive extraction of groundwater resources as a result of human activities, including agriculture and industrial demands, and not climate change. In order to provide useful solutions, these results should be taken into consideration by planners and managers. Considering these changes, by using proper management of water resources and considering all agriculture, drinking, industry and environmental aspects, the adverse effects of human factors and climate change on water resources of the region can be reduced. In recent years, many researches have investigated the effect of climate change on water level drawdown and groundwater recharge based on the fifth climate change report that indicate the undeniable effect of climate change on groundwater resources and the effect of choosing a climate model and emission scenario on the work (Epting et al. 2021; Costa et al. 2021; Nyembo et al. 2022). But in these researches, the uncertainty of climate change models has not been investigated by defining probability levels. Also, the separation of the contribution of human factors and climate change on the drop of the groundwater level was a prominent case that was discussed in this research. This makes managers and planners have a correct understanding of the aquifer conditions and provide more realistic solutions to solve the aquifer problem or to improve and restore lost groundwater reserves.