Streamflow prediction using a hybrid methodology based on variational mode decomposition (VMD) and machine learning approaches

Abstract

The optimal management of water resources depends on accurate and reliable streamflow prediction. Therefore, researchers have become interested in the development of hybrid approaches in recent years to enhance the performance of modeling techniques for predicting hydrological variables. In this study, hybrid models based on variational mode decomposition (VMD) and machine learning models such as random forest (RF) and K-star algorithm (KS) were developed to improve the accuracy of streamflow forecasting. The monthly data obtained between 1956 and 2017 at the Iranian Bibijan Abad station on the Zohreh River were used for this purpose. The streamflow data were initially decomposed into intrinsic modes functions (IMFs) using the VMD approach up to level eight to develop the hybrid models. The following step models the IMFs obtained by the VMD approach using the RF and KS methods. The ensemble forecasting result is then accomplished by adding the IMFs’ forecasting outputs. Other hybrid models, such as EDM-RF, EMD-KS, CEEMD-RF, and CEEMD-KS, were also developed in this research in order to assess the performance of VMD-RF and VMD-KS hybrid models. The findings demonstrated that data preprocessing enhanced standalone models’ performance, and those hybrid models developed based on VMD performed best in terms of increasing the accuracy of monthly streamflow predictions. The VMD-RF model is proposed as a superior method based on root mean square error (RMSE = 13.79), mean absolute error (MAE = 8.35), and Kling–Gupta (KGE = 0.89) indices.

Introduction

Streamflow forecasting is an important issue for water resource management, since it is necessary to develop flood warning systems, the optimal operation of dam reservoirs, and hydropower generation (Lin et al. 2021). Various equations and models for forecasting streamflow have been developed so far, including conceptual rainfall-runoff methods, time-series models, and hybrid techniques, all of which can be classified into two categories: physical models and data-driven models (Kartzert et al. 2018; Lin et al. 2021). Physical models are created from field data and are based on pre-existing mathematical correlations between various hydrological processes. Soil texture, land use, and vegetation cover in the basin are only a few data points (Beven 2020). As can be recognized in physical models, there are several aspects that influence the model’s outputs. Therefore, modeling is quite expensive. Furthermore, one of these models’ shortcomings is the requirement for extensive hydrological data. In other words, the presence of high uncertainty in the data required by physical models can lead to inaccurate predictions of complicated variables like streamflow (Lin et al. 2021; Biondi and De Luca 2013).

In recent years, data-driven strategies have made tremendous progress in overcoming the limitations of physical models. These techniques require less inputs, are less parameter-dependent, simpler to debug, and practical (Meng et al. 2021; Fang et al. 2019; Chen et al. 2018). Time-series models are one type of data-driven strategy that has been widely utilized to forecast river flow in many regions of the world (Adnan et al. 2017; Wen et al. 2019; Mehdizadeh et al. 2019). Autoregressive (AR), moving average (MA), autoregressive moving average (ARMA), and autoregressive vector (VAR) models are popular types of these models. In streamflow forecasting, time-series models imply a linear connection between inputs and outputs, which is harder to accomplish. In addition, the stationarity of the recorded data is a fundamental assumption in their implementation. Due to the trend, climate change, and other elements impacting streamflow, the stationarity criteria are critical to satisfying (Ghimire et al. 2021).

Unlike time-series models, machine learning approaches are better at recognizing complex relationships among the components of phenomenon and have been proposed as a feasible alternative method for estimating streamflow. (Meng et al. 2021; Lin et al. 2021). The following are some of the machine learning algorithms that have been frequently employed in hydrological modeling. Support vector machine (SVM) (Essam et al. 2022; Samantaray et al. 2022), gene expression programming (GEP) (Mehdizadeh et al. 2018; Esmaeili-Gisavandani et al. 2021), Bayesian regression (BR) (Wagena et al. 2020; Achieng and Zhu 2019), random forests (RF) (Ahmadi et al. 2022) and the K-star algorithm (KS) (Salih et al. 2020).

Human activities and climate changes are among the challenges that have a significant impact on machine learning methods performance with increasing non-stationarity in hydrological data (Meng et al. 2021). Machine learning models based on fundamental decomposition approaches have been developed to overcome this challenge. Streamflow series could be divided into multiple sub-series using these approaches. In this case, the characteristics of the data, including periodicity, trends and noises, are identified and directly provided to the models.

The performance of models is considerably enhanced when sub-series are added (Yilmaz et al. 2022; Ahmadi et al. 2022; Meng et al. 2021; Fang et al. 2019). Wavelet transform is a strong technique for detecting non-stationarity in dataset. By dividing the initial series into high and low frequencies, this strategy allows the model to identify data features. One of the most significant drawbacks of the wavelet transform approach is that it is dependent on the mother wavelet function, which means that each mother wavelet function generates different outputs for a series, and determining the appropriate mother wavelet function necessitates a try-and-error procedure to identify (Ahmadi et al. 2022).

Empirical mode decomposition (EMD) is a signal analysis technique created by Huang et al. (1998) that has undergone several improvements. When oscillations with the same time scale are stored in various intrinsic mode functions (IMFs), EMD runs into the problem of mode mixing. As a result of the influence of mixing modes, the EMD approach is rendered useless. The ensemble empirical mode decomposition (EEMD) approach is used to compensate for EMD’s flaws (Wu and Huang 2009). Trials with the addition of white noise to the signal reveal that the EEMD approach scales better than the EMD, and the resultant IMF does not exhibit linkages with other IMFs. The EEMD approach contains flaws, such as residual noise in reconstructed data. Therefore, Torres et al. (2011) developed the complete ensemble empirical mode decomposition (CEEMD). White noise is introduced to the signal numerous times in this approach, with the exception that the first IMF is extracted while adding white noise, and the steps are repeated by adding noise again to extract the remaining IMFs.

For signal analysis, Dragomiretskiy and Zosso (2013) presented the variational mode decomposition (VMD) approach. The VMD can decompose complicated series with more efficiency (Lahmiri 2015). He et al. (2020) found that using VMD rather than EEMD increases the performance of the GBRT model in runoff prediction. Sun et al. (2022) reported that the hybrid models using VMD is outperformed to other signal analysis approaches in estimating the daily flow of the Han River in China.

The literature review indicates that the VMD approach has received less attention in streamflow forecast research than other signal analysis methods. Therefore, in the present study, we evaluate the capability of the VMD-RF and VMD-KS hybrid models in predicting monthly river flow. In addition, some hybrid models are developed, and the performance of VMD-based hybrid models is compared with EMD-based and CEEMD-based hybrid models.

Methodology

Variational mode decomposition (VMD)

VMD is an emerging and powerful decomposition model employed for decomposing a stationary and non-stationary time series into a specified number of intrinsic mode functions (IMFs). Hence, modes are compact around its central frequency. Therefore, it can be ensured that the IMFs can reconstruct the Initial data series with the utmost accuracy (Dragomiretskiy and Zosso 2013). A restricted variational issue can be written as follows to achieve each mode and its central frequency (He et al. 2019):

$$ \left\{ \begin{gathered} \mathop {\min }\limits_{{\left\{ {u_{k} (t)} \right\},\left\{ {\omega_{k} (t)} \right\}}} \left\{ {\sum\limits_{k} {\left\| {\partial_{t} \left[ {(\delta (t) + \frac{j}{\pi t}) \otimes u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|}_{2}^{2} } \right\} \hfill \\ s.t.\sum\limits_{k} {u_{k} (t) = f(t)} \hfill \\ \end{gathered} \right. $$

(1)

where $t$ denotes time step, $\delta (t)$ is the Dirac distribution, $u_{k} (t)$ stands for the $k$ th mode, $\omega_{k} (t)$ shows corresponding center frequency, and $f(t)$ indicates the $t$ th data of the considered signal. Furthermore, the Hilbert transform of $u_{k} (t)$ is expressed by $(\delta (t) + \frac{j}{\pi t}) \otimes u_{k} (t)$, which can convert $u_{k} (t)$ into analytical data to create a one-sided frequency spectrum with only positive frequencies. Therefore, according to the index term $e^{{ - j\omega_{k} t}}$, the spectrum of modes can be transfer to a baseband. To convert the given optimization problem into a non-objective optimization term, two aspects should be considered: Lagrange multipliers $\lambda$ and the quadratic penalty parameter. The following is the equation for the augmented Lagrange function (Li et al. 2022):

$$ \begin{gathered} L(u_{k} ,\omega_{k} ,\lambda ) =\, \alpha \sum\limits_{k = 1}^{K} {\left\| {\partial_{t} \left[ {(\delta (t) + \frac{j}{\pi t}) \otimes u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } + \left\| {f(t) - \sum\limits_{k = 1}^{K} {u_{k} (t)} } \right\|_{2}^{2} + \hfill \\ \left\langle {\lambda (t)f(t) - \sum\limits_{k = 1}^{K} {u_{k} (t)} } \right\rangle \hfill \\ \end{gathered} $$

(2)

where $\left\| {f(t) - \sum\limits_{k = 1}^{K} {u_{k} (t)} } \right\|_{2}^{2}$ denotes a quadratic penalty function to reduce convergence time. The alternate direction method of multipliers (ADMM) is an optimization procedure that allows $u_{k} (t)$ and $\omega_{k} (t)$ to be updated in two different points to complete the VMD method. As a result, the modified equations are known as (He et al. 2019):

$$ u_{k}^{n + 1} = \frac{{f(\omega ) - \sum\nolimits_{i \ne k} {u_{i} (\omega ) + \frac{\lambda (\omega )}{2}} }}{{1 + 2\alpha (\omega - \omega_{k} )}} $$

(3)

$$ \omega_{k}^{n + 1} = \frac{{\int_{0}^{\infty } {\omega \left| {u_{k} (\omega )} \right|^{2} d\omega } }}{{\int_{0}^{\infty } {\left| {u_{k} (\omega )} \right|^{2} d\omega } }} $$

(4)

$$ \lambda^{n + 1} (\omega ) = \lambda^{n} (\omega ) + \eta \left( {f(\omega ) - \sum\limits_{k} {u_{k}^{n + 1} } } \right) $$

(5)

where n is the number of repetition, $\lambda (\omega )$, $f(\omega )$ and $u_{i} (\omega )$ are the Fourier transform parameters, and $\eta$ denotes the iterative factor. More details about the mathematical logic and algorithm of VMD can be found in Dragomiretskiy and Zosso (2013).

Empirical mode decomposition (EMD)

The EMD decomposes natural, or synthetic, data into a number of distinct oscillating trends. Except for the last extracted subcomponent, all subcomponents are denoted as intrinsic mode functions (IMFs), with the remnant being the final subcomponent that depicts the general trend of the data (Barge and Sharif 2016). The initial data are equal to the summation of all IMFs and the final residual subcomponent. Individual sub-series are only designated as IMFs if they satisfy the next two conditions:i) The number of extreme (minima and maxima) must be equal to the number of zero crossings or differ by no more than one, and ii) the average of the cubic spline interpolated envelope, specified by the local minima and maxima must have a value equal or near to zero (Lee and Ouarda 2012). EMD can decompose any complex data set ($x\left( t \right)$) into a confined number of IMFs through the sieving process. The sieving procedure for obtaining IFMs from a time series is described below.

• (1). To get the upper (lower) envelope, find all of the local extrema and use a smoothing approach to connect all of the local maxima (minimas). A cubic spline interpolation is a regularly used method (Lee and Ouarda 2012).

• (2). Use the following equation to find the mean value of the upper ($e_{{{\text{upper}}}}$) and lower ($e_{{{\text{lower}}}}$) envelopes:

• (3). $m(t) = \left[ {\frac{{e_{{{\text{upper}}}} (t) + e_{{{\text{lower}}}} (t)}}{2}} \right]$ (6)

• (4). Take the difference ($d(t)$) between the computed mean value and the time series ($x(t)$):

• (5). $d(t) = x(t){ - }m(t)$ (7)

• (6). Examine $d(t)$ to check if it satisfies the IMF’s specified conditions. If all of the conditions are met, $d(t)$ becomes the i th IMF, indicated as $C_{i} (t)$, and the residual $x\left( t \right)$ becomes the remaining residue $r\left( t \right)$, represented as $r\left( t \right) = x\left( t \right){ - }C_{i} \left( t \right)$, allowing the process to continue and the next IMF to be obtained. If the conditions are not met, the process is repeated with $d(t)$ substituting $x\left( t \right)$ in the above mentioned equation and all steps applied to the remaining $d(t)$ until $C_{i} (t)$ is found.

• (7). Repeat stages 1–4 until either $r\left( t \right)$ becomes a uniform function or the number of extrema becomes less than one or equal to zero.

• (8). Finally, the initial time series obtained from summation of the extracted IMFs as:

• (9). $x\left( t \right) = \sum\limits_{i = 1}^{n} {C_{i} \left( t \right) + } r\left( t \right)$ (8)

Complete ensemble empirical mode decomposition (CEEMD)

CEEMD is known as an improved version of EMD. CEEMD technique was applied in this study to decompose the monthly streamflow data into a series of relatively stationary components. In this method, the Gaussian white noise is added to the source data during the decomposition process to provide a uniform reference frame, which is then eliminated by averaging the relevant IMFs and residue. The decomposition process in CEEMD is detailed here.

• (1). To the time series $x\left( t \right)$, add some white noise $\varepsilon (t)$ as follows:

• (2). $x^{\prime}\left( t \right) = x(t) + \varepsilon (t)$ (9)

• (3). To extract the first component, decompose $x^{\prime}\left( t \right)$ using the EMD approach.

• (4). Steps 1 and 2 should be repeated with a different number of substantiation. This procedure is frequently repeated with $\tau$ number of times with each realization being distinct.

• (5). Then, as shown below, compute the mean of all $IMF_{1}$:

• (6). $IMF_{1} (t) = \frac{1}{\tau }\sum\limits_{k = 1}^{\tau } {\psi_{1} (x(t) + \eta .\varepsilon (t))}$ (10)

• (7). where $\psi_{1}$ denotes the k th IMF estimation and indicates the amplitude adjustment required to obtain an adequate signal.

• (8). As a result, the first residual component, also known as the residual component, is as follows:

• (9). $R_{1} (t) \, = x(t) \, {-}IMF_{1} (t)$ (11)

• (10). Following that, $IMF_{2}$ can be derived from the original signal as below:

• (11). $IMF_{2} (t) = \frac{1}{\tau }\sum\limits_{k = 1}^{\tau } {\psi_{1} \left[ {x(t) + \psi_{1} .\varepsilon (t)} \right]}$ (12)

• (12). To obtain the $IMF_{\beta + 1} (t)$ factor, the above-mentioned process is repeated.

• (13). $IMF_{\beta + 1} (t) = \frac{1}{\tau }\sum\limits_{k = 1}^{\tau } {\psi_{1} \left[ {x(t) + \psi_{\beta } .\varepsilon (t)} \right]}$ (13)

• (14). Finally, the residuals are averaged, revealing a gradual variation around the long-term average, which represents the general trend.

Random forests (RF)

The random forests (RF) algorithm is a popular machine learning algorithm from the field of artificial intelligence that belongs to supervised learning techniques. It can be used for classification and regression problems (Breiman 2001). It is based on the idea of group learning, which entails combining numerous classifiers to solve a complex problem and improve model performance. As the name implies, the random forest algorithm is a classifier that uses a variety of decision trees in different subsets of the data set (Cutler et al. 2012). Instead of using a decision tree, random forest forecasts each tree’s prediction based on the majority of votes and uses the final result as the output. With more trees in the forest, accuracy improves and overfitting is avoided (Breiman 2001). The following is a description of how the RF algorithm works (Ali et al. 2020).

• Step 1: Start by randomly selecting samples from a data set.

• Step 2: For each instance, RF generates a decision tree. The forecast result from each decision tree is then obtained.

• Step 3—Each expected result is voted on in this step.

• Step 4—As the final prediction result, choose the maximum forecast result.

K-star algorithm (KS)

The KS algorithm is an instance-based classification method that performs classification based on similar training cases and achieves the desired results compared to machine learning algorithms (Hernández 2015). Unlike other data mining methods that classify based on the entropy-based distance function, this method uses the similarity function to estimate different variables. The essential principle of instance classification is that cases belong to the same category. This algorithm considers K points at random first, resulting in K clusters with random points at their centers. Following an evaluation of the data, the data that are closest to each center are assigned to the appropriate cluster. After that, an average is taken from each cluster; this time, the averages are the centers of the categories, and any data that are farther from this average and closer to another cluster shift the cluster (Cleary and Trigg 1995). This cycle continues until all of the clusters are stable and data changes are no longer conceivable. Any digit can be used as K. This algorithm splits the data into the most similar categories and runs it multiple times with varied beginning points to achieve the optimal outcome, resulting in better integrated cluster components (Cleary and Trigg 1995).

Model development

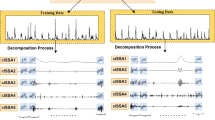
One of the most difficult aspects of modeling streamflow is selecting the appropriate inputs for the models. In order to establish suitable relationships between phenomena, models require inputs. As a result, the decomposed base (DB) method was employed to create hybrid models in this study. River flow data were initially decomposed into different IMFs using VMD, EMD, and CEEMD algorithms for this purpose. The following step is to choose the optimal delay for each IMF. The PACF approach is one of the statistical methods that has been utilized in many research to identify the optimum delay (He et al. 2019; He et al. 2020; Hu et al. 2021).Assume that the IMF(t) is to be estimated and is the model’s output; therefore, the IMF (t-i) will be considered as an input by the PACF technique during the delay i if it exceeds the 95 percent confidence interval. After determining the appropriate delays for each IMF, DB-RF and DB-KS hybrid methods were implemented. Finally, all estimated IMFs were combined to obtain the predicted river flow from the hybrid models. Figure 1 presents the development structure of the hybrid models in this study.

Fig. 1

Flowchart of the proposed hybrid models for streamflow modeling

Data and study area

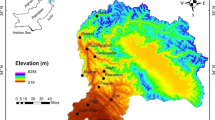
Monthly flow data from the Zohreh River were utilized to create hybrid models and assess their performance in this study. For this purpose, 10 operational hydrometric stations in the study area were surveyed. Meanwhile, the Bibijan hydrometric station was chosen to continue the investigation since it has a lengthy statistical period (1956 to 2017) and reliable data recording quality. The Zohreh River basin is located in Iran’s southwest (Fig. 2). According to the kind of terrain, the elevation of the Zohreh River basin can be divided into three categories: i) the basin’s high and mountainous sections in the north and northeast, ii) in the middle of the basin, there are submontane sections and semi-high hilly lands and iii) in the southern and southwestern parts of the basin, there are flat plains and lowlands. The basin has a maximum height of 3688 m and a minimum height of zero meters. With an average annual volume of 1655 million cubic meters, the Zohreh River is one of the most water-rich rivers in southwestern Iran, and it plays a vital role in the region’s economy and agricultural operations. In order to estimate the monthly streamflow of the Zohreh River, the data were divided into training and testing phase. Out of the 732 months recorded at the Bibijan (BJ) hydrometric station, 588 months (80% of data) were used for training and 144 months (20%) for model testing. Figure 3 depicts the time-series graphs of the observed monthly streamflow data at BJ station.

Fig. 2

Locations of the Zohreh River basin and considered hydrometric station in Iran

Fig. 3

Time series of the observed monthly streamflow data at Bibijan (BJ) station

Performance evaluation metrics

The root mean square error (RMSE), normalized root mean square error (NRMSE), mean absolute error (MAE), and Kling–Gupta efficiency (KGE) were implemented to assess the performance of the developed hybrid models in modeling the monthly streamflow. These four performance metrics are specified as follows:

$$ {\text{RMSE}} = \left( {\frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{n}} \right)^{0.5} $$

(14)

$$ {\text{NRMSE}} = 100 \times \frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } } }}{{O_{\max } - O_{\min } }} $$

(15)

$$ {\text{MAE}} = \frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{n} $$

(16)

$$ {\text{KGE}} = 1 - \sqrt {({\text{CC}} - 1)^{2} + (\frac{{P_{{{\text{SD}}}} }}{{O_{{{\text{SD}}}} }} - 1)^{2} + (\frac{{\overline{P} }}{{\overline{O} }} - 1)^{2} } $$

(17)

where $O_{i}$ are observed values, $P_{i}$ are estimated values, $\overline{O}$ and $O_{SD}$ represent the average and standard deviation of recorded monthly streamflow, $\overline{P}$ and $P_{SD}$ denote the average and standard deviation of estimated streamflow, $O_{\max }$ and $O_{\min }$ are maximum and minimum of observed data, CC is the correlation coefficient between observed and estimated streamflow and, n is the number of data. The developed hybrid model is selected as the most appropriate option for monthly streamflow prediction that has the lowest (highest) values of RMSE, NRMSE, and MAE (KGE).

Results

Data decomposition

The VMD, EMD, and CEEMD methods were used in this study to analyze streamflow time series. The proper decomposition level K and the penalty parameter for balancing the data-fidelity requirement α are two crucial parameters that must be set for the VMD approach (Meng et al. 2021). The bandwidth of IMFs is specified by α. Wider bandwidth is produced by a higher value of α, which is discovered through trial and error (Li et al. 2022). In this study, various values between 10 and 2000 were investigated, and ultimately α = 1000 produced the best results when monthly streamflow data were analyzed.

The number of VMD implementation steps is determined by choosing the appropriate decomposition level (K). The performance of the models is compromised if only a few decomposition levels are chosen since not all the data from the time series are retrieved. However, if a high level of decomposition is used, the original time series will be over-decomposed, and several IMFs will share the same information. The suitable K was chosen in this study by decomposing streamflow data from tow to nine levels using VMD. Then, for each IMF, central frequency diagrams were plotted. Figure 4 illustrates the outcomes of data analysis at various decomposition levels and their central frequencies. This figure shows that at level eight of decomposition, the center frequencies are close to one another, and there are no modal disruptions. Nevertheless, at the level of decomposition nine, mode mixing takes place. As a result, K should be set to eight (K = 8) for assessing the monthly streamflow data of the Zohreh River basin. Figures 5 and 6 show the outcomes of data decomposition using EMD and CEEMD methods, respectively.

Fig. 4

Results of monthly streamflow data decomposition using the VMD method

Fig. 5

Results of monthly streamflow data decomposition using the EMD method

Fig. 6

Results of monthly streamflow data decomposition using the CEEMD method

Input variables selection

Forecasting results are directly impacted by the kind and quality of input data. As a result, choosing the right approach for evaluating input data is crucial. The PACF approach was employed as a recognized technique to determine the optimum number of inputs for the RF and KS models (He et al. 2019). The PACF diagrams for the IMFs of the VMD approach are shown in Fig. 7. The suitable lag, as shown by this figure, begins at tow delays and go up to seven lags. Also, PACF diagrams were drawn for IMFs obtained by CEEMD, and EMD methods and the appropriate number of inputs were selected. The final results of determining the number of optimal inputs for the original time series of monthly streamflow and IMFs obtained from the decomposition methods are presented in Table 1.

Fig. 7

PACFs of the original streamflow data and the IMF series obtained by VMD at the Bibijan station

Table 1 Input features and output targets for VMD, CEEMD, and EMD decomposition sequences of raw data and their decomposition sequences at the Bibijan station

Results of standalone and hybrid models

The appropriate lag for the initial streamflow time-series modeling is equal to three, as shown in Table 1. The RF and KS models were subsequently examined with up to five delays. Table 2 displays the statistical results of the monthly streamflow forecast utilizing standalone models. The RMSE index in the test phase decreases with increasing lag in this table. In the fourth and fifth lags, the RMSE increases. These results demonstrate that the PACF approach performs satisfactorily in identifying the proper inputs. The best performance was achieved by the RF and KS models with the three lags input. The RMSE values for the KS and the RF method in the test phase may be compared, and it can be seen that they are 32.18 (m³/s) and 34.56 (m³/s), respectively. Additionally, when considering additional evaluation metrics, it is evident that the KS model performed better than the RF.

Table 2 The performance of various estimation models during the testing period for the Bibijan station in ZR basin. The best model, KS(3), is shown in bold

As can be seen from Table 2, the standalone approaches have a very large modeling error. In this study, a hybrid technique based on signal preprocessing was developed to increase the modeling accuracy. The data were initially decomposed for this purpose using VMD, EMD, and CEEMD methods. The RF and KS approaches were then used to model the obtained IMFs. The appropriate inputs were utilized to model IMFs using PACF. Tables 3 presents the statistical findings of the hybrid technique for estimating IMFs using RF and KS methods. This table shows that the RF model outperforms the KS model at predicting IMFs obtained using the VMD technique. For instance, in IMF4, the RF model’s RMSE value is 9.55, while the KS model’s RMSE value is 12.45. Additionally, IMFs four and five are the subjects of the most significant modeling error. This demonstrates that the performance of RF and KS models is most affected by the information gleaned from these IMFs. Therefore, if the original data are not decomposed, the machine learning models will receive less usable data.

Table 3 Statistical results of RF and KS models in estimating IMFs obtained from VMD, CEEMD, and EMD methods for monthly streamflow in the test phase

A radar diagram was utilized to more effectively assess how well the RF and KS models performed in estimating IMFs obtained using various decomposition techniques (Fig. 8). The RMSE index is depicted in Fig. 8. As can be seen, the RMSE index in estimating the IMFs of the VMD method varies between 0.83 and 12.45. However, the modeling error (RMSE index) for the EMD and CEEMD approaches varies from 0.26 to 31.78. Additionally, the RF model outperformed the KS technique in estimating the IMFs of the VMD method. In contrast, the KS model had a significant advantage over the RF method in estimating the IMFs obtained from EMD and CEEMD methods.

Fig. 8

The radar graph of the RMSE index for estimating IMFs obtained from VMD, EMD, and CEEMD methods using RF and KS models in the test phase

After modeling the IMFs using RF and KS models, the estimated series were combined, and the predicted monthly streamflow time series was reconstructed. Table 4 illustrates the statistical outcomes of hybrid and standalone models. This table shows that when compared to the standalone RF and KS models, the decomposition-based hybrid models are more accurate and less error-prone. Performance of standalone models and EMD-based method is pretty similar. In other words, using the EMD method for data analysis has not improved the information that the RF and KS models receive and has had almost no positive impact on increasing prediction accuracy. This is the result of EMD’s improper data decomposition. However, the performance and accuracy of RF and KS models have significantly improved with the adoption of CEEMD, and VMD approaches. For instance, the VMD-RF technique reduces the RMSE of the RF model from 34.56 to 13.76 (m³/s). At the same time, the RMSE is decreased from 32.18 to 14.76 (m³/s) for the VMD-KS hybrid model. Compared to VMD-RF and VMD-KS models, the performance increase for CEEMD-RF and CEEMD-KS hybrid models was less. The CEEMD-RF technique can only cut the RMSE index by 1.2 (m³/s), whereas the CEEMD-KS reduced RMSE by 5.37 (m³/s).

Table 4 Statistical results of hybrid and standalone models in predicting monthly streamflow in the test phase

Figure 9 shows the time series and scatter plots for the best case of standalone (KS(3) and RF(3)) and hybrid (VMD-RF and VMD-KS) models. This figure demonstrates that the standalone RF(3) model performs better than the KS(3) technique in estimating the maximum values. Additionally, a significant dispersion is visible around the one-to-one line in the scatter plots of both standalone models. Monthly streamflow estimation has been improved when using the hybrid technique and VMD data decomposition method. In the scatter plot, the observed streamflow and data from the VMD-RF model are close to the one-to-one line. Furthermore, hybrid VMD-RF and VMD-KS models are significantly better at estimating maximum values than single models. When the performance of the hybrid models is compared, it is clear that the VMD-KS technique still performs poorly at estimating maximum values and is unable to make reliable predictions. The distribution of the predicted and observed data cannot be fully understood from time series and scatter plots. Additionally, statistical indicators only represent model performance in numerical terms and offer no interpretation of the data’s mean or variation. Therefore, it is essential to examine the distribution of predicted values in order to better comprehend the performance of the studied models. The performance of the models can be assessed by comparing the distribution of observed and estimated data.

Fig. 9

Time-series and scatter plots of the observed against the modeled streamflow of the BJ station for the best hybrid and standalone models during the test phase

One technique for displaying the distribution of data and covering the shortcomings of scatter plots and statistical indicators is using violin plots. Another type of box plot is the violin plot. The violin plot is used to demonstrate the data distribution and probability density, while the box plot only displays the lowest, maximum, mean, and quarters of the data. Figure 10 shows the violin diagram for the best standalone and hybrid models. According to this figure, it is observed that single models have estimated the maximum values in the test phase more negligible than the observational values, which is a drawback of single models. Additionally, the KS(3) model performs the worst when estimating maximal values. It is clear by comparing the VMD-RF and VMD-KS violins that the estimation of maximum values in both models has significantly improved. However, the VMD-RF approach has been far more effective in this regard. Thus, it can be inferred from the justifications given that the VMD-RF model is the best suitable technique for forecasting the monthly streamflow.

Fig. 10

Violin plot of the best hybrid and standalone models in the test phase to predict the monthly streamflow

Discussion

In this research, hybrid models were constructed using the VMD, CEEMD, and EMD approaches. The outcomes demonstrated that RF and KS model performance could be enhanced by data preprocessing in general. Additionally, the findings indicate that, compared to other hybrid models developed in this study, the VMD-RF and VMD-KS models were more effective in estimating monthly streamflow. Similar findings have been reported by He et al. (2020), Hu et al. (2021), and Meng et al. (2021). The studies mentioned above demonstrate how hybrid models developed using the VMD approach have improved maximum values prediction. He et al. (2019) developed hybrid models based on EMD, EEMD, and VMD to forecast the daily streamflow of the Jing River in China. They stated that while estimating daily streamflow, the VMD-based model performed better. In other words, it can be concluded that, regardless of time scale, combining data-driven models with the VMD technique can provide better results. The findings of this study demonstrate that, in comparison with EMD and CEEMD, the VMD technique offers data-driven models better information.

One of the most widely employed techniques for developing hybrid models is the wavelet transform (Rahmati et al. 2020; Song et al. 2021). Considering studies like Saraiva et al. (2021), Ahmadi et al. (2022), Momeneh and Nourani (2022), and Yilmaz et al. (2022) as a comparison, it can be seen that wavelet transform is also quite effective in enhancing the performance of data-driven models. However, while applying the wavelet transform, the various mother wavelet functions must be compared, and the best ones for the data must be chosen. Due to the increase in processing steps, this is a significant restriction on using the wavelet transform method. In addition, selecting of the appropriate decomposition level in the wavelet transform method depends only on the number of data and no other variables are considered. In contrast, the VMD method does not require external functions to decompose the data, and its appropriate decomposition level can be easily identified based on the central frequency of the IMFs.

The non-stationary of the observed data is one of the substantial challenges that affects the performance of machine learning techniques. Decomposed based methods such as VMD can significantly reduce the non-stationary of the time series by smoothing the data (Lin et al. 2021). However, if the time-series decomposition approach is directly applied to the entire data set, the details related to the verification data will be included in the training data. In other words, using overall decomposition methods to train the model might be influenced by future knowledge, which would create an issue with backward induction and produce incorrect conclusions (Zhang et al. 2015). In the present study, this issue was resolved using an ensemble method for training models. The ensemble modeling method has been used and successfully tested in the investigations of He et al. (2019) and He et al. (2020), which is compatible with the findings of this study.

Conclusion

The RF and KS models have been used extensively in streamflow prediction. However, earlier research seldom took the data features into account while building the model, and prediction accuracy might still be increased. In this study, a hybrid monthly streamflow prediction approach based on data decomposition principles was presented to enhance the performance of monthly streamflow prediction, reduce the non-stationarity of the time series, and fully mine the embedded knowledge of the hydrological data. This method combines VMD, EMD, CEEMD, RF, and KS. The four phases for developing the hybrid models are as follows: (1) decomposing original monthly streamflow with VMD, EMD and CEEMD; (2) determination of the input variable using PACF; (3) developing hybrid decomposition based RF and KS models; and (4) ensemble predicted IMFs.

The findings demonstrated that the proposed model effectively extracts the characteristic data about the streamflow series while minimizing the non-stationarity and complexity of the original runoff series as well as its prediction difficulty. The proposed model uses VMD to decompose the original monthly streamflow series into some IMF components with low complexity and strong periodicity.

The VMD-RF and VMD-KS models are compared with four different models, namely RF, KS, EMD-RF, EMD-KS, CEEMD-RF, and CEEMD-KS. When comparing the studied models, hybrid techniques outperformed single models. EMD-based hybrid models, meanwhile, demonstrated poor performance. The VMD-RF model showed the best performance in predicting monthly streamflow. In comparison with the random forest model, this model was able to reduce the RMSE index by 60% and produce the most accurate forecast. In general, the accuracy has been much improved by combining the RF and KS models with the VMD approach.

The hybrid models developed in this study integrate data preprocessing techniques with machine learning methods to create a streamflow forecasting model that is more suited to being a practical and effective soft computing model to forecast streamflow series. It is recommended that VMD-based hybrid models be applied to forecast more hydrological parameters in subsequent studies. It is also advised to carry out more research on predicting streamflow using additional decomposed hydrological data. Future researches can also examine the impact of statistical period length on the VMD method’s analytical accuracy.