Introduction

Climate changes has significant effects on the earth and environment. Population growth has increased water demand for agricultural and food products. Agriculture is a sector that has been greatly affected by climate changes. These changes may adversely affect water resources and consequently water quality in arid and semi-arid regions and exacerbate water stress in these areas.

Increasing of EC in recent years has significantly reduced water quality in arid regions. Because of the global warming in the recent years, the PCP and flow discharge of the rivers in the Khuzestan province of Iran decreased and EC of water increased. Therefore, different scenarios must be considered for determining EC in the future. The following mentions some of the studies concerning the effect of climate change on the hydrological regime and quality of surface water.

Doulabian et al. (2021) evaluated the impact of climate change on the PCP and Tmean in Iran using representative concentration pathway (RCP) scenarios for the 2046–2065 period. According to their results, the Tmean is likely to rise in all months of the year. On the other hand, high uncertainty in the PCP parameter was observed in the simulation of the seasonal climate model. These results showed the importance of selecting a combination of GCMs in order to evaluate future changes in the weather of Iran. Birkinshaw et al. (2017) studied the effects of climate change on the runoff of the Yangtze River. They used 35 GCMs from the coupled model intercomparison project-phase 5 (CMIP5) report to examine the impact of climate change on the river during 2041–2070. The results of most of the GCMs indicated an increase in PCP for most months. The GCMs predicted a considerable rise for Tmean in the future period. Lotfirad et al. (2021) examined the effect of climate change on the runoff and hydrological drought trends in the Hableh Rood basin in central Iran. For this purpose, they utilized the daily minimum-temperature (Tmin), maximum-temperature (Tmax) and Tmean time series in the historical period (1982–2005). The results indicated maximum increases of 1.87 °C and 1.8 °C for Tmin and Tmax, respectively, in the south of the basin under the RCP8.5 scenario. The largest decrease in PCP is 54.88% in August under the RCP4.5 scenario. Based on the results, the annual runoff under the RCP4.5 and RCP8.5 scenarios decreases by 44.11% and 13.13%, respectively, relative to the historical period. Zamani and Berndtsson (2019) evaluated CMIP5 GCMs in southern and southwestern Iran using the technique for order of preference by similarity to ideal solution (TOPSIS) method. Bekele et al. (2021) evaluated the effect of climatic changes on river flow discharge in the Arjo-Didessa basin (upstream of the Nile watershed). They utilized the outputs of four climate models under the RCP4.5 and RCP8.5 scenarios. The results of the climate models for the future period (2041–2070) indicated that the climate change effects are fully dependent on the season. Specifically, the runoff increases during rainy seasons and decreases during dry seasons. The variations predicted under RCP8.5 were larger than those under RCP4.5.

In recent years, the following studies evaluated effects of climatic changes on runoff and EC:

Naderi and Saatsaz (2020), Okwala et al. (2020), Choudhury et al. (2022), Plunge et al. (2021), Al-Safi and Sarukkalige (2020), Donyaii (2021), Nourani et al. (2020), Nazari-Sharabian et al. (2019), Liu and Mizzi (2020), Fallah-Ghalhari et al. (2019), Fereidoon and Koch (2018) and Sinsin et al. (2022) applied different GCMs and estimated changes of PCP, Tmean, runoff or salinity in the future under different RCP scenarios.

This research studied the effect of climate change on the quality of the runoff of the Marun watershed as one of the most important watersheds of Iran. The relationship between runoff and EC changes in a large river (the main river of the watershed) in the future periods under the influence of climate change had not been studied in previous research. The Marun River is a tributary of the Jarrahi River. It supplies water to numerous cities and villages, thousands of hectares of agricultural land, gardens, groves, industrial zones, and a major part of the Shadegan Lagoon.

The objectives of this research are as follows:

  1. 1.

    Dividing the whole watershed into 5 regions and determining the best GCMs in each region using the TOPSIS technique

  2. 2.

    Combining the best GCM via KNN, projecting the PCP and Tmean of each region, and determining the regions that have the largest changes in PCP and Tmean under the RCP4.5 and RCP8.5 scenarios in the near and far future periods

  3. 3.

    Predicting the runoff in the Marun watershed and investigating about seasonal changes of runoff under the RCP4.5 and RCP8.5 scenarios in the near and far future

  4. 4.

    Establishing a suitable relationship between the flow discharge and EC and predicting the EC of the river in future periods

The novelties of this research are as follows:

  1. 1.

    Using the TOPSIS method for selecting the superior GCM and the KNN technique for combining the GCMs in order to simulate Tmean and PCP in the Marun watershed

  2. 2.

    Employing the MARS method to determine the relationship between runoff and EC in future periods

Materials and methods

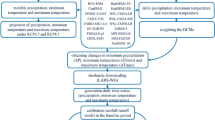
Stages of this study and research methodology flowchart

This study used the Tmean and PCP outputs of 35 downscaled GCMs from Coupled Model Intercomparison Project, Phase 5 (CMIP5). Unlike other GCM models, only these 35 models present Tmean and PCP data under RCP 4.5 and 8.5. This study uses identification of unit hydrographs and component flows from rainfall, evaporation and streamflow data (IHACRES) rainfall-runoff model for simulating runoff and this model needs to Tmean and PCP for this purpose. Therefore, other meteorological variables such as Tmin and Tmax were not considered.

The extracted PCP and Tmean data of the climate models in historical period (1966 to 2005) were compared with the observed PCP and Tmean. Then, the Nash–Sutcliffe efficiency (NS), ratio of root mean square error (RMSE) to the standard deviation of the observations (RSR), S-Taylor (ST), and mean absolute error (MAE) were calculated as performance criteria and GCMs were ranked using the TOPSIS method based on the performance criteria, and ten of the best GCMs were selected. Moreover, the GCMs were weighted using the KNN method, and the Tmean and PCP were obtained under RCP4.5 and RCP8.5 emission scenarios for the 40-years periods (2020–2059 and 2060–2099). These values were introduced as input to the calibrated IHACRES model for determine the runoff in the future periods. A relationship between the flow discharge and the EC during the historical period was obtained by the MARS technique. This equation was used to estimate EC in future periods. A flowchart of the research methodology is illustrated in the following (Fig. 1).

Fig. 1
figure 1

The research methodology flowchart

Full size image

Case study

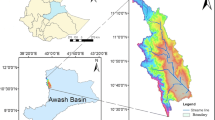
The Marun watershed is located in the southwest of Iran (49° 50′ to 51° 10′ E and 30° 30′ to 31° 20′ N). The area, average elevation, and slope of the watershed are 5401 km2, 1654 m (asl), and 1.4%, respectively. Moreover, this watershed is an arid region according to the Köppen climate classification (Köppen 1884). In addition, the minimum, mean, and maximum annual temperatures and the mean annual PCP are  − 6 °C, 22.8 °C, 53.3 °C, and 646.51 mm, respectively (Adib et al. 2021). The Idenak hydrometry station upstream of the Marun dam (in center of the watershed) records the flow discharge and EC of the Marun River, and the Idenak evaporation station records the PCP and temperature. The locations of these stations are illustrated in Fig. 2. The mean seasonal of Tmean is 12.1, 21.59, 33.26 and 24.38 °C and the mean seasonal of PCP is 411.94, 153.29, 1.05 and 80.23 mm in winter, spring, summer and fall, respectively. Also, The mean seasonal of flow discharge is 72.37, 90.06, 22.42 and 17.27 m3/s in winter, spring, summer and fall, respectively.

Fig. 2
figure 2

a The regions of the Marun watershed b The rivers of the Marun watershed and its location in Iran (Emamgholizadeh et al. 2011)

Full size image

In recent years, in the downstream areas of the watershed, EC has had a significant impact on the quality of drinking and agricultural water and has caused many economic, social and environmental problems for the people living in the downstream of the watershed. The EC is the best representative of mineral pollutants, whose increase leads to a decrease in water quality for various uses, too. Then, it is necessary to evaluate EC changes in future periods for water resources management and planning.

Data

The Idenak station locates in center of the Marun watershed (50° 28’ E and 30° 57’ N). The height of this station is 610 m (asl). The Iranian Ministry of Energy prepared daily data of this station for present study.

For the climatic modeling, the PCP and Tmean data of 35 CMIP5 GCMs were used for the historical, F1 and F2 periods. Also, the reanalysis climate research unit (CRU) data were utilized as the historical period data after bias correction. The Marun watershed divided into 5 regions with a resolution of 0.5° × 0.5° based on spatial resolution of the GCMs and the CRU. The Tmean and PCP data of the Idenak station in Region 3 were compared with data in the corresponding CRU cell. In order to increase the accuracy of the data, the CRU Tmean and PCP values were bias-corrected using linear regression. Finally, the R2 and RMSE of the CRU cell corresponding with the Idenak station (Region 3) were equal to 0.994 and 0.99 °C, respectively, for Tmean and 0.921 and 30.4 mm, respectively, for PCP. 480 EC and flow discharge data had been recorded during the historical period.

The difference between RCP4.5 and RCP8.5 scenarios

The Intergovernmental Panel on Climate Change (IPCC) fifth Assessment Report (AR5) presented these scenarios in 2014. The radiative forcing values in the year 2100 are 4.5 and 8.5 Watt/m2 for RCP4.5 and RCP8.5 respectively. RCP4.5 is an intermediate scenario. CO2, CH4 and SO2 emissions will peak around 2040 and then decline. By 2100, the average global temperature will rise between 2.5 and 3 °C compared to pre-industrial levels.

RCP8.5 is the worst scenario for global warming and climatic change in the future. CO2, CH4 and SO2 emissions continue to rise throughout the 21st century. By 2100, the average global temperature will rise 5 °C compared to pre-industrial levels (IPCC 2014).

Performance criteria

Correlation coefficient (r):

The correlation coefficient lies between  − 1 and  + 1. The correlation coefficient is determined from Eq. (1).

$$r = \frac{{\sum {\left( {X_{Cal} - \overline{X}_{Cal} } \right)\left( {X_{Obs} - \overline{X}_{Obs} } \right)} }}{{\sqrt {\sum {\left( {X_{Cal} - \overline{X}_{Cal} } \right)^{2} \sum {\left( {X_{Obs} - \overline{X}_{Obs} } \right)^{2} } } } }}$$
(1)

In the above equation, Xcal represents the value of the simulated variable, Xobs is the value of the observed variable, \(\overline{{X_{Cal} }}\) expresses the average value of the simulated variables, and \(\overline{{X_{Obs} }}\).denotes the average value of the observed variables.

RSR:

RSR is calculated using Eq. (2). In fact, it is the ratio of the RMSE to the standard deviation of the observed data.n expresses the number of months in the historical period. Moreover, RSR = 0 represents the optimal value and RSR > 0.7 indicates bad performance by the model (Moriasi et al. 2007).

$$RSR = \frac{RMSE}{{STDEV_{Obs} }} = \frac{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {X_{Obs} - X_{Cal} } \right)^{2} } } }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {X_{Obs} - \overline{{X_{Obs} }} } \right)^{2} } } }}$$
(2)

Mean absolute error (MAE):

MAE is calculated using Eq. (3). The lower MAE values, indicating the better performance of the model in simulating data (Adib et al. 2019).

$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\left( {X_{Cal} - X_{Obs} } \right)} \right|}$$
(3)

Nash–Sutcliffe efficiency coefficient (NS):

The NS values lie between −∞ and 1. A range between 0.5 and 1 is acceptable, while the best value of NSE is one. The NS coefficient is determined from Eq. (4) (Moriasi et al. 2007).

$$NS = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left( {X_{Obs} - X_{Cal} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {X_{Obs} - \overline{{X_{Obs} }} } \right)^{2} } }}$$
(4)

S-Taylor:

The S-Taylor is calculated from Eq. (5). R is the correlation coefficient between the observaed and simulated data, R0 is the theoretical value of the correlation coefficient, σ represents the ratio of the standard deviation of the simulated data to that of the observed data, and k is a constant that taken equal to 4 for Tmean and 2 for PCP.

The ideal value of the S-Taylor index is 1 when R and σ equal 1.

When R equals −1, the S-Taylor will equal zero (Esmaeili-Gisavandani et al. 2022; Zamani and Berndtsson 2019).

$$S_{T} = \frac{{4\left( {1 + R} \right)^{k} }}{{\left( {\sigma + \frac{1}{\sigma }} \right)^{2} \left( {1 + R_{0} } \right)^{k} }}$$
(5)

Kling Gupta efficiency (KGE) evaluation criterion:

Gupta et al. (2009) introduced this criterion and compared its advantages with those of NS. Later, this criterion was revised by Kling et al. (2012). This criterion is determined by Eq. (6), where r is the correlation coefficient between the simulated and observed data, α is the ratio of the standard deviation of the simulated data to that of the observed data, and β represents the ratio of the average of the simulated data to that of the observed data.

$$KGE = 1 - \sqrt {(r - 1)^{2} + (\alpha - 1)^{2} + (\beta - 1)^{2} }$$
(6)

The TOPSIS method

The steps in the TOPSIS method are as follows Hwang and Yoon (1981):

  • Step 1 Configuring the decision matrix consisting of m alternatives and n criteria:

    $$a_{ij} = \left[ {\begin{array}{*{20}c} {a_{11} } \\ {a_{12} } \\ \vdots \\ {a_{m1} } \\ \end{array} \begin{array}{*{20}c} {a_{12} } \\ {a_{22} } \\ \vdots \\ {a_{m2} } \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ {} \\ \cdots \\ \end{array} \begin{array}{*{20}c} {a_{1n} } \\ {a{}_{2n}} \\ \vdots \\ {a_{mn} } \\ \end{array} } \right]$$
    (7)

  • Step 2 Normalizing the matrix array using the following relationship:

    $$r_{ij} = \frac{{a_{ij} }}{{\sqrt {\sum\nolimits_{i = 1}^{m} {a_{ij}^{2} } } }}$$
    (8)

\({a}_{ij}\) and \({r}_{ij}\) represent the main and normalized elements of the decision matrix.

  • Step 3 Determining the weight of the criteria consisting of \(\sum_{i=1}^{n}{w}_{i}=1\) and multiplying the weights by the normal state

    $$v_{ij} = \left[ {\begin{array}{*{20}c} {w_{1} r_{11} } \\ {w_{1} r_{12} } \\ \vdots \\ {w_{1} r_{m1} } \\ \end{array} \begin{array}{*{20}c} {w_{2} r_{12} } \\ {w_{2} r_{22} } \\ \vdots \\ {w_{2} r_{m2} } \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ {} \\ \cdots \\ \end{array} \begin{array}{*{20}c} {w_{n} r_{1n} } \\ {w_{n} r{}_{2n}} \\ \vdots \\ {w_{n} r_{mn} } \\ \end{array} } \right]$$
    (9)

  • Step 4 The distance of Alternative i from the positive ideal \({A}^{+}\) and the negative ideal \({A}^{-}\)

Positive ideal:

$$A^{ + } = \left\{ {\left. {\left( {\max \,v_{ij} |\,j \in J} \right),\left( {\min \,v_{ij} |j \in J^{^{\prime}} } \right)} \right\}} \right.$$
(10)
$$A^{ + } = \left\{ {v_{{_{1} }}^{ + } ,v_{2}^{ + } } \right., \ldots ,\left. {v_{n}^{ + } } \right\}$$
(11)

Negative ideal:

$$A^{ - } = \left\{ {\left. {\left( {\min \,v_{ij} |\,j \in J} \right),\left( {\max \,v_{ij} |j \in J^{^{\prime}} } \right)} \right\}} \right.$$
(12)
$$A^{ - } = \left\{ {v_{{_{1} }}^{ - } ,v_{2}^{ - } } \right., \ldots ,\left. {v_{n}^{ - } } \right\}$$
(13)

  • Step 5 Determining the distance criteria for the positive ideal \({S}_{i}^{+}\) and the negative ideal \({S}_{i}^{-}\)

    $$S_{i}^{ + } = \sqrt {\sum\limits_{j = 1}^{n} {(v_{ij} - v_{j}^{ + } )^{2} } }$$
    (14)
    $$S_{i}^{ - } = \sqrt {\sum\limits_{j = 1}^{n} {(v_{ij} - v_{j}^{ - } )^{2} } }$$
    (15)

  • Step 6 Calculating the relative equation including \(S_{i}^{ + }\) and \(S_{i}^{ - }\)

    $$C_{i}^{*} = \frac{{S_{i}^{ - } }}{{S_{i}^{ - } + S_{i}^{ + } }}$$
    (16)

  • Step 7 Ranking the preferences based on descending \({C}_{i}^{*}\) values such that \({C}_{i}^{*}=1\) corresponds to the best rank and \({C}_{i}^{*}=0\) corresponds to the worst rank (Farajpanah et al. 2020).

KNN weighting method

KNN observational temperature-precipitation averaging is a method that can weigh the obtained Tmean or PCP from several GCMs in various months and create a combination of GCMs for the Tmean or PCP.

The KNN method extracts weights according to the distance between the variable (Tmean or PCP) derived from each GCM during the historical period and the corresponding observational value in each month, such that a weight is obtained for each model in each month. In this method, for each variable (Tmean or PCP), GCM, whose monthly long-term average is closer to the observed monthly long-term average, weighs more in that month. The weights for each month are calculated using Eqs. (17–20).

$$\Delta T_{m} = \mathop \sum \limits_{{G_{i} = 1}}^{n} \left( {WT_{m}^{{G_{i} }} \times TCF_{{G_{i} }} } \right)$$
(17)
$$TCF_{G} = \left( {\left( {\overline{T}_{m}^{F} } \right)_{{G_{i} }} - \left( {\overline{T}_{m}^{B} } \right)_{{G_{i} }} } \right)$$
(18)
$$\Delta P_{m} = \mathop \sum \limits_{{G_{i} = 1}}^{n} \left( {WP_{m}^{{G_{i} }} \times PCF_{{G_{i} }} } \right)$$
(19)
$$PCF_{G} = \left( {\frac{{\left( {\overline{P}_{m}^{F} } \right)_{{G_{i} }} }}{{\left( {\overline{P}_{m}^{B} } \right)_{{G_{i} }} }}} \right)$$
(20)

In the above equations, \(TCF_{G}\) represents the difference in Tmean between the future and historical periods for each GCM.

Moreover, \(PCF_{G}\) denotes the difference in PCP between the future and historical periods for each GCM.

Also, \(\left( {\overline{P}_{m}^{F} } \right)_{Gi}\) and \(\left( {\overline{T}_{m}^{F} } \right)_{Gi}\) indicate the 40-year averages of the PCP and Tmean, respectively, for each of the two future periods. n is number of GCMs. Finally, \(\Delta P_{m}\) and \(\Delta T_{m}\) express the variations in PCP and Tmean, respectively. The values estimated using Eqs. (17 and 18) are considered as a middle pattern for all the GCM outputs since their results are the most valid. Therefore, the middle climate change pattern is referred to the \(\Delta P_{m}\) and \(\Delta T_{m}\) values.

As a result, the GCM values are re-corrected. The GCMs whose TCFG value was smaller than ΔTm and whose PCFG value was larger than ΔPm are re-substituted into Eqs. (17 and 18). Finally, the climate change scenarios are applied to the observed values during the historical period according Eqs. (21 and 22) to calculate the Tmean and PCP values.

$$T_{i,j} = T_{Obs,j} + \Delta T_{i,j}$$
(21)
$$P_{i,j} = P_{Obs,j} + \Delta P_{i,j}$$
(22)

In these equations, \({T}_{i,j}\) and \({P}_{i,j}\) denote the predicted Tmean and PCP, respectively, of the ith model in the jth month during the future period. Furthermore, \({T}_{obsj}\) and \({\mathrm{P}}_{\mathrm{obs}j}\) are the Tmean and PCP in the jth month during the historical period.

IHACRES rainfall-runoff model

The IHACRES model (a lumped and continuous model), introduced by Jakeman and Hornberger (1993) is a conceptual integrated model for simulating rainfall-runoff. It has been successfully used in basins of various sizes (490 m2 to 10,000 km2). The application of this model is very simple and does not require a large number of parameters as input.

The most significant advantage of this model compared to other simulation models, which are mostly complex, is its good accuracy combined with its minimal use of input data and its simple structure. Hence, it has been recommended for arid and semi-arid regions. This model consists of a linear and a nonlinear unit hydrograph module. Esmaeili-Gisavandani et al. (2021) compared application of several lumped models such as IHACRES and the Soil and Water Assessment Tool (SWAT) model. The SWAT model is a distributed model. The IHACRES model simulated runoff well. Considering the shortage of meteorological and hydrometric data in Iran, the IHACRES model is a suitable tool for simulating runoff in semi-arid regions of Iran.

Multivariate adaptive regression splines (MARS) method

The MARS method was developed by Friedman (1991). This method is applied for detecting the hidden nonlinear pattern in datasets with a large number of variables. This technique aims to study the impact of independent variables on the dependent variable. MARS is employed to identify nonlinear relationships. The MARS method finds first the knots and then the straight lines between these knots and guarantees a continuous and classified response. The analysis of MARS method is carried out in two steps. First, all the possible basis functions are created. Second, the basis functions adversely affecting the model are eliminated from the model by the system.

This method is based on certain functions, called basis functions, which are defined as follows for each explanatory variable:

$$\max \left\{ 0 \right.,\left. {x - t} \right\}\,\,\,and\,\,\,\max \left\{ 0 \right.,\left. {t - x} \right\}$$
(23)

where t is called a knot, and x is a variable. The overall form of the MARS model is defined as follows:

$$Y = C_{0} + \sum\limits_{k = 1}^{M} {C_{k} B_{k} (X)}$$
(24)

In this equation, Y is the dependent variable, X represents the independent variable, \({C}_{0}\) is the constant term, Bk denotes the basis function, and Ck are coefficients determined by minimizing the residual sum of squares. Every basis function can be a linear spline function or a multiple of two or more of them, which represents mutual interaction. In the MARS method, the explanatory variable space is divided into separate regions using special knots that have produced the largest reduction in the mean squared error.

The reasons of selection of the MARS method in this study are:

  • High speed and automatic run (the MARS method can automatically separate relevant variables from unrelated variables and guarantees a correct and classified answer)

  • Determining the interrelationships between outputs and inputs of model

  • Performing additional testing to avoid overfitting

  • The output of the MARS method consists of a regression model that is easily extensible and can be applied to new inputs.

Results and discussion

Comparison of the CRU and observed data in the Idenak synoptic station and bias correction

In the first step, the data were sorted for historical period. Since there were gaps in collected data in the Idenak synoptic station, the CRU reanalysis data were used. The RMSE values for the estimated PCP and Tmean were calculated by comparing the collected data in the Idenak station (Region 3) and the corresponding CRU reanalysis data. In addition, the CRU PCP and Tmean data were adjusted according to the observed data to reduce the error in estimating the CRU reanalysis data in Idenak station. Two nonlinear regression equations were created, one for reducing the reanalysis Tmean error and the other for reducing the reanalysis PCP error.

These equations are:

$$P_{obs}^{adj} = \frac{{2259440 \times P_{CRU} }}{{866017 + P_{CRU} }}\quad {\text{For PCP}}$$
(25)
$$T_{obs}^{adj} = \frac{{10806700 \times T_{CRU} }}{{10552900 + T_{CRU} }}\quad {\text{For Tmean}}$$
(26)

Using these equations cannot increase r (for PCP, r = 0.921 and Tmean, r = 0.994). However it reduces RMSE considerably. For PCP, RMSE reduced from 61.5 mm to 30.4 mm and for Tmean, RMSE reduced from 1.15 °C to 0.69 °C.

GCMs results during the historical period and selecting the best GCM for the Idenak synoptic station region (region 3)

This study evaluated the performance of 35 GCMs in simulating the climatic variables (Tmean and PCP) in the Marun watershed. To examine the performance of each GCM, the mean long-term monthly (based on monthly downscaled time series) of each variable (Tmean and PCP) were compared to the corresponding values during the historical period. The applied performance criteria were r, RSR, MAE, NS, and ST.

The TOPSIS method was used to examine 35 GCMs. This method distinguished 10 GCMs with the highest ranks based on 5 performance criteria. Table 1 displays the highest-ranking GCMs for region 3. This table shows that the best GCM for PCP simulation is MRI-CGCM3 model with NS = 0.322, r = 0.996, RSR = 0.789, MAE = 2.688 mm and ST = 0.443. For Tmean simulation, the best model is MPI-ESM-LR model with NS = 0.932, r = 1, RSR = 0.249, MAE = 0.177 °C and ST = 0.998.

Table 1 The best GCMs in region 3 (ranked by TOPSIS method)
Full size table

Combination or weighting of the GCMs in region 3 in F1 and F2 periods

The weighting of the 10 best GCMs for the PCP and Tmean variables in Region 3 are shown in Appendix 1. As shown in Table 2 for F1 period, the variations of the monthly PCP and Tmean in Region 3 under the RCP4.5 and RCP8.5 scenarios indicated that the PCP under the RCP4.5 scenario has the largest increase, 116%, in September and the largest decrease,  − 14.27%, in January relative to the historical period. Moreover, under the RCP8.5 scenario, it experienced the largest increase, 65%, in September and the largest decrease,  − 7.7%, in January. As shown in Table 2, the variations of monthly Tmean in Region 3 in the F1 period indicate that the Tmean has largest increases, 2.294 °C, in September under RCP4.5 and 2.662 °C in September under RCP8.5.

Table 2 The monthly changes (%) of PCP and (°C) of Tmean in F1 (2020–2059) and F2 (2060–2099) periods compared to historical period (region 3)
Full size table

As shown in Table 2 for F2 period, the variations of the monthly PCP in Region 3 under the RCP4.5 scenario indicated that the PCP has the largest increase, 136%, in September compared to the historical period. This increase is 108% in September under the RCP8.5 scenario.

As shown in Table 2 for F2 period, the variations of monthly temperature in Region 3 indicated a maximum increase of 3.176 °C in September under RCP4.5 and 5.786 °C in September under RCP8.5.

The IHACRES rainfall-runoff model results

To simulate the runoff, first, the Tmean and PCP of the 5 regions of the watershed and observed flow discharge in the Idenak station during the historical period were introduced as input to the IHACRES model, and the model was calibrated (by comparison between the simulated and observed runoff). To simulate the runoff in the future periods, the Tmean and PCP time series were calculated by the Thiessen polygon method and Tmean and PCP time series in 5 regions.

Figure 3 compares the observed flow discharge in the Idenak station and the simulated flow discharge by IHACRES model in the historical period. This model has not good performance at high flows (under estimates high flows). However, it simulated low flows better than high flows. Since the number of low flows is more than high flows and the present research evaluate EC and low flows for establishment a relationship between runoff and EC, it can be said that the IHACRES model had acceptable performance. Due to the increase of EC value in drought and low flow, the IHACRES model can show high EC values well (Table 3).

Fig. 3
figure 3

Comparison between simulated and observed runoff in historical period

Full size image
Table 3 The performance criteria of IHACRES rainfall-runoff model
Full size table

The IHACRES rainfall-runoff model results for F1 and F2 periods

As shown in Fig. 4, the mean annual flow discharge in F1 period decreased, and it is almost 10.7% less than mean annual flow discharge during the historical period under the RCP4.5 scenario. For the RCP8.5 scenario, this reduction is 3.52%.

Fig. 4
figure 4

Comparison between simulated and observed mean long-term monthly flow discharge a F1 (2020–2059) period b F2 (2060–2099) period

Full size image

For F2 period, the mean annual flow discharge is 14.9% less than the mean annual flow discharge during the historical period under the RCP4.5 scenario and about 1.22% more than the mean annual flow discharge during the historical period under the RCP8.5 scenario.

The MARS method results

Using the obtained equation from the MARS method, the runoff (Q) and EC data during the historical period were normalized by the Box-Cox transformation. Then, they were introduced to the MARS method, and the future EC values were obtained. The NS, r, and RMSE are 0.5, 0.71 and 0.005 µs/cm, respectively. These values show an acceptable correlation between the two variables. Then, the obtained runoffs in F1 and F2 periods were introduced to the obtained equation from the MARS method, and the EC values in these periods were determined.

$$\begin{aligned} EC & = 1.7242 + (0.258 \times BF_{1} ) - (0.096 \times BF_{3} ) + (0.046 \times BF_{7} ) - (0.1 \times BF_{9} ) \\ & + (1.19 \times BF_{15} ) - (2.35 \times BF_{17} ) + (1.51 \times BF_{19} ) - (0.28 \times BF_{21} ) \\ & - (0.01 \times BF_{29} ) - (0.025 \times BF_{33} ) - (0.21 \times BF_{39} ) \\ \end{aligned}$$
(27)

The used Box-Cox transformation is:

$$Q_{i}^{(\lambda )} = \left\{ {\begin{array}{*{20}c} {\frac{{Q_{i}^{\lambda } - 1}}{\lambda }\,\,\,if\,\lambda \ne 0} \\ {\ln Q_{i} \,\,\,if\,\lambda = 0} \\ \end{array} } \right.$$
(28)

Results of the MARS method

Figure 5a indicates that EC will decrease in summer with an increasing in flow discharge. On the other hand, with a reduction in flow discharge in fall, EC will increase. Figure 5b indicates that the EC will decrease in spring with an increase in flow discharge. Figure 5c shows that EC will increase in fall with a decrease in flow discharge. Figure 5d shows that EC will decrease in winter with an increase in flow discharge.

Fig. 5
figure 5figure 5

Comparison between simulated and observed mean long-term monthly flow discharge and EC a F1(2020–2059) period under RCP4.5 scenario b F2 (2060–2099) period under RCP4.5 scenario c F1(2020–2059) period under RCP8.5 scenario d F2 (2060–2099) period under RCP8.5 scenario

Full size image

Results of the MARS method for different seasons

Figure 6a indicates an increase in EC with a reduction in the runoff in fall. In spring, with a decrease in flow discharge the EC will decrease. The reason of this matter is reduction of agricultural activity in future. In winter and summer, changes of flow discharge is low but the EC will decrease.

Fig. 6
figure 6

Comparison between simulated and observed mean long-term seasonal flow discharge and EC a F1 (2020–2059) period b F2 (2060–2099) period

Full size image

Figure 6b indicates an increase in EC with a reduction in the runoff in fall. In spring, with a decrease in flow discharge the EC will decrease. The reason of this matter is reduction of agricultural activity in future. In summer, changes of flow discharge and EC is low. In winter, Flow discharge will increase and EC will decrease.

Figure 6 indicates that the runoff changes have not significantly effect on EC during the historical period. Most likely, the EC of the river depends on the inflow of agricultural effluents into the river due to the increase in agricultural activities, and the flow discharge of the river did not considerably effects on the EC values. However, there is a reduction in agricultural activity in future periods under RCP4.5 and RCP8.5 due to increasing temperature and decreasing precipitation. Hence, the EC is more dependent on the flow discharge.

Discussion

Table 2 displays that Tmean will increase in F1 and F2 periods. In the F2 period, the amount of this increase is greater. This fact presents that climatic conditions get worse over time. Also, For RCP8.5 scenario, increasing Tmean is greater. This matter can show importance of preserving the environment. In summer and fall, increasing Tmean is greater (especially in summer). This can damage the agricultural activity in this watershed and make human life impossible.

Table 2 shows that PCP will increase in summer and fall. But the amount of PCP is low in these seasons (in summer, PCP is negligible). Therefore, increasing PCP in these seasons will not have a significant impact in the future.

Most of the PCP occurs from December to March in the Marun watershed. In these months, the PCP is almost constant in F1 period under RCP4.5 scenario and a small amount decreases in F2 period. However, the PCP will increase under RCP8.5 scenario (especially in F1 period). The amount of this increase is not considerable. Increasing the Tmean between 2 to 2.8 °C has the greatest effect on increasing PCP. Increasing the Tmean can increase evaporation and PCP. Increasing the Tmean by more than 3 °C prevents cloud formation and decreases PCP. The observed changes of Tmean, PCP and runoff in this study have been confirmed by Adib et al. (2021), Doulabian et al. (2021), Fallah-Ghalhari et al. (2019) and Fereidoon and Koch (2018).

The amount of runoff is dependent on the PCP (Fig. 6). The runoff is almost constant in summer and fall. It will decrease in spring (especially under RCP4.5 scenario) and the amount of this reduction is not considerable. In winter, the amount of runoff will increase under RCP8.5 scenario. Figure 6 shows that the EC will reduce in winter and spring and will increase in fall. The changes of EC is almost negligible in summer. This indicates that changes of EC is dependent on agricultural activity (importance of runoff is less than importance of agricultural activity). Because of increasing Tmean in future, agricultural activity will transfer from winter and spring to fall.

Conclusion

GCMs simulated Tmean better than PCP in the Marun watershed. The TOPSIS method showed that MPI-ESM-LR and MRI-CGCM3 models have the best performance for simulating Tmean and PCP, respectively, in the Idenak station (Region 3). The MARS method results during the F1 period under the RCP4.5 and RCP8.5 showed the maximum increase of EC will occur in July, August, September, and October, when the flow discharge has the largest decrease. Furthermore, the MARS method results during the F2 period under the RCP4.5 and RCP8.5 showed the maximum decrease of EC will occur in December, January, February, and March, when the flow discharge has the largest increase. The results of the MARS model during the historical period indicates that the runoff has not effect considerably on the EC. The reason for this matter is importance of agricultural activity in this watershed, and EC is mostly affected by the leakage of agricultural effluents into the river. The results of this study indicate a sharp increase in Tmean and evaporation in the future. Therefore, agricultural activity will reduce in the Marun watershed. This is more than the average Tmean increase in the world. This fact has been proved in recent years that increasing Tmean in the Middle East countries is more than other regions in the world. Then, protecting the environment in these countries is an essential task.