Introduction

Climate change (CC) is not a process that is just related to our era, and the Earth has always been confronted with such changes in different geological periods based on the available evidence (The Core Writing Team IPCC, 2015). The nature and acceleration of CC in the last few years are the factors that make our era distinctive relative to the previous changes. Numerous publications have investigated the mutual impact of CC on runoff in recent years. Moreover, hydrological drought causes a significant decrease in water availability in all its forms in the hydrological cycle, including streamflow (Nalbantis, 2008). Some studies have been conducted in conjunction with the effect of CC on runoff, which is referred to subsequently.

Birkinshaw et al. (2017) investigated the CC impacts on the Yangtze basin, which is among the most important rivers in China, under the Representative Concentration Pathway (RCP) 8.5 scenario during the period from 2041 to 2070, and their results represented variations of −3.6 percent to −14.8 percent in annual precipitation and variations of −29.8 percent to 16 percent in annual streamflow. Kamali et al. (2017) examined CC in the Karkheh river basin. They used the SWAT distribution hydrological model for runoff projection. They proposed the Drought Hazard Index (DHI), which is a combination of meteorological, hydrological, and agricultural droughts, and their results indicated the occurrence of drought based upon the DHI index. Carvalho-Santos et al. (2017) evaluated the effects of CC in a mountainous basin in Portugal, which indicated decreasing precipitation in spring and summer. They performed the hydrological modeling using the SWAT model for RCP 4.5 and 8.5 scenarios. They concluded that the construction of the second reservoir would lower water supply problems relative to the single-reservoir system. Zamani et al. (2017) evaluated the risk of climate change impacts on water requirement in agriculture in southwest Iran. The outcomes of the study demonstrated that the temperature would have a rising trend in all months of the future period and the precipitation variations will sometimes have decreasing and sometimes increasing trends. Also, the annual water demand for all agricultural products influenced by CC represented an increase of 4 to 10 percent. Ghimire et al. (2019) simulated the upstream daily streamflow of the Ayerawaddy River in Myanmar using the bias-corrected daily rainfall obtained from 8 general circulation models (GCM) in the HEC-HMS hydrological model. Their baseline was 1975–2014, and the projection of the future period was carried out in the intervals 2021–2060 and 2061–2100. The results indicated an upward in precipitation and monthly (except for October and November), seasonal (except for post-monsoon), annual, and decade streamflow. The high flows also increased compared to the baseline. Moghadam et al. (2019) evaluated the effect of CC uncertainty on runoff in the future period of the Khorramabad river basin utilizing five Atmospheric general circulation models (AOGCM) of the IPCC fourth assessment report. They explored the uncertainty by producing 100 time-series through the Monte Carlo method and by weighting them using the K-nearest neighbors and used the IHACRES rainfall-runoff conceptual model for estimating runoff. Maghsood et al. (2019) investigated the CC impacts on flood frequency and its source region in the Talar river basin employing 20 GCMs considering RCP 2.6 and 8.5 scenarios. They reported peak flow for the future period would increase. Vaghefi et al. (2019) evaluated the Tmin, Tmax, precipitation distribution, extreme events of temperature and precipitation, and the six largest floods resulting from them considering the statistics from 1980 to 2004 as the baseline. They applied 5 general circulation models for projection. Their results denoted a climate of extended drought conditions with intermittent heavy precipitation in such a way that some areas of Iran may become uninhabitable. Abdulai & Chung (2019) studied the meteorological and hydrological droughts caused by CC under the RCP 4.5 scenario in the Cheongmicheon watershed in South Korea. Their results referred to the occurrence of short-term severe or extreme droughts according to the Standardized Precipitation Evapotranspiration Index (SPEI) and Streamflow Drought Index (SDI). Moreover, by introducing the Reliability Ensemble Averaging (REA) technique, they also proposed a range of projections for uncertainty and reliability. Adib et al. (2021) investigated the CC impacts on the runoff inflowing to Karkheh Dam, as the biggest dam in Iran, which is located in southwest Iran. They reported an upward trend for the temperature of the Karkheh basin and a downward trend for the precipitation and streamflow of the Karkheh River. Babaeian et al. (2021) introduced a combination of adaptation pathway (AP) approaches that were used in conjunction with the SWAT model to evaluate the resilience of adaptation measures and design robust adaptation pathways taking into account the future climate uncertainty in the Hablehroud River Basin. Salimi et al. (2021) studied about effects of CC on hydrological and meteorological droughts. They used Standardized Precipitation Index (SPI), SPEI and Standard Stream flow Index (SSI) in the Navrood and Lighvan watersheds in north of Iran and observed high correlation between hydrological and meteorological droughts. Also, they concluded that CC is the most effective factor in the occurrence of future droughts. Afzal and Ragab (2020) used the Distributed Catchment-Scale Model (DiCaSM) and different hydrological and meteorological drought indices and three gas emission scenarios (low, medium and high) in the Eden catchment, north east of Scotland. They observed that CC will reduce surface water and groundwater resources (especially at the end of the twenty-first century).

Considering the studies mentioned, most of them have merely addressed the impacts of CC on runoff. Few studies have dealt with the changes in the hydrological regime and the hydrological drought. The Hablehroud river basin is in the arid and semiarid area; hence, the investigation of hydrological drought in the future period and its variations in comparison with the baseline period is of particular importance. Among the objectives followed in this study, one can refer to 1) comparing the observed and historical precipitation and temperature of GCMs in the baseline (1982–2005) and then applying climate projection using 23 Coupled Model Intercomparison Project, Phase 5 (CMIP5) and RCP 4.5 and RCP 8.5 scenarios for the future period (2025–2048), 2) applying the impact of CC on basin runoff with weighting the GCMs through K-nearest neighbors (KNN) algorithm, 3) simulating the streamflow of Hablehroud river streamflow based on the IHACRES model, 4) generating daily precipitation and temperature for the future period based upon variations in temperature and precipitation of the future period compared to the historical period using the Long Ashton Research Station Weather Generator (LARS-WG), 5) estimating the daily runoff of the future period using the daily precipitation and temperature of the future period as input to the IHACRES model calibrated with the data of baseline period and, 6) evaluating the trend and homogeneity of runoff variations in the baseline and future periods, and 7) calculating the short-, medium-, and long-term hydrological drought index and comparing them for the baseline and future periods.

Materials and methods

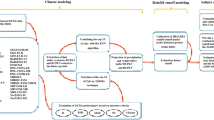
In this section, CC projection, which involves generating CC scenarios, weighting the output of the GCMs, and downscaling of GCMs using the LARS-WG model, is briefly explained. Afterward, the IHACRES rainfall-runoff model is proposed. This model is calibrated using data of baseline period, and then the runoff is obtained for the future period. The trend of monthly streamflow will also be examined. A flowchart of the procedure followed in this research is displayed in Fig. 1.

Fig. 1
figure 1

Flowchart of the methodology followed in this study

Full size image

Study area and data

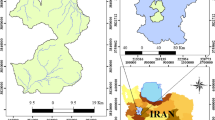
The Hablehroud Basin is located in East Tehran, north-central Iran. The main river of the basin, the Hablehroud River, originates in the Alborz Mountain Range and generally flows to the southwest and is discharged to the Garmsar Plain and the Kavir Desert (Fig. 2). The Hablehroud River has a length of 119.5 km, a drainage basin of 3261.2 km2. The average of Tmin, Tmax, PCP, and discharge of the basin, respectively, are 6.3 °C, 14.7 °C, 238 mm, and 7.6 m3/s for the period of 1982–2005. The regime of its principal tributaries, the Firuzkuh and the Namroud, is combination of rain-fed/snow-fed. Based on the climate classification procedure of Köppen-Geiger (Kottek et al., 2006), the climate of the Hablehroud Basin is mid-latitude arid (BWk) in the south, and mid-latitude semiarid (BSk) in the north (B: arid; W: desert; S: steppe; k: cold). Due to the lack of measured temperature data and its limited sequence, the daily the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5th Generation (ERA5)-Land reanalysis dataset was employed in this research, which was in extraordinary accordance with the few observed temperature data (Hersbach et al., 2020). The daily PCP data of 11 rain gauges were deployed in the basin. This study compared temperature data of the Firuzkuh synoptic station with temperature data of ERA5 and Climatic Research Unit (CRU) datasets. It is observed that the accuracy of temperature data of these datasets was acceptable. The spatial resolutions of ERA5 and CRU datasets are 0.1°and 0.5°, respectively. Therefore, the ERA5 dataset was selected for this study. Moreover, the daily discharge flow of the basin was used in the Bonkuh hydrometric gauge. The period of 1982–2005 was assigned as the baseline period, and all data were used on a daily scale. The average of Tmin, Tmax, and PCP in any of the five regions in the Hablehroud river basin area was achieved by Thiessen polygons. The data used in this study were gathered from the Iran Water Resources Management (IWRM) and Iran Meteorological Organization (IMO).

Fig. 2
figure 2

The location of the Hablehroud Basin

Full size image

Weighting GCM models

The GCMs are among the most advanced instruments for climate projection. In this study, 23 CMIP5 GCMs, which were BCSD (Bias Correction-Spatial Disaggregation) and spatial resolution of which was 0.5°, were acquired from the database http://gdo-dcp.ucllnl.org and employed under two RCP 4.5 and 8.5 scenarios. Unlike other GCM models, only these 23 models present Tmin, Tmax, and precipitation data under RCP 4.5 and 8.5.

The RCP 4.5 is a stabilization scenario, stating that the emissions peak in 2040 and then decline, and the total radiative will reach 540 ppm by 2100 before reaching a steady state. On the other hand, emissions in the RCP 8.5, a pessimistic scenario, continuously increase during the twenty-first century and reach 940 ppm by 2100 and increase for the next century. The dimensions of GCM cells are 0.5°*0.5° in this study. In addition, The Hablehroud river basin divided into 5 zones with dimensions 0.5°*0.5°. In the other words, this basin is placed within five cells of GCMs (Fig. 3).The Hablehroud river basin is placed within five cells of GCMs (Fig. 3). The GCM outputs for these five cells were extracted in the basin area. Considering the reliable meteorological data, the period of 1982–2005 was selected as the baseline to analyze the GCM outputs. In this study, Eqs. (1) and (2) were applied to computing the difference of observation data and their corresponding GCMs historical data.

Fig.3
figure 3

Division of the basin areas based on GCMs cells

Full size image

In this study, the 24 years (2025–2048) was designated as the future period. The weighting of GCM outputs revealed its impacts on the basin runoff very well. The GCM models have intrinsic uncertainty. For reduction of uncertainty in projections, multi-model ensemble of GCMs must be used. For this purpose, this study applied the KNN algorithm. This method calculates changes in climatic phenomena such as temperature and precipitation at each month based on long-term monthly changes in climatic phenomena in the baseline and future periods.

Therefore, the KNN algorithm was applied (Eqs. (3) and (4)). This algorithm uses the difference between the climatic parameters of the historical and observation periods. The weight of each GCM was then multiplied by the precipitation and temperature variations of the future to the baseline periods (Eqs. (5) and (7)); thus, the changes in temperature and precipitation were obtained for the future period. This technique will assign a higher weight to the GCM that is in better accordance with the data of the baseline period.

$$TE_{m}^{{G_{i} }} = \left| {(\overline{T}_{m}^{B} )_{{G_{i} }} - (\overline{T}_{m}^{B} )_{O} } \right|$$
(1)
$$PE_{m}^{{G_{i} }} = \left| {(\overline{P}_{m}^{B} )_{{G_{i} }} - (\overline{P}_{m}^{B} )_{O} } \right|$$
(2)

where \(TE_{m}^{{G_{i} }}\) and \(PE_{m}^{{G_{i} }}\) refer to the absolute error of GCMs to, respectively, survey temperature and precipitation. \(G\) indicates GCMs, and \(i\) is the number of GCMs. ͞ \(\overline{T}\) and \(\overline{P}\) indicate the mean temperature and mean precipitation within the 24-year records. Index \(B\) shows the baseline period of 1982–2005, and the index \(m\) is the abbreviation for the month. The index \(O\) indicates the observed data during 1982–2005.

$$WT_{m}^{{G_{i} }} = \frac{{{1 \mathord{\left/ {\vphantom {1 {TE_{m}^{{G_{i} }} }}} \right. \kern-\nulldelimiterspace} {TE_{m}^{{G_{i} }} }}}}{{\sum\nolimits_{i = 1}^{23} {({1 \mathord{\left/ {\vphantom {1 {TE_{m}^{{G_{i} }} }}} \right. \kern-\nulldelimiterspace} {TE_{m}^{{G_{i} }} }})} }}$$
(3)
$$WP_{m}^{{G_{i} }} = \frac{{{1 \mathord{\left/ {\vphantom {1 {PE_{m}^{{G_{i} }} }}} \right. \kern-\nulldelimiterspace} {PE_{m}^{{G_{i} }} }}}}{{\sum\nolimits_{i = 1}^{23} {({1 \mathord{\left/ {\vphantom {1 {PE_{m}^{{G_{i} }} }}} \right. \kern-\nulldelimiterspace} {PE_{m}^{{G_{i} }} }})} }}$$
(4)

where \(PE_{m}\) and \(TE_{m}\) show the difference between the average of simulated temperature and precipitation of the baseline period with the model i and the respective average for month \(m\) from the obtained average data; \(WP_{m}^{{G_{i} }}\) and \(WT_{m}^{{G_{i} }}\) are weights of each model \(i\) corresponding to the average long-term month \(m\); and \(i\) is the total number of GCMs.

$$\Delta T_{m} = \sum\limits_{{G_{i} = 1}}^{23} {\left( {WT_{m}^{{G_{i} }} \times TCF_{{G_{i} }} } \right)}$$
(5)
$$TCF_{G} = \left( {\left( {\overline{T}_{m}^{F} } \right)_{{G_{i} }} - \left( {\overline{T}_{m}^{B} } \right)_{{G_{i} }} } \right)$$
(6)
$$\Delta P_{m} = \sum\limits_{{G_{i} = 1}}^{23} {\left( {WP_{m}^{{G_{i} }} \times PCF_{{G_{i} }} } \right)}$$
(7)
$$PCF_{G} = \left( {\frac{{\left( {\overline{P}_{m}^{F} } \right)_{{G_{i} }} }}{{\left( {\overline{P}_{m}^{B} } \right)_{{G_{i} }} }}} \right)$$
(8)

in which \(TCF_{G}\) demonstrates the difference in temperature between the baseline and future for each GCM (°C), \(PCF_{G}\) indicates the difference in precipitation between the baseline and future for each GCM (%), and \(\left( {\overline{T}_{m}^{F} } \right)_{{G_{i} }}\) and \(\left( {\overline{P}_{m}^{F} } \right)_{{G_{i} }}\) denote the 24-year mean of temperature and precipitation for future period. \(\Delta T_{m}\) and \(\Delta P_{m}\) represent the variations of temperature and precipitation (Zareian et al., 2015).

Stochastic downscaling

The obtained results from GCM outputs only reveal variations in temperature and precipitation, and this feature is due to the large scale of the GCM. Thus, the downscaling techniques of Weather Generator (WG) are implemented to produce daily meteorological data. In this research, The LARS-WG model was applied for this purpose (Semenov and Barrow 2002). This model has been generated based on semiempirical distribution functions, which allows for the prediction of future wet and dry periods and validates this data generation by proposing KS, t, and F tests. In this model, the variations in Tmin, Tmax, and PCP of RCP 4.5 and 8.5 scenarios were introduced to the LARS-WG model (Ahmadianfar & Zamani, 2020). The accuracy of stochastic downscaling methods such as LARS-WG model is more than accuracy of non-stochastic downscaling methods such as change factor method (Hashmi et al., 2011). Considering the observation data in any of the five regions (Fig. 3) in the baseline (1982–2005), the daily data of the future period (2025–2048) were generated.

Evaluating the trend and homogeneity of hydrological streamflow

The trend is defined as the gradual changes in the mean value of the hydrological variable. The time series will have a trend if there is a significant correlation between observed values and time. Numerous methods have been proposed for estimating the trend on time-series, the most famous of which is the nonparametric Mann–Kendall (MK) test. The test was first introduced by Mann (1945) and then developed by Kendall (1975). Sen's slope estimator introduced by Sen (1968) is also employed for detecting the nonparametric trend. This nonparametric approach can determine the variation in time units. In this study, the nonparametric MK test and Sen's slope estimator were used at the 95% confidence level to check the trend governing the hydrological streamflow. To examine the homogeneity of the streamflow time series, the Pettitt test introduced by Pettitt (1979) was implemented at the 95% confidence level.

Assessing hydrologic drought

The early concept of the Streamflow Drought Index (SDI) was proposed by Nalbantis (2008) for analyzing the hydrological drought characteristics on multi-time scales. The method of calculating SDI is the same as calculating SPI. The future information about SDI and its performances can be reached from the related literature (Adib et al., 2020; Ashrafi et al., 2020; Adib & Tavancheh, 2019). In this research, based upon the Kolmogorov–Smirnov (KS) test, the time series of the baseline period and the future period of the Hablehroud river basin streamflow conform to the log-normal probability distribution (Srinivasan, 1971). Therefore, the SDI values for the baseline and future periods were computed with respect to log-normal probability distribution at 1, 3, 6, 9, and 12 time scale.

Rainfall-runoff simulation

IHACRES was first developed by Young & Beven (1991). A nonlinear module for converting observed rainfall into excess rainfall and a linear module for converting the estimated excess rainfall into river discharge are the main components of the IHACRES model. The IHACRES model was calibrated using daily mean precipitation, temperature, and runoff data in the baseline period and was utilized to estimate basin runoff under the impact of CC.

Performance criteria

This study applied four performance criteria including, correlation coefficient (R), RMSE-observations standard deviation ratio (RSR), Nash–Sutcliffe efficiency (NSE), and Kling-Gupta efficiency (KGE) (McCuen et al., 2006; Gupta et al., 2009; Knoben et al., 2019).

$$R = \frac{{{\text{cov}} (Q_{Obs}^{i} ,Q_{Cal}^{i} )}}{{\sigma_{Obs} \sigma_{Cal} }}$$
(9)
$$RSR = \frac{{RMSE}}{{STDE{V_{Obs}}}} = \frac{{\sqrt {\sum\nolimits_{i = 1}^n {{{(Q_{Obs}^i - Q_{Cal}^i)}^2}} } }}{{\sqrt {\sum\nolimits_{i = 1}^n {{{(Q_{Obs}^i - \overline Q _{Obs}^i)}^2}} } }}$$
(10)
$$NSE = 1 - \frac{{\sum\nolimits_{i = 1}^N {{{(Q_{Cal}^i - Q_{Obs}^i)}^2}} }}{{\sum\nolimits_{i = 1}^N {{{(Q_{Obs}^i - {{\overline Q }_{Obs}})}^2}} }}$$
(11)
$$KGE = 1 - \sqrt {(cc - 1)^{2} + (\alpha - 1)^{2} + (\beta - 1)^{2} }$$
(12)

where \({\text{cov}} (Q_{Obs}^{i} ,Q_{Cal}^{i} )\) is the covariance of the observed and calculated values; \(\sigma_{Obs}\) and \(\sigma_{Cal}\) are the corresponding standard deviations, \(Q_{Obs}\) and \(Q_{Cal}^{{}}\) are the observed runoff and calculated runoff, respectively, \(\overline{Q}_{Obs}^{i}\) is the average of observed runoff, R is the linear correlation coefficient,\(\alpha\) is standard deviation of the computed runoff to standard deviation of observed runoff, and \(\beta\) shows the average of calculated runoff.

Results

Evaluation of CC

In this paper, the variables of Tmin, Tmax, and PCP on a monthly scale of 23 general circulation models (GCMs) were used in the Hablehroud river basin. Weighing the GCMs, higher weight (or priority) will be allocated to a model that has a better performance in the baseline period. The Taylor diagram provides a perfect perspective on this subject (Farajpanah et al., 2020). Figure 4 shows the Taylor diagram of the long-term mean of Tmin, Tmax, and PCP in region 1.The Taylor diagrams of other regions are provided in Appendix (Figs. 14, 15, 16, 17). The radial distance from the reference point (REF), indicating the observed values, is the pattern root-mean-square deviation (RMSD), and the radial distance from the origin indicates the standard deviation, whereas the correlation coefficient is shown by the angle (Taylor, 2001).

Fig.4
figure 4

Taylor diagrams for PCP, Tmax, and Tmin of the region1 in the baseline period (1982–2005)

Full size image

The changes obtained from Eqs. (5) and (7), which suggest the variations of the future period to the baseline period under two scenarios (RCP 4.5 and RCP 8.5), were also introduced as a scenario file to the LARS-WG model, and daily temperature and precipitation values were produced. The criteria of the Kolmogorov–Smirnov (KS) test and the t test were at a favorable level.

Furthermore, changes of Tmin, Tmax, and PCP in the whole catchment in the future period compared to the baseline period are illustrated in Fig. 5. Similar diagrams for five regions are provided in the appendix (Fig. 18). As indicated in this figures, Tmin and Tmax considering two scenarios (RCP 4.5 and RCP 8.5) will rise in all regions. The highest increasing Tmin occurs in the south of the basin, i.e., region 1 and 2, which is located in Semnan province and has a low altitude (less than 1000 m). The lowest increase in the Tmin belongs to region 3, which is located in the east of Tehran at the foothills of Mount Damavand (Iran's highest peak). The highest increase in the Tmax also happens in the south of the basin, and the lowest increase in the Tmax takes place in region 3. However, PCP variations are different in the five regions; they have an ascending trend in some areas and a descending trend in the other areas. The highest increase in PCP is associated with region 2 for the RCP 8.5 scenario, and the highest decrease in PCP belongs to region 3 under the RCP 4.5 scenario. In Region 2, PCP will rise under the scenarios (RCP 4.5 and RCP 8.5) in most months. Region 3 will also encounter a reduction in precipitation in most months under scenarios RCP 4.5 and RCP 8.5. Except for three months, Jan, Feb, and Mar, the whole basin will experience a drop in precipitation for the remaining months, where this decrease is more severe under the RCP 4.5 scenario compared to RCP 8.5 scenario.

Fig. 5
figure 5

Future projections (2025–2048) compared to the baseline period: a Tmin b Tmax c PCP under scenarios (RCP4.5 and RCP8.5) in whole watershed

Full size image

The mean daily precipitation and temperature of the whole basin were calculated utilizing the Thiessen polygon technique and introduced as input to the IHACRES. Moreover, the daily discharge flow of the Bonkuh hydrometric gauge located at the outlet of the Hablehroud river basin was entered into the IHACRES model. The two periods of 1983–2001 and 2002–2005 were selected for the calibration and validation of the IHACRES model, respectively. Table 1 represents an accuracy of the IHACRES in the rainfall-runoff modeling. Figure 6 shows the simulated and observed streamflow in both periods of calibration and validation. According to the information in Table 1 and Fig. 6, the IHACRES model enjoys an acceptable accuracy. However, as is inferred from Fig. 6, the IHACRES model does not have a good performance for estimating the daily lowflows and highflows. So that the RSR values for lowflow and highflow are 0.6 and 1.1, respectively.

Table 1 Performance criteria for IHACRES model
Full size table
Fig. 6
figure 6

Comparison of the calibration and validation periods in the IHACRES rainfall-runoff model

Full size image

Figures 7 and 8 show the variations in the value of long-term monthly runoff in the future period compared to baseline period. In the future period, the Hablehroud river basin will experience a noticeable runoff decrease in autumn, winter, and spring, and the highest decrement is related to November considering two scenarios (RCP 4.5 and RCP 8.5). In contrast, it will face a runoff increase in summer. The reason for this can be attributed to the significant decrease in rainfall in the mentioned three months in regions 1 and 3 (west of the basin) in the future period.

Fig. 7
figure 7

The long-term mean monthly runoff in the baseline period and future period under two scenarios (RCP4.5 and RCP8.5)

Full size image
Fig. 8
figure 8

Percentage of monthly runoff changes in the future period under two scenarios (RCP4.5 and RCP8.5)

Full size image

According to Fig. 9, the trend of streamflow in the baseline period is always downward, and in all months except Apr, Jul, and Aug, this downward trend is significant at the 95% confidence level. Under the RCP 4.5 scenario, the streamflow trend is downward in all months for the future period, and this downward trend in Oct, Nov, Jan, and Feb is significant at the 95% confidence level. Under the RCP 8.5 scenario, the basin streamflow trend is upward in all months, and this upward trend is significant in spring and summer at the 95% confidence level. Figure 9 is associated with the Sen's slope and also indicates the decreasing trend of the streamflow in the baseline period under the RCP 4.5 scenario and the increasing trend of the streamflow under the RCP 8.5 scenario.

Fig. 9
figure 9

The trend of streamflow: a Sen's slope b Z-MK in the future period with respect to two scenarios (RCP4.5 and RCP8.5)

Full size image

Figure 10 illustrates the change point in the streamflow of the baseline period. Based on the Pettitt test, the mean streamflow value has an abrupt shift in nine months, such that this variation has led to a reduction in the mean streamflow value. This decline took place over the last decade of the baseline period (1955–2005). Figure 11 demonstrates the change point in the streamflow of the future period considering the scenario RCP 4.5, wherein in the Oct and Feb streamflow values we will observe an abrupt shift in time series that this change point is associated with decreasing discharge flow in the second half of the future period. Figure 12 represents the change points in the streamflow of the future period under the scenario RCP 8.5.

Fig. 10
figure 10

Homogeneity test for the long-term mean streamflow in the baseline period (1982–2005)

Full size image
Fig. 11
figure 11

Homogeneity test for the long-term mean streamflow in the future period under the scenario RCP4.5 (2025–2048)

Full size image
Fig. 12
figure 12

Homogeneity test for the long-term mean streamflow in the future period under the scenario RCP8.5 (2025–2048)

Full size image

In six months, an abrupt shift will be observed in the streamflow of the future period; in all of them, this shift will result in an increase in the mean streamflow value. This rise will occur during all six months of increasing streamflow in the second-half years (2035–2048) of the future period.

Figure 13 displays the occurrence of 1-month, 3-month, 6-month, 9-month, and 12-month hydrological droughts in the baseline and future periods. During the baseline period, the normal and wet conditions prevailed in the first two-thirds of the period, and hydrological drought occurred in the last one-third of the period. The occurrence of droughts in the future period under the RCP 4.5 scenario is the same as the baseline period. However, under the RCP 8.5 scenario, droughts in the future period are different. Based on the RCP 4.5 scenario, the normal and wet conditions prevail in the first two-thirds of the period that the drought will occur. Considering the RCP 8.5 scenario, drought dominates the hydrological streamflow of the basin in the first decade, and wet conditions happen in the second and third decades for the future period.

Fig. 13
figure 13

Short-term, middle-term, and long-term SDI in the baseline period and future period under the scenarios (RCP4.5 and RCP8.5)

Full size image

Figures 19, 20 and 21 provide the Streamflow Drought Index (SDI) in 1-, 3-, 6-, 9-, and 12-month scales. On a monthly (1 month) scale, the highest variations under the RCP 8.5 scenario occur in Dec, Jan, and Feb (winter), wherein non-drought conditions in the baseline period become drought conditions in the future period and cause Mild drought and Moderate drought conditions. Under the RCP 8.5 scenario, it will commonly face increasing Mild drought conditions in other months.

According to Fig. 20, non-drought conditions will be aggravated in three months Oct, Nov, and Dec under the RCP 4.5 scenario; however, at the same time, moderate drought conditions in the future period will increase. In three months, October, November, and December (OND), non-drought conditions decrease, and mild and moderate droughts increase under the RCP 8.5 scenario. In three months, January, February, and March (JFM), non-drought conditions decrease, and drought conditions increase under the two scenarios RCP 4.5 and RCP 8.5.

In the three months of April, May, and June (AMJ), there is an increase in severe drought occurrence under the RCP 4.5 scenario. The non-drought conditions enhance, and mild drought conditions decline, but moderate drought conditions will increase under the RCP 8.5 scenario. In three months, July, August, and September (JAS), the Hablehroud river basin will face a hydrological drought situation under the two scenarios (RCP 4.5 and RCP 8.5).

In the six months between Oct and Mar (autumn and winter), a reduction is observed in non-drought conditions and an increase in drought conditions under the two scenarios, RCP 4.5 and RCP 8.5. In the six months between Apr and Sep, non-drought conditions increase, and droughts decrease under the RCP 4.5 scenario (Fig. 21a, b). The non-drought conditions drop, and the drought conditions are exacerbated under the RCP 8.5 scenario.

In the nine months between Oct and Jun, increasing non-drought conditions and decreasing droughts under the RCP 4.5 scenario and little increase in non-drought conditions and a decrease in droughts under the RCP 8.5 scenario will be experienced (Fig. 21c).

Figure 21d reveals a 12-month drought from Oct to Sep. Considering two scenarios RCP 4.5 and RCP 8.5, the Hablehroud river basin will experience increasing non-drought conditions and decreasing drought conditions.

Discussion

For a long time, in various studies, outputs of the CMIIP3 and CMIP5 have been employed to evaluate the CC impacts on other systems such as the environment and human life (Shadkam et al., 2016; Vaghefi et al., 2019). Numerous GCM models have been developed on a global scale to forecast the climate conditions for the future period (Hoegh-Guldberg et al., 2019; Piao et al., 2019). Uncertainty is a pivotal component of GCMs such that natural variability and coarse resolutions can affect them. Thus, the spatial downscaling for the conformity between the GCMs output and the conditions of the study area is of particular importance (Zhou et al., 2020). Among the conventional downscaling techniques are stochastic downscaling (Nikakhtar et al., 2020). The LARS-WG model allows the user to generate daily weather data taking into account the variations in variables. Moreover, the IHACRES rainfall-runoff model, which is a conceptual and much-applied model, requires future temperature and precipitation to estimate the streamflow in the future period. Analyzing the characteristics of the future streamflow, including the existence of a significant trend or homogeneity, and also the occurrence of hydrological drought conditions to adopt an appropriate decision on the matters related to the Water Evaluation and Planning System of the basin is crucial.

The selection of models that are appropriate for the regional-scale climate is essential. Better conformity of the mean variables in the baseline represents a better performance in simulations. To illustrate the compliance of each model in the baseline period, the Taylor diagram was applied. The performance of all 23 GCMs was evaluated to be at a desirable level.

The examination of this study outcomes suggested better accuracy of GCMs to simulate the temperature compared to the precipitation. This result are directly agree with the previous researches (Zamani et al., 2017; Doulabian et al., 2021). Because of the conditional nature of the precipitation phenomenon, its projection is more complex relative to temperature (Ahmadalipour et al., 2017). In this research, the daily Tmin, Tmax, and PCP for the period of 24 years (1982–2005) were used. Besides, the weighting per se highlights the role of a suitable model, of which the result will be revealed well in the streamflow of the future period. Evaluation of the trend of variations in runoff and hydrological droughts is among the objectives achieved in this research.

As pointed out, the IHACRES rainfall-runoff model enjoys an appropriate potential in dry and even wet basins even though it requires a few input variables. However, among the disadvantages of this model, one may refer to its weak capability in the simulation of the daily peak flow; nevertheless, this weakness does not disrupt the study of hydrological drought, which is our primary objective.

In all regions, the temperature has an ascending trend in all months. The highest increases in the Tmin (1.87 °C) and Tmax (1.80 °C) are in the southern region of the river basin (region 1) under the RCP 8.5. The lowest variations in the Tmin and Tmax in region 3 under the RCP 4.5 were 1.24 °C and 1.57 °C, respectively.

Region 1 will face a decrease of 57.6% in PCP under the RCP 4.5 scenario in September. Region 2 will have an increase of 151% in PCP under the RCP 8.5 scenario in June. After that, Region 3 will experience an increase of 84% in rainfall under the RCP 8.5 scenario in September.

According to the results achieved from Fig. 8, the Hablehroud river basin will encounter a decline in streamflow in most months of autumn, winter, and spring except for the summer, which is due to increased PCP of the future period in the northern regions of the basin; this increase in rainfall is evident in Fig. 5. These results agree with the previous researches (Babaeian et al., 2021).

The whole Hablehroud river basin area will experience monthly short-term monthly and 3- and 6-month medium-term hydrological droughts in the future period, particularly in the first six months of the water year (from Oct to Sep). The adverse effects of CC, including decreasing precipitation and increasing temperatures, are felt more in the lowlands southern part of the Hablehroud river basin. However, 9- and 12-month long-term hydrological droughts in the future period imply a reduction in hydrological drought conditions. The rising temperature and declining precipitation in the southern parts of the basin can lead to evapotranspiration increase, the water requirement of crops, and including stress in periods of crop growth in the Garmsar plain, which is located at downstream of the Hablehroud river basin.

Despite change points that result in an increase in the mean runoff or an upward trend prevailing the streamflow in all months under the RCP 8.5 scenario, the long-term mean runoff in Jan, Apr, May, Oct, Nov, and Dec will still decline.

Although the Hablehroud river basin encounters a decrease in the long-term mean runoff in Jan, Apr, May, Oct, Nov, and Dec over the long run, the hydrological drought situation will be alleviated, and the non-drought conditions will be enhanced.

Conclusion

Hablehroud Basin drenches the Garmsar plain, which is highly significant from the agricultural aspect. The basin's climate is arid; the north of this basin has a temperate climate, and by approaching toward the basin's south, the climate becomes drier. One of the benefits of the present study is the separation of the basin area into five regions, such that all climate change analyses in each region were carried out separately. In this study, daily data sets including Tmin, Tmax, and PCP for a period of 24 years (1982–2005) were considered. Moreover, the output of 23 GCMs was utilized to simulate meteorological variables. GCMs are part of the uncertainty sources in the future period's runoff forecast. Thus, KNN method was implemented to combine the outputs of GCMs to reduce the mentioned uncertainty in forecasting.

The LARS-WG is one of the most applied weather generators, in which the meteorological data for the next daily period were generated by considering temperature and precipitation alterations under the climate scenarios of RCP 4.5 and RCP 8.5. According to the obtained results, the eastern part of the basin (regions 2, 4, and 5) PCP is increased, while it is decreased in the western part of the basin (regions 1 and 3). Generally, the entire basin's PCP in the future period is increased by 11.5% and 12.6% with respect to the scenarios RCP 4.5 and RCP 8.5, respectively. The highest increase rate of the Tmin and Tmax occurs in the southern region of the basin. According to the results, the Tmin of the basin in the future period will increase by 0.8 °C and 1.1 °C under the RCP 4.5 and RCP 8.5 scenarios, respectively. Furthermore, according to the results, the Tmax of the basin in the future period will increase by 1 °C and 1.2 °C under the RCP 4.5 and RCP 8.5 scenarios, respectively. Ultimately, the annual runoff amount of the future period with respect to the observational period will be reduced by 11.4% and 13.1%, under the RCP 4.5 and RCP 8.5 scenarios, respectively. Therefore, it can be stated that the impression of the basin's overall temperature increases on runoff, which also results in increase in potential evapotranspiration, is more significant than the impression of precipitation increase. Thus, the Hablehroud basin will have a decrease in runoff in the future period. Additionally, the base period runoff represents a downward trend with respect to the scenario RCP 4.5 and an upward trend under the RCP 8.5 scenario. Nevertheless, the upward trend will not increase the long-term average monthly runoff of the future period with respect to the base period. Moreover, the Hablehroud basin will suffer from short-term and medium-term hydrological droughts in the future period. Water scarcity is inherent in the arid regions of Iran, while water bankruptcy has been imposed. Considering that the main crops of Garmsar plain are irrigated wheat; therefore, varieties that are resistant to drought should be used instead of traditional wheat varieties. In general, the results of this study can be the stimulus for the government to achieve sustainable adaptation strategies for the water sector.