Development of a linear–nonlinear hybrid special model to predict monthly runoff in a catchment area and evaluate its performance with novel machine learning methods

Abstract

Accurate forecasting of runoff as an important hydrological variable is a key task for water resources planning and management. Given the importance of this variable, in the current study, a multivariate linear stochastic model (MLSM) is combined with a multilayer nonlinear machine learning model (MNMLM) to generate a hybrid model for the spatial and temporal simulation of runoff in the Quebec basin, Canada. Monthly hydrological data from 2001 to 2013, including precipitation and runoff data from nine stations and Normalized Difference Vegetation Index (NDVI) extraction of MODIS data, are applied as input to the proposed hybrid model. At the first step of the hybrid modeling, data normality and stationary were examined by performing various tests. In the second step, MLSM was developed by defining four different scenarios and as a result 15 sub-scenarios. The first and second scenarios were developed based on one exogenous variable (precipitation or NDVI). In contrast, the second and third scenarios were developed based on two additional variables. In the first and third scenarios, the data are modeled without preprocessing. In the second and fourth scenarios, a preprocessing step is performed on the data. Then, in the third step, various combinations based on different time delays from runoff data were applied for developing nonlinear model. The comparisons are made between observed and simulated time series at various stations and based on the root mean squared error (RMSE), mean absolute error (MAE), correlation coefficient (R) and Akaike information criterion (AIC). The efficiency of the proposed hybrid model is compared with a novel machine learning model that was introduced in 2021 by Sultani et al., and it was also compared with the results obtained from the linear and nonlinear models. In most stations, delays (t-1) and (t-24) are identified as the most effective delays in hybrid and nonlinear modeling of runoff. Also, in most stations, the use of climatic parameters and physiographic factors as exogenous variables along with runoff data improves the results compared to the use of one variable. Results showed that at all stations, proposed hybrid model generally leads to more accurate estimates of runoff compared with various linear and nonlinear models. More accurate estimates of peak runoff values at all stations were another excellence of proposed hybrid model than other models.

Introduction

One of the important challenges in the field of efficient watershed management is the accurate predicting of watershed runoff, which plays a key role in reducing the effects of floods and drought on hydraulic systems, controlling soil erosion and sedimentation (Al-Ghobari et al. 2020). To solve this challenge, various methods have been developed, which can be generally divided into three groups. The first group is conceptual models such as Clark model (Clark 1945), TANK model (Sugawara et al. 1974, 1983), Xinanjiang model (Zhao and Liu 1995) that use concepts for simulation of runoff. The second group is physically based models such as MIKE SHE (Refsgaard and Storm 1995); soil and water assessment tool (Arnold et al. 1998) that represents the actual process of runoff production. The third group is data-driven methods such as regression, time series and artificial neural network (ANN) models that estimate runoff based on a set of input variables (Fan et al. 2020). Conceptual and physics-based models convert precipitation into runoff using physical and empirical equations since these models rely on accurate knowledge of the physical mechanism of the phenomenon and use evaporation, infiltration, interception, soil moisture and land use components in the transformation process. As a result, they need a lot of information to model. In contrast, data-driven methods have become more popular due to the need for less knowledge of the physical behavior of the phenomenon. Nowadays, researchers are paying more attention to using simpler, cheaper and easier methods of modeling. Data-driven method is based on the relationship between input, internal and output variables (Lima et al. 2014). As a result, forecasting is easily done with this method and it is divided into two categories: linear (e.g., linear regression and time series models) and nonlinear (e.g., genetic programming (GP), adaptive neuro-fuzzy inference systems (ANFIS) and ANN models) statistical models. Among various linear statistical methods, time series forecasting technique is a well selection to model hydrological processes. Traditional time series techniques such as the Box-Jenkins technique (Box and Jenkins 1970) are widely used time series models. Most hydrological parameters can be modeled and predicted by this method (Moeeni et al. 2017; Bayesteh and azari 2019; Salih et al. 2020; Ebtehaj et al. 2020; Azari et al. 2021; Soltani et al. 2021). Also, numerous studies have been performed in the field of runoff modeling and prediction using stochastic models.

Valipour (2015) investigated the ability of the stochastic models for annual runoff forecasting and used only runoff data for modeling in various US states. His results showed that seasonal stochastic models produced better results than non-seasonal stochastic models. Wang et al. (2015) modeled the annual runoff in three reservoirs Biuliuhe, Dahuofang and Mopanshan, in China, using the stochastic model. Before modeling, they decomposed the time series using with the ensemble empirical mode decomposition (EEMD) technique and then performed the modeling. Their results showed that pre-processing through EEMD technique improved the runoff prediction results in these reservoirs. Hao et al. (2017) after calculating the annual runoff volume of input to Three Gorges Project as one of the largest hydropower projects in the world modeled the time series obtained from the annual runoff volume using the seasonal auto-regressive moving average (ARIMA) method and showed that the model has a high accuracy in modeling the annual runoff. Mishra et al. (2018) developed a stochastic model based on the data measured at site Panchratna of the river Brahmaputra basin and showed that the best performance for modeling does not depend only on the length of the data and that the existence of important patterns in modeling is important.

Among various nonlinear statistical methods, models based on Artificial Intelligence (AI) are a well selection to model hydrological processes (Kumar et al. 2019; Vidyarthi and Jain 2020; Jahan and Pradhanang 2020; Filipova et al. 2022) especially runoff (Vilanova et al. 2019; Niu and Feng 2021; Molajou et al. 2021; Gholami and Sahour 2022; Xu et al. 2022; Zhang et al., 2022). Among AI methods, neural network method is widely used for runoff modeling due to its flexibility in modeling complex processes. Numerous researchers have modeled runoff using ANN model and compared the results with the stochastic model. Valipour et al. (2013) compared stochastic and artificial neural network models to model the monthly flow at the Taleh-Zang station in Dez reservoir, in Iran. Their results showed that by performing non-seasonal differentiation and thus stationary of time series, it performs better than non-stationary mode and also ANN model performs better than the stochastic model. Nourani and Parhizkar (2013) modeled the runoff at two stations located in two different sub-basins of the Peace Tampa Bay watershed in Florida using three models: wavelet-ANN, ANN and ARIMA with exogenous input of rainfall. They showed that the wavelet-ANN model models runoff better than the other two methods due to preprocessing on the data. Nath et al. (2020) modeled runoff at Central Water Commission gauge station in India using Particle Swarm Optimization (PSO)-ANFIS, ANFIS and ARIMA models. In these modeling, runoff values with different time lags were used for modeling and showed that model PSO-ANFIS works better in runoff modeling than the other two methods.

In modeling hydrological phenomena through data-driven method (especially more complex phenomena such as runoff), some researchers by combining the linear and nonlinear models and creating a hybrid model that includes the characteristics of both models improve the modeling results compared to linear and nonlinear models (Moeeni and Bonakdari 2018; Lotfi et al. 2019; Mehdizadeh et al. 2019; Soltani et al. 2021). Zhang et al. (2011) by creating a hybrid model obtained from the combination of ARIMA and singular spectrum analysis (SSA), predicted the annual runoff in two reservoirs of Biliuhe and Dahuofang and showed that the hybrid model performs better than the ARIMA and SSA models. Chu et al. (2017) predicted runoff using a combination of a multiple linear regression model and a neural network. They used a combination of several climate variables to build the linear model and showed that using climate variables produces better results than not using them. Niu et al. (2019) predicted the monthly runoff in Three Gorges, in China, using the definition of a hybrid model and showed that the hybrid model performs better than the other models. Nourani et al. (2021) modeled the monthly and daily flow using two hybrid models in two watersheds and in each watershed in one station. Also, they compared the results with ANN and ARIMA models and showed that the hybrid model had more accurate results than other models.

A review of past researches shows that researches have been done on a single station in a watershed and data-driven modeling is limited at the watershed level and most studies at the watershed level have been done using conceptual and physical models. On the other hand, most linear and hybrid modeling has only used the climatic variables as additional variables, and since runoff process is a spatial and temporal phenomenon, various climatic factors such as duration, intensity and distribution of precipitation along with physiographic factors such as land use type, soil type, vegetation, catchment area, basin shape, height, slope, direction and type of drainage network are involved in the process. As a result, there is a need to consider both factors in modeling. One of the considerable methods widely applied in detecting land use, vegetation cover and land use change is Normalized Difference Vegetation Index (NDVI) (Nath 2014). The main purpose of this research is to develop a computer program in MATLAB software to create a hybrid model, which is a combination of two simple linear and nonlinear models, for modeling runoff in a watershed area. For this purpose, a multivariate linear model and a multilayer nonlinear model are used to construct proposed hybrid model and monthly runoff data measured from 2001 to 2013 at nine hydrometric stations located in the Saint Lawrence River watershed are used in order to evaluate the performance of the proposed model. Also, to obtain more accurate results, model construction is based on the definition of different scenarios. These scenarios are defined based on the type of additional exogenous and perform preprocessing before modeling begins. Additional exogenous considered for modeling includes NDVI and precipitation parameters as two effective parameters in runoff modeling and the effects of various transform functions including Box–Cox, logarithmic, standard logarithm and standard functions are investigated in scenarios involving preprocessing. Various tests are used to examine the structure of time series in terms of stationary and normality. Also, various statistical indicators and graphical interpretation are used to compare the efficiency and performance of the proposed model with multivariate linear model and a multilayer nonlinear model. Additionally, the obtained results of these models were compared with the results of the generalized structure of Group Method of Data Handling (GSGMDH) model. The GSGMDH is a new machine learning technique along with remote sensing and used as a multivariate nonlinear model for runoff estimation.

Regional description and data

In this study, part of Canada's third largest river watershed, the Saint Lawrence River, is studied. The Saint Lawrence River has a vital impact on energy, especially in transport (the main route for navigators and going to the North American continent) and region’s tourism. The total length of this river from Lake Ontario to outfall is 3058 km, of which 95 km is situated in the case study site. The assumed area with a maximum altitude of 688 m and an annual arithmetic average precipitation of 1141 mm is located in geographical position 46° 04′ to 46° 59′ N latitude and 72° 23′ to 72° 30′ W longitude. Figure 1 shows a map of situation of the study area. There are various climate and hydrometric stations in the region of study; of these, only nine hydrometric stations have complete data for 2001 to 2013 period. Thus, the monthly flow data were extracted from these nine stations. In Fig. 1, situation and names of hydrometric and climate stations are shown. As shown in the figure, the distribution of these stations in the study area is appropriate and in most places the hydrometric and climate stations are close to each other and only two stations are far apart. These stations are located at an altitude of less than 400 m above sea level. Among these stations, 02PB019 station with 1550 km2 has the highest gross drainage area and 02PH014 station with 195 km2 has the lowest gross drainage area.

Fig. 1

Location and elevation map of the study area and hydrometric stations

Monthly data at various stations in study area for 2001 to 2013 are gained from the Environment Canada website (EC) (https://wateroffice.ec.gc.ca, https://climate.weather.gc.ca/historical_data). The Normalized Difference Vegetation Index (NDVI) captured from the following website: (https://ladsweb.modaps.eosdis.nasa.gov/) and through Terra Moderate Resolution Imaging Spectroradiometer (MODIS) Vegetation Indices (MOD13Q1) Version 6, which creates two layers including NDVI and Enhanced Vegetation Index (EVI) layers. Consistent with precipitation and runoff data, monthly NDVI data are also computed for periods 2001 to 2013. Atmospheric corrections were performed on preprocessed data using the Google Earth Engine environment. Figures 2 and 1S in the supplementary file for details present the statistical analysis of data in box and whiskers plot at calibration and validation periods for runoff time series. According to the box and whisker plot for runoff data, almost identical statistical characteristics were observed during the calibration and validation periods. Comparing features in the data shows that the arithmetic average of runoff data at 02PB019 station, which has the largest gross drainage area, is much higher than the arithmetic average at other stations, and that the standard deviation of the runoff data at 02PB019 is also higher than other stations. This station with a median value of 84.80 has the highest median value than the other stations. The two stations 02PH011 and 02PH014, which are located close to each other, have almost the same statistical characteristics. All stations have positive skewness, and 02PJ034 station has slightly more skewed (skewness = 3.26) than other stations. The overall range of the data which represents the dispersion of data is greater for 02PB019 station, and the difference with other stations is completely visible. The Interquartile Range (IQR) of the calibration data varies between 2.88 and 40.85. After 02PB019 station with IQR equal to 40.85, 02PL005 with the dispersion of data between 10.17 and 25.7 has the most dispersion of data (IQR = 15.53). The lowest dispersion of data with an IQR equal to 2.76 is observed in the 02PJ034 station and in the validation period. All stations have potential outliers, and the farthest potential outlier’s value is for 02PB019 station. The 02PD010 and 02PB019 stations have the minimum and maximum amount of runoff, respectively.

Fig. 2

Statistical analysis of the runoff time series for all stations in calibration and validation periods

Methodology

Data pre-processing

Before starting the preprocessing and preparing the data for modeling, the data should be examined in terms of series length and predictability. One of the most popular methods for checking the length and predictability of time series is the Hurst coefficient. If the value obtained from this coefficient that statistic is obtained through Eq. 1 is greater than 0.5, the time series has a long memory and good predictability and includes the maximum and minimum runoff values. Otherwise, the length of the time series should be increased.

$$ H = \frac{{\log \left( {\frac{{D_{cd} }}{Sd}} \right)}}{{\log \left( {\frac{{N_{o} }}{2}} \right)}} $$

(1)

where H is the Hurst coefficient, Dcd denotes the difference between the least and highest amount of cumulative differences from the average of the data, Sd and No denote the standard deviation and the number of observations, respectively.

Data preprocessing is one of the most important steps in time series modeling. In examining the characteristics of time series, some time series may be very non-normal and asymmetric that this feature complicates the later stages of modeling and thus reduces the accuracy of modeling. In order to evaluate the normality of the data in this study, Jarque–Bera test (Jarque and Bera 1980) is used.

This test statistic is as follows:

$$ JB = N_{o} \left( {\frac{{S_{k}^{2} }}{6} + \frac{{\left( {E_{l} - 3} \right)^{2} }}{24}} \right) $$

(2)

$$ S_{k} = \frac{{\frac{1}{{N_{o} }}\sum\limits_{t = 1}^{n} {({\text{Ru}}_{t} - \overline{{{\text{Ru}}_{t} }} )^{3} } }}{{\left( {\frac{1}{{N_{o} }}\sum\limits_{t = 1}^{n} {\left( {{\text{Ru}}_{t} - \overline{{{\text{Ru}}_{t} }} } \right)^{2} } } \right)^{\frac{3}{2}} }} $$

(3)

$$ E_{l} = \frac{{\frac{1}{{N_{o} }}\sum\limits_{t = 1}^{n} {\left( {{\text{Ru}}_{t} - \overline{{{\text{Ru}}_{t} }} } \right)^{4} } }}{{\left( {\frac{1}{{N_{o} }}\sum\limits_{t = 1}^{n} {\left( {{\text{Ru}}_{t} - \overline{{{\text{Ru}}_{t} }} } \right)^{2} } } \right)^{2} }} $$

(4)

where Sk and El are the skewness and elongation of the sample (respectively), $\overline{\mathrm{Ru} }$ t is the arithmetic average of the data and No is the number of observations.

If the probability value (P-value) obtained from the statistics of this test is greater than 5%, then the time series has a normal distribution. Otherwise, the time series has a non-normal distribution and the customary method in this case is to use normalizing functions to reduce skewness and bring them closer to a normal distribution. There are several normalization functions for converting data to normal form and removing skew from them. Among these functions, logarithmic (Log), standard logarithm (Logstd), and Box–Cox functions are considered for data normalization in this study. The statistics of these functions are given in Table 1.

Table 1 Time series preprocessing methods

Given that most statistical methods for time series prediction use the stationary property of time series and on the other hand most hydrological series do not have such a property, it is necessary that the stationary of time series is to be examined. Each time series consists of two parts: stochastic and deterministic. Stochastic part consists of one term (S) and deterministic part consists of three terms: trend term (T), period (P) and jump (J). If there is any term of the deterministic part, the time series becomes non-stationary. As a result, these terms must be identified and removed from the time series. In order to survey the stationary in the time series, the PP and KPSS tests introduced by Phillips and Perron (1988) and Kwiatkowski et al. (1992), respectively, are selected to check existence (or absence thereof) of unit roots.

The PP test is given by:

$$ y_{i} = \alpha + \rho y_{i - 1} + \varepsilon_{i} $$

(8)

$$ Z_{\rho } = n(\mathop {\rho_{n} }\limits^{ \wedge } - 1) - \frac{1}{2}\frac{{n^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }^{2} }}{{S_{n}^{2} }}(\hat{\lambda }_{n}^{2} - \hat{\gamma }_{o,n} ) $$

(9)

$$ Z_{\tau } = \sqrt {\frac{{\hat{\gamma }_{o,n} }}{{\hat{\lambda }_{n}^{2} }}} \frac{{\left( {\hat{\rho }_{n} - 1} \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }} - \frac{1}{2}\left( {\hat{\lambda }_{n}^{2} - \hat{\gamma }_{o,n} } \right)\frac{1}{{\hat{\lambda }_{n} }}\frac{{n\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }}{{S_{n} }} $$

(10)

$$ \hat{\lambda }_{n}^{2} = \hat{\gamma }_{o,n} + 2\sum\limits_{j = 1}^{q} {(1 - \frac{j}{q + 1}} )\hat{\gamma }_{j,n} $$

(11)

$$ S_{n}^{2} = \frac{1}{n - k}\sum\limits_{i = 1}^{n} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{i}^{2} } $$

(12)

where ut is ordinary least squares residual; k and q are the number of covariates in the regression and Newey–West lags, respectively.

The KPSS test is given by:

$$ S^{2} (h) = \frac{1}{n}\sum\limits_{t = 1}^{n} {a_{t}^{2} } + \frac{2}{n}\sum\limits_{s = 1}^{h} {w(s,h)\frac{1}{n}} \sum\limits_{t = s1}^{n} {a_{t} a_{t - s} } $$

(13)

where at and n are the number of stages and the residuals of the time series and also w(s,h) is given by:

$$ w(s,h) = 1 - s(h + 1) $$

(14)

For “Level” and “Trend” stationary testing, the following statistics are used, respectively.

$$ {\text{KPSS}} = \frac{1}{{n^{2} }}\sum\limits_{t = 1}^{n} {\frac{{S_{t}^{2} }}{{S^{2} (l)}}} $$

(15)

where $S_{t}^{2}$ is the mean squares of errors.

In order to identify the type of deterministic term in the time series, various tests are applied. The ACF and PACF correlograms were applied to survey the existence of periodic terms in the time series. If the time series has a seasonal variation, sinusoidal fluctuations are evident in the graph. Any sudden or gradual change (decrease or increase) in the time series indicates the existence of trend or jump terms in the time series. The Mann–Whitney test was applied to survey the existence of the jump term in the time series. To perform this test, the data are divided into several subclasses and then, through the following statistics, the existence of the jump term is examined.

$$ U_{{{\text{MW}}}} = \frac{{\sum\limits_{t = 1}^{N} {\left( {R(B(t) - \frac{{{\text{Ru}}_{1} ({\text{Ru}}_{1} + {\text{Ru}}_{2} + 1)}}{2}} \right)} }}{{\sqrt {\frac{{{\text{Ru}}_{1} {\text{Ru}}_{2} ({\text{Ru}}_{1} + {\text{Ru}}_{2} + 1)}}{12}} }} $$

(16)

where Ru(t) is original series data, which are divided into two sub-series of length Ru1 and Ru2. B(t) is arranged in ascending order based on original data; R(B(t)) is the order of the function z(t).

The Mann–Kendall test (MK) and seasonal Mann–Kendall test (SMK) are applied to the existence of trend term in the time series.

The mathematical equation of MK test is as follows:

$$ U_{{{\text{MK}}}} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {({\text{MK}} - 1){\text{var}} ({\text{MK}})^{ - 0.5} } \hfill & {{\text{MK}}\rangle 0} \hfill \\ \end{array} } \\ {\begin{array}{*{20}l} 0 \hfill & {{\text{MK}} = 0} \hfill \\ \end{array} } \\ {\begin{array}{*{20}c} {({\text{MK}} - 1){\text{var}} ({\text{MK}})^{ - 0.5} } & {{\text{MK}}\langle 0} \\ \end{array} } \\ \end{array} } \right. $$

(17)

$$ {\text{MK}} = \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {{\text{sgn}} ({\text{Ru}}_{j} - {\text{Ru}}_{i} )} } $$

(18)

$$ {\text{var}} (MK) = \frac{1}{18}\left[ {N_{o} (N_{o} - 1)(2N_{o} + 5) - \sum\limits_{g}^{p} {N_{op} (N_{op} - 1)(2N_{op} + 5)} } \right] $$

(19)

where p is equal to the number of identical groups. Nop is the number of data in the p-group; sgn and No are the sign function and the number of observations, respectively.

The statistic of SMK test is as follows:

$$ R_{{{\text{sk}}}} = \sum\limits_{i = 1}^{{N_{k} }} {\sum\limits_{j = i + 1}^{{N_{k - 1} }} {{\text{sgn}} \left( {{\text{Ru}}_{ki} - {\text{Ru}}_{kj} } \right)} } $$

(20)

$$ {\text{SMK}} = \sum\limits_{k = 1}^{\omega } {(R_{sk} - {\text{sgn}} (R_{sk} ))} $$

(21)

$$ {\text{var}} ({\text{SMK}}) = \sum\limits_{j}^{\omega } {\frac{{N_{j} (N_{j} - 1)(2N_{j} + 5)}}{18}} + 2\sum\limits_{m = 1}^{\omega - 1} {\sum\limits_{n = i + 1}^{\omega } {\sigma_{mn} } } $$

(22)

$$ U_{{{\text{SMK}}}} = {\text{MK}}{\text{var}} ({\text{MK}})^{ - 0.5} $$

(23)

where Nj and σmn are Nth data from season j and covariance in the mth and nth seasons (respectively).

If the test results described above indicate that the time series is non-stationary, then the existing deterministic terms should be removed and retested. One of the popular methods for stationary is differentiation. This method is done in two forms of seasonal and non-seasonal differentiation. In non-seasonal differentiation, each of the data is subtracted from the previous data, and thus, the trend can be removed from the time series. Seasonal differentiation is done according to Eq. 24 and according to the season number, and thus, the season term can be removed from the time series. One of the suitable methods to remove the jump term from the time series is the standardization method. By removing the mean and standard deviation from the data, this method converts the time series to a time series with zero mean and standard deviation of one.

$$ {\text{Diff}}({\text{Ru}}) = {\text{Ru}}(t) - {\text{Ru}}(t - s) $$

(24)

$$ {\text{SStd}} = \frac{{{\text{Ru}}(t,i) - \overline{{{\text{Ru}}}} (i)}}{{S_{d} (i)}} $$

(25)

where s, Ru(t), $\overline{{{\text{Ru}}}}$ and Sd are the seasonal number, the train data set, the average and standard deviation of data, respectively.

Linear model

For complex problems, using only one variable is not enough, and solving such problems requires more variables. Thus, by adding exogenous variables to a simple linear regression model, a multivariate regression model can be created. These additional variables affect the predicted values. Due to the consideration of more information in modeling, they usually improve the results compared to simple linear regression models. In this study, the precipitation and NDVI are considered as exogenous input variables; that are applied to predict runoff values as the output. The complete relationship of multivariate linear stochastic model (MLSM) in the multivariate form with differencing and seasonality is as follows:

$$ {\text{Ru}}_{t} =\, \propto_{0} + \propto_{1,} V_{1,t} + ... + \propto_{m,} V_{i,t} + \frac{{\theta_{q} (B)\Theta_{Q} (B^{S} )}}{{\phi_{p} (B)\Phi_{P} (B^{S} )(1 - B^{S} )^{d} }}e_{t} $$

(26)

where p and P are the non-seasonal and seasonal auto-regressive operators, respectively; α₀ is the arithmetic average term; B is the backshift parameter; t is time; θ_q and Θ_Q are the non-seasonal and seasonal moving average operators, respectively; e_t is random term or the residuals; t indexes time Ru_t; S is the seasonal number; d is the differentiation by seasonal; V is external input variables and α₁, α₂, …, α_m are the parameters of independent variables input V_t.

Nonlinear model

The multilayer nonlinear machine learning model (MNMLM) has been employed for modeling of different systems with complex relationships. The main element in this model is neurons, which in three different layers, including input, hidden and output, are arranged. By connecting these neurons to each other in different layers, a system is created that acts like the human brain. In this way, the transfer and receipt of information are done through these communications. Input information to the system is obtained through various time delays from the runoff time series. These time delays were selected based on the ACF diagram at total stations in the study area. Thus, the number of neurons in the input layer is determined based on the defined combination. The used various combinations in this study are introduced below.

Model 1:	f(Rut-1)
Model 2:	f(Rut-1, Rut-2)
Model 3:	f(Rut-1, Rut-2, Rut-3)
Model 4:	f(Rut-1, Rut-2, Rut-3, Rut-4)
Model 5:	f(Rut-1, Rut-2, Rut-3, Rut-4, Rut-6, Rut-12)
Model 6:	f(Rut-1, Rut-2, Rut-3, Rut-4, Rut-6, Rut-12, Rut-24)
Model 7:	f(Rut-1, Rut-2, Rut-3, Rut-6)
Model 8:	f(Rut-1, Rut-2, Rut-3, Rut-6, Rut-12, Rut-24)
Model 9:	f(Rut-1, Rut-2, Rut-3, Rut-24)
Model 10:	f(Rut-1, Rut-2, Rut-4, Rut-6)
Model 11:	f(Rut-1, Rut-6)
Model 12:	f(Rut-1, Rut-12)
Model 13:	f(Rut-1, Rut-24)
Model 14:	f(Rut-6)
Model 15:	f(Rut-6, Rut-12)
Model 16:	f(Rut-12)

After receiving information on neurons located in the input layer, this information is transmitted to the hidden layer through weight communication, transfer function and bias. In the hidden layer, weighting functions are applied to the input values to these neurons, and when the value of a neuron in this layer reaches a threshold, a value is transmitted to the neuron in the next layer. The sum of the weight values transmitted from the neurons in the hidden layer is entered along with a bias value to the neurons in the next layer. The number of neurons in the hidden layer is determined by trial and error. Since the purpose of this study is to model runoff, a neuron in the output layer is considered. Finally, the value obtained in the neuron located in the output layer can be interpreted as the system's response to the input value.

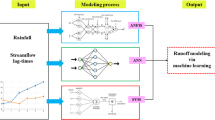
Proposed hybrid model methodology

To simultaneously use the advantages of linear and nonlinear methods in this study, a hybrid model for runoff modeling in a catchment is proposed. The proposed hybrid method for the catchment involves combining a multivariate linear method with a nonlinear method. In the linear method, in addition to runoff data, precipitation and NDVI data are also used to model the linear part. The proposed methodology is coded in MATLAB software, and its steps are shown in Fig. 3. The proposed methodology consists three substantial steps of data preparation (first step), multivariate linear modeling (second step) and nonlinear modeling (third step). In the first step, the length of time series, normality and stationary of data related to each station are evaluated. In the second step, the linear part was modeled by defining four main scenarios and 15 sub-scenarios. In Scenario 1, the data are modeled without pre-processing and using an additional variable (NDVI or precipitation). Therefore, for this scenario, two sub-scenarios were defined based on the type of input additional variable. In Scenario 2, which is based on the preprocessing technique and using an additional variable (NDVI or precipitation), eight different sub-scenarios were considered. These preprocessing comprise various normalization techniques (via Logarithm (Log), Box–Cox and Standard Logarithmic (Logstd) functions) and stationary technique via Standardization (Std) function. In Scenario 3 with one sub-scenario, the data are modeled without pre-processing and simultaneous use of precipitation and NDVI variables. In Scenario 4, modeling with preprocessing and simultaneous use of two variables of precipitation and NDVI as additional input variables led to the definition of four sub-scenarios. Then, by calculating different mathematical statistics and comparing the results obtained from different sub-scenarios, the superior linear model is selected, and by performing diagnostic check from the model residuals based on Ljung–Box test (Ljung and Box 1978), the linear model is validated.

Fig. 3

Flowchart of the proposed methodology for runoff modeling in catchment

In Ljung–Box test that statistic is obtained through Eq. 27, if the value of P-value obtained from this statistic is greater than 5%, then the residuals of the model are independent and there is no linear correlation between them. As a result, the residuals contain only the nonlinear component. Otherwise, the model should be reviewed. In the third step, the residuals of the model are modeled by a nonlinear model. In this step, 16 different input combinations based on various delay lags are used to model the nonlinear part. The considered input combinations are the same combinations used in “Nonlinear model” Section. At the end, the output of the linear model was added to the output of the nonlinear model for each combination and by comparing the results obtained from 16 different hybrid models; the best model was selected for each station.

$$ LB = N_{o} (N_{o} + 2)\sum\limits_{i = 1}^{q} {\frac{{r^{2} }}{{N_{o} - 1}}} $$

(27)

where No is the total observation data, the value of q is equal to a quarter of the length of the data, r is the ACF from residual at lag i.

Comparison measures

To compare the accuracy of results which are obtained from the implementation of various models, root-mean-square error (RMSE), mean absolute error (MAE), correlation coefficient (R) and Akaike information criterion (AIC) are used. The RMSE is obtained from the square root of the prediction errors, and MAE is obtained from the average of the prediction errors. These two criteria indicate the accuracy of modeling. R which is obtained by dividing the covariance by the standard deviation of each variable indicates the intensity of linear relationship between variables. The AIC that is obtained from the sum of the number of parameters used in modeling and the maximum log-likelihood of the model indicates the accuracy and complexity of the model. The RMSE, MAE, R and AIC are stated as

$$ {\text{RMSE}} = \frac{1}{{N_{o} }}\sqrt {\sum\limits_{t = 1}^{n} {({\text{Ru}}_{o(t)} - {\text{Ru}}_{p(t)} )^{2} } } $$

(28)

$$ {\text{MAE}} = \frac{1}{{N_{o} }}\sum\limits_{t = 1}^{n} {\left| {{\text{Ru}}_{o(t)} - {\text{Ru}}_{p(t)} } \right|} $$

(29)

$$ R = \frac{{\sum\limits_{t = 1}^{n} {\left( {{\text{Ru}}_{o(t)} - \overline{{{\text{Ru}}{}_{o}}} } \right)} \left( {{\text{Ru}}_{p(i)} - \overline{{{\text{Ru}}_{p} }} } \right)}}{{\sqrt {\sum\limits_{t = 1}^{n} {\left( {{\text{Ru}}_{o(i)} - \overline{{{\text{Ru}}_{o} }} } \right)} )^{2} \sum\limits_{i = 1}^{n} {\left( {{\text{Ru}}_{p(t)} - \overline{{{\text{Ru}}_{p} }} } \right)^{2} } } }} $$

(30)

$$ AIC = N_{o} \times \log ((RMSE)^{2} ) + 2 \times (NHN(NIP + 2) + 1) $$

(31)

where Ru_o (t) and Ru_p(t) denote the actual and predicted values, respectively. Also $\overline{{{\text{Ru}}{}_{o}}}$ and $\overline{{{\text{Ru}}_{p} }}$ are the arithmetic average actual and predicted values, respectively. N_o, NHN and NIP are the total number of data, number of neurons in the middle and first layers, respectively.

Results and discussion

Before starting the modeling, the data are first divided into two categories of training and testing, for which purpose 70% of the total data measured at each station is used to train the model and the rest of the data, which includes 30% of the data, are considered for model testing. Then, the predictability of the data was evaluated by Hurst test. This coefficient is computed, and the gained values are presented in Table 2 for all stations. All the numbers gained for H are bigger than 0.5 except for 02PH011, 02PH014 and 02PJ030 stations. In 02PH011, 02PH014 and 02PJ030 series with Hurst coefficients equal to 0.46, 0.47 and 0.49 (respectively), the length of the time series should be increased (Ebtehaj et al. 2019; Bayesteh and Azari 2019). Considering the total length of the time series for these three series and recalculating the Hurst coefficient for them, values 0.46, 0.48 and 0.51 were gained for 02PH011, 02PH014 and 02PJ030 stations, respectively. The value of the Hurst coefficient for the two stations did not exceed 0.5. This means that by increasing the number of the data by approximately 45%, the H coefficient does not improve properly. Based on previous studies, Cadenas and Rivera (2007) modeled the wind speed data using ARIMA and ANN models. These data are extracted from wind power stations. They showed that seasonal ARIMA models have better performance than other methods for the alignment and prediction of the wind speed and also showed that these models can be applied to forecast the wind speed. Cadenas et al. (2019) examined also the type of these data using Hurst coefficient and showed that using various methods including classical R/S analysis the structure of the studied data is antipersistent.

Table 2 Results of P-value for the Hurst coefficient (H) of runoff data

Given that our goal is to use all stations in modeling, thus we used the total stations for the modeling process.

The results of J-B test are given in Table 3 to check the normality of data in different stations. In all stations, the values gained from P-value of this test were lower than 5%; hence, the all of them are un-normal. Various transformations including Log, Logstd and Box–Cox were used for normalization of the original data. After the series was transferred using different functions, the normality test was performed on them again and results are also illustrated in Table 3. After transformation through logarithm and Box–Cox functions, the values gained of J-B test were higher than 5% for all of series. Thus, all of the series are normalized by these transfer functions. The Logstd function is able to normalize all series except for 02PC017 series. By transferring through the Log and Logstd function, among the runoff series, the 02PJ034 series is most affected and closer the normal distribution with a probable value of 90%. By transferring through the Box–Cox function, the 02PJ034, 02PH011 and 02PH014 series are most affected and have closer the normal distribution with a probable value greater than 90%. The least effect on normalization through the Log, Logstd and Box–Cox functions is observed in the 02PD010, 02PC017 and 02PB019 series, respectively. As shown in Table 3, the probability gained from this test for the Box–Cox conversion function is greater than the other transformations. Accordingly, the Box–Cox transformation has a greater ability to normalize data than the Log and Logstd transformations and performs better than other methods in the process of data normalization. The results for the rain data show that the values gained from P-value of J-B test were higher than 5% for all of the series but for the NDVI series show that the series were still un-normal.

Table 3 J-B test results for all stations

Based on the results of the stationary tests for all of the original data (Table 4), the time series were stationary, owing to the P-value for the KPSS test is above 5% and for the PP test is below 5%. In the case of transmitted series by Log function, four series out of nine series include 02PJ030, 02PH014, 02PJ034 and 02PL005 series become non-stationary based on KPSS test and the P-value is lower than 5%. Based on PP test and observing the results of P-value, the 02PB019, 02PC017, 02PL005 and 02PK009 series become non-stationary due to the P-value ascending above from the confidence level. Similar results were gained for the Box–Cox transfer and for PP test. In the case of the KPSS test, only the 02PJ034, 02PH014 and 02PL005 series have a P-value lower than 5% and are non-stationary. The result of the KPSS test for the transmitted series trough the Logstd function showed that only three series including 02PH014, 02PJ030 and 02PL005 have a P-value lower than 5% and therefore are non-stationary. Based on the result of the PP test, the gained P-value is above 5%, and therefore, all of the transmitted series trough the Logstd function are non-stationary except for 02PJ034. Based on the results of both tests, the transformation series via standardization method are stationary. Generally, it is concluded that using the Log, Box–Cox, Logstd functions all of the time series are non-stationary. Therefore, the non-stationary factor in time series must be considered.

Table 4 Results of stationary tests for all stations

The intuitive method is used to investigate the seasonal variation and ensure stationary. In order to, the ACF and PACF correlograms were drawn in supplementary figures for all stations (Figs. 4 and S2 in the supplementary file for details). A symmetrical peak with 12-lag repetition can be seen in all of the time series which confirms the existence of periodicity in this series. Also, in all of time series, PACF diagrams show the change of the sign after the first lag, which confirms the non-stationary time series.

Fig. 4

ACF and PACF plots for station 02PB019 and the original data in the calibration period

The P-value according to the MK and SMK test statistics is equal to 0.366–0.081, 0.513–0.567, 0.131–0.098 and 0.156–0.132 for 02PB019, 02PC017, 02PD010 and 02PK009 stations, respectively. As a result, due to the fact that the value of probability in both tests is greater than 5%, not all of these series have trends. On the other hand, other stations in the study area have trend term. The results of the Mann–Whitney test show that no jump exists for all series at the 95% confidence level except for 02PJ034, 02PH014 and 02PL005. In these three stations, the results of the Mann–Whitney test are equal to 0.019, 0.027 and 0.009, because the P-values are less than the critical value; the existence of a jump is confirmed in these stations. After checking the existence of the deterministic terms by several tests, if there are exist then removed in an appropriate method or their effect reduced. In series that have trend term, 1st differencing is used to eliminate the trend term. After differencing, all tests were used on differentiated series. The results of the PP and KPSS tests show that all of the time series are stationary and 02PJ034, 02PH011, 02PH014, 02PJ030 and 02PL005 series that had trend component; their trend is removed using differences. Also, through re-test, results show that the jump in these series was also eliminated, but they still have the periodic component. Thus, non- seasonal differencing is not only sufficient for stationary. As previously mentioned, standardization can use to reduce jumps in a time series, but after standardization, the results showed that in none of the series, this term is not reduced. The standardization method had the least impact on the series distribution. Thus, standardization is not a good way to eliminate jumps in these series. Generally, based on the results of various tests on the original data, there is a seasonal term for all stations, and also all of time series are un-normal. Consequently, in order to stationarize and normalization of the series, different transformation functions (such as Log, Logstd and Box–Cox functions) and seasonal differencing were applied. After differencing and transformation for all-time series, the total of the tests was reused (see Tables 1S to 9S in the supplementary file for details). The ACF and PACF plots are also drawn, and it can be concluded that all of time series are stationary (Figs. 5 and 3S in the supplementary file for details). Generally, all series have no seasonality, trend and jump terms based on ACF plot, Mann–Kendall trend test and Mann–Whitney test, respectively. It can be seen that by using different conversions including Box–Cox, Logstd and Log and then seasonal differentiation, all series are normal and stationary except the 02PL005 series that are un-normal and stationary. The Box–Cox transform was able to increase the normality of the data more efficient than other methods for all stations except 02PJ034, 02PL005 and 02PK009 series. In series that have trend and jump terms, the test results show that seasonal differentiation has been able to eliminate definite terms. Therefore, for all-time series only the seasonal differencing is sufficient to stationary them.

Fig. 5

ACF and PACF plots for 02PB019 station and the seasonal differentiation data in the calibration period

The results of linear model

At each station, by changing the seasonal and non-seasonal parameters, the simulation is performed for each sub-scenario. In scenarios 2 and 4, a pre-processing step is performed before stationary. In sub-scenarios 6, 10 and 15 before stationary through seasonal differentiation, one stage of stationary is done through standardization. In other sub-scenarios that involve preprocessing, a normalization step is performed on the Log, Box–Cox and Logstd functions. After modeling, for each sub-scenario and in each station, a model that has high accuracy and fewer parameters is selected as a suitable model. For this purpose, from between the models, the model that has less AIC is selected. Then, the Ljung–Box test is performed to validate the linear model. By calculating the residuals of the linear model and performing this test on the residuals, the independence of the residuals is examined. If the statistical value of this test for all lags is greater than 5%, the model is approved and therefore the model is suitable for predicting runoff. The results of the best models in all stations and for different scenarios are given in Table 10S in supplementary file for details. Then, the superior model for each station is selected by comparing the results of different sub-scenarios and selecting the sub-scenario that has the lowest value of AIC. The superior model for each station is given in Table 5.

Table 5 Mathematical criteria results of superior models in various stations for determining the best linear model

The superior model at 02PB019 station is obtained by running sub-scenario-13 which uses two variables of precipitation and NDVI with pre-processing. This sub-scenario with MAE = 16.71, RMSE = 23.75, AIC = 308.41 and R = 0.80 has the highest correlation value, the lowest error value and the lowest complexity value compared to other sub-scenarios. When using two additional variables in modeling, other normalization functions increase the complexity of the model and decrease its correlation and accuracy. At this station, although running through the Box–Cox function brings the data closer to normal, running the model through the logarithm produces better results. In this station, using the Box–Cox function as preprocessing and the use of two additional variables created the model with the highest complexity (AIC = 327.62). Comparison of the results of scenarios 1 and 3 shows that the use of two variables along with runoff data improves the modeling results compared to the model that the use of one additional variable. In case of using additional precipitation variable for modeling, the normalization preprocessing technique improves the modeling results in all criteria. If NDVI variable is used, the normalization preprocessing technique weakens the results and increases the complexity of the model and decreases the correlation and accuracy of the model.

At 02PC017, the lowest of R-value is gained base on sub-scenario 14 (R = 0.59) and the highest of R is registered to sub-scenarios 1, 6, 11 and 15 (R = 0.72). The AIC of sub-scenario 1 with the value gained equal to 126.05 was lower than other scenarios. The MLSM which is executed according to sub-scenario 1 is preferred than other models for 02PC017, because it has lower complexity and highest correlation than other models. The highest complexity (AIC = 142.53) is related to sub-scenario 14 which consists of two additional variables along with preprocessing via the Logstd function. This model has the highest number of parameters for modeling. The use of the additional variable of precipitation (sub-scenario 1) generates a more suitable result than the variable NDVI (sub-scenario 2), and on the other hand, the use of two additional variables (sub-scenario 11) with MAE = 2.67, RMSE = 3.68, AIC = 128.76 and R = 0.72) despite reducing the amount of error increases the complexity of the model. In this station, normalization through the Box–Cox function causes the data to be closer to the normal distribution. In the sub-scenarios 3 and 12 that use this function as preprocessing, better results are obtained than other functions. The highest complexity (AIC = 142.53) is related to the sub-scenario 14 which uses two variables of precipitation and NDVI with normalization via the Logstd function.

Comparing the sub-scenarios implemented from the first scenario at 02PD010 shows that the use of the additional variable NDVI produces better results in all the criteria evaluated. In contrast, the use of both additional variables (sub-scenario 11) weakens the results. Although the use of two additional variables increases the complexity and error of the model, using the normalization technique reduces the complexity and error of the model. By comparing the results presented from sub-scenarios that include preprocessing to sub-scenarios without preprocessing, preprocessing improves the results. In this station, although the Box–Cox function brings the data closer to the normal distribution, the performance of the logarithm function in modeling is better than the Box–Cox function. By comparing all sub-scenarios executed in this station, the least amount of complexity, the least error and the highest correlation are created through sub-scenario 13 with MAE = 3.50, RMSE = 4.56, AIC = 162.55 and R = 0.75. The maximum amount of complexity with AIC = 178.35 is created through sub-scenario 11, which shows the weakness of this model in runoff modeling.

At 02PH011, the MLSM that is executed according to sub-scenario 13 is preferable than other models, because it has the least complexity (AIC = 112.73) and highest correlation (R = 0.75) contrasted to other models. The lowest errors were gained for this station based on sub-scenario 3, which has the minimum MAE and RMSE equal to 2.12 and 2.78, respectively. Comparing scenarios 1 and 3, the results show that the use of two additional variables in modeling produces better results than the use of an additional variable. The normalization technique before the implementation of the model reduces the complexity of the model. In cases where there are two additional variables, the best preprocessing is using the logarithm function, and in cases where there is only one additional variable, the best preprocessing is using the Box–Cox function.

In the time series modeling of the 02PH014 station, comparing scenarios 1 and 3, the results show that using one additional variable produces better results than using two additional variables and the use of two variables increases the complexity of the model. Also, by comparing scenarios 1 and 2, the results show that performing preprocessing increases the complexity of the model and thus reduces the accuracy of runoff modeling. The comparison of scenarios 3 and 4 shows that using the Logstd function reduces the amount of complexity of the model, but the two logarithm and Box–Cox functions increase the complexity of the model. By implementing sub-scenario 14, a 13.5% decrease in the complexity of the model was observed compared to sub-scenario 11. The MLSM which is executed according to the sub-scenario 14 is preferable than other models. At this station, the weakest performance is related to sub-scenario 5 with AIC = 180.83, MAE = 3.62 and RMSE = 6.27.

At 02PJ030 station, comparing the results obtained from all sub-scenarios shows that the model implemented through sub-scenario 11 with the least amount of complexity (AIC = 243.90) and lowest error (MAE = 7.49) and highest correlation (R = 0.75) is the best model for runoff modeling at this station. Comparing scenarios 1 and 3, the results show that the implementation of the model using two additional variables has better results than using one additional variable. In all sub-scenarios that include preprocessing, preprocessing increases the complexity of the model compared to the non-preprocessing mode. At this station, the weakest performance is related to sub-scenario 7 with AIC = 258.42, MAE = 9.49 and RMSE = 9.76.

At 02PJ034 station, the AIC of sub-scenario 11 with the value gained equal to 101.84 was lower than other sub-scenarios. Also, the implementation of this sub-scenario shows the lowest amount of error (MAE = 2.13 and RMSE = 2.89) and highest correlation (R = 0.8) among all sub-scenarios. Therefore, the preferred model for this station is obtained through the implementation of this sub-scenario. At this station, by different pre-processing, the complexity of the model increases. Among the defined sub-scenarios without preprocessing, the results are improved using two additional variables including precipitation and NDVI.

At 02PK009, by comparing sub-scenarios 1 and 2, the results show that using the NDVI variable reduces the amount of complexity compared to using the precipitation variable. By using precipitation and NDVI at the same time, the results are better than using only the precipitation variable. But the results of using variable NDVI are still better than the other two cases. In case of using variable NDVI, preprocessing weakened the results. In this station, the use of preprocessing increases the complexity of the model. The lowest of AIC is registered to scenario 2 (AIC = 198.27).

At 02PL005 station, the lowest of AIC and highest correlation are registered to sub-scenario 12 (AIC = 259.37, R = 0.66). A comparison of the mathematical criteria for the third scenario shows that the model with the additional variable of precipitation with MAE = 12.03, RMSE = 16.31 has a lower error than the use of the NDVI variable with MAE = 15.07, RMSE = 18.64. A comparison of the mathematical criteria for the third scenario shows that the model with the additional variable of precipitation with MAE = 12.03, RMSE = 16.31 has a lower error than the use of the NDVI variable with MAE = 15.07, RMSE = 18.64, while using of the NDVI parameter has less complexity (AIC = 265.56) than the model with the additional variable of precipitation (AIC = 267.17).

Comparing the results of sub-scenarios that include two stages of stationary (first stage through standardization and the second stage through seasonal differentiation) with sub-scenarios that have only one stage of stationary through seasonal differentiation shows that standardization has no effect on runoff modeling and produces results quite similar to those of sub-scenarios that have only one stage of stationary.

The results of nonlinear models

At first, the input combinations to the nonlinear model were determined to model the monthly runoff in the catchment area. To determine these input combinations, the ACF and PACF diagrams of all stations were examined. Different combinations of important lags obtained from these diagrams were considered inputs for the nonlinear model. Lags 1, 2, 3, 4, 6, 12 and 24 are important lags obtained from the diagrams ACF and PACF. Considering different combinations of these lags, 16 different combinations were defined as inputs MNMLM. These input combinations were considered in a similar way for all stations in the study area. The MNMLM is trained with 70% of the runoff dataset, and the remaining data are utilized to test the model. Different mathematical metrics including MAE, RMSE, R and AIC were performed to test the performance of models and select the model with the best performance.

In the northern and eastern part of the study area, there are five stations named 02PB019, 02PC017, 02PD010, 02PH014 and 02PH011. According to the results obtained from these five stations, the lowest amount of complexity is related to Model 13 with the input combination including lags 1 and 24 (Figs. 6 and 4S in the supplementary file for details). Given that the best model is a model that in addition to high accuracy is as simple as possible. Therefore, in stations, the superior model is a model that, in addition to high accuracy, is also simple. The Model 13 with two input neurons produced better results than other models in these stations. In these stations, the lowest amount of error and the highest correlation according to MAE, RMSE and R criteria related to models 7 and 8, which have the highest number of input neurons compared to other models. On the other hand, these models have the highest amount of complexity, which indicates the poor performance of these models in runoff modeling. In all these stations, Model 7 has the highest level of complexity compared to other models. Therefore, the model based on the implementation of Model 13 is selected as best model for these stations due to the low complexity and is also one of the high precision models. The minimum value of correlation is observed to Model 14 while this combination is among the models with high error. At 02PB019 station, with the highest gross drainage area, the weakest performance in criteria of error and correlation is related to Model 1 with MAE = 26.94, RMSE = 37.83 and R = 0.26 (Fig. 6). In other stations located in the northern and eastern parts of the study area, the lowest correlation is related to Model 14, which is one of the models with the highest error value. In general, in the stations located in the northern and eastern parts of the study area, the best model for modeling runoff is Model 13 with the least amount of complexity and the weakest performance related to the results obtained from Model 7 with the highest amount of AIC. The lowest value of correlation was observed in the results obtained from Model 14.

Fig. 6

Results of mathematical metrics including MAE, RMSE, R and AIC for determining the best MNMLM models and for 02PB019 and 02PC017 stations in the study area

In the western and southern parts of the study area, two stations, 02PK009 and 02PL005, are located, respectively. Comparing the results obtained from different models for these two stations, it was observed that Model 13 with the least amount of complexity, the highest amount of correlation and the least amount of error is the best model for runoff modeling. In these two stations, according to the other stations, the lowest correlation value is related to Model 14. In 02PK009 and 02PL005 stations, Model 7 and Model 6 with AIC = 507.09 and 506, respectively, have the highest level of complexity compared to other models (Figs. 4S and 5S in supplementary file for details).

In the central part of the study area and at 02PJ034 station (Figs. 4S and 5S in supplementary file for details), the highest correlation is registered to Model 7 with input delays of 1, 2, 3, 4, 6, 12 and 24 months (R = 0.77), also the highest correlation in all stations is related to this station and this combination, while this combination has the highest value of complexity in this station (AIC = 463.68). The lowest AIC-value is equal to 122.61 and for Model 16. Besides, the minimum value of errors observed to combination Model 12 (MAE = 2.34, RMSE = 3.01). Overall, the model based on the implementation of Model 16 that has the lowest complexity is selected as preferred model for 02PJ034 station. The minimum value of correlation is observed to Model 14 (R = 0.09). Combination Model 1 has the maximum errors (MAE = 3.24, RMSE = 4.54) than other combinations. At 02PJ030 station (Fig. 4S in supplementary file for details), the highest correlation and the lowest RMSE are registered to Model 13 with input delays of 1 and 24 months (RMSE = 10.37, R = 0.71). The lowest AIC-value is equal to 252.21 and for Model 16 that the amount of MAE and RMSE errors in this combination is 2.7 and 2.64 higher than in combination Model 13. Overall, the model based on the implementation of Model 16 with having the minimum number of input neurons is selected as preferred model for 02PJ030 station. The minimum value of correlation is observed to Model 1 (R = 0.38). Combination Model 2 has the maximum errors (MAE = 10.79, RMSE = 13.94) than other combinations.

In general, in approximately 80% of the stations in the study area, Model 13 with the least amount of complexity and having only two input neurons with input delays of 1 and 24 months is the best model for runoff modeling, and in the remaining 20%, Model 16 with input delays of 12 month has the least complexity. Thus, lags 1, 12 and 24 are the most effective lags in runoff modeling in this study area. The use of combinations Model 7 and Model 8 for stations located in the northern and eastern parts of the study area causes fewer errors than other combinations. For stations located in the other parts, combinations Model 12 and Model 13 have fewer errors than other combinations. The highest level of correlation for stations located in the western and southern is obtained by using combination Model 13, for stations located in the central and eastern is obtained by using combination Model 7 and for other stations combination Model 8 and Model 10. In all stations, combination Model 6 and Model 7 has the highest complexity due to having the maximum number of input neurons. As a result, Model 6 and Model 7 are among the weakest models.

The result of hybrid models

To create a hybrid model, a suitable linear model is first created based on the definition of different scenarios. By performing different scenarios and comparing the results, it was found that in all stations except 02PC017 and 02PK009 stations, the use of two additional variables of precipitation and NDVI produced better results than one additional variable. In these stations, except for 02PJ030 and 02PJ034 stations, a normalization step using the normalization functions is required before the stationary stage and in other stations; a suitable linear model is built only with a stationary step (seasonal differentiation). At 02PC017 and 02PK009 stations, linear modeling is performed using the additional variables of precipitation and NDVI, without the need for normalization stage, respectively. At each station, after running the best linear model and confirming the model through test diagnostic, the residuals of the linear model are calculated. In the next step, the residuals of the linear model are modeled using the nonlinear model. In the nonlinear modeling step, various combinations of time delays are used. Then, the output of the nonlinear model is summed to the result of the linear model and runoff is modeled. The results of various mathematical criteria including error and linear correlation for all stations and all selected combinations are shown in Fig. 7. Also, the results related to the complexity of the model based on the AIC criteria are shown in this figure for all stations.

Fig. 7

Results of mathematic metrics including MAE, RMSE, R and AIC for determining the best hybrid models and for 02PL005 and 02PJ030 stations in the study area

At 02PB019 station (see Figs. 6S and 7S in supplementary file for details), Hyb-9 with delays of 1, 2, 3 and 24 creates the highest error (MAE = 20.00 and RMSE = 26.69) and Hyb-2 with delays of 1 and 2 creates the highest complexity (AIC = 319.45) and lowest correlation (R = 0.77), so these two models perform poorly in runoff modeling at this station. On the other hand, Hyb-13 reduced the complexity of the model by 7% by reducing the MAE and RMSE value by 13.29% and 17.46, respectively, and increasing the correlation by 23.38% compared to Hyb-2. At 02PC017 station (see Figs. 6S and 7S in supplementary file for details), Hyb-6 with delays of 1, 2, 3, 4, 6, 12 and 24 creates the highest error (MAE = 4.54 and RMSE = 5.40) and Hyb-5 with one less neuron at the input than model Hyb-6 creates the highest complexity (AIC = 136.46). The Hyb-13 has the least error (MAE = 2.34, RMSE = 3.02) and the least complexity (AIC = 110.97) and highest correlation (R = 0.79). The Hyb-13 increased the performance of the AIC and R over the Hyb-5 which has the highest amount of complexity and the lowest correlation with AIC = 136.47 and R = 0.69 compared to other combinations by 18.68% and 13.95%, respectively. Also, the Hyb-13 increased the performance of the MAE and RMSE over the Hyb-6 by 48.57% and 44%, respectively. As a result, considering that HYB-13 works better than other combinations in all criteria, it was selected as the preferred combination for this station. At 02PD010 station (see Figs. 6S and 7S in supplementary file for details), Hyb-8 with the highest error (MAE = 4.00 and RMSE = 5.30) and complexity (AIC = 177.65) and the lowest correlation (R = 0.66) showed the weakest performance in runoff modeling at this station. On the other hand, Hyb-13 with the least amount of complexity (AIC = 157.13) and the highest correlation (R = 0.79) has a good performance in runoff modeling. In station 02PJ034 (see Figs. 6S and 7S in supplementary file for details), the lowest error value (RMSE = 2.60), the highest correlation (R = 0.85) and the lowest complexity (AIC = 93.40) are provided through the implementation of Hyb-13. The Hyb-1 and Hyb-2 are among the models with poor performance in terms of error and complexity. At 02PH011(see Figs. 6S and 7S in supplementary file for details), the highest complexity (AIC = 118.73) and the lowest correlation (R = 0.7) were observed in Hyb-8 with 6 input neurons. On the other hand, by reducing the amount of neurons in the input to 2 neurons, it improved the modeling results, so that the amount of complexity in Hyb-12 decreased by 15.6% and the amount of correlation increased by 11.9%, and in Hyb-2 and Hyb-13, in Hyb-2 and Hyb-13, runoff was modeled with the least amount of error. At 02PH014 station (see Figs. 6S and 7S in supplementary file for details), Hyb-5 with MAE = 4.24, RMSE = 5.37, R = 0.57 and AIC = 118.93 creates the lowest correlation and highest error and complexity. On the other hand, Hyb-11 with two input neurons creates the least amount of error and complexity in runoff modeling than other models and improves the results in MAE, RMSE and AIC by 27.86%, 23.93% and 7.3%, respectively, compared to the results of Hyb-5. At 02PK009 (see Figs. 6S and 7S in supplementary file for details), the lowest complexity value (AIC = 165.17) is for Hyb-13 and the highest complexity value (AIC = 199.54) for Hyb-2. The Hyb-13 also produces the highest correlation values (R = 0.79) and the lowest RMSE values (RMSE = 5.71) in runoff modeling at this station. At 02PL005 (Fig. 7), Hyb-13 has the least error (MAE = 9.16, RMSE = 12.93) and the least complexity (AIC = 243.45) and highest correlation (R = 0.77). As a result, considering that HYB-13 works better than other combinations in all criteria, it was selected as the preferred combination for this station. The Hyb-13 increased the performance of the AIC and R over the Hyb-14 which has the highest amount of complexity and the lowest correlation with AIC = 264.01 and R = 0.61 compared to other combinations by 7.7% and 26.22%, respectively. At 02PJ030 (Fig. 7), the Hyb-6 with AIC = 247.30, MAE = 6.88, RMSE = 9.28 and R = 0.81 showed the weakest performance in runoff modeling at this station. In contrast, Hyb-13 showed the best performance in runoff modeling.

According to the results obtained, at all stations except 02PH011 and 02PH014 stations, the Hyb-13 model with input delays of 1 and 24 months has the least complexity. The Hyb-13 model has the highest correlation value among the models implemented for stations 02PB019 (R = 0.73), 02PC017 (R = 0.79), 02PD010 (R = 0.79), 02PJ034 (R = 0.86), 02PK009 (R = 0.79), 02PL005 (R = 0.77) and 02PJ030 (R = 0.81). Also, the Hyb-13 model according to both criteria RMSE and MAE at 02PL005 station (RMSE = 12.93 and MAE = 9.16), 02PC017 (RMSE = 3.02 and MAE = 2.34) and according to criterion RMSE in stations 02PJ030 (RMSE = 9.27), 02PK009 (RMSE = 5.71) and 02PJ034 (RMSE = 2.60) modeled the runoff with the least amount of error in these stations. At 02PC017 and 02PL005 stations (see Figs. 7, 6S and 7S in supplementary file for details), the Hyb-13 produces better performance than other models in all selected mathematical criteria. In all stations except 02PB019, 02PJ034 and 02PK009, the weakest performance was observed in models Hyb-5, Hyb-6 and Hyb-8. The used combinations in these models have more input neurons than other models, which leads to increased complexity in these models. At 02PB019 and 02PK009 stations, the highest value of AIC was observed in model Hyb-2 and at 02PJ034 in model Hyb-14.

In general, in approximately 80% of the stations in the study area which includes the total study area except the eastern part, the Hyb-13 with the least amount of complexity is the best model for runoff modeling, and in the remaining 20% which are located in the eastern part of the study area, Hyb-12 and Hyb-15 have the least complexity. In the study area and among the selected top models for stations, the values of complexity, correlation, RMSE and MAE fluctuate between 93.41 and 297.01, 0.68 and 0.73, 2.60 and 21.96 and 2.01 and 16.42, respectively. The lowest value of complexity and error is related to 02PJ034 station, and the highest is related to 02PB019 station. The lowest correlation is related to 02PH014 station, and the highest is related to 02PJ034 and 02PB019 stations.

Comparison of models

After modeling based on different methods, the best model was extracted from each method and for each station. Also, the results of these methods are compared with the results presented by Soltani et al. (2021). Figures 8 and 8S in the supplementary file present a comparison of the results of different methods for nine different stations located in the catchment area. In these figures, four indicators including AIC, MAE, RMSE and R are used to compare methods.

Fig. 8

Comparison of various mathematical criteria including MAE, RMSE, R and AIC for various models and for all stations located of Saint Lawrence River watershed

At 02PJ034 station (Fig. 8), comparison of MLSM and MNMLM methods shows that the linear method works better in all selected criteria than MNMLM method. The comparison of MLSM and hybrid methods shows that the hybrid method by reducing the error, increasing the correlation and reducing the complexity of the model works better than MLSM method in all selected criteria. As a result, among the methods implemented in this study, the proposed hybrid model works better than the other two methods. The comparing the results of the hybrid model with the Soltani et al. (2021) model shows that the hybrid model performs better in the two criteria R and AIC than the Soltani et al. (2021) model, and in the two criteria RMSE and MAE the two models have almost the same results.

At 02PH011 station (Fig. 8), MLSM and MNMLM models have almost the same results in MAE and RMSE criteria, but in both the AIC and R criteria, MNMLM performs much worse than MLSM model. Although the hybrid model works in both MAE and RMSE almost similar to the linear and nonlinear models, by reducing the amount of complexity by 11% compared to the linear method and 78% compared to the nonlinear method and increasing the amount of R, it performs better than the other two methods in runoff modeling. By comparing the results of hybrid, linear and nonlinear models with Soltani et al. 2021 method, Soltani et al. 2021 method performs better in error criterion than other methods and improves the accuracy of the model by reducing the error criteria by approximately 18%. In contrast, it operates weaker than the hybrid model in both the AIC and R criteria.

At 02PB019 station (see Fig. 8S in supplementary file for details), the lowest and highest of complexity were obtained in the hybrid and MNMLM methods with a value equal to 297.01 and 509.24, respectively. In the correlation criterion, Soltani et al. 2021 and hybrid models have the same value (R = 0.85) and the lowest correlation was obtained through the implementation of MNMLM method (R = 0.71). Less modeling error by examining the two criteria, MAE and RMSE, in all methods showed that Soltani et al. 2021 model has less error than other methods and caused a reduction of 5% of MAE and 4% of RMSE compared to the hybrid method. The weakest performance was obtained based on all evaluation criteria in Soltani et al. 2021. The best performance in terms of complexity was obtained in the hybrid model and in terms of error in Soltani et al. 2021 model.

At 02PC017 station (see Fig. 8S in supplementary file for details), by comparing the results of various criteria in four methods, it was found that the two methods of hybrid and Soltani et al. 2021 model in the error and correlation criteria have the same results and have better performance in runoff modeling than the other two methods. By comparing the results of MNMLM and MLSM methods, these two methods also have almost the same results in the error and correlation criteria. The difference between these methods is specified in the AIC criteria. Comparing the results of AIC criteria in various methods showed that the hybrid method with AIC equal to 110.97 and MNMLM method with AIC equal to 424.75, respectively, create the minimum and maximum amount of complexity in modeling this station. As a result, the hybrid model performs better than the other three methods and reduces the complexity by 74%, 32% and 12% compared to the MNMLM, Soltani et al. 2021 and MLSM methods, respectively.

At 02PD010 station (see Fig. 8S in supplementary file for details), by comparing the results of RMSE and MAE criteria, it was found that Soltani et al. 2021 method with MAE = 3.17 and RMSE = 4.12 creates the least amount of error in modeling. On the other hand, the two hybrid and Soltani et al. 2021 methods with the same correlation have the highest correlation values compared to other methods. In contrast, according to the AIC criterion, the hybrid method with an AIC equal to 156.57 has the least amount of complexity compared to other methods. Comparing the two methods, the Soltani et al. 2021 and hybrid shows that Soltani et al. 2021 method improves RMSE and MAE by 17% compared to the hybrid method, and in contrast, the hybrid method improves the complexity of the model by 19% compared to Soltani et al. 2021 method. Given that this criterion creates a balance between model accuracy and complexity, a model with a lower AIC will have better modeling.

At 02PH014 station (see Fig. S8 in supplementary file for details), the results presented in Fig. S8 show that MNMLM and Soltani et al. 2021 models with almost identical values in the error and correlation criteria produce the lowest amount of error in runoff modeling at this station. On the other hand, the lowest complexity and the highest correlation were observed in the hybrid model with an AIC equal to 102.24 and correlation equal to 0.75. Similar to 02PD010 station, although the Soltani et al. (2021) and MNMLM methods perform better than the hybrid and MLSM methods in terms of error, but it is due to the fact that these two models perform weaker in terms of complexity and their complexity is higher than hybrid and MLSM models. The hybrid method, with less complexity and more linear correlation, creates more appropriate modeling than other models.

At 02PJ030 station (see Fig. S8 in supplementary file for details), the highest error and the lowest correlation were obtained in the results of MLSM method, which were corrected by performing the hybrid model and reduced the MAE, RMSE and AIC criterion by 37.9%, 41.2% and 11.7%, respectively. The lowest error value was obtained based on RMSE and MAE criteria in Soltani et al. (2021) model. The hybrid and Soltani et al. (2021) methods created the highest correlation among the data (R = 0.81). By comparing the results, the lowest complexity value was obtained in the hybrid model. As a result, the hybrid method creates more appropriate modeling than other models.

By comparing the results obtained from different models in 02PK009 station, the lowest error value (MAE = 3.47 and RMSE = 4.43) and the highest correlation (R = 0.82) were obtained from Soltani et al. (2021) model. On the other hand, this model has the highest level of complexity compared to other models (AIC = 217.47). After Soltani et al. (2021) method, the hybrid model has the lowest amount of error (MAE = 4.79 and RMSE = 5.71) and the highest correlation (R = 0.79). This model also has the least amount of complexity (AIC = 163.7) compared to other models. The weakest performance was obtained based on the error and correlation criteria in the results of MNMLM model (MAE = 5.19, RMSE = 5.52 and R = 0.68).

At 02PL005 station (see Fig. 8S in the supplementary file for details), a comparison of the results of the MLSM and MNMLM models based on the criteria of complexity and accuracy indicates that the MLSM model performs better and increased the performance of AIC by 20.5% compared to the MNMLM model. In contrast, in other criteria, MNMLM model works slightly better than MLSM model. Comparison of linear, nonlinear and hybrid methods based on various criteria showed that the hybrid model improved the results compared to using linear or nonlinear models. The hybrid model has a more suitable efficiency in runoff modeling by increasing the AIC performance by 13.5% compared to Soltani et al. (2021) method. Also in other criteria, the results of the hybrid model are better than the results of the Soltani model. As a result, the proposed hybrid model with values of MAE, RMSE, R and AIC equal to 9.16, 12.93, 243.45 and 0.77 has less complexity and higher accuracy than other models.

The three statistical properties, including correlation coefficient, centered RMS error and standard deviation, which can be shown in the Taylor diagram, are plotted in Fig. 9S. This diagram is plotted for all hydrometric stations located of Saint Lawrence River watershed and for the four different methods used in this study including MLSM, MNMLM, hybrid, Soltani et al. (2021) methods. The superior model in terms of these three statistical indicators is a model that the distance between each model and observational values is less than the other models and thus reproduces a more realistic result for modeling observational data.

According to the results presented in Fig. 9 of four different methods studied in this study for 02PH011 station, although ULSM method has the closest variation to the observed values, it has the lowest correlation value and the highest RMS error compared to other methods and therefore has the lowest compatibility with the observed values. The hybrid method with the highest correlation and the lowest RMS error has the lowest radial distance with the observed values. As a result, this method is more compatible with the observed values than other methods. The Soltani et al. (2021) and MLSM methods have the same correlation, and although MLSM method has a standard deviation closer to the observed values, it has more RMS error than Soltani et al. (2021) method. In general, these two methods have the same radial relative to the observed values, and after the hybrid method is suitable methods for runoff modeling in this station. The hybrid model improves the RMS error results by 12.3% and 7.7%, respectively, compared to the MLSM and Soltani et al. 2021 methods.

Fig. 9

Taylor diagram for observations of four model estimates of the monthly runoff for 02PH011 and 02PJ034 stations in the study area

At 02PJ034 station (Fig. 9), the hybrid method with R = 0.86, RMS error = 2.56 and SD = 4.89 m³/s is more consistent with the observations than the other methods. Although Soltani et al. (2021) method has almost the same error and correlation (R = 0.83, RMS error = 2.58) with hybrid method, this method tends to underestimate the variability of runoff volume. These conditions indicate that Soltani et al. 2021 method does not adequately obtain runoff volume at points in the series when the runoff volume is high. On the other hand, the hybrid and MNMLM methods have a higher standard deviation than the observed values (SD = 4.61 m³/s). But MNMLM method estimates the runoff volume to be much higher than the actual value at peak points. Therefore, in this model, the amount of linear correlation (R = 0.52) decreases and the error increases sharply (RMS error = 7.31). In general, the two hybrid and Soltani et al. 2021 methods have the same radial distance to the location of the observed values, but due to the fact that the hybrid method performs better in modeling peak points, this method is a more suitable method for runoff modeling at this station.

At 02PB019 station (see Fig. 9S in supplementary file for details), it demonstrated that the observed variability which is obtained from the standard deviation is equal by 38.76 m³/s. All methods except MLSM method tend to underestimate the variation in runoff volume. The MNMLM model has more variation (SD = 25.27 m³/s), and the MLSM model with SD = 39 m³/s has the closest variation compared with the observations than other models. After MLSM method, the hybrid method with a SD equal to 37.51 m³/s has the closest variation compared to the observations. The MNMLM is significantly worse because it has RMS error equal to 31.32 m³/s which is the highest RMS error compared to other models. This model with correlation coefficients around 0.6 also has the lowest correlation value. On the other hand, the hybrid and Soltani et al. (2021) models with the highest correlation (R = 0.84) have better performance. The Soltani et al. (2021) had the lowest RMS error, with RMS error equal to 20.97. After Soltani et al. (2021) method, the hybrid method with a RMS error equal to 21.65 has the lowest amount of error compared to other models. The two methods hybrid and Soltani et al. (2021) with radial distance almost equal to the observed values are suitable methods for runoff modeling in this station. The MNLM method with the maximum radial distance has the weakest performance in runoff modeling.

At 02PL005 station, the variability of all models is clearly less than the observed variability (SD = 18.64 m³/s). The closest variability is related to the hybrid model with a standard deviation of 14.81m³/s, and the model of Soltani et al. (2021) (with SD = 12.01 m³/s) has more variability than the observation data. Although Soltani et al. (2021) method and MLSM (SD = 12.09 m³/s) have almost the same variability compared with the observations, Soltani et al. (2021) method has a higher correlation coefficient than the MLSM method. The best performance was obtained for hybrid model with a correlation of 0.77, and the worst performance for MLSM was obtained with a correlation of 0.66. The lowest value of RMS error was obtained with RMS error equal to 11.85 for hybrid model, and the highest value of RMS error was obtained for MLSM model. As a result, among various methods, the hybrid method has the highest compatibility with the observed values while the MLSM model has the least compatibility with the observed values. The hybrid model improves the RMS error results by 15.6% and 8%, respectively, compared to the MLSM and Soltani et al. (2021) methods.

At 02PC017 station, the two hybrid and Soltani et al. (2021) methods have the same radial distance from the point corresponding to the observed values. These two methods have almost the same results in both correlation and error criteria. But in terms of variability, the hybrid method with a standard deviation equal to 4.61 m³/s has the closest variability to the observed values (SD = 4.73 m³/s). Although MLSM and Soltani et al. (2021) methods have the same variability, MLSM method has less correlation and more error than Soltani et al. (2021) method. By comparing the results of different methods, the weakest performance is observed in MNMLM method and the hybrid method with the closest variability has the best performance in runoff modeling.

The hybrid model with the closest variability (SD = 3.68 m³/s), the highest correlation coefficient (R = 0.75) and the lowest RMS error equal to 2.75 compared to other methods has the best performance in runoff modeling at 02PH014 station. As shown in Fig. 9S, this method has the closest radial distance to the observational data location. In contrast, MLSM method with the highest standard deviation, the highest RMS error and the lowest correlation coefficient, and as a result, the largest radial distance from the place of observational values has the weakest performance in modeling. The hybrid method improved the results of RMS error and correlation by 42.8% and 19% compared to MLSM model, respectively. The Soltani et al. (2021) method models runoff with lower correlation, higher RMS error and less standard deviation than hybrid method. As a result, this method in modeling peak points with lower estimates than the hybrid method is poorer.

At 02PJ030 station, the Soltani et al. (2021) and MNMLM methods tend to underestimate the variation in runoff volume. In contrast, hybrid and MLSM methods with standard deviation equal to 14.35 m³/s and 14.57 m³/s, respectively, have slightly higher standard deviation than the standard deviation obtained from observational data. As a result, Soltani et al. (2021) and MNMLM methods are much weaker at estimating peak points than hybrid and MLSM methods. On the other hand, the MLSM method has a higher RMS error and less linear correlation than the hybrid method. The weakest performance in all evaluation criteria, which is plotted in the Taylor diagram, was observed in MNMLM, which had a greater radial distance from the observed values than other models.

At 02PD010 station, the variability of all models is clearly less than the observed variability (SD = 6.75 m³/s). The closest variability is related to the hybrid model with a standard deviation of 6.31 m³/s, and the model of MNMLM (with SD = 3.36 m³/s) has more variability than the observation data. The Soltani et al. (2021) model had the lowest RMS error, with RMS error equal to 4.12. As shown in Fig. 9S, the hybrid and Soltani et al. (2021) methods have the closest radial distance to the observational data location. The Soltani et al. (2021) method in RMS error criterion and hybrid method in variability work better than other methods.

At 02PK009 station, the Soltani et al. (2021) and the hybrid methods have almost the same correlation, and although hybrid method has a standard deviation closer to the observed values, it has more RMS error than the Soltani et al. (2021) method. The variability of all models except the hybrid model (SD = 8.17 m³/s) is less than the observed variability (SD = 7.45 m³/s). The Soltani et al. 2021 method has the closest radial distance to the observational data location. As a result, it has better adaptation to observational values, but on the other hand, due to the tendency to minimize variability of runoff volume in this model, peak point values are modeled less than the actual value.

Conclusion

To have an integrated management of water resources, it is vital to have precise information on the quantity and rate of runoff as one of the important hydrological variables from the land surface to the rivers, and with this information, many problems of development and management of the watershed can be avoided. A hybrid scenario-based method for runoff estimation in the Quebec basin, Canada, was presented in this study, which combined a multivariate linear stochastic model with a multilayer nonlinear machine learning model. The runoff data were extracted from 9 hydrometric stations located in different parts of the basin. In addition to runoff data, climatic parameters and physiographic factors are used as exogenous variables in the modeling. The proposed methodology for runoff modeling in the watershed includes three main stages of data preprocessing, linear modeling using MLSM and nonlinear modeling using MNMLM. In the preprocessing stage, the structure of the series was examined by performing normality and stationarity tests on all time series in the watershed. A summary of the results of this step is provided below:

• All time series have a non-normal distribution, and by performing the conversion using several normalization functions, all series have a normal distribution. Among the normalization functions, the Box–Cox function brings the data closer to the normal distribution.

• With using intuitive method, the existence of periods with 12 lag

• repetition in all time series was found. Although trend and jump components were present in some time series, the season component is the most important non-stationary factor in all stations. By using seasonal differentiation, time series were stationary and all non-stationary factors were removed from all time series.

In the second step with the definition of 15 different sub-scenarios for each station, a total of 135 sub-scenarios in an overall basin were defined and implemented. A summary of the results of this step is provided below:

• Although running through the Box–Cox function brings the data closer to normal, running the model through other functions produces better results and the model is modeled more accurately.

• The results of superior models for each station show that in most stations, the simultaneous use of precipitation and NDVI variables has a better performance than the use of only one variable.

• Comparing the results of sub-scenarios that include stages of normalization and stationary (the first stage through normalization and the second stage through seasonal differentiation) with sub-scenarios that have only one stage of stationary through seasonal differentiation shows that the use of normalization technique in some stations improved the modeling results while in other stations increased the model complexity and thus reduced the modeling accuracy. As a result, the use of modeling based on the definition of scenarios leads to more accurate modeling.

In the last step, by calculating the residuals of MLSM and performing modeling using 16 different combinations based on the combination of different delay lags for all stations, the following general results were obtained.

• In most stations, delays (t-1) and (t-24) are identified as the most effective delays in the hybrid modeling of runoff in the study area.

• In most stations, as the number of input neurons increases, the complexity of the model increases, and as a result, modeling accuracy decreases.

A summary of the comparison of the results of the hybrid model with the results obtained from modeling through the MLSM and MNMLM methods as well as the results obtained from the work of Soltani et al. (2021) is given below:

• Comparison of the results shows that in terms of complexity, which indicates the simplicity and accuracy of the model, the hybrid model performs much better than other methods in all stations. Also, this method creates better linear correlation in most areas of the region than other methods. But for error criteria, the Soltani et al. (2021) method works better than other methods.

• The results of comparing the predictions of the models through the Taylor diagram show that in almost all stations, the hybrid model performs better in the standard deviation index than the other methods. In index R and RMSD, the two methods of hybrid and Soltani et al. (2021) work better than other methods. In general, the weakest performance with the longest distance from the observed values was observed in MNMLM and the best performance, especially in predicting peak runoff values, was observed in the hybrid model.