Introduction

Groundwater is the main current water source used for public water supply in cities and surrounding areas. In other hand, groundwater and surface water are hydraulically connected in surrounding areas and a better understanding of their connectivity is essential for effective management of water resources. Therefore, hydraulics of groundwater flow modeling of aquifer systems is considered as an important topic in the hydraulic engineering science. For the groundwater management, hydraulics of groundwater flow modeling plays an important role in the design and operation of groundwater systems. Hence, for better management of available groundwater, it is essential to understand the hydraulics of groundwater flow behavior within the aquifer systems. The behavior of hydraulics of groundwater flow system may be described by techniques that have been developed to solve partial differential equations using either analytical or numerical methods (Mahdavi 2015; Mahdavi and Seyyedian 2013; Allen et al. 2010; Chesnaux 2015; Dong et al. 2012; Zhou et al. 2014; Gurarslan and Karahan 2015; King et al 2010; Monachesi and Guarracino 2011). Therefore, several investigators have studied numerically the hydraulics of groundwater flow problems by some techniques such as meshless methods (Swathi and Eldho 2014), finite element method (Zhou et al. 2017), or other methods.

Exact models play an important role in simulating the future behavior of hydraulics of groundwater flow system. Therefore, investigation of the exact models for hydraulics of groundwater problems is a hot topic for engineers and mathematicians. Exact models are mostly used for problems with simplification assumptions in geometry or boundary conditions. However, analytical modeling is a useful tool to verify numerical models of groundwater problems. Also, mathematical models include numerical methods have been investigated by several researchers (Avazzadeh et al. 2020; Nikan and Avazzadeh 2021; Nikan et al. 2022; Rasoulizadeh et al. 2021).

Sometimes, truncation errors may also occur in numerical models. One of the useful applications of the exact models is to analyze the sensitivity of controlling parameters. The advantage of exact models is that their equations offer quick answers to the proposed mechanism based on a few basic parameters. These models, therefore, allow an immediate system understanding and provide a meaning value for each parameter or group of parameters. Thus, numerous exact models have been developed to investigate the hydraulics of groundwater problems. Many researchers have investigated exactly the hydraulics of groundwater problems using Laplace transform or other methods (Sen 2013; Dong et al. 2016). Moutsopoulos and Tsihrintzis (2009) developed exact models for one-dimensional unsteady flow in an infinite double permeability aquifer using Laplace transform.

Prediction of the hydraulic head within an aquifer is an important hydraulic investigation due to its central role in the optimal utilization of groundwater resources. Hydraulic head variations are caused by many factors, including surface infiltration, evaporation, earth tides, ocean tides, pumping wells, interaction with an open water body and human activities. Surfacewater-groundwater interaction has been investigated by several researchers (Srivastava 2003; Singh 2004a, b; Rodríguez et al. 2006). Schilling et al. (2004) evaluated how variable groundwater recharge and channel bed lowering has affected the shape of the water table surface. They have developed a steady state, one-dimensional analytical model to describe the shape of the water table surface near an incised stream. Kisekka et al. (2014) investigated the effect of the proposed incremental raises in canal stage on water table elevation in agricultural lands. Mulligan and Ahlfeld (2016) studied the impact of withdrawals from pumping wells on stream flow in nearby streams. Basha (2013) obtained an approximate nonlinear solution of the one-dimensional Boussinesq equation using the traveling wave approach that describes the position of the water table as a function of time.

Numerous investigations have been studied to predict groundwater hydraulic head changes induced by variations in stream water level. Boufadel and Peridier (2002) derived an analytical expression using Laplace transform for the groundwater head in a stream-aquifer system. They investigated a simplified situation where a homogeneous confined layer is in contact with a stream whose level is rising linearly at a constant speed. Bansal and Das (2009) extended this model to an aquifer under recharge condition. The aforementioned solutions are obtained for a confined horizontal aquifer. In all these studies, linear stream water level rise is assumed, which is obviously a highly simplified version of a real-world hydrograph (Li et al. 2008). In reality, stream water level variation does not follow a specified pattern. Cooper and Rorabaugh (1963) derived solutions for the changes in hydraulic head as the result of a flood-wave stage oscillation. Ferris (1963) presented a solution for piezometric head due to sinusoidal variation in the stream water level. Pistiner (2008) derived an exact model for a semi-infinite porous medium possessing a boundary condition of the power law type. Peterson and Connelly (2004) simulated water movement beneath the shoreline region under the influence of a fluctuating river stage. Rodríguez et al. (2006) simulated numerically (with MODFLOW) groundwater flow and water exchange processes between the floodplain aquifer and the surrounding streams during an irrigation season.

Therefore, in the present research a more general function describing river level variation is considered, in which the linear, exponential and power of time variations are special cases. In addition, the principal purpose of this work is to present new exact models by means of the Laplace transform method for predicting the transient hydraulic head and flow rate in a leaky aquifer subjected to the time varying river level. In fact, in this research, new exact models have been obtained to analyze and estimate the groundwater hydraulic head and the water flow in the aquifer. A leaky, isotropic, incompressible and homogeneous aquifer, which is in contact with a constant river level at one end and a river of varying water level at the other end, has been investigated. A hypothetical example is considered to compare the results of the presented new exact models with the results of the exact model of Bansal and Das (2009) as well as MODFLOW. The results show that the presented new exact models are accurate, robust and efficient. In addition, the sensitivity of the hydraulic heads to the various parameters is analyzed. Also, in the present research a more general function describing river level variation is considered, in which the linear, exponential and power of time variations are special cases. Furthermore, the sensitivity of hydraulic heads to changes in recharge rate with different values of thickness, hydraulic conductivity, specific storage, and length is investigated. Hence, the presented new exact models can be utilized inversely to estimate the aquifer controlling parameters such as hydraulic conductivity or specific storage. Therefore, one of the advantages of the solutions is to investigate the sensitivity analysis of aquifer parameters, which has been carried out in this paper.

The groundwater hydraulic engineering science can be benefited by the results of this research in many practical problems such as evaluation of aquifer responses to river level variations, investigation of interactions between river and aquifer during a flood wave and determination of flow discharge, bank storage as well as travel time. Also, the new exact models presented in this research can be treated as guidelines for experimental works or a way to verify numerical methods.

This manuscript is organized as follows: at first, new exact models based on Laplace transformation to calculate the groundwater flow in river-aquifer systems are presented. Then, Results and discussion are provided. Also, in section the results of the present new exact models are successfully verified by the results obtained from the analytical solution of Bansal and Das. Furthermore, for more reliability the results are compared with those results of MODFLOW. After that sensitivity of the groundwater hydraulic head with respect to parameters such as hydraulic conductivity, specific storage, thickness and recharge rate is analyzed and also, in the next section, another scenario is considered to analyze the sensitivity of hydraulic heads to changes in recharge rate with different values of thickness, hydraulic conductivity, specific storage, and length. Finally in the last section conclusions are drawn.

Exact model

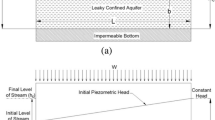
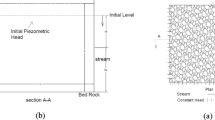
Figure 1 shows the schematic presentation of hydraulics of groundwater flow in a river-aquifer system. A leaky, isotropic, incompressible and homogeneous aquifer, which is in contact with a constant river level at one end and a river of varying water level at the other end, has been investigated. Also, it is recharged by surface infiltration. The conceptual flow system can be described as:

$$ T\frac{{\partial^{2} h}}{{\partial x^{2} }} + w = S\frac{\partial h}{{\partial t}}, $$
(1)
Fig. 1
figure 1

Schematic of groundwater flow in a river-aquifer hydraulic

Full size image

Subject to the initial condition:

$$ h{\kern 1pt} (x,{\kern 1pt} t = 0) = h_{c} - \frac{{h_{c} - h_{s} }}{L}x, $$
(2)

And the boundary conditions:

$$ h{\kern 1pt} (x = 0,{\kern 1pt} t) = h_{c} , $$
(3)
$$ h{\kern 1pt} (x = L,{\kern 1pt} t) = h_{s} + h_{0} \left( {u_{1} t} \right)^{m} e^{{ - u_{2} t}} ,\quad m = 1,2,3,...\quad . $$
(4)

where h is hydraulic head, \(S\) is storativity,\(T\) is transmissivity, L is the length of the aquifer, t is time, x is horizontal x-axis, \(h_{S}\) is initial and final level of river at the right end,\(h_{c}\) is constant river level at the left end, \(h_{0}\) is a parameter and \(m,{\kern 1pt} {\kern 1pt} {\kern 1pt} u_{1}\) and \(u_{2}\) are constants signifying the rate of the river level variation at the right boundary. Positive w represents downward constant recharge and negative one indicates upward evaporation. Figure 2 shows the variation in river level for various \(m,{\kern 1pt} {\kern 1pt} u_{1}\) and \(u_{2}\). The following parameters to achieve a dimensionless analysis are defined as follows:

$$ H = \frac{{h - h_{c} }}{{h_{s} - h_{c} }}\quad ,\quad X = \frac{x}{L}\quad ,\quad \eta = \frac{T}{{S{\kern 1pt} L^{2} }}t\quad ,\quad \rho_{1} = \frac{{S{\kern 1pt} L^{2} }}{T}u_{1} \quad ,\quad \rho_{2} = \frac{{S{\kern 1pt} L^{2} }}{T}u_{2} \quad \quad .\quad $$
(5)

where \(H,X,\eta ,\rho_{1}\) and \(\rho_{2}\) are the dimensionless hydraulic head, Dimensionless spatial coordinate, Dimensionless time, Dimensionless form of \(u_{1}\) and \(u_{2} {\kern 1pt}\), respectively.

Fig. 2
figure 2

Profile of the river level with \(h_{s} = 18m\) and \(h_{0} = 1m\)

Full size image

Applying the dimensionless parameters of Eq. (5), Eqs. (1)–(4) can be rewritten in a dimensionless form as follows:

$$ \frac{{\partial^{2} H}}{{\partial X^{2} }} + R = \frac{\partial H}{{\partial \eta }}. $$
(6)
$$ H{\kern 1pt} (X,{\kern 1pt} \eta = 0) = X. $$
(7)
$$ H{\kern 1pt} (X = 0,{\kern 1pt} \eta ) = 0. $$
(8)
$$ H(X = 1,{\kern 1pt} \eta ) = 1 + a\left( {\rho_{1} \eta } \right)^{m} e^{{ - \rho_{2} \eta }} . $$
(9)

where a and R are defined as follows:

$$ a = \frac{{h_{0} }}{{h_{s} - h_{c} }}\quad \quad ,\quad \quad R = \frac{{wL^{2} }}{{T{\kern 1pt} (h_{s} - h_{c} )}}\quad \quad . $$

Using the Laplace transform to Eqs. (6), (8) and (9), leads to:

$$ \frac{{d^{2} }}{{dX^{2} }}{\kern 1pt} \Lambda (X,{\kern 1pt} p) + \frac{R}{p} = p{\kern 1pt} \Lambda (X,{\kern 1pt} p) - H(X,\eta = 0), $$
(10)
$$ \Lambda (X = 0,{\kern 1pt} P) = 0, $$
(11)
$$ \Lambda (X = 1,{\kern 1pt} p) = \frac{1}{p} + a\rho_{1}^{m} \frac{\Gamma (m + 1)}{{(p + \rho_{2} )^{m + 1} }}. $$
(12)

where \(\Lambda\) denotes the Laplace transform of H and p is the Laplace variable for dimensionless time \(\eta\). Substitution of Eq. (7) into Eq. (10) yields:

$$ \frac{{d^{2} }}{{dX^{2} }}{\kern 1pt} \Lambda (X,{\kern 1pt} p) + \frac{R}{p} = p{\kern 1pt} \Lambda (X,{\kern 1pt} p) - X. $$
(13)

The ordinary differential Eq. (13) can be readily solved to get

$$ {\kern 1pt} \Lambda (X,{\kern 1pt} p) = \left\{ {A\sinh \left( {X\sqrt p } \right) + B\cosh \left( {X\sqrt p } \right)} \right\} + \frac{X}{p} + \frac{R}{{p^{2} }}. $$
(14)

where A and B are constants which can be determined by invoking Eqs. (11) and (12) in Eq. (14):

$$ \begin{aligned} B = - \frac{R}{{p^{2} }},\quad A = a\rho _{1} ^{m} \frac{{\Gamma (m + 1)}}{{\left( {p + \rho _{2} } \right)^{{m + 1}} \sinh \sqrt p }} \\ & \; + \frac{{R\cosh \sqrt p }}{{p^{2} \sinh \sqrt p }} - \frac{R}{{p^{2} \sinh \sqrt p }}. \\ \end{aligned} $$
(15)

Substituting these values in Eq. (14) and simplifying, we get:

$$ \begin{gathered} {\kern 1pt} \Lambda (X,{\kern 1pt} p) = a\rho_{1}^{m} \frac{{\Gamma (m + 1)\sinh \left( {X\sqrt p } \right)}}{{\left( {p + \rho_{2} } \right)^{m + 1} \sinh \sqrt p }} + \frac{{R\cosh \sqrt p \sinh \left( {X\sqrt p } \right)}}{{p^{2} \sinh \sqrt p }} - \frac{{R\sinh \left( {X\sqrt p } \right)}}{{p^{2} \sinh \sqrt p }} \hfill \\ - \frac{R}{{p^{2} }}\cosh \left( {X\sqrt p } \right) + \frac{X}{p} + \frac{R}{{p^{2} }}\quad .\quad \hfill \\ \end{gathered} $$
(16)

The inverse Laplace transform can be defined as follows:

$$ H(X,\eta ) = \sum\limits_{n = 1}^{\infty } {\mathop {{\text{Re}} s}\limits_{{p = p_{n} }} \left[ {e^{pt} \Lambda (X,p)} \right]} . $$
(17)

Applying Eq. (17) into Eq. (16) for m = 1 leads to:

$$ \begin{gathered} H\left( {X,\eta } \right) = - 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{\sin n\pi X}{{n^{3} \pi^{3} }}} + 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{( - 1)^{n} }}{{n^{3} \pi^{3} }}} \sin n\pi X + R\frac{{X - X^{2} }}{2} + X \hfill \\ - 2a\Gamma (2)\rho_{1} \sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{n\pi \sin n\pi X}{{\left( {\rho_{2} - n^{2} \pi^{2} } \right)^{2} }}( - 1)^{n} } \hfill \\ + e^{{ - \rho_{2} \eta }} a\rho_{1} \Gamma (2)\left[ {\frac{{\cot g(\rho_{2} )\sin (X\rho_{2} ) - Xcos(X\rho_{2} )}}{{2\rho_{2} \sin (\rho_{2} )}} + \frac{{\sin (X\rho_{2} )}}{{\sin (\rho_{2} )}}\eta } \right]. \hfill \\ \end{gathered} $$
(18)

Equation (18) represents the exact model of groundwater head in a leaky confined aquifer under the conditions mentioned in Eqs. (2)–(4).

Results and discussion

Assuming a unit cross-sectional area, the flow through a horizontal leaky confined aquifer can be expressed as:

$$ q = - K\frac{\partial h}{{\partial x}}. $$
(19)

where q is flow rate and k is hydraulic conductivity.

Based on the dimensionless variables in Eq. (5), Eq. (19) can be rewritten as:

$$ q = - K\frac{{h_{s} - h_{c} }}{L}\frac{\partial H}{{\partial X}}. $$
(20)

A dimensionless flow rate, Q, can be defined as follows:

$$ Q = \frac{\partial H}{{\partial X}} = - \frac{L}{{K(h_{s} - h_{c} )}}q. $$
(21)

where Q is Dimensionless flow rate.

Using this, an expression for flow rate is obtained as follows:

$$ \begin{gathered} Q\left( {X,\eta } \right) = - 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{\cos n\pi X}{{n^{2} \pi^{2} }}} + 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{( - 1)^{n} }}{{n^{2} \pi^{2} }}} \cos n\pi X \hfill \\ + 1 + R\frac{1 - 2X}{2} - 2a\Gamma (2)\rho_{1} \sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{n^{2} \pi^{2} \cos n\pi X}}{{\left( {\rho_{2} - n^{2} \pi^{2} } \right)^{2} }}( - 1)^{n} } \hfill \\ + e^{{ - \rho_{2} \eta }} a\rho_{1} \Gamma (2)\left[ {\frac{{\rho_{2} \cot g(\rho_{2} )cos(X\rho_{2} ) - cos(X\rho_{2} ) + X\rho_{2} sin(X\rho_{2} )}}{{2\rho_{2} \sin (\rho_{2} )}} + \frac{{\rho_{2} cos(X\rho_{2} )}}{{\sin (\rho_{2} )}}\eta } \right]. \hfill \\ \end{gathered} $$
(22)

Equation (22) calculates the flow rate along X-axis at time \(\eta\). The flow rates at the left and right ends of the aquifer can be obtained by setting X = 0 and X = 1, respectively. The hypothetical example programs are run in the MATLAB software to perform the exact simulation results of groundwater flow in river-aquifer systems. The computer configuration is that the CPU is Intel(R)/Core(TM)2/i7-6500U, CPU@2.250 GHz and the RAM@8.00 GB.

The accuracy and ability of the present new exact model, in the special case of linear river water variation, is verified by the results obtained from the analytical solution of Bansal and Das (2009). For the special case of (u2 = 0, u1 = 1 day−1and m = 1), Eq. 4 takes the form of linear variation in river water level similar to the work done by Bansal and Das (2009). In this case, by applying the inverse Laplace transform of Eq. 16 we get:

$$ \begin{gathered} H\left( {X,\eta } \right) = - 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{\sin n\pi X}{{n^{3} \pi^{3} }}} + 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{( - 1)^{n} }}{{n^{3} \pi^{3} }}} \sin n\pi X + R\frac{{X - X^{2} }}{2} + X \hfill \\ + a\Gamma (2)\rho_{1} \left[ { - 2\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{\sin n\pi X}{{n^{3} \pi^{3} }}( - 1)^{n} } + \frac{{X^{3} - X}}{6} + X\eta } \right]. \hfill \\ \end{gathered} $$
(23)

The typical value of Ss ranges from 10−4 to 10−6 m−1 (Rushton 2003). In addition, according to McWhorter and Sunada (1977) the standard value of hydraulic conductivity ranges from 2.5 to 45 m/day (\(2.88 \times 10^{ - 3}\) to \(5.20 \times 10^{ - 2}\) cm/s) for sand texture. Therefore, the parameter values are as follows:

\(L = 200\,m,\) \(b = 10\,m,\) \(K = 12\,m/day,\) \(S_{s} = 9 \times 10^{ - 5} \,m^{ - 1} ,\) \(w = 0.08\,m/day,\) \(h_{c} = 20\,m,\) \(h_{s} = 18\,m,\) and \(h_{0} = 0.5\,m\).

As shown in Fig. 3, the results of the present work (Eq. (23)) are compared with the results of the analytical solution of Bansal and Das (2009). It is observed that the results obtained from Eq. 23 agree very well with the results of Bansal and Das (2009). For more reliability, the results of Eq. 18 are compared with the results of MODFLOW. We consider u1 = 0.4 day−1, u2 = 0.03 day−1and m = 1. The other parameters are as stated earlier. As shown in Fig. 4, the results of the new exact model agree very well with the results of MODFLOW. In addition, Fig. 5 shows the hydraulic head versus time at different points of the aquifer.

Fig. 3
figure 3

Comparing the presented exact model with the analytical solution of Bansal and Das

Full size image
Fig. 4
figure 4

Comparison of the exact model with MODFLOW

Full size image
Fig. 5
figure 5

Profile of groundwater hydraulic head versus time at different points of the aquifer

Full size image

The flow rates at the left and right boundaries can be obtained by setting X = 0 and X = 1 in Eq. (22). The resulting expressions are:

$$ \begin{gathered} Q\left( {0,\eta } \right) = - 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{1}{{n^{2} \pi^{2} }}} + 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{( - 1)^{n} }}{{n^{2} \pi^{2} }}} + R\frac{1}{2} + 1 \hfill \\ - 2a\Gamma (2)\rho_{1} \sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{n^{2} \pi^{2} }}{{\left( {\rho_{2} - n^{2} \pi^{2} } \right)^{2} }}( - 1)^{n} } + e^{{ - \rho_{2} \eta }} a\rho_{1} \Gamma (2)\left[ {\frac{{\rho_{2} \cot g(\rho_{2} ) - 1}}{{2\rho_{2} \sin (\rho_{2} )}} + \frac{{\rho_{2} }}{{\sin (\rho_{2} )}}\eta } \right], \hfill \\ \end{gathered} $$
(24)
$$ \begin{gathered} Q\left( {1,\eta } \right) = - 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{\cos n\pi }{{n^{2} \pi^{2} }}} + 2R\sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{( - 1)^{n} }}{{n^{2} \pi^{2} }}} \cos n\pi + R\frac{ - 1}{2} + 1 \hfill \\ - 2a\Gamma (2)\rho_{1} \sum\limits_{n = 1}^{\infty } {e^{{ - n^{2} \pi^{2} \eta }} \frac{{n^{2} \pi^{2} \cos n\pi }}{{\left( {\rho_{2} - n^{2} \pi^{2} } \right)^{2} }}( - 1)^{n} } \hfill \\ + e^{{ - \rho_{2} \eta }} a\rho_{1} \Gamma (2)\left[ {\frac{{\rho_{2} \cot g(\rho_{2} )cos(\rho_{2} ) - cos(\rho_{2} ) + \rho_{2} sin(\rho_{2} )}}{{2\rho_{2} \sin (\rho_{2} )}} + \frac{{\rho_{2} cos(\rho_{2} )}}{{\sin (\rho_{2} )}}\eta } \right]. \hfill \\ \end{gathered} $$
(25)

Using Eqs. (24) and (25), the values of flow rate for w = 0 and 0.08 m/day are depicted in Fig. 6. The values of flow rates decrease at initial times, and then rise with time until attaining a steady-state value. Positive values of flow rate at the left and right boundaries indicate an inflow and outflow, respectively, whereas negative values indicate an outflow at the left boundary and inflow at the right boundary. It can be seen that the flow rate increases with recharge rate at the left boundary and decreases at the right boundary. In other word, the value of outflow from both boundaries increases with a rise in recharge rate.

Fig. 6
figure 6

Flow rate variations at the left and right boundaries

Full size image

The steady-state value of the flow rate can be calculated by setting \(\eta \to \infty\) in Eqs. (24) and (25). The resulting expressions are:

$$ Q\left( {0,\eta \to \infty } \right) = \frac{R}{2} + 1, $$
(26)
$$ Q\left( {1,\eta \to \infty } \right) = 1 - \frac{R}{2}. $$
(27)

Based on the dimensionless flow rate in Eq. (21) and substituting \(R = {{wL^{2} } \mathord{\left/ {\vphantom {{wL^{2} } {Kb{\kern 1pt} (h_{s} - h_{c} )}}} \right. \kern-0pt} {Kb{\kern 1pt} (h_{s} - h_{c} )}}\), Eqs. (26) and (27) can be rewritten as follows:

$$ q\left( {0,t \to \infty } \right) = - \frac{wL}{{2b{\kern 1pt} }} + \frac{{K(h_{s} - h_{c} )}}{L}, $$
(28)
$$ q\left( {1,t \to \infty } \right) = \frac{wL}{{2b{\kern 1pt} }} + \frac{{K(h_{s} - h_{c} )}}{L}. $$
(29)

where b is Aquifer’s thickness.

It can be deduced from Eqs. 28 and 29 that the flow rate is independent of specific storage when \(t \to \infty\).

The effects of the variation of \(K,\) \(S_{s} ,\) \(b\) and \(w\) on the groundwater hydraulic head

In this section sensitivity of the groundwater hydraulic head with respect to parameters such as hydraulic conductivity (K), specific storage (\(S_{s}\)), thickness (b) and recharge rate (w) is analyzed. The groundwater hydraulic head variations due to the change in hydraulic conductivity, specific storage, thickness and recharge rate are provided in Tables 1, 2, 3 and 4 for t = 10 and 60 days. As mentioned before, the typical value of Ss ranges from 10−4 to 10−6 m−1 (Rushton 2003). In addition, according to McWhorter and Sunada (1977) the standard value of hydraulic conductivity ranges from 2.5 to 45 m/day (\(2.88 \times 10^{ - 3}\) to \(5.20 \times 10^{ - 2}\) cm/s) for sand texture. Changed values of parameters are specified in tables. In all the tables, the values in the bold form indicate the groundwater mound height.

Table 1 The effect of variation in hydraulic conductivity (K) on the groundwater hydraulic head at t = 10 days and t = 60 days
Full size table
Table 2 The effect of variation in specific storage (\(S_{s}\)) on the groundwater hydraulic head at t = 10 days and t = 60 days
Full size table
Table 3 The effect of variation in thickness (b) on the groundwater hydraulic head at t = 10 days and t = 60 days
Full size table
Table 4 The effect of variation in recharge rate (w) on the groundwater hydraulic head at t = 10 days and t = 60 days
Full size table

Table 1 shows the sensitivity of the hydraulic head to the variations in hydraulic conductivity. It can be seen that with a rise in hydraulic conductivity the groundwater hydraulic head decreases. In addition, with a rise in hydraulic conductivity the location of groundwater mound drifts toward the left boundary at initial times. In Table 2, the values of groundwater hydraulic head for different values of specific storage are given. It can be deduced that the groundwater hydraulic head is too little sensitive to the variations in specific storage. From Table 3, it can be seen that the groundwater hydraulic head in a higher thickness aquifer grows slower than that of a lesser thickness aquifer. Table 4 shows the values of groundwater hydraulic head for different values of recharge rate. As expected, the groundwater hydraulic head increases with a rise in recharge rate. It can also be noticed that the spatial location of groundwater mound moves toward the left boundary as w decreases.

Variation in hydraulic head due to changes in recharge rate with different values of b, K, L and \(S_{S}\)

In this section, another scenario is considered to analyze the sensitivity of hydraulic heads to changes in recharge rate with different values of thickness, hydraulic conductivity, specific storage, and length. The curves of hydraulic head (h) versus recharge rate (w) for different times (t) and at x = 100 m are depicted in Figs. 7, 8, 9 and 10. Figure 7 shows variation in h with w for \(K = 8\,m/day,\) \(K = 22\,m/day\) and \(K = 44\,m/day\). It can be noticed that an aquifer with a lesser hydraulic conductivity is more sensitive to a change in the recharge rate than an aquifer with a greater hydraulic conductivity. In order to investigate the sensitivity of specific storage to the variations in recharge rate, three values of specific storage are considered, namely \(S_{s} = 3 \times 10^{ - 6} \,m^{ - 1} ,\) \(S_{s} = 1 \times 10^{ - 5} \,m^{ - 1}\) and \(S_{s} = 1 \times 10^{ - 4} \,m^{ - 1} .\) Figure 8 shows that the differences in hydraulic heads due to the increase in recharge rate are not significant for different values of specific storage. Figure 9 presents variation in h with w for \(b = 6\,m,\) \(b = 10\,m\) and \(b = 14\,m\). It can obviously be seen that an aquifer with a greater thickness is less sensitive to a change in the recharge rate than an aquifer with a smaller thickness. The sensitivity of hydraulic heads to recharge rate changes with \(L = 125\,m,\)\(L = 200\,m\) and \(L = 250\,m\) is illustrated in Fig. 10. It shows that a shorter aquifer is less sensitive to a change in the recharge rate than a longer aquifer.

Fig. 7
figure 7

Variation in hydraulic heads due to changes in recharge rate with different values of hydraulic conductivity

Full size image
Fig. 8
figure 8

Variation in hydraulic heads due to changes in recharge rate with different values of specific storage

Full size image
Fig. 9
figure 9

Variation in hydraulic heads due to changes in recharge rate with different values of thickness

Full size image
Fig. 10
figure 10

Variation in hydraulic heads due to changes in recharge rate with different values of length

Full size image

Conclusions

In this research, we use Laplace transform technique to derive new exact models to calculate and predict the transient hydraulic head in a leaky, isotropic, incompressible and homogeneous aquifer that is in contact with a constant river level at one end and a river of varying water level at the other end. Also, the aquifer is recharged by surface infiltration. We adopted a general mode of river water level variation in which linear, exponential and power of time variations can be treated as special cases. The presented new exact model has the ability to predict the groundwater hydraulic head for the various variation modes in the river level. In the case of a linear variation in river water level, the results of the present work are found to be in complete agreement with the work done by Bansal and Das. In addition, it is important to assess its robustness using comparisons with MODFLOW computations. Thus, for more reliability, the new exact model was verified by comparing its results with those obtained from the MODFLOW. The results show that the use of the new exact models is highly accurate, robust and efficient. The flow rates at both boundaries are obtained and it is shown that the steady-state value of the flow rate depends jointly on the values of w, L and b. It is observed that the value of outflow from both boundaries increases with a rise in recharge rate. Furthermore, sensitivity of the results with respect to hydraulic conductivity, specific storage, recharge rate and the thickness of the aquifer is analyzed. Also, the groundwater mound movement due to the variation in these parameters is investigated. Therefore, one of the advantages of the solutions is to investigate the sensitivity analysis of aquifer parameters, which has been carried out in this paper. The results of sensitivity analysis showed the following:

  • The average difference in groundwater hydraulic head height between thickness of 10 and 6 m was about 1.3 m, while this difference between thickness of 14 and 10 m was about 0.57 m. In other words, the groundwater hydraulic head in a higher thickness aquifer grows slower than in a lesser thickness aquifer.

  • The average difference in groundwater hydraulic head height between hydraulic conductivity of 8 and 22 m/day and between hydraulic conductivity of 22 and 44 m/day were about 1.9 and 0.55 m, respectively. In other words, with a rise in hydraulic conductivity the groundwater hydraulic head decreases.

  • Comparison of aquifer response for specific storage of \(3 \times 10^{ - 6}\), \(1 \times 10^{ - 5}\) and \(1 \times 10^{ - 4}\) \(m^{ - 1}\) illustrated that the average difference in groundwater hydraulic head height between specific storage of \(3 \times 10^{ - 6}\) and \(1 \times 10^{ - 5}\)\(m^{ - 1}\) and between specific storage of \(1 \times 10^{ - 5}\) and \(1 \times 10^{ - 4}\) \(m^{ - 1}\) were about 0.0002 and 0.003 m, respectively. It can be deduced that the hydraulic heads are too little sensitive to the variations in specific storage.

  • The aquifer response for three values of recharge rate of 0.03, 0.05 and 0.09 m/day is evaluated. Adding 0.03 and 0.04 m/day to the value of recharge rate caused 0.75 and 1 m rise in the water height, respectively.

  • The spatial location of groundwater mound moves toward the left boundary at initial times as K and b increase and w decreases.

In addition, variations in hydraulic head due to changes in recharge rate with different values of thickness, hydraulic conductivity, specific storage, and length are analyzed. Based on this analysis, the groundwater head in an aquifer with a lesser length, higher hydraulic conductivity or higher thickness is less sensitive to a change in the recharge rate than in an aquifer with a higher length, lesser hydraulic conductivity or lesser thickness. Furthermore, it is observed that the differences in hydraulic heads due to the increase in recharge rate are not significant for different values of specific storage.

Finally, the most important novelty of this research is providing new exact expressions to analyze hydraulic interactions between a leaky aquifer and river of varying water level in which the river level varies under a more general assumption than in previous works.