Introduction

Iran is located in one of the arid regions of the world, and due to low annual rainfall, its water resources are declining (Ghazvinian et al. 2021; Dehghanipour et al. 2021). In Iran, the agricultural sector accounts for the majority of total water consumption, which can be saved by improving applied water management and water productivity (WP). Accurate estimation of WP and crop yield is one of the most basic information to improve applied water management (Aliasgharzadeh and Sanainejad 2006; Khoshnavaz et al. 2016). Increasing demand for agricultural products and challenges in obtaining field data point to the need to use appropriate models to estimate WP and crop yield. Computer models have made it possible to analyze different management strategies (Bagheri et al. 2012a, b; Ghanizadeh et al. 2022; Fakharian et al. 2023). Most of these models require input parameters that are difficult to access or require significant time and cost. For this purpose, artificial neural networks and meta-heuristic algorithms are considered superior options (Shirdeli and Tavassoli 2015; Naderpour et al. 2020a, b; Rezazadeh Eidgahee et al. 2022). These models can predict changes in Intended variables with minimal measurement parameters and acceptable accuracy. Since wheat plays a crucial role in food security, predicting pre-harvest wheat production provides ample time to deal with food shortages (Dehghanisanij et al. 2021, Emami et al. 2019). To predict crop yield, it is necessary to identify yield-limiting factors. Grain yield when water is a yield constraint is a function of the amount of water available to the plant, water use efficiency, and individual yield. Grain yield (when water is a limiting factor) depends on the amount of water available, water productivity (WP), and specific gravity (Greaves and Wang 2017; Silva et al. 2020; Dehghanisanij et al. 2022). Nowadays, crop simulation models are proposed as a multi-purpose tool in agricultural research and management. There are different yield prediction models, one of the most common and straightforward of which is experimental regression models (Murthy 2004; Oteng-Darko et al. 2013; Chlingaryan et al. 2018; Fan et al. 2022). Researchers have evaluated the yield and WUE in orchards according to irrigation management and different surface irrigation methods (Zhang et al. 2005; Kaul et al. 2005; Alvarez 2009; Gonzalez-Sanchez et al. 2014; Matsumura et al. 2015). Chipanshi et al. (1999), by examining the limiting factors of dryland wheat growth, showed that the amount of soil moisture during vegetative growth and cluster growth is the most crucial determinant of dryland spring wheat yield. Farajzadeh (2000) predicted the dryland wheat yield using regression models in Urmia, Iran, and reported that rainfall during the growing season and full frost days are the most critical factors determining the dryland wheat yield. Tatari et al. (2008) studied the dryland wheat yield in the Khorasan region, Iran, using an experimental regression model and concluded the dryland wheat yield could be estimated only with acceptable accuracy based on rainfall factors. Gu et al. (2017) used a genetic algorithm-back propagation neural network (GA-BP) to predict corn yield under subsurface drip irrigation. The results showed that the GA-BP model provided more accurate predictions. Abrougui et al. (2019) predicted organic potato yield using tillage systems and soil properties by an artificial neural network (ANN) and multiple linear regression (MLR) and concluded that the MLR model estimated crop yield more accurately than the ANN model. Emami et al. (2019) estimated barley yield using radial basis function (RBF) and feed-forward neural (GFF) models in Torbat Heydariyeh, located in southeastern Iran. The results showed that the RBF model with the input parameter of irrigation water levels could better estimate the barley yield. Chen et al. (2020) evaluated a new irrigation decision support system (DSS) for improving WP and cotton yield in an arid climate. The results showed that the implementation of DSS increased WP and cotton seed yield by 20% and 32%, respectively, compared to the soil moisture sensor method. Naderpour et al. (2020a, b) introduced a new approach based on the group method of data handling to estimate the moment capacity of ferrocement members. The results showed that the GMDH model was ideally successful in estimating the moment capacity of ferrocement members. Shi et al. (2021) presented a crop growth model to investigate crop yield and WUE. The results showed that the presented model increased the WUE during the growth stages. Sharifi (2021) proved that the Gaussian process regression algorithm has the best performance in estimating barley yield. Prasad et al. (2021) used the random forest algorithm for estimating cotton crops at the regional level. The results indicated that the RF model had a high potential in predicting crop yield. Dehghanisanij et al. (2021) reported that irrigation-fertilizer and crop variety parameters are the most influential parameters in estimating the yield and water productivity of tomato crops. Eidgahee (2022) developed predictive models based on machine learning, using artificial neural networks (ANN), genetic programming (GP), and data handling combined group method (GMDH-Combi), for the dynamic module. The results showed that the ANN model is more accurate compared to the developed models based on GMDH and GP. Shada et al. (2022) used a hybrid wavelet-support vector machine (WSVM) model to predict the hourly flood of the Achankovil river in India. The results showed the acceptable efficiency of the WSVM model in flood prediction. Haque and Matin (2022) investigated the change in the Jamuna river shoreline using a multi-variate regression approach and reported that this model is effective in predicting lateral erosion.

Policymakers and managers need facts about WP and crop yield at different scales to devise appropriate management strategies. Estimating WP and crop yield is difficult and costly due to the scarcity of sufficient field details. Intelligent methods have high flexibility and can change the input parameters and select the most optimal parameters. Due to the need to replace complex crop models in evaluating yield and WP with simpler statistical models and limited previous studies, this study aims to present a model based on the hazelnut tree search algorithm (HTS) and extreme machine learning method (ELM) for estimating WP and wheat yield under the Lake Urmia basin. This study also presents the determining parameters in WP and yield and introduces the most effective ones. The contributions of this article are as follows:

  • Drip (tape) irrigation (DTI), sprinkler irrigation (SI), and basin irrigation (BI) methods are considered, and the superior irrigation method is selected.

  • Yield and WP factors are estimated using field results of the DTI method.

  • A hybrid approach called HTS–ELM is presented for estimating yield and WP.

  • The HTS–ELM approach is evaluated on the collected dataset, and its results are compared with previous intelligent methods.

Materials and methods

Study area

This research was carried out in Mahabad plain in the southeast of Lake Urmia in the 2020–2021 crop year. Mahabad’s geographic coordinates are 45° 43′ N, 36° 46′ E, and its altitude is 1320 m above sea level. The average annual rainfall is 413 mm and the average humidity is 53%. The average annual temperature and minimum temperatures are 12.8 °C and 6.7 °C, respectively. The average number of freezing days is 84 days. The average annual evaporation from the pan is 1860 mm, and the average evaporation from the free surface is 1560 mm (Bahramzadeh 2015). Mahabad plain has relatively prosperous agriculture with an irrigation and drainage network and potential lands. The main products of this plain include wheat, barley, sugar beet, alfalfa, oilseeds, tomatoes, weeds, vegetables, potatoes, apple orchards, peaches, nectarines, and grapes. Figure 1 shows the geographical location of the study area and selected farms.

Fig. 1
figure 1

Location of Mahabad plain and selected farms

Full size image

Description of treatments

Two wheat cultivated farms (F1 and F2) were selected in the study area under farmers’ management. Pishgam and Mihan wheat varieties were used in F1 and F2 farms, respectively. The selected farms were part of a regional project conducted by the Agricultural Engineering Research Institute (AERI) during the 2020–2021 crop growing season in the Lake Urmia basin to encourage farmers to decrease applied water while the yield is constant or improved. In the AERI project, different technologies were transferred to the farmers and farmers' knowledge improved accordingly. The impact of transferred technology was studied using on-farm and weather data collections and evaluations. Three experimental treatments for irrigation management were considered, including drip (tape) irrigation (DTI) and sprinkler irrigation (SI) in F1 and basin irrigation (BI) in F2 farms. The emitter's discharge under 1 bar pressure was ranging between 1.1 and 1.8 l/h in DTI, and that was 0.71 l/s for sprinklers in SI under 4 bar pressure. The distance between the drip (tape) lines was 20 cm, and the sprinkler array in SI was 15 m*18 m. The volume of applied water into each treatment was measured using a calibrated volumetric flow meter. The first irrigation water was applied to the DTI using the basin irrigation method to ensure crop growth and establishment.

The chemical and physical factors of soil and water are presented in Table 1. A sampling of disturbed and undisturbed soil was performed to determine physical and chemical properties, soil texture, pH, saturated moisture, field capacity, and permanent wilting point of 0–30 cm and 30–60 cm. The root zone depth of farms F1 and F2 was assumed to be 60 cm. Soil bulk density and soil texture were measured by cylindrical and hydrometric methods, respectively. The data in Table 1 were used to handle the irrigation schedule. The selected farms represent two different farms situation in the situation. The water quality in F1 is more saline but the soil type is lighter which causes salinity to wash out from the soil. OC and soil pH which are important for production are almost similar to other farms (https://zoom.earth/#view=36.779047,45.68245,10z/map=live).

Table 1 Physical and chemical factors of soil and water
Full size table

The studied area does not have spatial diversity and all treatments in F1 and F2 farms have the same soil texture. The soil survey and harvest calendar are shown in Table 2.

Table 2 Soil survey and harvest calendar
Full size table

The number of irrigation events in DTI, SI, and BI treatments was 9, 6, and 3, respectively. The irrigation date and volume of applied water in each treatment are presented in Table 3. Wheat rows were spaced 0.03 m apart with an in-row spacing of 0.11 m between plants, which accommodates 303 plants (per 1 m2). Planting and harvesting of wheat crops on both farms were done on November 04, 2020, and July 6, 2021, respectively.

Table 3 Applied water and effective rainfall in different treatments
Full size table

Irrigation scheduling

The potential evapotranspiration under standard conditions (ETo) was calculated by the Penman–Monteith method to calculate the water requirement. After determining the ETo, the crop coefficients (using the four-stage FAO method) were determined, and the amount of irrigation water required was calculated as follows (Gebremedhin et al. 2022; Nikolaou et al. 2023):

$${\text{IR}} = \frac{{\mathop K\nolimits_{{\text{c}}} *{\text{ET}}_{o} }}{{1 - {\text{LR}}}} - P_{{\text{e}}}$$
(1)

where IR indicates irrigation requirement (mm), Kc shows crop coefficient, LR indicates leaching coefficient, and Pe means effective rainfall. According to FAO recommendation (Rana et al. 2022), daily rainfall of more than 5 mm was used as effective rainfall.

Water productivity was calculated by considering the effective rainfall as follows (Rodrigues et al. 2022; Zhang et al. 2023):

$${\text{WP}} = \frac{{Y\,({\text{usually}}\,{\text{economical}}\,{\text{yield}})}}{{{\text{ET}}}}$$
(2)

where Y indicates the wheat grain yield (marketed product) (Kg ha−1) and ET shows the evapotranspiration (mm).

ET is calculated as follows:

$${\text{ET}} = \,I + \,P + \,D_{P} + \,R_{{{\text{off}}}} \pm \,\Delta S\,$$
(3)
$${\text{ET}} = \,I \pm \,\Delta S\,$$
(4)

where P indicates a wetted area (%), Roff shows surface runoff (mm), ΔS shows a change in soil moisture (mm).

Application efficiency indicates field losses in each irrigation were calculated as follows (Moursy et al. 2023):

$${\text{AE}} = \frac{{D_{{\text{z}}} }}{{ \, D_{{{\text{app}}}} }} \times 100$$
(5)

where AE shows application efficiency, Dz indicates the average water storage in the root zone depth (mm), and Dapp is the average water depth entering the irrigated area. There was no runoff at the end of any of the fields. Deep percolation losses (DP) (%) were calculated as follows (Dehghanisanij et al. 2022):

$$D_{P} = 100 - {\text{AE}}$$
(6)

Soil moisture was measured by a gravimetric method on both farms and at least three points on the farms (beginning, middle, and end).

Uniformity coefficient

To calculate uniformity, the distances of emitters and sprinklers were divided into several cells as 0.2 m*0.4 m and 15 m*18 m, respectively. A water collection can be placed in each cell to drain the droplets from the drippers and sprinklers. Plastic cans with an inner diameter of 15 mm were used for the experiments. After one hour of emitters and sprinklers work, water depth in cans was measured using a graduated cylinder. The uniformity coefficient was calculated as follows (Zhu et al. 2022):

$${\text{CU}}_{t} = \left(1 - \frac{{\sum\limits_{i = 1}^{n} {(D_{i} - \overline{D} )} }}{{\overline{D} \times n}}\right) \times 100$$
(7)

where \({\text{CU}}_{t}\) indicates Christiansen coefficient (%), \(\overline{D}\) reveals the average depth of water collected in cans (mm), \(D_{i}\) shows water depth in each can (mm), and n is the number of cans.

The uniformity coefficient of water distribution in the lower quarter was calculated as follows (Hui et al. 2022):

$${\text{DU}}_{t} = \left( {\frac{{D_{{{\text{lq}}}} }}{{\overline{D} }}} \right)$$
(8)

where \({\text{DU}}_{t}\) shows distribution uniformity in the lower quartile and \(D_{{{\text{lq}}}}\) represents the average water depth measured in a quarter of the lowest values.

Irrigation methods

Drip (tape) irrigation

Drip (tape) irrigation (DTI) is one of the drip irrigation equipment with a thinner wall than drip tubes. In the DTI method, water is applied to the ground near the crop root zone to wet a small area and depth from the soil surface (Dong et al. 2021; Guo et al. 2023).

Sprinkler irrigation

Sprinkler irrigation (SI) is a method in which water is distributed as rain on the ground. The SI method passes the water required for agriculture through a series of pipes using pumping. The sprinkler system gives the water needed for agriculture through a series of lines using pumping and falls to the ground by sprinklers (Solgi et al. 2022).

Basin irrigation

The Basin irrigation method (BI) is the simplest surface irrigation method used to irrigate all crops. In the BI method, the farm needs to be divided into plots with specific dimensions, and the slope of the farm is less than 1% (Pramanik et al. 2022; Ali Shah et al. 2022).

Hazelnut tree search (HTS) algorithm

Hazelnut tree search (HTS) is a multi-agent algorithm that provides the process of finding the most optimal hazelnut tree in a forest (Emami 2021). This algorithm has three operators: growth, fruit dispersion, and root dispersion. This algorithm starts with an initial population. In the growth stage, the effect of trees on each other in competition for shared resources is calculated. The algorithm in the fruit scattering phase examines the search space to find promising solutions beyond the current area. In the root propagation stage, an irregular local search is performed around the trees to exploit the optimal solutions. The growth stage, fruit dispersion, and root expansion are applied to the population several times to create the conditions for achieving the most optimal hazelnut tree in a forest (Emami 2021). Figure 2 shows the flowchart of the HTS algorithm.

Fig. 2
figure 2

Flowchart of the HTS algorithm

Full size image

Extreme learning machine (ELM)

The extreme learning machine (ELM) method generalizes single-layer backpropagation networks (Hu et al. 2022). Unlike conventional learning methods, the ELM randomly selects the input weights and biases of hidden layer neurons and can generate these parameters before viewing the learning data. The ELM neural network is a generalized single hidden layer feed forward neural network (SLFN) (Wang et al. 2014; Hu et al. 2022). Figure 3 shows the structure of SLFN.

Fig. 3
figure 3

SLFN network structure

Full size image

SLFN is formulated as follows (Tian et al. 2022; Hu et al. 2022):

$$\begin{gathered} y = g\left(b_{0} + \sum\limits_{j = 1}^{h} {w_{j0} v_{j} }\right ) \hfill \\ v_{j} - f_{i} \left(b_{i} + \sum\limits_{j = 1}^{h} {a_{i} s_{i} x_{i} } \right) \hfill \\ \end{gathered}$$
(9)

where Vj shows hidden layer neurons (j = 1,….,n), ai shows the weight of the connections between the input variable and the neuron in the hidden layer, wjo expresses the weight of the connections between neurons in the hidden layer and output neurons, bi represents the bias of neurons in the hidden layer, b0 shows the bias of the output neurons, fi and g show the activation function of neurons and output neurons, respectively, and si describes a binary variable (Tian et al. 2022; Hu et al. 2022):

The structure of the ELM is shown in Fig. 4.

Fig. 4
figure 4

ELM network structure

Full size image

The ELM output function is defined as follows (Tian et al. 2022; Hu et al. 2022):

$$f_{L} (x) = \sum\limits_{i = 1}^{L} {\beta_{1} h_{1} } (x) = h(x)\beta$$
(10)

where \(\sum\limits_{i = 1}^{L} {\beta_{1} h_{1} } (x) = h(x)\beta\) represents the output weight vector, m shows the output node,\(\sum\limits_{i = 1}^{L} {\beta_{1} h_{1} } (x) = h(x)\beta\) mapping is a nonlinear characteristic of a learning machine, and h1 is defined as follows (Hu et al. 2022):

$$h_{1} (x) = G(a_{i} ,b_{i} ,x),\,\,\,\,b_{i} \in R$$
(11)

where \(G(a_{i} ,b_{i} ,x)\) is a continuous nonlinear function.

HTS–ELM model

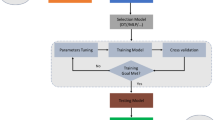
The parameters and structure of the ELM model need to be adapted and optimized. In the ELM method, generating more hidden nodes and irrelevant variables in the training dataset reduces the model's performance compared to other adjustable algorithms. To solve this problem, the number of neuron activation functions in the hidden layer, weights connectivity, the bias of neurons in the hidden layer, and the setting parameter (α) is determined using the HTS algorithm. HTS algorithm was compared with evolutionary algorithms, including particle swarm optimization (PSO) (Poli et al. 2007), covariance matrix adaptive evolutionary strategy (CMA-ES) (Hansen 2006), self-adaptive differential evolution (JDE) (Omran et al. 2005), grey wolf optimizer (GWO) (Mirjalili et al. 2014), social evolution and learning optimization (SELO) (Kumar et al. 2018), and provided more acceptable results (Emami 2021). Because the HTS–ELM model is superior in terms of solution quality and convergence rate compared to other algorithms, it was used in this study to estimate the wheat yield and WP. Figure 5 shows the process of the HTS–ELM model.

Fig. 5
figure 5

Flowchart of the HTS–ELM model

Full size image

Implementation criteria

Criteria coefficient of determination (R2), root-mean-square error (RMSE), normalized root-mean-square error (NRMSE), and efficiency criterion (NSE) were used to evaluate the performance of the HTS–ELM model (Emami et al. 2021). The desired criteria were shown by Eqs. 12–15.

$$R^{2} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {L_{i} - \overline{L} } \right)(K_{i} - \overline{K} )}}{{\mathop \sum \nolimits_{i = 1}^{n} \sqrt {(L_{i} - \overline{L} )^{2} } \mathop \sum \nolimits_{i = 1}^{n} \sqrt {(L_{i} - \overline{K} )^{2} } }}} \right]^{2}$$
(12)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\mathop {(\mathop L\nolimits_{i} - \mathop K\nolimits_{i} )}\nolimits^{2} } }$$
(13)
$${\text{RRMSE}} = \frac{{{\text{RMSE}}}}{{\sum\nolimits_{i = 1}^{n} {L_{i} } }}$$
(14)
$${\text{NSE}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {(L_{i} - \mathop K\nolimits_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {(L_{i} - \overline{K} )^{2} } }}$$
(15)

where \(L_{i}\) and \(K_{i}\) indicate the observed and estimated values of WP and yield, respectively. \(\overline{L}\) and \(\overline{K}\) are average observed and estimated values of WP and yield, respectively.

Results and discussion

Field results

A summary of the results of irrigation characteristics in different irrigation cycles is presented in Table 4. The DUt and CUt of the irrigation systems controlled for the first irrigation event which were 89.0% and 98.1% for DTI and 80.0% and 84.4% for SI, respectively. According to DUt values, Keller and Bliesner (2009) classified them as excellent, above 90%; good between 85 and 90%; acceptable up to 65% and unacceptable, below 65%. Little et al. (1993) suggested a classification of uniformity of a sprinkler irrigation system as very good, good, poor, and worse if the uniformity coefficient (CU) value equals 90%, between 80 and 89%, between 70 and 79%, and 78% to be the minimum acceptable performance level for economic system design. The average irrigation depth in DTI, SI, and BI treatments was 27.37 mm, 55.22 mm, and 142.20 mm, respectively, which indicates a reduction of 50% and 80% of irrigation depth in treatment DTI, respectively. Under DTI treatment, water loss due to evaporation and deep infiltration was mainly less than in SI and BI treatments. The low AE in BI and SI treatments shows the tendency of the farmer to over-irrigate. One of the reasons for low AE in treatment BI is the failure of the farmer to apply the flow reduction method. The maximum AE is related to the first and last irrigation, where the soil moisture deficit is significant and the irrigation depth is saved. The results showed that in all treatments, AE was higher during the spring than autumn growth period. The scarcity of effective rainfall in the spring growth period is the long intervals between irrigations and as a result, the soil moisture is low before irrigation. The average AE in SI and DTI treatments is high, and one of the important reasons is the irrigation method in both treatments. Deep penetration losses were lower in DTI and SI treatments than in BI treatment. One of the effective factors in the amount of applied water and deep penetration in DTI is the different irrigation method of this treatment. Irrigation depth values were greater than soil moisture deficit (SMD) for all irrigation events, so crops were not water stressed despite reduced applied water. Changing the irrigation method reduced the irrigation depth by 53.10%. Mean AE is higher in treatment DTI than in BI and SI, which is one of the important reasons for using the drip (tape) method. In SI and BI treatments, the entire field wet. On the other hand, the treatment DTI reduces the wetted surface area of the field and reduces losses due to deep penetration. The results showed that AE is higher in the spring growth period than in the fall, and one of the reasons for this is related to the lack of effective rainfall in the spring growth period and long intervals between irrigations, and as a result, low soil moisture before irrigation. The results obtained are consistent with the results of research by Yuan et al. (2003), Akhavan et al. (2007), Emami et al. (2019) and Dehghanisanij et al. (2021). Also, in the AE term, treatment DTI increased by 5% compared to SI and BI treatments.

Table 4 Mean values of irrigation parameters section
Full size table

In DTI, SI, and BI treatments, the measured yield was 5755 kg/ha, 5400 kg/ha, and 5050 kg/ha, respectively, which showed a 6.17% and 12.25% increase in yield in treatment DTI compared to SI and BI treatments. WP in DTI, SI, and BI treatments was calculated to be 1.70 kg/m3, 1.47 kg/m3, and 0.91 kg/m3, respectively. Thus, the application of DTI treatment increased water productivity by 0.23 kg/m3 and 0.79 kg/m3 compared to SI and BI treatments. Changing the irrigation method from basin and sprinkler to drip (tape) increased water efficiency and wheat yield. Crop yield is affected not only by irrigation, but by many other factors such as soil salinity, crop variety, crop management, soil fertility, pesticide and fertilizer applications. High WP values are the reason for the low amount of available water. The proposed treatment DTI improved AE, increased WP and reduced applied water. Mihan variety had the lowest seed yield with an average of 5000 kg/ha. The Pishgam variety has the highest seed yield due to the high number of seeds per panicle and number of panicles (in 1 m2). The results showed that with decreasing applied water, WP increases, which is consistent with the results of research by Afshar et al. (2020) and Dehghanisanij et al. (2022). Turknejad et al. (2006) by comparing drip irrigation (DI) systems and furrow irrigation in wheat cultivation, showed that WP in the DI system was almost doubled compared to furrow irrigation. Paltineanu et al. (1994) evaluated the effect of three DI, SI, and FI methods on winter wheat and reported that the highest grain yield and water use efficiency in drip irrigation at 6600 kg/ha ton and 2.97 kg/m3. Wang et al. (2009) and Qin et al. (2014), concluded that a slight reduction in irrigation water content did not have a significant effect on yield. Turknejad et al. (2006) showed that under the DI method, wheat grain yield increased by 11.40% compared to the FI method. Table 5 presents the values of yield and WP in research treatments.

Table 5 Yield and WP in research treatments
Full size table

After proving the efficiency of treatment DTI compared to SI and BI treatments, wheat yield and WP under irrigation with a DTI method were estimated.

Modeling results

Datasets used

Exhaustive range of irrigation parameters, soil texture and soil moisture, minimum and maximum temperature, rainfall, sunshine hours, average relative humidity, and minimum wind speed (http://tatweather.areeo.ac.ir/?LRef=6e50c40c-c972-47db-ad6a-273ee4197dce), and crop characteristics were considered independent modeling variables. This dataset was organized in a field with a length of 162.5 m, a width of 27.7 m, and an average slope of 0.0091 mm−1 (https://zoom.earth/#view=36.779047,45.68245,10z/map=live), in the 2020–2021 crop-year and 125 data. The datasets were classified into two categories: training and testing. 80% of the data were used for training, and the remaining 20% for model testing. The dataset parameters are presented in Table 6.

Table 6 Dataset parameter values
Full size table

The histogram of the input and output data is presented in Fig. 6.

Fig. 6
figure 6

a–h Histogram of input and output data

Full size image

Sensitivity analysis of input variables

The sensitivity analysis process shows the model’s sensitivity compared to its input variables. Accordingly, if the sensitivity coefficient of a variable is more than 1, that variable has a fundamental role in the variability of the output variable (Bagheri et al. 2012a, b). Table 7 presents sensitivity analysis results for the variables estimating wheat yield and WP. Based on the results, the variables of irrigation (I), effective rainfall (Pe), soil moisture (SM), and crop variety (V) were recognized as the most important input variables in estimating wheat yield and WP. After that, soil texture (ST), sunshine hours (Rn), and temperature (T) parameters were essential in estimating yield and WP, respectively.

Table 7 Sensitivity analysis results for wheat yield and WP estimation
Full size table

Based on Table 7, nine different input scenarios for estimating wheat yield and WP were presented. The accuracy of the HTS–ELM technique in estimating WP and wheat yield is presented in Table 8.

Table 8 Evaluation of the proposed technique in estimating WP and yield
Full size table

The superior model (χ12) estimates wheat yield and WP based on six-month effective rainfall (Pe), irrigation (I), soil moisture (SM) and crop variety (V). According to superior model, wheat yield and WP are positive with the amount of moisture at the field capacity point (FC) and negative with the amount of moisture at the permanent wilting point (PWP). The higher the moisture at the FC point, the greater the water holding capacity of the soil. The results of selecting variables showed that the model with I, V, Pe, and SM inputs using the HTS–ELM hybrid technique with R2 = 0.982, RMSE = 0.006, NRMSE = 0.008, and NSE = 0.980 has a high impact on the estimation of yield and WP. According to studies by Richards et al. (2001) and Tatari et al. (2008), wheat yield is a function of irrigation amount. Stone and Schlegel (2006) reported that 70% of changes in wheat yield in the US plains depend on soil water holding capacity. Dehghanisanij et al. (2021) concluded that irrigation parameters, effective rainfall, and crop variety are the most critical factors in estimating yield and WP in tomatoes crop. Arora et al. (1983) Tatari et al. (2008) and Dehghanisanij et al. (2021) reported the effect of rainfall during planting as one of the essential factors on plant germination and the final yield of wheat. Taliei and Bahrami (2002) showed that the amount of soil moisture at the time of planting is one of the factors determining the dryland wheat yield. Fredrich and Combertoa (1995) considered available water as one of the essential factors in wheat yield. Numerous studies have shown that soil texture affects the amount of available water to the plant (Koucheki and Alizadeh 1991; Mirkhani 2003). Soil texture parameters showed good performance in WP and yield estimation. Gupta and Larson (1979), reported that the amount of available water depends on the particle size, soil bulk density (B.D.), and percentage of soil organic matter. Due to the lack of organic matter in the soils of the study area, particle size and B.D. are a function of soil texture (Alizadeh 2004), so the positive relationship between the percentage of clay and wheat yield is acceptable. Vrindits et al. (2005), concluded that wheat yield depends on the rate of clay and the B.D of the soil.

After determining the superior model, yield and WP were modeled based on its parameters. Figures 7 and 8 show the observed and estimated values of yield and WP using the HTS–ELM technique in the test and testing stages.

Fig. 7
figure 7

a, b Comparison of estimated and observed yield

Full size image
Fig. 8
figure 8

a, b Comparison of estimated and observed WP

Full size image

The results show the accuracy of the proposed hybrid technique HTS–ELM in estimating yield and WP with a high correlation coefficient (R2 = 0.991 and R2 = 0.985, respectively, in the training and test stage) between the observed and estimated values.

Comparison technique

Since no extensive research has been done on wheat yield and WP estimation using soft computing techniques, therefore, in this section, the performance of the HTS–ELM hybrid technique with equivalent options, including the Gaussian process regression algorithm (GPR) (Sharifi 2021), tree growth optimization algorithm-adaptive neuro-fuzzy inference system (TGO-ANFIS) (Dehghanisanij et al. 2021), random forest (RF) (Prasad et al. 2021), season’s optimization-support vector regression (SO-SVR) (Dehghanisanij et al. 2021), and ANN (Abrougui et al. 2019), under the same conditions are compared. The results show the high relative efficiency of the HTS–ELM technique with values of R2 = 0.985 and RMSE = 0.005 compared to other intelligent methods. The results presented by the HTS–ELM technique and other counterparts are compared in Table 9.

Table 9 Comparison of intelligent techniques in estimating yield and WP
Full size table

Conclusion

In this paper, a new hybrid technique based on the hazelnut tree search algorithm-extreme machine learning technique called HTS–ELM for estimating wheat yield and WP under different irrigation levels was introduced. For this purpose, irrigation, meteorological and soil parameters were selected as model inputs. The HTS–ELM considering irrigation parameters, effective rainfall, soil moisture, and crop variety, developed superior results with R2 = 0.985, RMSE = 0.005, NRMSE = 0.008, and NSE = 0.980, respectively. The results showed that the WP and wheat yield has a direct relationship with the amount of moisture in the field capacity point. In comparison, the HTS–ELM technique performed better than the practical methods. Based on the results of using the HTS–ELM technique, an accurate estimate of WP and wheat yield was obtained in the Lake Urmia basin. Also, the output of the proposed model can be developed as user-friendly mobile applications. In the agricultural sector (for farmers), without much experimentation (even without research in several different areas), the best effective parameters in estimating yield and WP can be determined using intelligent methods, irrigation-fertilization scheduling, and even the cultivation pattern based on it. In general, the HTS algorithm is a fast convergence algorithm and outperforms the peer algorithms in optimizing the ELM parameters and thereby estimating the wheat yield and WP. Regardless, the HTS–ELM model requires to be parameterized, and the implementation of HTS–ELM is slightly less than ideal. In general, the HTS algorithm is a fast convergence algorithm and outperforms the peer algorithms in optimizing the ELM parameters and thereby estimating the wheat yield and WP. Regardless, the HTS–ELM model requires to be parameterized, and the implementation of HTS–ELM is slightly less than ideal. Consequently, in future studies, it was suggested to combine the HTS algorithm with SVR, ANN, and ANFIS models and artificial neural networks to enhance errors and supply generalizable results.