Introduction

In addition to protection against flood damages, flood routing is efficient for the optimal design of hydraulic structures. Generally, flood routing methods are divided into two categories including hydraulic and hydrological methods (Akbari et al. 2020). Hydraulic methods are based on the solution of differential continuity and momentum equations. Despite high accuracy, hydraulic methods require data such as flow depth, flow rate, roughness coefficient, river cross sections and bed slope (Bozorg-Haddad et al. 2019), and collecting these data requires spending time and cost. However, hydraulic methods are relatively simple and acceptably accurate, and only require one or more simultaneous inflow or outflow hydrographs of an event which are acquired from hydrometric stations (Bozorg-Haddad et al. 2020). The Muskingum model is one of the most known and applicable hydrological flood routing techniques. In this method, model parameters (decision variables) are estimated via optimization methods based on historical recorded inflow–outflow hydrograph data. Then, to specify an outflow hydrograph corresponding to an inflow hydrograph, the Muskingum routing equations are implemented (Das 2004). The Muskingum method is employed in river routing linearly and nonlinearly. In the linear model, a linear relationship is considered between storage and discharge, and other computations are conducted by assuming the existence of this relationship. The linear Muskingum model has been used by different researchers (Chow et al. 1988, Gill 1978, Norouzi and Bazargan 2019, O'donnell 1985, Wilson 1974). Since the storage–discharge relationship is usually nonlinear (Karahan et al. 2015, Niazkar and Afzali 2017), the linear Muskingum model is not enough accurate in the flood simulation. Thus, Gill (1978) presented the nonlinear version of the Muskingum method. The existence of a nonlinear relationship between storage and discharge in the river system is closer to reality and appears to be much more logical. Therefore, in recent years, the nonlinear Muskingum method has received more attention from researchers (Akbari et al. 2020, Barati 2013, Bozorg-Haddad et al. 2015, Bozorg-Haddad et al. 2019, Bozorg-Haddad et al. 2020, Chu and Chang 2009, Easa 2014, Gąsiorowski and Szymkiewicz 2020, Geem 2006, Ghaleni and Ebrahimi 2013, Hamedi et al. 2016, Kang et al. 2017, Karahan et al. 2015, Khalifeh et al. 2020, Khalifeh et al. 2021, Lu et al. 2021a, Niazkar and Afzali 2017, Xu et al. 2012). In order to increase the accuracy of the Muskingum model, researchers used other versions of the Muskingum model by alerting the storage equation adding the lateral flow term to it (Kang et al. 2017, Lu et al. 2021a, Ayvaz and Gurarslan 2017, O'donnell 1985, Zhang et al. 2016, Easa 2013, Karahan et al. 2015). In addition, the optimal estimation of the Muskingum model parameters (decision variables) is critically important in its exactness. For the optimal estimation of the parameters, meta-heuristic algorithms are usually used (Akbari and Hessami-Kermani 2022, Bazargan and Norouzi 2018, Bozorg-Haddad et al. 2015, Bozorg-Haddad et al. 2019, Bozorg-Haddad et al. 2020, Chu and Chang 2009, Das 2004, Easa 2014, Ehteram et al. 2018, Farahani et al. 2019, Geem 2011, Ghaleniand Ebrahimi 2013, Kang et al. 2017, Khalifeh et al. 2021, Kim et al. 2001, Niazkar and Afzali 2017, Norouzi and Bazargan 2020). In this research, the Muskingum fifth-type model presented by Bozorg-Haddad et al. (2015) is combined with the new lateral flow relation. Therefore, in the proposed Muskingum model, which includes a different storage equation compared to other types of Muskingum models, the accuracy of the proposed model in estimating the outflow hydrograph significantly increases compared to previous techniques. Another advantage of this method due to its efficiency is the smaller number of parameters (decision variables) compared to other models. Also, in this research, the artificial gorilla troops optimization algorithm (Abdollahzadeh et al. 2021) is used for the optimal estimation of the decision variables of the optimization model.

Materials and methods

Muskingum model

The Muskingum model is one of the hydrological river routing methods that was first proposed by (McCarthy, 1938) for flood control in Ohio, the USA. The first Muskingum linear model without considering the lateral flow (LMM) suggested by (McCarthy, 1938) is as follows:

$$\frac{{{\text{d}}S_{t} }}{{{\text{d}}t}} = I_{t} - O_{t}$$
(1)
$$S_{t} = K\left[ {{\text{XI}}_{t} + \left( {1 - X} \right)O_{t} } \right] \left( {{\text{LMM}}} \right)$$
(2)

In these relationships, St, It and Ot are, respectively, the storage volume, the inflow to the river reach and outflow from the river reach at time t, K is the time-storage coefficient of the river and has a logical value close to the flow passing time through the entire river reach (K > 0) and X is the weighting factor (0 < X < 0.5) (Geem 2006; Mohan 1997). The first to fifth types of the nonlinear Muskingum models without considering the lateral flow (NL) were, respectively, presented by these researchers: Chow (1959), Gavilan and Houck (1985), Gill (1978), Easa (2014) and Bozorg-Haddad et al. (2015).

$$S = K\left( {{\text{XI}}_{t}^{\alpha } + \left( {1 - X} \right)O_{t}^{\alpha } } \right) \left( {{\text{NL}}1} \right)$$
(3)
$$S = K\left( {{\text{XI}}_{t}^{{\alpha_{1} }} + \left( {1 - X} \right)O_{t}^{{\alpha_{2} }} } \right) \left( {{\text{NL}}2} \right)$$
(4)
$$S = K\left( {{\text{XI}}_{t} + \left( {1 - X} \right)O_{t} } \right)^{\beta } \left( {{\text{NL}}3} \right)$$
(5)
$$S = K\left( {{\text{XI}}_{t}^{\alpha } + \left( {1 - X} \right)I_{t}^{\alpha } } \right)^{\beta } \left( {{\text{NL}}4} \right)$$
(6)
$$S = K\left[ {X\left( {C_{1} I_{t}^{{\alpha_{1} }} } \right) + \left( {1 - X} \right)\left( {C_{2} O_{t}^{{\alpha_{2} }} } \right)} \right]^{\beta } \left( {{\text{NL}}5} \right)$$
(7)

In these relationships, K, X, C1, C2, α1, α2 and β are the parameters of the model. Also, various types of nonlinear models considering the lateral flow (Olat) have been presented by different researchers. O'donnell (1985) assumed that the lateral flow entering the river is proportional to \(O=\mathrm{a}\times {I}_{t}\) and presented the first Muskingum model with the lateral flow as follows:

$$S = K\left[ {(X + a)I_{t} + \left( {1 - X} \right)O_{t} } \right] \left( {{\text{LMM}} - L} \right)$$
(8)

Karahan et al. (2015) combined the NL2 model with the lateral flow \(O=a\times {I}_{t}\) and proposed the following model:

$$S = K\left( {\left( {X + a} \right)I_{t}^{{\alpha_{1} }} + \left( {1 - X} \right)O^{{\alpha_{2} }} } \right) \left( {{\text{NL}}2 - L} \right)$$
(9)

Zhang et al. (2016) combined the NL2 model with the lateral flow \(O=a\times {I}_{t}\) and proposed the following model:

$$S = K\left( {\left( {X + a} \right)I_{t}^{{\alpha_{1} }} + \left( {1 - X} \right)I_{t}^{\alpha } } \right)^{\beta } \left( {{\text{NL}}4 - L} \right)$$
(10)

The efficiency of the fifth type of the nonlinear Muskingum method (NL5) compared to the fourth type method (NL4) has been proven (Bozorg-Haddad et al. 2015). Therefore, in this paper, the Muskingum NL5 model with the advanced lateral flow equation (NL5-AL) is considered.

Proposed Muskingum model (NL5-AL)

In this paper, the amount of lateral flow is considered as Eq. (11) from the inflow to the reach.

$$O_{{{\text{lat}}}} = a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c$$
(11)

In this relation, sin and cos are the sine and cosine functions, and a, b, c, w1 and w2 are constant coefficients.

Therefore, if the lateral flow is included in Eq. (1), the following equations are obtained:

$$\frac{{{\text{d}}S_{t} }}{{{\text{d}}t}} = I_{t} + \underbrace {{a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c}}_{{O_{lat} }} - O_{t}$$
(12)

Therefore, the Muskingum NL5-type equation is obtained by considering the lateral flow in the form of Eq. (13).

$$S = K\left[ {X\left( {C_{1} I^{{\alpha_{1} }} } \right) + \underbrace {{a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c}}_{{O_{lat} }} + \left( {1 - X} \right)\left( {C_{2} O^{{\alpha_{2} }} } \right)} \right]^{\beta } \left( {{\text{NL}}5 - {\text{AL}}} \right)$$
(13)

Equation (13) is called the nonlinear Muskingum model with the advanced lateral flow equation (NL5-AL) and has 12 parameters (decision variables).

Model optimization

The parameter estimation of the NL5-AL model can be solved by expressing an optimization problem. In this optimization problem, the objective function (SSQ) is defined as the minimization of the sum of the squared errors between the measured outflow (\({\widehat{O}}_{t}\)) and the routed outflow from the river reach (Ot).

$${\text{SSQ}} = {\text{Minimize}}\mathop \sum \limits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - O_{t} } \right)^{2}$$
(14)

In this formula, SSQ is the objective function, and nt is the number of time steps in the outflow hydrograph. \({\widehat{O}}_{t}\) is the observed outflow from the river reach at the time step t, and Ot is the routed outflow from the river reach at the time step t which is computed by Eq. (15).

$$O_{t} = \left\{ {\frac{{\left( {\frac{{S_{t} }}{K}} \right)^{{\frac{1}{\beta }}} - \left[ {X\left( {C_{1} I_{t}^{{\alpha_{1} }} } \right) + a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c} \right]}}{{C_{2} \left( {1 - X} \right)}}} \right\}^{{\frac{1}{{\alpha_{2} }}}}$$
(15)

The steps to calculate the routed outflow (O) in the optimization model are as follows:

  • Step 1. Determining the minimum matrix of variables (lb) and the maximum matrix of variables (ub)

  • Step 2. Calculating S1 at the time step t = 1 from Eq. (16)

    $$S_{1} = K\left[ {X\left( {C_{1} I_{1}^{{\alpha_{1} }} } \right) + a \times \sin \left( {w_{1} \times I_{1} } \right) + b \times \cos \left( {w_{2} \times I_{1} } \right) + c + \left( {1 - X} \right)\left( {C_{2} O_{1}^{{\alpha_{2} }} } \right)} \right]^{\beta }$$
    (16)

  • Step 3. Calculating Ot for t>1 from Eq. (15):

  • Step 4. Calculating ∆S from the combination of Eqs. (12) and (15) as follows:

    $$\Delta S = \left[ {I_{t} + a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c - O_{t} } \right]\Delta t$$
    (17)

  • Step 5. Calculating S in step t+1 from Eq. (18)

    $$S_{t + 1} = S_{t} + {\Delta }S$$
    (18)

  • Step 6. Calculating the penalty function for cases where St+1 is smaller than zero or mixed:

    $${\text{S}}_{t + 1} = \left\{ {\begin{array}{*{20}c} {P_{{\text{s}}} \left| {S_{t + 1} } \right|} & {{\text{if}}} & {S_{t + 1} < 0} \\ {P_{{\text{s}}} \left| {{\text{Real}}(S_{t + 1} ) \times S_{t + 1} } \right|} & {{\text{if}}} & {{\text{image}}(S_{t + 1} ) \sim = 0} \\ \end{array} } \right.$$
    (19)

    In this regard, image (St+1) represents the imaginary part of St+1, Real (St+1) represents the real part of St+1, and PS is the penalty constant for S.

  • Step 7. Calculating Ot+1 from Eq. (20):

    $$O_{t + 1} = \left\{ {\frac{{\left( {\frac{{S_{t + 1} }}{K}} \right)^{{\frac{1}{\beta }}} - \left[ {X\left( {C_{1} I_{t}^{{\alpha_{1} }} } \right) + a \times \sin \left( {w_{1} \times I_{t} } \right) + b \times \cos \left( {w_{2} \times I_{t} } \right) + c} \right]}}{{C_{2} \left( {1 - X} \right)}}} \right\}^{{\frac{1}{{\alpha_{2} }}}}$$
    (20)

  • Step 8. Calculating the penalty function for cases where Ot+1 is smaller than zero or mixed:

    $$O_{t + 1} = \left\{ {\begin{array}{*{20}c} {P_{{\text{O}}} \left| {O_{t + 1} } \right|} & {{\text{if}} } & {O_{t + 1} < 0} \\ {P_{{\text{O}}} \left| {{\text{Real}}(O_{t + 1} ) \times O_{t + 1} } \right| } & {{\text{if}} } & {{\text{image}}(O_{t + 1} ) \sim = 0} \\ \end{array} } \right.$$
    (21)

    In this regard, image(Ot+1) represents the imaginary part of Ot+1, Real(Ot+1) represents the real part of Ot+1, and PO is the penalty constant for O.

  • Step 9. Repeating steps 3 to 8.

  • Step 10: Calculating SSQ from Eq. (14).

  • Step 11: Repeating steps 2 to 10 until the reaching the termination criterion.

  • Step 12: Determining the minimum SSQ

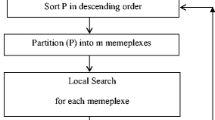
The flowchart of the optimization steps is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of model optimization steps

Full size image

Artificial gorilla troops optimization algorithm (GTO)

The artificial gorilla troops optimizer algorithm is one of the new meta-heuristic algorithms that was presented in 2021 by Abdollahzadeh et al. (2021). This algorithm was developed based on the social life of gorillas. Gorillas perform activities such as resting, traveling and eating during the day. The leader of the gorilla troop, the silverback gorilla, is a mature and strong male gorilla, usually more than 12 years old, known by the silver hair on his back, and he makes all the decisions. In conflicts between troop members, he plays the role of mediator and decides on the movement of the troop. Each silverback gorilla is the leader of a group of 5 to 30 individuals. The GTO algorithm uses different mechanisms for the optimization operation (exploration and exploitation). In the mechanisms used in the exploration phase, three different mechanisms of migration to an unknown place, migration to a known place and moving toward other gorillas are used. Each of these three mechanisms is chosen according to a general approach. A parameter called p is used to select the migration mechanism to an unknown place. The first mechanism is chosen when rand < p. If rand ≥0.5, the movement mechanism toward other gorillas is selected. If rand <0.5, the migration mechanism to a known place is selected. According to the used mechanisms, each of the mechanisms gives a great ability to the GTO algorithm. The first mechanism allows the algorithm to control the entire problem space well, the second mechanism improves the heuristic performance of the GTO, and finally, the third mechanism strengthens the GTO in escaping from local optimal points. Equation (22) is utilized to simulate the three mechanisms used in the exploration phase.

$${\text{GX}}(t + 1) = \left\{ \begin{gathered} \left( {{\text{UB}} - {\text{LB}}} \right) \times r_{1} + {\text{LB}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{if}}\;{\text{rand}}\;{\text{ < }}\;p \hfill \\ \left( {{\text{r}}_{2} - C} \right) \times X_{r} (t) + L \times H\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\,{\text{if}}\;{\text{rand}} \ge 0.5 \hfill \\ {\text{X}}({\text{i}}) - L \times \left[ {L \times (X(t) - {\text{GX}}_{r} (t)) + r_{3} \times \left( {X(t) - {\text{GX}}_{r} (t)} \right)} \right]\quad {\text{if}}\;{\text{rand}}\; < \;0.5 \hfill \\ \end{gathered} \right.$$
(22)

GX(t+1) is the gorilla position vector at iteration t+1. X(t) is the gorilla current position vector. In addition, r1, r2, r3 and rand are random values that are updated in the interval [0, 1] in each iteration. The value of the parameter p should be specified in the interval [0, 1] before the optimization operation. This parameter determines the probability of choosing the migration mechanism to an unknown place. UB and LB represent the maximum and minimum decision variables, respectively. Xr is one of the gorilla troop members randomly selected from the whole population, and GXr is one of the randomly selected gorilla candidate position vectors containing the updated positions at each step. Finally, C, L and H are calculated using Eqs. (23), (24) and (25), respectively.

$$C = F \times \left( {1 - \frac{{{\text{It}}}}{{{\text{Max}} {\text{It}}}}} \right)$$
(23)
$$F = {\text{Cos}} \left( {2 \times r_{4} } \right) + 1$$
(24)
$$L = C \times l$$
(25)

In Eq. (23), It is the number of the current iteration, Max It is the total number of iterations to perform the optimization operation, and the value of F is calculated from Eq. 24. In this equation, Cos is the cosine function and r4 is a random value in the interval [0, 1], and it is updated in every iteration. In Eq. (23), in initial iterations, the optimization values are created with sudden changes in a large interval, but this interval is reduced in final iterations. L is determined using Eq. (25), where l is a random value in the interval [1, 1]. Equation (25) is used to simulate silverback gorilla leadership. In the real world, the silverback gorilla may not make the right decisions to find food or control the troop due to the lack of experience in the early stages of leadership. However, it does gain enough experience to lead. Moreover, in Eq. (22), H is calculated using Eq. (26), and in Eq. (26), Z is computed using Eq. (27), which has a random value in the dimensions of the problem and is specified in the interval [−C, C].

$$H = Z \times X\left( t \right)$$
(26)
$$Z = \left[ { - C,\,C} \right]$$
(27)

At the end of the exploration phase, the cost function (objective) of all GX solutions is calculated, and if the objective function is GX(t) < X(t), the value of GX(t) is used instead of X(t). Therefore, the best solution produced in this stage is also considered as a silverback. There are two mechanisms in the exploitation stage including the possibility to choose the option of following the silverback gorilla and competing for adult female gorillas using the value of C in Eq. (23). If C≥W, the mechanism of following the silverback is chosen, but if C<W, the competition for mature female gorillas is done. The parameter W should be adjusted prior to the optimization operation. To simulate the mechanism of following the silverback, relation (28) is used.

$${\text{GX}}\left( {t + 1} \right) = L \times M \times \left[ {X\left( t \right) - X_{{{\text{Silverback}}}} } \right] + X\left( t \right)$$
(28)
$$M = \left[ {\left| {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} {\text{GX}}_{i} \left( t \right)} \right|^{g} } \right]^{\frac{1}{g}}$$
(29)
$$g = 2^{L}$$
(30)

In Eq. (28), X(t) is the gorilla position vector and Xsilverback is the silverback gorilla position vector (best solution). In addition, L is calculated using Eq. (25) and M by Eq. (29). In Eq. (29), GXi(t) represents the position vector of each gorilla candidate in the iteration t. N represents the total number of gorillas. g is also calculated using Eq. (30), and in this relation, L is also calculated using Eq. (15). If C<W, the mechanism of competition for adult female gorillas is selected in the exploitation phase. After some time, when the young gorillas reach puberty, they fight with other male gorillas and expand their group in choosing the adult female gorilla, and this competition is often violent. Equation (31) is used to simulate this behavior.

$${\text{GX}}\left( i \right) = X_{{{\text{Silverback}}}} - \left( {X_{{{\text{Silverback}}}} \times Q - X\left( t \right) \times Q} \right) \times A$$
(31)
$$Q = 2 \times r_{5} - 1$$
(32)
$$A = \beta \times E$$
(33)
$$E = \left\{ {\begin{array}{*{20}c} {N_{1} {\text{if rand}} \ge 0.5} \\ {N_{2} {\text{if rand}} < 0.5} \\ \end{array} } \right.$$
(34)

In Eq. (31), Xsilverback is the position vector of the silverback (best solution) and X(t) is the current gorilla position vector. Q is calculated from Eq. (32) to simulate the impact force. In equation (32), r5 is random values in the interval [0, 1]. A is the coefficient vector which is used to determine the level of violence in conflicts and calculated using Eq. (33). In Eq. (33), β is a parameter that should be determined prior to the optimization operation, and E is specified from Eq. (34) and used to simulate the impact of violence on the dimensions of the solutions. If rand ≥0.5, the E value is equal to random values in the normal distribution and problem dimensions, but if rand<0.5, E is equal to a random value in the normal distribution. rand is also a random value in the interval [0,1]. At the end of the exploitation stage, the group formation operation is performed, in which the cost function of all GX solutions is estimated, and if the cost function GX(t)<X(t), the GX(t) solution is taken as the X(t) solution and the best obtained solution is considered as a silverback among the whole population. The pseudo-code of the GTO algorithm is given below:

figure a

Evaluation criteria

To evaluate the NL5-AL model, the statistical indices of the ratio of error square to the standard deviation of the measured data (RSR), the difference between the peak flow in the measured and routed outflow hydrograph (DPO), the Nash–Sutcliffe efficiency index (NSE) and the percent bias (PBIAS) are utilized. RSR is a combination of two indices of root-mean-square error and standard deviation of measured data, and in the best case, its value is zero, which shows that the model has high efficiency (Moriasi et al. 2007). NSC varies between − ∞ in the worst case and 1 for the complete correlation (Nash and Sutcliffe 1970). With the PBIAS index, the closeness of the routed data to the average value of the measured data is calculated, whose optimal values are zero, while positive and negative values, respectively, indicate the estimation of routed values lower and higher than the measured values (Gupta et al. 1999). The relations of these indices are in the form of Eqs. (35–38).

$${\text{RSR}} = \frac{{{\text{RMSE}}}}{{{\text{STDEV}}_{{\hat{O}_{t} }} }} = \frac{{\sqrt {\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - O_{t} } \right)^{2} } }}{{\sqrt {\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - \hat{O}_{t}^{{{\text{mean}}}} } \right)^{2} } }}$$
(35)
$${\text{DPO}} = \left| {\hat{O}_{t}^{{{\text{Peak}}}} - O_{t}^{{{\text{Peak}}}} } \right|$$
(36)
$${\text{NSE}} = 1 - \frac{{\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - O_{t} } \right)^{2} }}{{\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - \hat{O}_{t}^{{{\text{mean}}}} } \right)^{2} }}$$
(37)
$${\text{PBIAS}} = \frac{{\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \left( {\hat{O}_{t} - O_{t} } \right)}}{{\mathop \sum \nolimits_{t = 1}^{{n_{t} }} \hat{O}_{t} }} \times 100$$
(38)

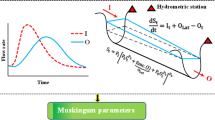
In these relationships, \({\widehat{O}}_{t}\) is the measured outflow from the river reach, \({\mathrm{O}}_{\mathrm{t}}\) represents the routed outflow from the river reach in the time step t, nt is the number of time steps of the outflow hydrograph, \({\widehat{O}}_{t}^{\mathrm{Peak}}\) is the peak discharge of the measured hydrograph, \({O}_{t}^{\mathrm{Peak}} \mathrm{denotes} \mathrm{the peak discharge of the}\) routed hydrograph, and \({\widehat{O}}_{t}^{\mathrm{mean}}\) represents the average measured outflow (Fig. 2).

Fig. 2
figure 2

Inflow, outflow and routed hydrographs for examples a Wilson flood b Wye River flood c Viessman and Lewis data d Sutculer flood e Karun River flood and f Dinavar River flood

Full size image

Results and Discussion

The performance of the NL5-AL model is evaluated by solving six routed problems. The first example is a single-peak smooth inflow hydrograph presented by Wilson (1974), the second example is a non-smooth inflow hydrograph of the Wye River in England presented by O'donnell (1985). The third example includes the hydrograph of the non-smooth inflow presented by Viessman et al. (2002). The fourth example includes the multi-peak inflow hydrograph presented by Lee (2021). The fifth example is the hydrograph related to the Karun River located in Iran which was presented by Orouji et al. (2013), and the sixth example is the data related to the Dinavar River in Iran, Kermanshah, which is presented in this study.

Example 1: Wilson flood data

The first example is the inflow and outflow hydrograph related to the studies reported by Wilson (1974). The data of this flood have been used in most of the previous studies to review different parameter estimation methods of different nonlinear Muskingum models (Bozorg-Haddad et al. 2015, Easa 2014, Geem 2006, Lee et al. 2018, Lu et al. 2021a, Zhang et al. 2016). The number of the time steps is equal to 21, and the length of each time step is 6 hours. This hydrograph is a single-peak hydrograph, in which the inflow increases from 22 cms to 111 cms in 30 hours and then decreases from 111 cms to 18 cms. Table (1) presents the inflow values, measured outflow and routed outflow. The NL5-AL model has 12 parameters (decision variables), which are determined through minimizing SSQ by GTO. The GTO parameters, i.e., w, p and β are set equal to 0.85, 0.03 and 3, respectively. The number of iterations is considered to be 500, and the population size is equal to 150. The optimal values of the NL5-AL model variables are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α2, α1, a, b, c, w1 and w2 are presented in Table (7). Also, the error indices for evaluating the NL5-AL model are given in Table (8). The values of the RSR, NSE, PBIAS, DPO and SSQ indices are obtained to be 0.008, 0.9999, 0.0066, 0.166 mcm and 0.799 (mcm)2, respectively. If 0≤RSR≤0.5, 0.75<NSE≤1 and PBIAS<±10, the model results are very good (Moriasi et al. 2007). So, the results of the new NL5-AL model are very appropriate. The low value of SSQ also shows that the NL5-AL model has a very good performance.

Table 1 Results related to Example 1 (Wilson flood data)
Full size table
Table 2 Results of the second example (Wye River data)
Full size table

Second example: the flood data of the Wye River

The second example is the flood that occurred in the Wye River in England in 1960. The inflow hydrograph is one-peak and non-smooth. The 69.75 Km path of the Wye River from Erwood to Belmont has no tributaries and has very small lateral flow. Therefore, this flood is a good case for testing routing methods (O'donnell, 1985). The inflow value varies from 54 cms to 1145 cms, and the flow reaches its maximum value in 84 hr. In this example, the time step is 6 hr, the number of time steps is 33, and the time period is 198 hr. The maximum outflow is 969 cms occurred in 102 hr. Some researchers used this case study to estimate the Muskingum parameters (Akbari and Hessami-Kermani 2022, Ayvaz and Gurarslan 2017, Bozorg-Haddad et al. 2020, Lee 2021, Lu et al. 2021b). In Table (2), the values of the inflow, measured outflow and routed outflow for the second example are presented. The NL5-AL model is linked to the GTO algorithm, and the GTO setting parameters are set as in the first example, and the number of iterations and the population size are considered to be 5000 and 150, respectively. The optimal values of the NL5-AL model variables are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α1, α2, a, b, c, w1 and w2 are presented in Table (7) are presented in Table (7) for the data of the Wye River. Also, the error indices for evaluating the NL5-AL model are presented in Table (8) for the data of the Wye River. The values of the RSR, NSE, PBIAS, DPO and SSQ indices are equal to 0.046, 0.9979, 0.1051, 12.93 mcm and 3459.09 (mcm)2, respectively. According to Moriasi et al. (2007), the results of the NL5-AL model are very suitable. The SSQ value also shows that the NL5-AL model has a very favorable performance, and the SSQ value for this example is the lowest compared to all previous studies.

Third example: Viessman and Lewis data

The third example is the third case study of a flood with a multi-peak discharge hydrograph that was introduced by Viessman and Lewis in 2003 (Viessman and Lewis 2003). This example contains Δt = 1 day and 24 time steps. The outflow hydrograph has two peaks on the 10th and 17th days. The inflow ranges from 143 cms to 1775.5 cms. The minimum and maximum outflow are 118.4 cms and 1509.3 cms, respectively. Some researchers used this case study to estimate the Muskingum parameters (Akbari et al. 2020, Ayvaz and Gurarslan 2017, Bozorg-Haddad et al. 2019, Lu et al. 2021a). In Table (3), the values of the inflow, measured outflow and routed outflow are presented for the third example. The GTO parameters, i.e., w, p and β are set equal to 0.85, 0.04 and 3, respectively. The number of iterations and the population size are considered to be 5000 and 150, respectively. The optimal values of the NL5-AL model variables are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α1, α2, a, b, c, w1 and w2 for the Viessman and Lewis data are presented in Table (7). Also, the error indices for evaluating the NL5-AL model for the Viessman and Lewis data are given in Table (8). The values of RSR, NSE, PBIAS, DPO and SSQ indices are 0.044, 0.9981, 0.0232, 3.625 mcm and 8449.46 (mcm)2, respectively. The results of the NL5-AL model are very suitable for the Viessman and Lewis data. The value of SSQ also shows that the NL5-AL model has a very favorable performance, and the value of SSQ for this example is evaluated as very appropriate compared to previous research.

Table 3 Results related to the third example (Viessman and Lewis data)
Full size table

Fourth example: Sutculer flood data

The fourth example includes the multi-peak inflow hydrograph presented by Karahan et al. (2015). This flood occurred in the center of Sutculer city at 102 Km ISparta as a result of heavy rainfall for four hours on November 4, 1995. This example contains Δt =1 hr and 30 time steps. The outflow hydrograph has two peaks in the third and fifteenth hours. The inflow ranges from 7.53 cms to 216 cms. In Table (4) the values of the inflow, measured outflow and routed outflow are presented for the fourth example. The GTO parameters, i.e., w, p and β are set equal to 0.85, 0.03 and 3, respectively. The number of iterations and the population size are considered to be 5000 and 150, respectively. The optimal values of the NL5-AL model variables are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α1, α2, a, b, c, w1 and w2 for the Sutculer flood data are presented in Table (7). Also, the error indices for evaluating the NL5-AL model for the Sutculer flood data are given in Table (8). The values of RSR, NSE, PBIAS, DPO and SSQ indices are 0.023, 0.9995, − 0.0632, 0.377 mcm and 33.5 (mcm)2, respectively. The values of the mentioned indices apply to inequalities of 0≤RSR≤0.5, 0.75<NSE≤1 and PBIAS<±10, so the results of the NL5-AL model are very suitable for the Sutculer flood data. The SSQ value also shows that the NL5-AL model has a very favorable performance, and the SSQ value for this example is the lowest compared to previous studies (Table 5).

Table 4 Results related to the fourth example (Sutculer flood data)
Full size table
Table 5 Results related to the fifth example (Karun flood data)
Full size table

Fifth example: Karun River flood data

The fifth example includes the inflow hydrograph of the Karun River, the largest river in southwest Iran, which was presented by Orouji et al. (2013). The hydrograph of this example is single-peak, Δt=2hr and has 30 time steps. The minimum and maximum outflow are 380 cms and 1300 cms, respectively. The inflow and outflow peak discharges occur at 48 hr and 56 hr, respectively. In Table (4), the values of the inflow, measured outflow and routed outflow are presented for the fifth example. By adjusting the parameters w, p and β of the GTO algorithm, the number of iterations and the population size are considered to be 5000 and 150, respectively. The optimal values of the decision variables of the NL5-AL model are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α1, α2, a, b, c, w1 and w2 for the Karun flood data are presented in Table (7). Also, the error indices for evaluating the NL5-AL model for the Karun flood data are given in Table (8). The values of RSR, NSE, PBIAS, DPO and SSQ indices are equal to 0.051, 0.9974, 0.048, 18.562 mcm and 9062.64 (mcm)2, respectively. The values of the mentioned indices apply to inequalities of 0≤RSR≤0.5, 0.75<NSE≤1 and PBIAS<±10, so the results of NL5-AL model are very good for Karun flood data. The SSQ value also shows that the NL5-AL model has a very favorable performance, and the SSQ value for this example is the lowest compared to previous studies.

Sixth example: Dinavar River flood data

The sixth example includes the inflow hydrograph of the Dinavar River, Iran, Kermanshah province, which is presented in this study. This example contains Δt=1hr and has 120 time steps. The minimum and maximum inflow are 14.9 cms and 121 cms, respectively. The inflow and outflow peak discharges occur at 51 hr and 54 hr, respectively. The hydrograph data are related to the Mianrahan and Heidarabad hydrometric stations, where the measurements were made by Kermanshah Regional Water Company. Through this path, the river flow is recharged by groundwater flows. In Table (6), the values of the inflow, measured outflow and routed outflow for the sixth example are given. The parameters w, p and β of the GTO algorithm are initialized, and the number of iterations of the algorithm and the population size are considered to be 500 and 150, respectively. The optimal values of the decision variables of the NL5-AL model are determined by different GTO runs. The values of the decision variables X, K, β, C1, C2, α1, α2, a, b, c, w1 and w2 for the Dinavar flood data are presented in Table (7). Also, the error indices for evaluating the NL5-AL model for the Karun flood data are given in Table (8) for the Dinavar flood data. The values of RSR, NSE, PBIAS, DPO and SSQ indices are equal to 0.041, 0.9983, − 0.1018, 2.456 mcm and 743.6 (mcm)2, respectively. The values of the mentioned indices apply to the inequalities of 0 ≤ RSR ≤ 0.5, 0.75 < NSE ≤ 1 and PBIAS <± 10, so the results of the NL5-AL model are very suitable for Dinavar flood data. The SSQ value also demonstrates that the NL5-AL model has a very favorable performance. The data related to the flood of the Dinavar River has not been used by the researchers. This river is also fed by the springs of the path.

Table 6 Results of sixth example (Dinavar River data)
Full size table
Table 7 NL5-AL model parameters for examples 1 to 6
Full size table
Table 8 Error indices for evaluating NL5-AL model in examples 1 to 6
Full size table

Another comparison that is made to evaluate the NL5-AL model in addition to the error indices is the comparison of the objective function of the NL5-AL model with the objective function of previous studies. This comparison is conducted in Table (9). This comparison is made for all types of Muskingum models including linear, nonlinear, fixed parameter and variable parameter. It should be noted that in Muskingum models with variable parameters, the decision variables of the optimization model increase with more partitioning of the inflow. For example, for the Muskingum model with three parameters and three inflow partitions, the decision variables of the model are 9. Therefore, the proposed Muskingum model with 12 decision variables is not very complicated compared to the presented models, and with little computational effort, the result is achieved with the GTO algorithm. The type of function considered for the lateral flow in the proposed model causes its accuracy to increase too much. As shown in Table (9), the values ​​of the best objective function (SSQ) of the recent studies for the Wilson flood data have very little difference with the SSQ value of the proposed model. For the second example, the SSQ of the proposed model is lower than the SSQ of all previous studies for the Wye River data. For the example of the Viessman and Lewis data, the SSQ value of the proposed model is equal to 8449 (mcm)2, where this SSQ value for the third example shows the very favorable performance of the NL5-AL model. For the Sutculer flood data (third example), the SSQ value is significantly different compared to the previous methods. The SSQ value of the proposed model is equal to 33.5, while the best SSQ value for previous studies is equal to 217.73, so the results of the proposed model are very suitable. The results of the NL5-AL model for the fifth example (Karun River flood) are evaluated very appropriate. The value of SSQ for the Karun flood which was done by Akbari et al. (2020) is equal to 11792 (mcm) 2 and the value of SSQ for the proposed model is equal to 9062.64. In the sixth example, the Dinavar River flood which is fed from the springs of the path during floods and the results of the proposed model are very suitable for estimating the routed outflow.

Table 9 Comparison of the NL5-AL results with previous studies for examples 1 to 6
Full size table

Conclusion

Due to the importance of flood forecasting, its role in the design of hydraulic structures, its control, flood routing are critically important for researchers, so that efforts have always been made to accurately and quickly predict floods. The investigations carried out in this research show the importance of increasing the accuracy of the Muskingum model and paying attention to the methods of estimating its parameters. The studies conducted in this field show that the issue of flood routing and investigation and research on different methods are among the goals and concerns of water resources engineers. In order to increase the accuracy of calculations and get closer to the actual outflow discharges, the Muskingum nonlinear model has been used in recent years. The Muskingum nonlinear model is an efficient technique in flood routing; however, the efficiency of this method is influenced by the parameters used in it. Therefore, in this paper, a new function for the lateral flow is proposed, which is combined with NL5. In this new Muskingum model, the value of the objective function that minimizes the squared difference of the measured, and routed outflow hydrograph was evaluated to solve six examples, which five of them have been used in previous studies. The results showed that the proposed model routed the outflow hydrograph with very good accuracy, and its comparison with previous research showed its high ability compared to other models. The GTO algorithm was used to determine the parameters of the proposed model and estimate them optimally. This algorithm is a powerful algorithm for solving optimization problems and performs exploration and exploitation steps properly and has high speed and accuracy in solving optimization problems. The proposed model had 12 decision variables and provided very good results so that it improved the value of SSQ in some of these examples by more than 30%.