Modelling nitrogen transformation in the Lake Bunyonyi ecosystem, South-Western Uganda

Abstract

Lake Bunyonyi is one of the major resources of social-economic potential in the districts of Rubanda and Kabale, South-Western Uganda. The lake’s sub-catchment faces environmental problems because of intensive agriculture, settlement, business and tourism activities, which consequently cause pollution of water in the lake’s system. This study, therefore, intended to determine the processes that govern nitrogen dynamism using a numerical model that takes into account various processes in the system using STELLA® 8.1.1 software. From the model simulation, it was found that mineralization, microbial uptake and nitrification were the major processes governing nitrogen transformation in the water phase, accounting for 47.8% (0.49 g/d m⁻²), 44.2% (0.45 g/d m⁻²), and 7.8% (0.05 g/d m⁻²), respectively. The developed model predicted reasonably well the behaviour of the lake evidenced by the validation results of observed and simulated data that showed good linear regression coefficients (R²) of organic nitrogen (0.48), ammonia–nitrogen (0.68), and nitrate–nitrogen (0.61). The model has proven suitable for application on lakes with characteristics similar to that of Lake Bunyonyi. The study recommended that a compressive investigation that puts into consideration all the possible sources of nutrient and water inflow into the lake system be done on Lake Bunyonyi.

Introduction

Worldwide anthropogenic activities are responsible for the excessive nutrient inflow into lake systems. The excessive nutrient loading into freshwater ecosystems causes eutrophication which is linked to oxygen depletion, development of harmful algal blooms, shifts in phytoplankton populations, and reduced water quality (Brooks et al. 2016). Ongore et al. (2013) reported that nutrients in combination with heavy metals from various anthropogenic activities like mining and industries caused the aquatic ecological degradation of the Lake Victoria catchment. In South-Western Uganda, Lake Bunyonyi is very important for the livelihoods of people in Kabale and Rubanda Districts. The wetland around the lake provides materials for thatching houses and handicraft making. In addition, the lake is the major source of water for domestic use, used for small-scale fish farming, and is a popular tourism destination site.

Nevertheless, the Lake is threatened by pollution from hotels, campsites and agricultural activities. Besides, population growth has caused degradation and destruction of hill slopes and wetlands, and nutrients are carried directly into the lake (Van Dam et al. 2007). To formulate deserving sustainable management strategies, a good understanding of nutrient transformation using a dynamic ecological model is considered necessary. Dynamic ecological models developed and applied have been demonstrated to be powerful tools for simulation of nutrient transformation and removal from lakes and wetland ecosystems (Van Dam et al. 2007; Tang et al. 2016; Biswas et al. 2018; Mayo et al. 2018; Radbourne et al. 2019). Nevertheless, no significant efforts have been made to model the processes that govern nutrient transformation and removal processes in small freshwater lakes like Lake Bunyonyi which suffer pollution from diffuse sources. This study, therefore, modelled the processes governing nitrogen transformation using a dynamic simulation model. Ultimately, the findings of the study will be used as the basis for the establishment of the best management strategies for Lake Bunyonyi while maintaining its ecological quality.

Materials and methods

Sample collection and examination

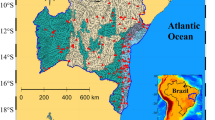
Water samples were collected for six months in both rainy (March–May 2020) and the dry season (June–August 2020). Samples from the inflow and the outflow rivers were collected from Rivers Kagoma and Heissesero (Fig. 1), respectively. Samples were collected into 1L plastic sampling bottles between 9:00 and 11:00 am prepared and then transported in an icebox with ice to the National Water and Sewerage Corporation (NWSC) Central Laboratories in Kampala for analysis within 24 h. While in the laboratory, samples were stored in the refrigerator at 4 °C before analysis. Water temperature, DO levels and pH were measured on-site during sampling. DO and water temperature were measured using the DO meter (DO 5510 M.R.C model). The pH was measured using a water-resistant hand-held pH meter (HI8314 HANNA instruments) following APHA (2017) standards. In the laboratory, samples were analysed for the determination of NH₃-N, NO₃-N and Org-N following the APHA (2017) standard procedures as described by Saturday et al. (2021). Besides, climatic secondary data such as air temperatures, sunshine, relative humidity, rainfall for a period of six months (March–May 2020) and June–August 2020 were collected from Uganda National Meteorological Authority, Kabale centre. The water inflow into the lake through the Kagoma River and outflow through the Heissesero River were measured onsite using the float-area method as described by Dahal and Dorji (2019).

Fig. 1

Map of the study area showing the sampling stations in the Lake Bunyonyi sub-catchment

Model development

Conceptual model of nutrient balance

A conceptual schematic model that encompasses the forcing variables, state variables and the activities governing nitrogen transformation processes is used (Fig. 2). The forcing variables considered in this model are the volume of water in the lake (Q), water temperature (T), pH, volume of water inflow (in) and outflow (out), and DO. The state variables are the major forms of nitrogen; Organic Nitrogen (Org-N), Ammonia Nitrogen (NH₃-N) and Nitrate Nitrogen (NO₃-N) as indicated by boxes connected by respective processes. The nitrogen transformation considered includes nitrification, denitrification, volatilization, mineralization, microbes’ ammonia and nitrates uptake, algae uptake, sedimentation and decaying processes. A complete materials balance includes lake inflow and outflow, nutrients contained in the inflow and outflow of the lake, precipitation, evaporation, solar radiations, and air temperature; all of which influence nitrogen dynamic processes in the lake system are considered in the model. The nutrient mass balance around state variables was done based on the simplified Eq. (1) (Jørgensen and Bendoricchio 2001).

$${\text{Accumulation }} = {\text{Input}} - {\text{Output}} \pm {\text{Reaction}}$$

(1)

Fig. 2

Conceptual model for nutrient transformation processes in Lake Bunyonyi

Here, Input = Nutrient load that enter the lake from diverse sources and through different ways; Output = Nutrient concentration that leaves the lake through different ways; Reaction = the way nutrients leave the lake system by chemical transformation into other substances.

As illustrated in the conceptual model diagram (Fig. 2), nitrogen enters the Lake Bunyonyi system majorly by inflow stream and runoff from agricultural land use activities. Besides nutrient inflow via stream discharges and agricultural runoff, nutrients enter into the lake system through direct rainfall on the lake. While in the lake, nutrients can be taken up by aquatic plants, animals and microbes but are released back into the lake system through excretion and decomposition after death. This precisely means that nutrients are temporarily stored in the biomass. It is generally expected that nutrient fixation is larger than release because organic matter cannot all be decomposed and therefore some nutrients remain fixed in organic matter. Besides, fish catches and water abstraction remove nutrients from the lake and some nutrients are adsorbed to the sediment and may be released when the sediments are suspended by waves.

The following assumptions were considered for the development of the Model.

• i. The inlet of water to the lake considered in the model is Kagoma River, while the other non-sources like runoff and precipitation are not included in the Model.

• ii. The outlet which has been considered in this model is the Heissesero River; other water loss ways like underground seepage and evaporation are not included in the model.

• iii. Similar microorganisms within the lake take up both NO₃-N and NH₃-N.

• iv. The rivers Kagoma (inlet) and Heissesero (outlet) are not seasonal; they continue to bring water into the lake and drain water from the lake throughout the year, respectively.

Based on these assumptions, the following equations for the mass balance of state variables and nitrogen transformation processes were derived.

Ammonia–nitrogen

Based on the mass balance, NH₃-N was added in the lake through Kagoma River, and within the lake by mineralization, regeneration from the sediments, while, volatilization, nitrification, uptake by plants and microorganism processes were reducing NH₃-N concentration within the lake and some were drained from the lake by Heissesero River as shown in Eq. (2).

$$\frac{{\partial \left[ {{\text{NH}}_{3} - {\text{N}}} \right]}}{\partial t} = \left( {\frac{{\partial Q_{IF} }}{\partial t} \frac{{\partial \left[ {{\text{NH}}_{3} - {\text{N}}_{{{\text{in}}}} } \right]}}{\partial A}} \right) + \left( {r_{m} + r_{{{\text{reg}}}} } \right) - \left( {\frac{{\partial Q_{OF} }}{\partial t} \frac{{\partial \left[ { {\text{NH}}_{3} - {\text{N}}_{{{\text{out}}}} } \right]}}{\partial A} + r_{g1} + r_{v} + r_{n} } \right).$$

(2)

where, $\frac{{\partial Q_{IF} }}{\partial t}$. = Water inflow rate (m³/d), $\frac{{\partial Q_{OF} }}{\partial t}$ = Water outflow rate (m³/d), $\frac{{\partial \left[ {{\text{NH}}_{3} - {\text{N}}_{{{\text{in}}}} } \right]}}{\partial A}$ = Ammonia–nitrogen loading in water inflow (g/d m⁻²), $r_{m}$ = Rate of mineralization of organic nitrogen (g/d m⁻²), r_reg = Rate of regeneration (g/d m⁻²), $\frac{{\partial \left[ {{\text{NH}}_{3} - {\text{N}}_{{{\text{out}}}} } \right]}}{\partial A}$. = Ammonia–nitrogen loading in water outflow (g/d m⁻²), $r_{g1}$. = Ammonia uptake by microorganisms, $r_{v}$ = Rate of volatilization (g/d m⁻²), $r_{u1 }$. = Uptake by the plant (g/d m⁻²), r_n = Rate of nitrification of ammonia (g/d m⁻²).

Nitrate–nitrogen

Based on the mass balance, NO₃-N was added to the lake through the Kagoma River. The nitrification, denitrification, and nitrate uptake by microorganisms and algae were the major processes reducing NO₃-N concentration within the lake and some were dined through Heissesero River as shown in Eq. (3).

$$\frac{{\partial \left[ {{\text{NO}}_{3} - {\text{N}}} \right]}}{\partial t} = \left( {\frac{{\partial Q_{IF} }}{\partial t} \frac{{\partial \left[ {{\text{NO}}_{3} - {\text{N}}_{{{\text{in}}}} } \right]}}{\partial A} + r_{n} } \right)\left( {\frac{{\partial Q_{OF} }}{\partial t}\frac{{\partial \left[ {{\text{NO}}_{3} - {\text{N}}_{{{\text{out}}}} } \right]}}{\partial A} + r_{g3} + r_{dm} } \right)$$

(3)

$\frac{{\partial Q_{{{\text{in}}}} }}{\partial t}$. = Water inflow rate (m³/d), $\frac{{\partial Q_{{{\text{out}}}} }}{\partial t}$ = Water outflow (m³/sec), $\frac{{\partial \left[ {{\text{NO}}_{3} - {\text{N}}_{IF} } \right]}}{\partial A} + r_{n}$. = Nitrate-nitrogen inflow (g/d m⁻²), r_g2 = Rate of nitrate uptake by microorganisms, $\frac{{\partial \left[ {{\text{NO}}_{3} - {\text{N}}_{OF} } \right]}}{\partial A}$ = Nitrate–nitrogen outflow (g/d m⁻²), $r_{n}$ = Rate of nitrification (g/d m⁻²), $r_{dn}$ = Rate of denitrification (g/d m⁻²).

Organic-nitrogen

Like NH₃-N and NO₃-N, Org-N was added into the lake through Kagoma River and within it by decomposition. On the other hand, mineralization, nitrification, denitrification, and nitrate uptake by microorganisms and algae were responsible for Org-N reduction within the lake and some were drained off it via Heissesero River as shown in Eq. (4).

$$\frac{{\partial \left[ {{\text{Org}} - N} \right]}}{\partial t} = \left( {\frac{{\partial Q_{{{\text{in}}}} }}{\partial t} \frac{{\partial \left[ {{\text{Org}} - N_{{{\text{in}}}} } \right]}}{\partial A}} \right) + \left( {r_{g1} + r_{g2} } \right) - \left( {\frac{{Q_{{{\text{out}}}} }}{\partial t} \frac{{\partial \left[ {{\text{Org}} - N_{{{\text{out}}}} } \right]}}{\partial A} + r_{m} + r_{s} } \right)$$

(4)

where, $\frac{{\partial Q_{{{\text{in}}}} }}{\partial t}$ = Water inflow rate (m³/d), $\frac{{\partial Q_{{{\text{out}}}} }}{\partial t}$ = Water outflow (m³/d), $\frac{{\partial \left[ {{\text{Org}} - N_{{{\text{in}}}} } \right]}}{\partial A}$ = Organic-nitrogen inflow (g/d m⁻²), $\frac{{\partial \left[ {{\text{Org}} - N_{{{\text{out}}}} } \right]}}{\partial A}$ = Organic-nitrogen outflow (g/d m⁻²), $r_{g1}$ = Rate of ammonia uptake by microorganisms, $r_{g2}$ = Rate of nitrate uptake by microorganisms (g/d m⁻²), $r_{m}$ = Rate of mineralization (g/m²/day), $r_{s}$ = Rate of sedimentation (g/d m⁻²).

Equations for nutrient dynamic processes

Mineralization

The mass balance for mineralization of organic nitrogen in the lake system was modelled using first-order kinetics as presented in Eq. (5).

$$\frac{\partial m}{{\partial t}} = r_{m} = \left[ {{\text{Org}} - N } \right] \times K$$

(5)

where, K = Mineralization rate of constant nitrogen (day⁻¹).

Nitrification

According to Fritz et al. (1979), the nitrification process model is based on the assumption that nitrite formation by Nitrosomonas is a rate-limiting step and is inhibited by dissolved oxygen, temperature, and pH. The nitrification process was modelled using Eq. (6). The temperature and pH influence on Nitrosomonas bacteria were explained by the empirical relationship presented by Eqs. (7) and (8), respectively.

$$r_{n} = \left[ {\left( {\frac{{u_{n} }}{{Y_{n} }}} \right) \times \left( {\frac{{{\text{NH}}_{3} - {\text{N}}}}{{K_{1} + {\text{NH}}_{3} - {\text{N}}}}} \right) \times \left( {\frac{{{\text{DO}}}}{{K_{2} + {\text{DO}}}}} \right) \times \left( {C_{T} } \right) \times \left( {C_{{{\text{pH}}}} } \right)} \right] \times \left[ {{\text{Org}} - {\text{N}} } \right]$$

(6)

where, $\mu_{n}$ = maximum Nitrosomonas growth rate (d⁻¹), $Y_{n}$ = Yield coefficient for Nitrosomonas bacteria (mg VSS/mg N), $K_{1}$ = Ammonia Nitrosomonas half-saturation constant (g/d m⁻²), $K_{2}$ = Oxygen Nitrosomonas half-saturation constant (g/d m.⁻²), $C_{T }$ = Temperature-dependent factor, $C_{{{\text{pH}}}}$ = Nitrosomonas growth-limiting factor for pH

$$C_{T} = {\text{exp}}\left[ {0.0098\left( {T - T_{O} } \right)} \right]$$

(7)

where, $C_{T}$ = Temperature dependence factor, $T$ = Temperature in °C, $T_{O}$ = Reference temperature (°C) = 15 °C

$$C_{{{\text{pH}}}} = \left\{ {\begin{array}{*{20}l} {1 - 0.83\left( {7.2 - {\text{pH}}} \right) \ldots } \hfill & {{\text{for}}} \hfill & {{\text{pH}} \ldots < 7.2} \hfill \\ {10 \ldots \ldots \ldots \ldots \ldots \ldots \ldots .} \hfill & {{\text{for}} \ldots } \hfill & {{\text{pH}} \ge 7.2} \hfill \\ \end{array} } \right..$$

(8)

Denitrification

To model the rate of denitrification, a combination of denitrifying bacterial activities is applied. The model expression is presented by Eq. (9).

$$r_{dm} = \left\lfloor {(DR_{ - 20 \times } \theta^{T - 20} } \right\rfloor \times \left[ {{\text{NO}}_{3 - } {\text{N}}} \right]$$

(9)

where, $DR_{ - 20}$ = Denitrification rate constant at 20 °C (d⁻¹), $\theta$ = Arrhenius constant microorganism growth temperature coefficient.

Ammonia uptake by microorganisms

In the model, it is assumed that ammonium uptake, i.e., MO (NH₃-N) would take place as long as is available in the lake since autotrophic bacteria prefer it to nitrates. Equation 10 is used to model NH₃-N uptake by microorganisms in the water phase.

$${\text{MO}} \left( {{\text{NH}}_{{3 - {\text{N}}}} } \right) {\text{Uptake}} = \left[ {\left( {u_{\max - 20} } \right){\text{Thita}}^{T - 20} \times \left( {\frac{{{\text{NH}}_{{3 - {\text{N}}}} }}{{K_{3} + {\text{NH}}_{{3 - {\text{N}}}} }}} \right)} \right] \times \left[ {\frac{{{\text{DO}}}}{{K_{2} + {\text{DO}}}}} \right] \times C_{{{\text{pH}}}} \times {\text{NH}}_{{3 - {\text{N}}}} \times P_{1}$$

(10)

where, $\mu_{{{\text{max}} - 20 }}$ = Maximum growth rate of bacteria at 20 °C (d⁻¹), $P_{1}$ = Ammonia uptake preference factor, $K_{3}$ = Ammonia uptake half-saturation constant (g/m³), $Thita$ = Microorganisms growth temperature coefficient.

Nitrate uptake rate by microorganisms

The nitrate uptake is done by autotrophic bacteria but it is assumed that it takes place after all the NH₃-N has been consumed and hence depleted from the system. Equation (11) is used to model the rate of nitrate uptake by microorganisms.

$${\text{MO}} \left( {{\text{NO}}3 - {\text{N}}} \right){\text{ Uptake }} = \left[ {\left( {U_{\max - 20} } \right) \times {\text{Thita}}^{T - 20} \times \left( {\frac{{{\text{NO}}_{3 - N} }}{{K_{4} + {\text{NO}}_{3 - N} }}} \right)} \right] \times \left[ {\frac{{{\text{DO}}}}{{K_{2} + {\text{DO}}}}} \right] \times C_{{{\text{pH}}}} \times P1 \times {\text{NO}}3 - {\text{N}}$$

(11)

$\mu_{{{\text{max}} - 20 }}$ = Maximum growth rate of bacteria at 20 °C (d⁻¹), $P_{1}$ = Nitrate uptake preference factor, $K_{4}$ = Nitrate uptake half-saturation constant (g/m³), $Thita$ = Microorganisms growth temperature coefficient.

Sedimentation rate

The transformation processes considered in the modelling of nitrogen in sediments in the lake system are sedimentation and ammonia–nitrogen regeneration. The organic nitrogen in sediments is mineralized by microorganisms, which ultimately regenerate NH₃-N to the water column. It is assumed that the rate of regeneration (rr) follows the first-order kinetics presented by Eqs. (12) and (13).

$$\frac{\partial S}{{\partial t}} = r_{s} - r_{r}$$

(12)

where, $r_{s} =$ Settling rate of organic-nitrogen to the bed (g/d m⁻²), $r_{r}$ = rate of ammonia regeneration (g/d m.⁻²)

$$r_{r} = r_{{{\text{reg}}}} \times N_{{{\text{sediments}}}}$$

(13)

where, $r_{reg }$. = Regeneration rate constant of ammonia (g/d m⁻²).

Ammonia volatilization

To model the rate of ammonia volatilization, the mass balance Eq. (14) is used.

$$r_{v} = \frac{{\left[ {NH_{3} - N} \right]}}{h} \times KL$$

(14)

where, h = Water depth in m, T = Temperature in °C, KL = Mass transfer coefficient = 0.056 exp (0.13 (T−20).

Model calibration

To run this model, the STELLA software (version 9.0.1) was used. The software has the capabilities to simulate the behaviour of nitrogen transformation in the Lake Bunyonyi system using conservation of mass principles. The mathematical equations presented in subsection 7.5.1 for the mass balance of ammonia–nitrogen, nitrate-nitrogen and organic-nitrogen along with forcing functions were entered in the STELLA software. Data collected from samples obtained from Lake Bunyonyi were used as inputs for the model calibration. These data include monthly averages for NH₃-N, NO₃-N, Org-N, DO, temperature, and pH (of the le system, inflows and outflows), rainfall, solar radiation, water inflows and outflows.

Nutrient mass balance

Total nutrient inflow was computed as the sum of the total volume of water that flows into the lake system multiplied by the concentration of nutrients in water inflows (Eq. 15). Total nutrient outflow was computed as a sum of the total volume of water outflow multiplied by the concentration of nutrients in the water outflows (Eq. 16).

$$Q_{{{\text{in}}}} C_{{{\text{in}}}} = Q_{{{\text{STMS}}}} C_{{{\text{STMS}}}}$$

(15)

$$Q_{{{\text{out}}}} C_{{{\text{out}}}} = Q_{{{\text{STM}}\left( {{\text{out}}} \right)}} C_{{{\text{STM}}\left( {{\text{out}}} \right)}}$$

(16)

To obtain the best values of coefficients, model calibration was performed. The model efficiency criterion by Nash and Sutcliffe (1970) was used to establish the efficiency of the model.

Results

Water inflow and outflow rate

The quantity of water inflow (Q_in) recorded varied from 20,044.80 to 73,612.80 m³/d with a mean value of 39,887.90 ± 22,959.58 m³/d (Fig. 3). The volume of water outflow (Q_out) from the lake ranged from 58,406.40 to 139,276.80 m³/d, obtained in July and March 2020 with the mean value of 103,867.20 ± 34,367.59 m³/d. These values of recorded water inflow and outflow volumes were used as input variables in modelling processes that govern nutrient dynamics in the lake system.

Fig. 3

Mean quantity of water inflow (Q_in) and outflow (Q_out) from Lake Bunyonyi. Error bars represent standard errors

Characteristics of physico-chemical parameters

To fully understand the processes governing nitrogen dynamics in Lake Bunyonyi, the physico-chemical parameters water temperature, pH, DO, NO₃-N, NH₃-N and Org-N were measured both at the inflow and outflow waters. Thereafter, the recorded values were used as inputs in the model. In the inflow waters (Table 1), water temperature varied from 20 to 22.40 °C with a mean value of 20.75 ± 0.94 °C; DO level between 7.10 and 9.70 mg/l/d with a mean value of 7.87 ± 0.93 mg/l/d, and pH values ranged 7.20 and 8.70 with a mean value of 7.90 ± 0.52 was recorded (Table 1). Similarly, nutrients ranged between 0.01 and 0.07 mg/l/d with a mean value of 0.05 ± 0.02 mg/L/d for NH₃-N; NO₃-N values ranged between 0.00 and 0.02 with a mean value of 0.01 ± 0.01 mg/l/d, while Org-N ranged from 0.10 to 2.80 with a mean value of 1.69 ± 1.16 mg/l/d (Table 1).

Table 1 Mean ± SD of the physical parameters measured at inflow and outflow rivers of Lake Bunyonyi (n = 12)

In the outflow waters, the mean value for water temperature was 20.74 ± 0.41 °C, DO ranged between 5.90 and 8.50 mg/l/d with a mean value of 7.39 ± 0.99 mg/l; pH values ranged between 7.00 and 8.20 with a mean value of 7.53 ± 0.43 (Table 2). Similarly, values for Org-N ranged from 0.00 to 1.40 mg/l/d with a mean value of 0.38 ± 0.51 mg/l/d, while NH₃-N and NO₃-N recorded mean values of 0.07 ± 0.03 mg/l/d and 0.02 ± 0.01 mg/l/d, respectively (Table 2).

Table 2 Mean ± SD of the nutrients measured at inflow and outflow rivers of Lake Bunyonyi (n = 12)

Modelling process

Model calibration and validation

Results of the calibration are shown in Table 3 together with some literature values for comparison. These calibrated parameters were used for modelling processes that govern nitrogen transformation and removal from the Lake Bunyonyi system. Figures 4, 5 and 6 depict graphs of simulated and observed NH₃-N, Org-N and NO₃-N, respectively, against time after running a calibrated model with a new data set and the forcing functions to reflect new conditions and to observe how well the model simulations fit the new data set. The simulation results were more or less related to the field data for all nitrogen species. The field data for NH_3-N tend to peak in the second month (April 2020) of data collection, while the model shows a gradual increase which peak in the third month (May 2020) of data collection. Both simulated and field data for NO₃-N slowdown in the second (April 2020) and third month (May 2020) of data collection and later gradually increased in the fifth month (July 2020) (Fig. 5). Both the simulated and measured Org-N data showed a gradual decline during months of data collection.

Table 3 Parameter optimized after model calibration

Fig. 4

Simulated versus Observed NH₃-N

Fig. 5

Simulated versus Observed NO₃-N

Fig. 6

Simulated versus Observed Org-N concentration

The efficiency of the model is demonstrated by Figs. 7, 8 and 9 for the observed and simulated NH₃-N, Org-N and NO₃-N, respectively. The model output showed a good agreement with observed values. The observed R squared values for NH₃-N, Org-N and NO₃-N were 0.62, 0.63 and 0.77, respectively, implying a good agreement between observed and simulated data.

Fig. 7

Linear regression analysis between Observed NH₃-N and simulated NH₃-N

Fig. 8

Linear Regression analysis between Observed Org-N and simulated Org-N

Fig. 9

Linear Regression analysis between Observed NO₃-N and simulated NO₃-N

Nutrient mass balance

Figure 10 depicts the flow of nutrients from one state variable to another. Organic nitrogen whose inflow value was 0.466 g/d m⁻² in the water had 0.000063 g/d m⁻² transported into the sediment phase. Nevertheless, out of this amount, 0.0002 g/d m⁻² was returned to NH₃-N into the water phase through NH₃-N regeneration leaving 0.00062 g/d m⁻², as the actual Org-N which was removed from the water phases through the sedimentation process. Likewise, algae take up 0.0003677 g/d m⁻² of nutrients in form of NO₃-N and NH₃-N for their cellular growth of which 0.00032 g/d m⁻² goes to the sediment through decomposition, leaving 8.85 × 10 ⁻⁹ g/d m⁻²as the actual nitrogen contained in algae cells.

Fig. 10

Nutrient mass balance (g/d m²) of Lake Bunyonyi

In addition, Org-N can as well be converted to NH₃-N through mineralization amounting to 0.49 g/d m⁻². Nevertheless, nitrification transforms 0.0455 g/d m⁻² NH₃-N to NO₃-N and the denitrification process which removes nitrogen from the lake system transforms 0.0795 g/d m⁻² of the total concentration value. The NO₃-N and NH₃-N inflow into the lake system was 0.00318 g/d m⁻² and 0.00012 g/d m⁻², respectively. Out of the total NO₃-N and NH₃-N in the water phase, 0.453 g/d m⁻² is taken up by microorganisms which subsequently transforms back to Org-N, leaving 0.44 g/d m⁻² and 0.008 g/d m⁻² as the actual NH₃-N and NO₃-N concentrations in the lake, respectively (Fig. 10). Based on results, it is evident that mineralization (45.8%), microbial uptake (42.4%), and denitrification (7.4%) were the three main processes responsible for nutrient transformation in the lake (Fig. 11). Other processes such as volatilization, sedimentation, nitrification and uptake by algae were responsible for 0.2% nutrient dynamism in the lake system (Fig. 11). Nutrients from the lake through outflow waters plus reactions account for 18.2% implying that nutrient accumulation accounts for 81.8%.

Fig. 11

Variability of the nutrient transformation processes in Lake Bunyonyi

Model application

The model developed is suitable for freshwater lakes. Its application requires the knowledge of the inflow and outflow concentrations of Org-N, NH₃-N and NO₃-N; the physical parameters: pH, temperature and DO level; the depth of lake; the quantity of inflow and outflow waters. Upon establishment of all the desired information, all the forcing functions, equations, parameters and constants values are entered into the model via the conceptual model (Fig. 2). In STELLA software, the selection of estimation for integration of the differential equations is provided using Runge–Kutta fourth-order Equation because of its low truncation error and fast convergence on given initial values. With the menu in the STELLA software, one can choose any state variable or process to be simulated.

Discussion

Based on the outputs of model calibration, the results revealed a good agreement between observed and simulated data. Related results have previously been observed by Mayo et al. (2018) in wetland systems who reported model coefficients (R²) of 0.54, 0.51 and 0.53 for NO₃-N, Org-N and NH₃-N, respectively. Besides, it can be observed that the model efficiency of the current study was slightly lower than that of Senzia (2003) whose regression value (R²) for NO₃-N was 0.82. These observed slight differences in the model efficiencies can be attributed to differences in the ecosystem setup. Besides, the model developed for the constructed wetland, where the flow was controlled while the current model developed is for uncontrolled environment.

The prominence of mineralization and microbial uptake as the main processes responsible for nutrient transformation in the lake is attributed to somewhat high DO, temperatures and pH that favour the said processes in the lake system. Volatilization was responsible for minimal nitrogen transformation and removal from the lake system perhaps due to average pH of less than 9 which does not encourage ammonia stripping.

The volume of water outflow was 61.6% higher than the water inflow implying that the volume of water in Lake Bunyonyi was not a true reflection of water inflows via rivers and streams. Precipitation and groundwater inflow are presumably the major sources of water in Lake Bunyonyi. The observed temperatures were within ideal ranges for the biological nitrogen transformation processes such as mineralization, denitrification, nitrification and volatilization. Similar temperature range values were obtained by Mayo and Hanai (2014) in a study conducted at the Pilot High Rate Pond in Dar es Salaam, Tanzania. Temperature influences the DO content of water, the rate of photosynthesis by aquatic plants and the metabolic rates of aquatic organisms (Bhateria and Jain 2016). The recorded average pH values are conducive for most biological nitrogen transformation processes including volatilization which requires values not greater than 8.0 (Dari et al. 2019). DO in the inflow and outflow waters of the lake that were greater than 7 mg/l are largely attributed to algal photosynthesis which produces oxygen. Besides, DO levels increased by 6.1% from the concentration level obtained from the inflow waters possibly due to photosynthesis taking place in the lake system. Besides, the level of DO contained in the outflow waters suggests sufficient aeration of the lake to support the biological oxidation of both organic and inorganic pollutants in the lake system.

The NH₃-N and NO₃-N decreased by 25.8% and 50%, respectively, from the inlet to the outlet of the lake system, which indicates high NH₃-N and NO₃-N in nutrient retention, in the lake. The reduction was attributed to uptake by microorganisms (algae and bacteria) and nitrification processes. The process of volatilization was unlikely since it requires pH above 9.4 (Reddy and Graetz 1988; Mayo and Hanai 2014; Dari et al. 2019). NH₃-N uptake by microorganisms was found to be one of the major pathways for NH₃-N reduction because it is a preferred source of nitrogen than nitrate (Neel et al. 1961; Fritz et al. 1979; Mayo and Hanai 2014).

Besides, Org-N concentration decreased by 0.9% from the inflow to the outflow of the system. This is equivalent to an accumulation rate of 99.1% of Org-N concentration from the inflow value of 0.466 to 0.00429 g/d m⁻². On other hand, low retention of Org-N was reported by Mwanuzi et al. (2003) due to the high export of Org-N from the wetlands fringing Lake Victoria. The study results further indicate that volatilization and nitrification processes were responsible for minimal nitrogen removal from the lake system. While the model emphasizes the importance of Org-N in the lake system, its accumulation lowers dissolved oxygen levels and affects the rate of nitrification. Possibly, this explains the observed low rates of nitrification and volatilization.

Conclusion

Based on the study results, we conclude that mineralization, microbial uptake, and denitrification were found to be the major processes that govern nitrogen dynamics in the lake system. Mineralization transforms 0.49 g/d m⁻² to NH₃-N, while nitrification transforms 0.05 g/d m⁻² to NO₃-N, and microbial uptake is responsible for the removal of 0.45 g/d m⁻² (NH₃-N and NO₃-N) from the water phase. Besides, denitrification can transform 0.08 g/d m⁻²of nutrients in the water phase. The developed model shows sensitive parameters that influence the output are Org-N levels, microbial uptake, mineralization rate and maximum growth rate at 20 °C. In addition, ammonia Nitrosomonas half-saturation constant, oxygen Nitrosomonas half-saturation constant, and ammonia Nitrosomonas half-saturation constant influence the model output. Much attention should be paid to the mentioned parameters during modelling to get results that reflect the reality in a lake system. Besides, the developed model will be useful for the prediction of nutrient dynamisms in lakes that share similar characteristics with Lake Bunyonyi.