Abstract
The hydraulic characteristics of the flow are measured using tools such as flumes, in the design and evaluation of furrow irrigation systems. Proper use of these tools, such as their immersion while working, is one of the important executive points in this field; in this study, trapezoidal flumes are used to measure the intensity of input and output flow in furrow irrigation. The proper method of installing these flumes was investigated in this article. For this purpose, during 60 irrigation operations, the results showed that in order to create free flow conditions in these flumes, and not to affect the downstream and upstream current, as well as increasing the accuracy of measurements, in addition to installing flumes in all directions, trapezoidal flume should be installed at a height of at least about 4 cm above the furrow bed; according to the irrigation operations, the percentage of immersion in the installation of the flume at a height of 4 cm from the furrow bed was observed as standard (less than 70% immersion) in order to reduce the percentage of flow measurement error in different depths of water entering the flume. The results also showed that for ensuring free flow in trapezoidal flumes, the flume should be installed at a height of 4 cm or more above the furrow bed, provided the input ridges are strengthened and the end flume is measured to measure the inflow to the furrow. The output current of the furrow should be installed in the floor of the furrow along the bed to prevent the passage of current, provided that after the outflow flume, the furrow bed should be deeper in terms of free flow. Observance of the points and results obtained in this study in furrow irrigation systems prevents errors in flow measurement and consequently increases the accuracy in the design and evaluation of furrow irrigation systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Generalities
Flow measurement in industries, especially in irrigation networks, is a basic need; for example, in surface irrigation, inaccuracy in measuring flow intensity causes error in infiltration calculations (Nafchi et al. 2022; Fattahi Nafchi et al. 2022; Abdollahi et al. 2021; Nafchi et al. 2021; Talebmorad et al. 2021; Salehi-Hafshejani et al. 2019; Vanani et al. 2017; Ostad-Ali-Askar et al. 2018a; Shayannejad et al. 2022; Talebmorad et al. 2020; Trout and Mackey 1988; Ostad-Ali-Askari and Shayannejad 2015). In this regard, management tools such as flow intensity flow-meters have been designed, which are open channels with a special shape and narrowed throat section. They can be made of concrete, metal or fiberglass. There are standard flume designs that can measure discharge over a wide range of flows. The two most commonly used types of flumes are partial flume and trapezoidal flume. Flumes are applied in a smooth, uniform channel, creating a relatively small drop in water head. Flow-meters can accurately measure a wide range of flow. The flume should not be submerged (return water in the throat), and care should be taken in its installation. If the flow is free, by measuring a height at the inlet of the flume, the amount of flow can be measured using the formula governing that flume (Derakhshannia et al. 2020; Eslamian et al. 2018b; Golian et al. 2020; Aminpour et al. 2020). Prefabricated flumes can easily be used in cold regions with frosty winters. The cost of on-site flumes is relatively expensive. The components of a flume are the throat, the convergence and divergence section, the slope of the wall, the scale for measuring the depth of flow in the flume, etc., which must be accurately constructed and applied to measure the flow correctly (Eslamian et al. 2018a; Pirnazar et al. 2018; Ostad-Ali-Askari et al. 2019; Ostad-Ali-Askari et al. 2020a; Li et al. 2020). The name of the flume is determined by the size of the flume with its throat width, for example, 6-inch flume means a flume whose throat width is 6 inches (Larsen 1992).
(Parshall flume)
Today, partial flumes are a common tool in many measurements. This type of standard flume is well known and has been used for decades (Ribeiro et al. 2021). This type of flume was designed by Parshall between 1915 and 1922 (Parshall 1926, 1936). The partial flume has three main components, including the convergent part (upstream), the throat part and the divergent part (downstream) (Fig. 1). According to Fig. 1, the partial flume starts with a convergence at the bottom of the flume, next a downward slope in the throat and then an upward slope in the divergent section. The amount of current can be obtained by measuring the levels of ha and hb. Measuring the effluent flow, lack of particle deposition and consequently reducing the measurement error, reducing the water head drop are among the advantages of using partial flume, which is mostly due to their special shape (Fig. 1) (Anonymous 1974 and 1981).
Trapezoidal flume
Specifications
A new type of flume was built with high measurement accuracy with the advantages of previous flumes. They are easier to make than partial flume. Throat width in these flumes is zero and measures low currents; for example, they are used in furrow irrigation. The similarity of the shape of this flume with the cross sections of the field has made them more used in the fields. The shape of the trapezoidal flume is such that its sides diverge from the floor of the flume to its surface relative to each other; therefore, it transmits more current than the partial flume, which is not the case (comparison of Figs. 1 and 2). The condition for using flumes is less than 70% submerged current, i.e., no upstream current does not affect the measurements. In trapezoidal flume, this percentage is higher than partial flume and above 80%, and therefore without using a correction factor (which should be used for reporting) flow rate can be shown with very little error (Ostad-Ali-Askari et al. 2021a; Ostad-Ali-Askari et al. 2017b; Ostad-Ali-Askari et al. 2020b; Ostad-Ali-Askari 2022b; Ostad-Ali-Askari et al. 2018b; Walker and Skogerboe 1987).
Installing trapezoidal flume
The installation method of trapezoidal flumes is similar to the partial flume and should be level in both longitudinal and transverse directions. However, if this flume is used on a sloping surface, the maximum allowable slope for installation should be observed, and the numbers read on the slope should be corrected according to the correction of the number zero on the slope; the depth of the flow (h1) is the height of the inlet cross-section floor to the flow surface. The depth h1 is measured to measure the flow rate, then placed in a formula for which the flow has already been calibrated and afterward the flow rate is measured. This formula is derived from the equation of energy and the equation of continuity (Dabrowski and Polak 2012). According to the mentioned cases, installing a trapezoidal flume depends on the slope of the channel if the maximum allowable slope is observed (mostly 0.0035 m/m or critical slope) the floor of the flume with the floor of the channel can be the same from the bottom of the canal. It is worth noting that the inlet of the flume is installed in such a way as to create a free flow, which requires the installation of a flume at a suitable height above the floor of the canal. If there is no free flow in the trapezoidal flume and the ratio of water depth at the outlet of the flume (h4) to water depth at the inlet of the flume (h1) (Fig. 2) is 80% or more, i.e., the upstream flow affects the downstream, the correction factor is used to calculate the current intensity (Fig. 3).
Considering the importance of the correct method of installing trapezoidal flume and the few scientific resources that exist in irrigation, especially furrow irrigation, in this article, the correct method of using trapezoidal flumes in furrow irrigation systems is examined. Providing the correct method for installing this flume creates free flow conditions. As a result, accurate flow measurement is one of the requirements for accurate infiltration calculation and consequently accurate design and evaluation of furrow irrigation systems (Fatahi Nafchi et al. 2021; Ostad-Ali-Askari et al. 2021b; Ostad-Ali-Askari 2022a; Ostad-Ali-Askari et al. 2021c).
Methods and materials
In this research, WSC type 2 trapezoidal flume was used in order to achieve the correct method of using trapezoidal flume and in furrow irrigation systems, and the experiments were repeated during 60 furrow irrigation operations finally the results were reviewed. The purpose of this article is to create non-submersible flow conditions with proper installation of this flume. Furrow irrigation operations were performed on farms located in Isfahan-Iran University of Technology. The length, width and depth of these furrows were 42 m, 60 and 20 cm, respectively, and the slope was 0.1% (with the maximum allowable slope). In these irrigation operations, a flume at the beginning of the furrow to measure the inflow and a flume at the end of the furrow to measure the output flow (using the calibrated formula in Table 1) were installed evenly in all directions. Therefore, this type of flume was installed 120 times in different ways and the flow was examined. Also, the soil around pounded and the flume was installed in this regard in order to prevent the flow of leakage around the flume. In all operations, in cases where free flow and submerged current were established, all the conditions for installing the flume, including the installation depth, etc., were recorded.
WinFlume software was also used to simulate the test conditions. The calculations required to calibrate the flume, determine its size and deploy it can be used by utilizing this software. The maximum and minimum error rates between the simulated discharge by this software and the actual measured discharge are 5% and 25%, respectively, and the average error is 13%. This model estimates the discharge more than the reality. The higher the flow rate through the flume, the lower the error. Also, the higher the sill height, the closer the flow in the gorge to the critical flow if the upstream and downstream slopes of the flume floor are equal (Wahl 2001).
Results and discussion
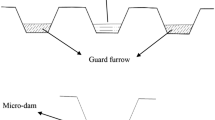
The results of 120 trapezoidal flume installations during various irrigation operations in this study showed that non-submersible flow occurs in this flume when the flume is installed at a height of at least about 4 cm from the bottom of the furrow. Because the allowable immersion percentage is less than 80% in this case. The flow will be measured with good accuracy (Fig. 4). Irrigation operations showed that the walls of the furrow should be hammered and tightened before installing the inflow (Fig. 4) in order to ensure the accuracy of measuring the inflow to the furrow in the primary flume, in addition to the above conditions, and the height of the walls should be increased as much as possible. Also, in the end flume to measure the output flow from the groove, the bottom of the flume should be the same as the bottom of the groove due to the blockage of the flow to pass, especially at the beginning of the flow time to the flume, which causes errors in calculations. Upon reaching it, the current is easily transferred from the bottom of the furrow to the bottom of the flume and passes easily through it. This should be done under the condition that the furrow surface should be at least 2 m deeper after the installation site to ensure non-submersible flow in the outlet flume.
The trapezoidal flume used in WinFlume software was simulated to further investigate and simulate irrigation operations. The results of modeling the existing flume (WSC flume type 2) by WinFlume software were as follows:
In this section, the percentage of immersion, which is the ratio of water height upstream and downstream, can be obtained. The above steps (Figs. 5, 6, 7 and 8) were for the height of 3.5 cm of flume floor from the furrow (sill height = 3.5 cm) repeated for different heights such as 3 cm and 4 cm and the percentage of immersion in the heights. Different water levels were obtained and compared. Table 2 is prepared for this purpose.
The results show that in sill height = 4 cm, the percentage of immersion is less than other installation heights, which indicates the accuracy of the results of field operations in this study. Also the higher the inlet flow rate (higher altitude), the higher the immersion percentage at a certain height.
The values of error percentage resulting in flow estimation by WinFlume software to the actual flow rate (measured by flume according to its formula) are shown in Table 3 based on the discharge operating range in the experiments of this study for flume.
The results showed that the higher the flow depth, the higher the software measurement error and the average measurement error at 3.5 and 4 cm flume floor heights is similar to the furrow and slightly lower at 4 cm depth; this shows the correct expression of the test results by WinFlume software.
Conclusions and recommendations
For this purpose, during 60 irrigation operations, the results showed that in order to create free flow conditions in these flumes, and not to affect the downstream and upstream current, as well as increasing the accuracy of measurements, in addition to installing flumes in all directions, trapezoidal flume should be installed at a height of at least about 4 cm above the furrow bed; according to the irrigation operations, the percentage of immersion in the installation of the flume at a height of four centimeters from the furrow bed was observed as standard (less than 70% immersion) in order to reduce the percentage of flow measurement error in different depths of water entering the flume. The results also showed that for ensuring free flow in trapezoidal flumes, the flume should be installed at a height of four centimeters or more above the furrow bed, provided the input ridges are strengthened and the end flume is measured to measure the inflow to the furrow. The output current of the furrow should be installed in the floor of the furrow along the bed to prevent the passage of current; provided that after the outflow flume, the furrow bed should be deeper in terms of free flow. Observance of the points and results obtained in this study in furrow irrigation systems prevents errors in flow measurement and consequently increases the accuracy in the design and evaluation of furrow irrigation systems.
Based on field experiments and simulations performed in this research, it is recommended that the WSC flume type 2 can be installed at least 4 cm from the bottom of the furrow to work in free-flow mode in furrow irrigation. It should be noted that the flow conditions for this result are the inlet flow to the furrow about one liter per second and the maximum allowable slope (0.0035 m per meter) and by pounding and strengthening the wall of the furrow at the inlet. This flume should be installed in the bottom of the furrow to create free flow conditions and also not to prevent it from passing, and in a few meters after installing this flume, conditions should be created in the bottom of the furrow so that the flow does not return to the flume. Obviously, the installation height of the boats varies according to the flow conditions. It is suggested to increase the accuracy of the studies, the appropriate method of using tools for this purpose before each test with respect to the importance of field measurements and the problems of their determination. Also tools are simulated, designed and calibrated by WinFlume, Flow3D to increase the accuracy of the experiments.
Data availability
All the data, including the experimental measurements, the data used for formulating empirical relations, and the code processing the data that support the findings of this study, are available from the corresponding author upon reasonable request.
References
Aminpour Y, Vatankhah AR, Farhoudi J (2020) Experimental modeling of flumes with two semi-cylinder contractions (free and submerged flows). Flow Meas Instrum 76:101844. https://doi.org/10.1016/j.flowmeasinst.2020.101844 (ISSN 0955-5986)
Anonymous. Water measurement manual, 2nd edn. Revised, reprinted 1974–reprinted 1981, United States department of the interior, Denver, p 327
Dabrowski W, Polak U (2012) Improvements in flow rate measurements by flumes. J Hydraul Eng ASCE 138(8):757–763. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000567
Eslamian S et al (2018a) Saturation. In: Bobrowsky P, Marker B (eds) Encyclopedia of Engineering Geology. Encyclopedia of Earth Sciences Series. Springer, Cham. https://doi.org/10.1007/978-3-319-12127-7_251-1
Eslamian S et al (2018b) Water. In: Bobrowsky P, Marker B (eds) Encyclopedia of Engineering Geology. Encyclopedia of Earth Sciences Series. Springer, Cham. https://doi.org/10.1007/978-3-319-12127-7_295-1
Hamid Raeisi V, Mohammad S, Ali Reza ST, Ostad Ali Askari K, Saeid E, Mohri-Esfahani E, Haeri-Hamedani M, Hossein J (2017) Development of a new method for determination of infiltration coefficients in furrow irrigation with natural non-uniformity of slope. Sustainable Water Resour Manage 3(2):163–169. https://doi.org/10.1007/s40899-017-0091-x
Hossein T, Abdollah A, Saeid E, Ostad Ali Askari K, Singh VP (2020) Evaluation of uncertainty in evapotranspiration values by FAO56-Penman-Monteith and Hargreaves-Samani methods. Int J Hydrol Sci Technol 10(2):135. https://doi.org/10.1504/IJHST.2020.106481
Hossein T, Jahangir A, Koupai S, Eslamian S, Farhad M, Samira A, Ostad Ali Askari K, Singh VP (2021) Evaluation of the impact of climate change on reference crop evapotranspiration in Hamedan-Bahar plain. Int J Hydrol Sci Technol 11(3):333. https://doi.org/10.1504/IJHST.2021.114554
Khosronejad A, Herb W, Sotiropoulos F, Kang S, Yang X (2021) Assessment of Parshall flumes for discharge measurement of open-channel flows: a comparative numerical and field case study. Measurement 167:108292. https://doi.org/10.1016/j.measurement.2020.108292 (ISSN 0263-2241)
Larsen DC (1992) Water measurement. University of Idaho. College of agriculture. 49:11–17
Li X, Jin L, Engel BA, Yang Z, Wang W, He W, Wang Y (2020) Influence of the structure of cylindrical mobile flumes on hydraulic performance characteristics in U-shaped channels. Flow Meas Instrum 72:101708. https://doi.org/10.1016/j.flowmeasinst.2020.101708 (ISSN 0955-5986)
Mohsen G, Homayoon K, Singh VP, Ostad-Ali-Askari K, Hamed T R (2020) Prediction of tunnelling impact on flow rates of adjacent extraction water wells. Q J Eng Geol Hydrogeol 53(2):236–251. https://doi.org/10.1144/qjegh2019-055
Mojtaba P, Hafez H, Arash ZK, Ostad Ali Askari K, Zahra G, Majedeh H, Hamedani E, Mohri E, Saeid E (2018) The evaluation of the usage of the fuzzy algorithms in increasing the accuracy of the extracted land use maps. Int J Global Environ Issues 17(4):307. https://doi.org/10.1504/IJGENVI.2018.095063
Mehdi D, Shahab D, Behrouz A, Ostad Ali Askari K (2020) Corrosion and deposition in Karoon River Iran based on hydrometric stations. Int J Hydrol Sci Technol 10(4):334. https://doi.org/10.1504/IJHST.2020.108264
Ostad-Ali-Askari K, Shayannejad M (2015) Developing an optimal design model of furrow irrigation based on the minimum cost and maximum irrigation efficiency. Int Bull Water Resour Dev 3(2):18–23
Ostad Ali Askari K, Mohammad S, Ghorbanizadeh-Kharazi H (2017a) Artificial neural network for modeling nitrate pollution of groundwater in marginal area of Zayandeh-rood River Isfahan Iran. KSCE J of Civil Eng 21(1):134–140. https://doi.org/10.1007/s12205-016-0572-8
Ostad Ali Askari et al (2017b) Deficit irrigation: optimization models. management of drought and water scarcity. Handb Drought Water Scarcity, vol 3. Taylor & Francis, Imprint: CRC Press, pp 373–389. eBook ISBN: 9781315226774. 1st Edn. https://doi.org/10.1201/9781315226774
Ostad Ali Askar K, Ruidan Su, Limin Liu (2018a) Water resources and climate change. J Water Climate Change 9(2):239–239. https://doi.org/10.2166/wcc.2018.999
Ostad Ali Askari K, Mohammad S, Saeid E, Bahareh N (2018b) Comparison of solutions of Saint-Venant equations by characteristics and finite difference methods for unsteady flow analysis in open channel. Int J Hydrol Sci Technol 8(3):229. https://doi.org/10.1504/IJHST.2018.093569
Ostad Ali Askari K, Hossein GK, Mohammad S, Mohammad JZ (2019) Effect of management strategies on reducing negative impacts of climate change on water resources of the Isfahan-Borkhar aquifer using MODFLOW. River Res Appl 35(6):611–631
Ostad Ali Askari Hossein K, Ghorbanizadeh K, Mohammad S, Mohammad JZ (2020a) Effect of climate change on precipitation patterns in an arid region using GCM models: case study of isfahan-borkhar plain. Nat Hazards Rev 21(2). https://doi.org/10.1061/(ASCE)NH.1527-6996.0000367
Ostad Ali Askari K, Mohammad S (2020b) Impermanent changes investigation of shape factors of the volumetric balance model for water development in surface irrigation. Model Earth Syst Env 6(3):1573–1580
Ostad Ali Askari K, Mohammad S (2021a) Quantity and quality modelling of groundwater to manage water resources in Isfahan-Borkhar Aquifer. Environ Dev Sustain 23(11):15943–15959
Ostad Ali Askari K, Mohammed S (2021b) Subsurface drain spacing in the unsteady conditions by HYDRUS-3D and artificial neural networks. Arab J Geosci 14(18). https://doi.org/10.1007/s12517-021-08336-0
Ostad Ali Askari K, Mohammad S (2021c) Computation of subsurface drain spacing in the unsteady conditions using Artificial Neural Networks (ANN). Appl Water Sci 11(2). https://doi.org/10.1007/s13201-020-01356-3
Ostad Ali Askari K (2022a) Developing an optimal design model of furrow irrigation based on the minimum cost and maximum irrigation efficiency. Appl Water Sci 12(7). https://doi.org/10.1007/s13201-022-01646-y
Ostad Ali Askari K (2022b) Management of risks substances and sustainable development. Appl Water Sci 12(4). https://doi.org/10.1007/s13201-021-01562-7
Parshall RL (1926) The improved venture flume. Trans ASCE 89(1):841–851
Parshall RL (1936) The Parshall measuring flume, Bull. Agric. Experiment Station, Fort Collins (Colorado), p 423
Ribeiro AS, Sousa JA, Simões C, Martins LL, Dias L, Mendes R, Martins C (2021) Parshall flumes flow rate uncertainty including contributions of the model parameters and correlation effects. Meas Sens 18:100108. https://doi.org/10.1016/j.measen.2021.100108 (ISSN 2665-9174)
Robinson AR (1966) Water measurement in small irrigation channels using trapezoidal flumes. Trans ASAE 9(3):0382–0385. https://doi.org/10.13031/2013.39986
Robinson AR (1968) Trapezoidal flumes for measuring flow in irrigation channels. Agric Res Serv. USDA ARS 41–140
Rouhallah F, Nafchi H, Samadi-Boroujeni H, Raeisi V, Ostad-Ali-Askari K, Milad KB (2021) Laboratory investigation on erosion threshold shear stress of cohesive sediment in Karkheh Dam. Environ Earth Sci 80(19). https://doi.org/10.1007/s12665-021-09984-x
Rouhallah F, Nafchi P, Yaghoobi H, Reaisi V, Ostad Ali Askari K, Jafar N, Bizhan M (2021) Eco-hydrologic stability zonation of dams and power plants using the combined models of SMCE and CEQUALW2. Appl Water Sci 11(7). https://doi.org/10.1007/s13201-021-01427-z
Rohallah F, Nafchi H, Raeisi V, Kobra N, Pashaee H, Samadi B, Ostad Ali Askari K (2022) Investigation on the effect of inclined crest step pool on scouring protection in erodible river beds. Nat Hazards 110(3):1495–1505. https://doi.org/10.1007/s11069-021-04999-w
Rouhallah F, Nafchi P, Yaghoobi H, Raeisi V, Ostad Ali Askari K, Jafar N, Bizhan M (2022) Correction to: Eco-hydrologic stability zonation of dams and power plants using the combined models of SMCE and CEQUALW2. Appl Water Sci 12(4). https://doi.org/10.1007/s13201-021-01563-6
Sara A, Meysam M, Ostad Ali Askari K (2021) Monitoring and investigating dust phenomenon on using remote sensing science geographical information system and statistical methods. Appl Water Sci 11(7). https://doi.org/10.1007/s13201-021-01419-z
Saeid SH, Mohammad S, Hossein SB, Ali R, Zarraty B, Soltani EM, Esfahani MH, Hamedani SE, Ostad Ali Askari K (2019) Determination of the height of the vertical filter for heterogeneous Earth dams with vertical clay core. Int J Hydrol Sci Technol 9(3):221
Shayannejad M, Ghobadi M, Ostad-Ali-Askari K (2022) Modeling of surface flow and infiltration during surface irrigation advance based on numerical solution of saint–venant equations using preissmann's scheme. Pure Appl Geophys 179(3):1103–1113. https://doi.org/10.1007/s00024-022-02962-9
Trout TJ, Mackey BE (1988) Inflow-outflow infiltration measurement accuracy. J Irrig Drain Eng ASCE 114(2):256–265
Wahl TL. 2001. User’s manual of WinFlume software version 1.05, September 2001. U.S. Bureau of Reclamation Water Resources Research Laboratory, D-8560 P.O. Box 25007 Denver, Colorado 80225–0007. http://www.usbr.gov/wrrl/winflume
Walker WR, Skogerboe GV (1987) Surface irrigation: theory and practice. Prentice-Hall, Englewood Cliffs, New Jersey, p 386p
Acknowledgements
Not applicable.
Funding
The authors received no specific funding for this work
Author information
Authors and Affiliations
Contributions
All authors designed the study, collected data, wrote the manuscript and revised it.
Corresponding author
Ethics declarations
Conflict of interest
There is no conflict of interest.
Consent to publish
All authors agree to publish this manuscript. There is no conflict of interest.
Ethical approval
The present Study and ethical aspect was approved by Department of Water Engineering, Shahrekord University, 88186-34141, Shahrekord, Iran and Department of Irrigation, College of Agriculture, Isfahan University of Technology, 8415683111, Isfahan, Iran.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vanani, H.R., Ostad-Ali-Askari, K. Correct path to use flumes in water resources management. Appl Water Sci 12, 187 (2022). https://doi.org/10.1007/s13201-022-01702-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-022-01702-7