Introduction

The difficulty to access water has become one of the fundamental issues globally through the twenty-first century (Gleeson et al. 2012; Elbeltagi et al. 2021). Most of the readily available fresh water on the earth’s surface is used up by the agricultural sector. The amount of water withdrawn from the surface of the earth in developing countries is estimated as ~ 81%, while the same is ~ 71% globally. Furthermore, irrigation plays a major role in the consumption of not less than 55% of the world’s freshwater reserves (Amarasinghe and Smakhtin 2014). Being able to provide food for the world’s population has become a conundrum amidst freshwater scarcity (Fischer et al. 2007; Shukla et al. 2021). Heightened demand for the limited water resources under rising climate change impacts and certain agricultural commodities have constantly hinted upon the need for ways to devise efficient use of the existing water resources at our fingertips. This will also require smart distribution of limited water resources in terms of appropriate time and through the right channel toward premium food production (Dhillon et al. 2019; Kushwaha et al. 2016). Gaining knowledge of the biophysical processes included in the uptake of water through the root zone of the soil and the processes of transpiration through the plant canopy has become essential. The sustenance of the development of irrigation and its processes depends on these aforementioned mechanisms. Hence, it becomes necessary to develop abilities for determining the precise amount of water requirements for an effective irrigation schedule (Rossini et al. 2013; Kushwaha et al. 2021). Reference evapotranspiration (ET0) is regarded as the principal component of the global hydrological cycle which has a direct effect on the yield of crops, water requirements, irrigation facilities, future plannings, as well as the management of water resources. It is considered as the aggregate term that combines the removal of water from the vegetative surface, which contains enough moisture, and the evaporation from the catchment surfaces. Certain factors such as certain management activities, characteristics of crops, condition of the weather, land type, and operations on the field are the major constituents that impact the process of ET0 (Sherma 2016). A substantially uniform field of alfalfa (commonly known as grass) is utilized worldwide for the reference surface. The properties of a reference surface crop include uniform height, soil properties, a specified amount of applied water, and the full growth of the crop in relation to at a certain period under the standard meteorological and agronomic conditions (Łabędzki et al. 2011).

Being able to estimate ET0 is paramount in the crop irrigation requirements at the regional and global scale as well as the preparation of water budget and also in the influence of the various climatic changes (Nouri et al. 2013; Vishwakarma et al. 2022). The further assessment of ET0 is of the essence in the fields of agro-meteorology and hydro-meteorology. In reference to Lu et al. (2010) and Zhao et al. (2013), serious challenges have been encountered in the accurate assessment of ET0 as a result of imperceptible processes exclusively in an ecosystem or a watershed spatial scale with the desired level of accuracy. In lieu of ET0 being a biophysical process that provides ample challenges on the land surface, the need for varying techniques and hydrological models was invented to assist in the estimation of ET0. As such, an accurate measurement of the ET0 plays other major roles which are not limited to just the study of climate change and in the assessment of water resources, but also toward effectively monitoring and providing adequate forecast on drought as well as in the proper use and growth of water resources (Zhao et al. 2013). As studied by (NOURI et al. 2013), the ET0 computation process has a profoundly high level of desirability in its impact on climate change, simulating and predicting crop water scheduling, in hydrological modeling (HM), and in situations of poor data situation and how it affects land use.

An accurate estimation of the ET0 values is essential to the estimation of the soil water balance; this, in turn, depicts the measure of water held within the body of the soil and can be related to checkbook balancing processes. In most cases, the function of the irrigation processes is to oversee the content of the soil water in other to promote proper development. Good irrigation planning and management are enhanced by determining the soil water balance, and hence, the process is of paramount importance. Knowing the soil’s water balance helps negate the risk associated with applying excessive water which enhances percolation and overflow. Irrigation scheduling is defined as the proper amount of water being applied at the appropriate period, and it is impossible without bearing knowledge of the water balance. There are varying methods and techniques applicable to estimate ET0, and they include indirect, direct, and machine learning models (Karimaldini et al. 2011).

The best choice for direct measurement of ET0 is by using lysimeters. However, it is a cumbersome field experimentation that is less time-efficient and expensive. In addition, the method is also not considered to be viable due to the lack of precision in its planning, while the indirect and soft computing models over the years have gathered importance in the estimation of ET0 from climate and meteorological data. The indirect methods utilized for estimating or calculating of ET0 include (1) empirical and semi-empirical equations, (2) pan evaporation methods, (3) energy budget methods, (4) mass transfer equations, (5) combination equations, and (6) radiation-based methods. Further information on indirect methods can be found in McMahon et al. (2013). In addition, empirical and semi-empirical equations based on the premise of Priestly–Taylor and Penman–Monteith methods (Vinukollu et al. 2011) have been widely adopted for estimation of ET0.

Coherently, one of the most widely accepted and well-known indirect methods for ET0 estimation has been introduced by the Food and Agriculture Organization (FAO) of the United Nations (Allen et al. 1989, 1994). The method includes the infusion of the Penman–Monteith equation which was modified and reformed by Allen et al. (1998) as a reference equation (FAO-PM56). This equation (FAO-PM56) is built on the premise that it has certain factors, such as various climatic, aerodynamic, and surface resistance parameters, which it control and influence them. They include (in terms of minimum and maximum magnitude) air temperature, relative air humidity, wind speed, solar radiation, saturation vapor pressure deficit, slope vapor pressure curve, and psychometric constant. Most weather stations are known to suffer anomalies to air temperature. The reliability and completion of other variables cannot be trusted in many locations (Rahimikhoob 2010). However, this might not be a valid case for developed countries, even though it comes across as a big challenge in developing countries where the integrity of the quantity and quality of data cannot be assured. According to Trajkovic and Kolakovic (2009), there are limitations to the reliability of weather datasets of radiation, relative humidity, and wind speed in developing countries. The need for geographic data (latitude, longitude, altitude) becomes essential for an adequate local adjustment of the different weather parameters. Such weather parameters are atmospheric pressure, extra-terrestrial radiations (Ra), and daylight hours (N) in the FAO-PM56 equation. Furthermore, the field measurement efforts and the experimental approaches used are not time-effective or even labor-intensive for the post-processing output processes. As a result, it is quite difficult to formulate the ET0 equation to overcome these effects that can produce reliable and verified results (Gavilan et al. 2007).

The modernization and invention of machine learning algorithms are making it easier to tackle nonlinear processes (ET0) in various disciplines (Kumar et al. 2011). The major problem associated with the estimation of ET0 is its nonlinear dynamic and high complexity nature. Instead of this, machine learning algorithms provide an essential alternative for ET0 estimation. The functionality of these algorithm works on the principles associated with the computational intelligent system which aims to eradicate imprecision and vulnerability in producing results. The proficiency associated with dealing with complex problems makes these methods well accepted. More so, there is the added superiority of using these methods to deal with complex problems using just a set of available data (Ibrahim 2016).

Currently, machine learning models, based on robust algorithms, are applied in mapping nonlinear processes, using input and output (target) variables. Raza et al. (2021a, b) reviewed ET0 estimation based on accuracy, structure, and its usefulness for the study period 2012–2020. The primary objective of the reported researches was to develop an alternative soft computing model against FAO-PM56 against the limitation of requiring large quantity of climate data as input and limited availability of such data in the public domain across developing countries. The study found that designing soft computing models using all the usable data is not effective (similar to FAO-PM56). Besides, limited studies are available that aimed for the development of a generalized ET0 model for the accurate ET0 estimation in all stations within an area (Raza et al. 2021a, b). This becomes significant in the case of developing countries where climate data from most stations are either missing or not available due to technical issues and lack of technology. Thus, the development of ET0 model with fewer climatic inputs (e.g., temperature data) is mainly requisite. For this purpose, different types of machine learning algorithms were developed in ET0 modeling, for example, support vector machine (SVM) (Kisi and Imen 2009; Kushwaha et al. 2021; Mehdizadeh et al. 2017; Ferreiraand and Cunha 2020), least square support vector machine (Kisi 2013; Guo et al. 2011), genetic programming (Traore et al. 2016; Valipour et al. 2019; Mattar 2018), extreme learning machine (ELM) (Shamshirband and Kamsin 2016; Abdullah et al. 2015), tree-based models (Raza et al. 2021a, b) such as M5 model tree (Fan et al. 2018a, b; Granata 2019), random forest (Feng et al. 2017a, b; Fang et al. 2018; Saggi and Jain 2019), and extreme gradient boosting (XGBoost) (Ferreira and Cunha 2020; Fan et al. 2018a, b; Han et al. 2019), artificial neural networks (ANNs) (Torres et al. 2011; Tang et al. 2018; Walls et al. 2020), and adaptive neuro-fuzzy inference system (ANFIS) (Nourani et al. 2019; Tabari et al. 2013).

In recent studies, data intelligence and hybrid metaheuristic algorithms have been applied in ET0 estimation on New Delhi and Ludhiana stations located in north India due to its capability of detecting patterns and changes in time-series data (Kushwaha et al. 2021). Moreover, these algorithms can also grab series data without discretization. The perfect handling of time-series data makes their use successful in various engineering problems, especially ET0 estimation. Wu et al. (2021) conducted a study on ET0 estimation in south China and applied ELM in combination with a clustering approach. The study recommended using proposed machine learning models in ET0 estimation. Roy et al. (2021) estimated ET0 using the ANFIS model along with various algorithms in combination and concluded that hybrid models outperformed single machine learning models. Similarly, Ahmadi et al. (2021) compared ET0 estimation with novel data intelligent models and another commonly used genetic expression programming (GEP) and SVM single machine learning model. The study concluded that the proposed novel data intelligent model in combination with SVM has outperformed and found best in comparison with the empirical model. Sattari et al. (2021) applied five data intelligent machine learning models for estimating ET0 using several input meteorological combinations and found that combining machine learning (hybrid) models increase predictive ability in results. Malik et al. (2019) estimated ET0 using five machine learning models using different meteorological input combinations and concluded that accuracy in results and efficiency can be increased by using hybrid machine learning models. It can be inferred from aforesaid studies that data intelligent and hybrid metaheuristic machine learning algorithms are recommended in ET0 modeling and can be considered the best alternative to conventional FAO-PM56 equation. Thus, this study applied five data intelligent and hybrid metaheuristic machine learning algorithms, namely additive regression (AR), AR-bagging, AR-random subspace (AR-RSS), AR-M5P, and AR-REPTree, for estimating monthly mean daily ET0. Coherently, the contributions of the current study in scientific literature are as follows: (1) developing and evaluating the potential of AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree in ET0 estimation; (2) determining effective meteorological input combination by performing sensitivity analysis; and (3) investigating best performing hybrid data intelligent and hybrid metaheuristic machine learning algorithms based on different standard statistical indices.

Materials and methods

Study area, data preparation, and preprocessing

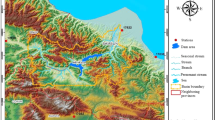
The study area is comprised of two stations, namely Faisalabad and Islamabad of Pakistan located in semi-arid climatic regions based on aridity and continentality indices as found in Raza et al. (2021a, b). Climatic parameters of maximum and minimum temperature (Tmax, Tmin, °C), an average of the maximum and minimum relative humidity (RHavg, %), average wind speed of 24 h at 2 m height (U, km/day), and sunshine hours (N, h) are obtained from Pakistan Meteorological Department (PMD), Lahore, Pakistan. The data duration for each station is from 1987 to 2016. The geographical location of the study area is shown in Fig. 1. In addition, properties of geographic parameters such as latitude (Lat), longitude (Lon), altitude (Alt), and an average of each meteorological variable for both climatic stations are presented in Table 1. It can be observed from Table 1 that mild temperature was recorded for Faisalabad and Islamabad (semi-arid climate). However, wind speed for Faisalabad station is recorded highest (386.28 km/day) among all the selected stations due to its geographical position. Also, severe types of the thunderstorm were observed every year due to western cold wind direction. Further, it has humid summer and dry winter seasons. The statistical values of each meteorological variable used in the training and testing of machine learning algorithms are also presented in Table 1.

Fig. 1
figure 1

Location map of the study stations

Full size image
Table 1 Parameter of the selected algorithms
Full size table

Methodology

Regression and sensitivity analysis for best input combination

The performance of the combination of different input variables on model outputs is identified by conducting sensitivity analysis coupled with regression algorithm−based analysis. In machine learning, the regression is preferably calculated by an algorithmic process that results in the estimation of the value of a numerical dependent variable (the output). For example, standard statistics, such as coefficient of regression and root mean square error, are used for evaluating sensitivity, while regression analysis was based on statistics, such as mean absolute error, relative absolute error, and root-relative mean square error, apart from using root mean square error and correlation coefficient. This is discussed in depth in Sect. 2.3.

The present study has employed the three scientific tools for testing the models, thereby selecting the best model, viz. (1) MATLAB 9 (MathWorks Inc., Natick, MA, USA) used for validating the regression algorithms; (2) R 3.4 (R Foundation, Vienna, Austria) used for testing the algorithms based on regression trees; and (3) Weka 3.8.1 (The University of Waikato, Hamilton, New Zealand) containing different types of decision trees used for conducting linear regression, k-nearest neighbors, Bayes networks, logistic regression, K* algorithm, locally weighted learning, rule-based methods, etc.

Additive regression (AR)

In recent years, Bayesian additive regression trees (BART), which are a flexible prediction machine learning approach, have gained popularity among the research community due to their widespread applications (Sparapani et al. 2021; Tan and Roy 2019). This study has used BART for additive regression using MATLAB. This study has a continuous outcome for ET0 (say y) and p covariates x = (x1, …, xp). The BART model, which aims for the prediction, can define complex relations between the aforesaid x and y by estimating f(x) from models of the form y = f (x) + ε, where ε ∼ N(0, σ2). Further, a sum of m regression trees is used, i.e., f(x) = ∑ g (x; Tj, Mj) ranging between j = 1 and j = m which allows estimation of f(x). The expression for BART is shown in Eq. 1.

$$ y = f\left( x \right) + \varepsilon = \mathop \sum \limits_{j = 1}^{m} g\left( {x;T_{j} ,M_{j} } \right) + \varepsilon. $$
(1)

Bagging

Bootstrap aggregation or bagging is generally employed to decrease variance within a noisy dataset. It follows the ensemble learning method such that when an algorithm overfits (high variance and low bias) or underfits (low variance and high bias) to its training set, ensemble methods can then account for the generalization of the model to new datasets (Breiman 1996). Considering this, in the present study, a random sample of data in a training set was selected with replacement. This allowed the selection of individual data points more than once; however, the models so generated were weak because, on an individual level, its performance may not be significant due to high variance or high bias. Post-generation of several data samples, these weak models were then trained independently, given regression and classification. In general, the aggregation of these weak models allowed reducing biases and variances, thereby yielding improved model performance.

Random Subspace (RSS)

The random subspace (RSS) ensemble is a machine learning algorithm introduced by Ho (1998). The algorithm combines multiple classifiers and their outputs (predictions) from multiple decision trees via a voting approach. It has overcome one of the critical shortcomings of traditional decision trees (Lasota et al. 2013). This has been achieved by addressing the decision-making tree classifier overfitting issue (i.e., high variance and low bias). Further, it ensures that the precision of the training results remained protected. Skurichina and Duin (2002) classified inputs of the RSS algorithm into four categories, viz. (1) training dataset (Tx), (2) base classifier (Cw), (3) size of subspaces (SL), and (4) number of subspaces (Sds). In general, the procedure follows selecting a random subset of input features (columns) for each model in the ensemble and thereby fitting the model on the model in the entire training dataset. It can be implemented using bootstrap or random sample (rows) in the training dataset.

M5P

Quinlan (1992) introduced the M5 algorithm which was further reconstructed to develop the M5P model tree. This integrates the traditional decision tree with the linear regression function. Wang and Witten (1996) described the four steps in the M5P algorithm, viz. (1) splitting of input spaces; (2) developing a linear regression model; (3) pruning process; and (4) smoothing process. Besides, the M5P algorithm has been recognized as a robust algorithm due to its greater efficiency while dealing with missing data problems. Since M5P can efficiently handle and process large datasets so as to ensure reduced errors in the output, this study has considered it for analyzing and predicting the ET0 process in the study area.

The present study acquired information about the splitting criteria for the M5P model tree based on the error calculated at each node. (Linear regression functions are assigned on terminal nodes.) The standard deviation of the class values is used for analyzing the error at each node. The attribute at each node is tested so as to select a particular attribute for splitting. This selection is majorly driven by determining the attribute that maximizes the expected error reduction, which can be obtained by standard deviation reduction (SDR), as shown in Eq. 2.

$$ {\text{SDR}} = {\text{SD}}\left( A \right)\mathop \sum \limits_{1}^{i} \frac{{\left| {A_{i} } \right|}}{\left| A \right|}{\text{SD}}\left( {A_{i} } \right) $$
(2)

where A represents the set of instances that attain the node, Ai represents the subset of illustrations that have the ith product of the possible set, and SD represents the standard deviation.

REPTree

Quinlan (1987) introduced the reduced error pruning tree (REPTree) algorithm as a representative technique to explain decision tree learning problems. REPTree is an ensemble of a traditional decision tree, wherein it generates a decision regression tree by using the gain ratio information and by separating and pruning the regression tree. More precisely, in this algorithm, the training data are split into two sets, viz. training and pruning set, such that ~ 75% of the data are used for training purposes (training the decision tree), while the remaining data are used for pruning purposes (pruning data help determine accuracy measurement). As pruning decreases the decision tree size by error elimination of individual trees (Rahman et al. 2021), this study has considered the REPTree algorithm as a standard model for predicting evapotranspiration.

Model performance indicators

This study included different statistical indices for evaluating the model performance, such as mean absolute error (MAE), relative absolute error (RAE), root mean square error (RMSE), root-relative mean square error (RRMSE), and correlation coefficient (r). MAE statistics represent the mean absolute deviation of forecasted values from the observed values of time series, as shown in Eq. 3, while RAE statistic represents the ratio of the absolute error of the measurement to the actual measurement which helps to determine the magnitude of the absolute error in terms of the actual size of the measurement. RMSE statistics represent the root mean square deviation of forecasted values from the observed values of time series, as shown in Eq. 4. More precisely, the relative error provides inferences about the strength of measurement with reference to the actual measurement. RRSE statistic normalizes the total squared error by dividing it with the simple predictor (average of the actual values), thereby allowing reducing the error to the same dimensions as the quantity being forecasted, mathematically shown by Eq. 5. The correlation coefficient represents the measure of linear association between the dependent and independent variables, as shown in Eq. 6.

$$ {\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {{\text{ET}}_{{{\text{pi}}}} - {\text{ET}}_{{{\text{oi}}}} } \right| $$
(3)
$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {{\text{ET}}_{{{\text{pi}}}} - {\text{ET}}_{{{\text{oi}}}} } \right)^{2} } $$
(4)
$$ {\text{RRMSE}} = \frac{{{\text{RMSE}}}}{{{\text{ET}}_{{{\text{pi}}}} }} = \frac{{\sqrt {\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left( {{\text{ET}}_{{{\text{pi}}}} - {\text{ET}}_{{{\text{oi}}}} } \right)^{2} } }}{{{\text{ET}}_{{{\text{pi}}}} }} $$
(5)
$$ r^{2} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {{\text{ET}}_{{{\text{pi}}}} - {\text{ET}}_{{\text{p}}} } \right)\left( {{\text{ET}}_{{{\text{oi}}}} - {\text{ET}}_{{\text{o}}} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {{\text{ET}}_{{{\text{pi}}}} - {\text{ET}}_{{\text{p}}} } \right)^{2} } \sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {{\text{ET}}_{{{\text{oi}}}} - {\text{ET}}_{o} } \right)^{2} } }} $$
(6)

where ETpi and ET0i are ith ET0 values predicted/forecasted and observed/calculated by FAO56-PM, respectively, and ETp and ET0 are average values of ET0 predicted/forecasted and observed/calculated by FAO56-PM, respectively. Besides, N represents the number of data, while the range between zero and the closest value indicates good performance for all indices except r2, such that the best value for r2 is 1.

Results

Best subset regression and sensitivity analysis

Selection of best input combination

The best input combination has been selected using the six statistical criteria (i.e., MSE, determination coefficients (R2), adjusted R2, Mallows' Cp, Akaike's AIC, and Amemiya's PC) at two stations, and the results are given in Tables 1 and 2. From Table 1, it can be seen that four number of input variables is identified as the best input combination, as it has the lowest values of Mallows' Cp of 4.002 and Amemiya's PC of 0.058 and has the highest values of R2 (0.943) and high adj-R2 (0.943) among all input combinations at Faisalabad station. Similarly, at Islamabad station, the four number of input variables is identified as the best input combination with the lowest values of Mallows' Cp of 6.696 and Amemiya's PC of 0.045 and the highest values of R2 (0.956) and high Adj-R2 (0.955) among all input combinations, as given in Table 2. In this study, whole datasets for both the stations are divided into two segments, viz. training dataset and testing dataset. Seventy-five percentage of datasets were allocated for training the models and the remaining 25% were considered for validating the models.

Table 2 The best subset regression analysis for determining the best input combinations at Faisalabad station
Full size table

Sensitivity analysis

The sensitivity analysis of the input variables has been carried out through regression analysis to identify the most effective input parameters in the prediction of ET0 using machine learning models. The obtained results from the regression analysis are given in Tables 3 and 4 and Figs. 2 and 3. The results of performed regression analysis on all input parameters proved that Tmin, RHAvg, Ux, and n by having absolute standard coefficients (0.634, −0.225, 0.384, and 0.070) were identified as the most influential input parameters, respectively, for prediction of ET0 at Faisalabad station. In the case of Islamabad station, the findings of performed regression analysis on all input parameters revealed that Tmin, RHAvg, Ux,, and n by having the highest standard coefficients (0.661, −0.212, 0.312, and 0.168) were identified as the most influential input parameters, respectively.

Table 3 The best subset regression analysis for determining the best input combinations at Islamabad station
Full size table
Table 4 The regression analysis for identifying the most effective parameters for ETo estimation at Faisalabad station
Full size table
Fig. 2
figure 2

The standardized coefficients of input variable for sensitivity analysis at Faisalabad station for reference evapotranspiration

Full size image
Fig. 3
figure 3

The standardized coefficients of input variable for sensitivity analysis at Islamabad station for reference evapotranspiration

Full size image

Implementation of machine learning algorithm at two different gauging stations

The ET0 at two different meteorological stations was estimated by applying novel hybrid machine learning algorithms. The performances of the applied algorithms were evaluated and compared based on performance indicators (i.e., MAE, RMSE, RAE, RRSE, and r). The model with a high r and lowest values of MAE, RMSE, RAE, and RRSE with close to zero is considered the higher accuracy in the prediction of ET0. The general trend of MAE, RMSE, RAE, RRSE, and r is presented in Tables 5 and 6. The M5P algorithm has improved the performance of AR in the prediction of ET0 with greater accuracy as compared to other hybrid algorithms at selected (both) meteorological stations.

Table 5 The regression analysis for identifying the most effective parameters for ETo estimation at Islamabad station
Full size table
Table 6 RMSE, NSE, WI, and r for meta-heuristics algorithms-based models during the training and testing span at Faisalabad station
Full size table

Prediction of ET0 at Faisalabad station

The performance of the applied algorithms, namely additive regression (AR), AR-bagging, AR-RSS, AR-M5P, and AR-REPTree, was assessed using performance indicators (i.e., MAE, RMSE, RAE, RRSE, and r) at Faisalabad station and is presented in Table 6. It is apparent from Table 6 that the hybrid AR-RSS algorithm performed better during the training period and the AR-M5P models performs better than other applied algorithms during the testing period. The additive AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree provided MAE = 0.468, 0.489, 0.430, 0.459, and 0.477, RSME = 0.669, 0.658, 0.620, 0.638, and 0.684, RAE = 23.03, 24.06, 21.16, 22.57, and 23.47%, RRSE = 29.04, 28.55, 26.88, 27.665, and 29.66%, and r = 0.957, 0.959, 0.963, 0.961, and 0.955 during training the period and MAE = 0.726, 0.692, 0.656, 0.570, and 0.679, RSME = 0.999, 0.994, 0.915, 0.789, and 0.984, RAE = 32.38, 30.87, 29.30, 24.45, and 30.34%, RRSE = 39.08, 38.88, 35.78, 30.90, and 38.49%, and r = 0.927, 0.928, 0.934, 0.957, and 0.934 during the testing period, respectively. Therefore, the value of correlation coefficient was highest and error parameters were obtained lowest for the AR-M5P model as compared to the other models testing span and considered as the best model in estimation of ET0 at Faisalabad meteorological station.

Figure 4a–e shows the time-series plot (left side) and scatter plot (right side). In scatter plots, the regression line provided the coefficient of determination (R2) as 0.860 for the AR, 0.826 for the AR-bagging model, 0.872 for the AR-RSS, 0.915 for the AR-M5P model, and 0.872 for the AR-REPTree model (Fig. 4a to e). The regression line (RL) was located below the best fit (1:1) for all the applied models, which means these models underestimated the ET0 values concerning the observed ET0 values. The AR-M5P model provided the RL near to the best fit line and showed superior performance among other models.

Fig. 4
figure 4

Observed vs estimated reference evapotranspiration (ET0) values by the AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree models during testing at Faisalabad station

Full size image

In addition to the above, the performance of the applied models was assessed using a radar chart of the best-calculated value of RMSE. Having a better diagnostic analysis of the efficiency of all models, the values of RMSE are shown in Fig. 5. It can be inferred that the AR-M5P model has a lower value of RMSE; this revealed that the AR-M5P model performed better than other models. Further comparative analysis (AR) model was located furthest. The AR-M5P model was located nearest to the observed point based on the standard deviation, correlation, and RMSE. This showed AR as the worst model and AR-M5P as the best model among the selected models.

Prediction of ET0 at Islamabad station

The results obtained for ET0 estimation at Islamabad station are shown in Table 7. It is revealed that the AR-bagging model was superior with r = 0.964, MAE = 0.355, RMSE = 0.470, RAE = 423.85% and RRSE = 26.73% in the training period, whereas the AR-M5P model showed superiority among other models during testing period with r = 0.961, MAE = 0.437, RMSE = 0.570, RAE = 27.86%, and RRSE = 31.37%. It is revealed that the AR-M5P model performs superior to the applied models.

Table 7 RMSE, NSE, WI, and r for meta-heuristics algorithms-based models during the training and testing span at Islamabad station
Full size table

The scatter plots (right side in Fig. 6) and time-series graphs (left side in Fig. 6) of the observed ET0 against the predicted ET0 of the additive regression (AR), AR-bagging, AR-RSS, AR-M5P, and AR-REPTree models over the testing span are shown in Fig. 6a–e. The RL provided the coefficient of determination (R2) as 0.850 for the AR, 0.886 for the AR-bagging model, 0.908 for the AR-RSS, 0.923 for the AR-M5P model, and 0.834 for the AR-REPTree model. The RL of the AR-M5P model is located just above the best fit 1:1 line. This reveals that the AR-M5P model has high accuracy in the estimation of ET0 values at the Islamabad station.

Fig. 5
figure 5

Observed vs estimated reference evapotranspiration (ET0) values by the AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree models during testing at Islamabad station

Full size image
Fig. 6
figure 6

Radar charts display the best value of RMSE for AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree models during testing at Faisalabad station

Full size image

Figure 7 represents the radar chart for the best-calculated values of the RMSE. It can be inferred that the AR-M5P model has higher accuracy in estimating streamflow values as the model has a lower value of RMSE. Further comparison among the applied models has been made using the Taylor diagram. The AR-M5P model (in Fig. 8) showed the highest correlation coefficient with a low value of RMSE and located near the observed point. The AR-REPTree model is located farthest from the observed point with a lower value of correlation coefficient and a high value of RMSE. The AR-M5P model can be considered as the best model in the estimation of ET0 at Islamabad station.

Fig. 7
figure 7

Radar charts display the best value of RMSE for AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree models during testing at Islamabad station

Full size image

Pearson correlation matrix and Heat Maps

Figure 10a, b presents the Pearson correlation matrix and heat maps of Faisalabad and Islamabad stations resulting from input dataset for explaining the relation between explanatory and response variables. The input parameters, namely minimum temperature and sunshine hours, exhibited equally strong positive correlation with actual and AR-M5P ET0 which was computed as 0.91 and 0.73 for Faisalabad station, but 0.84 and 0.73 for Islamabad station, respectively. Strong negative correlation was found between average RH and actual (PM56) ET0 (0.39, 0.48) in Faisalabad station. Similar relation was found between average RH and AR-M5P ET0 (0.36, 0.49) in case of Islamabad station. Interestingly, wind speed parameter was also found strongly correlated with the AR-M5P ET0 in positive direction (0.85) in Faisalabad, but looked weakly correlated, i.e., 0.57 in case of Islamabad station. This indicated that wind speed plays a vital role and should be considered as an effective climatic parameter for ET0 estimation at Faisalabad station. In addition, wind speed for Faisalabad station was recorded highest (386.28 km/day) due to its geographical position. Also, severe types of the thunderstorm were observed every year due to western cold wind direction. Further, it has humid summer and dry winter seasons which also support our above-mentioned results.

Discussion

The performance of hybrid machine learning algorithms was assessed for the estimation of reference ET0 values at two different meteorological stations. The results revealed that machine learning algorithms have the prediction potential for ET0. More specifically, the AR-M5P model showed the superior result. The scatter plot between the observed and estimated ET0 values at different locations is presented in Figs. 4 and 5. It can be inferred that the RL provided the high value of the R2 with reference to the AR-M5P model at both the selected stations. This showed the superiority of the AR-M5P model. Further comparison among AR alone and hybrid algorithms was made using a radar chart (Figs. 6, 7) of best-calculated value of RMSE. The result revealed that the AR-M5P model predicted ET0 more precisely at both stations, as it has a lower value of RMSE. The Taylor diagram (Figs. 8, 9) showed the more comparable depiction of model performance in ET0 values. The AR-REPTree model was located furthest and the AR-M5P model was located nearest to the observed point based on the standard deviation, correlation, and RMSE at both the selected meteorological stations. This showed AR-M5P model has higher accuracy in the prediction of ET0 values as compared to other selected algorithms.

Fig. 8
figure 8

Taylor diagrams of AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree during testing span at Faisalabad station

Full size image
Fig. 9
figure 9

Taylor diagrams of AR, AR-bagging, AR-RSS, AR-M5P, and AR-REPTree during testing span at Islamabad station

Full size image
Fig. 10
figure 10

Pearson’s correlation matrix and heat maps between explanatory and response variables

Full size image

The results obtained from this study were also compared with the recent work (Kisi et al. 2015; Kisi 2015; Feng et al. 2017a, b; Shriri, 2018; Fan et al 2018a, b; Wang et al. 2017a; Wang et al. 2017b; Malik et al. 2018) conducted in different continents of the world. Kisi et al. (2015) investigated the comparative performance of four different artificial neural network algorithms, namely multi-layer perceptron-artificial neural networks (MLP-ANN), ANFIS with grid partition (ANFIS-GP), ANFIS with subtractive clustering (ANFIS-SC), and GEP, in predicting monthly ET0 from 50 meteorological stations in Iran. The study concluded that the ANFIS-GP model was better than the others applied models. Similarly, Kisi (2015) explored the applications of LSSVM, MARS, and M5Tree in simulating monthly pan evaporation for the locations of Antalya and Mersin in Turkey. MARS's performance was better than that of the LSSVM and M5Tree. Feng et al. (2017a, b) computed daily ET0 for southwestern China between 2009 and 2014 using RF and GRNN models utilizing meteorological information. The RF method was deemed to be superior even though both methods were judged to be suitable. Shiri (2018) estimates ET0 by weather data via the combined wavelet random forest approach (WRF). It was concluded that outcomes were better when the WRF hybrid model. Fan et al. (2018a, b) investigated the potential for the daily ET0 modeling of restricted weather data using the K-fold-validation approach in terms of gradient boosting decision-making (GBDT), extreme gradient boosting (XGBoost), RF, and M5 modeling tree (M5Tree). The authors also applied SVM and ELM models to compare the outcomes. They employed meteorological variables from a variety of climates to validate the models from 1961 to 2010 in China. The study suggested using GBDT and XGBoost models to estimate ET0 in China's varying climate. Wang et al. (2017b) applied models, such as the multi-layer perceptron (MLP), the fuzzy genetic (FG), the long short-term memory (LSVM), the multi-layer perceptron (MLR), and the SS models, to predict pan evaporation in China. They claimed that soft computing strategies outperformed both the MLR and SS models in terms of performance. A study conducted by Wang et al. (2017a) examined the ability of the FG, ANFIS-GP, and M5Tree models to predict monthly pan evaporation in the Yangtze River Basin in China. The results revealed that the FG model outperformed the other models in terms of estimated proficiency. Granata (2019) used meteorological data from central Florida, USA, with four distinct neural network models such as bagging, RF, M5P regression tree, and support vector regression. These algorithms were tested in the humid subtropical climate conditions and compared with the observed ET0 value. Experimental results showed that the M5P model produced the greatest results when coupled with meteorological data and soil moisture content. The study also confirmed that the AR machine learning algorithms performed better with M5P algorithms and have higher accuracy than other applied hybrid models in the prediction of ET0 at both stations.

Conclusions

This study applies five data intelligent and hybrid metaheuristic algorithms, namely additive regression (AR), AR-bagging, AR-random subspace (AR-RSS), AR-M5P, and AR-REPTree, in order to investigate their potential for reference evapotranspiration (ET0) prediction. The input dataset of 30 years (1987–2016) for two meteorological stations from semi-arid climatic conditions has been used in this study. In addition, ET0 was determined using the global standard FAO-PM56 method and used as the benchmark for selected data intelligent and hybrid metaheuristic algorithms. The reduction in climatic parameters was performed using sensitivity analysis through regression methods. The study found that minimum temperature, average relative humidity, wind speed, and sunshine hours are prime climatic parameters for ET0 prediction at studied stations. Based on the result of performing indices, it was concluded that AR-M5P ranked at first place compared with other machine learning algorithms using limited meteorological input for the ET0 modeling process. Experimental results showed that AR machine learning algorithms performed better with M5P algorithms and have higher accuracy than other applied hybrid models in prediction of ET0 at both stations.