Introduction

The contamination of wastewater by phenol and phenolic compounds is a severe environmental problem. Phenols are considered priority wastewater contaminants because they are highly toxic and harmful to organisms even at low concentrations. The toxic levels usually range between the concentrations of 10–24 mg/L for humans and the toxicity level for fish between 9 and 25 mg/L (Thakurta et al. 2018). Phenol causes several dreaded acute and chronic toxic effects on human health including a wide range of symptoms such as headache, vomiting, fainting, liver and kidney damage, and other mental disorders (Pal et al. 2014). The industries associated with phenol contaminated effluents are petrochemical, coal conversion, resin manufacturing, coal gasification operating units, pulp and paper mills, liquefaction processing units, dye synthesis units, petroleum refineries, and phenol producing industries (Hamad 2020; Naguib and Badawy 2020). There is a need for the decontamination of phenol-contaminated effluents through an efficient wastewater treatment technique before they are discharged into natural receiving waters.

Some wastewater treatment techniques have been investigated for the removal of phenol from wastewater, such as membrane separation (Raza et al. 2019), electrocoagulation (Jeong et al. 2019), solvent extraction (Chen et al. 2017), solar photo-catalytic system (Abid et al. 2019), and adsorption (Dehmani et al. 2020). Adsorption is most widely used, and it is a highly efficient technique for treating industrial effluents (Bousba and Meniai 2014). The preference for adsorption is mostly because it is less expensive in terms of design, land space, and operating cost and more efficient in comparison with other processes (Mahmoud 2016; Patel 2019). The efficiency of the adsorption process is mainly due to the characteristics of the adsorbent such as high surface area, high adsorption capacity, micro-porous structure, and special surface reactivity.

The adsorption process can be carried out in a batch or dynamic (column) process. The batch process is used mainly for treating a small volume of effluents. The results of the batch study, however, may not be directly applied for field applications in wastewater treatment systems. The column adsorption technique is usually considered for large-scale industrial wastewater treatment because it is simple to operate, has high contaminant removal efficiency, and can easily be scaled-up from a laboratory process. The most commonly used adsorbent is activated carbon which has a high affinity for pollutants in wastewater mainly because of its high surface area, micro-porous structure, and a high degree of surface reactivity. Commercial activated carbon is quite expensive; hence, there is a need for extensive research on the preparation of activated carbon from renewable materials, especially agricultural wastes. Some of the agricultural biomass that has been investigated for phenol removal from simulated and industrial wastewater include eggshell (Giraldo and Moreno-Piraján 2014), onion dry scales (Naguib and Badawy 2020), wheat bran (Achak et al. 2014), and palm kernel shell (Aremu et al. 2020).

Rice husk is a waste product of the agricultural process in Nigeria. The hard protective coatings of the grains of rice are rice husks. When the rice grains are detached, the husks are usually thrown away as waste. Hence, rice husks running into millions of tons are dumped as waste annually. They are usually discarded and burnt or dumped as refuse. Most times, they constitute environmental pollution. Nigeria is among the top producers of rice in sub-Saharan Africa. In 2017, Nigeria produced over 5.8 million tons of rice (Udemezue 2018). It is, therefore, necessary to find a sufficient and economic utilization of this abundant agro-waste material. The performance of rice husk for phenol removal in a packed bed column has not been widely investigated, the few available reports focused on batch studies.

To understand the nature and kinetics of the dynamic adsorption process and for the prediction of the breakthrough curves, some mathematical models have been developed, viz. Thomas, Adam Bohart, Yoon–Nelson, Wolborska, etc. The experimental data are fitted to the models to estimate the model parameters. The linear least square regression technique is the most widely used approach in fitting the experimental data to the dynamic adsorption models. However, the linear regression technique necessitates the transformation of the nonlinear form of the model equations to linear form. The linearization procedure leads to alteration of the error structures, violation of the error variance, and normality assumptions of the standard least squares (Pal et al. 2014), and this leads to bias in the fitted model parameters between linear and nonlinear versions of the model equations (Ho 2006). In contrast to the linear regression, the nonlinear regression does not involve model transformation; hence, the error structure is unaltered. Nonlinear regression analysis of adsorption models has gained the attention of researchers recently but majorly for batch adsorption studies. There is a scarcity of reports on the analysis of dynamic adsorption models via the nonlinear regression method. It could be because of the complex nature of the nonlinear forms of dynamic adsorption models which makes the nonlinear regression process more rigorous than the linear regression. Till now, no work is available in the literature on nonlinear regression analysis of phenol adsorption onto rice husk-activated carbon (RHAC) in a packed bed column. A detailed evaluation of the adsorption characteristics of dynamic adsorption of phenol is also inadequate in the literature. Further, the authors noted, to the best of their knowledge, that the use of RHAC for adsorptive phenol removal in a dynamic mode operation is not readily available in the literature.

To this end, the present study focuses on the linear and nonlinear kinetics analysis and adsorption characteristics of phenol adsorption onto activated carbon synthesized from locally and abundantly available rice husk biomass in a packed bed column. The dynamic adsorption models considered include Thomas, Adams–Bohart, Yoon–Nelson, and Wolborska models. Microsoft Excel's Solver Extension software program was employed for the nonlinear regression of the models, and the result was compared with that of the traditional linear regression technique. The error distribution in the prediction of the model parameters was assessed using various error functions. The parameters depicting the adsorption characteristics were generated by the breakthrough analysis of the dynamic adsorption process at different solution flow rates, influent phenol concentration, bed height, and adsorbent particle size. The characteristic parameters estimated include (a) the amount of phenol loaded in the column at breakthrough (min,b) and saturation (min,ss); (b) the amount of phenol that left the column unadsorbed at breakthrough (mout,b) and saturation (mout,s); (c) the amount of phenol adsorbed in the column at breakthrough (mads,b) and saturation (mads,s); (d) the adsorption capacity at breakthrough (qb); (e) the equilibrium (maximum) adsorption capacity (qe) at saturation; (f) the length of mass transfer zone (MTZ); (g) the volume of effluent treated at saturation (Veff,s); (h) the empty bed contact time (EBCT); (i) the degree of sorbent used (DoSU) and; (j) the sorbent usage rate (SUR).

Materials and methods

Materials

The rice husk biomass was sourced from Wisdom Pack Global Rice Mills at Awka, Nigeria. The reagents such as phenol, tetraoxophosphoric acid (H3PO4), and distilled water used were of analytical grade and purchased from the Chemicals and Reagents market, Bridge Head, Onitsha, Nigeria.

Adsorbate preparation

Simulated aqueous wastewater was prepared by dissolving a calculated amount of phenol in distilled water. The solutions with a concentration of 100 mg/L, 200 mg/L, and 300 mg/L were used for the column experiments. The 100 mg/L phenol solution was prepared by weighing 100 mg (0.1 g) of phenol crystals into a 1000 ml standard volumetric flask and dissolved with distilled water; then, the volume was made up to 1000 ml with distilled water. The 200 and 300 mg/L solutions were similarly prepared by dissolving 200 and 300 mg of phenol crystals, respectively, in distilled water, and the volume was made up to 1000 ml in each case. The pH value was in the range of 6–7. A similar study by Karunarathne and Amarasinghe (2011) showed that effective phenol removal could be achieved under solution pH in the range of 6–7.

Preparation of activated carbon

The activated carbon was prepared according to the method described by Joseph et al. (2017). The rice husk was washed with tap water to remove muds and other impurities. Then, the material was washed with distilled water three times and sun-dried. The dried sample was broken into small pieces and further sun-dried. This helps to further reduce the moisture content of the sample. The dried sample was activated by mixing it with 45% concentration of tetraoxophosphoric acid (H3PO4) and kept in an oven at 110 °C for 24 h. Thereafter, the activated sample was washed severally with deionized water until a pH of 7 was obtained. The activated rice husk was placed in a furnace at the appropriate temperature and time to undergo carbonization. The operating conditions for the carbonization process were a carbonization time of 4 h, and a carbonization temperature of 575 °C. The prepared RHAC sample was put into distilled water and was recovered by filtering. Recovered RHAC was dried at a temperature of 110 °C for 24 h and finally ground and sieved to separate dust carbon particles into different sizes. RHAC particles of 300 μm, 600 μm, and 800 μm sizes were used for the experiments.

Characterization of the adsorbent

Produced rice husk-activated carbon (RHAC) was characterized for physical properties, BET surface area, pore size distribution, and other selected properties. The bulk density was determined using the water displacement method according to Das et al. (2015). Moisture content, ash content, volatile matter, fixed carbon, porosity, iodine number were analyzed as per standard procedures described by Joseph et al. (2017). The surface area and the pore volume were determined using the BET nitrogen (N2) adsorption–desorption isotherms measured at 77 K using N2 gas sorption analyzer according to Sivakumar et al. (2012). The instrumental analysis was done with the aid of the Fourier transform infrared spectrophotometer (FTIR) and scanning electron microscope (SEM). An FTIR-8400S Fourier transform infrared spectrophotometer, made by SHIMADZU, was used for the FTIR analysis. For the SEM analysis, a JOEL scanning electron microscope (model, JSM 6400) was used. The micrograph was done at 500× and 1000× magnifications.

Packed bed column studies

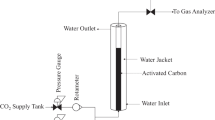
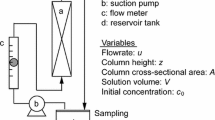
A laboratory-packed bed column was used for this study. A glass column of 30 cm high and an internal diameter of 30 mm were used. Figure 1 gives the schematic diagram of the column adsorption process. The adsorbent was separately packed in the column with glass wool at the bottom of the column. A peristaltic pump (BQ 50-IJ-A) was used to pump the phenol solution into the column. A flow controller was used to vary and regulate the flow rate. Different flow rates of 9 mL/min, 13 mL/min, and 18 mL/min were considered. Other process variables include packed bed heights (5 cm, 7.5 cm, and 10 cm), influent phenol concentrations (100 mg/L, 200 mg/L, and 300 mg/L), and adsorbent particle sizes (300 μm, 300 μm, and 800 μm). The phenol solution was placed at an elevation in a small cylindrical tank and connected to the column for delivery. The effluent sample was collected at different time intervals of 1 h up to 24 h until the adsorbents became saturated. The absorbance was measured using a UV–Vis spectrophotometer at a wavelength of 290 nm.

Fig. 1
figure 1

Schematic diagram for packed bed adsorption process

Full size image

The fitness of the experimental data to the Thomas, Yoon–Nelson, Adams–Bohart, and Wolborska kinetic models was evaluated via linear and nonlinear regression.

Packed bed adsorption column design parameters

The performance of a dynamic adsorption system is evaluated through the analysis of the breakthrough curve. This is achieved by calculating the breakthrough curve parameters from the experimental data. The breakthrough curve is plotted as the ratio of pollutant effluent concentration to influent concentration as a function of time or volume of effluent for a given bed height (Patel 2019). Breakthrough and saturation times have been defined as the time when the effluent concentration reached 5 and 95% of the influent concentration, respectively (Chatterjee and Schiewer 2011; Dwivedi et al. 2008). The breakthrough parameters computed include breakthrough adsorption capacity (qb), equilibrium (maximum) adsorption capacity (qe) at saturation, length of mass transfer zone (MTZ), the volume of effluent treated at saturation (Veff,s), empty bed contact time (EBCT), degree of sorbent used (DoSU), and sorbent usage rate (SUR). The above parameters are defined and estimated as detailed below (Chatterjee and Schiewer 2011):

The amount of phenol that was loaded in the column at breakthrough and saturation (min,b, and min,ss, mg, respectively) are given by inlet concentration (C0, mg/L) multiplied by flow rate (Q, L/h) and time (t, h) according to Eqs. (1) and (2):

$$ m_{{{\text{in}},{\text{b}}}} = C_{o} Qt_{{\text{b}}} $$
(1)
$$ m_{{{\text{in}},{\text{s}}}} = C_{o} Qt_{{\text{s}}} $$
(2)

The amount of phenol that left the column unadsorbed at breakthrough and saturation (mout,b, and mout,s, mg, respectively) are given by the product of the area under the dimensionless breakthrough curve of Co/C versus time (h) up to time tb and ts, inlet concentration (C0, mg/L) and flow rate (Q, L/h) according to Eqs. (3) and (4):

$$ m_{{{\text{out}},{\text{b}}}} = C_{o} Q\mathop \smallint \limits_{0}^{{t_{{\text{b}}} }} \left( {\frac{C}{{C_{o} }}} \right){\text{d}}t $$
(3)
$$ m_{{{\text{out}},{\text{s}}}} = C_{o} Q\mathop \smallint \limits_{0}^{{t_{{\text{s}}} }} \left( {\frac{C}{{C_{o} }}} \right){\text{d}}t $$
(4)

The amount of phenol adsorbed in the column at breakthrough and saturation (mads,b and mads,s, mg, respectively) are given by Eqs. (5) and (6), respectively:

$$ m_{{{\text{ads}},{\text{b}}}} = m_{{{\text{in}},{\text{b}}}} - m_{{{\text{out}},{\text{b}}}} $$
(5)
$$ m_{{{\text{ads}},{\text{s}}}} = m_{{{\text{in}},{\text{s}}}} - m_{{{\text{out}},{\text{s}}}} $$
(6)

The adsorption capacity at breakthrough (qb) and the equilibrium (maximum) adsorption capacity (qe) at saturation is determined as the total amount of phenol adsorbed at breakthrough and saturation to the mass of adsorbent in column (M, g) according to Eqs. (7) and (8) (Chatterjee and Schiewer 2011; Madan et al. 2019):

$$ q_{{\text{b}}} = \frac{{m_{{{\text{ads}},{\text{b}}}} }}{M} = \frac{{C_{o} Q}}{M}\mathop \smallint \limits_{0}^{{t_{{\text{b}}} }} \left( {1 - \frac{C}{{C_{o} }}} \right){\text{d}}t $$
(7)
$$ q_{{\text{e}}} = \frac{{m_{{{\text{ads}},{\text{s}}}} }}{M} = \frac{{C_{o} Q}}{M}\mathop \smallint \limits_{0}^{{t_{{\text{s}}} }} \left( {1 - \frac{C}{{C_{o} }}} \right){\text{d}}t $$
(8)

DoSU is calculated as the ratio of adsorption capacity at breakthrough (qb) to the adsorption capacity at equilibrium (qe) according to Eq. (9):

$$ {\text{DoSU}} = \frac{{q_{{\text{b}}} }}{{q_{{\text{e}}} }} $$
(9)

According to Chatterjee and Schiewer (2011), DoSU is connected to the effective use of the column because, in an ideal reactor, breakthrough and saturation times would be equal suggesting 100% utilization of the column’s maximum capacity, i.e., DoSU = 1.

SUR (g/l) denotes the mass of RHAC needed for obtaining a unit volume of clean effluent (before breakthrough); it is calculated according to Eq. (10), where M is the mass of adsorbent (g), and Vb stands for the breakthrough volume.

$$ {\text{SUR}} = \frac{M}{{V_{{\text{b}}} }} = \frac{M}{{Qt_{{\text{b}}} }} $$
(10)

The estimation of the length of the mass transfer zone (MTZ, cm) is accomplished using Eq. (11), where Z is the height of the bed (cm) (Madan et al. 2019):

$$ {\text{MTZ}} = Z\left( {1 - \frac{{q_{{\text{b}}} }}{{q_{{\text{e}}} }}} \right) $$
(11)

The volume of the effluent treated (Veff,s, mL) at saturation is given by Eq. (12).

$$ V_{{{\text{eff}},{\text{s}}}} = Qt_{{\text{s}}} $$
(12)

The empty-bed contact time (EBCT, min) shows the relation between the bed packed with the material in the column and the linear flow rate of solvent with solute (Madan et al. 2019). It is estimated using Eq. (13), where VC (L) is the volume of adsorbent in the bed. Other parameters are as initially defined.

$$ {\text{EBCT}} = \frac{{V_{c} }}{Q} $$
(13)

Column adsorption kinetic models

The kinetics of the dynamic adsorption process was analyzed by subjecting the experimental data to four adsorption kinetic models, viz. Thomas, Adam–Bohart, Yoon Nelson, and Wolborska models. The details of the linear and nonlinear forms of the model equations are presented in Table 1.

Table 1 Linear column kinetic model equations
Full size table

Error analysis

The error distribution in the prediction of the model parameters was evaluated using root mean square error (RMSE), Chi-square function (χ2), and Sum of Squares Errors (SSE). The fitness of the models to the experimental data was assessed using the coefficient of determination (R2). Table 2 presents the mathematical equations used in evaluating the error functions.

Table 2 The mathematical expressions of the error functions
Full size table

Results and discussion

Characterization of the adsorbent

Physical properties of raw rice husk and RHAC

The analyses of the physical properties of the raw rice husk and the rice husk activated carbon (RHAC) involve the determination of bulk density, pH, ash content, moisture content, volatile matter, and fixed carbon. The influence of the activation process on the physical properties of the rice husk was evident in the results as presented in Table 3. The bulk density increased from 0.092 (raw rice husk) to 0.448 g/ml (RHAC), depicting a higher mass per volume of the adsorbent particles, and this would lead to an increase in the adsorption capacity. The decrease of the ash content and volatile matter from 20.53 to 64.29% (raw rice husk) to 5.79% and 30.82% (RHAC), respectively, highlights the successful removal of a significant amount of the ash and volatile materials associated with the raw sample thereby opening up the pores for enhanced adsorption process. The pH was not significantly affected by the thermal activation process, the values being 7.4 and 6.8 for the raw and activated samples, respectively. The moisture content was found to decrease from 10.74 (raw rice husk) to 6.50% (RHAC). Moisture content represents the presence of a liquid particularly water, often in trace amounts in an adsorbent material. It has been reported that moisture content does not have a significant effect on the adsorptive power of an adsorbent unless it increases the weight and hinders the porous nature of the adsorbent (Adugna et al. 2020).

Table 3 Physical properties of raw rice husk and RHAC samples
Full size table

Surface area and pore size distribution of raw rice husk and RHAC

The results of the analyses of the BET surface area, pore width, micropore volume, and pore radius are presented in Table 4. The findings provide insight into the pore structure of the raw rice husk and the synthesized bio-adsorbent. It can be seen that the surface area of the activated sample (RHAC) is about 4758% higher than that of the raw rice husk. The micropore volume of the RHAC was higher than that of the raw rice husk, the values being 0.179 and 0.006 cm3/g, respectively. The average pore width increased significantly from 2.79 (raw rice husk) to 6.247 nm (RHAC), while the pore radius increased from 7.13 (raw rice husk) to 16.20 Å (RHAC). The activation of the rice husk provided the activated carbon with enhanced surface area, pore width, micropore volume, and pore radius. The rice husk changed from non-porous biomass to microporous sorbent after thermal activation. This underscores the significance of activation in improving the sorption properties of a biomaterial.

Table 4 BET surface area and pore size distribution of raw rice husk and RHAC samples
Full size table

Scanning electron microscope (SEM)

SEM images were used to study the morphology of solid samples. The SEM images of the raw rice husk at 500× and RHAC at 500× and 1000× magnification are presented in Fig. 2. The analysis was performed using solid samples sieved at 200 μm. The difference in the morphology of the raw rice husk and the activated carbon produced from it can be seen in Fig. 2a–c. The morphology of the raw sample (Fig. 2a) has a highly packed surface with non-distinctive pores and cavities. Conversely, the texture and surface morphology of the RHAC (Fig. 2b, c) was characterized by rough surfaces. The interspatial pores seen within the matrix of the activated carbon suggest that the produced adsorbent has good adsorption properties. The large pores observed in Fig. 2b, c are likely because the associated volatile matter has been eliminated during carbonization at a high temperature. The macropores were visible after activation facilitating the easy diffusion of more phenol molecules into the pore structure of the adsorbent.

Fig. 2
figure 2

SEM images a Raw rice husk at 500×, b RHAC at 500×, c RHAC at 1000×

Full size image

Fourier transform infra-red

The FTIR technique is an important tool used to identify the characteristic functional groups, which are instrumental in the adsorption of aromatic compounds. The FTIR spectrums of the raw and activated samples are presented in Fig. 3. The range of the wavenumbers is 3693.8 to 670 cm−1 with peaks from 96.68 to 83.45 cm−2 as seen (Fig. 3). In order to identify the functional groups at the distinctive peaks, the spectra results of the FTIR analysis were matched with the standard signature of identified materials available in the FTIR library (Stuart 2000). Compounds like esters, ethers, carboxylic acids, and nitro compounds seemed to be more distinctive to the spectroscopy after the activation. This is likely due to the exposure to high temperature and the chemical activities of the inorganic acid used in the activation which revealed the presence of these compounds. The O–H stretching of the carboxylic acid group is depicted in the absorption band region of 3600 cm−1, while the O–H bending of the alkanol group is visible in the region of 3200 to 3300 cm−1. The wavenumbers in the band region of 2900–3000 cm−1 depict the presence of the C–H stretching of the alkanes and alkyls groups, while 2200–2210 cm−1 correspond to the C–O–C stretching of esters. The presence of N–H bending of the amides group is indicated in the region of 1035–1050 cm−1.

Fig. 3
figure 3

FTIR spectrum: a raw rice husk; b RHAC

Full size image

Effect of process parameters on breakthrough curves

Effect of flow rate

The experiments for the effects of flow rate on breakthrough curves were carried out at an influent phenol concentration, 100 mg/L, bed height, 10 cm, particle size, 300 µm, and flow rates of 9 mL/min, 13 mL/min, and 18 mL/min. The breakthrough curves are shown in Fig. 4a. The details of the breakthrough parameters are presented in Table 5. The results showed that as the flow rate increased from 9 to 18 mL/min, the breakthrough curves become steeper and the breakthrough and saturation times decreased. Also, the adsorption capacity decreased with an increase in the flow rate of the solution. This variation in the slope of the breakthrough curves and adsorption capacity could be explained based on mass transfer fundamentals (Dwivedi et al. 2008). At a high flow rate, the phenol solution leaves the column before equilibrium occurs thus leading to a reduction in the breakthrough and saturation times. Also, increased flow rate depicts a decrease in residence time of the phenol solution, and since phenol did not have sufficient time to diffuse into the active pores of the adsorbent they thereby leave the column unadsorbed, resulting in a decrease in the adsorption capacities of the adsorbent at breakthrough and equilibrium. These observations corroborate with the reports of Chittoo and Sutherland (2020) in a similar study. It could also be seen (Table 5) that the amount of phenol loaded in the column, the amount adsorbed in the column, the amount that left the column unadsorbed at the breakthrough point, and the degree of sorbent usage (DoSU) decreased as the flow rate increased. The reason is connected to the adsorbate not having sufficient residence to time to diffuse into the pores of the adsorbent. However, MTZ, SUR, and Veff,s increased with an increase in flow rate. This is in agreement with the result reported by Chatterjee and Schiewer (2011) in a similar study.

Fig. 4
figure 4

Effects of operating parameters on breakthrough curves a Effect of flowrate, b Effect of inlet phenol concentration, c Effect of bed height, d Effect of particle size

Full size image
Table 5 Breakthrough parameters for the adsorption of phenol onto RHAC
Full size table

Effect of influent phenol concentration

The influence of influent phenol concentration on the breakthrough curves was investigated at influent phenol concentrations of 100 mg/L, 200 mg/L, and 300 mg/L as shown in Fig. 4b. This was carried out at a constant bed height of 10 cm, a flow rate of 9 mL/min, and a particle size of 300 µm. The dynamic adsorption parameters of the breakthrough curves can be seen in Table 5. It could be observed that as the influent phenol concentration increased from 100 to 300 mg/L, the breakthrough and saturation times decreased. At increased adsorbate concentration, breakthrough and equilibrium are attained faster. Also, as the influent phenol concentration increased the adsorption capacities at breakthrough and equilibrium decreased as shown in Table 5. At lower influent phenol concentration, the inflow phenol molecules do not saturate the active sites on the surface of the sorbent. However, the available active sites are saturated earlier at high influent phenol concentration, resulting in a decrease in adsorption capacity. This is an indication that the diffusion of the adsorbate into the pores of the adsorbent is highly dependent on the concentration gradient. However, as shown (Table 5), MTZ and SUR increased with an increase in influent phenol concentration. This is likely because as the concentration of the feed increases, phenol loading rate increases, so does the driving force for mass transfer, leading to an increase in the mass transfer zone. This corroborates with the report of Dwivedi et al. (2008) in a similar study. As the sorbent mass and the volumetric flow rates of the solution are constant a reduction in Veff,s was observed as the sorbent molecules increased. And, since the solution flow rate and bed height were constant, the EBCT was constant as the influent phenol concentration varied.

Effect of bed height

The effect of bed height on breakthrough curves was studied at the influent phenol concentration of 100 mg/L, a flow rate of 9 mL/min, and a particle size of 300 µm. The bed heights considered were 5 cm, 7.5 cm, and 10 cm as shown in Fig. 4c. The details of the breakthrough parameters are presented in Table 5. It could be deduced from the results that breakthrough and saturation times increased as bed height increased from 5 to 10 cm as a result of the availability of more number of sorption sites. Less time is taken to saturate the bed in smaller bed heights. A higher bed height corresponds to a higher amount of adsorbent; consequently, the breakthrough and equilibrium adsorption capacities were observed to increase with an increase in bed height (Table 5). These findings are in agreement with the results reported by Sarkar and Das (2016) in a similar study. Other parameters that increased with bed height include MTZ, DoSU, and Veff,s. A higher bed height depicts a higher amount of adsorbent and mass transfer zone; consequently, the degree of sorbent usage and the volume of effluent treated would increase. However, EBCT was found to decrease proportionally with an increase in bed height, owing to an increased availability of sorbents.

Effect of particle size

The influence of particle size on breakthrough curves was investigated at a constant influent phenol concentration of 100 mg/L, a flow rate of 9 mL/min, a bed height of 10 cm, and varying particle sizes of 300 μm, 600 μm, and 800 μm as shown in Fig. 4d. The breakthrough parameters obtained at the respective particle sizes are presented in Table 5. The breakthrough and saturation times decreased as the particle size increased. This is likely because a larger particle size depicts a reduced surface area of the adsorbent and this will result in a less active site available for the sorption of the adsorbate. Conversely, a reduced particle size represents an improved surface area and this will enhance the number of active sites available for the sorption of phenolic ions. Accordingly, qb, qe, DoSU, and Veff,s increased with a decrease in particle size. Nonetheless, because the adsorption capacity is reduced at a higher particle size, the space required for mass transfer would increase; hence, MTZ was found to increase with an increase in particle size. At inlet phenol concentration of 100 mg/L, a solution flow rate of 9 mL/min, bed height of 10 cm, and particle size of 300 µm, a maximum equilibrium adsorption capacity of 14.57 mg/g was obtained, and the volume of effluent treated was 11.88 L. The result of the maximum adsorption capacity obtained in this study was compared with the results of other authors for different adsorbents and presented in Table 6.

Table 6 Comparison of maximum equilibrium adsorption capacity for different adsorbents
Full size table

Column kinetics study

Thomas model

Thomas’s model is based on the assumptions of Langmuir isotherm for equilibrium and second-order reversible reaction kinetics (Ajmani et al. 2020). In Thomas model, mass transfer resistance from both fluid film and intraparticle diffusions is neglected. Thus, this model assumed that surface reaction between ion molecules and unoccupied sites controlled the adsorption rate (Sazali et al. 2020). The linear and nonlinear forms of the Thomas model are as given in Eq. (14) and (15), respectively. A linear regression analysis was executed on the experimental data by plotting the graph of Ln (Co/Ct − 1) against time (Figure not given). The model parameters generated from the linear plots are shown in Table 7. The results indicated that the adsorption capacity decreased with an increase in the solution flow rate, influent phenol concentration, and particle size but increased with an increase in bed height. At a high solution flow rate, the aqueous solution containing the adsorbate does not have sufficient residence time to contact with the solute in the column to a point of equilibrium before they exit the column, while the contact between the adsorbent and the adsorbate is enhanced at a low solution flow rate. This is responsible for the inverse relationship between the solution flow rate and the adsorption capacity. Similarly, an increased influent phenol concentration results in an early saturation of the active sites available for sorption, leading to a decrease in adsorption capacity. Further, smaller particle size represents an improved surface area for contact between the adsorbent and adsorbate, this is responsible for the decrease in adsorption capacity with an increase in particle size. On the other hand, the rate constant (kTH) decreased with an increase in bed height but did not show a linear relation with other process parameters.

Table 7 Kinetics parameters obtained via linear regression
Full size table

The nonlinear regression was accomplished using the Excel's Solver Extension software of the Microsoft office program. The results are presented in Table 8. It could be deduced from the results of the nonlinear regression that the maximum adsorption capacity (qe) is influenced by the process parameters similarly as already stated for the linear regression. Assessment of the regressed lines revealed that the Thomas model showed a better fit to the experimental data when analyzed via the nonlinear regression. A direct comparison of the maximum adsorption capacity predicted by the linear regression and nonlinear regression is presented in Table 8. The correlation coefficients ranged from 0.8359 to 0.9918 and 0.9997 to 1.0000 for the linear and nonlinear regression, respectively, indicating a better correlation between the experimental data and the nonlinear regressed lines of the Thomas model. The maximum adsorption capacity obtained experimentally and via nonlinear regression analysis were 14.57 and 14.88 mg/L, respectively, at the same experimental condition, while 9.78 mg/L was obtained via the linear regression. This is an indication that the nonlinear regression should be preferred for a better analysis of the Thomas model and the prediction of its parameters. Selected error functions, viz. RMSE, χ2, and SSE, were further used to assess the error distribution between the experimental data and the model (nonlinear) predicted data. In all cases, the values of the error functions were less than zero indicating a minimal error distribution in the prediction of the model parameters.

Table 8 Kinetics parameters obtained via nonlinear regression
Full size table

Adams–Bohart model

The theoretical model proposed by Adams–Bohart assumes that the adsorption rate is proportional to both the residual capacity of the adsorbent and the concentration of the adsorbing species (Cruz-Olivares et al. 2013). The model is used only for the description of the initial part of the breakthrough curve, i.e., up to the breakpoint or 10–50% of the saturation point (Cruz-Olivares et al. 2013; Sarin et al. 2006). The linear form of the model is represented by Eq. (16). The No and kAB values were evaluated from the slopes and intercepts of the linear plots of Ln Ct/Co against time. Adams–Bohart’s model parameters can be seen in Table 7. It could be deduced from the results that No increased with an increase in flow rate but decreased with an increase in bed height and particle size. The increase of No with an increase in flow rate could be attributed to the larger mass transfer driving force connected with the high flow rate. The decrease of No with bed height is probably because higher bed height depicts an increased amount of adsorbent, the number of active sites competing for the same number of influent phenol ions will increase thereby reducing the saturation concentration (No) of the column. On the other hand, kAB was found to decrease with an increase in flow rate and influent phenol concentration but increased with an increase in bed height and particle size. According to Li et al. (2018), the decrease of the rate constant as solution flow rate and influent adsorbate concentration increases shows that the external mass transfer was the dominant kinetics at a low flow rate and low influent concentration for the adsorption of the adsorbate. The linear correlation coefficient for the linear regression analysis ranged from 0.9024 to 0.9898, indicating a good correlation with the experimental data.

The nonlinear form of the model is illustrated by Eq. (17). The results are presented in Table 8. The process parameters influenced the values of the model parameters No and kAB in a similar manner as discussed above for the linear analysis. The correlation coefficient obtained in the nonlinear approach was 1.0000 in most cases indicating an excellent correlation with the experimental data. The error functions as presented (Table 8) for the nonlinear regression analysis were less than zero in all cases depicting minimal error distribution in the prediction of the model parameters. Comparison of the correlation coefficient of the results obtained via linear and nonlinear regression analysis indicated that the nonlinear form of the model analyzed the experimental data better.

Wolborska model

Wolborska’s model describes the initial stage of the adsorption dynamics and concentration distribution in the bed at low concentrations (Wolborska 1989). The linear form of the model is illustrated by Eq. (18). The model parameters were estimated from the linear plots of Ln (Ct/Co) against adsorption time in the linear regression technique. The Wolborska model parameters can be seen in Table 7. The No values obtained in the Wolborska model are the same as in the Adams–Bohart model this affirms the similarity in the mathematical expressions of both models. As the influent solution flow rate increased from 9 to 18 mL/min, β decreased from 0.5177 to 0.5127 h−1, and No increased from 1564.06 to 1771.17 mg/l. This same trend was observed as the influent concentration increased from 100 to 300 mg/L. Both No and β decreased with an increase in bed height and particle size. A similar trend was reported by Shanmugam et al. (2016) who indicated that β is an effective coefficient that reflects the influence of mass transfer in the liquid phase and axial diffusion.

The nonlinear form of the model is illustrated by Eq. (19). The nonlinear model parameters are presented in Table 8. No, and kAB values were found to depend on solution flow rate, influent phenol concentration, bed height, and particle size as discussed above for the linear regression. The fitness of both model forms to the experimental data was analyzed using the correlation coefficient (R2). The R2 values for the linear regression ranged from 0.9024 to 0.9898, and the nonlinear regression values ranged from 0.9991 to 1.0000. This indicates that the model parameters predicted by the nonlinear regression have a better correlation with the experimental data. Error functions (RMSE, χ2, and SSE) were further used to assess the error distribution between the experimental data and the nonlinear model predicted data. In all cases, the values of the error functions were less than zero indicating a minimal error distribution in the model analysis and prediction of the model parameters.

Yoon–Nelson model

The Yoon–Nelson model assumes that the probability of adsorption of each molecule is directly proportional to the probability of adsorbate breakthrough on the adsorbent and the probability of adsorbate adsorption (Ajmani et al. 2020; Yoon and Nelson 1984). The model parameters were estimated from the linear plots of Ln (Ct/Co—Ct) against time according to Eq. (20). The generated model parameters are shown in Table 7. The results showed that as the flow rate increased from 9 to 18 mL/min, τ decreased from 6.07 to 0.02 h, this is likely due to an increase in the flow velocity of the solution associated with a higher solution flow rate, ultimately leading to a higher rate of supply of phenol ions to the available active sites. As the influent phenol concentration increased from 100 to 300 mg/L, τ decreased from 9.07 to 0.24 h likely due to the high supply of phenol ions to the available active sites, resulting in a reduction in the time required to achieve a 50% breakthrough. Similarly, an increase in the sorbent particle size from 300 to 800 µm resulted in a decrease in τ from 5.53 to 0.483 h. Conversely, as the packed bed height increased from 5 to 10 cm, τ increased from 1.99 to 10.75 h. This is because the number of adsorption sites increases with an increase in bed height, at an increased number of adsorption sites more time would be required to achieve a 50% adsorbate breakthrough. The Yoon–Nelson constant, kYN increased with an increase in influent phenol concentration, flow rate, and particle size but decreased with an increase in packed bed height. This trend of the relation between the Yoon–Nelson model parameters and the process parameters corroborates with the report of Ajmani et al. (2020) in a related study. At 300 mg/L influent phenol concentration, a low R2 value of 0.6827 was obtained from the linear regression, and however, the R2 was as high as 0.9863 at 18 mL/min solution flow rate.

The nonlinear form of the Yoon–Nelson model is represented by Eq. (21), and the results obtained from the nonlinear regression analysis are presented in Table 8. It could be deduced from the results that both the τ and kYN values obtained via the nonlinear regression are influenced by the process variables in the same manner as was with the linear regression. The R2 values of the nonlinear regression were higher than those of the linear regression, ranging from 0.9958 to 1.0000. This indicated that a better model analysis would be achieved with the application of the nonlinear regression. The error functions were also low, less than zero in some cases, and greater than zero in a few other cases. Regarding the R2 values and error functions, it is evident that the Thomas, Adams–Bohart, and Wolborska models gave better fits to the experimental data than the Yoon–Nelson model.

Comparative study of the experimental and model (linear and nonlinear regression) maximum adsorption capacities

Table 9 presents the values of experimental and model adsorption capacities with their corresponding R2 values.

Table 9 Comparison of the linear and nonlinear maximum adsorption capacities with the experimental values
Full size table

It is evident (Table 9) that the nonlinear predicted adsorption capacities have a better correlation with the experimental values than those of the linear regression. A maximum adsorption capacity value of 14.57 mg/g was obtained experimentally, at the same experimental conditions, 14.88 mg/g was predicted by the nonlinear regression, while 9.78 mg/g was predicted by the linear regression of the Thomas model. The R2 values ranged from 0.8359 to 0.9918, and from 0.9997 to 1.0000 for the linear and nonlinear regression, respectively. These are shreds of evidence that nonlinear regression is most appropriate for the accurate analysis of dynamic adsorption models.

Conclusions

The results of linear and nonlinear regression analysis and adsorption characteristics for the uptake of phenol from an aqueous solution were presented in this work. The study was carried out in a packed bed column system. Activated carbon was synthesized from locally and abundantly available rice husks biomass for this purpose. The RHAC was characterized for physical properties, BET surface area, and pore size distribution and analyzed via FTIR and SEM. The analyses and characterization of the produced adsorbent revealed that the adsorbent possesses favorable adsorption properties and characteristics. The results of the column adsorption studies indicated that phenol adsorption onto RHAC is dependent on solution flow rate, influent phenol concentration, particle size, and packed bed height. The linear and nonlinear regression analyses of the Thomas, Adams–Bohart, Yoon–Nelson, and Wolborska kinetics models showed that the regressed lines of the four models provided good fits to the experimental data. However, the R2 values for the linear regression ranged from 0.6827 to 0.9918, and 0.9958 to 1.0000 for the nonlinear regression. A direct comparison of the predicted model coefficients showed that the values predicted by the nonlinear regression analysis correlated better with the experimental data compared to those obtained via linear regression. Hence, the nonlinear regression is considered more appropriate for the regression analysis of phenol adsorption onto RHAC in a packed bed column. The results of the study also confirmed that rice husks, an agro-waste, can effectively be used as adsorbent material for the adsorption of phenol from aqueous effluents. The dynamic adsorption characteristic-parameters equally presented will be useful for the design of a packed bed adsorption column for phenol removal from phenol-contaminated effluents.