Introduction

Groundwater is among the most indispensable resources of the earth that takes place below the surface of the earth (Naghibi et al. 2015) on which near about 2.5 billion human beings depend on these fresh water resources in daily basis (Alcaide and Santos 2019). Groundwater varies spatially in both quality and quantity; however, it is very important for socio-economic development because groundwater meets certain demands of mankind, namely water for drinking, for irrigation, for forestry, for industrial purpose and to support livestock (Naghibi et al. 2016). Utilization of groundwater is hygienic and more reliable than surface water because groundwater is less exposed to environmental degradation (Kim et al. 2019; Lee et al. 2020). In most part of the globe, uncontrolled use of groundwater has depleted this resource. Since the last few decades, the availability of freshwater resource has become challenging issue because of its high demand for domestic, agricultural, industrial purposes (Chakraborty et al. 2021; Shit et al. 2019, Chen et al. 2019), insufficient rainfall, surface water scarcity and population growth (Panahi et al. 2020) which can lead the shortage of groundwater globally by 2025 (Nguyen et al. 2020). Being world's leading groundwater consumer, the consumption rate of India has been stated 230 cubic km per year (Fienen and Arshad 2016). Thus, mapping the GWPZ has become an essential and central part in the management system of watershed (Verma et al. 2018; Bhunia et al. 2018; Kulkarni et al. 2018).

Groundwater mapping has been carried out with direct filed surveys in recent past in expensive and time-consuming manner (Prasad et al. 2020). But now the integration of remote sensing and GIS is capable of accumulating, maneuvering and demonstrating various forms of data which result into the construction of thematic maps (Band et al. 2020; Rukhsana 2020; Karimi-Rizvandi et al. 2021). Besides, this platform is time as well as cost-effective and also applicable in large area (Prasad et al. 2020). The occurrence of groundwater varies over place to place in accordance with hydrology, climate, topography, geology, ecology, soil, slope, etc., of the region (Karimi-Rizvandi et al. 2021). Therefore, such factors are used in GIS to prepare the GWPZs.

Review of the literature suggests that researchers across the globe have used various methods to delineate GWPZs. Among them Analytical Hierarchy Process (Maity and Mandal 2019), Logistic regression (Park et al. 2017), Frequency Ratio (Ozdemir 2011), Weights of evidence (Madani and Niyazi, 2015) are very commonly used for this purpose. Besides, various techniques under machine learning are now broadly accepted in order to delimit GWPZs. These include Random Forest (Naghibi et al. 2016), SVM (Support vector machine) (Lee et al. 2018), BRT (boosted regression trees) (Naghibi and Pourghasemi 2015), linear discriminant analysis (Naghibi et al 2017), Naïve Bayes (Miraki et al. 2018), classification and regression tree (Naghibi et al. 2016) and artificial neural network (Lee et al. 2018). Despite being used in different parts of the planet all these techniques have some drawbacks. Identification of groundwater potential zones based on one single method is now not justifying the study.

AHP reduces the mathematical complexity in decision making (Abhijit 2020), thereby widely used. Frequency Ratio has been also successfully used with very high and precise accuracy by Ozdemirin 2011. Moreover, hypothesis or postulation is not obligatory in the allocation of revealing factors in RF model and enables mixed use of categorical data and numeric data (Aertsen et al. 2010). Even NB model is very simple and does not necessitate for estimation of parameter (Wu et al. 2008). Both RF (Naghibi et al. 2016) and NB (Miraki et al. 2018) models have been successfully implemented by several researchers across the globe with high accuracy. Among the machine learning model, Random Forest (RF) and Naïve Bayes (NB) are the most acceptable and high accuracy models depicted in previous studies' results (Naghibi et al., 2017; Pham et al., 2021; Miraki et al., 2018). It helps the model selection for GWPZs. Therefore, present study tries to map the probable groundwater sites by using with AHP, Frequency Ratio (FR), Random Forest (RF) and Naïve Bayes (NB) in Gandheswari River Basin of Bankura District, West Bengal. Gandheswari Watershed is composed with hard crystalline rock mainly granite gneiss which is not preamble; therefore, occurrence groundwater is not widely spread over the region. Thus, the main objective of the current work is to compare among multi-criteria decision approach, bivariate statistic method and machine learning algorithms for the delineation of groundwater potential zone (GWPZ) of the study area.

Description of study area

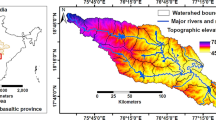
Gandheswari Watershed has been selected to delineate the GWPZs. Gandheswari River is the 32-km-long tributary of Dwarakeshwar River and flows through the four CD Blocks of Bankura district of West Bengal after originating from Santuri CD Block of Purulia district of West Bengal. The study area extends between 86° 53′ 20.526″ E and 87° 08′ 20.681″ E longitudes and 23° 13′ 43.376″ N and 23° 31′ 15.417″ N latitudes. The watershed occupies nearly 394.96 km2 (Fig. 1). This watershed is mainly situated in the peripheral region of Chota Nagpur Plateau; thereby, the studied region consists with undulating plane (below 120 m), an eroding plateau (120–220 m) and the Susunia Hill Zone (220–437 m) (Sinha 2016). Thick layer of ‘mottled clay’ is very abundant in Gandheswari basin, and most part of the study area consist granitic gneissic of Pre-Cambrian which results into moderate to low storage of groundwater (Ghosh et al. 2020).

Fig. 1
figure 1

Location of the study area: a India, b West Bengal, and c Gandheswari Watershed

Full size image

Material and methods

Data from different sources are used for spatial modeling and GWPZ analysis (Table 1). After converted the data into spatial database in accordance with our requirements AHP, FR, RF and NB methods have been applied to conduct the study. Figure 2 represents overall framework of the study.

Table 1 Data sources and type of data required in the research
Full size table
Fig. 2
figure 2

Methodological design of the study: starting from criteria selection to model validation

Full size image

Preparation of inventory map

Researchers, across the globe, have prepared inventory dataset for groundwater mapping by using location of springs, wells and quant. However, present study selects 85 well points and 85 non-well points (where occurrence of groundwater is minimum) to construct the inventory map. SOI toposheets (73I/15, 73 M/3 and 73 M/4) and Central Ground Water Board (CGWB) data have been used here. Of the 170 sites, 70% (119) have been randomly used for modeling and 30% (51) have been randomly used for validation purpose.

Factors affecting groundwater potential zone

Selection of effective parameters of GWPZ is crucial task for researchers (Naghibi et al. 2016). Literature review (Table 2) has helped to identify twelve such parameters. The thematic maps (Fig. 3a–i) based on the selected parameters have been prepared by using ArcGIS software. Details of these factors are as follows:

Table 2 Literature review of factors used to delineate groundwater potential zones (GWPZ)
Full size table
Fig. 3
figure 3

Distribution of six causative factors used in this study: a elevation, b slope, c drainage density, d TWI, e distance from the river, f lineament, g NDVI, h soil, i rainfall, j lithology, k geomorphology and l LULC

Full size image

Elevation has tremendous impact on groundwater potential mapping (Naghibi et al. 2016) as it is contrariwise related to the reserve of groundwater (Karimi-Rizvandi et al. 2021). Figure 3a reveals that elevation of Gandheswari Watershed varies from 13 to 383 m.

Slope is another important factor that controls rate of infiltration and run-off in any part of the globe. Higher slope adversely effects on groundwater storage; thereby, groundwater potential zones are generally associated with lower slope region (Maskooni et al. 2020). Highest slope in the study area is recorded as 43.24 degree, and lowest is recorded as zero degree (Fig. 3b). Drainage density is directly related to run-off and inversely related to groundwater storage (Magesh et al. 2012). In this area, drainage density extends from 0 to 0.75 km2 (Fig. 3c). TWI value ranges from 26.21 to 2.66 in the study area (Fig. 3d). TWI uncovers the saturated portions in said watershed. The index indicates effects of topography on accumulation of water in a region (Biswas et al. 2020), and hence, steep slope and higher elevation have greater run-off and thus reduce the capacity of water accumulation; on contrary, low-lying area has greater potential of topographical wetness or accumulation of water in the study area. The formula, given by Moore et al. (1991), is used to compute the TWI in present research. Distance from the river can be a vital controlling factor of groundwater storage. In this specific research, the distance from river ranges from 0 to 1511.67 m (Fig. 3e). Lineament density is among the most influential variables as it is positively related to groundwater storage. Lineaments act as the place of secondary porosity (Ghosh et al. 2020) and thereby very important in this study because most parts of the Gandheswari River Basin are composed with granite gneiss whose primary porosity is assumed to be low. The lineament density varies 0–0.59 km2 (Fig. 3f) in the studied watershed. Rainfall acts as natural sources of groundwater which helps the amount of infiltration (Karimi-Rizvandi et al. 2021). The mean annual rainfall in mentioned area fluctuates between 97.5 and 114.83 cm (Fig. 3i). Nature of soil also determines the storage of groundwater because soil properties determine the permeability of the region (Karimi-Rizvandi et al. 2021). Figure 3h unveils that current study area consists of four types of soil group, namely coarse loamy, clayey loamy, fine loamy and fine silt. Among those groups, coarse loamy soil can recharge the groundwater more efficiently than the others. Storage of groundwater is also shaped by geomorphology of any region (Biswas et al. 2020). Figure 3k uncovers five distinct features explicitly residual hill, pediment, pediplain, valley fill and water bodies. These features may be advantageous (valley fill, pediplain) for groundwater storage and residual hill and pediment may retard groundwater storage. Water bodies in the selected region act as the direct source of GWPZs. Lithological configuration of the studied watershed can be considered as primary controlling factor that determines the permeability and porosity of the region. Figure 3j reveals that most part of the watershed is composed with granite gneiss. This lithological constrain reduces the primary infiltration here, and thereby, groundwater storage is heavily depended on either secondary infiltration (through the cracks and joints) or the area having recent deposits (Ghosh et al. 2020). NDVI also significantly affects the groundwater storage capacity. Higher value of NDVI suggests thick coverage of vegetation coverage, and vegetation reduces run-off and helps in recharging the groundwater. In our area of interest, the NDVI value ranges from 0.47 to  − 0.19 (Fig. 3g). LULC of any region controls the groundwater movements. Evapotranspiration, surface runoff and groundwater recharge are largely controlled by LULC (Karimi-Rizvandi et al. 2021). Our study (Fig. 3i) has divided entire basin into six prominent LULC classes, namely water bodies, forests, agricultural lands, built-up area, sandy lands and other lands.

Accuracy assessment of groundwater-influencing factors

The important part of the research work is selection of the groundwater-influencing factors. The current work has used two methods for the selection of factors that influences groundwater storage. Firstly, variance inflation factors (VIF) (Dormann et al. 2013) method uncovers the multicollinearity among the selected parameters. In the current research, multicollinearity validates the possibility of association among the twelve parameters. Multicollinearity between parameters specifies that variables which are linked can be estimated by other factors. Therefore, the multicollinearity affected variable is needed to be removed from the model. The VIF values of > 10 and < 0.1 denote such problems (Khosravi et al. 2019).

Secondly, Information Gain Ratio (IGR) method unveils the relative importance of every influencing parameter (Chen et al. 2017). The Average Merit is computed through this method which quantifies the pattern of influence. Greater Average Merit signifies greater effect on the groundwater availability and vice versa.

Methods for GWPZ

AHP method

Analytical Hierarchical Process (AHP), invented by Saaty (1971), is the hierarchical additive weighting approaches for multi-criteria decision problems, and it is broadly used by researchers across the globe. This method analyzes parameters based on their relative relevance when compared to one another. Moreover, it is able to determine the subject, along with their rank and precedence, which is computed by pairwise comparison matrix to arrange the criteria in hierarchical order. Each parameter is given a set of weights (Table 3). Next step is to normalize the data. The consistency index (CI) coupled with consistency ratio (CR) is then computed to test the constancy of these weights. This AHP method has been gone through several steps. First of all, formation of a hierarchy is necessary from the problems. AHP begins with identifying the criteria to be used in evaluating several options, which are arranged in a treelike hierarchy. After that, data have been collected by comparing criteria at each level of the hierarchy and alternatives in pairs. Then estimation of the relative importance of selected criteria and alternatives is taken places, which is followed by validating the constancy in the pairwise comparisons (Table 4). The weights of each criterion were then normalized, and their average weights were determined (Table 5). The consistency vector has been calculated by multiplying the average weight of each criterion. The following equations have widely been used to check the CI and CR from the pairwise comparison matrix of all the parameters.

$$CI = \frac{{\left( {\lambda_{\max } - n} \right)}}{{\left( {n - 1} \right)}}$$
(1)

Here, n is the total number of criteria and \({\varvec{\lambda}}{\varvec{m}}{\varvec{a}}\) x (lambda) is simply the average value of consistency vector.

$$CR = \frac{CI}{{RI}}$$
(2)
Table 3 Random inconsistency indices for n = 15
Full size table
Table 4 Pairwise comparison matrix
Full size table
Table 5 Normalized pairwise comparison matrix
Full size table

Here, RI is the random index from Table 3

The present research finds the followings: maximum eigen value (λmax) = 13.673, consistency index (CI) = (λmax − n)/(n − 1) = 0.15209, random index (RI) = 1.54 (for n = 12), consistency ratio (CR) = (CI/RI) = 0.0987 or 9.9 (acceptable).

The weighted overlay analysis is very much useful tools for any suitable area analysis. This method has the ability to assigning and combining the multilayers to create an integrated analysis. The weighted values calculated by AHP method are used in weighted overlay tools to identify prominent factor through this process (Parimala and Lopez 2012).

$$S = \sum\limits_{i = 1}^{n} {W_{i} *X_{i} }$$
(3)

where S is the suitability index for each pixel map. Wi is the weight of the ith layer and Xi score of the ith criteria layer. n is the number of suitability layer.

Frequency Ratio (FR)

The Frequency Ratio (FR) is a statistic-based bivariate approach and has been developed to discover the groundwater potential area by evaluating the relationships among the controlling factors (Oh et al. 2011; Naghibi et al. 2016). The model has been applied here to uncover the quantitative link between distribution of well occurrence and predictor factors. Frequency Ratio has been calculated based on the following equation:

$$FR = \frac{W/TW}{{CP/TP}}$$
(4)

where W represents the number of pixels having linked with well from each thematic map, whereas TW represents the total number of pixels across the area under concern. CP and TP represent number of pixels in each thematic map and in area under concern, respectively.

Random Forest (RF)

Random Forest (RF) is a very popular and accurate machine learning algorithm (Wang et al. 2021). RF is basically a tree-based method, which has an authentic and great expectation execution by joining an enormous number of decision trees to determine the relationship between the factors affecting groundwater and dug well occurrence (Kim et al. 2018). Random forest creates many trees for making a ‘forest,’ where trees are created by bootstrapped data (Rahmati et al. 2017). The data are produced by the aid of classification and regression tree methods followed by Rahmati et al. (2017). RF method is further carried out by following the works of Naghibi et al. (2016), Lee et al. (2017) and Wang et al. (2021). The advantage of this method in comparison with other methods is as follows: (i) the overfitting problems of the datasets, (ii) manage big datasets with various dimensionality in nature, (iii) it does not need any hypotheses within the response variable and explanatory variables, (iv) it does not require any previous data to rescale and transform the datasets (Arabameri et al. 2019). The RF classification adopted resampling methods by randomly transferring the predictive factors to enhance the diversity in every tree (Naghibi et al. 2017). The notation of the predictive variable is defined as log 2 (M+1), where M is the total input number within the algorithm. The RF model determines the split at each node with the help of predictive variables and the number of trees (Kim et al. 2018). The average prediction of the tree is computed as:

$$Gp = \frac{1}{k}\sum {k^{th} } v^{response}$$
(5)

where Gp is any groundwater prediction and k represents the separate trees in the method.

Naïve Bayes (NB)

Naïve Bayes (NB) model is based on postulation that there are no dependent attributes to capitalize on the subsequent possibility in determination of the class for categorization (Soni et al. 2011). NB classification scheme is a term in Bayesian statistics which supervises an easy probabilistic classifier determined by Bayes' hypothesis (Bhargavi and Jyothi, 2009). The major benefit of the NB classifier is that it is simple to build and iterative parameter estimation schemes are not needed in it (Wu et al. 2008).

xI is the vector of the 12 controlling factors of groundwater potential zone, and yi is the vector of classifier variable (potential zone or non-potential zone). The NB is based on following equations.

$$\gamma_{NB} = \prod\limits_{{\left[ {yi = potential\_zone\_or\_non\_potential\_zone} \right]}}^{\arg \max p(yi)} {_{i = 1}^{12} } p\left[ {\frac{xi}{{yi}}} \right]$$
(6)

where P(yi) is the prior probability of yi that can be estimated based on the proportion of the observed cases with output class yi in the training dataset. P(xi/yi) is the conditional probability that can be calculated by the following equation:

$$p\left( {\frac{xi}{{yi}}} \right) = \frac{1}{{\sqrt {2\pi \alpha } }}e^{{\frac{{ - (xi - n)^{2} }}{{2\alpha^{2} }}}}$$
(7)

where η is the mean and \(\alpha\) is the standard deviation of xi.

Model validation

Validation of any model is fundamental steps for scientific research (Naghibi et al 2016). The performance of GWPM by four methods has been evaluated by ROC curve and the statistical measures of accuracy (ACC), mean absolute error (MAE), root-mean-square error (RMSE), Kappa index (K) and coefficient of determination (R2). The formulas that are used here are as follows:

$$Accuracy = \frac{TP + TN}{{TP + TN + FP + FN}}$$
(8)
$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{i = n} {(X_{ei} - X_{oi} )^{2} } }$$
(9)
$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{i = n} {\left| {X_{ei} - X_{oi} } \right|}$$
(10)
$$Kappa(k) = \frac{{P_{c} - P_{cxp} }}{{1 - P_{cxp} }}$$
(11)

where \(P_{c}\) indicates numeral of pixels to be matched accurately as well or non-well pixels;\(P_{cxp}\) denotes estimated results. \(X_{oi}\) and \(X_{ei}\) are the \(i^{th}\) observed and model predicted values, respectively, and \(n\) is the amount of data point (Khosravi et al. 2019).

The present study also uses ROC curve to unveil overall validity of the models applied here. The ROC curve significantly predicts the occurrence or non-occurrence of wells by sensitivity on Y-axis and specificity on X-axis (Prasad et al. 2020). The region below the curve is called area under curve. AUC is very much essential for model efficiency (Karimi-Rizvandi et al. 2021). The value of AUC ranges from 0 to 1and near to 1 represents higher accuracy of the models (Naghibiet al.2016; Chen et al. 2018; Prasad et al.2020).

Results

Importance of factors

IGR and VIF technique have been employed to identify the influence of selected parameters in groundwater potential map (GPM) and to unveil the multicollinearity issues in the selected parameters, respectively. The results of IGR and VIF are portrayed below (Table 6). The table discloses that VIF values of all factors are smaller than 10; therefore, no multicollinearity problem is existed among the selected parameters. Apart from VIF, IGR values also uncover the factorwise influence upon GWPZ.

Table 6 The evolution of the influencing factors using VIF and IGR test (Average Merit)
Full size table

Table 6 also demonstrates that for the river basin, geomorphology has the highest (0.94) importance in GWPZ, followed by slope (0.88) and rainfall (0.87). Besides, distance from the river (0.69), elevation (0.67) has moderate influence in the storage of groundwater. Moreover, LULC (0.08) has the least effect on groundwater storage and followed by soil (0.22) and topographical wetness index (0.23). So, the results unveil that all the selected factors have some impact on GWPZ; therefore, all these factors have been included in model development.

Groundwater potential zone mapping

Based on four different models GWPZ has been prepared for the Gandheswari Watershed (Fig. 5 a-d). ArcGIS has helped to classify GWPZ into five different classes such as Very good (VG), Good (G), Moderate (M), Poor (P) and Very Poor (VP). Based on expertise thoughts, pairwise comparison matrix and normalized pairwise comparison matrix are computed in Tables 4 and 5, respectively, to make decisions via AHP model. Weight overlay analysis techniques have been performed based on the result in ArcGIS, and GWPM has been created by AHP model (Fig. 4a).

Fig. 4
figure 4

Result of AHP (a), FR (b), NB (c) and RF (d) model for GWPZ

Full size image

Table 7 demonstrates percentagewise area of each class in each GWPM. According to the AHP model (Table 7), the percentages for the class VP, P, M, G and VG potential zones are 12.76, 27.88, 26.33, 26.81 and 6.21%, respectively. In case of the FR technique 9.66, 29.07, 28.41, 27.55 and 5.31% area falls into the class of VP, P, M, G and VG, respectively. RF model depicts (Table 7) that 12.66, 29.09, 28.87, 25.59 and 3.68 percentages area falls under the class of VP, P, M, G and VG potential categories, respectively. Finally, NB technique uncovers that percentages for the class VP, P, M, G and VG potential categories are 14.16, 29.52, 27.21, 25.98 and 3.02%, respectively.

Table 7 Area under groundwater potential zones of different models
Full size table

Based on the very good potential and very poor potential zone a final overlay map has been created in ArcGIS platform to show the common area across the four model under the category of very good and very poor category. This overlay map (Fig. 5) presents the location where water can be easily accessible in near future. This map depicted that 10.41 km2 areas are under the very good and 20.77 km2 areas is under the very poor category of groundwater probability. This result may help in watershed management as the result provides the sites where wells are to be drilled and sites where well should not be drilled.

Fig. 5
figure 5

Final very good and very poor groundwater potential map

Full size image

Model validation

The analytical performance of four GWPZ models has been measured by several measures, namely accuracy, Kappa coefficient, RMSE, MAE and R2 (Table 8). The results clearly unveil that proposed machine learning-based Naïve Bayes model has the highest value of accuracy (87.36%), Kappa coefficient (0.85), coefficient of determination (0.86) and lowest value of MAE and RMSE as 0.16 and 0.19, respectively, in the validation phase. This result significantly represents a very high level of satisfaction in mapping of GWPZ through this model. The performance analysis of the four models in the validation stage follows the descending order: NB > RF > FR > AHP.

Table 8 The accuracy assessment of AHP, FR, NB and RF model for training and testing data using error measures
Full size table

The ROC curve (Fig. 4) unveils that NB model has (AUC = 85.5%) outperformed the RF (AUC = 85.3%), FR (AUC = 0.81.0%) and AHP (AUC = 78.8%) models in the validation phase (Fig. 6). The prediction percentage depicts that all the models have performed well, but machine learning-based RF and NB models show highest prediction effectiveness over statistical-based FR and MCDM-based AHP models.

Fig. 6
figure 6

ROC for models’ validation

Full size image

Discussion

The groundwater potentiality mapping is expected to very useful for water resource management in the studied Gandheswari river basin because most parts of the basin consist of hard rock and thereby exhibit very low primary porosity. Methodological approach for the study having high accuracy is based on logical consideration among twelve commonly used groundwater contributing factors. The elevation and slope were very low in the southeastern portion of this Gandheswari watershed. Groundwater recharge is negatively related to the elevation (Pham et al. 2021). Thus, locations that are located in low-elevation areas represent high groundwater potential in particular regions of the study area rather than the overall study area. Since the Gandheswari watershed is situated on the Pre-Cambrian granitic and gneissic rocks, the movement and occurrence of groundwater are found to be moderate to low (Etikala et al. 2019). In the current study area, shallow aquifers are of great importance as source of water (Central Ground Water Board 2017). Groundwater supports various sectors, namely agriculture, industry and many more to the human society. But recently irrational exploitation of this resource has led water shortage (Miraki et al. 2018). Reduction of surface water along with the misuse of existing groundwater has brought some key challenges to planet earth. Thus, managing the groundwater has become necessary. The current study has aimed at the exploration of GPZ in Gandheswari Watershed with the help of widely used AHP, statistical-based method FR and two machine learning algorithms, namely RF and NB. During model building for the study, the VIF has showed there is no multicollinearity problem and thus all the selected twelve parameters have been used during model building. Furthermore, InGR method has revealed that geomorphology followed by slope have the highest impact in the mapping of GWPZ.

The study unveils that the selected techniques have made a substantial contribution to map the potential groundwater sites into following categories: VP, P, M, G and VG with high accuracy. The result reveals that less than 2.71% area of Gandheswari Watershed is very good potential zone for easy access to groundwater across all models and nearly 50 to 55% area indicate moderate to good potential zone. The watershed is mostly composed of granite gneiss of Archean era; therefore, porosity and permeability are assumed to be low, besides geomorphology of the area also suggests existence of residual hill (for example Susunia Hill) which may negatively affect groundwater storage. The ROC curve uncovers that the accuracy level for AHP, FR, RF and NB is 78.8, 81.0, 85.3 and 85.5%, respectively. That definitely depicts that NB method has more accurately identified the potential groundwater sites followed by RF method. Furthermore, the research can be used by engineers and decision-makers to the refill of world’s most vital and precious resources.

Conclusions

Groundwater potential mapping using various factors is one of the significant aspects in groundwater studies. In the current research, the performance of four relatively new data mining models such as AHP, Frequency Ratio (FR), Random Forest (RF) and Naïve Bayes (NB) models has been assessed. Therefore, multi-criteria decision approach, bivariate statistic method and machine learning algorithms were employed and investigated in groundwater potential mapping. Accordingly, area under curve for prediction dataset was computed as 78.8, 81.0, 85.3 and 85.5% for AHP, FR, RF and NB models, respectively. Therefore, it can be concluded that NB had the best performance. Also, it can be suggested that data mining models performed generally well and could be considered in this field of study. This research showed that among the various approaches of the delineation of groundwater potential zone, machine learning algorithms are the most accurate and acceptable method. Moreover, it was seen that geomorphology, slope and rainfall had high importance in groundwater potential mapping, while LULC had the lowest importance. The output of the study showed that less than 2.71% area of Gandheswari Watershed is very good potential zone for easy access to groundwater across all models and nearly 50–55% area indicate moderate to good potential zone. Moreover, this work may lead appropriate selection of drilling wells and augmentation of available water resource by sustainable aquifer management. Apart from this, the present research may be further modified with the integration of some factors, i.e., the rate of abstraction of groundwater, amount of groundwater used by domestic purpose, quality of groundwater, etc., in order to find out the future potential sites for collecting water resource. Therefore, this approach can be applied in other parts of fringe area of Chota Nagpur Plateau having similar type of lithological features with or without necessary modifications.