Introduction

Water loss is a global problem. It may interrupt operations of water distribution systems (WDSs), waste pumping energy costs (Reis et al. 1997; Araujo et al. 2006; Nicolini and Zovatto 2009), and may cause contamination intrusion in water pipeline at low pressure nodes threatening human health (Kouchi et al. 2017). Mathematically, water leakage amount at a node in a WDS is proportional to the pressure at the node (Ulanicki et al. 2000) and thus the amount of water leakage increases as the WDS operates at highly excessive pressure (Savić and Walters 1996). For this reason, reducing excessive pressure tends to also reduce water losses as well as the possibility of pipe burst (Savić and Walters 1996; Reis et al. 1997; Araujo et al. 2006; Nicolini and Zovatto 2009; Adedeji et al. 2017). In general, the reduction of average pressure in the WDS will lead to the decrease of water leakage level accordingly. This is actually important, especially in pumped systems, because we can estimate the amount of water volume, and thus energy, saved over a time horizon (i.e., a year). Water pressure management can be accomplished through control of water levels in storage tanks (Nazif et al. 2010; Carmona-Paredes and Carmona-Benítez 2018), installing and optimizing operations of pressure reducing valves (PRVs) to decrease excessive pressure in WDSs (Dai and Li 2016), and simultaneously optimizing operations of pressure reducing valves and water levels in the storage tank to achieve water leakage reduction (Gupta et al. 2017).

It is due to the fact that PRVs can maintain the downstream node pressure at a preset value regardless how large the pressures at the upstream nodes are (Ulanicki et al. 2008), they are commonly installed in WDSs to regulate operational pressure of WDSs. The choice of positions for placing PRVs in WDSs is of important because proper placement of PRVs will reduce significant water leakage amount. This engineering problem can be casted into a mixed integer nonlinear program (MINLP) where binary variable for each link has to be introduced to represent the PRV position (i.e., 1 means a PRV is present and 0 not present on the link) (Eck and Mevissen 2012).

Many works in the literature have proposed modeling and solution approaches to solve such the MINLP. Hindi and Hamam (1993) applied the linear approximation technique to transform the MINLP into a mixed integer linear program (MILP). Although this approach is efficient due to the fact that only the MILP needed to be solved, it could not be applied for large-scale WDSs due to large error of approximation. Savić and Walters (1996) and Reis et al. (1997) addressed the optimal PRV localization for minimizing water leakages using Genetic Algorithm (GA). Since GA is a stochastic optimization algorithm, it can handle well nonlinear and non-smooth optimization problem, however it requires a burden of computation time. To increase the efficiency of GA solution approach, Araujo et al. (2006) applied a GA based on two-phase method to identify optimal locations of PRVs and their pressure settings. In the first phase, the number of possible valves was determined by solving a nonlinear program (NLP) where roughness coefficients of pipes are considered as decision variables. As a result, links associated with small values of roughness coefficients will be considered as potential link candidates for placing PRVs. In the second phase, the pressure settings of PRVs were determined so that a compromise between the leakage reduction amount and the valve installing cost can be attained. The short coming of the approach lies on the first phase where possible combinations of PRV locations are determined in such an heuristic way based on their frequency of appearance. Similarly, Liberatore and Sechi (2009) also solved the localization and regulation of PRVs in two phases. In contrast to the methods used in (Araujo et al. 2006), in the first phase, the number of link candidates for PRV locations is determined by using a pressure reference method (PRM) (i.e., without having to solve an optimization problem). In the second phase, a scatter search approach was employed to calculate the pressure settings of PRVs. Although the pressure reference method is capable of reducing solution search space, this method is highly sensitive to the reference pressure value (HPRM) as well as the maximum pressure (Hmax). More importantly, with the method, it is impossible to identify PRV link candidate sets for multiple demand patterns.

Nicolini and Zovatto (2009) applied NSGA-II technique for operational pressure management under multiple demand scenarios with two objective functions, the number of valves and the amount of water leakages. Creaco et al. (2010) applied a multi-objective genetic algorithm to optimize placement of isolated valve to minimize the valve installing cost and weighted average demand short fall. Later, Creaco and Pezzinga (2014) employed a hybrid algorithm combining GA and linear programming (LP) for valve placements and pipe replacements. The efficiency of the approach lies in the fact that LP is used to calculate PRV pressure setting while GA is applied to determine optimal locations of PRVs. Ali (2014) also applied GA for solving the problem of optimal locations of PRVs. The knowledge of WDSs, like significant pipes, is incorporated into the optimization model to reduce the search space and therefore improve the overall efficiency of GA. Also, Covelli et al. (2016) proposed a new hydraulic model for WDS where water leakage is distributed along links instead of nodes. The hydraulic model is coupled with a GA to optimize PRV locations and their pressure settings for real and complex WDSs. The results have been shown that a large amount of water leakage has been saved when the pressure is properly regulated. De Paola et al. (2017) proposed new methodology, namely harmony search (HS) model, to optimize localization of PRVs and their pressure settings. The results were shown to be more favorable than the ones reported in the other methods in Eck and Mevissen (2012) and Araujo et al. (2006) in term of computation time. However, it is noted that the performance of the approach was evaluated when considering only one demand pattern in peak hour for optimal locations of PRVs. Therefore, it may be different when considering multiple demand patterns as used in other approaches. Gupta et al. (2018) proposed a modified pressure reference method to determine link candidates for PRV locations. NSGA-II was used to choose the best combinations of PRVs among the link candidates as well as pressure setting of PRVs. Recently, Cao et al. (2019) proposed an approach based on the k-means++ method to simultaneously place pressure sensors and localizing PRVs for the purpose of control system design for on-line pressure control. Mehdi and Asghar (2019) introduced a new Valve Selection Index (VSI) and that the links with high values of VSI will be chosen as potential links for placing valves. The Particle Swarm Optimization was then used to determine optimal pressure settings of PRVs by maximum the nodal pressure reliability index in the WDS. In general, the heuristic algorithms can be applied to solve complex nonlinear optimization problems, however they usually require high computation time and sometimes cannot locate highly accurate solutions (Bagirov et al. 2012).

About the mathematical programming approach, Eck and Mevissen (2012) firstly developed a mixed integer nonlinear program (MINLP) for optimal localization of PRVs. The resulting MINLP was hard to be solved by standard MINLP solvers based gradient methods (Dai and Li 2014). Consequently, its solution for large scale WDSs usually lacks robustness, reliability, and efficiency (Pecci et al. 2017). Later, the new MINLP model with more linear equality constraints as compared with the MINLP model in (Eck and Mevissen 2012) is proposed by (Pecci et al. 2017). However, in general, solving such the MINLPs for large scale WDSs requires a huge computation time. The outer algorithms (OA) were demonstrated to be suitable for solving such kind of the MINLP formulation (Pecci et al. 2017), but for large scale WDSs, it is still not trivial.

To solve large scale MINLPs, a class of primal heuristics that are based on reformulating the MINLP problem into a mathematical program with complementarity constraints (MPCCs) is employed (Schewe and Schmidt 2019). The MPCCs is solved by using regularization schemes and as a result a sequence of regularized NLPs is solved. If such the sequence of regularized problems is chosen carefully, the NLP solutions will converge to a stationary point of the MPCCs, which is the solution of MINLP. Dai and Li (2014) and Pecci et al. (2017) have applied the MPCC formulation for solving the optimal PRV localization, the results have shown that this approach can be efficiently applied for large scale WDSs. Later, Pecci et al. (2017) theoretically developed penalty and relaxation schemes to solve the MPCC problem for optimal PRV localization. However, the quality of the stationary point of the MPCCs has not been investigated yet. The efficiency of the MPCC approach depends on solving the regularized NLPs. With the existing MPCC model, the regularized NLP is very high nonlinear and thus the stationary point is likely to be trapped into a bad local solution, especially at large penalty parameter values. This paper proposed a new MINLP model for optimal PRV localization where new constraints are used to describe whether PRVs are placed on links or not instead of complex constraints used in (Eck and Mevissen 2012). These new constraints make the regularized NLP being solvable with reliable solutions. In addition, since the regularized NLP at high penalty parameter value is very nonlinear, we proposed a soft heuristic method for extracting MINLP’s local solutions from a sequence of NLP solutions allowing MINLP’s local solution can be found from the first iteration, which will improve the quality of MINLP solution. Numerical experiments on our new optimization model have demonstrated that by applying our new MPCCs and MPCC computation framework beside the computation time for solving the MINLP is significantly reduced, the quality solution is indeed improved and more reliable as compared with other solution approaches in the literature can be obtained.

The remainder of this paper is organized as follows. Existing and new constraints for describing the appearances of PRVs on links are presented in section 2. Section 3 presents a new formulation of MINLP for optimal PRV localization. The MPCC algorithm and a soft heuristic method are presented in Sect. 4. Case study is presented in Sect. 5 to demonstrate the efficiency of our new MPCC model. Conclusions of this paper are provided in Sect. 6.

Existing and new constraints for modeling appearances of PRVs on links

Existing constraints for modeling PRVs placing on links (Eck and Mevissen 2012)

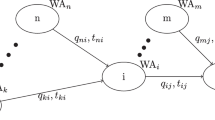
The MINLP model in Eck and Mevissen (2012) employed the following constraints (from Eq. (1) to Eq. (4) ) for modeling the appearance of PRVs on links, i.e., for forward flows, the head loss equation is

$$\begin{aligned} {Q_{i,j,k}}\left( {{H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}}} \right) \ge 0 \end{aligned}$$
(1)
$$\begin{aligned} {H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} - {M_{i,j}}{v_{i,j}} \le 0 \end{aligned}$$
(2)

Similarly, for backward flow for load scenario k, the head loss equation of a link is

$$\begin{aligned} {Q_{j,i,k}}\left( {{H_{j,k}} - {H_{i,k}} - {\varDelta } {H_{j,i,k}}} \right) \ge 0 \end{aligned}$$
(3)
$$\begin{aligned} {H_{j,k}} - {H_{i,k}} - {\varDelta } {H_{j,i,k}} - {M_{j,i}}{v_{j,i}} \le 0, \end{aligned}$$
(4)

where \(j,i=1,...,N_p\) and the pipe head loss \({\varDelta } {H_{i,j,k}}\) can be computed either by the Hazen-Williams equation

$$\begin{aligned} {\varDelta } {H_{i,j,k}} = \frac{{10.67{L_{i,j}}}}{{{D^{4.87}}}}{\left( {\frac{{{Q_{i,j,k}}}}{C}} \right) ^{1.852}} \end{aligned}$$
(5)

or by the Darcy–Weisbach equation

$$\begin{aligned} {\varDelta } {H_{i,j,k}} = \frac{{8L_{i,j}f_{i,j}}}{{g{\pi ^2}{D^5_{i,j}}}}\left| {{Q_{i,j,k}}} \right| {Q_{i,j,k}}, \end{aligned}$$
(6)

where \(L_{i,j}\), \(D_{i,j}\) and \(C_{i,j}\) are the length, diameter and Hazen–William coefficient of pipe, respectively; The friction factor \(f_{i,j}\)

The constraints in Eq.(1) and Eq.(3) are very complex and highly nonlinear. As a result, the relaxed NLP is complicated and its solution is likely to be trapped into bad local solutions. In this paper, we propose more sophisticated constraints replacing such the above constraints.

New constraints for modeling PRVs placing on links

The new and more sophisticated constraints are proposed to replace constraints in Eq.(1) and Eq.(3). In fact, instead of using Eq.(1), we use the non-smooth constraint, \(\max \left( {0,{H_{i,k}} - {H_{j,k}}} \right) - {\varDelta } {H_{i,j,k}} \ge 0\). By setting \({\beta _{i,j,k}}=\max \left( {0,{H_{i,k}} - {H_{j,k}}} \right)\), such the non-smooth constraint is equivalent with following constraints

$$\begin{aligned} {\beta _{i,j,k}} - {({H_{i,k}} - {H_{j,k}})} \ge 0 \end{aligned}$$
(7)
$$\begin{aligned} {\beta _{i,j,k}}\left( {{\beta _{i,j,k}}} - {({H_{i,k}} - {H_{j,k}})} \right) \le \varepsilon \end{aligned}$$
(8)
$$\begin{aligned} {\beta _{i,j,k}} - {\varDelta } {H_{i,j,k}} \ge 0 \end{aligned}$$
(9)

for backward flows, instead of using Eq.(3), the following constraint is employed

$$\begin{aligned} {H_{j,k}} - {H_{i,k}}+{\beta _{i,j,k}} - {\varDelta } {H_{j,i,k}} \ge 0 \end{aligned}$$
(10)

The constraints from Eq.(7) to Eq.(10) combined with constraints in Eq.(2) and Eq.(4) are new constraints for modeling the appearances of PRVs on links.

We will show that these constraints exactly describe whether PRVs are placed on links or not. At first, we consider the case as \({H_{i,k}} \ge {H_{j,k}}\) since \(\beta _{i,j,k}={H_{i,k}} - {H_{j,k}}\), from constraints in (9) and (2), we obtain \({H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} \ge 0\) and \({H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} - {M_{i,j}}{v_{i,j}} \le 0\). In this case, if \(v_{i,j}=0\) then these constraints are the model equation of a normal pipe. Otherwise, if \(v_{i,j}=1\) then these constraints describe the model equation of a PRV because \({H_{i,k}} - {H_{j,k}} \ge {\varDelta } {H_{i,j,k}}\). In addition, from constraints (10), we have \({H_{j,k}} - {H_{i,k}}+{H_{i,k}} - {H_{j,k}}- {\varDelta } {H_{j,i,k}} = -\frac{{10.67{L_{i,j}}}}{{{D_{i,j}^{4.87}}}}{\left( {\frac{{{Q_{j,i,k}}}}{C_{i,j}}} \right) ^{1.852}} \ge 0\), which results in \(Q_{j,i,k}= 0\) and indicates that PRVs cannot be placed on the link with direction from j to i. Similarly, in the case \({H_{j,k}} > {H_{i,k}}\), model equations describing whether a PRV is placed on link ij with direction from j to i can be deduced in the same fashion. With the new constraints, the relaxed NLP will be more suitable for NLP solver.

A new MINLP formulation for optimal localization of PRVs

We will formulate the MINLP with our newly proposed constraints for optimal PRV localization. Considering a WDS with \(N_n\) nodes, \(N_p\) links, \(N_r\) reservoirs, and \(N_L\) demand patterns, the aim of our optimization problem is to determine optimal locations for placing PRVs so as to minimize the excessive pressure. Therefore, the objective function is defined as the minimization of the total excessive pressure of all nodes under multiple demand patterns (Germanopoulos and Jowitt 1989).

Objective function

$$\begin{aligned} \mathop {\min }F = \sum \limits _{i = 1}^{{N_n}} {\sum \limits _{k = 1}^{{N_L}} {\left( {{H_{i,k}} - H_{i,k}^L} \right) } } \end{aligned}$$
(11)

Hydraulic constraints

The continuity equation at node i for scenario k

$$\begin{aligned} \sum \limits _{j,k} {{Q_{j,i,k}}} - \sum \limits _{j,k} {{Q_{i,j,k}}} - {d_{i,k}} - {l_i} = 0 \end{aligned}$$
(12)

\(k=1,...,N_L,\); \(i=1,...,N_n\)

The leakage amount associated to node i is calculated by (Araujo et al. 2006).

$$\begin{aligned} {l_i} = {C_L}{L_{t,i}}p_i^\gamma \end{aligned}$$
(13)
$$\begin{aligned} {L_{t,i}} = 0.5\sum \limits _j {{L_{i,j}}}, \end{aligned}$$
(14)

where \(i=1,...,N_n\); \(C_L=10^{-5}\) is the discharge coefficient of the orifice (Araujo et al. 2006); \(L_{i,j}\) is the length of pipe ij; \(p_i\) is the pressure at node i

Constraints for modeling whether PRVs are placed on links

Our newly proposed constraints for describing whether PRVs are placed on links or not are given in Eq.(2), Eq.(4), Eq.(7), Eq.(8), Eq.(9), and Eq.(10).

Constraints for ensuring that only one PRV can be placed on the link and maximum number of PRVs

$$\begin{aligned} 0 \le {v_{i,j}} + {v_{j,i}} \le 1 \end{aligned}$$
(15)

Moreover, if a maximum \(N_{prv}\) of PRVs are to be placed in the system, there should be

$$\begin{aligned} \sum \limits _{i,j} {({v_{i,j}} + {v_{j,i}}) = N_{prv}} \end{aligned}$$
(16)

Operational constraints

$$\begin{aligned} {H^L} \le {H_{i,k}} \le {H^U} \end{aligned}$$
(17)
$$\begin{aligned} 0 \le {Q_{i,j,k}} \le {Q^U} \end{aligned}$$
(18)
$$\begin{aligned} 0 \le {Q_{j,i,k}} \le {Q^U} \end{aligned}$$
(19)
$$\begin{aligned} {v_{i,j}},{v_{j,i}} = {\left\{ {0,1} \right\} ^{2{N_p}}} \end{aligned}$$
(20)

Constant reservoir heads

$$\begin{aligned} {H_{i,k}} = {{\overline{H}}}_i, \end{aligned}$$
(21)

where \(i=1,..., N_r\)

The formulated MINLP has \(3{N_p}\times T\) + \({N_n}\times T\) continuous variables, \(2{N_p}\) binary variables, and \(6{N_p} \times T + {N_n}\times T+ {N_p}+ 1\) constraints. It can be recognized that as compared with the MINLP in (Eck and Mevissen 2012), our new MINLP has more \(2{N_p}\times T\) constraints (i.e., equality constraints in (7) and (8)) among which \({N_p}\times T\) constraints are linear (i.e., constraints in (7)). As demonstrated in the next section, although our MINLP model has more constraints, it is simpler than the one in (Eck and Mevissen 2012). In general, the MINLP is written in the following form.

$$\begin{aligned} \begin{array}{l} \min f\left( {{\mathbf{x}},{\mathbf{z}}} \right) \\ {\mathrm{s}}{\mathrm{.t.}}\\ {\mathbf{g}}\left( {{\mathbf{x}},{\mathbf{z}}} \right) = {\mathbf{0}}\\ {{\mathbf{x}}^L} \le {\mathbf{x}} \le {{\mathbf{x}}^U}\\ {\mathbf{z}} = {\left\{ {0,1} \right\} ^{2{N_p}}}, \end{array} \end{aligned}$$
(22)

where \(\mathbf{x}\) and \(\mathbf{z}\) represents the vector of continuous variables and vector of binary variables, respectively; \(\mathbf{g}\) represent constraints of the MINLP.

The mathematical complementarity constraints (MPCCs) and a soft heuristic strategy for local solution extraction

The MPCC formulation

In general, the MINLP is reformulated by the MPCC model as (Herty and Steffensen 2012; Schewe and Schmidt 2019)

$$\begin{aligned} \begin{array}{l} \min f\left( {{\mathbf{x}},{\mathbf{z}}} \right) \\ {\mathrm{s}}{\mathrm{.t.}}\\ {\mathbf{g}}\left( {{\mathbf{x}},{\mathbf{z}}} \right) = {\mathbf{0}}\\ {z_i} \bot \left( {1 - {z_i}} \right) = 0\\ 0 \le {z_i} \le 1\\ {{\mathbf{x}}^L} \le {\mathbf{x}} \le {{\mathbf{x}}^U}\\ i = 1,...,2{N_p} \end{array} \end{aligned}$$
(23)

To solve the MPCCs, the complementarity constraints (i.e., \({z_i} \bot \left( {1 - {z_i}} \right) = 0\)) are replaced by NCP functions. One of such the form is the Fischer–Burmeister function proposed by Fischer in (Fischer 1992)

$$\begin{aligned} \phi = a + b - \sqrt{{a^2} + {b^2}} \end{aligned}$$

The non-differentiability in \(\left( {a,b} \right) = \left( {0,0} \right)\) which typically resolved by regularizing the square root with a positive small value,\(\tau\), giving

$$\begin{aligned} \phi = a + b - \sqrt{{a^2} + {b^2} + \tau } \end{aligned}$$

In our MPCC, by applying \(a = {z_i}\) and \(b = 1 - {z_i}\), we obtain

$$\begin{aligned} \phi = 1 - \sqrt{{{\left( {1 - {z_i}} \right) }^2} + z_i^2 + \tau } \end{aligned}$$

As seen, when \(\phi\) gets a sufficiently small value, the relaxed binary variables (i.e., \(0 \le {z_i} \le 1\)) will get approximated binary values. In addition, the direct use of constraint \(\phi =0\) will cause serious numerical problems (Schewe and Schmidt 2019). For this reason, we employ the penalty regularization scheme (i.e., minimize \(\phi\)) to solve the NCP problems, and at \(\rho ^k\), the resulting regularized \(NLP(\rho ^k)\) is

$$\begin{aligned} \begin{array}{l} \min f\left( {{\mathbf{x}},{\mathbf{z}}} \right) + {\rho ^k}\sum \limits _{i = 1}^{2{N_p}} {\left( {1 - \sqrt{{{\left( {1 - {z_i}} \right) }^2} + z_i^2 + \tau } } \right) } \\ {\mathrm{s}}{\mathrm{.t}}\\ {\mathbf{g}}\left( {{\mathbf{x}},{\mathbf{z}}} \right) = {\mathbf{0}}\\ 0 \le {z_i} \le 1\\ {{\mathbf{x}}^L} \le {\mathbf{x}} \le {{\mathbf{x}}^U}\\ i = 1,...,2{N_p} \end{array} \end{aligned}$$
(24)

It is recognized that as \(\rho ^k\rightarrow \infty\), \(\phi \rightarrow 0\) and the stationary point will be a solution of the MINLP.

The MPCC algorithm and local solution extraction

Remark

Solving the NLP with a particular penalty parameter will results nonzero values of \(v_{ij}\) and \(v_{ji}\). The links associated with nonzero values of \(v_{ij}\) and \(v_{ji}\) are considered as potential links for placing PRVs and that it is possible to choose any combinations of links among these links for placing PRVs without causing infeasibility of the MINLP.

Proof

It is clear that the considered WDS has excessive pressure and that PRVs are placed to decrease these excessive pressure. In this case, as no PRV is placed (i.e., by fixing all \(v_{ij}\) and \(v_{ji}\) to 0.0), the WDS still works and the model equations of the WDS are always satisfied. Now, we assume that after solving the NLP, links ij having nonzero \(v_{ij}\) (or \(v_{ji}\)), from the constraints in (9) and (??), we have \({H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} \ge 0\) and \({H_{i,k}} - {H_{j,k}}- {\varDelta } {H_{i,j,k}} - {M_{j,i}}{v_{j,i}} \le 0\). By selecting a number of links for placing PRVs, it will be equivalent to fix some \(v_{ij}\) (or \(v_{ji}\)) to 0.0 and some \(v_{ij}\) (or \(v_{ji}\)) to 1.0. This will leads to some constraints with the kind of \({H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} = 0\) and some constraints with \(0 \le {H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}}- {M_{j,i}} \le 0\). These constraints are always satisfied, because \(0 \le {H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}}- {M_{j,i}} \le 0\) covers the case \({H_{i,k}} - {H_{j,k}} - {\varDelta } {H_{i,j,k}} = 0\) which are always satisfied. Therefore, the remark is proved. A heuristic method for identifying local solutions: From the lema, in this paper, a more soft heuristic strategy for extracting earlier local solution is proposed. In fact, at first, in each iteration, we define a set of link ij and rank them according to their values of \(v_{ij}\) or \(v_{ji}\), namely \(B_{k}=\{ij, v_{ij} (v_{ji})\ge v_{mn}(v_{nm}); ij=1,..., N_{p}; ij\ne mn\}\). Then, we choose the first \(N_{prv}\) links, \(P_k=\{ij_{(1)},ij_{(2)},...,ij_{(N_{prv})}\}\), as a combination of links for placing PRVs. The MINLP with fixed locations of PRVs now becomes the NLP and it is solved by a NLP solver. Better solution is updated if it results in lower objective function value. The MPCC algorithm is terminated when the stationary point is reached, i.e., number of links with nonzero values of \(v_{ij} (v_{ji})\) is equal to number of PRVs installed in the WDS (\(|B_{p}|= N_{prv}\)). To the end, along with the strategy of finding the stationary point (solution) of the MPCC, the local solution will be extracted with hope that the better solution can be found. The MPCC combined with the heuristic algorithm is given in Table 1. \(\square\)

Table 1 Computation framework
Full size table

Case studies

Case study 1a: PRV localization for a benchmark WDS

The new MPCC will be applied to determine optimal locations for placing PRVs in a benchmark WDS studied by (Sterling and Bargiela 1984; Jowitt and Xu 1990; Reis et al. 1997; Vairavamoorthy and Lumbers 1998; Araujo et al. 2006) as shown in Fig. 1. The system comprises 22 nodes, 3 reservoirs, and 37 links. The emitter coefficients were determined through the methodology developed by (Araujo et al. 2006). In addition, the leakage exponent (\(\gamma\)) was fixed to 1.18 for all the nodes. The 24 demand patterns and 24 heads of reservoirs 23, 24, and 25 are given in (Araujo et al. 2006). The head loss equation is calculated by Hazen-Williams equation as in (5). Optimal PRV localization will be formulated for 24 demand patterns and ensure that the minimum pressure at all demand nodes are kept at a value of 30.0 m.

Fig. 1
figure 1

WDS benchmark for PRV localization (Sterling and Bargiela 1984; Jowitt and Xu 1990)

Full size image

The resulting MINLP problem has 3192 continuous variables, 74 binary variables, and 5894 constraints. Several scenarios on number of PRVs (\(N_{prv}=1,2,3,4,5,6\)) are considered, and IPOPT solver is used to solve the regularized \({NLP(\rho ^k)}\). All computation experiments are accomplished on computer desktop Intel(R) Core(TM)i5-6500CPU@3.2GH, RAM 8GB. For all scenarios, we set \({\rho ^0}\) to 1.0 and the \(\sigma =1.1\). The link combinations for placing PRVs and computation times for each scenario are given in Table 2. It can be seen that using our new MPCC model and algorithm, computation times for solving the MPCC are significantly reduced as compared with those reported in (Dai and Li 2014). In particular, for the case \(N_{prv}=2\), in each iteration, a potential combination of links for placing PRVs is identified and the corresponding objective function values are found. As seen in Fig. 2, using our soft heuristic method for local solution extraction, the best combination of links, 1 and 11, resulting in the objective function value of 1777.2 m is identified. It is also seen that if we implement the MPCC algorithm alone ( without the heuristic method), the stationary point is also reached but with the combination of links 11 and 21. This combination results in the objective function value of 2037.35 m. In this case, our proposed heuristic method for local solution extraction is indeed beneficial.

Table 2 Comparison of solving the MINLPs
Full size table

Next, we consider the case \(N_{PRV}=3\). As seen in Fig. 4, from the \(1st\) iteration to \(20th\) iteration, using our algorithm, the combination of links of 1, 11, 29, is identified and the corresponding objective function value is 1664.37 m. From \(21th\) iteration to \(64th\) iteration, links 1,11,21 is found for placing PRVs resulting in the objective function value of 1690.46 m. From the \(65th\) iteration, the best combination of links 11,20,21 is found with the objective function value of 1326.45 m. In this case, the MPCC converges to the best solution.

Fig. 2
figure 2

Profile of objective function values for \(N_{prv}=2,3, 4\)

Full size image

Now for \(N_{PRV}=4\), using our MPCC algorithm, a combination of links is extracted in each iteration. It is seen in Fig. 2, from \(1st\) to \(62th\) iterations, a combination of links 1,11,21,29 is identified resulting in the excessive pressure of 1465.91 m. From \(63th\) iteration, using the local solution extraction method, the best combination of links 1,11,20, and 29 is found with the objective function value of 1164.03 m. In this case, at the final iteration, the MPCC algorithm converges to such the best solution.

Fig. 3
figure 3

Potential links for the case \(N_{prv}=5\) a Iterate 1st, b Iterate 3rd, c Iterate 52th, d Iteration 55th

Full size image

Similarly, in the cases of \(N_{prv}=5\) and \(N_{prv}=6\), as seen in Fig. 4, we see that by applying the heuristic strategy, it is possible to identify better solution before the MPCC converges to the stationary point (i.e., at final iteration). In particular, for the case of 5 PRVs, using our approach, the best combination of links, 1,11,20,21,29, is found at the \(55th\) iteration, and the MPCC converges to the same solution at the \(68th\) iteration. In particular, as seen in Fig. 3 at the first iteration, a combination of links 1,11,23,22,29 is found corresponding with the objective function value of 1551.41 m, then better solution with a combination of links 1,11,21,23,29 is identified at the \(52th\) iteration with the objective function values of 977.18 m. The best combination of links, 1,11,20,21,29 is found at the \(55th\) iteration, and the MPCC also converges to this solution at the final iteration. Similarly, in the case of 6 PRVs, the best combination of links of 1,11,20,21,29 is found at \(65th\) and the MPCC also converges to the same solution. It is also seen in Fig. 4 that when \(N_{prv}\) increases, many links can be candidates for placing PRVs therefore the changes of objective function values are not flat as in the case number of PRVs is small.

Fig. 4
figure 4

Profile of objective function values for \(N_{prv}=5, 6\)

Full size image

The comparison of our new MPCC and the one using the MINLP developed by (Eck and Mevissen 2012) on solving the optimal PRV localization is given in Table 2. It can be seen that the same solution is found for all scenarios. However, using our new optimization model, the computation time is significantly reduced. After an extensive investigation, we reveal that the MPCC reformulated from the MINLP Eck and Mevissen (2012) is highly sensitive to the initial guesses, therefore in the MPCC solution framework in Dai and Li (2014), the solution of the \(NLP(\rho ^k)\) is not used as initial value for the \(NLP(\rho ^{k+1})\), instead randomly initial guesses are used. This strategy significantly increase the computation time while the good solution is not always ensured. To demonstrate this point, in Fig. 5, we run both MPCC formulations with the same value of \(\rho ^0\) and \(\sigma\), for both cases of \(N_{prv}=4, 5\) the best solution found by using our optimization model are better than the one found by using the existing MPCCs.

Fig. 5
figure 5

Profiles of objective function values

Full size image

The reduction of average pressure in the WDS will lead to the decrease of water leakage flows. In order to evaluate such the water leakage decrease (after placing PRVs), the case of 6 PRVs is investigated. The results of optimal pressure settings for these PRVs indicated that among 6 PRVs only three PRVs on links 1, 11, and 21 are operated in active modes while the others are worked in closed mode in the whole time horizon. The optimal pressure settings of these PRVs working in active modes are shown in Fig. 6. It can be seen in the figure that the pressure settings of PRV 21 are adjusted in a range of values from 32.0 to 32.5 m while the pressure settings of PRV 1 are around values of 30.0 m. On the contrary, pressure settings of PRV 11 are changed more significantly (i.e., from 30.5 m to 32.5 m) to adapt with variation of the water demand factors. In particular, during the periods of low demand factors (i.e., from 0 to 6:00), the pressure settings are set to low values, while in the ones with high demand factors (i.e., from 7:00 to 22:00), the pressure settings are set to higher values to ensure that the pressures at nodes are at least of 30.0 m.

Fig. 6
figure 6

Optimal pressure settings for PRVs

Full size image

For water leakage decrease evaluation, at first, we consider the case as \(\gamma\) is set to 1.18 and with 6 PRVs installed in the WDS, the results of water leakage flows are compared with the ones where no pressure control is made (no PRV is placed) and they are given in Table 3. It can be seen that, an amount of 498.45 m\(^3\) water will be saved for a day and it is about 179,442.000 m\(^3\) for a year demonstrating the benefit of installing and regulating PRVs for pressure control in the WDS.

Table 3 Comparisons of water leakage flows with \(\gamma =1.18\)
Full size table

Now, we consider the case as \(\gamma\) is set to 0.5, with the same PRV positions, the optimal pressure settings are found by solving the NLP (i.e, the MINLP with fixed binary variables). The comparisons of water leakage flows are given in Fig. 7. It can be seen that, for this case, a decrease of 19.47 m\(^3\) of water per day is achieved with installation of 6 PRVs. As compared with the case \(\gamma =1.18\), the water leakage flows decrease significantly. This is reasonable because, according to Eq.13, the water leakage amounts (\(l_i\)) at nodes are much reduced as \(\gamma\) decreases.

Fig. 7
figure 7

Water leakage flows for the case \(\gamma =0.5\)

Full size image

To the end, it can be concluded that, as the average pressure in the WDS is regulated to an appropriate level (i.e., ensuring that the minimization of excessive pressure is achieved), the water leakage flow is decreased significantly. In addition, with different values of \(\gamma\), different water leakage flows are observed and that higher value of \(\gamma\) will result in higher water leakage level.

Case study 1b: PRV localization for a large benchmark WDS

To demonstrate the efficiency of our new optimization, we apply it to determine optimal locations for placing PRVs for EXNET network (Farmani and Walters 2004), the largest scale benchmark WDS. The system consists of 2465 links, 1890 nodes, and 2 reservoirs as shown in Fig. 8.

Fig. 8
figure 8

WDS benchmark for PRV localization (Farmani and Walters 2004)

Full size image

The data of the WDS are given in (Dai and Li 2014) where the allowable minimum pressure is kept at 8.0 m. Reservoir heads are fixed to 80.0 m. We consider the demand pattern multiplier of 1.0. The head loss equation is calculated by Eq. (6). This WDS is a benchmark case study investigated in (Farmani and Walters 2004; Eck and Mevissen 2012) only for purpose of optimal pressure management and that the water leakage incidents are not taken into account in the model, i.e., the discharge coefficient of the orifice (\(C_L\)) is set to zero for all nodes. For this reason, our algorithm is implemented with such the model without leakage incidents although it can handle the model with leakage incidents and with specified values of \(\gamma\). Numerous scenarios on numbers of PRVs placed in the WDS are used, i.e., \(N_{prv}=1\) to 10. The resulting MINLP model has 4930 binary variables, 9285 continuous variables, and 19147 constraints. Such the MINLP is certainly not trivial to be solved by standard MINLP solvers. Our proposed MPCC algorithm is implemented with \({\rho ^0}=1.0\) and \(\sigma =1.1\) and optimal locations for placing PRVs are given in Table 4 together with the optimal solutions reported in (Dai and Li 2014). It can be seen that using our new MPCC better solution can be achieved in all scenarios. Fig. 9 demonstrates the profiles of objective function values for the whole iterations corresponding with \(N_{prv}=3,4,5,6\), once again, it is seen that most good solutions are identified by our heuristic solution extraction before the stationary point of the MPCC is reached.

Fig. 9
figure 9

Objective function values for the case \(N_{PRV}=3,4,5,6\)

Full size image

In these Figures, the MPCC algorithm terminates at the \(58th\) iteration. It can be seen that in early iterations, the changes of objective function values are small while they are large at late iterations. The reason is that at late iterations penalty parameter values are relatively high, and solving such the regularized NLP will result in relaxed variables, \(v_{ij} (v_{ji})\) swinging around binary values (0,1). The changes of variables from values from 1 to 0 or reversely leading to the significant changes of the objective function values. This is seen in in Figs. 9 and 10 that our heuristic algorithm for extracting local solution is extremely beneficial in finding good solutions because the \({NLP(\rho ^k)}\) with a high value of \(\rho ^k\) becomes strongly non-convex and stationary points (i.e., at the final iteration) are likely trapped into bad local solutions.

Table 4 Optimal PRV locations for the EXNET network
Full size table

It is also seen in Table 4, installation of PRVs in the WDS significantly lowers excessive pressure, i.e., considering the case of 10 PRVs, the total decrease of excessive pressure is 9960.06 m as compared with the case no PRV is installed.

Fig. 10
figure 10

Objective function values for the case \(N_{PRV}=7,8,9,10\)

Full size image

Case study 2

The new optimization model with a soft heuristic method for solution extraction will be used to determine optimal locations of PRVs for a real-world water distribution system in Thai Nguyen City in Vietnam as shown in Fig. 11. The system consists of 99 nodes, 116 links, and 4 reservoirs.

Fig. 11
figure 11

Water distribution system in Thainguyen City

Full size image

The network structure and pipeline data are from the local water company. The water demand profiles are from the historical data of the network operation and are given in Table 5 while the constant total heads of reservoirs 150, 151, 152 and 153 are fixed to 111.74 m, 75.21 m, 69.57 m, and 69.46 m, respectively. To demonstrate the reduction in water leakage flow (i.e., after installing PRVs) in the WDS, the water leakage incidents are assumed to be at nodes 13, 25, and 78 where corresponding emitter coefficients (equivalent to \(C_LL_{t,i}\) in Eq. (13)) are 0.2, 0.1, and 0.1 L/m\(^{\gamma }\), respectively. In addition, \(\gamma\) is set to a value of 1.18. The WDS is modeled in EPANET 2 (Rossman 2001). Similar to case study 1, our new MPCC model are formulated for optimal PRV locating problem with three demand patterns, 0.36, 0.86, and 1.34. The resulting MINLP model has 1329 continuous variables, 232 binary variables, and 2490 constraints, respectively. The minimum allowable pressure at demand nodes is maintained at 17.0 m. We implement the MPCC algorithm with \({\rho ^0}=1.0\) and \(\alpha =1.1\). The optimal locations for placing PRVs found for numerous scenarios by applying the MPCC algorithm are given in Table 6 together with those found by using the existing MPCC. It is seen that our new MPCC outperforms the existing one for the case \(N_{prv}=6,5,3\), while they identified the same solution for the rest cases. The profiles of objective function values for scenarios for whole iterations are given in Fig. 12, if we implement the MPCC algorithm alone (i.e., without extracting local solution method) only with the case \(N_{prv}=6\), the MPCC algorithm converges to the best solution as found by the heuristic method.

Table 5 Daily water demand pattern factors
Full size table

In particular, we consider the strategy of extracting local solution for the case \(N_{prv}\)=5 in detail. From the \(2nd\) to \(55th\) iterations, a combination of links, 1, 3, 5, 100, 121 is identified with the corresponding objective function value of 2583.29 m. From the \(56th\) to \(60th\) iterations, we found links 1, 3, 5, 100, and 104 with the objective function value of 2449.40 m. The best combination of links 1,3,5,69, and 100 is identified from the \(76th\) iteration with the corresponding objective function value of 2449.31 m. As seen in Fig. 12, the stationary point (solution of the MINLP) is found with the combination of links 1, 3, 5, 100, and 104, which is a bit worse than the best solution found by the soft heuristic method.

Fig. 12
figure 12

Objective function values for the case \(N_{PRV}=2,3,4,5,6\)

Full size image

Similarly, for the case of \(N_{PRV}\)=6, by applying the heuristic method, we at first found the combination of links 1, 3, 5, 18, 102, 121 with the objective function value of 2890.25 m, and the best combination of link, 1, 2, 3, 5, 69, 100, is found with the objective function value of 2306.51 m at the \(70th\) iteration. In this case, the MPCC converges to the stationary point, which is the same as the solution extracted by using our heuristic method as seen in Fig. 12.

Table 6 Optimal PRV locations for the WDS
Full size table
Fig. 13
figure 13

Pressure settings of 6 PRVs

Full size image

To demonstrate the efficiency of pressure management by placing PRVs, we consider the case of 6 PRVs in WDS, the respective optimal pressure settings of PRVs for 24 hours are demonstrated in Fig. 13, it can be seen that, at low demand pattern periods, i.e., from, 1 a.m to 5:00 a.m, according to high pressure appearing in the WDS, pressure settings of PRVs are regulated to sufficiently small values to decrease the system pressure, this is reasonable. On the contrary, at large demand pattern periods, i.e., from 6:00 a.m to 20:00, the pressure settings of PRVs tend to be higher to ensure that pressures are sufficient to satisfy pressure requirement (i.e., minimum pressures at demand nodes are larger than 17.0 m) from supplying water.

The distribution of pressure in the WDS for three demand pattern values is shown in Fig. 14. It is seen that, when PRVs are properly placed in the WDS, the excessive pressure of the system is significantly decreased. In particular, at low demand pattern of 0.36 and without pressure management, high excessive pressure is observed (see Fig. 14a). However, with PRV installation, much more reduction in excessive pressure is attained (see Fig. 14b). Similarly, at medium demand pattern value of 0.86, as seen in Fig. 14c, d, pressures at most of nodes in the WDS with PRV installation are less than 25.0 m while they are larger than 25.0 m for the case no PRV is installed. At high demand pattern value of 1.34, since large flows are consumed making the system pressure decreased. In this case, pressure settings of PRVs are set to appropriate values to ensure that pressures are sufficient at low pressure zones, while it is at acceptable level at high pressure zones.

Fig. 14
figure 14

Distribution of pressures with 6 PRVs (right) and without PRVs (left) with various demand pattern factors. Demand pattern of 0.36 a without PRVs b with 6 PRVs; Demand factor of 0.86 c without PRVs d with 6 PRVs; Demand factor of 1.34 e without PRVs f with 6 PRVs

Full size image

For water leakage decrease evaluation, we consider the case of 6 PRVs installed in the WDS. The results of water leakage flows are given in Table 7 together with the ones when no pressure control is made (without installation of PRVs). It can be seen in the table that much more water leakage amount is decreased as PRVs are placed for pressure regulation. In particular, for a day, it is possible to save an amount of 1044.30 m\(^3\) of water, and for a year, it is about 375,960.000 m\(^3\). Drinking water is valuable for countries worldwide, especially when water resources now becoming scarcity according to exhaustive exploitation and the intrusion of seawater into the land increases salinity of groundwater. For this reason, savings of drinking water have been becoming one priority task for water utilities and this can be accomplished in such an efficient manner by regulation of average pressures in WDSs to economic levels.

Table 7 Comparisons of water leakage flows with \(\gamma =1.18\)
Full size table

Conclusion

We have presented a new optimization model and MPCC algorithm for identifying optimal locations for placing PRVs in WDSs in order to minimize excessive pressure and thus decrease water leakage flows. The new optimization model is suitable and easier to be solved by standard NLP solvers. As a result, the MPCC algorithm can be accomplished in such an efficient manner. In addition, the MPCC algorithm is enhanced by a soft heuristic strategy, which will choose potential links for placing PRVs basing on their values of relaxed binary variables in each iteration. Using this heuristic strategy, it is possible to determine early potential combinations of links for placing PRVs and thus, in the case the stationary point of the MPCC has bad quality (i.e., which likely occurs at large values of penalty parameter), better solution still can be found. Numerical experiments on solving the optimal PRV localization for two benchmark WDSs and a real-world WDS in Vietnam demonstrated that our new optimization model and the MPCC algorithm are indeed efficient and outperforms the existing one in terms of optimal solution and computation time.