1 Introduction

The aim of a water distribution system (WDS) is to supply water with proper pressure and quality. On the one hand, a minimum operational pressure is required for an adequate water supply (Brentan et al. 2021). On the other hand, higher pressure can lead to breaks and higher water losses if leaks are present (Kourbasis et al. 2020). Therefore, pressure management represents an important task for WDS operation. In addition, water quality for drinking purposes should be ensured. Water age is an essential indicator of water quality. High levels of water age give rise to serious effects on human health (AWWA with assistance from Economic and Engineering Services, Inc. 2002; Wu et al. 2005; Wang et al. 2014). Therefore, in addition to pressure management, it is also necessary to perform water age management so that WDSs can be operated with minimum water age.

The installation and operation of a certain number of pressure reducing valves (PRVs) in a WDS has been considered as an effective measure for pressure management (Dai and Li 2016; Fontana et al. 2018; Gupta et al. 2018; Cao et al. 2019). Its basic idea is to operate the PRVs in such a way that the working pressure, and thus, the water loss in a WDS is minimized. Determining the optimal positions and settings of the PRVs leads to a complicated mixed-integer nonlinear programming (MINLP) problem that has been solved through the development of sophisticated optimization approaches and, as a result, the total pressure can be considerably reduced (Nicolini and Zovatto 2009; Eck and Mevissen 2012; Dai and Li 2014; Pecci et al. 2017). In this study, we are concerned with the question: Is it possible to use such PRVs simultaneously for pressure and water age management?

To answer this question, we need a model that describes the relationship between water age and its influencing factors. Water age can be affected by daily water demand, system design such as pipe dimensions as well as distribution network structure, and WDS operation such as pressure and water flow (Shu et al. 2010). Since the PRVs installed in a WDS can be operated to manipulate the pressure and flow, their operation will affect water age. Water age, or mean hydraulic residence time, is the average time it takes for water to travel from a source to a particular location in a WDS. It can be understood as the length of piping from the location to the water source divided by the average flow velocity (American Water Works Association 1999). In a looped network, different flow paths are possible, i.e. determined by the varying demands at different locations in the WDS. A change between a potentially existing short flow path from the source (a lower water age) and a long flow path from the source (a higher water age) can result in a different water quality at that location (Best 2005).

According to Murray et al. (2009), the average water age of a WDS in a time period can be assessed as the median of the summed water age at all junctions and time points. Murray et al. (2015) describe different computation approaches that consider water age if it is above a certain threshold indicating potential water quality problems. A more rigorous model was presented in Rossman and Boulos (1996), where water age is considered as a reactive constituent whose growth follows zero-order kinetics. As a result, the water age at a junction can be calculated by solving the classical one-dimensional advection equation describing fluid transport through the pipes to the junction. Rossman and Boulos (1996) showed that this method is highly efficient and has therefore been implemented in EPANET (Rossman et al. 2020). However, for the purpose of water age management using an optimization approach, such a model can be highly complicated in the formulation and solution of the optimization problem.

A simple, easy-to-use water age model was proposed in Wang et al. (2009) using a junction-by-junction approach. Its basic idea is to calculate the water age at a junction based on the known water age of the neighboring nodes and the flow rate of the connecting links. A comparative study in Chen et al. (2018) showed that the difference between the water age results from EPANET and the junction-by-junction method is quite small and can be neglected. In addition, it is shown that water age and pressure can be controlled indirectly by appropriate localization of PRVs.

The most common way to minimize the operating pressure in a WDS is to install PRVs at optimal locations in the network, which leads to a mixed-integer optimization problem. This problem is typically solved using appropriate algorithms from the genetic algorithm (GA) family. Mahdavi et al. (2010) formulated an optimization problem for optimal locations of a fixed number of PRVs and solved it using a single objective GA. PRV installation was considered as part of network modifications (along with pipe replacement and duplication or tank enlargement) by Roshani and Filion (2014) to minimize the capital and operational costs of the network, where a fast-elitist non-dominated sorting GA (NSGA-II) was used as the solution method. Similar works were done by Vassiljev and Puust (2016) and Covelli et al. (2016).

Mixed-integer optimization has been widely used for optimal design and operation of WDSs (Ulanicki et al. 2007; Pulido-Calvo and Gutiérrez-Estrada 2011; Cassiolato et al. 2024; Price and Ostfeld 2013; Belotti et al. 2013; Pecci et al. 2021). Eck and Mevissen (2012) proposed a MINLP formulation for the placement and setting of PRVs, which was extended to dynamic demand scenarios in Pecci et al. (2017). In Dai and Li (2016), a reformulation approach was developed to solve the MINLP problem for determining optimal locations of PRVs in WDSs to minimize water leakage. The MINLP problem is reformulated as a mathematical program with complementarity constraints (MPCC), which can be efficiently solved by an NLP algorithm.

Recent studies have also considered pressure and water age management simultaneously, mostly using a random search approach (e.g., GA) combing the simulation tool EPANET (Zeidan et al. 2018; Desta et al. 2022). The impact of pressure management on water age was analyzed in Salomons and Ostfeld (2017) and Kravvari et al. (2018) by dividing the network into district metered areas (DMAs) and placing PRVs at each entry node of a DMA. This work was extended for a trade-off between water age and pressure with pressure regulations in the Kos network (Patelis et al. 2020). In Kourbasis et al. (2020), GA was used to find an optimal layout of closing pipes throughout the network to form DMAs and install PRVs, showing that the use of PRVs leads to reduced system pressure but increased water age.

According to Chondronasios et al. (2017), water age is affected by the number of DMAs and the location of closed valves on certain pipes, showing that the optimal solution requires inclusion of the competing objectives of water age and operating pressure. As noted in Brentan et al. (2021), simultaneous optimization of water age and pressure in a WDS is possible using a heuristic technique when these parameters are optimized together, which focuses on optimal valve operation by given PRV locations. Recently, Shmaya and Ostfeld (2022) proposed a method for PRV placement with the goal of reducing water age based on the graph theory so that shorter paths or higher flow velocities can result.

Based on the above literature review, it can be seen that many studies have been carried out for pressure and/or water age management using optimization approaches. So far, a few studies have been conducted using heuristics, GA, and graph theory to minimize water age and pressure simultaneously. However, a clear relationship between pressure and water age considering user preference has not been investigated. In this study, a MINLP approach is developed to solve the optimal positioning and setting of PRVs for simultaneous minimization of water age and pressure. The MINLP problem consists of a weighted pressure and water age objective function, hydraulic equations and water age functions at junctions as equality constraints, and pressure, flow, and water age operating limits as inequality constraints. A binary variable is assigned to each link in the water supply network to describe the option of placing a PRV or not. The advantage of a weighted objective function is that the weighting factor can be easily adjusted to fit the bi-objective optimization, taking into account the user’s preferences.

The remainder of the paper is organized as follows. In Section 2, mathematical modeling of water age and pressure in WDS is outlined, where we show the mechanisms to improve water age while reducing pressure levels by properly positioning PRVs in the distribution network. The formulation of the optimization problem using a MINLP approach is presented in Section 3. Section 4 contains two illustrative case studies that demonstrate the performance of the proposed optimization method. Brief concluding remarks are given in Section 5.

2 Modeling Water Age and Pressure in WDS

In this section, we present the model of water age and pressure in a WDS used to formulate our optimization problem. The junction-by-junction method is employed to calculate the water age and its performance will be compared with the results of EPANET.

2.1 Water Age Model

In this study, we use a simple but quite accurate water age model (Wang et al. 2009). The water age at a node is calculated based on that of the neighboring nodes and the flow rate of the connecting links, resulting in a junction-by-junction approach. The travel time of water through a link between nodes k and i is calculated as (Chen et al. 2018)

$$\begin{aligned} t_{ki} = \dfrac{l_{ki}}{v_{ki}} = \dfrac{l_{ki}\,A}{q_{ki}} \end{aligned}$$
(1)

with the length \(l_{ki}\) of the pipe, the average water flow velocity \(v_{ki}\) between nodes k and i, the volumetric flow rate \(q_{ki}\) and the cross-sectional area A of the pipe. This scheme can be extended to obtain the water age (WA) at a particular node in a WDS where water is flowing from a source to demand nodes.

Figure 1 shows a general network description that is used to explain how the water age is calculated at the nodes when applying the junction-by-junction approach. It is assumed that the water entering node i blends entirely and instantaneously, i.e. the sum of water at nodes k to n represents the set of nodes from which water flows into node i. The velocity \(v_{ki}\) of the flow between points k and i is calculated based on the Bernoulli formula (Larock et al. 1999)

$$\begin{aligned} v_{ki} = \sqrt{2 \, g \, \left( h_{k} - \Delta h_{ki} - \dfrac{p_{i}}{\rho \, g} - z_{i}\right) } \end{aligned}$$
(2)

with the gravitational acceleration g, the pressure \(p_i\) and the elevation head \(z_i\) at the downstream node i, the density of the fluid \(\rho\), the total head \(h_k\) at the upstream node k and the frictional head loss \(\Delta h_{ki}\) between the two nodes. From Eqs. (1) and (2), the water age \(\text {WA}_i\) at node i can be calculated as (Chen et al. 2018):

$$\begin{aligned}&\text {WA}_i = \dfrac{\sum _{k=1}^{n} [q_{ki} \, (\text {WA}_{k} + t_{ki})]}{\sum _{k=1}^{n} q_{ki}} = \dfrac{\sum _{k=1}^{n} \left[ q_{ki} \, \left( \text {WA}_{k} + \dfrac{l_{ki}}{v_{ki}}\right) \right] }{\sum _{k=1}^n q_{ki}} \end{aligned}$$
(3a)
$$\begin{aligned} =&\dfrac{\sum _{k=1}^{n} \left[ q_{ki} \, \left( \text {WA}_{k} + \dfrac{l_{ki}}{\sqrt{2 \, g \, \left( h_{k} - \Delta h_{ki} - \dfrac{p_{i}}{\rho \, g} - z_{i}\right) }}\right) \right] }{\sum _{k=1}^n q_{ki}}. \end{aligned}$$
(3b)
Fig. 1
figure 1

General description of calculating the water travel time

Full size image

Since not all nodes are inside a distribution network and therefore have inflows and outflows, special cases must be considered. For instance, if the set of inflow nodes is empty (i.e. \(\sum _{k=1}^n \text {WA}_{k}=0\)), node i is a reservoir. Thus, the water age at such a node depends on its initial value \(\text {WA}_{i,0}\). It is also necessary to distinguish between tanks and reservoirs. Reservoirs are water quality source points, which means that this infinite external source always has an initial water age of zero, regardless of its inflow, if any. Tanks, on the other hand, have a storage capacity, and thus the water age of the stored volume can vary over time (Rossman and Boulos 1996).

If the considered node has no outflow (i.e. \(q_{ij}=0\)), it represents an end node or a dead end. For example, as shown in Fig. 1, the water age \(\text {WA}_j\) at the end node j with inflow nodes i to m is calculated as follows:

$$\begin{aligned}&\text {WA}_j = \dfrac{\sum _{i=1}^{m} [q_{ij} \, (\text {WA}_{i} + t_{ij})]}{\sum _{i=1}^{m} q_{ij}} = \dfrac{\sum _{i=1}^{m} \left[ q_{ij} \, \left( \dfrac{\sum _{k=1}^{n} [q_{ki} \, (\text {WA}_{k} + t_{ki})]}{\sum _{k=1}^{n} q_{ki}} + t_{ij}\right) \right] }{\sum _{i=1}^{m} q_{ij}} \end{aligned}$$
(4)

where m is the number of upstream nodes that have an inflow to node j. As a result, an iterative water age calculation algorithm is established that takes into account the water flow through each link (Chen et al. 2018).

From Eq. (2), it can be seen that there is a relation between \(\text {WA}_i\) and \(p_i\). An increase of the pressure \(p_i\) at the downstream node i leads to a decrease of the flow velocity \(v_{ki}\). In turn, the water travel time between node k and i will increase, and thus the water age at the downstream node i will increase (see Eq. (3b)). However, in the case of a complicated network structure, there will be no explicit relationship between water age and pressure. Nevertheless, the implicit effect of pressure on water age can be used for optimal design and operation of WDSs, especially when PRVs are used for this purpose.

Now we use a simple network, as shown in Fig. 2, to verify the junction-by-junction water age calculation and to illustrate the effect of installing a PRV on water age. Assume that a PRV between nodes 3 and 5 is operated either open or closed, resulting in two different network structures.

Fig. 2
figure 2

A simple network with a PRV in pipe L6 which can be open or closed, affecting water age and pressure

Full size image

The values of water age calculated by the junction-by-junction model and EPANET (Rossman et al. 2020) of the two network structures are shown in Table 1. It is seen, due to the symmetric structure, that the water age at nodes 2 and 4 is the same. In addition, Table 1 shows that the values calculated by the two methods are identical, demonstrating the high accuracy of the junction-by-junction model. Moreover, it is shown in Table 1 that the water age at the nodes (except node 3) with an open PRV is higher than that with a closed PRV. This is because the flow velocity is lower when the PRV is open than when it is closed, illustrating a clear effect of a PRV on water age.

Table 1 Water age calculated by the junction-by-junction method and EPANET in the simple network (Fig. 2)
Full size table

2.2 Pressure Model

The frictional head loss \(h_{f_\kappa }\) across a pipe \(\kappa\) can be calculated by the semi-empirical Hazen-Williams (HW) formula in the SI units (Dai and Li 2014):

$$\begin{aligned} h_{f_\kappa } = \frac{10.67 \, l_\kappa }{D_\kappa ^{4.871}} \left( \dfrac{q_\kappa }{C_\kappa }\right) ^{1.852} \end{aligned}$$
(5)

where \(l \in \mathbb {R}^{n_p}, C \in \mathbb {R}^{n_p}, D \in \mathbb {R}^{n_p}\) are the length, roughness and diameter of the pipe, respectively. \(q \in \mathbb {R}^{n_p}\) is the flow rate in the pipe with \(n_p\) pipes in the considered WDS. We chose this model instead of the Darcy-Weisbach (DW) equation due to its direct solvability of the head loss.

From Eq. (5), the influence of pipe length l, pipe diameter D and flow rate q on head loss \(h_f \in \mathbb {R}^{n_p}\) (5) as well as water age \(\text {WA} \in \mathbb {R}^{n_n}\) (1) is shown in Table 2. If the flow rate \(q_\kappa\) of the pipe \(\kappa\) is raised by a factor \(\chi\), the head loss will also increase by \(\chi ^{1.852}\), whereas the water age will decrease by \(\dfrac{1}{\chi }\). Increasing the flow rate and thus the flow velocity will result in a higher head loss but a lower pressure and a lower water age.

Table 2 Influence of q, D, l by respective factors \(\chi , \psi , \omega\) on the head loss \(h_f\) and water age \(\text {WA}\)
Full size table

Increasing the pipe diameter \(D_\kappa\) by a factor of \(\psi\) decreases the head loss by \(\dfrac{1}{\psi ^{4.871}}\) but increases the water age \(\text {WA}\) by \(\psi ^2\). This can be explained by the decrease in flow velocity. Note that the change in flow rate q and pipe diameter D has a greater effect on head loss than on water age. This can be confirmed later in our case study in Section 4.

Increasing the pipe length l by a factor \(\omega\) leads to a proportional rise of both head loss and water age by \(\omega\), as shown in Section 2.1. A larger head loss implies a smaller pressure, since the head of a downstream node j is given by

$$\begin{aligned} H_j = H_i - h_{f_{ij}} \end{aligned}$$
(6)

where \(H_i\) is the head of the upstream node i and \(h_{f_{ij}}\) is the head loss of the connecting pipe between nodes i and j. As a result, inserting a PRV between the two nodes will result in a lower head of the downstream node and a lower pressure at this node, i.e., a lower PRV setting. Mathematically, this can be described by Bermúdez et al. (2021)

$$\begin{aligned} \Delta H_{PRV} = \frac{q\left| q \right| }{(r\,E)^2} \end{aligned}$$
(7)

where r is the opening of the PRV, q is the flow, and \(E=C_v \, A_v \, \sqrt{2g}\) with the discharge coefficient representing the losses through a fully open valve \(C_v\), the cross-sectional area of the valve orifice \(A_v\) and the acceleration of gravity g. Throttling the PRV will lead to a smaller pipe diameter in Eq. (1) and thus a higher velocity, then the water age in Eq. (2) will be reduced.

To see the effect of PRVs on the operation of a WDS, the simple network shown in Fig. 2 is reconsidered. Now we close the PRV on pipe L6 to simulate a looped WDS with the following data. All pipes have a length of \(l=1000m\) and a roughness of \(C=100\). All pipes have a diameter of \(D=0.2m\) except pipe L2 which has a doubled diameter to show possible effects on water age and head loss. The reservoir has an elevation of \(e_R=500m\) while all other nodes are at level zero. The demand at nodes 2, 4, 5 is \(d=0.025 \frac{m^3}{s}\) and at node 3 it is zero. Assume that the initial water age in the network is zero.

Three different scenarios are simulated with EPANET: one without any PRV, and two with a closed PRV on either pipe L2 or L4. The results of the total velocity and head loss of the pipes, pressure and water age at the nodes are shown in Table 3. In the case of no PRV, the water flows through both branches, resulting in lower flow rates and thus lower head losses, as shown in Table 3. Consequently, the total pressure and the total water age are higher than those in the other two scenarios with a PRV. Comparing these two scenarios, it can be seen that a closed PRV on L4 leads to a lower total velocity and head loss than that of a closed PRV on L2. This is due to the fact that L2 is twice the diameter of L4. Accordingly, the total pressure and water age are higher when water flows through L2 and L3 than through L4 and L5.

Table 3 Total values of velocity v, head loss \(h_f\), pressure p and water age \(\text {WA}\) for different scenarios in the simple network with a closed PRV on pipe L6 (Fig. 2)
Full size table

3 MINLP Formulation

Consider the situation where we have a certain number of PRVs to be placed in a WDS. Our optimization goal is to determine the position and setting of the PRVs in the WDS to simultaneously minimize the total pressure and water age at the nodes. This means that our optimization approach will provide the optimal solution for a given number of PRVs \(n_\beta\). Meanwhile, the water demand and all operational constraints should be satisfied. Our formulation of the optimization problem considers a WDS with

  • \(n_0\) water sources (e.g., reservoirs or tanks),

  • \(n_n\) nodes (e.g., consumer household or industry),

  • \(n_p\) pipes connecting the water sources and nodes.

As a result, a WDS can be interpreted as a directed graph with \(n_n + n_0\) vertices and \(2 n_p\) links (Pecci et al. 2017). This sets up a bidirectional positive flow expressed as the node-edge incidence matrices \(A^\top _{12} \in \mathbb {R}^{n_n \times 2 n_p}\), \(A^\top _{10} \in \mathbb {R}^{n_0 \times 2 n_p}\) and \(A_{1} = [A_{12};A_{10}]\). By doubling the pipes to \(2n_p\), it is possible to allow the change of direction of the water flow. The matrices A are constructed to represent the linking of each pipe via the nodes. A "1" in the matrix corresponds to a linkage of a pipe to a node or water source with a positive flow direction. On the other hand, a "0" in the matrix A indicates that there is no connection.

The objective of the optimization problem is to minimize a weighted sum of the total pressure p, and the total water age WA:

$$\begin{aligned} \underset{\text {WA},p}{\min } \, \sum _{i=1}^{n_n} \left( \alpha \, \text {WA}_i + (1-\alpha ) \, p_i \right) \quad \text {with} \; \alpha =[0,1] \end{aligned}$$
(8)

subject to

$$\begin{aligned} A^\top _{1} \, q - d&= 0 \end{aligned}$$
(9)
$$\begin{aligned} q (- A_{1} (\underbrace{p + e}_{\text {head}}) - h_f)&\ge 0 \end{aligned}$$
(10)
$$\begin{aligned} - A_{1} (p + e) - h_f - M \, \beta&\le 0 \end{aligned}$$
(11)
$$\begin{aligned} \beta&\in \{0,1\}^{2n_p} \end{aligned}$$
(12)
$$\begin{aligned} \beta _\kappa + \beta _{n_p+\kappa }&\le 1, \qquad \qquad \forall \kappa =1,\cdots ,n_p \end{aligned}$$
(13)
$$\begin{aligned} \sum _{\kappa =1}^{2 n_p} \beta _{\kappa }&= n_\beta \end{aligned}$$
(14)
$$\begin{aligned} p_{\min } \le p&\le p_{\max } \end{aligned}$$
(15)
$$\begin{aligned} 0 \le \text {WA}&\le \text {WA}_{\max } \end{aligned}$$
(16)
$$\begin{aligned} 0 \le q&\le q_{\max } \end{aligned}$$
(17)

with pressure \(p \in \mathbb {R}^{n_n}\ \text {in } [m]\), flow \(q \in \mathbb {R}^{2 n_p}\ \text {in } [LPS]\), elevation \(e \in \mathbb {R}^{n_n}\ \text {in } [m]\), demand \(d \in \mathbb {R}^{n_n}\ \text {in } [LPS]\), frictional head loss \(h_f \in \mathbb {R}^{n_p}\ \text {in } [m]\) (see Eq. (5)), and the diagonal matrix of sufficiently big constants \(M \in \mathbb {R}^{2 n_p}\). The big-M constants can be computed as follows (Dai and Li 2014):

$$\begin{aligned} M_{\kappa } := (h_{max})_{\kappa }-(h_{min})_{\kappa } \end{aligned}$$
(18)

where \(h_{max}\) and \(h_{min}\) are the maximum and minimum possible hydraulic heads \(h \in \mathbb {R}^{n_n}\) at node j, which is the downstream node given that \(i \overset{\kappa }{\rightarrow }\ j\).

In Eq. (8), \(\alpha\) is a user-defined weighting factor. The value for this parameter may vary depending on the user’s preference for pressure or water age minimization. If the WDS is prone to water leaks, decision makers or operators may want to focus on minimizing the pressure in the network (i.e. a lower value of \(\alpha\)). If there is no deviation in WDS operation, improving the water quality will be considered (i.e. a higher \(\alpha\) value).

Equations (9–11) state the mass and energy conservation laws that are satisfied for each demand pattern. \(\beta\) in (12) is a vector of binary variables describing whether a PRV is present on a pipe or not. The dimension of this vector is \(2 n_p\), since bi-directional flow is considered. These binary variables are constrained by Eq. (13), i.e. only one direction will be active, and Eq. (14), i.e. the total number of PRVs should be \(n_\beta\).

The inequality constraints (15–17) allow the pressure p, the water age \(\text {WA}\) and the flow q to be within the specified bounds. Since a bidirectional flow is considered by defining \(2 n_p\) links, only positive flow values are accepted (see inequality (17)). The pressure bounds \(p_{min}\) and \(p_{min}\) are defined based on the network operation specifications, while the upper bound of water age \(\text {WA}\) (see inequality (16)) can be set to satisfy the government health safety restriction (AWWA with assistance from Economic and Engineering Services, Inc. 2002). In the inequality (16), the water age \(\text {WA}_i\) at node i described by Eq. (3a) is rewritten as follows:

$$\begin{aligned} \text {WA}_i = \frac{\sum _{\kappa =1}^{2 n_p} A_{12}^{\top } \left[ ( A_{12} \, \text {WA}_\kappa ) q_\kappa + \overbrace{(\frac{D_\kappa }{2 \cdot 1000})^2 \frac{\pi }{3.6} l_\kappa }^{\text {t}_{ij}} \right] }{ A_{12}^{\top } \, q} . \end{aligned}$$
(19)

This means that the water age at node i is equal to the sum of the water age at the nodes that have an inflow to node i plus the time spent in the pipes divided by the total inflow to node i.

The mixed-integer nonlinear programming (MINLP) problem (5, 8–19) has \(n_n+2n_p\) continuous variables including head loss, pressure, flow and water age, and \(2n_p\) binary variables for the placement of PRVs (Pecci et al. 2017). We implemented this problem formulation in the GAMS software package (GAMS Development Corporation 2023) and solved it using the BONMIN solver (Bonami and Lee 2011) for two WDSs as case studies presented in the next section.

4 Case Studies

In this section, we present the results of solving the MINLP problem for two networks. The optimal values of the decision variables are provided as inputs to the corresponding EPANET models to verify the results.

4.1 Net4

Net4 is a simple network with two reservoirs, nine nodes, and four loops as shown in Fig. 3. This network is a benchmark in EPANET 2.2 (Rossman et al. 2020) for demand-driven analysis. The technical design values of Net4 can be found in literature (U.S. Environmental Protection Agency 2017). The reservoirs were modified to elevations of \(e_{R1}=220 m\) and \(e_{R2}=225 m\). The length of the pipelines was increased to 5000m, and the length of the outlet pipe of the reservoirs were extended to 7000m to have a clearer effect on the water age parameter. The flow directions shown in Fig. 3 are only one option and may vary with changing parameters and placement of PRVs.

Fig. 3
figure 3

The network of Net4 (U.S. Environmental Protection Agency 2017)

Full size image

The lower and upper bounds of the pressure at each node are \(p_{\min }=5\,m\) and \(p_{\max }=60\,m\), the flow rate in the pipes is restricted to \(q_{\min }=0\,LPS\) and \(q_{\max }= 200\,LPS\), and the water age at the nodes is constrained to \(\text {WA}_{\min }=0.01\,h\) and \(\text {WA}_{\max }=9\,h\), respectively. Now we consider two scenarios by setting the weighting factor in the objective function (8) to \(\alpha =0\) and \(\alpha =1\) and solve the MINLP problem accordingly.

With \(\alpha =0\), the aim of the optimization is only to minimize the total pressure at the nodes in the WDS. Figure 4a shows the resulting total pressure and water age when using different numbers of PRVs. It can be seen that the pressure decreases as the number of PRVs increases due to the increase of the degrees of freedom for the optimization problem. However, the total water age at the nodes increases with the number of PRVs, indicating a contradictory effect between total pressure and water age.

Fig. 4
figure 4

Total pressure and water age in Net4 with different number of PRVs and different \(\alpha\) values

Full size image

In addition, Fig. 4a shows strong nonlinear behavior as the number of PRVs is increased from 0 to 3. This is largely due to the binary decision variables used to localize the PRVs. Table 4 shows the optimized positions and settings in the cases of placing 1, 2 and 3 PRVs. It can be seen that the PRVs should be placed close to the reservoirs to reduce the total pressure in the network, but regardless of the water age.

Table 4 Optimal PRV location and setting for Net4 when \(\alpha =0\)
Full size table

In the second scenario, water age is considered as high preference, i.e. \(\alpha =1\). By solving the corresponding MINLP problem, Fig. 4b shows that the total water age is indeed reduced by installing more PRVs.

However, due to the strong nonlinearity, the reduction in total water age from 0 to 1 PRV and from 2 to 3 PRVs is almost negligible. This effect can be explained in Table 5, which shows the optimal position and setting of the PRVs. It can be seen that when comparing the use of 2 PRVs and 3 PRVs, in both cases two PRVs are placed on L3 and L7 with the same setting values. In the case of using 3 PRVs, the setting of the additional PRV on pipe L1 is large enough to have little effect on the flow rates.

Table 5 Optimal PRV location and setting for Net4 when \(\alpha =1\)
Full size table

Moreover, when comparing the total water age values shown in Fig. 4, it can be seen that the total water age values are lower when \(\alpha =1\). This is due to the optimal locations of the PRVs, which cause higher velocities in the pipes than those in the first scenario where \(\alpha =0\).

We also solved the MINLP problem for two further scenarios with \(\alpha =0.5\) and \(\alpha =0.8\), respectively. All the results from the four scenarios are summarized in Fig. 5a for the total pressure and in Fig. 5b for the total water age which show a clear trend.

Fig. 5
figure 5

Total pressure and water age in Net4 with different \(\alpha\) values and different number of PRVs

Full size image

It can be seen that as \(\alpha\) increases, the total pressure will increase while the total water age will decrease. However, this trend does not hold when using 0 or 1 PRV. The absence of an additional degree of freedom in the former case and the negligible effect of varying the distribution of water flows in the network when using only one PRV in the latter case explain this deviation.

Furthermore, there is an unreasonable phenomenon in Fig. 5a: the total pressure decreases as \(\alpha\) increases from 0.8 to 1. This may be due to the fact that the MINLP problem is nonconvex and we obtained a local solution.

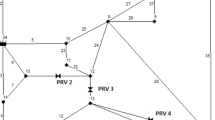
4.2 The 25-node System

The 25-node system is a more intricate network originally proposed in Sterling and Bargiela (1984) and depicted in Fig. 6. It consists of 37 pipes connecting three reservoirs with 22 nodes. Accordingly, the MINLP problem has 96 continuous and 74 binary variables. In addition, we define the lower and upper bounds of the continuous variables in the problem formulation as follows:

  • The pressure at each node: \(p_{\min }=20\,m\), \(p_{\max }=45\,m\),

  • The flow rate in each pipe: \(q_{\min }=0\,LPS\), \(p_{\max }= 150\,LPS\),

  • The water age at each node: \(\text {WA}_{\min }=0.01\,h\), \(\text {WA}_{\max }=45\,h\).

The initial water age in reservoirs R23-R25 is 0. The flow of water between R23 and R24 through pipe L2 has no effect on the water age in reservoir R24, as explained in Section 2.1.

Fig. 6
figure 6

The structure of the 25-node system (Sterling and Bargiela 1984)

Full size image

First, we consider a scenario of simultaneous minimization of total water pressure and water age by using \(\alpha =0.8\), which leads to the results shown in Fig. 7. It can be seen that both total pressure and water age will be reduced as the number of PRVs is increased. A reduction in total pressure of \(53.1\%\) and water age of \(9.2\%\) is achieved when four PRVs are placed in the WDS. However, it is shown that the addition of the third PRV does not have a significant impact. The reason for this can be explained by the positioning of the valve, which hits the lower bound of the pressure constraint, i.e., the PRV on L34 has its setting as 20m as seen in Table 6.

Fig. 7
figure 7

Total pressure and water age in the 25-node system using different number of PRVs when \(\alpha =0.8\)

Full size image
Table 6 Optimal PRV location and setting for the 25-node system when \(\alpha =0.8\)
Full size table

If we minimize only the total water age, i.e. \(\alpha =1\), a smaller decrease in total pressure will be obtained, while the decrease in total water age is considerable, as shown in Fig. 8a. A peak in the total water age is observed when four PRVs are placed in the 25-node system. Again, this may be due to the non-convexity of the MINLP problem and thus a local solution is found. However, this peak value is lower than all values of the total water age except for 5 PRVs obtained when \(\alpha =0\), i.e. when the focus is on minimizing the total pressure, as shown in Fig. 8b. It can be seen that the total pressure is indeed reduced much more compared to the case of \(\alpha =1\) shown in Fig. 8a.

Fig. 8
figure 8

Total pressure and water age in the 25-node system with different \(\alpha\) values

Full size image

The optimal positions for using different numbers of PRVs with \(\alpha =0\) and \(\alpha =1\), respectively, are listed in Table 7. It is evident that the valve positions for the two cases are significantly different. In the case of only minimizing the total pressure (\(\alpha =0\)), it is shown that the valves are positioned near the reservoirs to reduce the total pressure as much as possible. In contrast, when the focus is on minimizing the total water age (\(\alpha =1\)), the positioning of the PRVs leads to PRV locations inside the WDS to manipulate the flow distribution in favor of reducing the total water age.

Table 7 Optimal PRV location for the 25-node system with \(\alpha =0\) and \(\alpha =1\)
Full size table

To analyze the behavior of the network in more detail, we solved the MINLP problem with different numbers of PRVs to be installed and more cases of \(\alpha\) values. The influence of these factors on total pressure and water age is shown in Fig. 9. It can be seen that the use of PRVs always leads to an improvement in both pressure and water age. This means that, tendentiously, the higher the number of PRVs to be used, the lower both the total pressure and the total water age. The lowest total pressure values are obtained with \(\alpha =0\) (see Fig. 9a), since this corresponds to the highest preference for pressure minimization. Increasing the value of \(\alpha\) results in an increasing total pressure. Furthermore, Fig. 9b shows a clear decrease of the total water age corresponding to the increase of the \(\alpha\) value, as expected.

Fig. 9
figure 9

Total pressure and water age in 25-node system with different \(\alpha\) values and different number of PRVs

Full size image

5 Conclusion

This paper proposes an optimization approach to simultaneously minimize pressure and water age in WDSs through optimal placement and operation of PRVs. A weighting factor is used to reflect the user’s preference for a trade-off between the two criteria. Compared to previous heuristic optimization approaches, we formulated and solved a MINLP problem to determine the optimal positions and settings of the PRVs. The optimal position of the PRVs depends on the defined value of the weighting parameter. Pure pressure minimization will result in PRVs being positioned near the reservoirs, which will not be advantageous for the water age. However, if water age is added to the objective function, water quality will be improved along with minimizing the pressure when the PRVs are optimally located in the network. The results of two case studies demonstrate the effectiveness of the proposed approach.

In addition to introducing the weighting parameter, another strength of our approach is the use of a junction-to-junction water age model, which makes it possible to include water age directly in the MINLP formulation. As a result, the MINLP problem can be solved with a mathematical optimization method in GAMS, leading to a significant reduction in computation time compared to the stochastic search methods such as GA. The CPU time to solve the two case study problems was only several minutes using a standard PC.

Nevertheless, due to the non-convexity of the MINLP problem, some unreasonable behaviors are observed in the results. Therefore, the development of a global solution approach will be a meaningful future work. In addition, the simultaneous minimization of pressure and water age under uncertainty will also be a focus of our work in the near future. Furthermore, practical case studies will be considered.