Assessment of soil erosion, flood risk and groundwater potential of Dhanari watershed using remote sensing and geographic information system, district Uttarkashi, Uttarakhand, India

Abstract

Quantitative morphometric analysis of Dhanari watershed has been done using remote sensing and Geographical Information System (GIS). The impact of climate, lithology, tectonics, structural antecedents, vegetation cover and land use on hydrological processes is assessed by quantifying geomorphic parameters. The Dhanari River (a tributary of the Bhagirathi River) and its tributaries Dhanpati Gad and Kali Gad forms Dhanari watershed covering 91.8  Km² area. Several geomorphic aspects viz. linear, areal, relief were computed to comprehend potentials of soil erosion, groundwater, flood vulnerability and the geomorphic response of watershed. LISS-III image is used to generate the Land Use and Land Cover (LULC) map and assess the watershed dynamics. Values of computed hypsometric integral and morphometric parameters viz. drainage density ($D_{{\text{d}}}$), stream frequency ($F_{{\text{s}}}$), stream length ratio ($L_{{{\text{ur}}}}$), bifurcation ratio ($R_{{\text{b}}}$), rho coefficient (ρ), drainage texture ($D_{{\text{t}}}$), circularity ratio ($R_{{\text{c}}}$), relief ratio ($R_{{{\text{hl}}}}$), elongation ratio ($R_{{\text{e}}}$), form factor ($F_{{\text{f}}}$), basin shape ($B_{{\text{s}}}$), drainage intensity ($D_{{\text{i}}}$), compactness coefficient ($C_{{\text{c}}}$) and infiltration number ($I_{{\text{f}}}$) have shown a moderate and steady erosion rate, with low groundwater potential and low to moderate flood vulnerability in the watershed. Hypsometry presents a dependable geomorphic parameter to understand the erosion and geomorphic response of a watershed to hydrological processes. Hypsometric integral value (0.51) of Dhanari watershed suggests a mature topography with steady erosion in the watershed.

Introduction

Himalayan mountains have one of the most complex and dynamic drainage systems. The rivers and their tributaries are important geographical units in the region as they are the primary source of fresh water in most parts of the Himalaya. The river and streams also act as driving forces for any ongoing fluvial activity. The fluvial activities play a vital role in shaping and modifying the landforms of the Himalayan terrain. In Dhanari watershed, the population relies on surface runoff water for their need for freshwater; as the groundwater resources in the Dhanari watershed are sparse, most of the watershed population resides along the river and its tributaries. The area residents are practicing agricultural activities in the loose and fertile alluvium of the Dhanari River and its tributaries. The Dhanari watershed is highly susceptible to soil erosion as heavy rainfall occurs during pre-monsoon and monsoon season (average annual rainfall of 1693 mm), increasing the surface runoff. It becomes necessary to have proper watershed management plans to check the soil loss during any watershed management activity. It is essential to understand the hydrological nature of rocks before morphometric analysis (Singh et al. 2014).

Morphometric assessment of earth surface, shape and landforms is done by quantitative measurement and numerical analysis (Clarke 1966; Biswas et al. 2014). Morphometric analysis methods were introduced by Horton (1932, 1945) to present its relationship with the natural agents like climate, geology, vegetation, soil and hydrology. In the quantitative morphometric analysis, vital unit is a stream network; it expresses the watershed's geological, structural and hydrological framework. To further understand the origin of landform from drainage networks the technique is improved, modified and studied in detail by Strahler (1952, 1964), Miller (1953), Schumm (1956), Chorley (1957), Melton (1957), and Faniran (1968). In past few decades, more precise, cheaper and dependable techniques like remote sensing combined with GIS are being used by many researchers viz Sreedevi et al. (2005), Biswas et al. (2014), Rai et al. (2018) and Sharma et al. (2018) for the geomorphic study of landforms. Geomorphic aspects viz drainage network, basin geometry, drainage texture and relief aspect were computed to derive Dhanari watershed features.

Hypsometric assessment is the study of the distribution of ground surface area or horizontal cross-sectional region of a landmass with respect to altitude; hypsometry indicates the stage of basin development and upliftment rate in a watershed (Strahler 1952; Schumm 1956; Singh et al. 2008). Langbein (1947) introduced hypsometry as a dimensionless parameter for comparing watersheds regardless of their scale. Hurtrez et al. (1999) suggested that the soil mass volume and extent of erosion occurred in a basin against the remaining mass is related to the Hypsometric curve (HC). The hypsometric integral (HI) measurement is based on the plot of the contour height measured and the covered area produced by the DEM and using the empirical elevation relief formulas proposed by Pike and Wilson (1971). Hypsometric integral quantifies the erosion proneness and the geomorphological stage of the watershed. The hypsometric curve and hypsometric integral signifies the watershed condition (Ritter et al. 2002). The variation in the shape of curves and the HI values are linked to the degree of uncertainty among erosive and tectonic forces (Weissel et al. 1994).

The remote sensing data is processed in the GIS environment to generate quick and precise data for morphometric and hypsometric analysis. An attempt has been made to use hypsometry and various geomorphic aspects to establish a relationship between the drainage network and hydrology, geology, climate, vegetation, and soil. The present study encompasses studying the geomorphic parameters of the Dhanari watershed to assess the groundwater potential and erosion and flood susceptibility. The objective is to use remote sensing coupled with GIS for systematic planning of soil and water management.

Drainage basin setup

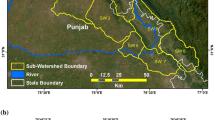
The Dhanari watershed is located in the Uttarkashi and Tehri district of Uttarakhand (Fig. 1), formed by the Dhanari River, a tributary of Bhagirathi River covering an area of 91.8 km². Dhanari watershed falls in the survey of India topographic map no. 53 J/6/NW, 53 J/6/SE, 53 J/6/NE, 53 J/10/NW between Latitude 30º 35' 00''–30º 42' 00'' N and Longitude 78º 21' 00''–78º 31' 00'' E. Dhanari Gad runs for 19.594  Km; it has two major tributaries Dhanpati Gad and Kali Gad; several small stream segments of lower order form the watershed drainage network (Fig. 2a). The streams are mostly rain-fed; the main channel reaches its threshold during monsoon; springs available in the upper region of the watershed fed by snowmelt and rainwater recharge the streams during summers. The watershed elevation varies from 920  meters above mean sea level (MSL) at the confluence with the Bhagirathi River near Dunda village to 2924  meters at the highest point near Nagni Thank (Fig. 2b). The climate of Dhanari watershed is hot and humid during the summers and receives snowfall for a short duration during winters at higher altitudes and during monsoons receives high precipitation.

Fig. 1

Location map of the study area

Fig. 2

Thematic layers showing a drainage map, b digital elevation model, c geological setup (after Jain 1971; Fuchs and Sinha 1978; Valdiya 1980) and d land use and land cover pattern of the Dhanari watershed

The Dhanari watershed lies in the Lesser Garhwal Himalaya region with immature, rugged, highly dissected topography. Denudation and deposition by the Dhanari River and its tributaries form fluvial landforms with sub-montane soil type. The watershed in the higher altitudes has thick vegetation along gentle slopes, while lower altitudes have sparse to dense vegetation with most of the agricultural activities concentrated along the river. The watershed is characterized by prominent ridges where the majority of them are trending NNW-SSE and WNW-ESE; though, in some part of the Western margins, the trend is in N-S and NW-SE direction.

The study area lies in Lesser Himalayan region of Garhwal Himalaya having low to medium grade metamorphic rocks. The geology of the region is studied in detail by Jain (1971) and later on by Fuchs & Sinha (1978) and Valdiya (1980); they identified two major tectonic units in Dhanari watershed viz. Dunda Thrust and Singuni Thrust dipping NE and SW, respectively (Fig. 2c). The litho-units of Dhanari watershed viz. Dhanari Formation, Dunda Formation and Berinag Formation (locally known as Gamri Quartzite Formation) are of Garhwal Group, while Debguru Porphyroid Formation is of Ramgarh Group. The Dunda thrust running NW–SE separates the Gamri Quartzite Formation in the NE from Dhanari Metabasic Formation in SW; Singuni thrust trending NW-SE separates Gamri Quartzite Formation in the SW from Debguru Porphyroid Formation in NE. The watershed lithology comprises Dichli Dolomites and Gamri Quartzites of Berinag Formation; Khattukhal Limestone; Dhanari Slate and Dunda Quartzite of Dunda Formation; Augen Mylonitic Gneisses and Metabasic rocks of Debguru Porphyroid Formation (Jain 1971; Valdiya 1980).

Methodology

The morphometric analysis of the Dhanari watershed was completed using the Survey of India topographic map No. 53J/6/NW, 53J/6/SE, 53J/6/NE and 53J/10/NW on a 1:25,000 scale. The topographic map was scanned, georeferenced and digitized to produce the drainage network of the Dhanari watershed in the ArcGIS-10.5. Drainages are classified based on drainage order (Strahler, 1964) and saved in feature files. Watershed boundary is delineated by using pour point method from SRTM-DEM (Shuttle Radar Topographic Mission- Digital elevation model) in ArcGIS-10.5 software. Quantitative analysis of various geomorphic aspects viz. basin geometry, drainage network, drainage texture and relief characteristics are derived by extracting data from digitized drainages. The SRTM-DEM data with a spatial resolution of 30 meters is downloaded from the United State Geological Survey (https://earthexplorer.usgs.gov/) website to generate thematic maps. To generate LULC (Land Use and Land Cover) map of the Dhanari watershed (Fig. 2d) ortho corrected IRSP-LISS-III (Indian Remote Sensing Program-Linear Integrated Self-Scanning Sensor) image with a spatial resolution of 23.5  meters is used. The LISS-III image was taken on October 22, 2016, by Resourcesat-2 satellite and downloaded from the National Remote Sensing Center (https://bhuvan.nrsc.gov.in/bhuvan_links.php). The LISS-III image is then processed in ArcGIS software where spectral band combination (band combination used in the study is 4, 3, 2) is used to generate false color composite (FCC). In the next step, the supervised classification of the processed image is done to generate the LULC map.

The hypsometric study for the watershed is done to determine the erosion status and runoff capacity. The HC and HI are used to assess the erosion status, sediment accumulation, and topography influence in surface runoff. The hypsometric curve presents the distribution of the area at different elevations for the watershed. The HC is shown diagrammatically by plotting the cumulative area (a/A) along the abscissa and cumulative altitude (h/H) along the ordinate (Strahler 1952). The HC is the diagrammatic representation, while HI is the numerical expression for the HC. The data acquired for area and elevation is collected from SRTM-DEM in ArcGIS. The HI can be calculated using four methods viz. integration of hypsometric curve, leaf area meter, planimeter equipment and the elevation relief ratio relationship (Singh et al. 2008). In the current analysis, we used the elevation relief ratio relationship method proposed by Pike and Wilson (1971), as it offers comparatively more minor error than the other three techniques. The equation for the technique can be expressed as:

$$E \approx HI = \frac{{Elev_{{mean}} - Elev_{{\min }} }}{{Elev_{{\max }} ~{-}Elev_{{\min }} }}$$

(1)

where E = elevation relief ratio (equivalent to His); Elev_mean= weighted mean elevation, Elev_min and Elev_max are the minimum and maximum elevation.

Result and discussion

The development of watershed drainage networks depends upon geology and precipitation apart from other factors like thrust, fault and anthropogenic activities. Among major geological structures in the watershed, Dunda thrust shows a remarkable example of a drainage-tectonics relationship. Kali Gad and the Dhanari River flows more or less parallel to Dunda thrust (Fig. 2c). The regional structure and tectonics lead to deformation of rock, making them more susceptible to erosion as exhibited by the presence of a window structure (Dunda window) within the Dhanari watershed (Fig. 2c). The watershed receives high precipitation during monsoons resulting in erosion of these weak and deformed rocks. The study was conducted to infer the hydrological response of Dhanari watershed for soil erosion, groundwater potential and flood vulnerability. The morphometric parameters were studied under four broad geomorphic aspects viz. drainage network, basin geometry, drainage texture analysis and relief characteristics.

Drainage network

The streams in a watershed are placed in the hierarchical order to delineate stream order (S_u) for drainage basin analysis (Strahler 1952). In the Dhanari watershed, first-order stream segments have the highest frequency, while higher order has the lowest frequency (Fig. 2a). The watershed highest stream order is the fifth order carrying all the discharge of water and sediments from its lower-order streams. The higher frequency of lower-order stream influences the topography and hydrology of the watershed. The higher number of lower-order streams increases the erosion activities along slopes during rainfall; the increased surface runoff provides a very short interval for water percolation, thus decreasing the groundwater recharge. The watershed topography is affected by the stream frequency as several new channels or gullies are formed along the slopes where vegetation cover is sparse, and the gradient is high.

The sum of all stream of each order in a watershed is recognized as the stream number (${N}_{u}$). The $N_{{\text{u}}}$ is associated with surface runoff in the watershed. Horton (1945) stated that “sum of stream segments of every order forms an inverse geometric succession with each stream order” (Fig. 3a). The high percentage (78%) of first-order stream number (Table 1) represents low infiltration and permeability and increased erosion. In contrast, less number (Table 1) of the higher-order stream suggests moderate-to-low erosion and infiltration.

Fig. 3

Graph showing a Relationship between the stream order and stream number, and b relationship between the stream order and stream length

Table 1 Linear aspects of Dhanari watershed

Surface runoff characteristics of a watershed can be assessed by stream length ($L_{{\text{u}}}$) parameter, where stream segments of shorter length represent a steep slope gradient and those traveling for long distances suggest gentle or flat topography. The geometrical relationship is preserved generally in the watershed of increasing stream order (Strahler 1957), where stream length decreases with increasing stream order (Fig. 3b). The stream length of the Dhanari watershed is computed in the GIS environment and given in Table 1. In the Dhanari watershed, the fourth- and fifth-order stream segments length suggests gently sloping topography, while first-, second-, and third-order stream segments indicate steeply inclined slopes. The higher stream length in lower orders suggests high stream frequency resulting in high erosion intensity. The mean stream length ($L_{{{\text{um}}}}$) of the Dhanari watershed varies from 0.43 to 13.4  Km (Table 1). The $L_{{{\text{um}}}}$ is obtained by the sum of the stream length of an order from the sum of stream segments of that order. It reveals the characteristic size of the drainage elements and their contributing surface. The alteration in $L_{{{\text{um}}}}$ values suggest a variation in slope and topography of the watershed. Unlike $L_{{\text{u}}}$ , the lower orders in $L_{{{\text{um}}}}$ show low values, which increase with increasing stream orders. The $L_{{{\text{um}}}}$ in the area with lower orders in the watershed indicate that erosion is higher and slope are steeply inclined, while higher value suggests an extended peak flow with low erosion and gentle gradient.

Stream length ratio ($L_{{{\text{ur}}}}$) as suggested by Horton (1945) is the ratio of the mean length of a higher stream order to the mean length of the lower stream order ($L_{{\text{u}}}$-1), which tends to be successive throughout a basin. The values of stream length ratio vary from 1.19 to 4.9 for Dhanari watershed (Table 1). The results indicate that mean stream length of stream segments of each of the subsequent stream orders tend to approximate a direct geometric sequence in which the first stream length is the average length of segments of the first order. The mean stream length ratio ($L_{{{\text{urm}}}}$) of the watershed is 2.67 (Table 1). The difference in the values of $L_{{{\text{ur}}}}$ suggests a variation in the topography and gradient of the watershed. It is also associated with surface flow discharge and the erosional phase of the watershed. The weighted mean stream length ratio ($L_{{{\text{uwm}}}}$) is obtained by summation of $L_{{{\text{ur}}}}$ multiplied by $L_{{{\text{ur}}}}$ of successive order divided by stream length used in the ratio. The $L_{{{\text{uwm}}}}$ value for Dhanari watershed is 1.51 (Table 2). The main channel length ($C_{{\text{l}}}$) is the length of main stream majored from the point where two or more streams merged to form a major channel, while valley length ($V_{{\text{l}}} {\text{)}}$ is calculated from the farthest point in the watershed from where a stream is originated. The $C_{{\text{l}}}$ and $V_{{\text{l}}}$ value of Dhanari watershed is 19.59 and 19.7, respectively (Table 2), indicating a stable topography with low tectonic activity.

Table 2 Results of various morphometric parameters for the Dhanari watershed

Bifurcation ratio ($R_{{\text{b}}}$) is one of the most critical parameters of the morphometric analysis, “it is the ratio of $N_{{\text{u}}}$ of lower order to $N_{{\text{u}}}$ of higher order” (Strahler 1964). The $R_{{\text{b}}}$ values indicate the shape of the watershed and structural control on drainage network; higher values of $R_{{\text{b}}}$ are associated with circular watershed and structural control on stream network, while lower values of $R_{{\text{b}}}$ suggests elongated watershed and homogenous rock controlling stream network (Soni 2017). The $R_{{\text{b}}}$ value for first-to-third-order streams Dhanari watershed varies from 4.55 to 6 and mean bifurcation ratio ($R_{{{\text{bwm}}}}$) is 4.72 (Table 1) which suggests the homogenous basement rocks controls the drainage network; $R_{{\text{b}}}$ for fourth-order show comparatively higher value (Table 1) suggesting significant structural control on stream segments. The mean $R_{{\text{b}}}$ for the Dhanari watershed (Table 1) indicates an elongated shape, high surface runoff, high discharge, and low infiltration. The $R_{{{\text{bwm}}}}$ for the Dhanari watershed is 4.55 (Table 2), which suggests that peak discharge is produced by lower order streams, while higher order stream shows extended peak flow in the watershed.

The rho coefficient (Rho) coefficient suggests the relationship between drainage density and topographic development of a watershed. It helps assess the storage capacity of drainage networks and is also the final scale factor for developing drainages in a given watershed (Horton 1945; Biswas et al. 2014). The climate, geology, vegetation, geomorphology and anthropogenic factors control the parameter. The rho value of the Dhanari watershed is 0.56 (Table 2) suggesting steep hydrological storage in the watershed at the time of floods and the higher risk of erosion.

Basin geometry

The watershed shape is affected by several factors like climate, structure, lithology and relief. Several geomorphic parameters were studied to understand the role of these factor in controlling the basin geometry. According to Schumm (1956), length of the basin ($L_{{\text{b}}}$) is “the longest path of the basin parallel to the main channel of the watershed.” The Dhanari watershed length is 15.536 Kilometers (Table 2) determined by using the GIS method following Schumm's approach (1956). A simple power function associates stream length and basin area for a large number of basins (Hack 1957), which is expressed by length area relation ($L_{{{\text{ar}}}}$). The $L_{{{\text{ar}}}}$ value of Dhanari watershed is 21.07 (Table 2). The $L_{{{\text{ar}}}}$ value suggests that the watershed is elongated in shape with high surface runoff. Schumm (1956) established that basin area (A) and the sum of stream lengths have an interesting relationship, assisted by the contributing areas. The area, perimeter (P) and width ($W_{{\text{b}}}$) of the watershed are computed using GIS software. The area, perimeter and width of the Dhanari watershed are 91.8 Km², 45.55 km and 11.5 Km, respectively (Table 2). The relative perimeter ($P_{{\text{r}}}$) of the Dhanari watershed is 2.02 (Table 2), calculated by dividing the watershed area by its parameters.

The relative space between stream segments is measured as Drainage texture ($D_{{\text{t}}}$) in a fluvially dissected topography. It is a product of drainage density and stream frequency. The factors like climate, precipitation, vegetation cover, soil, rock type, water infiltration properties and geomorphic stage influences $D_{{\text{t}}}$. The $D_{{\text{d}}}$ and $F_{{\text{s}}}$ directly influence the infiltration capacity of the watershed; Horton (1945) used infiltration capacity as the basis to classify $D_{{\text{t}}}$ of the watershed by which he divided the $D_{{\text{t}}}$ values into very coarse (< 2), coarse (2–4), moderate (4–6), fine (6–8) and very fine (> 8) classes. The Dhanari watershed is placed in the very fine category as the $D_{{\text{t}}}$ computed is 16.77 (Table 2), which suggests lower infiltration chances and high risk of soil erosion. Schumm (1956) identified texture ratio ($R_{{\text{t}}}$) as a significant factor in determining basement rocks nature; thus, the aspect directly relates to lithology, infiltration capacity, and watershed relief. Texture ratio for Dhanari watershed is computed 13.08 (Table 2), categorized as moderate, suggesting basement rocks support infiltration and are relatively permeable.

To determine the slope of the watershed Chorley et al. (1957) used Lemniscate (k). The lemniscate value for the Dhanari watershed is 4.22 (Table 2) signifying the watershed occupies the maximum area in its regions, beginning with a large sum of lower order streams. The value of shape factor ratio $R_{{\text{s}}}$ is computed similar to lemniscate by dividing the square of basin length from the total area; but unlike lemniscate, the shape factor ratio is a shape parameter and determine the shape of the watershed. The $R_{{\text{s}}}$ value (Table 2) suggests that the Dhanari watershed is elongated and susceptible to erosion and flood.

The shape of the watershed is categorized using the elongation ratio ($R_{{\text{e}}}$). Schumm (1956) described $R_{{\text{e}}}$ as “the ratio between the diameter of a circle with the same area as that of the basin and maximum length of the basin.” The shapes of the watershed are categorized as circular (0.9-1.0), oval (0.8-0.9), less elongated (0.7-0.8), elongated (0.5-0.7), and more elongated (<  0.5) based on the index of $R_{{\text{e}}}$ (Rai et al. 2018). High $R_{{\text{e}}}$ value represents high infiltration and less runoff, while lower value suggests lower infiltration and high surface runoff. The $R_{{\text{e}}}$ of Dhanari watershed is 0.55 (Table 2), suggesting an elongated watershed with high surface runoff. Form factor ($F_{{\text{f}}}$) is the basin area ratio to the square of the basin length as described by Horton (1932). Smaller the value of $F_{{\text{f}}}$, more elongated will be the watershed and water flows for a longer duration, in case value is high the water exits the watershed in the short period. The Dhanari watershed has very low $F_{{\text{f}}}$ value of 0.23 (Table 2), and suggests an elongated shape with water flowing for longer duration in the watershed.

The external form of the watershed is measured by circularity ratio ($R_{{\text{c}}}$). It is a dimensionless unit; Miller (1953) and Strahler (1964) defined $R_{{\text{c}}}$ as “ratio of watershed area to the area of a circle having the same perimeter.” Circularity ratio is influenced by structure, geology, relief, slope, stream frequency, relief, climate and LULC of the watershed. The $R_{{\text{c}}}$ value ranging between 0.4 and 0.7 indicates a homogenous extremely permeable basement rock with mature and elongated watershed (Miller 1953). The $R_{{\text{c}}}$ value of Dhanari watershed is 0.56 (Table 2), which suggests watershed has high infiltration capacity with permeable and homogenous rocks, high risk of erosion, elongated shape, mature topography and dendritic pattern of the stream network. The circularity ration ($R_{{cn}}$) is the ratio of watershed area to perimeter of the watershed. The $R_{{{\text{cn}}}}$ for Dhanari watershed is 2.02, which indicate an elongated shape.

Gravelius (1914) described compactness coefficient ($C_{{\text{c}}}$) as “the ratio of the watershed perimeter to the circumference of a circular area having equal area as the watershed.” Compactness coefficient depends upon the slope of the watershed and is independent of dimension. The $C_{{\text{c}}}$ of Dhanari watershed computed is 1.34 (Table 2), suggesting the elongated shape of the watershed and minor side flow for shorter duration and the high main flow for a longer period and low flood hazard vulnerability. Melton (1957) signified the topographic fitness ratio ($R_{{\text{f}}}$) as the ratio of the main channel length to the length of watershed perimeter. The $R_{{\text{f}}}$ for Dhanari watershed is 0.43 (Table 2). Smart & Surkan (1967) defined another parameter wandering ratio ($R_{{\text{w}}}$) as “the ratio of the main stream length to the basin length.” The $R_{{\text{w}}}$ for Dhanari watershed is 0.99 (Table 2).

Drainage texture analysis

The prolonged erosion by channel network results in dissected topography. The amount of landscape dissection done by channels defines the texture of watershed. Several geomorphic parameters were studied to assess the texture of Dhanari watershed. Stream frequency ($F_{{\text{s}}}$) was introduced by Horton (1932, 1945) as “the number of stream segments per unit area.” It is directly related to the drainage density ($D_{{\text{d}}}$) of the watershed and controlled by lithology of the watershed. Dhanari watershed has $F_{{\text{s}}}$ of 8.32 (Table 2), which suggests fine texture, moderate groundwater recharge, and erosion and flood vulnerability. ($D_{{\text{d}}}$) is “length of stream per unit area in the watershed” (Horton 1945; Strahler 1952; Melton 1957). The $D_{{\text{d}}}$ is a computable expression for analyzing the change in landform. The factors like vegetation, climate, lithology and soil influences the $D_{{\text{d}}}$. The $D_{{\text{d}}}$ value has a direct relationship with infiltration, permeability, surface runoff and soil erosion. Drainage density for Dhanari watershed is 4.25 km² (Table 2) suggesting moderate class (Fig. 4a), indicating high susceptibility for erosion, moderate infiltration by basement rock, high relief and thick vegetation cover. Faniran (1968) defined drainage intensity ($D_{{\text{i}}}$) as the ratio of the $F_{{\text{s}}}$ to $D_{{\text{d}}}$. The Dhanari watershed has $D_{{\text{i}}}$ value 1.95 (Table 2) which is of lower class and implies that $D_{{\text{d}}}$ and $F_{{\text{s}}}$ has a low impact on reducing the land surface by denudation. The low value of $D_{{\text{i}}}$ suggests that surface runoff stays for a longer duration in the watershed signifying high susceptibility for landslide, flood and gully erosion.

Fig. 4

a Drainage density map b Relief map c Slope map and d Slope aspect map

Schumm (1956) introduced constant of channel maintenance (C) as “the ratio between the drainage basin area and the sum of stream length of all channels in the watershed.” Schumm (1956) used the inverse of $D_{{\text{d}}}$ or the ‘C’ as a property of landforms. The ‘C’ provides a quantitative expression for the unit area needed to develop and sustain a 1 km long channel. The ‘C’ of the Dhanari watershed is 0.23  Km² (Table 2), which stipulates that the lower-order stream covers a larger area than higher-order streams with no or less structural control on the drainage network. Low ‘C’ value suggests a reduced overland flow, resulting in the rapid discharge of the water from the watershed. Infiltration number ($I_{{\text{f}}}$) of a watershed is the product of $D_{{\text{d}}}$ and $F_{{\text{s}}}$ suggesting the dissection and runoff potential. The computed $I_{{\text{f}}}$ for the Dhanari watershed is 35.36 (Table 2) suggesting low infiltration and high surface runoff.

Drainage pattern ($D_{{\text{p}}}$) reflects the effect of gradient, bedrock and structure in a watershed. The $D_{{\text{p}}}$ analysis helps identify the geomorphic stage of erosion cycle and structural behavior of basement rocks of the watershed (Horton 1932). The $D_{{\text{p}}}$ of the Dhanari watershed suggests a dendritic pattern (Fig. 2a) with homogeneous rock, low structural control on drainages and a long process of watershed evolution. The $D_{{\text{p}}}$ suggests that watershed has resistant basement rocks with high channel flow. Horton (1945) used length of overland flow ($L_{{\text{g}}}$) to study the extent of surface runoff in a watershed; he defined it as “the length of the stream segment over the surface before it gets concentrated in a channel.” Meanwhile, the low value of $L_{{\text{g}}}$ i.e., 0.11 (Table 2) for Dhanari watershed suggests low infiltration, high surface runoff, short flow path, high relief and vulnerability to flash floods.

Relief characteristics

In the morphometric analysis, relief characteristics bring the role of relief and aspect in the watershed to our knowledge. The difference between the highest point in the watershed/maximum elevation point (Z) and lowest altitudinal point/minimum elevation (z) of the watershed is defined as total basin relief (H) is. The Z value for Dhanari is 2894 meters, and z value is 920 meters (Fig. 2b). The H value for the Dhanari watershed is 1974  meters, suggesting a mountainous high relief terrain formed by the denudation and erosion. Absolute relief ($R_{{\text{a}}} )$ is “the difference between elevations from MSL to a point in the watershed.” The Dhanari watershed has $R_{{\text{a}}}$ value of 2894  meters.

Relief ratio ($R_{{{\text{hl}}}}$) is defined as “the ratio of total relief of the watershed to basin length” (Schumm 1956). The $R_{{{\text{hl}}}}$ value is closely related to relief and erosion as the low value suggests resistant basement rocks and gentler slopes, while the higher value suggests high relief and weak basement rocks. The $R_{{{\text{hl}}}}$ value of Dhanari watershed is 0.10 (Table 2), suggesting drainage has moderate to high relief and moderate slopes (Figs. 4b, c). The relative relief ratio ($R_{{{\text{hp}}}}$) value is the ratio of H and the watershed parameter (Table 2). The $R_{{{\text{hp}}}}$ computed for the watershed is 4.33 (Table 2), indicating high relief mountainous terrain with moderate slope class.

The ruggedness of topography denotes the smoothness and roughness of the terrain in the watershed. Ruggedness number ($R_{{\text{n}}}$) is a product of H and $D_{{\text{d}}}$ (Strahler 1958). The Melton ruggedness number ($MR_{n}$) is a dimensionless unit of gradient index that provides a precise depiction of relief ruggedness within the watershed (Melton 1965). It separates watershed vulnerable to flood from debris flow and debris floods (Melton 1965). The $R_{{\text{n}}}$ values suggest extent of instability of land surface in the watershed (Strahler 1957); while $MR_{n}$ values provide a preliminary classification of flow processes (Melton 1965). The $R_{{\text{n}}}$ value for Dhanari watershed is 8.39 (Table 2) suggesting rugged topography, high susceptibility to soil erosion and low influence of structure on drainage network. The $MR_{n}$ value of the watershed is 0.010 (Table 2) which is classified low suggesting ordinary flow in main stream without added debris flow.

The factor inferring degree of vertical erosion in a watershed explaining the phase the landform development in a region are assessed by Dissection index ($D_{{{\text{is}}}}$) (Singh and Dubey 1994). Lower values of the s$D_{{{\text{is}}}}$ suggest the absence of vertical erosion with flat topography while the higher value represents vertical erosion with steep slopes. The $D_{{{\text{is}}}}$ value for Dhanari watershed is 0.52 (Table 2), which suggests the watershed has moderately dissected topography with the intermediate class of slopes.

The slope of the watershed ($S_{{\text{w}}}$) is one of the most crucial parameters; it suggests the degree of erosion, developmental stage and topography of a watershed (Strahler 1957; Melton 1965). More the percentage of slopes higher will be the vulnerability to erosion, if all other factors are kept constant. The slope category for Dhanari watershed lies between gentle and steep class (Fig. 4c) with a mean gradient (Ѳ_s) averaging 5.8% (Table 2). Gradient ratio ($R_{{\text{g}}}$) is a parameter of channel inclination enabling analysis of the runoff volume (Sreedevi et al. 2005). The quantified $R_{{\text{g}}}$ for Dhanari watershed is 0.10 (Table 2), indicating moderate to high relief terrain with main channel flowing in gently sloping terrain.

The HI of Dhanari watershed is done by using elevation relief method for the estimation of HI. Denudation and sediment loss by surface runoff during heavy precipitation are the major problem related to Dhanari watershed. HI is utilized as a proxy to understand the erosion stage of the watershed and geomorphic response to erosion. The HI value for Dhanari watershed is 0.51 (Fig. 5), suggesting a mature stage of erosion in the watershed and is forwarding toward the peneplanation stage. The value of HI indicates that the erosion is predominantly done by the incision of channel beds, removal of soil mass, mass wasting of bedrock material and erosion of the top-soil from the slopes and channel bank. The HI value also suggests that 51% of the in situ rock mass is still intact in the watershed. The HI measures erosion status of the watershed, the information can be used for conservation, planning, and management. The modern conservation techniques should be implemented with requisite tools to reduce or stop sediment loss from the watershed.

Fig. 5

Hypsometric curve for Dhanari watershed

Soil erosion characteristics

In Dhanari watershed, crucial soil erosion factors are climate, lithology, slope, hydrology and regional structures. The precipitation is the most important factor influencing erosion; loose weathered material and top-soil are eroded by rainwater in surface runoff from the watershed. Precipitation is the highest during monsoon in the watershed, and the main channel receives the highest sediment load during this period. Several channel or streams are formed along slopes as a result of gully erosion. Hydrological behavior of the watershed also alters with increased erosion, as the drainage frequency and texture changes in the watershed. Surface runoff is influenced by the nature of slope in the watershed, as the slope gradient increase the risk of erosion also grows. The lithology and regional structure affect the topography of the watershed significantly. The susceptibility of rocks to erosion depends on rock type and geological structures, such as thrust and faults in the vicinity. The rocks with higher resistance and less structural disturbance remain intact and are resistant to erosion, while structurally disturbed and weaker rocks are easily eroded.

Soil erosion susceptibility of Dhanari watershed is assessed by computing geomorphic aspects and is classified into three classes (Fig. 6). Morphometric parameters viz. $D_{{\text{d}}}$_,, $F_{{\text{s}}}$, $L_{{{\text{ur}}}}$, $R_{{\text{b}}}$, Rho, $D_{{\text{t}}}$, $L_{{\text{g}}}$ and HI have a direct relationship with soil erosion where it increases with increasing values, while other parameters like $R_{{\text{e}}}$, $F_{{\text{f}}}$, $B_{{\text{s}}}$, $D_{{\text{i}}}$, $C_{{\text{c}}}$ and $I_{{\text{f}}}$ show an inverse relationship with erosion potential where it increases with decreasing value. Numerical analysis of the morphometric parameters of Dhanari watershed (Table 2) has suggested that most areas are moderate to highly susceptible to soil erosion. The Dhanari watershed needs proper management and planning for conservation of natural resources in the region of high susceptibility.

Fig. 6

Soil erosion and flood vulnerability map of Dhanari watershed

Groundwater recharge potential

The factors like lithology, hydrology, structure, slope and rock mass properties, play a significant role in groundwater recharge. In Dhanari watershed lithology includes quartzite, limestone, dolomite and gneiss rocks (Fig. 2c). The limestone and dolomites rocks are distributed over a small area in the watershed; these rocks are good aquifer and can conduct and store water efficiently. Limestone and dolomite are in contact with Dunda thrust and Singuni thrust, which results in shearing and fracture. Mylonitized gneiss rocks are in contact with Singuni thrust. The gneisses are sheared and fractured near thrust zone and are confined to a small region in the watershed. The gneisses do not conduct or store water efficiently in the watershed, thus have a low potential for water storage. The quartzite rocks are distributed in the majority of the watershed and are sheared and jointed. Quartzites near thrust zone are sheared and highly jointed but gradually become massive with fewer joints when moving away from these structural anomalies. The quartzites in the upstream region of the watershed are jointed because of regional deformation; several springs were encountered in the watershed, suggesting the rocks are efficient in both conducting and storing the water. The colluvial and fluvial deposit forms shallow aquifers in the Dhanari watershed; these aquifers conduct water efficiently. Their discharge increases during monsoon, but they have low storage capacity and are mostly seasonal.

The slope class for Dhanari watershed ranges from moderate to high (Fig. 4c), suggesting that surface runoff is fast and gives a short recharge duration. The slope condition needs to be satisfied for healthy groundwater recharge; if the slope condition is not favourable, the groundwater recharge is difficult even though watershed has favorable rock type. Another parameter which is very critical to understand is drainage characteristics, which is assessed by quantitative analysis of geomorphic parameters. The geomorphic parameters like $F_{{\text{s}}}$,$D_{{\text{d}}}$,$D_{{\text{t}}}$,$R_{{\text{c}}}$,$R_{{\text{t}}}$,$C$,$L_{{\text{g}}}$ and $I_{{\text{f}}}$ are quantified as they indirectly related to groundwater infiltration, recharge, and surface runoff. The computed values of geomorphic parameters are high (Table 2), suggesting that the watershed has moderate-to-high surface runoff and a very short infiltration period. We interpret that several factors influence the groundwater recharge potential of Dhanari watershed. The study shows that the watershed has poor infiltration and low groundwater recharge due to high surface runoff. We suggest that conservation and management plan for the Dhanari watershed should start in headwater regions with vegetative and mechanical tools to reduce the surface runoff.

Flood vulnerability

The flood vulnerability of Dhanari watershed is assessed by computing morphometric parameters directly related to flood susceptibility. Morphometric parameters viz. $F_{{\text{s}}}$, $D_{{\text{d}}}$, $D_{{\text{t}}}$, $L_{{\text{g}}}$, $R_{{\text{c}}}$ and $R_{{{\text{hl}}}}$ suggests the flood susceptibility of the watershed during a high precipitation event. For Dhanari watershed the $F_{{\text{s}}}$ and $D_{{\text{d}}}$ have high values which give the drainage network very fine texture resulting in rapid surface runoff and increased susceptibility for floods. Lower values of $L_{{\text{g}}}$ in the watershed suggest quicker runoff of smaller streams into the main channel resulting in high flood proneness. The $R_{{{\text{hl}}}}$ when computed suggests low to moderate risk of flood in the watershed. The $R_{{\text{c}}}$ is the most critical parameter to assess flood vulnerability as it highlights potential flood susceptibility of the watershed. The higher value of $R_{{\text{c}}}$ suggests a higher probability of floods and the lower value indicates a low risk of floods. The $R_{{\text{c}}}$ value for the Dhanari watershed indicates moderate to high risk of flood hazards. The morphometric parameters are considered to classify the flood risk or susceptibility of the watershed into three classes (Fig. 6). Natural resources conservation in the watershed needs proper planning and management; the first step is prioritizing based on susceptibility zones. The present study also envisaged that the zones with high soil erosion susceptibility are closely associated with thrust faults dissecting the Dhanari watershed (Figs. 2c and 6). Therefore, special consideration should be given to delineate structural discontinuities for soil erosion and flood vulnerability zonation.

In the present study, we tried to discuss most of the geomorphic aspect of Dhanari watershed. For future studies, the authors suggest following research work can be carried out complementary to the current investigation: (i) Land suitability modeling study (e.g., Danesh et al. 2020); (ii) Prioritization of watersheds for conservation measures (e.g., Meshram et al. 2020); (iii) Determination of flood risk (e.g., Şen and Kahya 2017) and (iv) Mapping of Groundwater Recharge Potential Zones (e.g., Ganapuram et al. 2009; Achu et al. 2020).

Conclusion

The quantitative analysis of drainage characteristics coupled with remote sensing and GIS reveals the influence of hydrological characteristics on a watershed. Quantitative analysis of geomorphic aspects suggests that hydrology, geology, climate, and vegetation directly impact the watersheds hydrological processes. The results indicate that Dhanari watershed is prone to moderate to high erosion; potential groundwater zones in the watershed are scanty because of low infiltration. Flood vulnerability of the Dhanari watershed lies in moderate-to-high class and reaches the highest during monsoons when the discharge is at its peak. Hypsometry of the watershed suggests that the watershed is in a mature development stage with a moderate-to-high erosion rate. Hydrological processes have resulted in the watersheds elongated shape, developed from slow and steady sheet erosion; deposition occurs in low relief. The Dhanari watershed has moderately resistant and homogenous bedrocks; there is low-to-moderate structural control on drainages. Watershed planning, conservation and mitigation measures can be taken to prevent soil erosion and flooding during the peak discharge by using requisite methods, tools and technique. Finally, we feel the modus operandi adopted here would be beneficial in future for the zonation of soil erosion and flood vulnerability in different watersheds across the Himalaya.