Introduction

Mercury (Hg), Lead (Pb), and Cadmium (Cd) considered as toxic metals. Their presence in the aquatic environment above recommended limits is critical to human health and the ecosystem. The presence of mercury in the aquatic environment and the ecosystem remains an area of research interest because of the toxic nature of mercury to humans. The characteristic of non-biodegradability supports the persistency of mercury ions in the system (Šapanin et al. 2019). Mercury ions released into the environment from ores, industries, and agricultural waste. These ions are transported along the eco-chain into humans resulting in food poisoning, liver, kidney malfunctioning, and carcinogenicity (Mousavi et al. 2011; Alam et al. 2019; Avigliano et al. 2019).

There is a need to reduce the presence of Hg(II) ions from solution. The techniques in current use include membrane filtration, oxidation, sedimentation, distillation, ion exchanger, and adsorption (Abdel-Ghani et al. 2014; Abdolali et al. 2014). All these process and techniques have several setbacks range from high cost, the high volume of waste, and the inability to achieve the limits required by the international community (Páez-Hernández et al. 2005). Mercury ion removal using adsorption is considered an accepted technique since it is simple, less expensive, and environmental friendly (Chen et al. 2019).

The use of activated carbon as an adsorbent in mercury ion removal exists. The desirability to use activated carbon stems from the fact that activated carbon contains well oriented structural carbon atoms. However, the extra cost of growing bio-materials is problematic, thus readily grown bio-materials such as the African palmae is an added advantage (Thambiliyagodage et al. 2018; Sadegh et al. 2017). The development of activated carbon takes different forms inclusive pyrolysis at high temperature (physical activation) and the use of chemical reagents at low temperature (Jankovi et al. 2019). The use of chemical reagents is preferable since low temperature and shorter time is involved. Besides, the extra surface area added to improve on the reactivity of the activated carbon (Di Stasi et al. 2019). Among the activating reagents, potassium hydroxide is considered the best since it generates high surface area and high porosity of the activated carbon (Yacob et al. 2010; Yang et al. 2019; Wan et al. 2019; Vazquez et al. 2002). The interaction of activated carbon and some mercury ions controlled by the adsorption characteristics of net proton charge and the surface area (Ghaith et al. 2019; Skinner et al. 2007). A Weber-Morris model is an excellent tool in the validation of intra-particle diffusion (Ghannad and Lotfollahi, 2019). The Freundlich isotherm and the extended forms are useful in validating the reaction kinetics of the reaction processes {Yang et al. 2019; Fuadi et al. 2014; Lotfy et al. 2012).

There are several spilt cases of mercury in the environment. Some of these cases could be due to the careless release of mercury from the laboratories, manufacture, and mining operations. In this study, the treatment of mercury in solution with a well prepared and characterized, activated carbon derived from Palmae biomass is done.

Materials and experimental methods

Material preparation

Local communities in Nigeria provide the sampled Palmae shells used as precursor used for the formulation of the activated carbon. The samples were cleaned and air-dried using tap water at a moisture content of 10%. The samples were carbonized and fractionated into powdered and granular forms of 0.6 mm and 1.5 mm, respectively (Ani et al. 2020). The purpose for the fraction is to understand the role of particle fractions in the efficiency of the activated carbons.

Formulation of activated carbon

The carbonization process involved heating of the shells to 4000 °C until the shells turned into a large volume of charcoal. The charcoal was then chemically activated using 75% potassium hydroxide at a moderate temperature of 400 °C for 5 h. The activation was carried out in the ratio of 3:1(carbon: activator) to form a paste. A muffle furnace in an atmosphere of neutral gas (N2) used to heat the paste until dried. The content rinsed with distilled water at ambient temperature. Subsequently, the rinsed and dried content was dried at 105 °C for 24 h to ensure wholistic drying. Again, the content subjected to further pulverization to achieve the PAC-0.6 mm and GAC-1.5 mm fractions. The content ready for adsorption experiments (Bani et al. 2018; Hui and Zaini, 2015). A set of reactions occurring during the activation process is provided:

$$ {\text{C}} + 2{\text{KOH}} \to 2{\text{K}} + {\text{H}}_{2} + {\text{CO}}_{2} $$
(1)
$$ {\text{C}} + 2{\text{KOH}} \to 2{\text{K}} + {\text{H}}_{{2}} {\text{O}} + {\text{CO}} $$
(2)
$$ {\text{CO}}_{2} + 2{\text{KOH}} \to {\text{K}}_{{2}} {\text{CO}}_{{3}} + {\text{H}}_{2} {\text{O}} $$
(3)

Characterization of biomass and activated carbon

Proximate analysis

A carbonized shell contains physical and chemical components distributed over the carbon structure. These include the water present in the sample (i.e., moisture content), gases and vapors (i.e., volatile matter), and the fixed carbon contained in the sampled. The moisture content was determined by heating the sample at 105 °C for 2 h in a petri dish and recording the difference in weight before and after heating of the sample. The volatile matter was determined by heating the sample in a crucible at 925 °C for 7 min and recording the difference in weight before and after heating of the sample. The ash content was evaluated by heating the sample at 725 °C for 1 h and recording the difference in weight before and after heating of the sample. The fixed carbon content was evaluated by recording the difference between % of moisture content, volatile matter content, and ash content from 100 (Budianto et al. 2019).

Ultimate analysis (CHNS)

The determination of carbon, hydrogen, nitrogen, and sulfur in biomass CHNS analysis. This Dumas technique centered on the full oxidation of the precursor expressed, in the CHNS components. The % of oxygen-derived by recording the difference between the CHNS and 100 (Fleck 1965). The CHNS Analyzer LabX, Ontario, Canada was used for the ultimate analysis. The reaction of the precursor and excess oxygen releases carbon dioxide, water, nitrogen dioxide, and sulfur dioxide, respectively. A chromatographic column was used for the separation of these components, detected by a thermal conductivity detector (TCD.). The signals from the TCD were related to the concentration of the components of the biomass (Zheng et al. 2019).

Determination of the point of zero charges of activated carbon

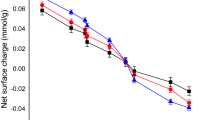
The point of zero charges (pHpzc) indicates a pH value of zero. This parameter indicates the interface between the positive and negative charges at the active sites. A potentiometric titration involving 0.001 M, 0.01 M, and 0.1 M of NaCl electrolyte, and 1 g activated carbon reacted for 24 h was used to evaluate this parameter. The titration curves generated by a plot of net proton charges versus the suspension pH were used to determine the pHpzc.

Morphological study of the activated carbons

The scanning electron microscopy (SEM–EDX method) (EMLS-Canada) was used to perform the image analysis of the activated carbons. A high vacuum mode (HV) was used to observe the analyzed samples at the accelerated voltage of 20 kV or 10 kV using an SE secondary electron detector.

Determination of surface area of activated carbon

The physical adsorption of nitrogen gas on the surface of the AC was used to evaluate the equivalent nitrogen gas adsorbed to a single layer on the activated carbon surface. monomolecular layer on the surface. A micromeritics (ASAP 2020) surface area analyzer LabX, Ontario, Canada was used to degas the sample at 300 °C in liquid nitrogen flow condition (Stoeckli and Centeno, 2005).

Regeneration of the activated carbon

Thermal regeneration of the spent activated carbon was carried out by treating it with 1 M nitric acid, thus resulting to 60% regain. The extracted activated carbon was heated to 500 °C for 24 h (Shahadat, and Isamil 2018).

Adsorption experiments

All chemicals and materials used for analyses were of analytical grade purity obtained from BDH (England), Loba Chemie (India). 1 g of mercury chloride was dissolved in distilled and made up to a liter. This content is the stock solution, and several standards were prepared from the stock solution. The equilibrated experiments on batch mode adsorption were administered using 20 g/50 mL of mercury solution. The suspension since agitation for 30 min except for contact time experiments and filtered with 0.45 µm membrane was measured for Hg(II) ions remaining in a solution using ICP-OES analyzer (CAP6300, Thermo, USA). The adsorption capacity of the AC Qe (mg/g) was determined (Eq. 1):

The adsorption capacity of the AC Qe (mg/g) was calculated using the following Eq. (1):

$$ Q_{e} = [C_{0} - C_{e} ]{\raise0.7ex\hbox{$V$} \!\mathord{\left/ {\vphantom {V M}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$M$}} $$
(4)

Herein, C0 and Ce define the concentration at the start of reaction and concentration at the steady- state of the Hg(II) ions (mg/L) and contaminated water interaction, respectively, V is the volume of the solution (L), and m is the mass of AC used (g). The exchange of protons has a constant defined by an isotherm deduced from the plot of the change in pH versus lg Kd as provided (Eqs. (5) and (6):

$$ \alpha {\text{SOH}} \leftrightarrow {\text{SO}}^{ - } + \alpha {\text{H}}^{ + } $$
(5)
$$ 1g\;{\text{Kd}} \leftrightarrow 1g(K_{p} \{ {\text{SOH}}\} \alpha ) + \alpha pH $$
(6)

Herein, SOH represents an AC surface-reactive site, SO − is the surface-bound Hg(II), lgKp is the apparent equilibrium-binding constant, and α is the coefficient of protonation, which represents the number of protons displaced when one mole of Hg(II) binds to the AC surface.

Also, the mass transfer rate and intraparticle diffusion were derived from Eqs. (8)– (9):

$$ Q_{t} = [C_{0} - C_{t} ]{\raise0.7ex\hbox{$V$} \!\mathord{\left/ {\vphantom {V M}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$M$}} $$
(7)

Herein, C0 is the initial Hg(II)concentration (mg·L−1) at time t = 0; Ct is the concentration (mg·L−1) at time t; V is the total suspension volume, and m is the mass of the AC (g) (Ojemaye et al. 2017).

An intraparticle diffusion model by Weber–Morris also, was used to describe the reaction mechanism as provided (Eq. 8) (Dong, 2012):

A reaction kinetic involving AC charged with Hg(II) ions was deduced from the mass transfer constant Kf. Here, Ct/C0 versus time provided the slopes of the curves derived from Eq. (8) {Joseph et al. 2019}.:

$$ \left[ {\frac{{d\left( {{\raise0.7ex\hbox{${C_{t} }$} \!\mathord{\left/ {\vphantom {{C_{t} } {C_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{0} }$}}} \right)}}{dt}} \right]_{t = 0} \cong - K_{f} S_{s} $$

Herein, C0 and Ct represent the Hg(II) initial concentration at time t, Ss is the exposed surface area of an AC, and Kf is the coefficient of mass transfer. These models as derived from the Freundlich isotherm have been reviewed previously and adopted to describe the adsorption of Hg(II) ions(Mohan and Chander 2001).

$$ Q_{t} = K_{{t^{0.5} }} + C $$
(9)

Herein, Ki is the intraparticle diffusion constant (mg·g−1·min−1), and the intercept (C) represents the effect of the layer boundary. The value of Ki is derived from the slope (Ki) of the plots of Qt vs. t0.5. A linear plot of Qt versus t0.5 indicates that intraparticle diffusion was involved in the process of adsorption [Li et al. 2016]. For validation of an intraparticle diffusion, a 10 mg·L−1 Hg(II) solution was charged with 20 g of AC made up to 50 mL at 4 ≤ pH ≤ 10. This mixture was treated for 30, 60, 90, 120, 150, 180, and 210 min. A Hg(II) ions remaining in solution were determined using the ICP-OES. In all experiments, the adsorption efficiency of AC was calculated from Eq. (10):

$$ {\text{Adsorption}}\;{\text{efficiency}}\;(\% ) = \frac{{C_{0} - C_{e} }}{{C_{0} }} \times 100 $$
(10)

Herein, C0 and Ce (mg·L−1) are the concentrations at the start of reaction and concentration at the steady-state Hg(II) concentrations in solution, respectively (Zbair et al. 2019; Awual, 2017).

Besides the Freundlich isotherm and its derivatives used in this study, the Langmuir adsorption isotherm is used to describe the adsorption kinetics. A linear regression (y = A + B · x) and Langmuir equation are represented

$$ {\raise0.7ex\hbox{${C_{e} }$} \!\mathord{\left/ {\vphantom {{C_{e} } {q_{e} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${q_{e} }$}} = \tfrac{1}{{q_{m} *b}} + \tfrac{{C_{e} }}{{q_{m} }} $$
(11)

Herein, Ce is the equilibrium concentration of cadmium(mg/L) in solution, qe is the adsorption capacity of the activated carbon at equilibrium (mg/g), qm is the maximum adsorption capacity of the activated carbon (mg/g) and b(L/mg) is a constant linked to the energy of adsorption. A plot of \({\raise0.7ex\hbox{${C_{e} }$} \!\mathord{\left/ {\vphantom {{C_{e} } {q_{e} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${q_{e} }$}}\) versus \(C_{e}\) gives a slope of \(\tfrac{1}{{q_{m} }}\) and an intercept \(\tfrac{1}{{q_{m} *b}}\).

y = A + B*x; y = \({\raise0.7ex\hbox{${C_{e} }$} \!\mathord{\left/ {\vphantom {{C_{e} } {q_{e} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${q_{e} }$}}\); x = \(C_{e}\); A = \(\tfrac{1}{{q_{m} *b}}\); B = \(\tfrac{1}{{q_{m} }}\) (12).

If the adsorption process falls in line with the Langmuir model, then the plot provides a straight line, and the values of qm and b (L/mg) are evaluated from the plot.

Effect of pH on the removal of Hg(II) removal

At a constant contact time (30 min), dosage (20 g), and some mercury concentration (20 mg/L) the effect of pH was also studied. 20 g of the activated carbon was introduced into a 50 mL plastic vial. The content was made up to 50 mL by adding the mercury-contaminated carnal water and 0.1 M of NaOH was used to regulate the pH to pH 4, 5, 6, 7, 8, 9, and 10. The solution was shaken and filtered with 0.45 µm filter paper. The Remaining mercury in solution was determined using inductively coupled plasma optical emission spectrometer (ICP-OES analyzer CAP6300, Thermo, USA).

Effect of contact time on the removal of Hg (II) Removal

At a constant pH of 6.05, 20 g dosage and some mercury concentration of 20 mg/L, the effect of contact time on mercury removal was also studied at a range of 30, 60, 90, 120, 150, 180, and 210 min. 20 g of the activated carbon was introduced into a 50 mL plastic vial. The content was sealed and placed in a mechanical shaker and agitated at 20 rotation per minute (rpm), for each of the different contact times (30, 60, 90, 120, 150, 180, and 210 min). The content of each was filtered and analyzed with ICP-OES analyzer (CAP6300, Thermo, USA) to determine the amount of mercury remaining in the solutions.

Effects of Hg concentration on its removal by activated carbon

At a constant pH of 6.05, a contact time of 30 min and 20 g dosage of activated carbon, the effect of Hg concentration on its removal by activated carbon was studied. 20 g of the activated carbon was introduced into a 50 mL plastic vial. The content was made up to 50 mL by adding variable concentrations of mercury solutions at 40 mg/L, 20 mg/L, 15 mg/L, and 10 mg/L. The content was sealed and placed in a mechanical shaker and agitated at 20 rotations per minute (rpm). The content was filtered and analyzed with ICP-OES analyzer (CAP6300, Thermo, USA) to determine the amount of mercury remaining in the solutions.

The effect of dosage of activated carbon on the removal of Hg(II) ions

At a constant pH of 6.05, a contact time of 30 min a mercury concentration of 20 mg/L, the effect of dosage of activated carbon on mercury removal was studied. 10, 20, 30, and 40 g of the activated carbon were introduced into a 50 mL sample vial. The content was made up to 50 mL by adding 20 mg/L of mercury solution. The content was sealed and agitated in a mechanical shaker at a speed of 20 rotations per minute (rpm). The content was then filtered and analyzed with ICP-OES analyzer (CAP6300, Thermo, USA) to determine the amount of mercury remaining in the solutions.

Results

Characterization

This study has made available the component distribution of moisture content, volatile matter, and the fixed carbon contained in the biomass. Besides, the CHNS components have been provided (Tables 1 and 2). Thermal treatment of biomass decreased the content of the biomass to 39.2%. The sudden increase in the amount of fixed carbon and decrease in the amount of hydrogen may be linked to volatile matter removed during carbonization and subsequent activation of the biochar. Palmae shell does not carry nitrogen as a component, rather it was introduced during the carbonization process. Also, a significant amount of oxygen is lost during the activation process.

Table 1 Proximate and ultimate analysis of powdered palmae shells and granular palmae shells
Full size table
Table 2 Proximate and ultimate analysis of powdered activated carbon and granular activated carbon
Full size table

The pHpzc of activated carbon is 7.01 (Figs. 1 and 2). This value indicates that above the pHpzc, the active surface of the activated carbon is negatively charged. The actual mineral surface subject to reaction is controlled by the specific surface area. This is determined using the Brunauer–Emmett–Teller (BET) method. The powdered and granular forms of the activated carbon generated a surface area 3520 m2/g and 2950 m2/g, respectively. Equations (1) and (2) and a graphical plot (Fig. 3) were used to evaluate the proton coefficient (α), of the reactions. The graph provided a linear fit trend (Table 3). The value of α for powdered (PAC) and the granular (GAC) forms of activated carbon as provided by the slopes are 1.12 and 0.38, respectively.

Fig. 1
figure 1

Plot of net surface charge versus suspension pH of activated carbon for determination of the point of zero charges

Full size image
Fig. 2
figure 2

SEM micrographs of activated carbons a without treatment and b treated with mercury ions,

Full size image
Fig. 3
figure 3

Plot of lg Kd versus final pH for proton coefficient for PAC and GAC

Full size image
Table 3 Linear fit parameters derived from Fig. 2
Full size table

Thus, lg Kd versus pH plot provided a peak distribution coefficient (Kd) of 23.68 L/g and 2.15 L/g for powdered and granular forms of activated carbon, respectively. The mass transfer of Hg(II) ions from the surface to the reactive boundary ( Eq. 4) is generated from a plot of Ct/C0 versus contact time (Fig. 4 and Table 3). The rate of particle diffusion in the reaction processes (Eqs. 5–6) is used to plot and provide slope values for the constant (Fig. 4, and Table 4).

Fig. 4
figure 4

Ct/Co for Hg(II) versus contact tim

Full size image
Table 4 Analysis of mass transfer constant derived from Fig. 3
Full size table

The thermal regeneration of the spent activated carbon revealed a regain of 60% adsorption capacity. Thermal heating of the extracted activated carbon provided a 90% removal efficiency (Fig. 5).

Fig. 5
figure 5

A plot of adsorption capacity of PAC and GAC versus square root of contact time (min) for intra-particle diffusion

Full size image

Adsorption studies

The results obtained from the adsorption studies are shown Eq. (Figs. 6, 7, 8, 9, 10 and 11 and Tables 3, 4, 5, 6 and 7).

Fig. 6
figure 6

Hg removal (%) versus Contact Time (mins) for powdered activated carbon (PAC) and granular activated carbon (GAC) (20 g adsorbent, pH = 6.05, 40.41 mg/L Hg(II) ions

Full size image
Fig. 7
figure 7

Hg(II) removal (%) versus Hg concentration (mg/L) for powdered activated carbon (PAC) and granular activated carbon (GAC) at 30 min. contact time, 20 g adsorbent, pH = 6.05

Full size image
Fig. 8
figure 8

Hg(II) removal (%) versus pH for powdered activated carbon (PAC) and granular activated carbon (GAC) at contact time 30 min, 20 g adsorbent, 40.41 mg/L Hg(II) ions

Full size image
Fig. 9
figure 9

Hg(II) removal (%) versus dose of powdered activated carbon (PAC) and granular activated carbon (GAC) at contact time 30 min,pH = 6.05, 40.41 mg/L Hg(II) ions

Full size image
Fig. 10
figure 10

Plot of Ce/qe versus Ce for Langmuir isotherm for PAC

Full size image
Fig. 11
figure 11

Plot of Ce/qe versus Ce for Langmuir isotherm for GAC

Full size image
Table 5 linear fit analysis derived from Fig. 3 for PAC and GAC
Full size table
Table 6 Langmuir parameters for mercury adsorbed by powdered activated carbon
Full size table
Table 7 Langmuir parameters for mercury adsorbed by granular activated carbon
Full size table

The Langmuir isotherm parameters are provided (Tables 2 and 4). The Langmuir constants for PAC are higher than that of the GAC, and the maximum adsorption is equally slightly higher for the PAC compared to the GAC.

Effect of contact time on a Hg(II) removal

The efficiency removal of mercury was plotted against contact time using Eq. 7 and found in Fig. 5. Two critical components of the plot revealed a steady increase in adsorption supported by an equilibrium outlook over time. The adsorption response is 78% and 74.5% at the 18th mins for both PAC and GAC activated carbons, respectively.

Effect of initial Hg(II) concentration on its removal

The efficiency removal of mercury was plotted against Hg(II) concentration using Eq. 7 and found in Fig. 6. Two critical components of the plot reveal a decrease in Hg(II) removal as the concentration increases and subsequently achieved an equilibrium state over time. The maximum removal efficiencies are 87.5% and 81.25% for both the powdered and granular forms of activated carbons.

Effect of pH on Hg(II) removal

In the range of pH studied, uptake of both charged and uncharged Hg(II) species exist with the latter dominating in solution. The uptake of Hg(II) ions appeared to increase increased pH as the hydronium increased. Within the alkaline range, the uptake of Hg(II) ions decreased and achieved a steady-state, The pH is critical to the adsorption of Hg(II) ions in solution (Reddy et al. 2014). At pH = 7.01, both the positives and negatives at the reactive surface are balanced, and adsorption is by coulombic forces. However, above the isoelectric point an equilibrium state of the reaction is achieved (Fig. 7). The maximum removal efficiencies are 88% PAC and 86.1% for both the powdered and granular forms of activated carbons.

Effect of dosage of activated carbon on Hg(II) removal

The efficiency removal of mercury was plotted against the dosage of the activated carbons using Eq. 7 and found in Fig. 8. Two critical components of the plot revealed a steady increase in adsorption supported by an equilibrium state over time. Herein, the maximum removal efficiencies are 71.5% and 64.5% for both the powdered and granular forms of activated carbons.

Discussion

Adsorption and reaction mechanism

The reaction mechanisms are characterized by the proton coefficient, diffusion of intraparticle and the transfer of Hg(II) ions from the boundary layer to the reactive sites (Ghannad and Lotfollahi, 2019). Here, when Hg(II) ions were charged with the activated carbons, the proton coefficients are less than one. There is a suggestion that the removal of Hg(II) ions is not solely a process initiated by the formation and utilization of protons. Instead, the diffusion of intraparticle with slopes 3.22 × 10–3 and 3.22 × 10–3 (mgg-1 min-0.5) with a non-zero intercept for both the powdered and granular activated forms of activated carbons, respectively. The critical regions are the transfer of Hg(II) ions and the diffusion of activated carbon particles. The boundary layers controlled the diffusion process thus making the plot to possess a non-zero intercept.

Adsorption and reaction kinetics

The contact time of the reaction is the critical component of the reaction kinetics. (Fig. 5). The criteria for evaluation include a contact time range of 30—210 min at a constant temperature, mercury concentration of 20 mg/L and pH = 4–10. Again, two critical components of the reaction are presented. These are a steady increase in adsorption until an equilibrium state is achieved. Before the steady-state, Hg(II) ions are deposited at available reactive sites (Rafatullah et al. 2011). and consequently, filled since and become saturated (Anirudhan and Sreekumari 2011; Vazquez et al. 2002). Besides, the higher exposed surface area for the powdered activated carbon and the lower surface area for the granular form of activated carbon differentiated the adsorption efficiencies. Both of the Freundlich and Langmuir isotherms indicate greater values for PAC compared to the GAC.

Effect of Hg (II) concentration on its removal by activated carbons

In nature, aquatic systems possess a variable range of Hg concentrations. A mercury increase in solution decreased the adsorption of Hg(II) ions (Fig. 6) for both forms of activated carbons. The surface-reactive sites are occupied steadily until saturation is reached. Thus, there are retention of Hg(II) ions on activated carbon at a low concentration, and there is ready removal of Hg(II) ions at this stage of the reaction process.

Effect of pH on mercury removal

pH promotes the attachment of Hg(II) ions to the reactive functional groups of active carbon (Fig. 7). pH increase increased the deprotonation of these active carbon sites, thus, enhancing a negative charge (Burakov et al. 2018). There is a generation of bonding based on electrostatic attraction. Around the pHzpc, there is reduced protonation and improved hydroxylation, which enhances Hg(II) removal from solution. Thus, intraparticle diffusion sets in and reorganized the reactive sites of the active carbon surfaces (Banerjee & Chattopadhyaya 2017). The decrease in pH decreased Hg(II) removal. There is a competition for reactive sites between hydronium and Hg(II) ions, thus, impeding the removal of mercury ions in the solutions (Zheng et al. 2017).

Effect of dosage of active carbon on the removal of Hg(II) ions

The interaction of doses of active carbon and Hg(II) ions is represented (Fig. 8). The increase in the dosage of active carbon increased Hg(II) removal. When active carbon is increased, there is a consequent increase in active sites supported by increased surface area due to a increase in available reactive sites and surface area of active carbon. At the onset of coagulation of active particles, a steady-state of reaction is achieved (Fig. 8).

Comparison of performance of adsorption parameters

In comparing, the parameters of the adsorption of Hg(II) ions pH recorded the highest adsorption efficiency of 88% PAC and 86.1% for GAC at pH a range of pH-8–10 and pH = 9–10, respectively. This parameter is followed by the concentration of mercury in solution. This parameter recorded 87.5% and 81.25% for GAC at 10 mg/L of Hg(II) concentration. The contact time was found to record 78% and 74.5% (i.e., for PAC and GAC), respectively, at the range of 150–210 min. The dosage of active carbon recorded the lowest adsorption efficiencies of 71.5% and 63.5% using powdered and granular forms of activated carbon.-

Conclusions

Both forms of active carbons are novel in removing Hg(II) ions from aqueous systems Protonation and deprotonation controlled by pH regulates the adsorption process. A two-interaction process namely mass transfer of active particles and intraparticle diffusion controlled by a boundary layer are involved in the removal mechanism for Hg(II) ions. There is evidence that two-reaction steps namely a step whereby the reaction is gradual and a steady-state at equilibrium. There is evidence that the active sites at carbon surfaces get filled over time, thus, promoting the two-step reaction. The presence of hydronium ions promotes the hydroxylation of the system, thus, creating a reorganization of the active. Both of the Freundlich and Langmuir isotherms fit into the experimental data.