Adsorption of cadmium ion from aqueous solutions by copper-based metal organic framework: equilibrium modeling and kinetic studies

Abstract

In the present study, the adsorption behavior of copper-based metal organic framework (Cu-MOF) in the removal of cadmium ion (Cd²⁺) from aqueous solution was investigated. The Cu-MOF prepared by solvothermal method was characterized by BET, FTIR, SEM and EDX techniques. Effect of adsorption parameters such as initial Cd²⁺ concentration (20–100 mg/L), contact time (20–60 min) and adsorbent dosage (0.1–0.5 g) on the removal efficiency and equilibrium adsorption capacity was investigated at fixed pH and temperature. The results obtained from the batch mode adsorption studies revealed that at initial Cd²⁺ concentration of 20 mg/L, contact time of 60 min and adsorbent dosage of 0.5 g, the removal efficiency and equilibrium adsorption capacity of Cd²⁺ from the process were 98.62% and 1.9724 mg/g, respectively. The experimental data were evaluated by Langmuir and Freundlich isotherm models. The data fitted well with the Langmuir isotherm, and monolayer adsorption capacity of the Cu-MOF was 219.05 mg/g. The kinetic data were analyzed by using pseudo-first-order, pseudo-second-order and intraparticle diffusion models. The kinetic studies showed that pseudo-second-order model exhibited high correlation coefficients for all the initial Cd²⁺ concentrations studied, thus indicating that the theoretical amount of Cd²⁺ adsorbed agreed to the experimental values of Cd²⁺ adsorbed.

Introduction

Persistence increase in concentration of heavy metals in water bodies has been attributed to population explosion and proliferation of industries. Heavy metals are toxic, persistence in nature and highly soluble in water. The destructive effects of toxic heavy metals on humans are well known. For instance, cadmium ion (Cd²⁺) is one of the most toxic heavy metal ions to which man can be exposed in the environment (Bernard 2008). Cd²⁺ causes lung cancer, proteinuria, kidney failure and osteomalacia (Ekanem 2017). Therefore, there is need to treat heavy metal-contaminated effluent before its release into water bodies. Various treatment methods such as reverse osmosis, ion exchange, coagulation, electrocoagulation, electrochemical, precipitation and adsorption have been used for the removal of heavy metals from aqueous environment (Kamaraj et al. 2013; Vasudevan et al. 2010; Osasona et al. 2018). Among the aforementioned techniques, adsorption has been widely accepted because it is cheap, simple, effective and environmentally friendly (Gorzin and Abadi 2017; Osasona et al. 2018).

Adsorption is a percolation process in which a fluid is passed through porous material (adsorbent) which has the affinity to alter the concentration of the fluid. Various adsorbents such as activated carbon (Osasona et al. 2018), zeolite (Kussainova et al. 2018), molecular sieve (Rao et al. 2015), silica gel (Tzvetkova and Nickolov 2012) and so on have been used for the removal of heavy metals from aqueous environment. However, these adsorbents are less effective due to their low surface area and adsorption capacities. In recent time, researchers have centered their studies on the development of adsorbent with better properties. In particular, a highly active and porous synthetic material such as metal organic frameworks (MOFs) is still ongoing. Numerous researchers have synthesized MOFs from different sources and applied them in gas separation and storage (Senkovska and Kaskel 2008), sensing devices (Chen et al. 2008), catalysis (Lee et al. 2009), drug storage and delivery (Horcajada et al. 2008), as electrode material for super-capacitor (Liu et al. 2010), liquid and gas adsorption (Ahmed et al. 2013) and many more. MOFs are referred to as porous crystalline materials in which both metal ions and ligands are linked together (Abassi et al. 2017). Many studies on the use of MOFs as adsorbents to remove inorganic and organic contaminants from wastewater have been conducted and documented (Bakhtiari et al. 2015; Abassi et al. 2017; Lin and Hsieh 2015). Shooto et al. (2017) studied the adsorption behavior of iron-based MOF for removal of lead ion from aqueous solution. Maleki et al. (2015) synthesized cobalt-based MOF and employed as adsorbent to separate hexavalent chromium from aqueous solution. A MOF-derived nanoporous carbon adsorbent was synthesized by Bakhtiari et al. (2015) for removing copper ions from simulated solution. However, the literature survey reveals that few studies on the use of MOFs as adsorbents for removing heavy metal ions from aqueous solution have been reported. Moreover, to the best of our knowledge, detailed kinetic study on Cd²⁺ adsorption by MOF has not been reported.

In the present study, copper-based metal organic framework which is referred to as Cu-MOF was synthesized via solvothermal method, characterized and employed as adsorbent to remove cadmium ion (Cd²⁺) from simulated solution. The effects of variables affecting adsorption process such as the initial Cd²⁺ concentration, contact time and adsorbent dosage were investigated. Equilibrium adsorption isotherm and kinetic models were applied to evaluate the acquired experimental data.

Experimental

Material

Copper nitrate trihydrate [Cu(NO₃)₂∙3H₂O, BDH], cadmium nitrate tetrahydrate [Cd(NO₃)₂∙4H₂O], benzene 1,3,5-tricarboxylic acid [C₆H₃–1,3,5-(COOH)₃ (H₃BTC), 98%] and methanol (CH₃OH, 99.5% synthesis grade) were all purchased from Nizo chemical enterprise, Lagos, Nigeria. All the chemical compounds were used as received without subjecting them to further purification.

Preparation of Cu-MOF adsorbent

The procedure employed to prepare Cu-MOF adsorbent in this study was reported by Vakiti (2012). Cu(NO₃)₂∙3H₂O (0.25 g, 1.03 mmol) was dissolved in 10 mL of distilled water, and H₃BTC (0.10 g, 0.53 mmol) was dissolved in 10 mL of methanol. The two resulting mixtures were vigorously mixed and 5 mL of deprotonating agent (Trethyl amine) was added. The slurry was then refluxed at 130 °C for 2 h under constant stirring. The light blue crystals obtained were filtered, washed with methanol severally until clear crystals were obtained, after which it was dried in an oven at 55 °C for 30 min and employed immediately as an adsorbent for Cd²⁺ removal from aqueous solution.

Characterization of Cu-MOF adsorbent

The properties of the as-synthesized Cu-MOF adsorbent were determined using Brunauer–Teller–Emmett (BET) surface area measurement, Fourier transform infrared (FTIR) spectroscopy and scanning electron microscopy-energy-dispersive X-ray (SEM–EDX). The textural characteristics of the as-prepared adsorbent were determined by a Quantachrome instrument (NOVA station A, version 11.03, USA) based on the principle of adsorption/desorption of nitrogen at 77 K and 60/60 s (ads/des) equilibrium time. The FTIR spectrophotometer (IR Affinity-1S, Shimadzu, Japan) was employed to determine the surface functional groups of the Cu-MOF adsorbent, and the IR spectra of the sample studied were collected in the range of 4000–400 cm⁻¹, while SEM image of the prepared adsorbent was viewed through a microscope (SEM, JEOL-JSM 7600F) in order to examine its surface morphology. The elemental composition of the Cu-MOF adsorbent was also evaluated by the microscope equipped with EDX analyzer.

Preparation of cadmium ion solution

Stock solution of Cd²⁺ was prepared by dissolving 1.85 g of Cd(NO₃)₂∙4H₂O in 1 L of distilled water. From the stock solution, 20, 40, 60, 80 and 100 mg/L, the initial Cd²⁺ concentration was made by dilution method and subsequently used for batch adsorption experiment.

Batch adsorption experiment

The adsorption studies were conducted via batch mode by charging required quantity of adsorbent into 250-mL conical flasks containing 50 mL of Cd²⁺ solution. The mixture of Cu-MOF adsorbent and Cd²⁺ solution contained in a set of each conical flasks was placed and agitated in a temperature-controlled water bath shaker (SearchTech Intrument SHZ-82 Thermostatic, India) operated at a constant stirring speed of 150 rpm. The process was conducted by considering various adsorption conditions as follows: the initial Cd²⁺ concentration (20–100 mg/L), contact time (20–60 min) and adsorbent dosage (0.1–0.5 g). All the adsorption experiments were carried out at fixed pH and room temperature of 4.0 and 30 °C, respectively.

After the attainment of the equilibrium, each sample was centrifuged at high speed for 10 min and decanted. The concentration of Cd²⁺ left un-adsorbed in the collected solution was determined by atomic absorption spectrophotometer (AAS, Buck Scientific 210VGP, USA). The Cd²⁺ removal efficiency, R (%), and amount of Cd²⁺ adsorbed per unit mass of Cu-MOF, $q_{\text{e}}$ mg/g, are calculated by Eqs. (1) and (2), respectively.

$$R = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)}}{{C_{\text{o}} }} \times 100\%$$

(1)

$$q_{\text{e}} = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)V}}{W}$$

(2)

where $C_{\text{o}}$ and $C_{\text{e}}$ (mg/L) are the initial and equilibrium concentrations of Cd²⁺ in aqueous solution, V (L) is the volume of the Cd²⁺ solution and W (g) is the weight of the Cu-MOF sample used.

Equilibrium adsorption isotherm

The correlation between the amount of Cd²⁺ adsorbed onto Cu-MOF and the equilibrium concentration of Cd²⁺ in the aqueous phase was evaluated using two-parameter isotherm models. The experimental data acquired were analyzed by Langmuir and Freundlich models.

The Langmuir isotherm model is employed based on monolayer adsorption of adsorbate on homogeneous active sites, and thus, saturation is attained, beyond which no further attachment of adsorbate on adsorbent takes place. It also operates with the principle that there is no interaction between the adsorbed molecules on adjacent sites (Oyedoh and Ekwonu 2016). The nonlinear model which was described by Langmuir (1918) is presented in Eq. (3).

$$q_{\text{e}} = \frac{{q_{\hbox{max} } bC_{\text{e}} }}{{\left( {1 + bC_{\text{e}} } \right)}}$$

(3)

where $q_{e}$ (mg/g) is the amount of Cd²⁺ adsorbed at equilibrium, $C_{\text{e}}$ (mg/L) is the equilibrium concentration of Cd²⁺ in aqueous solution, $q_{\hbox{max} }$ (mg/g) is the maximum adsorption capacity and b is the Langmuir equilibrium constant.

The separation factor (R_L) whose value determines the nature of the isotherm shape is the important feature of the Langmuir isotherm. It can either be favorable (0 < R_L < 1), unfavorable adsorption (R_L > 1), linear (R_L = 1) or irreversible adsorption (R_L = 0). The dimensionless parameter is given by Eq. (4).

$$R_{\text{L}} = \frac{1}{{\left( {1 + bC_{\text{o}} } \right)}}$$

(4)

where $C_{\text{o}}$ (mg/L) is the maximum initial Cd²⁺ concentration and b (L/mg) is the Langmuir equilibrium constant.

The Freundlich isotherm is the two-parameter model which is applied based on multilayer adsorption on heterogeneous surface and is expressed as follows (Freundlich 1906):

$$q_{\text{e}} = k_{\text{F}} C_{\text{e}}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}}$$

(5)

where $C_{\text{e}}$ (mg/L) is the equilibrium concentration of Cd²⁺ in solution, $k_{\text{F}}$ (mg/g(L/mg)^1/n) indicates the adsorption capacity of the adsorbent and n is a Freundlich exponent.

Adsorption kinetics

Kinetic data provide adequate information regarding the adsorption mechanism that is important for the process efficiency. A kinetic model is a mathematical representation of the rate at which physical or chemical process takes place. However, the rate at which adsorption mechanism occurs varies from very rapid to very slow stage (Owabor and Oboh 2012). In the present study, three different adsorption kinetic models, namely pseudo-first-order, pseudo-second-order and intraparticle diffusion, were applied to evaluate the extent of utilization of the adsorption capacity with respect to contact time between the cadmium ions (adsorbate) and the Cu-MOF (adsorbent). The linearized forms of the pseudo-first-order (Langergren 1898), pseudo-second-order (Ho and Mckay 1998) and intraparticle diffusion (Wu et al. 2009) models are expressed in Eqs. (6)–(8), respectively, as follows:

$$\log \left( {q_{\text{e}} - q_{\text{t}} } \right) = \log q_{\text{e}} - \left( {\frac{{k_{1} }}{2.303}} \right)t$$

(6)

$$\frac{t}{{q_{\text{t}} }} = \frac{1}{{k_{2} q_{\text{e}}^{2} }} + \left( {\frac{1}{{q_{\text{e}} }}} \right)t$$

(7a)

$$h = k_{2} q_{\text{e}}^{2}$$

(7b)

$$q_{\text{t}} = k_{\text{D}} t^{1/2} + C$$

(8)

where $q_{\text{t}}$ and $q_{\text{e}}$ are the amount of Cd²⁺ adsorbed (mg/g) at time t in min and at equilibrium, respectively. $k_{1}$ (min⁻¹) and $k_{2}$ (g/mg min) are the rate constants for pseudo-first order and pseudo-second order, respectively. h is the initial sorption rate (mg/g min). $k_{\text{D}}$ is the intraparticle diffusion rate constant (mg/g min^0.5), and C is the intercept.

Modeling of batch adsorption system

A batch mode adsorption system shown in Fig. 1 is to be used to separate cadmium ions from effluent containing volume (V) of Cd²⁺ solution with the initial concentration $C_{\text{o}}$ mg/L. The concentration of Cd²⁺ after equilibrium is to be reduced to $C_{\text{e}}$ mg/L in the process. In the treatment process, W (g) Cu-MOF is fed into the adsorber containing the effluent and the amount of Cd²⁺ adsorbed at equilibrium changes from $q_{\text{o}}$ (it is zero initially) to $q_{\text{e}}$.

Fig. 1

A single-batch adsorption system

The total material balance around the batch mode adsorption system is given by

$$VC_{\text{o}} + q_{\text{o}} W = VC_{\text{e}} + q_{\text{e}} W$$

(9)

$$V\left( {C_{\text{o}} - C_{\text{e}} } \right) = W\left( {q_{\text{e}} - q_{\text{o}} } \right)$$

(10)

Since $q_{\text{o}}$ is zero at the initial stage of the treatment, Eq. (10) reduces to

$$\frac{W}{V} = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)}}{{q_{\text{e}} }}$$

(11)

If the adsorption of Cd²⁺ onto Cu-MOF is assumed to be well predicted by the Langmuir isotherm model, then $q_{\text{e}}$ in Eq. (11) can be replaced by Eq. (3) and adsorbent mass (W)/solution volume (V) ratio for the single-stage batch adsorption system is obtained as:

$$\frac{W}{V} = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)}}{{q_{\text{e}} }} = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)\left( {1 + bC_{\text{e}} } \right)}}{{q_{\hbox{max} } bC_{\text{e}} }}$$

(12)

where $C_{\text{o}}$ and $C_{\text{e}}$ (mg/L) are the initial and equilibrium concentrations of Cd²⁺ in aqueous solution, V (L) is the volume of the Cd²⁺ solution and W (g) is the weight of the Cu-MOF sample used.$q_{\hbox{max} }$ (mg/g) is the maximum adsorption capacity and b is the Langmuir equilibrium constant.

Results and discussion

Characterization of prepared Cu-MOF adsorbent

Textural properties determination

The specific surface area of the prepared adsorbent was evaluated using multipoint BET method, while total pore volume and pore diameter of the adsorbent were determined by Barrett–Joyner–Halender (BJH) method. The detailed results are presented in Table 1. The BET surface area, pore volume and pore diameter of the Cu-MOF adsorbent before adsorption were determined to be 1057 m²/g, 0.207 cm³/g and 2.137 Å, respectively. The BET surface area of the Cu-MOF studied can be compared to those values reported by Lin and Hsieh (2015) for Cu-MOF and Tranchemotagne et al. (2008) for MOF-74. Meanwhile, the textural properties of Cu-MOF diminished after adsorption due to coverage and saturation of the adsorbent surface by Cd²⁺ (adsorbate). Nevertheless, the Cd²⁺-loaded Cu-MOF adsorbent still possessed better textural properties, thus indicating that the surface of the active sites can still accommodate more adsorbates.

Table 1 Textural properties of Cu-MOF adsorbent before and after adsorption

FTIR analysis

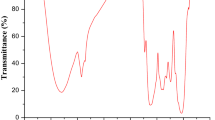
In order to evaluate the Cd²⁺ adsorption mechanism and also identify the various functional groups on the prepared Cu-MOF adsorbent, the FTIR analysis was performed. The FTIR spectra of the adsorbent before and after adsorption of Cd²⁺ are depicted in Fig. 2 and Table 2. It was revealed that those functional groups found on the prepared Cu-MOF adsorbent include alcohol (O–H), saturated aliphatic (C–H), unsaturated aliphatic (C=H and C≡C), carboxylic acid (C–O, C=O and O–H), carbonyl (C=O and C–O–H), amine (N–H and C–N) and phosphine (P–H). The presence of carboxylic groups (C–O and C=O) on the as-synthesized Cu-MOF was attributed to the use of H₃BTC as ligand (Lin and Hsieh 2015). Some peaks were shifted, disappeared and new ones were developed after adsorption. Those shifts observed in some FTIR absorption bands after Cd²⁺ adsorption onto Cu-MOF indicated that no force of attraction was between the surface of the adsorbent and the adsorbed solute (Osasona et al. 2018). Meanwhile, formation of those new peaks as can be seen in Table 2 is an indication that those functional groups found on the surface of the adsorbent were actively involved in adsorption process (Hameed et al. 2009).

Fig. 2

FTIR spectra of the prepared MOF a without Cd²⁺ adsorption and b with Cd²⁺ adsorption

Table 2 FTIR of Cu-MOF adsorbent

SEM–EDX analysis

The SEM image of the as-synthesized Cu-MOF adsorbent in Fig. 3 showed irregular clusters of spherical particles fused together. At magnification of 10,000, agglomeration of small particle was clearly seen; thus, better adsorption behavior is anticipated for the as-prepared adsorbent. The EDX spectrum of Cu-MOF (Fig. 4 and Table 3) confirmed the presence of copper (Cu), oxygen (O) and carbon (C). The percentage composition of the elements contained in the Cu-MOF was found in the following order: C > O > Cu. As can be seen in Table 3, C and O constitute a larger content. However, detected elements in the EDX spectrum indicate that the Cu-based MOF was successfully synthesized and these elements would constitute active sites on the surface of the prepared adsorbent, thus resulting in electrostatic interaction between the adsorbent and adsorbate (Shooto et al. 2017).

Fig. 3

SEM image of as-synthesized Cu-MOF adsorbent

Fig. 4

EDX spectrum of Cu-MOF adsorbent

Table 3 Elemental composition of Cu-MOF adsorbent

Effects of various variables studied during adsorption process

Effect of the initial Cd²⁺ concentration

The effects of the initial concentration (20–100 mg/g) on the removal of Cd²⁺ from aqueous solution via batch mode adsorption were studied. As shown in Fig. 5, the removal efficiency of Cd²⁺ decreased from 98.77 to 92.65%, while the equilibrium adsorption capacity increased from 1.98 to 9.27 mg/g by increasing the initial adsorbate concentration from 20 to 100 mg/L. This finding could be attributed to the fact that the same molecular adsorption sites on the adsorbent surface were available for the increasing adsorbate concentration, thus resulting in overloading of the adsorption sites on the Cu-MOF adsorbent. The same results were also reported for Cd²⁺ adsorption onto activated carbon derived from brewery waste¹ (Osasona et al. 2018) and Cd²⁺ adsorption onto wheat straw (Muhamad 2008).

Fig. 5

Effect of the initial Cd²⁺ concentration on the adsorption of Cd²⁺ onto Cu-MOF at adsorbent dose = 0.5 g/50 mL, contact time = 60 min, pH = 4.0 and temperature = 30 °C

Effect of contact time

The effect of varying the contact time (20–60 min) was also investigated with Cu-MOF adsorbent. As shown in Fig. 6, both the Cd²⁺ removal efficiency and adsorbent loading capacity increased as the contact time increased. The reason for this observation might be attributed to the large surface area of the Cu-MOF, which was available throughout the adsorption process. This is corroborated by BET surface area analysis and is the main reason why Cu-MOF adsorbent exhibited better performance. A similar observation was reported by Gaur et al. (2018) for the adsorption of lead and arsenic ions on soya bean adsorbent.

Fig. 6

Effect of contact time on the adsorption of Cd²⁺ onto Cu-MOF at adsorbent dose = 0.5 g/50 mL, initial Cd²⁺ concentration = 20 mg/L, pH = 4.0 and temperature = 30 °C

Effect of adsorbent dose

The influence of adsorbent dose on the adsorption of Cd²⁺ on Cu-MOF adsorbent was investigated at fixed pH and temperature of 4 and 30 °C, respectively. Figure 7 reveals that Cd²⁺ removal efficiency increased with the increase in the quantity of Cu-MOF adsorbent, while the adsorption capacity of Cu-MOF decreased from 8.91 to 1.99 mg/g when the adsorbent dosage increased from 0.1 to 0.5 g. The reason for this behavior was due to availability of enough active sites on the surface of adsorbent, which remained unsaturated during the Cd²⁺ adsorption process. The result obtained herein followed the same trend with the one reported by Osasona et al. (2018) for adsorption of Cd²⁺ onto activated carbon derived from brewery waste.

Fig. 7

Effect of adsorbent dosage on the adsorption of Cd²⁺ onto Cu-MOF at initial Cd²⁺ concentration = 20 mg/L, contact time = 60 min, pH = 4.0 and temperature = 30 °C

Equilibrium adsorption isotherm

An adsorption isotherm was studied in order to examine the correlation between the quantity of Cd²⁺ adsorbed and its concentration in the liquid phase. Since the adsorption isotherms help in describing the interaction of adsorbate with the adsorbent, it is highly important for the modeling of adsorption system. Accordingly, two-parameter isotherm models, namely Langmuir and Freundlich, were employed to study the interaction between adsorbate and adsorbent. Another experimental runs were conducted at the optimum conditions (contact time = 60 min, adsorbent dose = 0.5 g, pH = 4.0 and temperature = 30 °C) and at different initial Cd²⁺ concentration of 20, 40, 60, 80 and 100 mg/L.

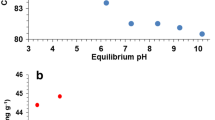
Figure 8 shows the nonlinear plots of Langmuir and Freundlich models, $q_{\text{e}}$ (mg/g) versus $C_{\text{e}}$ at fixed temperature of 30 °C. The values of constant parameters contained in Langmuir ($q_{\hbox{max} }$ and b) and Freundlich ($k_{\text{F}}$ and n) models were all determined from the plots. The values of the models constants are presented in Table 4 with their correlation coefficients ($R^{2}$). The best model was selected based on the $R^{2}$ value, and it was found that Langmuir model provided the best fit with the experimental data. This indicates that the Cu-MOF adsorbent surface is dominated by the monolayer and homogeneous active sites. A similar result was reported for Cd²⁺ removal from aqueous solution by treated rice husk (Kumar and bandyopadhyay 2006), wheat straw (Muhamad 2008) and activated carbon made from spent brewery barley husks (Osasona et al. 2018). The value of R_L (0.012) as indicated in Table 4 is less than 1, which suggests favorable adsorption process. This is confirmed by the magnitude of Freundlich exponent n (2.68) which also indicates favorable adsorption condition, because n is greater than 1.

Fig. 8

Two-parameter isotherm models for adsorption of Cd²⁺ onto Cu-MOF adsorbent at 30 °C

Table 4 Two-parameter isotherm constants and correlation coefficients for adsorption of Cd²⁺ onto Cu-MOF adsorbent

In order to ascertain the efficiency of the as-synthesized Cu-MOF adsorbent, a comparison of the Cd²⁺ adsorption of this present study and other similar studies is reported. The maximum adsorption capacity ($q_{\hbox{max} } )$ is the most important parameter used for the comparison. Table 5 lists a comparison of maximum monolayer adsorption capacity ($q_{\hbox{max} } )$ of Cd²⁺ on different adsorbents. Cu-MOF adsorbent is found to possess a relatively large adsorption capacity of 219.05 mg/g, and this implies that the adsorbent is highly effective for the treatment of water and wastewater containing heavy metals.

Table 5 Comparison of monolayer adsorption capacities of different adsorbents for Cd²⁺ removal from aqueous system

Kinetic modeling

In this current study, three different kinetic models were applied to evaluate the experimental data obtained at various initial Cd²⁺ concentrations from 20 to 100 mg/L.

Pseudo-first-order model was initially used to analyze the obtained experimental data. The plot of $\log \left( {q_{\text{e}} - q_{\text{t}} } \right)$ versus t shown in Fig. 9 gave a straight line at different initial adsorbate concentrations from which $q_{\text{e}}$ and $k_{1}$ were evaluated. The values of the pseudo-first-order kinetic parameters ($q_{\text{e}}$ and $k_{1} )$ computed at different adsorbate concentrations are presented in Table 6. The results revealed that the predicted $q_{\text{e}}$ values did not agree with the experimental $q_{\text{e}}$ values at all adsorbate concentrations studied with low correlation coefficients. Thus, the experimental data could not be predicted by the pseudo-first-order model and further kinetic analysis was conducted using pseudo-second-order model.

Fig. 9

Pseudo-first-order model for adsorption of Cd²⁺ onto Cu-MOF at different initial concentrations

Table 6 Kinetic models and parameters of adsorption of Cd²⁺ onto Cu-MOF adsorbent

The values of pseudo-second-order model parameters ($q_{\text{e}}$ and $k_{2} )$ (Eq. 7a) are evaluated from the plot of $t/q_{\text{t}}$ versus t shown in Fig. 10, and the results are presented in Table 6. The values of calculated $q_{\text{e}}$ at various adsorbate concentrations were found to be approximately equal to the experimental values of $q_{\text{e}}$ with high coefficients of correlation (R²) in the range 0.9973–1.00. The R² values for the pseudo-second-order model were relatively larger than those of the pseudo-first-order model for the various adsorbate concentrations. The obtained results indicate that the adsorption of Cd²⁺ onto Cu-MOF adsorbent could be well predicted by the pseudo-second-order model.

Fig. 10

Pseudo-second-order model for adsorption of Cd²⁺ onto Cu-MOF at different initial concentrations

Furthermore, high linearity of Fig. 10 is an indication that the pseudo-second-order kinetic model agrees reasonably well with the chemisorption as a rate determining step and it can be deduced that the role of the chemisorption in the rate controlling step cannot be ignored (Lim and Lee 2015). In addition, it was observed that there was decrease in values of the initial rate of adsorption (h) with an increase in the cadmium ions concentration as depicted in Table 6. These results imply that there was rapid movement of adsorbate from the bulk fluid with lower initial concentration to the surface of the adsorbent due to the concentration gradient (Hameed et al. 2009).

In order to further analyze the experimental data and evaluate the diffusion mechanism, the intraparticle diffusion model (Eq. 8) was employed. The plot of $q_{\text{t}}$ versus $t^{1/2}$ shown in Fig. 11 gave a straight line at different adsorbate concentrations from which $k_{\text{D}}$ and C were obtained as slope and intercept, respectively. The computed values for intraparticle diffusion constants ($k_{\text{D}}$ and C) and R² are presented in Table 6. The linearity of the plots implies that the intraparticle diffusion played a significant role in the adsorption of Cd²⁺ from aqueous solution by Cu-MOF. However, since the R² values for the intraparticle diffusion model were lower than those of pseudo-second-order model for the various initial Cd²⁺ concentrations, the intraparticle diffusion kinetic model could not be regarded as a rate-limiting step. This fact was affirmed by the fact that the plots did not pass through the origin. Hence, the obtained experimental data were well predicted by the pseudo-second-order kinetic model.

Fig. 11

Intraparticle diffusion model for adsorption of Cd²⁺ onto Cu-MOF at different initial concentrations

Modeling of batch adsorption system

Depicted in Fig. 12 is a series of plots of adsorbent dose against volume of Cd²⁺ solution at different removal efficiencies. The obtained data points were evaluated from the model equation (Eq. 12) describing the adsorption of Cd²⁺ by Cu-MOF in a single-stage batch adsorber in which different volumes (1, 2, 3, 4 and 5 L) of cadmium solution with the initial concentration of 20 mg/L were charged. The quantity of Cu-MOF needed for the 60% uptake of Cd²⁺ from aqueous solution was 6.19, 12.37, 18.56, 24.74 and 30.93 g, respectively, for Cd²⁺ solution of volumes of 1, 2, 3, 4 and 5 L. It can be deduced from Fig. 12 that the amount of Cu-MOF required for the effective removal of Cd²⁺ in a single-stage adsorber depends on the aqueous solution volume.

Fig. 12

Adsorbent dose (W) against treated Cd²⁺ solution volume (V) at different removal efficiencies

Conclusions

The adsorption capacity of Cu-MOF adsorbent in the removal of Cd²⁺ from aqueous solution had been investigated. The synthesized adsorbent possessed large BET surface area and pore volume with active functional groups on its surface as revealed by the FTIR analysis. EDX result showed that Cu-MOF comprised of Cu, C and O, which might facilitate formation of charges and functionalities on the adsorbent surface. The amount of Cd²⁺ adsorbed onto Cu-MOF adsorbent was found to increase with the increase in contact time, initial concentration and adsorbent dose. Equilibrium adsorption isotherm analysis showed that the Langmuir isotherm best fitted with the experimental data (R² = 0.9958), thus indicating a monolayer adsorption of Cd²⁺ on homogeneous active sites of the Cu-MOF adsorbent. Analysis of kinetic data showed that pseudo-second-order model provided the best fit with the experimental data.