Abstract
This study aimed at quantitative analysis of morphometric parameters of Agula watershed and its sub-watersheds using remote sensing data, geographic information system, and statistical methods. Morphometric parameters were evaluated from four perspectives: drainage network, watershed geometry, drainage texture, and relief characteristics. A sixth-order river drains Agula watershed and the drainage network is mainly dendritic type. The mean bifurcation ratio (R b) was 4.46 and at sub-watershed scale, high R b values (R b > 5) were observed which might be expected in regions of steeply sloping terrain. The longest flow path of Agula watershed is 48.5 km, with knickpoints along the main river which could be attributed to change of lithology and major faults which are common along the rift escarpments. The watershed has elongated shape suggesting low peak flows for longer duration and hence easier flood management. The drainage texture analysis revealed fine drainage which implies the dominance of impermeable soft rock with low resistance against erosion. High relief and steep slopes dominates, by which rough landforms (hills, breaks, and low mountains) make up 76% of the watershed. The S-shaped hypsometric curve with hypsometric integral of 0.4 suggests that Agula watershed is in equilibrium or mature stage of geomorphic evolution. At sub-watershed scale, the derived morphometric parameters were grouped into three clusters (low, moderate, and high) and considerable spatial variability was observed. The results of this study provide information on drainage morphometry that can help better understand the watershed characteristics and serve as a basis for improved planning, management, and decision making to ensure sustainable use of watershed resources.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Morphometric analysis is an important aspect of characterization of watersheds. It involves computation of quantitative attributes of the landscape related to linear, aerial and relief aspects from elevation surface and drainage networks within a watershed. Over the past several decades, morphometric analysis to evaluate watersheds and to describe the characteristics of surface drainage networks with reference to land and water management has been a major emphasis in geomorphology. Pioneer studies by Horton (1932, 1945) demonstrated the significance of quantitative morphometric analysis to better understand the hydrologic and geomorphic properties of watersheds. Since then, several methods of watershed morphometry were further developed (e.g., Miller 1953; Strahler 1954, 1957, 1964; Schumm 1956; Melton 1957; Faniran 1968) that enabled morphometric characterization at watershed scale to extract pertinent information on the formation and development of land surface processes.
Morphometric analysis represents a relatively simple approach to describe the hydro-geological behavior, landform processes, soil physical properties and erosion characteristics and, hence, provides a holistic insight into the hydrologic behavior of watersheds (Strahler 1964). The hydrological response of watersheds is interrelated with their physiographic characteristics, such as size, shape, slope, drainage density, and length of the streams (Gregory and Walling 1973). Recent studies demonstrated that quantitative morphometric analysis has several practical applications that include land surface form characterization (Reddy et al. 2004; Thomas et al. 2012; Magesh et al. 2013; Kaliraj et al. 2014; Banerjee et al. 2015), watershed prioritization for soil and water conservation (Gajbhiye et al. 2014; Meshram and Sharma 2015), environmental assessment (Magesh et al. 2011; Al-Rowaily et al. 2012; Rai et al. 2014; Babu et al. 2016), and evaluation and management of watershed resources (Pandey et al. 2004). Furthermore, comparison of the quantitative morphometric parameters helps understand the geomorphological effects on the spatial variation of hydrological functions (Romshoo et al. 2012; Sreedevi et al. 2013). Understanding drainage morphometry is also a prerequisite for runoff modeling, geotechnical investigation, identification of water recharge sites and groundwater prospect mapping (Sreedevi et al. 2005; Fenta et al. 2015; Roy and Sahu 2016). As such, morphometric analysis is an important procedure for quantitative description of the drainage system; thus enabling improved understanding and better characterization of watersheds.
Earlier studies successfully applied conventional methods of morphometric characterization based on map measurements or field surveys (e.g., Horton 1932, 1945; Strahler 1952, 1954, 1957, 1964); however, it has been recognized that such methods of generating information especially for large watersheds are expensive, time-consuming, labor intensive and tedious. Recently, increasing availability of remote sensing datasets with improved spatial accuracy, advances in computational power and geographical information system (GIS), enable evaluation of morphometric parameters with ease and better accuracy (Grohmann 2004). On the one hand, remote sensing enables acquisition of synoptic data of large inaccessible areas and is very useful in analyzing drainage morphometry. On the other hand, GIS provides a powerful tool and a flexible environment and as such the information extraction techniques are less time-consuming than ground surveys for morphometric characterization through manipulation and analysis of spatial data. Integrating remote sensing data and GIS tools, therefore, allow automated computation of morphometric parameters and have been successfully employed by several researchers (e.g., Magesh et al. 2011; Thomas et al. 2012; Kaliraj et al. 2014; Banerjee et al. 2015; Roy and Sahu 2016) for generating updated and reliable information to characterize watershed physiographic attributes.
Significant advances in remote sensing technology have led to availability of higher quality digital elevation models (DEMs). For instance, availability of Shuttle Radar Topography Mission (SRTM) and Advanced Space-borne Thermal Emission and Reflection Radiometer (ASTER) DEMs free of charge via http://earthexplorer.usgs.gov/ has provided new potentials in watershed scale quantitative morphometric analysis. In the past decade, several studies used SRTM (90 m resolution) and/or ASTER (30 m resolution) DEMs in a GIS environment to derive morphometric characteristics of watersheds with different geological and hydrological settings (e.g., Romshoo et al. 2012; Thomas et al. 2012; Gajbhiye et al. 2014). These studies demonstrated that SRTM and ASTER DEMs provide reliable datasets with global coverage that enabled evaluation of morphometric properties and various relief features. A recent comparative study by Thomas et al. (2014) showed that topographic attributes extracted from the space-borne (SRTM and ASTER) DEMs are in agreement with those derived from topographic maps. Their study also revealed that despite the coarser resolution (i.e., 90 m), SRTM DEM shows relatively higher vertical accuracy and better spatial relationship of topographic attributes than the finer resolution (i.e., 30 m) ASTER DEM when compared with topographic maps.
Turcotte et al. (2001) demonstrated that morphometric analysis solely based on automated DEM-based approaches has limitations in representing the actual drainage structure of a watershed, and ways to recondition DEMs for improved performance have been suggested (e.g., Hellweger 1996; Soille et al. 2003). Studies by Turcotte et al. (2001) and Callow et al. (2007) showed that DEM reconditioning using stream networks digitized from topographic maps greatly improves replication of stream positions and reduces error introduction in the form of spurious parallel streams. Therefore, in the present study, a more rational approach of morphometric analysis has been employed using SRTM DEM with relatively fine spatial resolution (i.e., 30 m) and natural stream networks digitized from topographic maps (scale 1:50,000). The natural stream networks were used to recondition the DEM prior to the computation of flow direction and flow accumulation grids. The objective of this study was to derive morphometric parameters related to drainage network, watershed geometry, drainage texture, and relief characteristics of Agula watershed and infer their implications by integrating remote sensing data, GIS tools and statistical methods. In general, watershed management practices and water resources development schemes are often implemented without proper assessment of the watershed characteristics. Such a study, therefore, provides pertinent information for an enhanced perceptive of the hydro-geologic and erosion characteristics of watersheds. Given the wide range of applications of derived morphometric parameters, this study presents selected parameters for a better understanding of watershed characteristics and can serve as a basis for improved planning, management and decision making to ensure sustainable use of watershed resources.
Materials and methods
Description of the study area
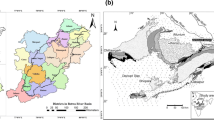
Agula watershed is located between 13°32′44″ to 13°54′49″N latitude and 39°34′40″ to 39°47′42″E longitude in Eastern Tigray region, northern Ethiopia (Fig. 1). It is bounded by the mountain ranges of the western flank of the Ethiopian rift valley in the east, May-Mekden watershed in the south and Genfel watershed in the north. The area of the watershed is 442 km2, and drains east to west bordering the Agula rural town in the south to join Geba River which is tributary of the Tekeze River basin. Elevation in the watershed ranges from 1980 meters above sea level (masl) in the valley to 2887 masl on the hills with a mean value of 2341 masl. As described by Gebreyohannes et al. (2013), the dominant geological formations are Limestone with Shale intercalations (43%) in the east and south, Meta-volcanic (22%) in the north having a gradational contact with its adjacent units, deeply weathered Agula Shale (18%) in the center and south (Fig. 2). Also, Sandstones (Adigrat and Enticho sandstone formations) cover about 10%, while the remaining consists of Dolerites and localized Meta-sediments along the river valley. Based on meteorological data (1992–2012) from Atsbi and Wukro stations, the mean annual rainfall is 593 mm mainly concentrated during the wet season (June–September); the mean daily minimum and maximum temperature is 10 and 26 °C, respectively. Based on our recent studies (Fenta et al. 2016, 2017), grass land, cultivated land, shrub land, forest, bare land, and settlement are the main land use/land cover (LULC) types in Agula watershed. Between 1990 and 2012, cultivated land was the dominant LULC type which covered about 52% of the watershed. Shrub land was the second dominant LULC type which accounted for about 21 and 26% of the watershed in 1990 and 2012, respectively. Fenta et al. (2016, 2017) reported considerable changes in LULC through increased shrub land (24%) and forest cover (32%) and decreased bare land (81%) in the period 1990–2012. The dominant tree species of the watershed are Juniperus procera, Ficus vasta, Olea europaea L. subsp. cuspidata, Acacia saligna, and Eucalyptus species, while the common shrub species are Acacia etbaica, Dodonaea angustifolia, and Euclea schimperi (Getachew 2007).
Geological map of Agula watershed (based on Gebreyohannes et al. 2013)
Data sources
Topographic maps (scale 1:50,000) for year 1997 were obtained from the National Mapping Agency (NMA) of Ethiopia. The study area was covered by four topographic maps with index: 1339-B1, 1339-B2, 1339-B3 and 1339-B4. The scanned topographic maps were geometrically rectified and geo-referenced to the Universal Transverse Mercator (UTM) map projection (Zone 37 N), Adindan datum and Spheroid—Clarke 1880 by taking the printed corner coordinates. The rectified topographic maps were then mosaicked to form a single topographic map from which stream networks were digitized and used to recondition the SRTM DEM. SRTM generated the most complete digital topographic database for the Earth using two antenna pairs operating in C- and X-bands to acquire interferometric radar data (Rabus et al. 2003). Commonly, SRTM data with global coverage are readily available at 3 arc-seconds (~90 m) and 30 arc-seconds (~1 km) resolutions. However, recently (starting April 2015), the SRTM data for Africa are available in 1° × 1° tiles with relatively high resolution at 1 arc second (~30 m) via http://earthexplorer.usgs.gov/. In the present study, the 1 arc second data of tile N13E39 were downloaded and re-projected to a similar projection and datum with that of the topographic maps for further use. Several studies (e.g., Rabus et al. 2003; Slater et al. 2006; Farr et al. 2007; Yang et al. 2011) provide more elaborated details of SRTM datasets including issues such as data processing, accuracy, errors, and applications.
Methodology
Watershed boundary delineation
ArcHydro tools extension of the ArcGIS software was used for watershed delineation which is automated and more consistent compared with a manual approach. The procedure used for watershed delineation in ArcHydro involved sequence of steps accessed through the toolbar menus. The first of these was the reconditioning of the SRTM DEM data to reconcile with the digitized stream network from topographic maps using the AGREE method. AGREE is a surface reconditioning system for DEMs and enables to adjust the surface elevation of the DEM to be consistent with digitized stream networks. This helps increase the degree of agreement between stream networks delineated from the DEM and the input vector stream networks (Hellweger 1996). The next step was to fill the sinks (artifact features from DEM) and remove local depressions to assure flow continuity for proper determination of flow direction and flow accumulation grids. The D8 algorithm (O’Callaghan and Mark 1984) was used to determine flow direction of a grid cell based on elevations in a 3 × 3 window around it. The direction of each grid cell was determined by one of its eight surrounding grid cells with steepest descent. Based on cumulative number of the upstream cells draining to each cell in the flow accumulation grid, stream networks for each of the watersheds were generated. In the present study, the rivers and streams digitized from topographic maps (scale 1:50,000) were well represented/captured when stream definition threshold was set at 25 pixels of the flow accumulation layer. It should be noted, however, that the threshold area is an average indicator and different physiographic regions may have different thresholds for defining rivers and streams. Then, boundaries of Agula watershed and its sub-watersheds were delineated using point delineation functionality of the ArcHydro tools.
Morphometric analysis
A number of morphometric parameters which signify the watershed characteristics were computed in a GIS environment. In this study, Agula watershed was discretized into twenty-six sub-watersheds which include streams of at least three different orders following the work of Biswas et al. (2014). Areas of the sub-watersheds along with their perimeter, elevation information, basin length, and number and length of stream networks were extracted for further analysis. In addition, the longest flow path (from outlet point to the water divide line) and its longitudinal profile were also derived from SRTM DEM with the ArcHydro tools and 3D-analyst extension. A smoothing process (smooth 3D line) was carried out to remove kinks from the longitudinal profile. The derived morphometric parameters were evaluated from four different aspects: drainage network, watershed geometry, drainage texture, and relief characteristics (Table 1). Overall, twenty-seven morphometric parameters were computed for Agula watershed and for each of the sub-watersheds. The computations of morphometric parameters were based on mathematical equations (Table 1), and the values of some of the watershed characteristics required for computing morphometric parameters are shown in Table 2. Furthermore, landforms of Agula watershed were topographically modeled from combinations of slope class and local relief produced from SRTM DEM following the procedures suggested by Sayre et al. (2009). This approach of generating landforms from DEM is on the basis of applying a moving neighborhood analysis window and a land surface classification method modified from Hammond (1964). In this study, slope was generated using 3D analyst tools and classified as gently sloping or not gently sloping using a slope threshold of 8%. Local relief was calculated using neighborhood analysis of the spatial analyst tools in a 3 × 3 moving window. Local relief was then divided into five classes with ranges: 0 to ≤15, >15 to ≤30, >30 to ≤90, >90 to ≤150, and >150 m. Slope classes and relief classes were subsequently combined to produce eight land surface form classes (flat plains, smooth plains, irregular plains, escarpments, low hills, hills, breaks/foothills, and low mountains).
Hypsometric analysis was also carried out to develop relationship between horizontal cross-sectional drainage area and elevation. This involved generating Hypsometric Curve (HC) which provides quantitative means for characterizing the topographic structure of a watershed. To generate the HC, the watershed is assumed to have vertical sides rising from a horizontal plane passing through the watershed outlet and under the entire watershed. According to Strahler (1952), the HC is a plot of the continuous function relating relative elevation to relative area. The relative elevation (h/H) is calculated as the ratio of height of a given contour above the base plane (h) to the maximum basin elevation from the outlet (H); whereas the relative area (a/A) is calculated as a ratio of the area above a particular contour (a) to the total area of the watershed (A). Thus, the HC describes the relative proportion of the watershed area that lies above a given height relative to the total relief of the watershed. In this study, following the procedures suggested by Davis (2010), the HC was produced from the SRTM DEM by creating a binned histogram (100 classes of equal interval) with the reclassify tool; then the area and elevation values were normalized by total area and total relief of the watershed. Strahler (1952) noted that differences in the shape of the HC for a particular landform provide a measure of the erosion state or geomorphic age of a watershed. Hence, hypsometric analysis has been widely used in the past and recent researches dealing with erosional topography (e.g., Willgoose and Hancock 1998; Bishop et al. 2002; Singh et al. 2008; Thomas et al. 2012).
According to Harlin (1978), the HC can be considered as a cumulative probability distribution function of elevations and, in this approach, the HC is represented by a continuous polynomial function with the form:
where f(x) is a polynomial function fitted to the HC by regression and a 0, a 1, a 2, … a n are the coefficients. For the entire watershed, the area under the HC also called the Hypsometric Integral (HI), which represents the relative fraction of landmass that remains above the base plane, was calculated by the integration of f(x) between the limits of the unit square. Following Harlin (1978), the result of this integration can be solved as:
In addition to the exact integration approach, there are several approximation methods available for computing HI: one of which is the elevation-relief ratio method suggested by Pike and Wilson (1971) is less cumbersome and faster method used to calculate HI for the sub-watersheds of Agula. The statistical moments for the distribution of the HC and its density function (first derivative of the curve) were derived to characterize the planimetric and topographic structure of the watershed. Harlin (1978) defined the statistical moments as: skewness of the HC (hypsometric skewness, SK), kurtosis of the HC (hypsometric kurtosis, KUR), skewness of the hypsometric density function (density skewness, DSK) and kurtosis of the hypsometric density function (density kurtosis, DKUR). The first moment of f(x) about the x-axis (μ 1) for the unit square which represents the x-mean can be defined as:
In the same way, the ith moment of f(x) about the x-mean can be expressed as:
The second moment (μ 2) of f(x) about the x-mean is known as the variance, and can be solved as a summation expression by following a similar development as in Eqs. (2) and (3). The third (μ 3) and fourth (μ 4) moments about the x-mean are termed as the SK and KUR of the distribution function, respectively. Based on Harlin (1978), the SK and KUR are dimensionless coefficients defined as:
By following the same reasoning as for f(x), the moments and coefficients of density function (first derivative of the curve) were derived to obtain the DSK and DKUR. When applied to the probability distribution function of the HC, the statistical moments can be interpreted in terms of erosion and watershed slope. As such, based on Harlin (1978), the SK indicates the amount of headward erosion in the upper reach of a watershed; DSK represents slope change; a large value of KUR indicates erosion on both upper and lower reaches of a watershed, and DKUR represents mid-basin slope. These statistical moments can be used to describe and characterize the shape of the hypsometric curve and, hence, to quantify changes in the morphology of the watershed.
Cluster analysis of morphometric parameters
Given the large number of sub-watersheds and morphometric parameters, hierarchical clustering was used to group the sub-watersheds into three major categories (that represent low, moderate, and high values) according to the four morphometric aspects. In this method, the sub-watersheds are grouped into successively larger clusters based on distance or similarities between data points. As such, hierarchical clustering produces dendrograms by which the sub-watersheds are grouped and presented as a tree-like hierarchical diagram. Euclidean distance was used for measuring similarity between pairs of sub-watersheds, and Ward method was chosen as a clustering technique, which is based on mutually exclusive subsets of the data set and is most appropriate for quantitative variables (Ward 1963). Furthermore, to understand how the different morphometric parameters interact and influence each other, a correlation matrix was produced. Some of the morphometric parameters were excluded as they depend totally on some other parameters which are already included (e.g., constant of channel maintenance is the inverse of drainage density and was therefore excluded).
Results and discussion
Quantitative description of drainage network, watershed geometry, drainage texture, and relief characteristics has been carried out for Agula watershed and its sub-watersheds. In the following sections, the various morphometric parameters and their implications are discussed for the entire watershed and the sub-watersheds based on the derived cluster groups (Fig. 3).
Drainage network
The network of drainage channels and tributaries forms a particular drainage pattern as determined by local topography and subsurface geology (lithology and structures). Drainage channels develop where surface runoff is enhanced and Earth materials provide the least resistance to erosion. Hence, the drainage pattern of a watershed helps understand the topographic and structural/lithologic controls on the water flow. As shown in Fig. 4, the drainage pattern of Agula watershed can be described as dominantly dendritic; however, in some sub-watersheds trellis and parallel patterns also co-exist. Dendritic drainage patterns form where the underlying rock structure does not strongly control the position of stream channels. Hence, dendritic patterns tend to develop in areas where the river channel follows the slope of the terrain and the subsurface geology has a roughly equal resistance to weathering (Ritter et al. 1995; Twidale 2004). Further, the preferred direction of alignment of streams reflected fracture/lineament control on drainage network. Stream ordering of a drainage network represents a measure of the extent of stream branching within a watershed. As such, designation of stream order is the first step in morphometric characterization of watersheds and, in the present study, the stream ordering was done based on hierarchical ranking method proposed by Strahler (1964). The first-order stream has no tributaries; the second order has only first order as tributaries, similarly third-order streams has first- and second-order streams as its tributaries and so on. The order-wise stream numbers and stream length of Agula watershed are given in Table 2. A sixth-order river drains Agula watershed with four 5th order stream tributaries, namely Adi Felesti in the northeast, Adi Siano in the northwest, Era in the east and Mezerbei in the southeast.
Stream orders of Agula watershed (ranked according to Strahler 1964)
The first-order streams accounted for about 74% of the total number of streams, and based on Macka (2003), such a high proportion of first-order streams indicates the structural weakness present in the watershed dominantly in the form of fractures/lineaments. The total length of the stream segments (L u) was 1150 km (Table 2) of which the first- and second-order streams constituted about 74%. Mean stream length (L m) is a dimensional property revealing the characteristic size of components of a drainage network and its contributing areas. The Lm of a given order was higher than that of the next lower order, but lower than that of the next higher order, indicating that the evolution of the watershed followed the laws of erosion acting on homogeneous geologic material with uniform weathering-erosion characteristics. Stream length ratio (R L) considered as an important factor in relation to both drainage composition and geomorphic development of watersheds was also computed. Variation existed in R L values between the streams of different order (Table 2), which according to Horton (1945) might be attributed to morphological changes in slope and relief. The bifurcation ratio (R b) values ranged between 3.75 and 5.75 for the Agula watershed (Table 2), with mean R b value of 4.46. The R b was designated as an index of relief and dissection by Horton (1945), with higher values indicating mountainous or highly dissected watersheds. In this study, the obscure trends in R b values between various stream orders confirmed the substantial influence of geology and relief on drainage branching. Relatively, high R b values in sub-watersheds belonging to cluster C3 (Fig. 3a; Table 3) suggested the significant influence of structural elements on the drainage network and presence of highly dissected sub-watersheds. By contrast, low R b values of sub-watersheds under cluster C1 are the characteristics of structurally less disturbed watersheds with minimal distortion in drainage pattern. Based on Horton (1945), natural drainage systems are generally characterized by R b values between 3.0 and 5.0; however, anomalous R b values (e.g., R b < 3.0 and R b > 5.0) were reported in several studies (e.g., Gajbhiye et al. 2014; Roy and Sahu 2016). These anomalous values were considered as indirect manifestations of substantial structural controls. In some sub-watersheds, abnormally high bifurcation ratios (R b > 5.0) were observed which might be expected in regions of steeply sloping terrain where narrow strike valleys are confined between ridges. The rho coefficient (ρ) signifies the storage capacity of a watershed and determines the relationship between drainage density and physiographic development of the watershed. Sub-watersheds belonging to C1 (Fig. 3a; Table 3) having high value of ρ are subject to a greater risk of being eroded by excess discharge during flood.
The longest flow path of Agula watershed is about 48.5 km and its longitudinal profile is shown in Fig. 5. The resultant longitudinal profile was continuous, with values at intervals of 30 m (or 42.42 m where the streamline moves diagonally) along the entire stream. The longitudinal profile (Fig. 5) showed that in the upper reach of the river, the gradient was steep (0.018 m m−1 for L 1), but gradually flattened out as the river eroded towards its outlet (0.008 m m−1 for L 4). This indicated that in the upper course, the river has high gravitational energy and so is the energy to erode vertically, whereas in the lower course, the river has less erosive power and hence deposits its load. It is worth noting that knickpoints (Fig. 5a–c) with steep reaches developed along the main river at some 44, 37, and 28 km, respectively, from the watershed outlet. Such abrupt changes in slope of the longitudinal profile could be attributed to change of lithology along the main river (e.g., from Meta-volcanic to Meta-sediments) resulting in differential erosion as well as the presence of major faults which are common along the rift escarpments. If a river flows over two or more rock types, there is often a slope break at the contact, especially where the adjoining rocks have varying resistance to erosion. According to Hack (1973), when the rock type of a river bed changes from a resistant rock to a less resistant one, the river erodes the less resistant rock faster producing a sudden change in the gradient of the river with the resistant rock being higher up than the less resistant rock; this creates a higher hydraulic head. Hence, as the river flows over the resistant rock, it falls onto the less resistant rock, eroding it and creating a greater height difference between the two rock types, producing the knickpoints. Also, Bishop et al. (2005) suggested that knickpoints can be the result of disequilibrium steepening in response to a relative fall in base level, where the base level of the river falls giving it some extra gravitational energy to erode vertically. Computation of the longest flow path and its longitudinal profile is also an important step in hydrologic modeling as it helps estimate the time of concentration in empirical models.
Watershed geometry
The shape of a watershed is controlled by geological structure, lithology, relief and climate, and varies from narrow elongated forms to circular or semicircular forms. The shape mainly governs the rate at which water is supplied to the main channel. In the present study, four parameters, namely: form factor (F f), elongation ratio (R e), circularity ratio (R c), and compactness coefficient (C c) were used for characterizing watershed shape, which is an important parameter from hydrological perspective. For Agula watershed, the F f, R e, R c, and C c values were 0.25, 0.57, 0.15 and 2.55, respectively (Table 1). Based on Schumm (1956), R e values can be grouped into five categories, i.e., circular (0.9–1.0), oval (0.8–0.9), less elongated (0.7–0.8), elongated (0.5–0.7), and more elongated (<0.5). Horton (1932) also suggested that the smaller the value of F f (<0.45), the more the basin will be elongated. For Agula watershed, low values of F f, R e, and R c and high value of C c implied that the watershed has elongated shape. For the sub-watersheds, the value ranges for the shape parameters were F f (0.15–0.60), R e (0.43–0.87), R c (0.17–0.33), and C c (1.75–2.43). Sub-watersheds that belong to cluster C2 (Fig. 3b) have low F f, R e, and R c values (Table 3); and by implication these sub-watersheds have elongated shape. According to Thomas et al. (2012), watersheds with elongated shape are characterized by flat hydrograph for longer duration with low slope of the rising and recession limbs. Furthermore, the low F f, R e, and R c values of these sub-watersheds suggested a lower chance of occurrence of heavy rainfall covering the entire area, and hence lesser vulnerability to flash floods and as a result easier flood management than those of the circular basins (Pandey et al. 2004). Sub-watersheds in cluster C1 (Fig. 3b) have more circular shape as suggested by moderately high F f, R e, and R c values (Table 3). The more circular sub-watersheds have shorter lag time and higher peak flows of shorter duration compared to the elongated sub-watersheds (Thomas et al. 2012). As such, the more circular sub-watersheds are more efficient in the discharge of runoff than elongated sub-watersheds. However, more circular sub-watersheds have a greater risk of flash floods as there will be a greater possibility that the entire area may contribute runoff at the same time, and may result in high risk of erosion and sediment load (Reddy et al. 2004). It is noteworthy, however, that the hydrologic response of watersheds is affected by several other factors, such as the rainfall event properties, soil type, LULC and slope. The correlation analysis revealed that the F f, R e, and R c showed significant positive correlation to one another (p < 0.05), whereas a significant negative correlation was observed between C c and the other shape parameters (Table 4). Moreover, the F f, R e, and R c were negatively correlated with ruggedness number (R n) and dissection index (D is), but positive correlation was observed between C c and the relief characteristics R n and D is (Table 4).
Drainage texture analysis
Drainage texture indicates the amount of landscape dissection by a channel network and includes parameters such as stream frequency (F s), drainage texture (D t), drainage density (D d), infiltration number (I f), length of overland flow (L o), and constant of channel maintenance (C). These are important parameters as they are related to the dynamic nature of the network of streamlines and area of watersheds. These parameters largely reflect the inter-relationships among geomorphological elements like lithology, geological structure, topography, vegetation, hydrology and climate. As such, the drainage texture parameters can help predict watershed processes such as runoff and sediment yield as well as magnitude of dissection of terrain. The computed F s, D t, D d, and I f values of Agula watershed were 5.05, 11.74, 2.6 and 13.15 (Table 1) and these values are indicative of moderately dissected steep terrain. Based on Smith (1950), D t has four categories: coarse (D t ≤ 4), moderate (4 < D t ≤ 10), fine (D t > 10) and ultra-fine or badlands topography (D t > 15). From such classification, the drainage of Agula watershed is categorized as fine drainage texture, which, in general, indicates that the watershed is dominated by low permeability soft rock with low resistance against erosion. This is in agreement with the geology map (Fig. 2) which showed that about 60% of the watershed is Shale and Limestone intercalations characterized by low permeability and low resistance to erosion. Further, fine drainage texture is favored in areas where basin relief is high and consequently the landscape is susceptible to erosion (Magesh et al. 2011). At sub-watershed level, the value ranges of F s, D d, and I f were 3.49–6.30, 2.3–2.95, and 8.33–16.29, respectively. High values of F s, D d, and I f were found in sub-watersheds under cluster C1, whereas sub-watersheds under cluster C2 registered relatively low values (Fig. 3c; Table 3). This indicates that sub-watersheds under cluster C1 are characterized by weak and impermeable subsurface material with sparse vegetation, high relief and steep slope landscape, which has high tendency to generate surface runoff. By contrast, watersheds under cluster C2 are likely to have highly resistant permeable subsurface material with good vegetation cover and low relief, which would result in more infiltration capacity and comparably could be good sites for ground water recharge.
In general, resistant surface materials and those with high infiltration capacities exhibit widely spaced streams, consequently yielding low F s, D d, and I f. As surface permeability decreases, runoff is usually accentuated by the development of a greater number of more closely spaced channels, and thus F s, D d, and I f tend to be higher. Horton (1945) demonstrated that high transmissibility (as evidenced by infiltration capacity) leads to low drainage density, high base flow and a resultant low magnitude peak flow. By contrast, an impermeable surface will generate high drainage density and efficiently carry away runoff, with high peak discharge but low base flow. However, Dingman (1978) noted that the relationship between D d and flow may be overridden by other factor such as flood plain and channel storage; and in areas where saturated overland flow is the major source of runoff, D d may not be related to the efficiency at which the watershed is drained. Further, D d has also been used as an independent variable in the framing of L o and C (Table 1); both have a reciprocal relationship with D d. Hence, sub-watersheds with high values of F s, D d, and I f have corresponding low values of L o and C, and vice versa (Table 3). The L o is of great importance from hydrologic perspective as it indicates the distance which water must travel before reaching stream channels. It also bears a close relation to the hydrology of a watershed since the greater the L o, the greater, in general, is the infiltration and the less the direct surface runoff (Horton 1945). For Agula watershed, the computed L o value was 0.19 (Table 1), which indicated the presence of short flow paths and steep ground slopes associated with more runoff. Thomas et al. (2012) also noted that relatively shorter L o is characteristics of areas with steeper slopes and fine texture that lead to high surface runoff generation. For the sub-watersheds of Agula, the C value ranged between 0.34 and 0.43. High values of C for sub-watersheds of cluster C3 suggested strong control of lithology with a surface of high permeability; and by implication more area is required to produce surface flow. For sub-watersheds under cluster C1, low values of C indicated limited percolation/infiltration and hence more surface runoff (Sreedevi et al. 2013). The correlation analysis showed statistically significant (p < 0.05) positive correlations among the drainage texture parameters (Table 4).
Relief characteristics
Relief characteristics can help understand landforms of a watershed, drainage networks development, overland flow, and erosional properties of terrain. In the present study, relief ratio (R h), relative relief (R hp), ruggedness number (R n), and dissection index (D is) were used as these parameters reveal the runoff and erosion potential of a watershed. The total relief of Agula watershed is 907 m (Table 1). Such a high value indicated the high potential erosive energy of the watershed above a specified datum available to move water and sediment down the slope. The relief characteristic values of R h (0.02), R hp (0.48), R n (2.36), and D is (0.31) (Table 1) indicated that Agula watershed is characterized by high relief, steep slopes and is moderately dissected. For the sub-watersheds, the Rh value ranged from 0.03 to 0.1 with low values in sub-watersheds under cluster C1 and high values in sub-watersheds under cluster C3 (Fig. 3d; Table 3). In a similar study, Kaliraj et al. (2014) attributed the low value of Rh mainly to resistant basement rocks and low degree of slope. Thomas et al. (2012) considered relatively high Rh values as indicative of comparatively steeply sloping terrain and consequently higher basin energy manifested as high intensity of erosion processes operating along the hillslopes as well as sediment transport capacity. As such, runoff is generally faster in sub-watershed with high R h producing more peaked discharges and hence greater erosive power. For the sub-watersheds of Agula, the R n and D is values ranged from 0.41–1.63 to 0.07–0.22, respectively. Similar to the R h, high values of R n and D is were found in sub-watersheds under cluster C3, whereas sub-watersheds under cluster C1 registered low R n and D is values (Fig. 3d; Table 3). The high R n and D is values indicated the presence of long and steep slopes and high degree of dissection which implied lower time of concentration of overland flow and possibilities of flash floods and high susceptibility to soil erosion than watersheds with low R n and D is. A study by Patton and Baker (1976) demonstrated that watersheds with high flash flood potential have greater R n than low potential watersheds in several physiographic regions of the United States. Further, R h, R n, and D is bear statistically significant (p < 0.05) positive correlations (Table 4).
In addition to the morphometric parameters related to relief characteristics, classification of terrain into various geomorphic classes (or landforms) was carried out. Following the approach of Sayre et al. (2009), five landform classes were generated for Agula watershed from combinations local relief and slope (Fig. 6). The relations among slope, relief, and landform class are depicted in Table 5. The smooth and irregular plains and low hills classes had a very low occurrence and, hence, were combined with the flat plains and hills, respectively. Breaks/foothills and low mountains were the dominant landforms each accounting for about 35% of the watershed, and the low mountains dominated the central/middle parts of the watershed. Overall, three rough landforms including hills, breaks, and low mountains make up 76% of the watershed, whereas flat plains and escarpments comprised 18 and 6% of the watershed, respectively (Table 5; Fig. 6). Based on Wilcox et al. (2007), the rough landforms such as the hills, breaks, and low mountains are characterized by high runoff generation and minimal groundwater recharge. It is also obvious that physiographic and land surface forms strongly influence the distribution of terrestrial ecosystems, and landform is a key part of the ecosystem delineation process. As such, understanding landforms of a watershed helps predict the distribution, physical and chemical properties of soils, and type of LULC, and is a very essential input for comprehensive watershed planning and management.
Landforms of Agula watershed derived from SRTM DEM following the procedure of Sayre et al. (2009)
Hypsometric attributes
Identification of geomorphic stages and erosional surfaces of watersheds have been more suitably done by the analysis of area–altitude relationship in general and hypsometric analysis in particular. The HC of Agula watershed is S-shaped with HI value of 0.4 (Fig. 7). The HC expresses the volume of rock mass in the watershed and the area below the curve represents the amount of material left after erosion. For Agula watershed, a 0.4 HI value indicated that about 40% of the original rock masses still exist in the watershed. The gradient of the HC was higher in its upper part (Fig. 7), which indicated that the amount of material left after erosion is smaller (Harlin 1978; Luo 2000). Keller and Pinter (2002) related such higher gradient of the HC with maturity of a watershed, since it implied that lateral erosion must have been intensive in the river head. In addition, the HC was more concave upward in the upper portion of the curve (Fig. 7), which according to Luo (2000) indicated more erosion in the upper reaches of the watershed. With reference to threshold limits recommended by Strahler (1952), HI ≥ 0.60 are typical of a youthful stage; 0.30 ≤ HI ≤ 0.60 are related to a maturity stage; and HI ≤ 0.30 are indicative of a peneplain/old stage. Taking this classification scheme, Agula watershed is categorized as in the equilibrium or mature stage of geomorphic evolution. At sub-watershed scale, however, those under cluster C1 with relatively high values of HI (Table 3; Fig. 3d) considered to be at youthful stage which are less dissected landscapes subject to erosion, whereas sub-watersheds with low HI values belonging to cluster C3 were at equilibrium or mature stage which are relatively stable, but still developing landforms. Willgoose and Hancock (1998) have a slightly different take on HI and, as such, watersheds with HI values >0.5 are relatively highland dominated by diffusive hillslope processes, whereas those having HI values <0.5 are considered dominated by fluvial erosion (channel processes play a larger role). The correlation matrix (Table 4) revealed negative correlation between HI and relief characteristics, but test statistics was not significant at p < 0.05. Similarly, Strahler (1952) also demonstrated that HI is inversely correlated with total relief, slope steepness, drainage density, and channel gradients; however, it is expected to correlate positively with rates of erosion.
The HC was fitted to a fifth-order polynomial function by regression using the least square fit (R 2 = 0.99) to get the coefficients a 0 = 0.95, a 1 = −3.58, a 2 = 11.46, a 3 = −20.80, a 4 = 18.72, and a 5 = −6.73. With these coefficients, it was possible to compute the statistical moments of the HC (SK and KUR) and its density function (DSK and DKUR) using Eqs. (2)–(5) defined by Harlin (1978). The derived statistical moments of the HC were SK (0.48), KUR (2.14), DSK (0.41), and DKUR (1.59). These derived hypsometric attributes are sensitive to subtle changes in overall watershed development as mass is removed by erosion over a long geological time period. According to Harlin (1978), the high value of SK for Agula watershed showed headward development of the main stream and its tributaries as these streams encroached the upper reaches of the watershed. DSK interprets the behavior of slope change in the watershed with positive (negative) values pointing to high erosion amounts in the upper (lower) regions of the watershed; hence, the positive value of DSK was an indication of accelerated forms of erosion in the upper reaches and dominance of fluvial landforms (Luo 2000). The relatively high KUR value confirmed that erosional processes have occurred in both the upper and lower reaches of the watershed, whereas the platykurtic nature of the DKUR value was an indication that mid-basin slope is moderate. Several studies (e.g., Luo 2000; Bertoldi et al. 2006; Vivoni et al. 2008) demonstrated that analysis of the HC and its statistical attributes are also useful metrics for inferring changes in watershed runoff response, which may result from landscape evolution.
Conclusions
In the present study, efforts were made to demonstrate the role of integrated remote sensing and GIS-based morphometric analysis to derive watershed characteristics for a case study site of Agula watershed and its sub-watersheds. Analysis of morphometric parameters was carried out from four aspects: drainage network, watershed geometry, drainage texture, and relief characteristics. A sixth-order river drains Agula watershed and the drainage network is dominantly dendritic type. A mean bifurcation ratio of R b = 4.46 for the entire watershed is indicative of mountainous and moderately dissected terrain. However, at sub-watershed scale, high R b values (R b > 5) were observed which might be expected in regions of steeply sloping terrain. The longest flow path of Agula watershed is about 48.5 km, and the longitudinal profile showed changes in slope of the river with steep gradient (0.018 m m−1) at the upper reach of the river which gradually flattened near its outlet (0.008 m m−1). Knickpoints with abrupt changes in elevation also developed along the main river which could be attributed to change of lithology along the main river resulting in differential erosion as well as the presence of major faults which are common along the rift escarpments. Based on the results of watershed shape parameters, Agula watershed has elongated shape, suggesting low peak flows for longer duration, lesser vulnerability to flash floods and easier flood management. The drainage texture parameters revealed that Agula watershed is characterized by fine drainage texture, implying that the watershed is dominated by impermeable soft rock with low resistance against erosion and sparse vegetation cover. Furthermore, high relief and steep slopes dominate, by which rough landforms including hills, breaks, and low mountains make up 76% of the watershed. The S-shaped hypsometric curve with hypsometric integral of 0.4 indicated that Agula watershed is in the equilibrium or mature stage of geomorphic evolution. At sub-watershed scale, the derived morphometric parameters from four perspectives (drainage network, watershed geometry, drainage texture, and relief characteristics) were further grouped into three clusters (that represented low, moderate, and high values) and considerable spatial variability was observed. The results of this study provide information on drainage morphometry that can serve as a database of initial assessment for strategic planning, management and decision making that include watershed prioritization for soil and water conservation, assessment of surface and groundwater potential, soil erosion studies, flash flood hazard assessment, etc.
References
Al-Rowaily SL, El-Bana MI, Al-Dujain FA (2012) Changes in vegetation composition and diversity in relation to morphometry, soil and grazing on a hyper-arid watershed in the central Saudi Arabia. Catena 97:41–49
Babu KJ, Sreekumar S, Aslam A (2016) Implication of drainage basin parameters of a tropical river basin of South India. Appl Water Sci 6:67–75
Banerjee A, Singh P, Pratap K (2015) Morphometric evaluation of Swarnrekha watershed, Madhya Pradesh, India: an integrated GIS-based approach. Appl Water Sci. doi:10.1007/s13201-015-0354-3
Bertoldi G, Rigon R, Over TM (2006) Impact of watershed geomorphic characteristics on the energy and water budgets. J Hydrometeorol 7:389–403
Bishop MP, Shroder JF, Bonk R, Olsenholler J (2002) Geomorphic change in high mountains: a western Himalayan perspective. Glob Planet Change 32(4):311–329
Bishop P, Hoey TB, Jansen JD, Artza IL (2005) Knickpoint recession rate and catchment area: the case of uplifted rivers in eastern Scotland. Earth Surf Proc Land 30(6):767–778
Biswas A, Majumdar DD, Banerjee S (2014) Morphometry governs the dynamics of a drainage basin: analysis and implications. Geogr J. doi:10.1155/2014/927176
Callow JN, Van Niel KP, Boggs GS (2007) How does modifying a DEM to reflect known hydrology affect subsequent terrain analysis. J Hydrol 332(1):30–39
Davis J (2010) Hypsometric tools. http://arcscripts.esri.com/details.asp?dbid=16830. Accessed Jan 2016
Dingman SL (1978) Drainage density and streamflow: a closer look. Water Resour Res 14(6):1183–1187
Faniran A (1968) The index of drainage intensity: a provisional new drainage factor. Aust J Sci 31(9):326–330
Farr TG, Rosen PA, Caro E, Crippen R, Duren R et al (2007) The shuttle radar topography mission. Rev Geophys 45(2):RG2004
Fenta AA, Kifle A, Gebreyohannes T, Hailu G (2015) Spatial analysis of groundwater potential using remote sensing and GIS-based multi-criteria evaluation in Raya Valley, northern Ethiopia. Hydrogeol J 23(1):195–206
Fenta AA, Yasuda H, Shimizu K, Haregeweyn N, Negussie A (2016) Dynamics of soil erosion as influenced by watershed management practices: a case study of the Agula watershed in the semi-arid highlands of northern Ethiopia. Environ Manag 58(5):889–905
Fenta AA, Yasuda H, Shimizu K, Haregeweyn N (2017) Response of streamflow to climate variability and changes in human activities in the semi-arid highlands of northern Ethiopia. Reg Environ Change. doi:10.1007/s10113-017-1103-y
Gajbhiye S, Mishra SK, Pandey A (2014) Prioritizing erosion prone area through morphometric analysis: an RS and GIS perspective. Appl Water Sci 4(1):51–61
Gebreyohannes T, De Smedt F, Walraevens K, Gebresilassie S, Hussien A et al (2013) Application of a spatially distributed water balance model for assessing surface water and groundwater resources in the Geba basin, Tigray, Ethiopia. J Hydrol 499:110–123
Getachew B (2007) Birki integrated watershed management study report. Tigray Bureau of Water Resources, Mekelle
Gravelius H (1941) Flusskunde. Goschen’sche Verlagshandlung, Berlin
Gregory KJ, DE Walling (1973) Drainage basin form and process: a geomorphological approach. Wiley, the University of Michigan, Ann Arbor
Grohmann CH (2004) Morphometric analysis in geographic information systems: applications of free softwares. Comput Geosci 30:1055–1067
Hack JT (1973) Stream profile analysis and stream gradient index. J Res US Geol Survey 1(4):421–429
Hammond EH (1964) Analysis of properties in land form geography: an application to broad-scale land form mapping. Ann Assoc Am Geogr 54(1):11–19
Harlin JM (1978) Statistical moments of the hypsometric curve and its density function. Math Geol 10(1):59–72
Hellweger R (1996) AGREE—DEM surface reconditioning system. Center for Research in Water Resources, the University of Texas, Austin
Horton RE (1932) Drainage basin characteristics. Trans Am Geophys Union 13(1):350–361
Horton RE (1945) Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol Soc Am Bull 56(3):275–370
Kaliraj S, Chandrasekar N, Magesh NS (2014) Morphometric analysis of the river Thamirabarani sub basin in Kanyakumari district, south west coast of Tamil Nadu, India, using remote sensing and GIS. Environ Earth Sci 73(11):7375–7401
Keller EA, Pinter N (2002) Active tectonics: earthquakes, uplift, and landscape. Prentice Hall, Upper Saddle River, New Jersey
Luo W (2000) Quantifying groundwater sapping landforms with a hypsometric technique. J Geophys Res 105(1):1685–1694
Macka Z (2003) Structural control on drainage network orientation an example from the Loucka drainage basin, SE margin of the Bohemian Massif (S Moravia Czech Rep.). Landf Anal 4:109–117
Magesh NS, Chandrasekar N, Soundranayagam J (2011) Morphometric evaluation of Papanasam and Manimuthar watersheds, parts of western Ghats, Tirunelveli district, Tamil Nadu, India: a GIS approach. Environ Earth Sci 64(2):373–381
Magesh NS, Jitheshlal KV, Chandrasekar N, Jini KV (2013) Geographical information system-based morphometric analysis of Bharathapuzha river basin, Kerala, India. Appl Water Sci 3(2):467–477
Melton MA (1957) An analysis of the relations among elements of climate, surface properties and geomorphology. Project NR 389-042, Tech Rep 11, Columbia University
Meshram SG, Sharma SK (2015) Prioritization of watershed through morphometric parameters: a PCA-based approach. Appl Water Sci. doi:10.1007/s13201-015-0332-9
Miller VC (1953) A quantitative geomorphologic study of drainage basin characteristics in the Clinch mountain area, Virginia and Tennessee. Technical report 3, Columbia University, New York
O’Callaghan JF, Mark DM (1984) The extraction of drainage networks from digital elevation data. Comput Vis Graph Image Process 28(3):323–344
Pandey A, Chowdary VM, Mal BC (2004) Morphological analysis and watershed management using geographical information system. J Hydrol 27(3–4):71–84
Patton PC, Baker VR (1976) Morphometry and floods in small drainage basins subject to diverse hydrogeomorphic controls. Water Resour Res 12(5):941–952
Pike RJ, Wilson SE (1971) Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Geol Soc Am Bull 82(4):1079–1084
Rabus B, Eineder M, Roth A, Bamler R (2003) The Shuttle Radar Topography Mission: a new class of digital elevation models acquired by spaceborne radar. ISPRS J Photogramm Remote Sens 57(4):241–262
Rai PK, Mohan K, Mishra S, Ahmad A, Mishra VN (2014) A GIS-based approach in drainage morphometric analysis of Kanhar River Basin, India. Appl Water Sci. doi:10.1007/s13201-014-0238-y
Reddy OGP, Maji AK, Gajbhiye SK (2004) Drainage morphometry and its influence on landform characteristics in a basaltic terrain, Central India—a remote sensing and GIS approach. Int J Appl Earth Obs Geoinformatics 6(1):1–16
Ritter DF, Kochel RC, Miller JR (1995) Process Geomorphology. Waveland Press, Long Grove
Romshoo SA, Bhat SA, Rashid I (2012) Geoinformatics for assessing the morphometric control on hydrological response at watershed scale in the upper Indus basin. J Earth Syst Sci 121(3):659–686
Roy S, Sahu AS (2016) Effectiveness of basin morphometry, remote sensing and applied geosciences on groundwater recharge potential mapping: a comparative study within a small watershed. Front Earth Sci 10(2):274–291
Sayre R, Comer P, Warner H, Cress J (2009) A new map of standardized terrestrial ecosystems of the conterminous United States. USGS professional paper 1768
Schumm SA (1956) Evaluation of drainage system and slopes in badlands at Perth Amboy, New Jersey. Geol Soc Am Bull 67(5):597–646
Singh O, Sarangi A, Sharma MC (2008) Hypsometric integral estimation methods and its relevance on erosion status of north-western Lesser Himalayan watersheds. Water Resour Manag 22(11):1545–1560
Slater JA, Garvey G, Johnston C, Haase J, Heady B et al (2006) The SRTM “finishing” process and products. Photogramm Eng Remote Sens 72(3):273–274
Smith K (1950) Standards for grading textures of erosional topography. Am J Sci 248:655–668
Soille P, Vogt J, Colombo R (2003) Carving and adaptive drainage enforcement of grid digital elevation models. Water Resour Res 39(12):1366
Sreedevi PD, Subrahmanyam K, Ahmed S (2005) The significance of morphometric analysis for obtaining groundwater potential zones in a structurally controlled terrain. Environ Geol 47:412–420
Sreedevi PD, Sreekanth PD, Khan HH, Ahmed S (2013) Drainage morphometry and its influence on hydrology in an semi-arid region: using SRTM data and GIS. Environ Earth Sci 70(2):839–848
Strahler AN (1952) Hypsometric area-altitude analysis of erosional topography. Geol Soc Am Bull 63(11):1117–1142
Strahler AN (1954) Quantitative geomorphology of erosional landscapes. In: 19th International geologic congress, Section XIII, pp 341–354
Strahler AN (1957) Quantitative analysis of watershed geomorphology. Trans Am Geophys Union 38(6):913–920
Strahler AN (1964) Quantitative geomorphology of drainage basins and channel networks. In: Chow VT (ed) Handbook of applied hydrology. McGraw Hill Book Company, New York, pp 4–11
Thomas J, Joseph S, Thrivikramji K, Abe G, Kannan N (2012) Morphometrical analysis of two tropical mountain river basins of contrasting environmental settings, the southern western Ghats, India. Environ Earth Sci 66(8):2353–2366
Thomas J, Joseph S, Thrivikramji KP, Arunkumar KS (2014) Sensitivity of digital elevation models: the scenario from two tropical mountain river basins of the western Ghats, India. Geosci Front 5(6):893–909
Turcotte R, Fortin JP, Rousseau AN, Massicotte S, Villeneuve JP (2001) Determination of the drainage structure of a watershed using a digital elevation model and a digital river and lake network. J Hydrol 240(3):225–242
Twidale CR (2004) River patterns and their meaning. Earth Sci Rev 67(3):159–218
Vivoni ER, Di Benedetto F, Grimaldi S, Eltahir EA (2008) Hypsometric control on surface and subsurface runoff. Water Resour Res 44. doi:10.1029/2008WR006931
Ward JH (1963) Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58(301):236–244
Wilcox BP, Wilding LP, Woodruff CM (2007) Soil and topographic controls on runoff generation from stepped landforms in the Edwards plateau of central Texas. Geophys Res Lett 34. doi:10.1029/2007GL030860
Willgoose G, Hancock G (1998) Revisiting the hypsometric curve as an indicator of form and process in transport-limited catchment. Earth Surf Proc Land 23:611–623
Yang L, Meng X, Zhang X (2011) SRTM DEM and its application advances. Int J Remote Sens 32(14):3875–3896
Acknowledgements
The two anonymous reviewers are gratefully acknowledged for providing valuable comments on the earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fenta, A.A., Yasuda, H., Shimizu, K. et al. Quantitative analysis and implications of drainage morphometry of the Agula watershed in the semi-arid northern Ethiopia. Appl Water Sci 7, 3825–3840 (2017). https://doi.org/10.1007/s13201-017-0534-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-017-0534-4