Abstract
The necessity of flow prediction in rivers, for proper management of water resource, and the need for determining the inflow to the dam reservoir, designing efficient flood warning systems and so forth, have always led water researchers to think about models with high-speed response and low error. In the recent years, the development of Artificial Neural Networks and Wavelet theory and using the combination of models help researchers to estimate the river flow better and better. In this study, daily and monthly scales were used for simulating the flow of Gamasiyab River, Nahavand, Iran. The first simulation was done using two types of ANN and ANFIS models. Then, using wavelet theory and decomposing input signals of the used parameters, sub-signals were obtained and were fed into the ANN and ANFIS to obtain hybrid models of WANN and WANFIS. In this study, in addition to the parameters of precipitation and flow, parameters of temperature and evaporation were used to analyze their effects on the simulation. The results showed that using wavelet transform improved the performance of the models in both monthly and daily scale. However, it had a better effect on the monthly scale and the WANFIS was the best model.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Rainfall–runoff modeling is a very complicated natural phenomenon because it is nonlinear and multi-dimensional. Flow prediction as a key parameter plays a significant role in the modeling. To model this process, various models are used. These models can be classified into three categories: physical, conceptual, and black-box models. In theory, physical and conceptual models must be very precise because their principles are based on the complex physical processes that affect the conversion of rainfall or runoff. On other hand, the complexity of natural systems and the number of processes that successively contribute to rainfall–runoff phenomena make modeling very difficult, so the performance of these models is highly dependent on the quality and quantity of the input data. Hence, the fuzzy models (ANFIS) are used because of their flexibility in modeling of nonlinear phenomena such as rainfall–runoff.
Wu et al. (2009) offered methods to improve neural network performance for daily flow prediction in two watersheds of China. In this work, three techniques of data processing, including moving average, singular spectrum analysis (SSA), and wavelet multi-resolution analysis (WMRA) in combination with artificial neural networks, were used to improve the estimation of daily flows. Six models, including an original model of neural network with no data processing, were reviewed and launched. In terms of prediction, the performance of ANN was poor because data normalization was not conducted. Wu and Chau (2011) made their rainfall–runoff modeling using ANN coupled with SSA and concluded that the neural ANN has a better performance in comparison with SSA. Thus, this method is used in the combination with other techniques because of the proper structure of the neural networks. The following cases are some of the uses of neural networks in combination with other methods. Asadi et al. (2013) offered a new combination of ANN for modeling rainfall–runoff in Aq Chay Basin, Iran. The proposed model was a combination of data processing methods, genetic algorithms, and Levenberg–Marquardt Algorithm for training the neural network input. Results showed that this method is more accurate, in predicting runoff, than ANN and ANFIS.
The use of wavelet analysis in hydrology is a new subject and some researchers have started using it. Nakken (1999) might be the first one who used wavelet analysis to characterize the temporal changes of rainfall–runoff and their relationships. In the following, Demyanov et al. (2001) used wavelet analysis and geostatistical tools (kriging) for survaying spatial variation of rainfall and the results were compared with the results of the hybrid model of ANN and kriging. Jayawardena et al. (2004) also used wavelet decomposition combined with Markov model to simulate daily rainfall of Chao Phvraya watershed in Thailand. Salerno and Tartari (2009) have conducted a study with a combined approach of surface hydrological modeling and wavelet analysis to understand the base flow components of river discharge in karst environments. They examined the advantages of wavelet analysis in this field.
A hybrid WANN model is provided for the precipitation prediction of Ligvan Chai (Tabriz, Iran) watershed. The results showed that the proposed model could predict both short- and long-term precipitation events because of using multi-scale time series as the ANN input layer (Nourani et al. 2009a). Daily rainfall prediction for Varayeneh station was conducted using WANN hybrid model and it was compared with ANFIS models. The results showed that WANN model functioned better for estimating daily precipitation (Solgi et al. 2014a, b). The performance evaluation of intelligent systems for predicting monthly precipitation using ANN and ANFIS models has been studied as well. The results showed that the performance of the two models is similar; however, in terms of estimating extreme points, the ANFIS model functioned better (Solgi et al. 2014a, b). Modeling and prediction of monthly river flow using WANN method in the Eastern Black Sea, Turkey have been conducted. Results of this study showed that WANN hybrid model could increase the forecast accuracy and perform better than MLP, MLR and, AR models (Kisi 2008). One method based on discrete wavelet transform (DWT) and ANN, which was applied to predict flow of seasonal river in semi-arid watershed in Cyprus, was presented. The WANN model for flow prediction was more accurate than the ANN. The results indicate that WANN models are promising new methods for predicting short-term flow in non-perennial rivers in semi-arid watersheds such as those found in Cyprus (Adamowski and Sun 2010). Rainfall–runoff modeling of Susurluk Catchment with ANN and ANFIS is carried out. The results showed that ANFIS model and ANN have the similar performance (Dorum et al. 2010). Two hybrid methods of Artificial Intelligence (AI) for modeling rainfall–runoff for two watersheds in Azerbaijan, Iran were presented. The first was the Seasonal Auto Regressive Integrated Moving Average with Exogenous Input-ANN (SARIMAX-ANN) model and the second was the WANFIS model. The results showed that the second model is relatively more efficient (Nourani et al. 2011).
Talei et al. (2013) predicted runoff using a Takagi–Sugeno neuro-fuzzy model with online learning. For this purpose, local learning of neural fuzzy system (NFS) for rainfall–runoff modeling program was performed. Results obtained by local learning model were better than those obtained by the physical model. Moreover, real time of launching the local learning model without re-training has better results as compared with launch time of fuzzy neural system.
An extraction method based on the self-organizing map (SOM) feature and the WANN model was devised for modeling the rainfall-runoff. A two-stage procedure was presented to model the rainfall–runoff process of the Delaney Creek and Payne Creek Basins, Florida, USA. The two-stage procedure includes data preprocessing and model building. The results proved that the proposed model leads to better outcome, especially in terms of determination coefficient for detecting peak points (DC peak) (Nourani and Parhizkar. 2013). Monthly flow predictions using linear genetic programming (LGP) were conducted and compared to WANN. The results showed that the linear LGP has better performance than WANN (Danandeh Mehr et al. 2013).
Application of hybrid models of wavelet-artificial intelligence has been studied. Results of this study show that the reason for considering wavelet transform is the benefit and usefulness of multilateral resolution analysis, the removal of signal-related disorders, and the powerful capability of artificial intelligence in optimization, versatility, and estimation of processes (Nourani et al. 2014). Different models were compared based on WANN for rainfall–runoff modeling. The results showed that Discrete Wavelet Transform Multilayer Perceptron Neural Network (DWTMLPNN) and Discrete Wavelet Transform Radial Basis Function (DWTRBFNN) at the decomposition level of 9 with Db8 Mother Wavelet have the best performance. Moreover, the results showed that decomposition of rainfall signals leads to the increase in the models’ performance for rainfall–runoff modeling (Shoaib et al. 2014).
Due to the importance of the topic of river flow and the need for having precise and accurate models in this field, in this research a combination of models is used. In other words, in this study two hybrid models are used to predict the river flow of Gamasyab River. The WANFIS and WANN models were used and compared with ANN and ANFIS models to study the effect of wavelet transform on them to obtain an accurate model for the river flow prediction.
Materials and methods
Study area
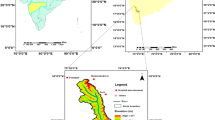
Karasti Springs, located in the south-west of Nahavand, is the source of Gamasiab River. This river, which is about 200 km long and 20–50 m wide and with a depth of 0.5–2 m, is a major tributary of Karkheh River and its hydrometer station is Verayneh, including hydrometric, pluviometry, and evaporimeter stations. This station is located at 48°24′15″E and 34°04′32″N. This station is 1795 meters above the sea level (Fig. 1). In this study, precipitation, temperature, evaporation and flow data, from 1969 to 2011, were used (Table 1).
Since inputting raw data reduces the accuracy and speed of the network, data normalization method, which prevents the excessive reduction of the weights and early saturation of the neurons, is used. By normalization method, each number is converted to a number between 0 and 1 to be applicable to the neural network function (Riad et al. 2004). For this purpose, the following equations are used:
In which x is the data, \(\bar{x}\) is the average of the data, x max is the max value of the data, x min is the min value of data, and y is the standardized data. Then, 75% of the data were used for training data and 25% are considered for simulation data.
Artificial neural network
An artificial neural cell is a physical element with some inputs which are applied with various intensities and has one output that is displayed as a nonlinear function of the input. If the sum of the weighted inputs is larger than the threshold level, the nerve is stimulated and shows a certain potential in the output. Neural networks are presented based on the mathematical model of the neural networks and human perceptual approach with the following hypotheses. Generally, information processing occurs in many units, known as neurons. Like in natural neurons, electrical signals are responsible for transferring information. Each connection to the neuron has its own weight and this weight is multiplied by transmitted signal. The body of the each neural cell is composed to two parts. The first part is called combination function. The task of the combination function is combining all inputs and turns them into one number. Transfer function cell is in the second part of the neural cell which is also called stimulation function.
When the combined inputs reach some certain threshold, the neural cell is stimulated and produces output signal. By comparing network output with the considered optimum, error vector is calculated and using various algorithms, this vector spreads from the end to beginning of the network, so that in the next cycle error is reduced. To launch the artificial neural network according to the input parameters, five structures were examined with regard to Table 2 in which Q t , P t , T t , and E t are flow, evaporation, temperature and precipitation, respectively, and Q t−1, P t−1, T t−1 and E t−1 are flow, precipitation, temperature and evaporation in the previous period and Q t+1 is the flow in the future period.
Effective parameters in ANN modeling
For modeling neural networks, several important parameters have to be determined:
-
1.
The number of neurons in different layers
-
2.
The number of network layers
-
3.
The number of repetitions (Epoch)
-
4.
Training rules
-
5.
Transfer Functions
For more information, refer Solgi et al. (2014a, b). There are two kinds of functions called linear function and Sigmoid function(karamouz and Araghinejad 2011). An activity function, which needs to be solved by ANN, is selected. Practically, limited activity functions are used. Table 3 shows transfer functions used in this study (Alborzi 2001). Other important functions in ANN are training functions. Table 4 shows training functions used in this study.
Wavelet transform
Wavelet theory is a method in mathematics, derived from Fourier theory which was presented in nineteenth century, but it has been in use for about one decade. The current concept of wavelet theory was presented by Morlet and a team in Marcel Research Center for Theoretical Physics under the supervision of Alex Grossmann in France.
Wavelet transform is an efficient mathematical transformation in the field of signal processing. Wavelets are the mathematical functions which present the scale time shape of time series and their functions for the analysis of time series, which include variables and non-constants. Wavelet analysis offers long-time intervals for information with low frequency and shorter time intervals for information with higher frequency.
Wavelet analysis is able to show various aspects, which other signal analysis methods may not be able to show, of different data, breakpoints, and discontinuities.
The wavelet function has two important features of fluctuation and of being short-lived. \(\psi (x)\) is the wavelet function if and only if its Fourier transform \(\psi (x)\) satisfies the following condition (Mallat 1998).
This condition is known as an admissibility condition for the wavelet. The above equation can be considered equivalent to Eq. (7).
This feature of functions, the average being equal to zero, is not a strict filter and many functions can be considered as the wavelet functions based on it. \(\psi (x)\) is the mother wavelet function that uses functions in analysis by two math practices called translation and scale, which causes changes in the size and place of the analyzed signal.
Finally, wavelet coefficient could be calculable in every point of signal (b) and for every scale value of (a) by Eq. (9) (Mallat 1998).
In Eq. (9), a does the scale task and b does the transform task. For the value of T, different values of a and b were obtained. Whenever, T has the highest positive value, the highest adjustment occurs. There is no adjustment for T equal to zero and for negative value of T the adjustment is reversed or the biggest difference occurs. Wavelet functions are different types and depending on their application their accuracy varies.
Wavelet functions
Depending on their application, the wavelet functions have different types with different levels of precision. The most commonly used wavelet functions are followed as Haar Wavelet function. Haar wavelet function is the simpler and one of the first wavelets. Daubechies wavelet function is one of the most efficient wavelet functions in discovering local discontinuities in signals. Symlet wavelet function has properties similar to those of the Daubechies family. Functions Sym6 and Sym4 are almost symmetric and are used in the discovering damages. Other wavelets include Gaussian, Morlet, Meyer, Coif, Mexican hat, and Bior.
One of the important key points in choosing mother wavelets is natural occurrence and type of time series. Thus, patterns of mother wavelet functions, which can geometrically be adapted to a time series curve, do better adaptation and the obtained results would be better. In this study in accordance with the various mother wavelets tests and according to the above point, Haar, Coif1, Sym3, Db4, and Db2 mother wavelets were selected. In Fig. 2, wavelet functions used in this study, are shown.
Adaptive neural fuzzy inference system (ANFIS)
Fuzzy theory is proposed by Professor Lotfi Asgarzadeh known as Zade in 1965 and has been widely used in many fields. This theory is a powerful and flexible tool for modeling uncertainty and lack of clarity in the real world and is considered as a tool for expressing speech–language phrases derived from human experience and knowledge in the form of mathematical equations.
Complexity and uncertainty in hydrological systems, lack of information in the hydrological processes, and vagueness of the data promoted cause the use of fuzzy theory in the field of hydrology and rainfall- runoff, which are the main processes of the hydrology, increases (Ross 1995). However, the main problem of fuzzy logic is the lack of kinematic approach for fuzzy controller. In other words, the neural network has this ability to be trained by its environment. Also, it is able to arrange its input and output pairs and structures, and find a relation between inputs and outputs.
For this purpose, Jang et al. (1997) proposed neural network-adaptive fuzzy system which has the ability to combine these two methods (Ross 1995). This method practically has been developed in the engineering field. Based on the fuzzy optimum theory, new fuzzy neural networks are introduced to predict runoff. ANFIS uses learning algorithm of the neural network and fuzzy logic to design a nonlinear mapping between the input and output spaces. Furthermore, due to the capability in combining linguistic power of a fuzzy system with numerical strength of a neural network, it is very useful in the modeling of processes such as hydrologic reservoir management and suspended sediment load estimation (Nayak et al. 2004, Kişi 2009).
ANFIS model works based on the changes in the amount and range of membership functions, belonging to different frequencies, to achieve the appropriate network with the minimum error. Takagi–Sugeno Inference method is used in the ANFIS model. The number and type of inputs and the shape of membership functions are some of the factors that affect the neuro-fuzzy model (Jang et al. 1997).
Membership functions
Transfer functions calculate the output vector of each layer. The only existing limitation related to input and output vector is that they should be in the same dimension. Each transfer function can be assigned to different layers of the network. To generate a certain output, a transfer function can be used. This function draws a wide range of input values to a specific value. For example, each output value can be mapped to the binary value of 0 or 1.
The most popular transfer functions which are used in the network structure of the adaptive neural fuzzy inference will be explained below (Fig. 3). The simplest membership functions are formed using straight lines. Triangular membership function is the simplest membership function which is named “Trimf”. This function is nothing more than a set of three points to make up a triangle. Trapezoidal membership functions of “Trapmf” are indeed a broken triangular curve whose upper part is trimmed and flatted. The straight line of this membership functions has the advantage of easy application. Two membership functions make up the Gaussian distribution curve, a simple Gaussian curve and a two-way combination of two different Gaussian curves. These two functions are “Gaussmf” and “Gauss2mf”. The bell-shaped membership function is generalized by three specific parameters and is known as “Gbellmf” function. It has one parameter more than Gaussian membership function; therefore, if the free parameter is adjusted it can achieve a non-fuzzy set. Because of their softness and decompression, membership functions of bell-shaped and Gaussian are powerful membership functions for training inference fuzzy-adaptive neural networks. Both these curves have the advantage of softening and non-zeroing in all the points. However, although Gaussian and bell-shaped membership functions can acquire their soft state, they are unable to determine some specific and important requirements of the asymmetric transfer functions. The other membership function is “sigmoidal” which is openly defined from left or right sides. Close and asymmetric transfer functions, which are not open from left or right sides, constructed by two sigmoidal functions. Thus, in addition to the original “sigmf”, the difference between sigmoidal function named “Dsigmf” and multiplication of two Sigmoidal function named “Psigmf” is significant and transfer function of Pi curve due to its appearance has the same. Membership functions which are used in the networks training need more space for explication and because of their popularity they are chosen for analysis in this study.
For more details on these functions, you can see MATLAB toolbox.
To implement this model, different structures are designed based on Table 5 in which Q t , P t , T t , and E t are flow, evaporation, temperature, and precipitation, respectively, Q t−1, P t−1, T t−1, and E t−1 are flow, precipitation, temperature, and evaporation, respectively, in the last period and Q t+1 is the flow in the next period.
Wavelet-artificial neural networks (WANN)
The data are analyzed using wavelet analysis and the output of this analysis is used as an input to ANN model. Then, a hybrid model is obtained. Precipitation and flow parameters are decomposed by wavelet transform and depending on the study and their mother wavelet transform they are turned into several time sub-series. These time sub-series are entered as input to ANN (Fig. 4). In this figure, a schematic view of the wavelet neural network is presented as well. The sub-series are \(P_{a} (t),\;T_{a} (t),\;Q_{a} (t),\;E_{a} (t)\) which are related to the overall scale of the final end; the other sub-series are related to the small scale of level 1 to the final level.
Wavelet-adaptive neural fuzzy inference system (WANFIS)
Figure 4 shows the schematic diagram of WANFIS model. First, the time series of precipitation and flow were decomposed by wavelet transform and then they were fed into the ANFIS model to form hybrid models of WANFIS.
Model evaluation criteria
The aim of model evaluation is to obtain the error rate of model according to the input data for training purposes and it is based on various criteria of error calculation. In this study, the following criteria were used to evaluate the model:
-
1.
Root mean square error or RMSE:
$${\text{RMSE}} = \sqrt {\frac{{\sum {(P_{\text{obs}} - P_{\text{pre}} )^{2} } }}{n}} .$$(10) -
2.
Coefficient of determination or \(R^{2}\):
$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {P_{\text{obs}} - P_{\text{pre}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {p_{\text{obs}} - \bar{p}} \right)^{2} }}.$$(11)
RMSE is the root mean square error and R 2 is the coefficient of determination. In these equations, Q is the observed flow prediction, \(Q_{\text{Pre}}\) is the predicted flow and \(\bar{Q}\) is the mean flow. The other index that is used in this research is the Akaike index. Based on this index, the best model is the one with a lesser Akaike index.
In Eq. (12), m is the number of input data and N par is the number of trained parameters.
Results and Discussion
According to Table 6, using normalizing formula (standardizing), number 1, has smaller simulation error and bigger coefficient of determination in simulating stage. Therefore, we used formula (1) for normalization in this study.
In the neural network, different training rules and stimulus functions for different neurons of middle layer were studied. This was done with trial and error. In the neural network, the input layer neurons were considered equal to input parameters of the network and the number of neurons in the middle layer was considered from 3 to 20 with trial and error and the neurons of output layer were considered as one. Structures and the results are presented in Table 7.
To model ANFIS, MATLAB software and the related ANFIS toolbox were used. Different structures were analyzed in the each different architecture of the ANFIS model. This means that each structure was examined with different membership functions and the different number of iterations. Table 8 shows the best structures for the each architecture of the ANFIS model for daily and monthly periods. Figure 5 displays the coefficient of efficiency for daily and monthly time series of the different ANFIS structures. Thus, it is clear that in both daily and monthly periods, architecture 5 was better than the other architectures and it means that adding evaporation and temperature data has improved the model’s performance.
By comparing membership functions, it has also become clear that membership function of “Trapmf” has better performance than other membership functions. As it is clear, this model has a better performance in the daily period (R 2 = 0.94) than monthly period (R 2 = 0.74). Therefore, using this model for the daily periods yields better results.
By comparing the results of the root mean square error (RMSE) criterion, it can also be concluded that the 5th architecture has a better performance and “Trapmf” membership function has the lesser RMSE than the rest of membership functions and it meant that it has better performance.
In the hybrid model WANN, at first, the signal of the input parameters was decomposed using wavelet transform. Then, sub-signals are used as inputs to the ANN. For this purpose, it is suggested that the degree of decomposition be calculated by Eq. (13) (Nourani et al. 2009b).
In this equation, L is the proposed decomposition degree and N is the number of time series. In this study, N = 516, L = 2 were determined and to be more precise, 1–4 decomposition degree were examined. The number of neurons in the first layer depends on the degree of wavelet decomposition. The number of input neurons to the network is m*(j + 1) which j is the wavelet decomposition degree and m is the number of input parameters. For example, for j = 1, according to the input parameters, which is 4 (precipitation, flow, temperature and evaporation), the number of input neurons is equal to 8. The output layer also has one neuron. The number of the middle layer neurons is variable and is obtained by trial and error. However, in this study the number of neurons in the middle layer, which varied from 3 to 20, has been analyzed. In this case, modeling was done using different training functions and different transfer functions for different neurons of hidden layers. Moreover, all the transfer functions are studied and various structures with the results are shown in Table 9.
By reviewing Tables 9 and 10, it is concluded that 5th architecture has the best performance and it is also observed that the number of neurons of the middle layer is less than 10 in the superior structures. This means that the optimal solution can be reached with a lower number of neurons. Moreover, in Architecture 1, the best structure has 3 middle layers, which means, in the neural networks, that the study of one intermediate layer should not be confined. It is true that in most cases, one intermediate layer is recommended but to achieve the optimum solution a number of different intermediate layers should be examined.
Besides wavelet function of Db4 has a better performance than other wavelet functions in every time period. It has the best performance in the daily period in the 5th level and in the monthly period in the second level. For this reason, WANFIS model for membership functions and wavelet functions in the daily period of level 5 and in the monthly period of level 2 was examined in Fig. 6. According to Fig. 6, db4 wavelet function has better performance than the other wavelet functions and Trapmf wavelet function was the best function. Indeed the combined use of these types yielded better performance.
In Figs. 7 and 8, the observed flow and the predicted one are presented for various models in the daily and monthly periods.
According to Fig. 7, two ANN and WANN models in the daily period have almost similar performance, but ANN model has a better performance in predicting minimum points, while ANFIS model has a better performance in predicting maximum points. However, in terms of coefficient of efficiency, ANFIS model has a better performance.
According to Fig. 7, comparison of two ANN and WANN models based on coefficient of efficiency shows that using wavelet transform improved the performance of the model. This is also true for the two models of ANFIS and WANFIS which shows direct and effective impact of the wavelet transform on flow prediction. This issue is completely clear in the monthly models, having big difference in the coefficient of determination, because they have less data in comparison with daily periods. Also, it is obvious that the WANFIS model has a better performance in predicting the minimum and maximum points.
According to Fig. 8, in predicting the maximum points, ANFIS model functions are better, while ANN model has a better performance in predicting minimum points. However, in terms of coefficient of efficiency, ANFIS model has a better performance. For both models of WANFIS and WANN because of the abundance of data in the daily models, it is observed that the performance of both models is similar. However, during monthly period, WANFIS model function is better for predicting the maximum point. Generally, the WANFIS model is the optimal model of this study. Finally, the best structures of different models are compared with each other and the results are shown in Table 11.
Based on Table 11 and the examined Akaeik criteria, it is also concluded that the WANFIS model has lesser Akaeik criteria than other models in both daily and monthly periods. Despite the fact that in the daily period, Akaeik criteria of two models are very close to each other and in the monthly period WANFIS has better performance than WANN. Therefore, in general, it can be said that WNFIS and WANN show no significant difference in the daily period, but in the monthly period the difference between these two models must be considered. In the Figs. 9 and 10, the comparison between modeling in the daily and monthly periods of two models is presented.
The results of this study are similar to those of the Dorum et al. (2010) and Solgi et al. (2014a, b) in terms of the performance similarity of the two models with little advantage of the neural fuzzy system in determining the extent points. Moreover, the results correspond with those of the Nourani et al. (2011) based on the performance WANPIS model compared with WANN model.
Conclusion
In this study, two models of ANN and ANFIS are used for predicting the flow of the Gamasyab River using daily and monthly data of the Verayneh Station. Then, we used wavelet transform and decomposed the input data at different levels with the used wavelet functions. Next, the obtained signals were used as the inputs of ANN and ANFIS to obtain hybrid model of WANN and WANFIS. By evaluating different structures, it is concluded that the performances of WANN and WANFIS are similar in the daily period, but in the monthly period, WANFIS has better performance for predicting the maximum points and considering coefficient of efficiency and other evaluation, it was cleared that WANFIS was better in the monthly period. Moreover, after examining different structures, it is determined that 5th architecture functions are better in the various models, in the daily and monthly periods of the architecture. It means that using the data of evaporation and temperature makes the performance of the models better than the architecture in which these data are not used. Accordingly, the use of temperature and evaporation parameters is suggested in the other studies in addition to flow and precipitation parameters. Moreover, after examining different training functions, it was concluded that the usage of all training functions, because of being time-consuming, is not suggested. Therefore, as proposed, the three Levenberg–Marquardt, BFGS Quasi-Newton, and Bayesian Regularization are recommended for future studies due to their better performance.
After examining different stimulus functions, it is recommended that four types of Tansig, Logsig, Satlin, and Poslin” stimulus functions can be used for future study because of their better performance. By reviewing the membership functions, it is determined that Trapmf membership function has better performance than other membership functions especially in the monthly model. Generally, the number of 2 and 3 middle layers is considered in the superior structure of the neural network model and shows that in the reviewing of the structures, the number of middle layers should also be examined and one single middle layer is not sufficient to consider.
References
Adamowski J, Sun K (2010) Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds. J Hydrol 390:85–91
Alborzi M (2001) Familiar with artificial neural networks. Institute of Publishing Sharif University of Technology, Iran
Asadi S, Shahrabi J, Abbaszadeh P, Tabanmehr S (2013) A new hybrid artificial neural networks for rainfall–runoff process modeling. Neurocomputing 121:470–480
Danandeh Mehr A, Kahya E, Olyaie E (2013) Streamflow prediction using linear genetic programming in comparison with a neuro-wavelet technique. J Hydrol 505:240–249
Demyanov V, Soltani S, Kanevski M, Conu S, Maignan M, Savelieva E, Timonin V, Pisaren KV (2001) Wavelet analysis residual kriging vs neural network residual kriging. Stoch Environ Res Risk Asses 15:18–32
Dorum A, Yarar A, Faik Sevimli M, Onüçyildiz M (2010) Modelling the rainfall–runoff data of susurluk basin. Expert Syst Appl 37(9):6587–6593
Jang JSR, Sun CT, Mizutani E (1997) Neuro-fuzzy and soft computing: a computational approach to learning and machine intelligence. Prentice-Hall International, Upper Saddle River
Jayawardena AW, Xu P, Tsang FLL (2004) Rainfall predication by wavelet decomposition. In: Asia Pacific Association of Hydrology and Water Resources Conference, Singapore
Karamouz M, Araghinejad S (2011) Advanced Hydrology. Amirkabir University of Technology Press (Tehran Polytechnic), Tehran
Kisi O (2008) Stream flow forecasting using neuro-wavelet technique. Hydrol Process 22:4142–4152
Kişi Ö (2009) Evolutionary fuzzy models for river suspended sediment concentration estimation. J Hydrol 372(1–4):68–79
Mallat SG (1998) A wavelet tour of signal processing. Academic Press, San Diego. doi:10.1016/B978-012466606-1/50000-3
Nakken M (1999) Wavelet analysis of rainfall–runoff variability isolating climatic from anthropogenic patterns. Environ Model Softw 14(4):283–295
Nayak PC, Sudheer KP, Rangan DM, Ramasastri KS (2004) A neuro-fuzzy computing technique for modeling hydrological time series. J Hydrol 291(1–2):52–66
Nourani V, Parhizkar M (2013) Conjunction of SOM-based feature extraction method and hybrid wavelet-ANN approach for rainfall–runoff modeling. J Hydroinform 15(3):829–848
Nourani V, Alami MT, Aminfar MH (2009a) A combined neural-wavelet model for prediction of Ligvanchai watershed precipitation. Eng Appl Artif Intell 22(3):466–472
Nourani V, Komasi M, Mano A (2009b) A multivariate ANN-wavelet approach for rainfall–runoff modeling. Water Resour Manag 23:2877–2894
Nourani V, Kisi Ö, Komasi M (2011) Two hybrid artificial intelligence approaches for modeling rainfall–runoff process. J Hydrol 402:41–59
Nourani V, Hosseini Baghanam A, Adamowski J, Kisi O (2014) Applications of hybrid wavelet–Artificial Intelligence models in hydrology: a review. J Hydrol 514:358–377
Riad S, Mania J, Bouchaou L, Najjar Y (2004) Rainfall–runoff model usingan artificial neural network approach. Math Comput Model 40(7–8):839–846
Ross TJ (1995) Fuzzy logic with engineering application. McGraw Hill Inc., New York
Salerno F, Tartari G (2009) A coupled approach of surface hydrological modelling and Wavelet Analysis for understanding the baseflow components of river discharge in karst environments. J Hydrol 376:295–306
Shoaib M, Shamseldin AY, Melville BW (2014) Comparative study of different wavelet based neural network models for rainfall–runoff modelling. J Hydrol 515:47–58
Solgi A, Nourani V, Pourhaghi A (2014a) Forecasting Daily Precipitation Using Hybrid Model of Wavelet-Artificial Neural Network and Comparison with Adaptive Neuro Fuzzy Inference System (Case Study: Verayneh Station, Nahavand). Adv Civil Eng 2014:1–12
Solgi A, Radmanesh F, Pourhaghi A, Bagherian Marzouni M (2014b) Evaluation of artificial intelligence systems performance in precipitation forecasting. TI J Agric Sci Dev 3(7):256–264
Talei A, Chua LHC, Quek C, Jansson PE (2013) Runoff forecasting using a Takagi–Sugeno neuro-fuzzy model with online learning. J Hydrol 488:17–32
Wu CL, Chau KW (2011) Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J Hydrol 399(3–4):394–409
Wu CL, Chau KW, Li YS (2009) Methods to improve neural network performance in daily flows prediction. J Hydrol 372(1–4):80–93
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Solgi, A., Zarei, H., Nourani, V. et al. A new approach to flow simulation using hybrid models. Appl Water Sci 7, 3691–3706 (2017). https://doi.org/10.1007/s13201-016-0515-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0515-z