Abstract
Correct estimation of soil loss at catchment level helps the land and water resources planners to identify priority areas for soil conservation measures. Soil erosion is one of the major hazards affected by the climate change, particularly the increasing intensity of rainfall resulted in increasing erosion, apart from other factors like landuse change. Changes in climate have an adverse effect with increasing rainfall. It has caused increasing concern for modeling the future rainfall and projecting future soil erosion. In the present study, future rainfall has been generated with the downscaling of GCM (Global Circulation Model) data of Mandakini river basin, a hilly catchment in the state of Uttarakhand, India, to obtain future impact on soil erosion within the basin. The USLE is an erosion prediction model designed to predict the long-term average annual soil loss from specific field slopes in specified landuse and management systems (i.e., crops, rangeland, and recreational areas) using remote sensing and GIS technologies. Future soil erosion has shown increasing trend due to increasing rainfall which has been generated from the statistical-based downscaling method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Climate change is an important factor in the present scenario for planning and management of water resources. Global Circulation Models (GCMs) are tools that are used in the simulation of the present and future climate changes. These are numerical models that represent the various physical processes of the earth-atmosphere–ocean system (Wilby and Wigley 1997; Prudhomme et al. 2003). However, hydrological variability at the local scale is required for the assessment of the regional climate. Therefore, downscaling of the GCM data to the regional scale is done with various approaches. These methods are support vector machines, multiple linear regressions, and artificial neural networks (Ghosh and Mujumdar 2006; Raje and Mujumdar 2009; Aksornsingchai and Srinilta 2011). The SDSM model (Wilby and Dawson 2007) applies multiple linear regression for future climate change analysis.
Soil erosion is a diffuse process varying spatially over a typical landscape. Soil erosion is caused by detachment and removal of soil particles from land surface. It is a natural physical phenomenon which helped in shaping the present form of earth’s surface (Das 2002). Modeling soil erosion is the process of mathematically describing soil particle detachment, transport, and deposition on land surface.
Direct measurement of soil erosion at many points across a region is impractical. Physically, erosion is difficult to measure, and variation of climate requires at least 10 years of data to obtain an accurate measure of average annual erosion. Consequently, researchers commonly use erosion prediction methods to make regional assessments of the impact of erosion on crop productivity, off-site sedimentation, or in selecting conservation methods for specific fields.
Planning for conservation measures within an area requires assessing the magnitude of soil erosion, which enables resource planners in deciding what is considered acceptable, and the effects of different conservation strategies can be determined. What is required, therefore, is a method of predicting soil loss under a wide range of conditions (Morgan et al. 1984).
Soil erosion is one of the major environmental hazards today experienced by the human community. It has been estimated that in India about 5344 m-tonnes of soil is being detached annually due to different reasons (Narayan and Babu 1983). These huge soil losses are not only responsible for the reduced storage reservoir capacity in India but also reduction in nutrient laden agricultural land at many areas. Several researchers have attempted to estimate the soil erosion loss in the different regions of the country utilizing remote sensing and GIS technologies (Jain et al. 2001; Chowdary et al. 2004; Pandey et al. 2007; Dabral et al. 2008; Ismail and Ravichandran 2008; Dalu et al. 2013; Gajbhiye et al. 2014). Effect of climate change on soil erosion has been observed by Routschek et al. (2014) due to changes in the rainfall, and a study shows that increased intensity of various climatic parameters, particularly rainfall, has caused an increase in the sediment load (Mukundan et al. 2013). Higher rate of soil erosion is observed by various researchers in different parts of India using the MMF (Morgan–Morgan-Finney), USLE (Universal Soil Loss Equation), and RUSLE (Revised Universal Soil Loss Equation) models (Prasannakumar et al. 2012; Patel and Kathwas 2012; Pandey et al. 2009).
The main objective of the study is the assessment of the impact of future change in climate (rainfall) on the soil erosion of the Mandakini basin area with the USLE (Universal Soil Loss Equation) and SDSM model. The SDSM model (Wilby and Dawson 2007) has been used in the present study for future climate change analysis with the HadCM3 data of A2 scenario.
Description of the study area
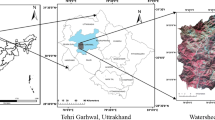
The Mandakini basin draws its name from the river Mandakini, one of the tributaries of river Alaknanda, started from Kedarnath which is one of the most auspicious shrines in India. The basin falls in the district of Rudraprayag, Uttarakhand, and comprises an area of 1646 km2 (approx). The Mandakini river runs for a length of 80 km up to the confluence, where it meets with Alaknanda river at Rudraprayag with an average slope of 4.50 in percentage. The annual rainfall in the region is about 1000–2000 mm. The maximum rainfall is observed in the monsoon months. The region witnesses comparatively cooler climate from the main Indian land with maximum temperature ranges from 30 to 36 °C while minimum between 0 and 8 °C. The relative humidity is high in the monsoon season generally exceeding 70 %. The climate in the study area is tropical monsoon type with most of the rainfall concentrating in the months of June to October. The region has steep valley slopes with land slide and sediment movement, as debris flow is frequent in these reaches. The population density in the area is generally thin. The location map of the study area is shown in Fig. 1.
Methodology
Climate change
The daily observed predictor data of atmospheric variables was derived from the National Center of Environmental Prediction (NCEP) on 2.5° latitude × 2.5° longitude grid-scale for 41 years (1961–2001) from the website of Canadian Climate Impacts Scenarios (CCIS) (http://www.cics.uvic.ca/scenarios/sdsm/select.cgi). The predictors of Hadley Center’s GCM (HadCM3) of A2 scenario for 139 years (1961–2099) on 2.5° × 3.75° grid-scale are obtained from the Canadian Climate Impacts Scenarios (CCIS) website (http://www.cics.uvic.ca/scenarios/sdsm/select.cgi). The SDSM model was used here which requires two types of daily data for downscaling. One is ‘Predictand’ (rainfall) which are local data, and the other one is ‘Predictors’(NCEP and simulated GCM data), which are large-scale data of different atmospheric variables. Model calibration is done to develop an empirical relationship between the predictand and predictors. The NCEP data from 1961 to 1991 are used for model calibration, and the rest (1992–2001) is used for validation.
Soil erosion model: the universal soil loss equation (USLE)
The Universal Soil Loss Equation developed by Wischmeier and Smith (1958 and 1978) was used to predict the gross soil erosion (average annual soil loss) and its spatial distribution on the basin. The USLE estimates soil loss for a given area as product of six erosion factors, whose values are determined separately using the area specific empirical equation. The USLE is limited for predicting long-term average of soil loss, and is expressed as follows:
where A is average annual soil loss rate (t ha−1year−1), R is rainfall erosivity factor (MJ mm ha−1h−1year−1), K is soil erodibility factor (t ha h ha−1MJ−1mm−1), LS is topographic factor expressed as slope length and steepness, C is crop management factor, and P is conservation supporting practice factor. The flow chart showing the processes is given in Fig. 2.
Development of database for USLE
Rainfall erosivity (R) factor
R factor is a function of the falling raindrop and rainfall intensity (Wischmeier and Smith 1958) and is estimated as the product of the kinetic energy (E) of the raindrop and the maximum intensity of rainfall (I 30) over duration of 30 min in a storm. The erosivity of rain is calculated for each storm, and these values are summed up for each year. The kinetic energy is calculated by the following formula (Wischmeier and Smith 1978):
where E is the total kinetic energy of rainfall (t m ha−1cm−1), E i is the rainfall kinetic energy of the ith increment per storm (mt ha−1cm−1), I i is the average intensity of rainfall during the ith increment for each storm (cm ha−1), and N is the total number of discrete increment.
In this study, the storm wise rainfall data were not available for the computation of rainfall erosivity factor (R); therefore, the relationship between seasonal value of R and average seasonal (June–September) rainfall has been used, recently defined by RamBabu et al. (2004). The rainfall erosivity factor has been defined by following equation:
where R is the average seasonal erosivity factor (metric tonnes ha−1 cm h−1 100−1), and X is the average seasonal rainfall (mm).
In and around the study average rainfall of 10 years have been taken from the rain gauge station for the estimation of rainfall erosivity. The rainfall erosivity factor (R) has been calculated using Eq. 3 for annual average rainfall of observed and simulated data. The values from R have been adopted in this study to calculate soil erosion using USLE.
Soil erodibility (K) factor
The K factor is an expression of the inherent erodibility of the soil or surface material at a particular site under standard experimental conditions. It is a function of the particle-size distribution, organic-matter content, structure, and permeability of the soil or surface material. As per the soil codes and soil types available in the study area, the soil has been classified in five major categories. Fine-textured soils with high clay content are resistant to detachment, thereby considered a low K factors ranging from 0.05 to 0.15. Coarse-textured soils, such as sandy soils, also have low K values from 0.05 to 0.2 because of high infiltration resulting in low runoff even though these particles are easily detached. Medium-textured soils, such as a silt loam, have moderate K values (about 0.25), because they are moderately susceptible to particle detachment and they produce runoff at moderate rates. Soils having high silt content are highly susceptible to erosion and have high K values, which can range from 0.25 to 0.4; thus, an average value of 0.325 is assigned. Soil with very severe soil erosion is considered a K value of 0.4. The various classes of soil and the values of K are given in Table 1 as below:
Prior to the preparation of the K map, soil map for the area has been generated. Then, K map is prepared for the Mandakini basin by considering the soil map after assigning suitable K values for the different types of soils, as given in Table 1. The K map, finally, generated in GIS environment and is presented in Fig. 3. Table 2 describes the existing soil status in the study area.
Topographic (LS) factor
The LS factor is an expression of the effect of topography, specifically hill slope length and steepness, on rates of soil loss at a particular site. The value of ‘LS’ increases as hill slope length and steepness increase, under the assumption that runoff accumulates and accelerates in the down-slope direction. This assumption is usually valid for lands experiencing overland flow, but may not be valid for forest and other densely vegetated lands.
Hill slope-length factor (L)
The L-factor was calculated based on the relationship developed by Weismeier and Smith (1965). The equation is as follows:
where λ = slope length measured from the water divide of the slope (m), m = exponent dependent upon slope gradient and may also be influenced by soil properties and type of vegetation. m is taken as 0.5 for slopes exceeding 5 %, 0.4 for 4 % slopes, and 0.3 for slopes less than 3 %. In the study, the percent slope was determined from the DEM, accordingly m has been taken as 0.4. Different slope classes in the study area are shown in Fig. 4.
Hill slope-gradient factor (S)
The hill slope-gradient factor, S, reflects the effect of hill slope-profile gradient on soil loss. The slope-gradient factor (S) is the ratio of soil loss from a plot of known values of the factor S. In this study, slope-gradient factor (S) is calculated using the following equation (McCool et al. 1987),
where \(\theta\) = field slope in degrees = tan−1(field slope/100).
Therefore, the final LS map has been prepared in the ARC GIS environment by multiplying L & S factor using above Eqs. 5, 6 and shown in Fig. 4. Different LS classes in the study area are presented in Table 3.
Crop management (C) factor
The C factor is an expression of the effects of surface covers and roughness, soil biomass, and soil-disturbing activities on rates of soil loss at a particular site. The value of C decreases as surface cover and soil biomass increase, thus protecting the soil from rain splash and runoff. In the present study, the landuse/land cover map was generated from the satellite images and used in the allocation of C factor for different landuse classes. Table 4 furnishes the crop management factors used in the model under different landuse/land cover. The spatial distribution of C-values is shown in Fig. 5.
Conservation practice (P) factor
The P factor is an expression of the effects of supporting conservation practices, such as contouring, buffer strips of vegetation, and terracing, on soil loss at a particular site. It is the ratio of soil loss with specific support practice to the corresponding loss with up- or down-slope cultivation. In the present study, the P factor has been considered as one, assuming no conservation practices followed in the area, thereby the soil loss estimated by the model will be very high.
GIS database preparation
Different layers were created in vector format for the analysis of study area as given in Table 5. Most of the analysis and overlay operations are easily and efficiently done in the raster model, and therefore, all maps in vector model were converted into raster structure using the Arc GIS software. Boundary, soil, and landuse maps which were already in polygon form were rasterized through polygon to raster mode.
Landuse classification
Using Landsat imageries of resolution 30-m landuse/land cover map was prepared. Unsupervised classification was done using the ERDAS 9.0 software. The study area has been classified into six different landuse classes namely: (1) water body, (2) open forest, (3) dense forest, (4) barren outcrop, (5) scrub, and (6) snow cover that were generated for study area. The classified map depicting various landuse/land cover classes of the study area is shown in Fig. 5. The landuse/land cover statistics of the study area is also presented in Table 6.
The overall kappa statistics (\(\mathop {\rm K}\limits^{ \wedge }\)) estimated based on the minimum 120 samples taken from different landuse categories are 0.80. A kappa value of 1 indicates a perfect agreement between the categories. A value greater than 0.75 indicates a very good-to-excellent agreement, while a value between 0.40 and 0.75 indicates a fair-to-good agreement. A value less than or equal to 0.40 indicates a poor agreement between the classification categories (Manserud and Leemans 1992). Based upon these criteria, the kappa value indicates a good-to-excellent agreement. The accuracy assessment parameters for different classifications are presented in Table 7.
Results and discussion
Downscaling
The predictors and their corresponding correlation coefficients, partial correlation, and P value are provided in Table 8.
The model calibration process is based on the multiple regressions between the predictand (observed rainfall) and NCEP predictors (Table 8). Since the relationship between the predictand and predictor is governed by the occurrence of wet-day, a threshold value of 0.3 mm of rainfall has been considered during model calibration. The calibration (1961–1991) and validation (1992–2001) results of the model are given in Table 9. The observed results show that the SDSM model has good agreement between the observed and simulated daily mean rainfall, standard deviation, and variance. The correlation coefficient is 0.59 and 0.48 during calibration and validation, respectively. The root mean square error (RMSE) value for calibration is 17.25 and validation is 19.85, the normalized mean square error (NMSE) value for calibration is 10.47 and for validation is 12.95, the NashSutcliffe coefficient (NASH) value for calibration is 0.85 and validation is 0.82, and the Correlation coefficient (CC) value for calibration is 0.82 and for validation is 0.80. Similar types of model performance methods have also been used in the studies of soil erosion by Mondal et al. (2016b, c).
The annual average rainfall corresponding to future erosion is presented in Table 10. The result depicts an increase in annual rainfall successively. In the 2020s, the simulated rainfall is about 270 mm higher than the present scenario. Likewise, 2050 and 2080 rainfalls are 1595.21 and 1977.89 mm, respectively.
Soil erosion
The results obtained after analyzing different data are presented in Table 10 that shows future erosion of the catchment in the 2020s, 2050s, and 2080s due to changing rainfall. The rainfall erosivity factors (R) estimated for the study area are 459, 558, 646, and 784 metric tonnes ha−1 cm h−1 100−1 for 1961–2001 (current), 2020s, 2050s, and 2080s, respectively. Increased rainfall has caused changes or increase in the soil erosion in the future. There is a prominent increase in the future than the current or observed period, but the percentage of change in the 2020s and 2080s are higher than the 2050s. However, sediment load of 2050s is higher than 2020s, which indicates that the sediment load in the future is gradually increasing due to rainfall change.
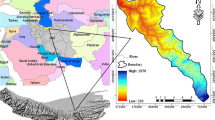
The magnitude and spatial distribution of predicted soil loss in the Mandakini basin are shown in Fig. 6. Areas covered by different erosion classes are <5, 5–20, 21–50, 50–100, and >100 t ha−1 year−1. The last three classes with higher erosion rate need an immediate attention and its conservation and management are suggested. Major part of the basin area is experiencing a soil loss of 5–20 t ha−1 yr−1 in the current year, which shows a gradual increase in the future. Mostly, the northern part of the basin is showing highest erosion of >100 t ha−1 yr−1, and the extreme north shows lowest erosion of <5 t ha−1 yr−1. As observed from the current map, erosion of <5 t ha−1 yr−1 is observed in a few areas in the south and southeast, which is observed to have converted into areas with higher erosion rate, as projected in the future maps. Hence, in the 2080s projection, reduction in the areas of low-rate soil erosion and increased areas with higher soil erosion is observed. Since a further increase in soil erosion in the catchment is expected, vegetative and structural control measures are urgently needed to minimize the menace of soil erosion.
Soil erosion is occurring in many parts of India and is considered as grave due to loss of soil productivity. Climate change is causing changes in the behaviour of rainfall, which is also a major factor influencing soil loss. Increased future rainfall is predicted by many researchers in different parts of India. Increased rainfall is observed in the works of Kannan and Ghosh (2011) and Rupa Kumar et al. (2006). Increased rainfall is also observed in the works of Meenu et al. (2013) and Mondal et al. (2014) in different parts of India. An increase in the rate of soil erosion due to changes in rainfall in the future is observed in the works of Mondal et al. (2014, 2016a), showing differences in erosion due to change in slope of the area in the central part of India. Increase in soil erosion and rainfall erosivity due to climate change is also observed in the other parts of the world in the studies of Simonneaux et al. (2015) in Morocco and Maeda et al. (2010) in Kenya.
Conclusions
A quantitative assessment of the annual soil erosion loss with respect to the climate change was done in the Mandakini river basin— a hilly catchment of Uttarakhand, India. Climate change scenario in the future has been used with the HadCM3 GCM data (A2 scenario) by the SDSM software, which is a regression-based model. Model output is showing increasing rainfall in the future. The well-known USLE soil loss estimation model is used to identify the priority erosion prone region in the catchment. The different USLE parameters are estimated using remote sensing and GIS. Future soil erosion has been calculated using the future rainfall data. Only rainfall has been considered in the study, which shows there will be increase in soil erosion with increasing rainfall. However, other parameters (soil type, landuse, DEM) are taken as constants in the future. Therefore, the estimation of spatial soil erosion loss can be made utilizing remote sensing and GIS techniques. Although the output from the USLE model during the study have been cross-checked with reference to other governmental reports for the region in 2011, however, the study requires further validation of the model output with the observed data from available gauging networks in the basin outlet. The soil erosion study reveals that there is an urgent need for soil conservation measures in the catchment, where the area is found under critical erosion condition with high and very high soil erosion. The study shows the climate change will be very much responsible for soil erosion in the future.
References
Aksornsingchai P, Srinilta C (2011) “Statistical downscaling for rainfall and temperature prediction in Thailand.” Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hong Kong, Vol. I, March 16–18
Chowdary VM, Yatindranath KS, Adiga S (2004) Modelling of non-point source pollution in a watershed using remote sensing and GIS. Ind J Rem Sens 32(1):59–73
Dabral PP, Baithuri N, Pandey A (2008) Soil erosion assessment of a hilly catchment of North Eastern India using USLE, GIS and remote sensing. Water Resour Manage 22:1783–1798
Dalu T, Tambara EM, Clegg B, Chari LD, Nhiwatiwa T (2013) Modeling sedimentation rates of Malilangwe reservoir in the south-eastern lowveld of Zimbabwe. Appl Water Sci 3(1):133–144
Das G (2002) Hydrology and Soil Conservation Engineering Practice. Hall India
Gajbhiye S, Mishra SK, Pandey A (2014) Relationship between SCS-CN and sediment yield. Appl Water Sci 4(4):363–370
Ghosh S, Mujumdar PP (2006) Future rainfall scenario over Orissa with GCM projections by statistical downscaling. Curr Sci 90(3):396–404
Ismail J, Ravichandran S (2008) RUSLE2 model application for soil erosion assessment using remote sensing and GIS. Water Resour Manage 22:83–102
Jain SK, Kumar S, Varghese J (2001) Estimation of soil erosion for a himalayan watershed using GIS technique. Water Resour Manage 15:41–54
Kannan S, Ghosh S (2011) Prediction of daily rainfall state in a river basin using statistical downscaling from GCM output. Stoch Env Res Risk Assess 25(4):457–474
Maeda EE, Pellikka PKE, Siljander M, Clark BJF (2010) Potential impacts of agricultural expansion and climate change on soil erosion in the Eastern Arc Mountains of Kenya. Geomorphology 123:279–289
Manserud RA, Leemans R (1992) Comparing global vegetation maps with the kappa statistics. Ecol Model 62:275–279
McCool DK, Brown LC, Foster GR (1987) Revised slope steepness factor for the Universal Soil Loss Equation. Trans ASAE 30:1387–1396
Meenu R, Rehana S, Mujumdar PP (2013) Assessment of hydrologic impacts of climate change in Tunga-Bhadra river basin, India with HEC-HMS and SDSM. Hydrol Process 27(11):1572–1589
Mondal A, Khare D, Kundu S, Meena PK, Mishra PK, Shukla R (2014) Impact of climate change on future soil erosion in different slope, landuse and soil type conditions in a part of Narmada river basin. J Hydrol Eng (ASCE), C5014003-1–C5014003-12
Mondal A, Khare D, Kundu S (2016a) Impact of climate change on future soil erosion and SOC loss in different slope, soil and landuse condition. Nat Hazards. doi:10.1007/s11069-016-2255-7
Mondal A, Khare D, Kundu S (2016b) Uncertainty Analysis of Soil Erosion Modeling Using Different Resolution of Open Source DEMs. Geocarto Int Taylor Francis Publ. doi:10.1080/10106049.2016.1140822
Mondal A, Khare D, Kundu S, Mukherjee S, Mukhopadhyay A, Mondal S (2016c) Uncertainty of soil erosion modeling using open source high resolution and aggregated DEMs. Geosci Front. doi:10.1016/j.gsf.2016.03.004
Morgan RPC, Morgan DDV, Finney HJ (1984) A predictive model for the assessment of erosion risk. J Agric Eng Res 30:245–253
Mukundan R et al (2013) Suspended sediment source areas and future climate impact on soil erosion and sediment yield in a New York City water supply watershed, USA. Geomorphology 183:110–119
Narayan DVV, Babu R (1983) Estimation of soil erosion in India. J Irrig Drain Eng 109(4):419–431
Pandey A, Chowdary VM, Mal BC (2007) Identification of critical prone areas in the small agricultural watersheds using USLE, GIS and remote sensing. Water Resour Manage 21:729–746
Pandey A, Mathur A, Mishra SK, Mal BC (2009) Soil erosion modeling of a Himalayan watershed using RS and GIS. Environ Earth Sci 59:399–410
Patel N, Kathwas AK (2012) Assessment of spatio-temporal dynamics of soil erosional severity through geoinformatics. Geocarto Int 27:3–16
Prasannakumar V, Vijith H, Abinod S, Geetha N (2012) Estimation of soil erosion risk within a small mountainous sub-watershed in Kerala, India, using revised universal soil loss equation (RUSLE) and geo-information technology. Geosci Front 3:209–215
Prudhomme C, Jakob D, Svensson C (2003) Uncertainty and climate change impact on the flood regime of small UK catchments. J Hydrol 277:1–23
Raje D, Mujumdar PP (2009) A conditional random field-based downscaling method for assessment of climate change impact on multisite daily precipitation in the Mahanadi basin. Water Resour Res 45:1–20
RamBabu R, Dhyani BL, Kumar N (2004) Assessment of erodibility status and refined Iso- Erodent Map of India. Ind J Soil Conserv 32(2):171–177
Routschek A, Schmidt J, Enke W, Deutschlaen Th (2014) Future soil erosion risk—results of GIS-based model simulations for a catchment in Saxony/Germany. Geomorphology 206:299–306
Rupa Kumar K, Sahai AK, Kumar KK, Patwardhan SK, Mishra PK, Revadekar JV, Kamala K, Pant GB (2006) High-resolution climate change scenarios for India for the 21st century. Curr Sci 90(3):334–345
Simonneaux V, Cheggour A, Deschamps C, Mouillot F, Cerdan O, Bissonnais YL (2015) Land use and climate change effects on soil erosion in a semi-arid mountainous watershed (High Atlas, Morocco). J Arid Environ 122:64–75
Weismeier WH, Smith DD, (1965) “Predicting rainfall Erosion losses from Crop Land East of Rocky Mountain.” Agriculture Handbook, No.282 R.S. USDA
Wilby RL, Dawson CW (2007) “User manual on SDSM 4.2-a decision support tool for the assessment of regional climate change impacts,” 1–94
Wilby RL, Wigley TML (1997) Downscaling general circulation model output: a review of methods and limitations. Prog Phys Geogr 21:530–548
Wischmeier WH, Smith DD (1958) Rainfall Energy and its relationship to soil loss. Eos, Trans Am Geophys Union 39:285–291
Wischmeier WH, Smith DD, (1978) “Predicting Rainfall Erosion Losses. A Guide to Conservation Planning.” United States Department of Agriculture, Agricultural Handbook #537
Acknowledgments
The authors are thankful to the Indian Meteorological Department (IMD) for the rainfall data and the National Bureau of Soil Science (NBSS) for soil data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Khare, D., Mondal, A., Kundu, S. et al. Climate change impact on soil erosion in the Mandakini River Basin, North India. Appl Water Sci 7, 2373–2383 (2017). https://doi.org/10.1007/s13201-016-0419-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0419-y